The Influences of π-Conjugated Aliphatic Chains in Ionic Liquids of Antimony Pentachloride with Pyridine Imidazolium Hybrid Salts: A DFT Study

Abstract

A theoretical study was performed using Density Functional Theory (DFT) to investigate the impact of π-conjugated aliphatic chain growth on the chemical and electronic properties of hybrid antimony pentachloride salts with pyridine- and imidazolium-based cations. Ten molecular systems were optimized to determine their ground-state geometry. Using conceptual DFT, parameters such as chemical hardness, electrophilicity index, electroaccepting power, and electrodonating power were studied. The energy gap was obtained for all ten molecular systems, ranging from −4.038 to −3.706 eV as the chain length increased, favoring intramolecular charge transfer in long-chain systems. Natural bond orbital (NBO) analysis showed charge redistribution between anion and cation as the π-conjugated aliphatic chain grows. At the same time, non-covalent interaction (NCI) studies revealed key attractions and repulsive interactions, such as H···Cl and Cl···π, which are modulated by chain length. These results demonstrate that the structural modification of the cation allows for the fine-tuning of the electronic properties of ionic liquids (ILs). Increasing the conjugated aliphatic chain length was observed to reduce the chemical hardness and electrophilicity index, as well as affecting the Egap of the molecular systems. This work demonstrates that there is an optimal size for the inorganic ion, allowing it to form an optimal IL compound.

1. Introduction

Ionic liquids (ILs) are organic structures that are usually composed of a cation and an anion [1,2]. The study of these compounds continues to gain momentum within the scientific community, in fields such as electrochemistry, organic chemistry, biochemistry, and green chemistry. All of the above is attributed to the exceptional properties that these materials present, such as high chemical and thermal stability, low vapor pressure, high ionic conductivity, and interesting properties as solvents [3]. According to the above, ILs have versatility in terms of their applications, such as gas separation, heat transfer, electrolysis in sensors, and electrochemical devices, including batteries, solar cells, and light-emitting electrochemical cells (LEECs) [4,5,6,7,8,9]. Multiple properties of ILs can be analyzed, but one of those evaluated is their optical properties, which are influenced by the electronic and structural information that they provide. In recent years, nonlinear optics (NLO) has garnered particular attention due to the potential applications of these materials, such as photorefractive media and electro-optical modulators [10,11,12].

Furthermore, hybrid NLO materials exhibit high nonlinear responses, with the particularity of being fine-tuned through subtle changes in their molecular structure, thereby allowing for the convenient optimization of desired properties through molecular engineering [13]. In general, the NLO properties of these materials, such as hyperpolarizability and optoelectronic properties, can be enhanced by the presence of strong donor/acceptor groups when their orbitals overlap [14].

In ILs, it is important to have strong donor and acceptor groups in the cationic and anionic parts, respectively; thanks to this, the geometric structure of the anion and cation and their combinations can be manipulated as desired [2]. ILs are mainly composed of organic ions, which means that they have a greater diversity of structures compared to inorganic species [15]. The unique properties of ILs are achieved by modifying their ionic structure. Due to their non-volatile properties, ILs can be studied with various techniques as if they were solids; in this way, their electronic structure and photophysical properties can be investigated. In a study by Nishi and co-workers, results were reported using soft X-ray emission spectroscopy (SXES) to determine the occupied upper states and the unoccupied lower states of the compounds [C_nmim]⁺[BF₄]⁻ and [C_nmim]⁺[PF₆]⁻ (n = 4, 8, 10). This research employed molecular orbital (MO) calculations to interpret the measured spectra [16]. Density Functional Theory (DFT), as a computational method, has shown wide application to calculate the electronic properties of ILs step by step [17,18,19,20,21].

Based on the relevance of ILs in diverse technological applications and their structural sensitivity to molecular modifications, this work presents a detailed theoretical study of a series of hybrid salts formed by the antimony pentachloride anion and organic cations derived from pyridine and imidazolium with π-conjugated aliphatic chains of different lengths (see Figure 1). The objective was to evaluate how π-conjugated aliphatic chain growth influences the chemical and electronic properties of these systems. To this end, DFT calculations were employed using one of the new functional forms of the Minnesota density functionals (MN15), as this functional form is designed to account for non-covalent interactions, enabling the analysis of reactivity parameters, frontier molecular orbitals, non-covalent interactions, and charge distribution. This approach allows us to explain how minor structural modifications in the cation can significantly modulate the electronic behavior of the system, which is crucial for the rational design of new functional materials based on ionic liquids (ILs).

2. Results and Discussion

2.1. Molecular Structure Analysis

Ground-state geometry optimization was calculated for ten ionic liquid molecular systems, as shown in Figure S1. These systems consisted of an antimony pentachloride with a distorted square-based pyramidal geometry anion and a cation composed of an organic molecule based on pyridine and imidazole, with modifications involving the lengthening of the π-conjugated aliphatic chain (see Figure S1). The structures of the liquid ions presented here were verified by calculating vibrational frequencies, which did not present imaginary frequencies. Figure S2 shows the IR spectra, with the characteristic vibrational frequencies for each of the molecular systems studied. These spectra provide valuable insights into the structure and behavior of the molecules under investigation.

The optimized molecular systems were analyzed in terms of specific geometric parameters between the anion and the cation. In liquid ions, it is important to understand the intermolecular interactions between the anion and the cation, as these modify their electronic properties [22,23].

To identify significant non-covalent interactions, the interatomic distances between the chlorine atoms of the anion and the hydrogens and aromatic rings of the cation were measured from the optimized geometries (using the scheme in Figure 2). These calculated distances were then compared against established interaction thresholds reported in the literature, specifically H···Cl 3.30 Å and Cl···π 3.80 Å [24,25,26,27,28].

Table 1. The most important non-covalent interactions for the ten molecular systems.

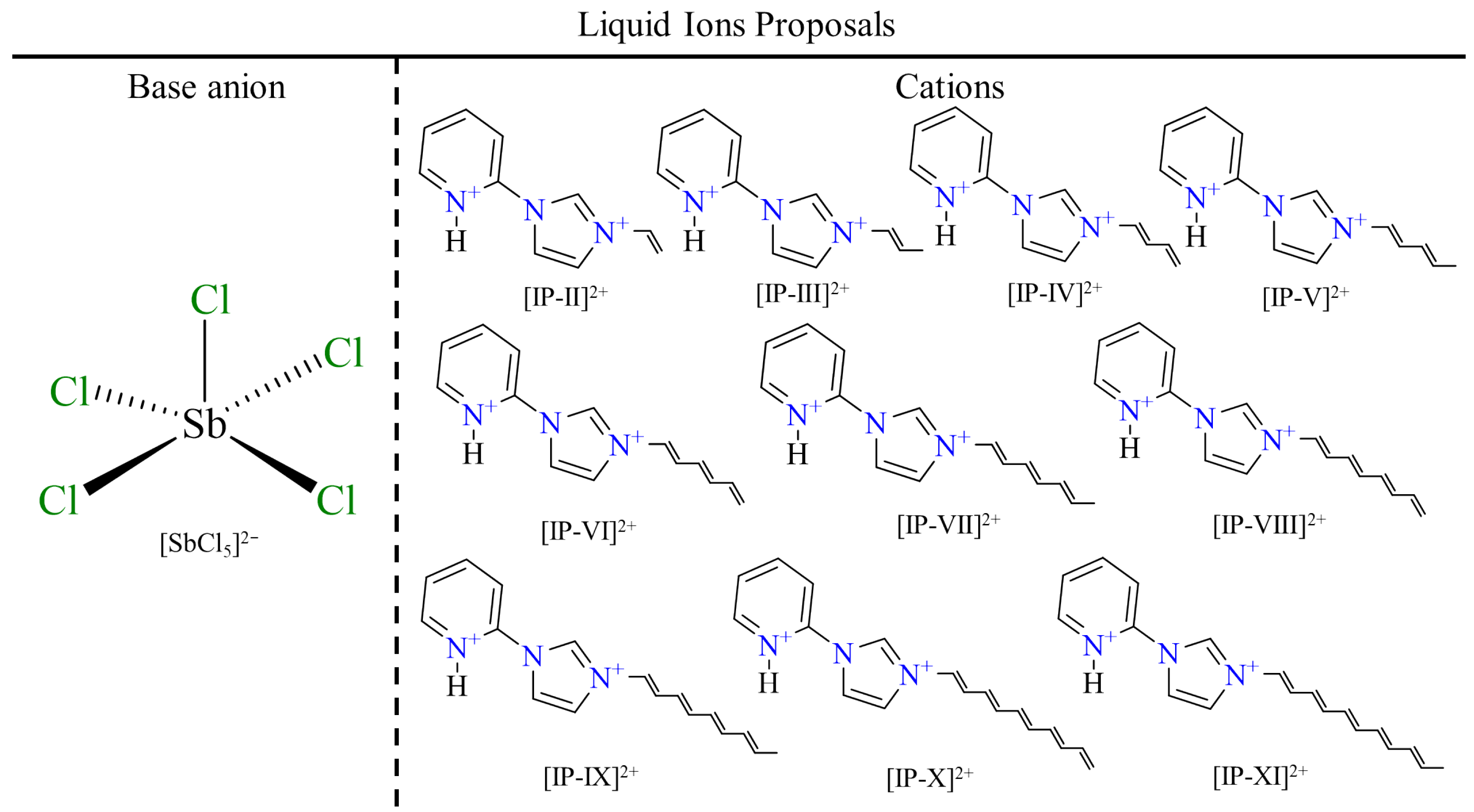
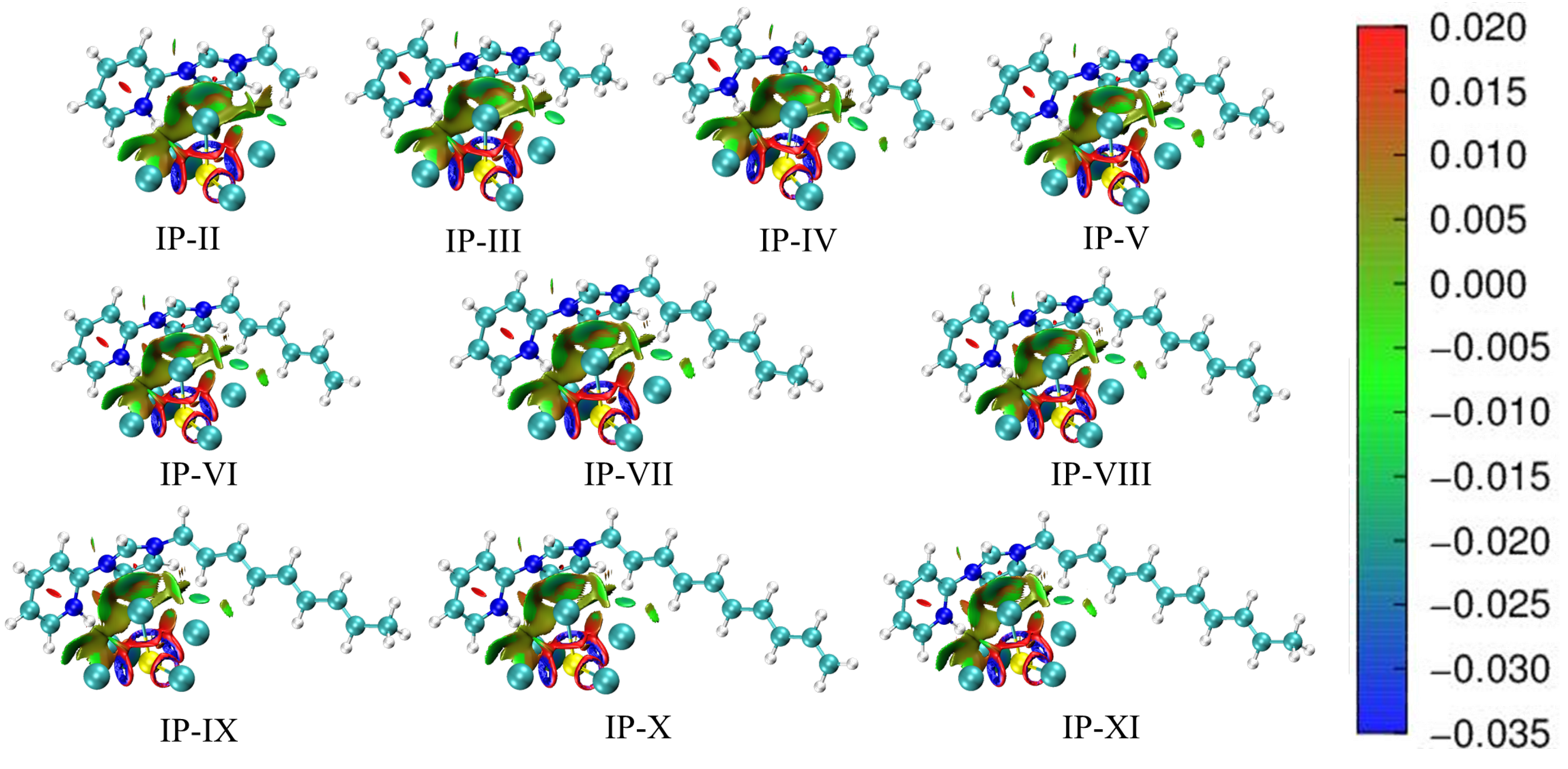
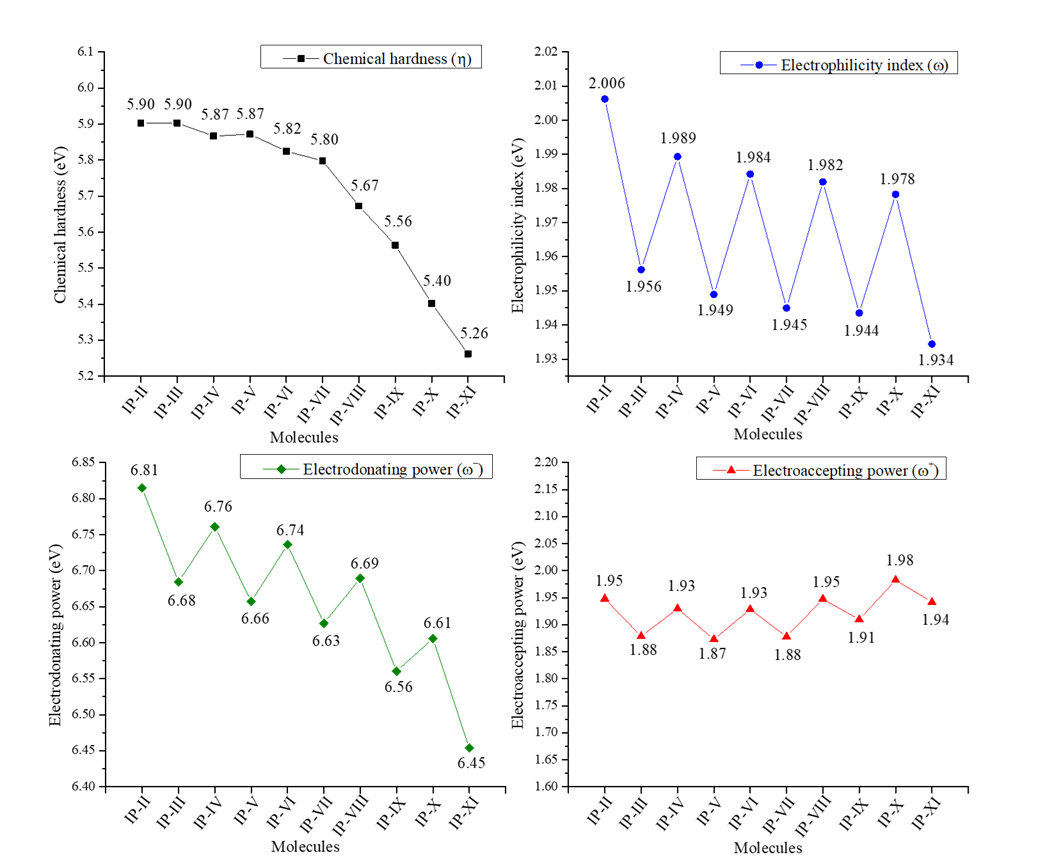
Molecule	Ha···Cla	Hb···Cla	Hc···Clc	Hd···Clc	He···Clc	Clb···πa	Clb···πb
	Angstrom (Å)
IP-II	1.687	2.484	3.056	2.512	-	3.816	3.048
IP-III	1.704	2.497	3.113	2.501	4.576	3.812	3.048
IP-IV	1.708	2.508	3.203	2.452	3.409	3.850	3.028
IP-V	1.716	2.525	3.263	2.461	3.231	3.848	3.028
IP-VI	1.719	2.526	3.290	2.453	3.538	3.855	3.025
IP-VII	1.721	2.529	3.323	2.462	3.135	3.839	3.032
IP-VIII	1.718	2.524	3.297	2.453	3.165	3.833	3.032
IP-IX	1.719	2.520	3.277	2.462	3.550	3.829	3.033
IP-X	1.720	2.530	3.300	2.454	3.132	3.846	3.027
IP-XI	1.723	2.530	3.324	2.469	3.110	3.849	3.026

summarizes the interactions identified through this analysis.

An analysis of the interactions shown in Table 1 reveals that the hydrogen found in the protonated pyridine (H_a) is the closest to the anion. Furthermore, we can observe that, from IP-II to IP-IX, this H_a∙∙∙Cl_a interaction decreases as the distance increases, in the same order in which the length of the π-conjugated aliphatic chain increases, namely, IP-II (1.687 Å), IP-III (1.704 Å), IP-IV (1.708 Å), IP-V (1.716 Å), IP-VI (1.719 Å), IP-VII (1.721 Å), IP-VIII (1.718 Å), IP-IX (1.719 Å), IP-X (1.720 Å), and IP-XI (1.723 Å). Finally, we can note that, from IP-VII, this trend is broken, which is also exhibited for H_b∙∙∙Cl_a and H_c∙∙∙Cl_c. The remaining intermolecular interactions do not exhibit a trend, and the values remain relatively close to one another. In the case of the C–H_e···Cl_c interactions shown in Table S1, it can be appreciated that, for all liquid ion proposals (IP-IV to IP-XI), they do not exceed the sum of the Van der Waals radius (3.45 Å), except for IP-III having a distance of 4.578 Å, which exceeds the sum of the Van der Waals radius for carbon (1.70 Å) and chlorine (1.75 Å) [29,30]. The distances N⁺–H and C–H, as well as the distances from the hydrogen donor to the acceptor and their angles, are shown in Table S1. To provide detailed information on any geometric parameters, the XYZ coordinates of the optimized molecular structures, calculated with the MN15/def2-SVPD and MN15/6-31G(d)+LANL2DZ levels of calculation, are provided in the Supplementary Materials. A more detailed explanation of non-covalent interactions will be provided in Section 2.2.

2.2. Non-Covalent Interaction (NCI)

In ionic liquids (ILs), the most prevalent interactions that dictate the behavior of these materials at the macro and micro scales are non-covalent interactions (NCIs). NCIs are attraction forces between atoms or molecules in which electrons are not shared, as occurs in covalent bonds. Although these interactions are weaker than covalent bonds, they play a crucial role in the formation of structures and the functioning of ionic liquids [31]. NCI analysis is based on electron density (ρ) and the reduced density gradient (RDG) (s), and it is used to identify regions where non-covalent interactions can occur. This mathematical model does not rely on bonding models, but rather directly on the characteristics of electron density.

The reduced density gradient (RDG) is defined by Equation (1):

$$s\left(r\right)= {\displaystyle \frac{1}{{2\left(3{\pi }^2\right)}^{\frac{1}{3}}}} {\displaystyle \frac{\left|\nabla \rho \left(r\right)\right|}{{\rho \left(r\right)}^{\frac{4}{3}}}}$$

(1)

where s(r) is the reduced density gradient, and ∇ρ(r) represents the null value of the density gradient. Critical points in the density are characterized by three principal curvatures λ₁ < λ₂ < λ₃, which correspond to the eigenvalues of the Hessian matrix. When a critical point has two negative eigenvalues and a positive eigenvalue, it is called a bond critical point (bcp) [32,33].

By analyzing the product of the reduced gradient of s(r) and the sign of the second eigenvalue λ₂, we can identify zones of non-covalent interaction and distinguish their strength based on the magnitude of ρ(r). If λ₂(ρ) < 0, it is considered to be an attraction interaction, such as those occurring between hydrogens covalently bonded to electronegative atoms (C and N in this case), shown in blue. If λ₂(ρ) ≈ 0, it represents a Van der Waals interaction, typical of regions with electronic resonance, such as aromatic rings (shown in green). If λ₂(ρ) > 0, it is interpreted as a repulsive interaction, such as steric hindrance due to the size and proximity of the atoms (shown in red) [34].

A three-dimensional representation of the optimized ILs at the MN15/def2-SVPD level of theory is shown in Figure 3. Green areas indicate weak attraction interactions, such as Van der Waals forces, resulting from soft ionic interactions. In these regions, the value of λ₂(ρ) ≈ 0, which is common in organic ionic salts, where there are soft couplings between charged fragments. In all systems, these interactions occur between the chlorines coordinated to antimony and the organic cation, with a primary focus on the interactions between the hydrogen bonds of the cation and the chlorines of the anion. In systems IP-II and IP-III, a H_d···Cl_c interaction is observed with distances of 2.512 and 2.501 Å, respectively. The decrease in this distance is attributed to chain growth. In systems IP-IV to IP-VII, a H_e···Cl_c interaction appears, which decreases as the number of chain members increases. From IP-VIII onwards, this trend is broken, which is attributed to the repulsion generated by the increase in chain length.

The anion in all molecular systems is composed of pentacoordinate antimony with five chlorines, forming a distorted square-based pyramidal geometry. NCI analysis reveals that the anion features five rings positioned perpendicular to the Sb-Cl bonds. The disc-like shape with a blue/green center and a red rim is a characteristic of strong interactions bordering on weak covalent character, as shown across all images in Figure 3. The hole in the middle of the disc indicates a region of high electron density (the bond critical point), while the outer red rim indicates some static repulsion at the periphery of the interaction, but it represents a strong, localized attractive interaction between the antimony and the chlorine.

The red ovals present in both aromatic rings indicate repulsive interactions resulting from electronic overlap within the rings. These rings are oriented toward Cl_b, located at the tip of the anion’s pyramid geometry, with distances ranging from 3.812 to 3.855 Å for the Cl_b-π_a centroid situated in the center of the pyridinium ring, and from 3.025 to 3.048 Å for the Cl_b-π_b centroid located in the center of the imidazolium ring.

2.3. Natural Bond Orbital

In this work, a population analysis study was conducted using the natural bond orbital (NBO) charge analysis criteria [35,36], employing the MN15/def2-SVPD level of calculation. The point charge values were grouped into three distinct segments: the anion segment, composed of the inorganic negative counterion SbCl₅; and the cation segment, divided into two parts: (i) the part where the aromatic rings of the organic molecule are based on pyridine and imidazole, and (ii) the part composed of the π-conjugated aliphatic chain that was growing in this research, as shown in Figure 4.

Because these systems are salts, the sum of the net charges is equal to zero, where the negative point charge is found in the inorganic anion part and the positive part in the organic cation. To analyze the behavior of the organic part, it was divided into two parts: the part with the rings and the part with the chain. The behavior of charge change (Δq) between the rings and the cation chain as the chain grew was analyzed. In the group of systems with a methylene chain termination (GA), it can be observed that the value of the change in charge (Δq) decreases according to the following trend: IP-II(0.937) < IP-IV(0.945) > IP-VI(0.940) > IP-VIII(0.934) > IP-X(0.931), in which the longer the chain, the lower the value of the change in charge, except for IP-II, which is the only one that does not follow the trend. This is because IP-II is the system with the smallest chain and, therefore, the system with the least charge in the chain. The same trend is observed in the chain growth of systems with a methyl group termination (GB): IP-III (0.941) > IP-V (0.937) > IP-VII (0.933) > IP-IX (0.928) > IP-XI (0.927), as shown in

Table 2. NBO charge analysis by segments, and the difference between the anionic and the cationic parts of the molecular system.

Molecules	Ring	Chain	Anion	Ring–Chain (Δq)	Anion–Chain (Δq)
IP-II	1.26190	0.32449	−1.58638	0.93741	−1.26189
IP-III	1.26957	0.32885	−1.59845	0.94072	−1.26960
IP-IV	1.27139	0.32653	−1.59793	0.94486	−1.27140
IP-V	1.27058	0.33327	−1.60385	0.93731	−1.27058
IP-VI	1.27239	0.33200	−1.60437	0.94039	−1.27237
IP-VII	1.27021	0.33736	−1.60758	0.93285	−1.27022
IP-VIII	1.26998	0.33549	−1.60545	0.93449	−1.26996
IP-IX	1.26767	0.33994	−1.60763	0.92773	−1.26769
IP-X	1.26880	0.33756	−1.60637	0.93124	−1.26881
IP-XI	1.26802	0.34051	−1.60853	0.92751	−1.26802

.

Based on the information in Table 2, it can be assumed that chain growth in all systems directly affects the charge transfer behavior in the organic part, and this is consistent with the charge transfer from the inorganic part to the organic part, which is consistent with HOMO–LUMO transitions, where the electron density is observed to have a charge transfer from metal to ligand behavior, as will be seen in Section 2.5.

Table S2 contains similar information, calculated with the MN15 functional and the 6-31G(d)+LANL2DZ basis sets. The most important analysis of this comparison is that there are qualitative trends at both levels of theory. Both methods predict the same fundamental behaviors: an anion-to-cation charge transfer and a progressive redistribution of positive charge from the aromatic ring fragment to the aliphatic chain fragment as the latter is elongated. This qualitative agreement indicates that there is no dependence on the basis set used, but rather on characteristics of the electronic structure of these ionic liquids.

2.4. Chemical Reactivity Parameters

The chemical reactivity parameters of antimony pentachloride-based liquid ions were calculated using conceptual DFT, and the results are presented in Figure 5. The chemical hardness parameter is inversely related to intramolecular charge transfer; specifically, the lower the chemical hardness, the better the intramolecular charge transfer [37,38]. Therefore, determining this parameter is crucial for this type of material.

To simplify the analysis of the salt trends, they were divided into two groups: the methylene group (GA), comprising IP-II, IP-IV, IP-VI, IP-VIII, and IP-X; and the methyl group (GB), comprising IP-III, IP-V, IP-VII, IP-IX, and IP-XI.

The chemical hardness for all salts is shown in Figure 5, which decreases significantly with the growth of the chain. The chemical hardness of the GA group decreases in the following order: IP-II (5.90 eV) > IP-IV (5.87 eV) > IP-VI (5.82 eV) > IP-VIII (5.67 eV) > IP-X (5.40 eV); for the GB group, the order is IP-III (5.90 eV) > IP-V (5.87 eV) > IP-VII (5.80 eV) > IP-IX (5.56 eV) > IP-XI (5.26 eV). According to this analysis, it can be observed that an increase in the chain generates a decrease in the chemical hardness in both groups, which can be attributed to the presence of a greater amount of π-conjugated carbon atoms in the chain in both cases, making it more rigid, allowing the flow of electronic charge through it more efficiently.

The electrophilicity index represents the stability of a molecular system in the presence of external charges; a high value indicates greater stability [39]. Based on this, both groups were analyzed. The electrophilicity index shown in Figure 4 was analyzed in groups (GA and GB), presenting the following order for the GA group: IP-II (2.006 eV) > IP-IV (1.989 eV) > IP-VI (1.984 eV) > IP-VIII (1.982 eV) > IP-X (1.978 eV); for group GB, the order was IP-III (1.956 eV) > IP-V (1.949 eV) > IP-VII (1.945 eV) > IP-IX (1.944 eV) > IP-XI (1.934 eV). A slight variation can be observed in the electrophilicity index between the two groups, demonstrating similar stability for the ten salts. However, the GA group with methylene in the termination is more stable than the GB group with methyl. It can be noted that the ionic systems with the shortest chain and the smallest volume have the highest electrophilicity index. Notably, IP-II has a value of 2.006 eV, making it the most stable of all. IP-XI, with a value of 1.937 eV, is the least stable.

The electroaccepting power can determine the acceptor characteristics of a molecular system; a higher value indicates an improved ability to accept electrons from an outsourced system [40]. Figure 4 shows the electroaccepting power for both groups of all molecular systems. They were analyzed in the following order: for group GA, IP-II (1.95 eV) > IP-IV (1.93 eV) ≈ IP-VI (1.93 eV) < IP-VIII (1.95 eV) < IP-X (1.98 eV); for the GB group, IP-III (1.88 eV) > IP-V (1.87 eV) < IP-VII (1.88 eV) < IP-IX (1.91 eV) < IP-XI (1.94 eV). This analysis reveals that, in both groups, the electroaccepting power exhibited no significant variation across all molecular systems, with values consistently below 0.11 eV. It can be observed that ω⁺ first decreases and then increases as the chain grows. This was observed for the molecular systems in the GA group, where IP-II > IP-IV ≈ IP-VI, with the latter being the system with the lowest electroaccepting power and, therefore, assumed to be less likely to accept electrons from other systems. On the other hand, in group GB, the order is IP-III > IP-V < IP-VII, with values around 1.87–1.88 eV. It can be observed that, after IP-VI and IP-VII, the increase in the number of chain members in both groups increases the electroaccepting power. This is linked to the electron affinity of these molecular systems.

According to Gázquez et al., it is important to consider that the lower the value of the electrodonating power, the greater the capacity to donate electrons [40]. The electrodonating power of the two groups was analyzed, which decreased with growing chain length as follows: for the GA group, IP-II (6.81 eV) > IP-IV (6.76 eV) > IP-VI (6.74 eV) > IP-VIII (6.69 eV) > IP-X (6.61 eV); for the GB group, IP-III (6.68 eV) > IP-V (6.66 eV) > IP-VII (6.63 eV) > IP-IX (6.56 eV) > IP-XI (6.45 eV). The molecular system with the highest electrodonating power was the methylene group, specifically IP-II, with an electron affinity of 6.81 eV. For the methyl group, it was the IP-III molecular system, with an electrodonating power of 6.68 eV. It can be observed that the group with methyl (GB) presents lower values of electrodonating power; therefore, the methyl-terminated GB group has the best donating capacity, with IP-XI being the best molecular system in terms of donating capacity.

A comprehensive analysis of chemical reactivity parameters reveals that these systems exhibit varying chemical behavior as the number of π-conjugated aliphatic chain members increases. The systems with larger π-conjugated aliphatic chains exhibit lower hardness, a lower electrophilicity index, and a greater donating capacity. However, the electroaccepting power first decreases and then increases. If it is considered that the molecular systems were modified in the cation part, then it is expected that it would be more convenient to have a greater accepting capacity; therefore, IP-X could be a better option for ILs. Nevertheless, all of the molecular systems have a similar electroaccepting power, and any of those could be a good option for ILs.

Figure S3 presents the reactivity parameters calculated with the MN15/6-31G(d) level of calculation. The agreement between the two methods for both chemical hardness and the global electrophilicity index is very good. Both levels of calculation correctly predict the defining chemical trend for these systems—for example, a systematic decrease in hardness and electrophilicity as the π-conjugated aliphatic chain is elongated. The absolute differences in the calculated values are minimal, with a maximum deviation of only 0.12 eV for both parameters across the entire series of ten molecules. This quantitative agreement demonstrates that the prediction of these global reactivity descriptors is not drastically sensitive to the differences between these two basis sets and ECP schemes. When analyzing the electrodonating and electroaccepting powers, both methodologies again capture the identical qualitative trends. While the values for ω⁻ and ω⁺ exhibit a small, systematic offset between the two methods (approximately 0.5 eV and 0.3 eV, respectively), this is a well-understood consequence of differences in the basis sets. Our understanding and ability to explain these offsets in detail provide confidence in the depth of our analysis and the reliability of our results.

2.5. Frontier Molecular Orbitals

One of the most important aspects of the theoretical study of molecular systems is the analysis of frontier molecular orbitals, which can provide essential information about the distribution of electron density within the system [41]. Within the frontier orbital theory, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), along with their related orbitals, are crucial for determining the electronic properties of chemical compounds, such as liquid ions, due to the electrostatic interactions and non-covalent interactions involved [42].

In ionic systems, such as those presented in this work, anions act as electron donors within the molecular system due to their negative formal charge; therefore, the HOMO electron density is expected to be concentrated in the ion. Cations, on the other hand, act as electron acceptors due to their positive formal charge, primarily due to the presence of protons (N⁺) in both of the rings (pyridinium and imidazolium), which confers an electron acceptor behavior; therefore, the LUMO electron density is expected to be concentrated in this ion. The energy gap (Egap) between the HOMO and LUMO has been used to correlate properties related to intermolecular charge transfer (ICT), which is reflected in the chemical activity of the molecular systems [43,44].

Figure 6 shows the mapping of the HOMO−1, HOMO, LUMO, and LUMO+1 molecular orbitals for the 10 molecular systems (IP-II to IP-XI). It can be observed that, from IP-II to IP-IX, the charge transfer from the HOMO to the LUMO involves a shift in electron density from the anion to the cation, as expected in this type of ionic system, indicating an intermolecular charge transfer. However, in systems IP-X and IP-XI, the HOMO–LUMO charge transfer is expected to become intramolecular transfer in the organic molecule. In the HOMO−1-to-LUMO and HOMO−1-to-LUMO+1 transitions, IP-VI to IP-IX also exhibit intramolecular transfer in the organic molecule. In IP-X and IP-XI, the HOMO–1 still displays intermolecular charge transfer, while the HOMO reflects intramolecular charge transfer, with electron density localized in the cation chain. This behavior may be due to the presence of a greater number of π-conjugated bonds in the aliphatic chain of these systems compared to the systems IP-II to IP-IX.

A direct relationship is observed between the electron density of the HOMOs and the number of pi-conjugated bonds, both in the rings and in the chain. In systems IP-II to IP-V, the chain lacks sufficient π-conjugated bonds to facilitate intramolecular charge transfer, and anion–cation transfer is maintained in all transitions. From systems IP-VI to IP-IX, the position of HOMO–1 electron density changes to localize over the cation, which can be attributed to the chain growth. In systems IP-X and IP-XI, the HOMO–1 is localized in the anion part, whereas the position of the HOMO electron density is on the cation part. Consequently, the HOMO–LUMO transition exhibits an intramolecular transfer, where the electron density shifts from the chain to the ring, as shown in Figure 6.

On the other hand, it can be observed how the number of members in the chain modifies the interaction of the cation with the anion, making the N−H_a···Cl_a interaction shorter as the chain grows, as shown in Table 2. It is assumed that this phenomenon may be caused by the increase in the electronic density due to the presence of more electrons as the chain grows in the organic molecule, as shown in Figure 6. In a potential application of the molecular systems, such as liquid ions, the anion-to-cation intermolecular transfer is important. Based on the above, IP-II to IP-V are suggested as the best option, as they all exhibit a HOMO-to-LUMO transition and the HOMO–1-to-LUMO+1 transition, thereby exhibiting anion-to-cation intermolecular transfer.

2.6. Energy Gap Analysis

It can be clearly seen in the data displayed in Figure 7 that the energy corresponding to the anion [SbCl₅]⁻² (HOMO level) and the rings (LUMO+1 and LUMO) remains relatively constant across all systems, while the energy levels corresponding to the chain (HOMO–1) increase significantly (become less stable). This phenomenon can be attributed to the increase in chain length and the increase in π-conjugated bonds in the cation. According to the frontier molecular orbital (FMO) plots in Figure 6, the HOMO becomes progressively localized on the growing π-conjugated aliphatic chain. Therefore, the Egap reduction is almost entirely driven by the destabilization of the HOMO on the cation chain. The system with the lowest Egap is IP-XI, with a value of −3.706 eV, which presents a chain with a methyl group.

For the HOMO and HOMO–1, both groups show energy-increasing behavior. In particular, the HOMO–1 show an apparent increase as the chain grows: for group GA, IP-II (−7.686 eV) < IP-IV (−7.670 eV) < IP-VI (−7.396 eV) < IP-VIII (−6.901 eV) < IP-X (−6.724 eV); for group GB, IP-III (−7.647 eV) < IP-V (−7.635 eV) < IP-VII (−7.105 eV) < IP-IX (−6.701 eV) < IP-XI (−6.689 eV).

With these energy values and the electron density mappings of the frontier molecular orbitals, it can be highlighted that there is a change in the expected behavior of the HOMO−1 in systems IP-VI to IP-IX and the HOMO in systems IP-X and IP-XI, attributable to the increase in the length of the π-conjugated aliphatic chain.

Figure 6. Frontier molecular orbitals (HOMO−1, HOMO, LUMO, and LUMO+1) for all of the IL molecular systems.

Figure 6. Frontier molecular orbitals (HOMO−1, HOMO, LUMO, and LUMO+1) for all of the IL molecular systems.

Figure 7. HOMO−1, HOMO, LUMO, and LUMO+1 energy levels for all of the IL molecular systems.

Figure 7. HOMO−1, HOMO, LUMO, and LUMO+1 energy levels for all of the IL molecular systems.

3. Materials and Methods

3.1. Computational Details

All computational calculations were performed with Density Functional Theory (DFT) [45,46] using the Gaussian 16 computational package [47]. In our study, we explored several initial configurations to ensure that the lowest-energy structures were located at the global minimum. To ensure the robustness of the results, minimal-energy structures were determined using two levels of theory. The primary methodology, used for all results presented in the main text, employed the MN15 global hybrid exchange–correlation density functional [48] with the def2-SVPD basis set [49,50] for all atoms. This modern basis set provides a balanced description and is consistently paired with a def2 effective core potential (ECP) for the heavy antimony (Sb) atom, which accounts for scalar relativistic effects. For validation, a second set of calculations was performed, using the 6-31G(d) basis set [51,52] for the C, Cl, H, and N atoms, and the Los Alamos National Laboratory (LANL) 2 double-zeta (DZ) pseudopotential “LANL2DZ” [53,54,55] for the Sb atom. The results from this second methodology are provided in the Supplementary Materials.

All compounds were calculated in the gas phase, corroborating that no imaginary frequencies were present. The conceptual DFT reactivity parameters were calculated by post-processing the final single-point energy results obtained from Gaussian 16. The calculated parameters were as follows: electrophilicity index (ω) [39], electrodonating power (ω⁻), electroaccepting power (ω⁺) [40], and chemical hardness (η) [56].

The non-covalent interactions (NCIs) and reduced density gradient (RDG) were calculated, and three-dimensional figures were generated using the VMD [57] and MultiWFN 3.8 software packages [58,59,60]. For a better understanding of these interactions, a population analysis of the natural bond orbital (NBO) for the title molecular systems and electronic structure was carried out using the MN15/def2-SVPD level of calculation to determine the atomic charge of each atom in each molecular system [61].

Given the strong congruence of the results, the data calculated using the MN15/6-31G(d)+LANL2DZ level of calculation serves as a powerful independent verification of our findings. The corresponding graphs and data, included in the Supplementary Materials, provide not just additional but thorough support for the reported trends, demonstrating that our results are independent of minor variations in the levels of theory.

3.2. Theoretical Background

The ionization potential (I) is determined by the difference between the ground-state energy of a system with N₀ − 1 electrons (cation energy) and the energy of a system in the ground state with N₀ electrons (neutral state) [62].

$$I=(E_{N_0-1}-E_{N_0})$$

(2)

The electron affinity (A) is determined by the difference between the energy of a system in the ground state with N₀ electrons (neutral state) and the energy of a system in the ground state with N₀ + 1 electrons (anion energy) [62].

$$A=(E_{N_0}-E_{N_0+1})$$

(3)

The ionization potential (I) is considered to be the minimum energy needed to remove an electron from molecular system or atom (gaseous phase) in its ground state, and the electron affinity (A) is the energy released when a neutral system (gaseous phase) captures an electron.

The molecular chemical hardness (n) is defined as the resistance to charge transfer, and it is determined by the differences between the ionization potential (I) and the electron affinity (A) [56].

$$n=(I-A)$$

(4)

The electrophilicity index (ω) was proposed by Parr and defined as follows: the change in the energy of a molecular system immersed in an environment saturated with electrons, which can be calculated by the square of the sum of the ionization potential (I) and the electron affinity (A), divided by eight times the chemical hardness (n) [39].

$$\omega ={\displaystyle \frac{{(I+A)}^2}{8(I-A)}}$$

(5)

The electrodonating power (ω⁻) is defined as the propensity to donate charge, which can be calculated by the square of the quantity three times the ionization potential (I) plus the electron affinity (A), divided by sixteen times the chemical hardness (n) [40].

$${\omega }^{-}={\displaystyle \frac{{(3I+A)}^2}{16(I-A)}}$$

(6)

The electroaccepting power (ω⁺) is defined as the ability of the chemical species to accept charge; this can be calculated as follows: the square of the quantity three times the electron affinity (A) plus the ionization potential (I), divided by sixteen times the chemical hardness (n) [40].

$${\omega }^{+}={\displaystyle \frac{{(I+3A)}^2}{16(I-A)}}$$

(7)

4. Conclusions

In this theoretical study, we have established clear structure–property relationships that govern the chemical and electronic behavior of a series of hybrid antimony pentachloride salts. We have shown that the elongation of the cation’s π-conjugated aliphatic chain is a key factor in molecular engineering. Our DFT calculations reveal several key trends: increasing the chain length systematically reduces the chemical hardness and the HOMO–LUMO energy gap (Egap), while also inducing a critical shift in the nature of the primary electronic excitation, from intermolecular (anion-to-cation) to intramolecular (within the cation) charge transfer.

These findings go beyond a purely theoretical description and offer actionable principles for the rational design of functional materials based on ionic liquids. The predictable tuning of the Egap, for instance, has direct applications in the engineering of ILs for optoelectronic applications, such as electrolytes in dye-sensitized solar cells or as active components in light-emitting electrochemical cells (LEECs). This practical insight can significantly advance the development of these technologies.

Moreover, the distinct transition from intermolecular to intramolecular charge transfer presents a clear design switch for materials science. For applications where the ILs primarily serve as an electrolyte (e.g., in batteries or supercapacitors) and charge separation between ions is crucial, cations with shorter chains are optimal. Conversely, for applications in fields like nonlinear optics (NLO), where the cation itself is the functional chromophore, longer conjugated chains are ideal. These systems support efficient intramolecular charge transfer, a key mechanism for enhancing the molecular hyperpolarizability required for NLO materials. This adaptability underscores the versatility of our research.

By modulating non-covalent interactions and chemical reactivity parameters, we have paved the way for fine-tuning the physicochemical properties of these ILs. This has significant implications for their performance as designer solvents in catalysis or as optimized media for gas separation. Our work provides a computational roadmap for synthesizing next-generation antimony-based ILs with electronic properties tailored for specific technological applications.