Abstract
The recently synthetically prepared endohedral CH4@C60 was characterized here using calculations—namely its structure, energetics, thermodynamics, and vibrational spectrum. The calculations were carried out with DFT (density-functional theory) methods, namely by the DFT M06-2X functional and MP2, as well as B2PLYPD advanced correlated, treatments with the standard 6-31++G** and 6-311++G** basis sets, corrected for the basis set superposition error evaluated using the approximative Boys–Bernardi counterpoise method. The symmetry of the endohedral obtained in the geometry optimizations was tetrahedral T. The energetics of CH4 encapsulation into C60 was attractive (i.e., with a negative encapsulation-energy term), producing a substantial energy gain of −13.94 kcal/mol at the most advanced computational level, B2PLYPD/6-311++G**. The encapsulation equilibrium constants for CH4@C60 were somewhat higher than previously found with the CO@C60 system. For example at 500 K, the encapsulation equilibrium constant for CH4@C60 had a value one order of magnitude larger than for CO@C60. The encapsulation thermodynamic characteristics suggest that high-pressure and high-temperature synthesis could in principle also be possible for CH4@C60.
1. Introduction
Fullerenes can encapsulate not only single metals and their aggregates but also non-metals and their molecules. Thus, species like N2@C60, CO@C60, and N2@C70 have been produced [1], namely by application of high pressures at high temperatures. Moreover, N2@C60 can also be prepared [2,3] by implantation of the nitrogen ion into the C60 cage, though this technique is preferentially used for the preparation of N@C60 [2,3,4,5,6,7,8,9]. Other non-metallic endohedrals encapsulate noble-gas atoms [10,11,12,13,14], again produced [10] by high pressures at high temperatures and with the help of catalytic action [13]. Moreover, with an entirely different method, an ingenious synthetic approach, hydrogen molecules [15] or even water [16] were first placed inside open fullerene cages that were subsequently closed through synthetic steps [17,18]. More recently, such elegant treatments even enabled [19] preparation of (H2O)2@C70. Similarly, carbon monoxide [20,21] as well as hydrogen peroxide [22,23] were also deposited inside derivatives of open C60 cage. Such fullerene encapsulations of non-metals have also been calculated, for example in works [24,25,26,27,28,29,30,31,32,33,34,35] (for a survey, see ref. [36] and references therein) with the first calculations [24] dating from the year 1991. These calculations mostly deal with encapsulations in the C60 cage; however, C70 and C84 [25,36], C59N [33,34], and even C60Hn [25] cases have also been studied.
The present report continues with the latter efforts and describes quantum chemical characterization of the structural and vibrational spectral features, encapsulation energetics, and thermodynamics of the recently prepared [37] CH4@C60 species.
2. Calculations
The calculation treatment started with structure optimizations carried out with a DFT (density-functional theory) approach, viz the DFT M06-2X functional considered [38] the most reliable technique for various species and aspects, including hydrogen-bonded systems and long-range interactions. The M06-2X functional was combined with the conventional 6-31++G** basis set [39] (the treatment is labeled here as M06-2X/6-31++G**). Subsequently, in the localized M06-2X/6-31++G** hypersurface stationary points, a GF (harmonic) vibrational analysis was performed, which allowed checking the nature of the stationary points; i.e., if local energy minima had really been found (and not activated complexes or even higher types of hypersurface stationary points). For numerical integration with the DFT functional, a so called ultrafine grid was applied. Moreover, the tight SCF (self-consistent field) convergency criterion was used. Finally, the wave function stability was tested throughout, in order to eliminate unstable SCF solutions lacking real physical significance.
The M06-2X/6-31++G** calculated energetics of the encapsulation process was further checked and refined by more advanced, correlated quantum chemical methods, namely by the second-order perturbation Møller-Plesset (MP2) treatment [40], considering all electrons (MP2 = FU) with the conventional 6-31++G** and 6-311++G** basis sets in the previously optimized M06-2X/6-31++G** structure. Moreover, an even more advanced and recently introduced technique known as B2PLYPD = FU [41] (again with all electrons) was also employed for refining the encapsulation energetics. The B2PLYPD technique is based on the MP2 method, however combined with the DFT approach and with inclusion of dispersion correction (D). In addition, the so-called basis set superposition error (BSSE) was also evaluated for the encapsulation energy, namely by the approximative Boys–Bernardi counterpoise method (also known as CP2) [42], since this was recently considered [43] with metallofullerenes. The Boys–Bernardi approach to the BSSE correction term is an approximative scheme that ensures that every reaction component of a studied chemical process is formally described using the same number of basis functions. The required situation is realized by rather artificial (also called ghost) atoms possessing no electrons. The BSSE issue is essentially rooted in the fact that the considered basis sets are always finite. In other words, the BSSE term would disappear in a situation with a basis set with an infinite number of basis functions (of course, such an infinite scheme cannot practically be handled). The BSSE correction term represents an important addition to the energetics of any encapsulation process—without the BSSE correction, the energy gain created by encapsulation would be exaggerated (endohedrals would be artificially over-stabilized). The molecular partition functions used in the thermodynamic treatment are approximated by the rigid rotator and harmonic oscillator (RRHO) description [36], as this treatment represents the only approach applicable to such relatively large systems with the computer resources available at present. All the reported calculations were performed with the program Gaussian 09 [44]. The calculations were carried out with computers operating in parallel regime, mostly with 8–24 processors (with a computational frequency up 3 GHz each and with available operational memory up to 60 GB).
3. Results and Discussion
The presented calculations deal with the encapsulation equilibrium process in the gas-phase:
connected with the encapsulation change in the potential energy and also described by the encapsulation equilibrium constant , defined by the partial pressures p of the individual reaction components:
The equilibrium constant for encapsulation (1) is related, as usual, to the standard reaction Gibbs energy change (at a temperature T):
where R denotes the gas constant. Finally, the standard encapsulation Gibbs energy change is related to the standard change of the encapsulation enthalpy at temperature T, , as well as to the standard encapsulation entropy change at temperature T:
Both latter terms were evaluated here through a statistical mechanical treatment based on the RRHO partition functions. As these calculations deal with the species in the gas-phase, no solvent effects needed to be included.
The molecular–structure optimizations began from selected different initial arrangements for the CH4@C60 complex. The optimized potential energy minimum exhibited tetrahedral T symmetry (Figure 1). The C-H bond length was only slightly influenced by the encapsulation. In the free CH4, its calculated M06-2X/6-31++G** C-H bond length was equal to 1.091 Å while after the encapsulation, the C-H bond at the M06-2X/6-31++G** level equaled 1.088 Å. Similarly, the changes in the C-C bond lengths on the C60 cage were also small. The 6/6 and 5/6 C-C bond lengths for the empty C60 were calculated at the M06-2X/6-31++G** level as 1.388 and 1.452 Å, respectively. In the CH4@C60 endohedral at the same level, the 6/6 bonds spanned an interval 1.389–1.390 Å, while for the 5/6 bonds this was 1.451–1.454 Å.
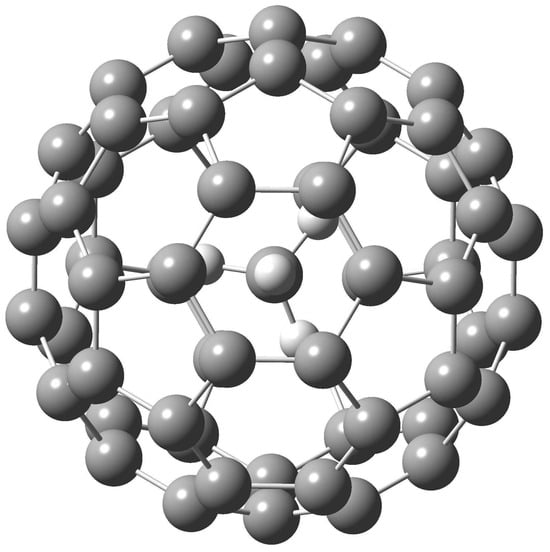
Figure 1.
M06-2X/6-31++G** optimized structure of CH4@C60.
With respect to the thermodynamic evaluations, it should be mentioned that some common quantum chemical programs can erroneously work with an incorrect symmetry number for the Ih icosahedral C60 cage. In fact, they simply deal with a value of one instead of the proper [36] (and used here) value of sixty. Actually, the Ih symmetry number was only discussed for the first time [36] in the year 1989, soon after the discovery of C60, as previously there was no usage of the term. Before C60 studies, only two other icosahedral molecules were known (dodecahedrane C20H20 and dodecaborate ion B12). At present, on the other hand, there is a whole series of (topological) icosahedral fullerenes, like C20, C80, C120, C180, etc., though some of them undergo Jahn–Teller conditioned symmetry reduction in quantum chemical structural optimizations; for example, C20 and C80. The Jahn–Teller effect in such icosahedral cages can still be suppressed by the charge transfer present in metallofullerenes. Such restoration of symmetry happens, for example, in La2@C80 derived from the icosahedral C80 cage (which is actually [36] the most populated isomer of La2@C80—in contrast to the set of the empty C80 cages where the icosahedral cage is, on the contrary, the least populated).
In particular, application of a simple symmetry number of one for C60, instead of the correct value of sixty, would imply a change in equilibrium constant by a huge multiplication factor of 60. Incidentally, a somewhat similar issue also appears [45] with the contribution of chirality to the partition functions; i.e., a factor equal to 2. Both issues are obviously important for thermodynamic stability evaluations. The encapsulation equilibrium constant from Equation (2) can be expressed [36] by a compact formula using the molecular partition functions (the partition functions also have to correspond to the selected standard state, i.e., here an ideal gas phase at 1 atm = 101,325 Pa pressure) and the standard encapsulation enthalpy change at absolute zero temperature :
where the symbol stands for the Avogadro number. The standard encapsulation enthalpy change at the absolute zero temperature actually has the meaning of the ground-state energy change; i.e., it contains the encapsulation reaction change in the vibrational zero-point energy (ZPE):
Let us note that the form of Formula (5) should allow some partial cancellation of higher contributions [36] beyond simple RRHO approximation like anharmonicity corrections. As for the symmetry numbers, they have their roots in the rigorous quantum mechanical requirements for the symmetry behavior of wave functions. Practically speaking, the symmetry number is equal to the number of rotations of the molecule that convert it into an identical position; hence, this is given by the order of the rotational subgroup of the related molecular point group of symmetry. The symmetry numbers appear in the rotational contributions to the molecular partition functions in Equation (5) and can thus significantly contribute to the values of equilibrium constants.
The situation is more complex with fullerene endohedrals, as their encapsulates can exhibit rotational motions in the cages (or at least large amplitude oscillations). The internal motions can effectively recover [36,37,46,47,48] the original cage symmetry, especially at higher temperatures, thus simplifying the NMR patterns. The collective motions of encapsulates inside the cages yield a time-averaged equalizing environment on the NMR timescale. The aspects of symmetry are reflected in the so-called [36] free, fluctuating, or floating encapsulate model (FEM), originally developed for relative thermodynamic stabilities or populations of isomeric mono-metallofullerenes (where the calculated results consistently agreed [36] with the available observed data). In our situation, the endohedral symmetry should also be treated like the isomeric metallofullerenes, i.e., as the highest (topological) symmetry for the empty cage. Thus, we dealt here with just the dynamic symmetry of CH4@C60, i.e., Ih, not with its static tetrahedral symmetry T found from the geometry optimizations. The symmetry number for CH4@C60 (and for similar endohedrals based on C60) was therefore here taken as [36] sixty (generally speaking, the RRHO and FEM treatments could in fact bracket out some bounds for thermodynamic terms). Incidentally, this treatment also removed the chirality feature of the T symmetry in this case. Obviously, the change in the symmetry number (from 12 for T to 60 for Ih) was quite profound and the consequences for the thermodynamic stabilities were substantial.
The Mulliken charges on atoms calculated at the M06-2X/3-21G level indicated that there was a (small) negative charge transfer of −0.069 (in elementary charge units) from CH4 to the C60 cage (so that there was an electrostatic contribution to the stabilization, cf. H2O@C59N [33,34]). Such a rather negligible charge transfer, however, stands in clear contrast to the substantial charge transfers known [36] for metallofullerenes. Mulliken charges on the cage carbons have values between −0.007 and +0.003. The Mulliken charge on the carbon in the free CH4 at the same level was equal to −0.787, while in the encapsulated CH4 this amounted to −0.764 (on H atoms of the encapsulated CH4 it was +0.208). Let us mention for completeness that the Mulliken charges on atoms, due to their historical construction, were calculated using smaller sets of basis functions, like for example the standard 3–21 G basis set used here. Mulliken charges on atoms calculated with the 3–21 G basis set are known [49] to produce a good agreement with the available observed charges [50]. In addition, there are also more general methodological reasons [51,52] why some larger basis sets should not be applied in the calculation of the Mulliken atomic charge on atoms.
Table 1 presents the encapsulation energy for CH4@C60 evaluated with the four selected approaches. The term was always negative—there was an energy gain upon the encapsulation, responsible for the complex stabilization. At the DFT M06-2X level, both considered basis sets produced about the same values. Similarly, the correlated MP2 and B2PLYPD encapsulation energies were quite close. As the B2PLYPD treatment is the most sophisticated among the four approaches considered in Table 1 (and also very close to the value in [35]), the value of −13.94 kcal/mol was used in the subsequent evaluations of the thermodynamic stability. After the addition of the M06-2X/6-31++G** term, the corresponding encapsulation enthalpy change at absolute zero temperature amounted to −11.38 kcal/mol. The encapsulation energy of −13.94 kcal/mol was comparable with the energy gain found in [36] for the encapsulation producing CO@C60 (−12.5 kcal/mol) or for the encapsulation yielding [36] N2@C60. Moreover, CH4@C60 had a significantly larger energy gain than the endohedrals [36] H2@C60, Ne@C60, or [36] NH3@C60 (though not as high as that found in [36] for (H2O)2@C70, (H2O)2@C84). For example, the formation of NH3@C60 was calculated [36] to be connected with an encapsulation energy of just −5.23 kcal/mol at the MP2 = FC/6-31G** level.

Table 1.
The encapsulation energy for CH4@C60 calculated with the selected approaches a and with inclusion of BSSE correction.
The temperature interplay between the standard change of the encapsulation enthalpy and the standard entropy change yielded the encapsulation equilibrium constants (Table 2). The presented values were higher than those found in [36] for the CO@C60 formation. For example, at 500 K, the encapsulation equilibrium constant for CH4 had a value of 0.0114 atm−1, while in the case of CO@C60 its value in [36] was lower by one order of magnitude, namely 0.00118 atm−1. The finding suggests that production of CH4@C60 by applying high pressures at high temperature could in principle be possible. However, there is not only thermodynamic, but also kinetic, aspects. An efficient reaction mechanism is needed for encapsulation with high pressure at high temperature [1,7], which should temporarily open a window in the fullerene cage. In fact, a catalytic (or autocatalytic) action [13,53,54] is required for the window opening (and also for its closure). The standard encapsulation changes in enthalpy for process (1) consistently exhibit a negative sign. In the view of the van’t Hoff relationship,
the encapsulation equilibrium constant must exhibit a decreasing course with increasing temperature—as indeed seen in both Table 2 and Figure 2.

Table 2.
The standard a enthalpy , entropy , Gibbs energy changes, and the equilibrium constants for the gas-phase equilibrium formation (1) of CH4@C60 evaluated b at the selected temperatures T.
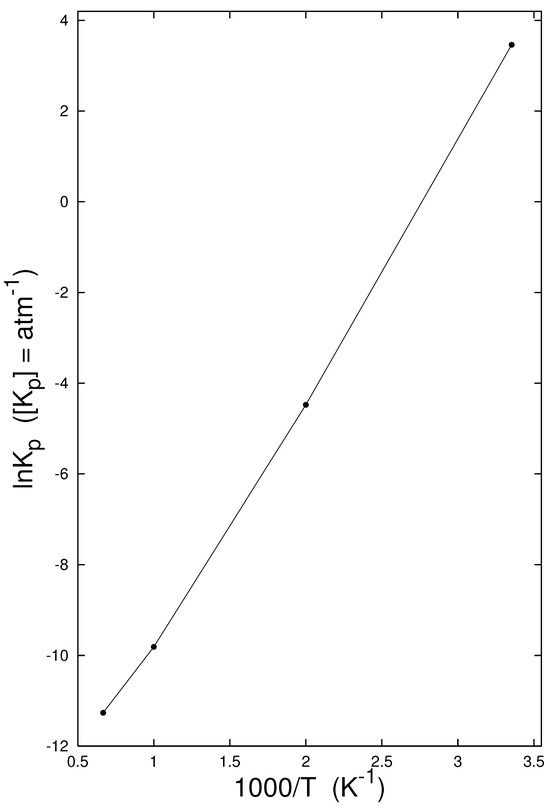
Figure 2.
Temperature dependency of the equilibrium constant (2) for CH4 encapsulation in C60.
GF vibrational analysis was used here for confirmation that the energy minimum was indeed found (no imaginary frequency) and as input for the RRHO partition functions. Figure 3 shows the M06-2X/6-31++G** calculated IR and Raman harmonic vibrational spectrum of CH4@C60. The high Ih symmetry [55] of the free C60 grossly simplifies its IR vibrational spectrum [56]. The symmetry representation of the 174 vibrational modes of C60 was as follows [57]:
where A, T, G, and H denote one-, three-, four-, and five-fold degenerate modes, respectively (so that we deal with a number of modes 3 × 1 + 16 × 3 + 12 × 4 + 15 × 5 = 174 = 60 × 3 − 6). This high symmetry actually led to only 46 distinct vibrational frequencies [57], with four of them () active in the IR and ten of them (, ) in the Raman spectra. However, if the high symmetry of the cage was reduced by encapsulation, the spectral symmetry selection rules should also be relaxed. Nevertheless, even the CH4@C60 IR spectrum primarily consisted of four (broader) bands. The CH4 vibrational modes appeared in the CH4@C60 spectrum, with low intensities in the regions around 1300 cm−1 (the bond-angle deformation, in the free CH4 at the M06-2X/6-31++G** level amounted to 1349 cm−1) and around 3200 cm−1 (bond stretching, in the free CH4 3192 cm−1). The CH4@C60 endohedral had 189 vibrational modes—174 of them actually originated from the vibrational modes of the free C60 and 9 from the vibrational modes of the free CH4, though their frequencies were somewhat shifted and the exact degeneracies had been removed. The remaining six vibrational modes had the nature of hindered rotational motions or hindered translational motions of CH4 in the C60 cage (the translational motions can also be viewed as the encapsulate vibrations between the cage walls). The hindered collective motions actually possessed the lowest frequencies in the vibrational spectrum, about 173 cm−1 for the hindered rotations and about 247 cm−1 for the hindered translations (though their IR intensities were negligible, while the modes around 247 cm−1 should have still been a bit more active in the Raman spectra). In contrast to the straightforward FEM treatment of the relative thermodynamic stabilities or populations in sets of isomeric monometallofullerenes [36], the lowest vibrational modes in our case were important for the description of the overall encapsulation thermodynamics. The six lowest vibrational modes were also primary contributors to the encapsulation reaction change of the vibrational zero-point energy in Equation (6).
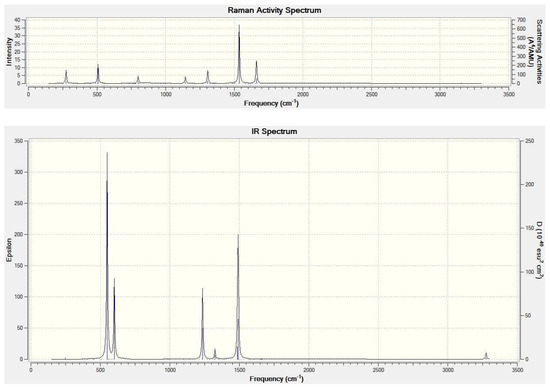
Figure 3.
M06-2X/6-31++G** computed IR and Raman (top) spectrum of CH4@C60.
In addition to C60, the C84 cages could also be of interest for the CH4 accommodation. C84 is a relatively well known system of isomeric fullerenes, in particular the two most common isomers, and , conventionally also labeled [58] as 22 and 23, (22)-C84 and (23)-C84. The structure is the lowest-energy isomer, but it is located only about 0.5 kcal/mol below the species [59]. The M06-2X/6-31++G** water dimer encapsulation energy into the (22)-C84 cage was calculated [36] as −17.4 kcal/mol, while for (23)-C84, it was −14.4 kcal/mol. On the other hand, the inclusion of the water dimer into C60 was repulsive [26]. Incidentally, our ongoing calculations on CO2@(23)-C84 at the M06-2X/6-31+G* level preliminary gave an encapsulation energy of −13.6 kcal/mol. Hence, CH4@C84 should also be of computational interest in further studies.
In future, still higher methodological levels for the molecular structure optimization and energetics, as well as more advanced descriptions of the motions of the encapsulate in the cage, with related modifications of the RRHO approximation (including the combination [36] of the RRHO and FEM treatments), should be considered. Another more advanced approach [60] treats the motions of a monoatomic encapsulate (for example in He@C60) as the quantum problem of a particle in a sphere (a similar approach [60] can also be developed for encapsulate motions in nanotubes using a model cylinder). This approach produces contributions to thermodynamic functions, showing for example an interesting temperature development [60,61] of the heat capacity. Further generalizations of this approach could lead to a more realistic description of the encapsulation thermodynamics. A generalization of the classical Pitzer description [62] of the hindered internal rotations in molecules should also be studied [55,63] for this purpose. Moreover, there have been some promising results [36] for anharmonicity considerations based on quantum chemical calculations, too. Finally, let as mention for completeness that topological, non-numerical approaches [64,65,66,67] can also be useful in understanding some encapsulation issues.
Such expected future progress should in turn encourage studies of still more complex nanocarbon systems [68,69,70,71] via applications of Gibbs energy treatments. The results of such more advanced calculations with an even higher accuracy could also be used in the search for non-metallic fullerene endohedrals in the interstellar spectra (diffuse interstellar bands, DIBs). This would be a subsequent step after the discovery [72,73,74] of the empty C60 and C70 in interstellar space and hypotheses [75,76,77] of their origin there. One of the possible endohedral candidates is [78] H2O@. For the application, the calculations should also be adjusted for charged species (including electronic spectra).
4. Conclusions
The previously synthetically prepared endohedral CH4@C60 was characterized through calculations. The symmetry of the endohedral was found to be tetrahedral T symmetry. The calculated encapsulation energetics were attractive, with a substantial energy gain of −13.94 kcal/mol at the most advanced computational level. The encapsulation equilibrium constants for CH4@C60 were somewhat higher than previously found with the CO@C60 system—this finding suggests that high-pressure and high-temperature synthesis could in principle be possible for CH4@C60. In future, these computational approaches should be developed further, for both encapsulation energetics and description of the motions of the encapsulate in the cage. The presented results encourage studies of still more complex endohedral and other nanocarbon systems.
Author Contributions
Conceptualization, Z.S., T.A. and X.L.; methodology, Z.S. and L.A.; hardware and software, Z.S., F.U. and L.A.; models validation, Z.S., T.A., X.L. and L.A.; analysis and interpretation, Z.S., F.U., T.A. and X.L.; writing—original draft preparation, Z.S. and F.U. All authors have read and agreed to the published version of the manuscript.
Funding
The reported research has been supported by the National Natural Science Foundation of China (21925104 and 92261204), the Hubei Provincial Natural Science Foundation of China (No. 2021CFA020), and the International Cooperation Key Project of Science and Technology Department of Shaanxi; and by the Charles University Centre of Advanced Materials/CUCAM (CZ 02.1.01/0.0/0.0/15_003/0000417), the MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) computing facilities.
Data Availability Statement
The data presented in this study are available in article.
Acknowledgments
An initial phase of the research line was supported by the Alexander von Humboldt-Stiftung and the Max-Planck-Institut für Chemie (Otto-Hahn-Institut).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peres, T.; Cao, B.P.; Cui, W.D.; Khong, A.; Cross, R.J.; Saunders, M.; Lifshitz, C. Some new diatomic molecule containing endohedral fullerenes. Int. J. Mass Spectr. 2001, 210/211, 241–247. [Google Scholar] [CrossRef]
- Suetsuna, T.; Dragoe, N.; Harneit, W.; Weidinger, A.; Shimotani, H.; Ito, S.; Takagi, H.; Kitazawa, K. Separation of N2@C60 and N@C60. Chem. Eur. J. 2002, 8, 5079–5083. [Google Scholar] [CrossRef] [PubMed]
- Suetsuna, T.; Dragoe, N.; Harneit, W.; Weidinger, A.; Shimotani, H.; Ito, S.; Takagi, H.; Kitazawa, K. Separations of N2@C60 and N@C60 (vol 8, pg 5079, 2002). Chem. Eur. J. 2003, 9, 598. [Google Scholar] [CrossRef]
- Murphy, T.A.; Pawlik, T.; Weidinger, A.; Höhne, M.; Alcala, R.; Spaeth, J.-M. Observation of atomlike nitrogen in nitrogen-implanted solid C60. Phys. Rev. Lett. 1996, 77, 1075–1078. [Google Scholar] [CrossRef]
- Knapp, C.; Dinse, K.-P.; Pietzak, B.; Waiblinger, M.; Weidinger, A. Fourier transform EPR study of N@C60 in solution. Chem. Phys. Lett. 1997, 272, 433–437. [Google Scholar] [CrossRef]
- Pietzak, B.; Waiblinger, M.; Murphy, T.A.; Weidinger, A.; Höhne, M.; Dietel, E.; Hirsch, A. Buckminsterfullerene C60: A chemical Faraday cage for atomic nitrogen. Chem. Phys. Lett. 1997, 279, 259–263. [Google Scholar] [CrossRef]
- Cao, B.P.; Peres, T.; Cross, R.J.; Saunders, M.; Lifshitz, C. Do nitrogen-atom-containing endohedral fullerenes undergo the shrink-wrap mechanism? J. Phys. Chem. A 2001, 105, 2142–2146. [Google Scholar] [CrossRef]
- Kobayashi, K.; Nagase, S.; Dinse, K.-P. A theoretical study of spin density distributions and isotropic hyperfine couplings of N and P atoms in N@C60, P@C60, N@C70, N@C60(CH2)6, and N@C60(SiH2)6. Chem. Phys. Lett. 2003, 377, 93–98. [Google Scholar] [CrossRef]
- Wakahara, T.; Matsunaga, Y.; Katayama, A.; Maeda, Y.; Kako, M.; Akasaka, T.; Okamura, M.; Kato, T.; Choe, Y.K.; Kobayashi, K.; et al. A comparison of the photochemical reactivity of N@C60 and C60: Photolysis with disilirane. Chem. Commun. 2003, 39, 2940–2941. [Google Scholar] [CrossRef]
- Saunders, M.; Jiménez-Vázquez, H.A.; Cross, R.J.; Poreda, R.J. Stable compounds of helium and neon: He@C60 and Ne@C60. Science 1993, 259, 1428–1430. [Google Scholar] [CrossRef] [PubMed]
- Saunders, M.; Jiménez-Vázquez, H.A.; Cross, R.J.; Mroczkowski, S.; Freedberg, D.I.; Anet, F.A.L. Probing the interior of fullerenes by 3He NMR spectroscopy of endohedral 3He@C60 and 3He@C70. Nature 1994, 367, 256–258. [Google Scholar] [CrossRef]
- Cross, R.J.; Saunders, M.; Prinzbach, H. Putting helium inside dodecahedrane. Org. Lett. 1999, 1, 1479–1481. [Google Scholar] [CrossRef]
- Cross, R.J.; Saunders, M. Catalyzed incorporation of nobel gases in fullerenes. In Recent Advances in the Chemistry and Physics of Fullerenes and Related Materials, Volume 11—Fullerenes for the New Millennium; Kadish, K.M., Kamat, P.V., Guldi, D., Eds.; The Electrochemical Society: Pennington, NJ, USA, 2001; pp. 298–300. [Google Scholar]
- Rubin, Y.; Jarrosson, T.; Wang, G.-W.; Bartberger, M.D.; Houk, K.N.; Schick, G.; Saunders, M.; Cross, R.J. Insertion of helium and molecular hydrogen through the orifice of an open fullerene. Angew. Chem. Int. Ed. Engl. 2001, 40, 1543–1546. [Google Scholar] [CrossRef]
- Carravetta, M.; Murata, Y.; Murata, M.; Heinmaa, I.; Stern, R.; Tontcheva, A.; Samoson, A.; Rubin, Y.; Komatsu, K.; Levitt, M.H. Solid-state NMR spectroscopy of molecular hydrogen trapped inside an open-cage fullerene. J. Am. Chem. Soc. 2004, 126, 4092–4093. [Google Scholar] [CrossRef]
- Iwamatsu, S.-I.; Uozaki, T.; Kobayashi, K.; Re, S.; Nagase, S.; Murata, S. A bowl-shaped fullerene encapsulates a water into the cage. J. Am. Chem. Soc. 2004, 126, 2668–2669. [Google Scholar] [CrossRef] [PubMed]
- Komatsu, K.; Murata, M.; Murata, Y. Encapsulation of molecular hydrogen in fullerene C60 by organic synthesis. Science 2005, 307, 238–240. [Google Scholar] [CrossRef] [PubMed]
- Kurotobi, K.; Murata, Y. A Single molecule of water encapsulated in fullerene C60. Science 2011, 333, 613–616. [Google Scholar] [CrossRef]
- Zhang, R.; Murata, M.; Aharen, T.; Wakamiya, A.; Shimoaka, T.; Hasegawa, T.; Murata, Y. Synthesis of a distinct water dimer inside fullerene C70. Nat. Chem. 2016, 8, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Iwamatsu, S.; Stanisky, C.M.; Cross, R.J.; Saunders, M.; Mizorogi, N.; Nagase, S.; Murata, S. Carbon monoxide inside an open-cage fullerene. Angew. Chem. Intl. Ed. 2006, 45, 5337–5340. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.J.; Yang, D.Z.; Colombo, F.; Yu, Y.M.; Zhang, W.X.; Gan, L.B. Punching a carbon atom of C60 into its own cavity to form an endohedral complex CO@C59O6 under mild conditions. Chem. Eur. J. 2013, 19, 16545–16549. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lou, N.; Xu, D.; Pan, C.; Lu, X.; Gan, L. Oxygen-delivery materials: Synthesis of an open-cage fullerene derivative suitable for encapsulation of H2O2 and O2. Angew. Chem. Int. Ed. 2018, 57, 14144–14148. [Google Scholar] [CrossRef]
- Gan, L. Molecular containers derived from [60] fullerene through peroxide chemistry. Acc. Chem. Res. 2019, 52, 1793–1801. [Google Scholar] [CrossRef] [PubMed]
- Cioslowski, J. Endohedral chemistry: Electronic structures of molecules trapped inside the C60 cage. J. Am. Chem. Soc. 1991, 113, 4139–4141. [Google Scholar] [CrossRef]
- Charkin, O.P.; Klimenko, N.M.; Charkin, D.O.; Mebel, A.M. Theoretical study of host-guest interaction in model endohedral fullerenes with tetrahedral molecules and ions of MH4 hydrides inside the C60H36, C60H24, C84, and C60 cages. Russ. J. Inorg. Chem. 2004, 49, 868–880. [Google Scholar]
- Ramachandran, C.N.; Sathyamurthy, N. Water clusters in a confined nonpolar environment. Chem. Phys. Lett. 2005, 410, 348–351. [Google Scholar] [CrossRef]
- Shameema, O.; Ramachandran, C.N.; Sathyamurthy, N. Blue shift in X-H stretching frequency of molecules due to confinement. J. Phys. Chem. A 2006, 110, 2–4. [Google Scholar] [CrossRef] [PubMed]
- Mazurek, A.P.; Sadlej-Sosnowska, N. Is fullerene C60 large enough to host an aromatic molecule? Int. J. Quantum Chem. 2011, 111, 2398–2405. [Google Scholar] [CrossRef]
- Rodríguez-Fortea, A.; Balch, A.L.; Poblet, J.M. Endohedral metallofullerenes: A unique host-guest association. Chem. Soc. Rev. 2011, 40, 3551–3563. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R. Can a single molecule of water be completely isolated within the subnano-space inside the fullerene C60 cage? A quantum chemical prospective. Chem. Eur. J. 2012, 18, 15345–15360. [Google Scholar] [CrossRef]
- Farimani, A.B.; Wu, Y.B.; Aluru, N.R. Rotational motion of a single water molecule in a buckyball. Phys. Chem. Chem. Phys. 2013, 15, 17993–18000. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef]
- Hashikawa, Y.; Murata, M.; Wakamiya, A.; Murata, Y. Orientation of a water molecule: Effects on electronic nature of the C59N cage. J. Org. Chem. 2017, 82, 4465–4469. [Google Scholar] [CrossRef]
- Zhu, G.-Z.; Liu, Y.; Hashikawa, Y.; Zhang, Q.-F.; Murata, Y.; Wang, L.-S. Probing the interaction between the encapsulated water molecule and the fullerene cages in H2O@ and H2O@C59N−. Chem. Sci. 2018, 9, 5666–5671. [Google Scholar] [CrossRef]
- Jaworski, A.; Hedin, N. Local energy decomposition analysis and molecular properties of encapsulated methane in fullerene (CH4@C60). Phys. Chem. Chem. Phys. 2021, 23, 21554–21567. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Adamowicz, L. Theoretical predictions of fullerene stabilities. In Handbook of Fullerene Science and Technology; Lu, X., Akasaka, T., Slanina, Z., Eds.; Springer: Singapore, 2022; pp. 111–179. [Google Scholar]
- Bloodworth, S.; Sitinova, G.; Alom, S.; Vidal, S.; Bacanu, G.R.; Elliott, S.J.; Light, M.E.; Herniman, J.M.; Langley, G.J.; Levitt, M.H.; et al. First synthesis and characterization of CH4@C60. Angew. Chem. Int. Ed. 2019, 58, 5038–5043. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Moller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Double-hybrid density functionals with long-range dispersion corrections: Higher accuracy and extended applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the difference of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Akasaka, T.; Nagase, S. Computed stabilities in metallofullerene series: Al@C82, Sc@C82, Y@C82, and La@C82. Int. J. Quant. Chem. 2011, 111, 2712–2718. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Rev. D.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Slanina, Z.; Uhlík, F.; François, J.-P.; Ōsawa, E. Thermodynamic Data Bases and Optical Isomerism. Croat. Chem. Acta 2000, 73, 1047–1055. [Google Scholar]
- Akasaka, T.; Nagase, S.; Kobayashi, K.; Wälchli, M.; Yamamoto, K.; Funasaka, H.; Kako, M.; Hoshino, T.; Erata, T. 13C and 139La NMR studies of La2@C80: First evidence for circular motion of metal atoms in endohedral dimetallofullerenes. Angew. Chem. Intl. Ed. Engl. 1997, 36, 1643–1645. [Google Scholar] [CrossRef]
- Kurihara, H.; Lu, X.; Iiduka, Y.; Mizorogi, N.; Slanina, Z.; Tsuchiya, T.; Akasaka, T.; Nagase, S. Sc2C2@C80 rather than Sc2@C82: Templated formation of unexpected C2v(5)C82 and temperature-dependent dynamic motion of internal Sc2C2 cluster. J. Am. Chem. Soc. 2011, 133, 2382–2385. [Google Scholar] [CrossRef]
- Kurihara, H.; Lu, X.; Iiduka, Y.; Nikawa, H.; Hachiya, M.; Mizorogi, N.; Slanina, Z.; Tsuchiya, T.; Nagase, S.; Akasaka, T. X-ray Structures of Sc2C2@C2n (n = 40–42): In-depth understanding of the core-shell interplay in carbide cluster metallofullerenes. Inorg. Chem. 2012, 51, 746–750. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Nagase, S.; Akasaka, T.; Adamowicz, L.; Lu, X. Eu@C72: Computed comparable populations of two non-IPR isomers. Molecules 2017, 22, 1053. [Google Scholar] [CrossRef]
- Takata, M.; Nishibori, E.; Sakata, M.; Shinohara, H. Charge density level structures of endohedral metallofullerenes determined by synchrotron radiation powder method. New Diam. Front. Carb. Technol. 2002, 12, 271–286. [Google Scholar]
- Hehre, W.J. A Guide to Molecular Mechanics and Quantum Chemical Calculations; Wavefunction: Irvine, CA, USA, 2003; p. 435. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry; Wiley: Chichester, UK, 2017; p. 319. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Adamowicz, L.; Lee, S.-L. Computations of the catalytic effects in the Stone-Wales fullerene isomerizations: N and CN agents. Int. J. Quantum Chem. 2004, 99, 634–639. [Google Scholar] [CrossRef]
- Hao, Y.; Tang, Q.; Li, X.; Zhang, M.; Wan, Y.; Feng, L.; Chen, N.; Slanina, Z.; Adamowicz, L.; Uhlík, F. Isomeric Sc2O@C78 related by a single-step Stone-Wales transformation: Key links in an unprecedented fullerene formation pathway. Inorg. Chem. 2016, 55, 11354–11361. [Google Scholar] [CrossRef] [PubMed]
- Slanina, Z. Some aspects of mathematical chemistry of equilibrium and rate processes: Steps towards a completely non-empirical computer design of syntheses. J. Mol. Struct. (Theochem) 1989, 185, 217–228. [Google Scholar] [CrossRef]
- Frum, C.I.; Engleman, R., Jr.; Hedderich, H.G.; Bernath, P.F.; Lamb, L.D.; Huffman, D.R. The infrared emission spectrum of gas-phase C60 (buckmisterfullerene). Chem. Phys. Lett. 1991, 176, 504–508. [Google Scholar] [CrossRef]
- Slanina, Z.; Rudziński, J.M.; Togasi, M.; Ōsawa, E. Quantum-chemically supported vibrational analysis of giant molecules: The C60 and C70 clusters. J. Mol. Struct. (Theochem) 1989, 202, 169–176. [Google Scholar] [CrossRef]
- Manolopoulos, D.E.; Fowler, P.W. Molecular graphs, point groups, and fullerenes. J. Chem. Phys. 1992, 96, 7603–7614. [Google Scholar] [CrossRef]
- Bakowies, D.; Kolb, M.; Thiel, W.; Richard, S.; Ahlrichs, R.; Kappes, M.M. Quantum-chemical study of C84 fullerene isomers. Chem. Phys. Lett. 1992, 200, 411–417. [Google Scholar] [CrossRef]
- Uhlík, F.; Slanina, Z.; Ōsawa, E. Thermodynamic properties of He@C60. Fullerene Sci. Technol. 2000, 8, 453–460. [Google Scholar] [CrossRef]
- Suzuki, H.; Nakano, M.; Hashikawa, Y.; Murata, Y. Rotational motion and nuclear spin interconversion of H2O encapsulated in C60 appearing in the low-temperature heat capacity. J. Phys. Chem. Lett. 2019, 10, 1306–1311. [Google Scholar] [CrossRef] [PubMed]
- Pitzer, K.S. Potential energies for rotation about single bonds. Discuss. Faraday Soc. 1951, 10, 66–73. [Google Scholar] [CrossRef]
- Gilson, M.K.; Irikura, K.K. Symmetry mumbers for rigid, flexible, and fluxional molecules: Theory and applications. J. Phys. Chem. B 2010, 114, 16304–16317. [Google Scholar] [CrossRef] [PubMed]
- Ōsawa, E. The evolution of the football structure for the C60 molecule: A retrospective. Phil. Trans. R. Soc. Lond. A 1993, 343, 1–8. [Google Scholar]
- Slanina, Z.; Lee, S.-L.; Yu, C.-H. Computations in treating fullerenes and carbon aggregates. Rev. Comput. Chem. 1996, 8, 1–62. [Google Scholar]
- Díaz-Tendero, S.; Alcamí, M.; Martín, F. Fullerene C50: Sphericity takes over, not strain. Chem. Phys. Lett. 2005, 407, 153–158. [Google Scholar] [CrossRef]
- Vukicevic, D.; Cataldo, F.; Ori, O.; Graovac, A. Topological efficiency of C66 fullerene. Chem. Phys. Lett. 2011, 501, 442–445. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Basiuk, E.V. Noncovalent complexes of Ih-C80 fullerene with phthalocyanines. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 69–75. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Tahuilan-Anguiano, D.E. Complexation of free-base and 3d transition metal(II) phthalocyanines with endohedral fullerene Sc3N@C80. Chem. Phys. Lett. 2019, 722, 146–152. [Google Scholar] [CrossRef]
- Li, M.; Zhao, R.; Dang, J.; Zhao, X. Theoretical study on the stabilities, electronic structures, and reaction and formation mechanisms of fullerenes and endohedral metallofullerenes. Coor. Chem. Rev. 2022, 471, 214762-1–214762-12. [Google Scholar] [CrossRef]
- Li, Y.B.; Biswas, R.; Kopcha, W.P.; Dubroca, T.; Abella, L.; Sun, Y.; Crichton, R.A.; Rathnam, C.; Yang, L.T.; Yeh, Y.W.; et al. Structurally defined water-soluble metallofullerene derivatives towards biomedical applications. Angew. Chem. Int. Ed. Engl. 2023, 62, e202211704-1–e202211704-10. [Google Scholar]
- Cami, J.; Bernard-Salas, J.; Peeters, E.; Malek, S.E. Detection of C60 and C70 in a young planetary nebula. Science 2010, 329, 1180–1182. [Google Scholar] [CrossRef]
- Campbell, E.K.; Holz, M.; Gerlich, D.; Maier, J.P. Laboratory confirmation of C60+ as the carrier of two diffuse interstellar bands. Nature 2015, 523, 322–323. [Google Scholar] [CrossRef]
- Hansen, C.S.; Peeters, E.; Cami, J.; Schmidt, T.W. Open questions on carbon-based molecules in space. Commun. Chem. 2022, 5, 94-1–94-4. [Google Scholar] [CrossRef]
- Berné, O.; Tielens, A.G.G.M. Formation of buckminsterfullerene (C60) in interstellar space. Proc. Natl. Acad. Sci. USA 2012, 109, 401–406. [Google Scholar] [CrossRef]
- Berné, O.; Montillaud, J.; Joblin, C. Top-down formation of fullerenes in the interstellar medium. Astronom. Astrophys. 2015, 577, A133-1–A133-9. [Google Scholar] [CrossRef] [PubMed]
- Berné, O.; Montillaud, J.; Joblin, C. Top-down formation of fullerenes in the interstellar medium (Corrigendum). Astronom. Astrophys. 2016, 588, C1-1. [Google Scholar] [CrossRef]
- Rademacher, J.; Reedy, E.S.; Negri, F.; Alom, S.; Whitby, R.J.; Levitt, M.H.; Campbell, E.K. Gas-phase electronic spectroscopy of nuclear spin isomer separated H2O@ and D2O@. Mol. Phys. 2023, 122, e2173507-1–e2173507-11. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).