Next Article in Journal
Guardians of the Genome: Iron–Sulfur Proteins in the Nucleus
Previous Article in Journal
Phase Relations in the Pseudo-Binary BiFeO3–EuFeO3 System in the Subsolidus Region Derived from X-Ray Diffraction Data—A Machine Learning Approach
Previous Article in Special Issue
A Comparison of β–Phenyl Elimination in Nickel and Palladium Alkyl Complexes: A Potentially Relevant Process in the Mizoroki–Heck Reaction
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 12
Issue 12
10.3390/inorganics12120315
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Investigations of Para-Methoxystyrene/Styrene Polymerization Catalyzed by Cationic Methyl- and Dibenzobarrelene-Based α-Diimine Palladium Complexes

by
Ling Zhu
1,
Yi Luo
1,3,*,
Xin Wen
1,
Wenzhen Zhang
1 and
Guangli Zhou
2,*
1
State Key Laboratory of Fine Chemicals, School of Chemical Engineering, Dalian University of Technology, Dalian 116024, China
2
School of Chemistry and Chemical Engineering, Linyi University, Linyi 276000, China
3
PetroChina Petrochemical Research Institute, Beijing 102206, China
*
Authors to whom correspondence should be addressed.
Inorganics 2024, 12(12), 315; https://doi.org/10.3390/inorganics12120315
Submission received: 25 October 2024 / Revised: 22 November 2024 / Accepted: 3 December 2024 / Published: 5 December 2024
(This article belongs to the Special Issue Revealing Reaction Mechanisms in Homogeneous Transition Metal Catalysis, 2nd Edition)
Browse Figures
Versions Notes

Abstract

:
The polymerization mechanism of para-methoxystyrene catalyzed by cationic α-diimine palladium complexes with various ancillary ligands was rigorously examined using density functional theory. In the classical methyl-based α-diimine palladium complex [{(2,6-iPr2C6H3)-N=C(Me)-C(Me)=N-2,6-iPr2C6H3)}PdMe]+ (A+), the 2,1-insertion of para-methoxystyrene is favored over the 1,2-insertion, both thermodynamically and kinetically, during the chain initiation step. The resulting thermodynamically favored η3-π-benzyl intermediates face a substantial energy barrier, yielding only trace amounts of polymer, as experimentally verified. In contrast, the dibenzobarrelene-based α-diimine palladium complex [{(2,6-iPr2C6H3)-N=C(R)-C(R)=N-2,6-iPr2C6H3)}PdMe]+ (R = dibenzobarrelene, B+) shows similar energy barriers for both 2,1- and 1,2-insertions. Continuous 2,1/2,1 or 2,1/1,2 insertions are impeded by excessive energy barriers. However, theoretical calculations reveal that the 1,2-insertion product can seamlessly transition into the chain propagation stage, producing a polymer with high 1,2-regioselectivity. The observed activity of complexes A+ or B+ towards para-methoxystyrene polymerization stems from the energy barrier differences between the 1,2- and 2,1-insertions, influenced by the steric hindrance from the ancillary ligands. Further investigation into the effects of steric hindrance on the chain initiation stage involved computational modeling of analogous complexes with increased steric bulk. These studies established a direct correlation between the energy barrier difference ∆∆G (1,2–2,1) and the van der Waals volume of the ancillary ligand. Larger van der Waals volumes correspond to reduced energy barrier differences, thus enhancing the regioselectivity for para-methoxystyrene polymerization. Moreover, the experimental inertness of complex B+ towards styrene polymerization is attributed to the formation of stable kinetic and thermodynamic 2,1-insertion intermediates, which obstruct further styrene monomer insertion due to an extremely high reactive energy barrier. These findings contribute to a deeper understanding of the mechanistic aspects and offer insights for designing new transition metal catalysts for the polymerization of para-alkoxystyrenes.

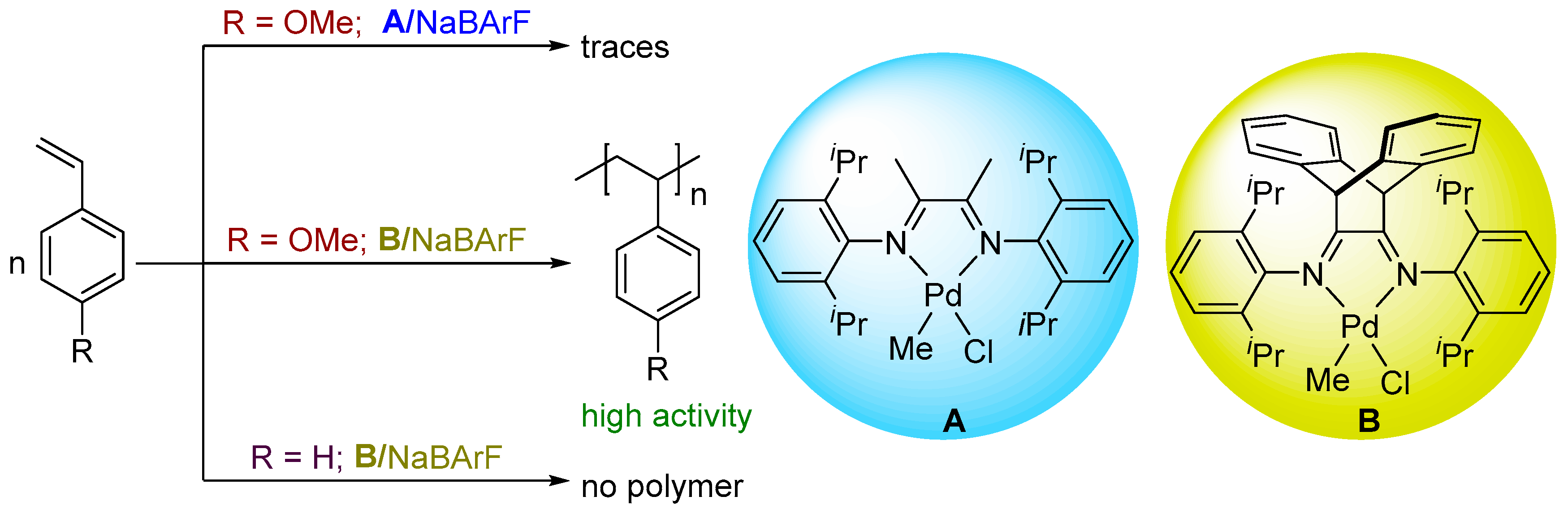
1. Introduction

Functionalized polyolefins, which incorporate polar functional groups into polyolefins, represent a promising class of materials due to their distinctive properties such as wettability, adhesion, printability, and compatibility. These properties significantly expand their potential applications [1,2,3]. The successful introduction of polar functional groups into polyolefins has been achieved through various polymerization techniques including cationic polymerization [4,5], radical polymerization [6,7], and coordination-insertion polymerization [8,9,10,11]. Among these, coordination-insertion polymerization, facilitated by transition metal catalysts, has proven to be an efficient and straightforward method. This technique offers mild reaction conditions and allows precise control over the polymer’s structure and composition.
Early transition metal catalysts, including group 4–6 metals, are susceptible to poisoning due to their strong Lewis acidity, which facilitates the easy coordination of polar monomers [12,13,14]. In contrast, late transition metal catalysts, such as square planar d8 nickel and palladium complexes, exhibit low oxophilicity and enhanced tolerance to functional groups, making them ideal for synthesizing functionalized polyolefins. Over the past decades, the development of late transition metal catalysts for polar monomer polymerization has garnered significant interest in functional polyolefin research [15,16,17,18]. For instance, Mecking in 2009 first demonstrated the continuous insertion of methyl acrylate using a neutral phosphinesulfonato palladium(II) catalyst, achieving only trace amounts of oligomers [19]. Subsequently, the same group explored the polymerization behavior of diallyl ether catalyzed by identical palladium(II) complexes [20]. This catalyst displayed moderate catalytic activity for diallyl ether polymerization. Conversely, the homopolymerization of allyl ethyl ether resulted in products with significantly lower molecular weights and reduced productivity. The Pellecchia group developed a series of Ni(II) complexes with pyridylimino ligands, demonstrating high productivity but lower selectivity in methyl acrylate insertion for the copolymerization of ethylene with methyl acrylate [21]. However, the overall activity, selectivity, and insertion rates of polar monomers in these polymerization processes remain generally low, making it challenging to achieve the desired high molecular weights and high rates of polar monomer insertion.
Recently, considerable efforts have been invested in enhancing the polymerization performance of metal catalysts through modifications to ligand backbones, substituents, and metal centers. While some experimental instances have demonstrated success, a general lack of theoretical understanding concerning the regulation of catalytic activity, polymer molecular weight, and polar monomer insertion rates by late transition metals often leads to inefficiency and a measure of trial-and-error in research. Consequently, it is essential to investigate the influence of the ligand backbone, substituents, and metal centers within metal complexes on polymerization activity at the molecular level.
In 2020, Gao and colleagues reported that the classical α-diimine palladium complex A catalyzed the polymerization of para-methoxystyrene (pMOS), yielding only trace amounts of the product. In contrast, the dibenzobarrelene-based α-diimine palladium species B demonstrated high activity, rapidly producing poly(para-methoxystyrene)s with high molecular weights. However, this catalyst B was inert when used for the polymerization of styrene (Scheme 1) [22]. This observation underscores the significant influence of the auxiliary ligands and the type of monomer on the catalytic activity and microstructure of the polymerization process. Consequently, this study systematically investigates the mechanisms and origins of the activity in the polymerization of pMOS by late transition metal palladium complexes with varying auxiliary ligands. Additionally, it examines the monomer specificity of dibenzobarrelene-based α-diimine palladium species using density functional theory (DFT) calculations. These investigations aim to provide a theoretical foundation for designing and synthesizing new catalytic systems.

2. Results and Discussion

2.1. Mechanism of pMOS Polymerization by Cationic Species A+

The cationic palladium alkyl species A+ was synthesized by reacting Pd–Cl with sodium tetrakis(3,5-bis(trifluoromethyl)phenyl)borate NaBArF from complex A. As depicted in Figure 1, the chain initiation and propagation processes of pMOS polymerization, catalyzed by the α-diimine palladium complex A+, were modeled using DFT calculations. The chain initiation can proceed via two pathways: 1,2-(black line) and 2,1-(green line) insertion of pMOS. In the 1,2-insertion, coordination of the C=C bond of pMOS with the palladium species A+ leads to the formation of the stable 1,2-coordination complex A1pMOS12 (ΔG = −11.6 kcal/mol). This is followed by the insertion of the C=C bond of pMOS into the Pd−C bond via the four-center transition state ATS1pMOS12, requiring an energy barrier of 20.8 kcal/mol (8.3–(−12.5)) and resulting in an exergonic reaction of 17.4 kcal/mol, forming the intermediate A3pMOS12. Conversely, in the 2,1-insertion, pMOS π-coordinates with species A+ to form the 2,1-coordination complex A1pMOS21. This complex then undergoes insertion via the four-center transition state ATS1pMOS21, forming the complex A2pMOS21 which exists with an agostic interaction, then it subsequently transforms into a more stable π-η3-benzyl chelate intermediate A3pMOS21. The 2,1-insertion process has a lower free energy barrier of 18.0 kcal/mol (5.5–(−12.5)), which is 2.8 kcal/mol less than the 1,2-insertion. Additionally, the chain initiation product A3pMOS21, resulting from the 2,1-insertion, releases 29.8 kcal/mol of energy, making it thermodynamically more stable than A3pMOS12 by 12.4 kcal/mol. These calculations indicate that the 2,1-insertion mode is more favorable than the 1,2-insertion mode, both kinetically and thermodynamically, at the chain initiation stage. Thus, the subsequent chain propagation process was modeled based on the 2,1-insertion product A3pMOS21.
During the chain propagation stage, both 1,2- and 2,1-insertion modes of pMOS were examined. The coordination of pMOS with the intermediate A3pMOS21 to form A4pMOS12 and A4pMOS21 is endergonic, with energy increases of 10.9 and 12.9 kcal/mol, respectively. Furthermore, the energy barrier for the 1,2-insertion, as modeled by the transition state ATS2pMOS12, was calculated to be notably high at 33.1 kcal/mol. Similarly, the transition state for the 2,1-insertion, ATS2pMOS21, also exhibited a significant energy barrier of 29.9 kcal/mol. These calculated free energy barriers for the chain propagation pathways are prohibitively high, considering the experimental reaction conditions at 30 °C, aligning with the observed trace amounts of polymer produced under these conditions.

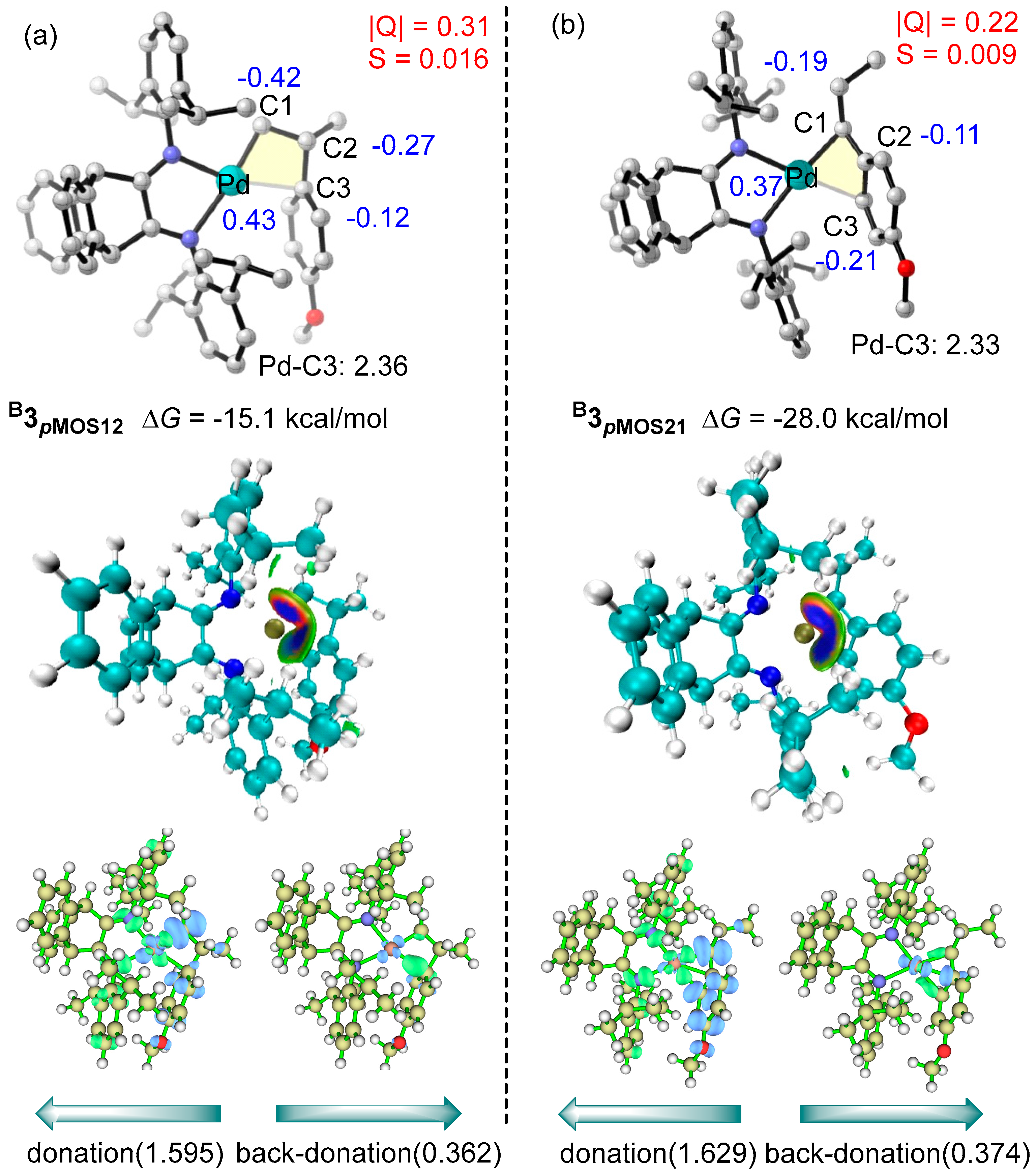
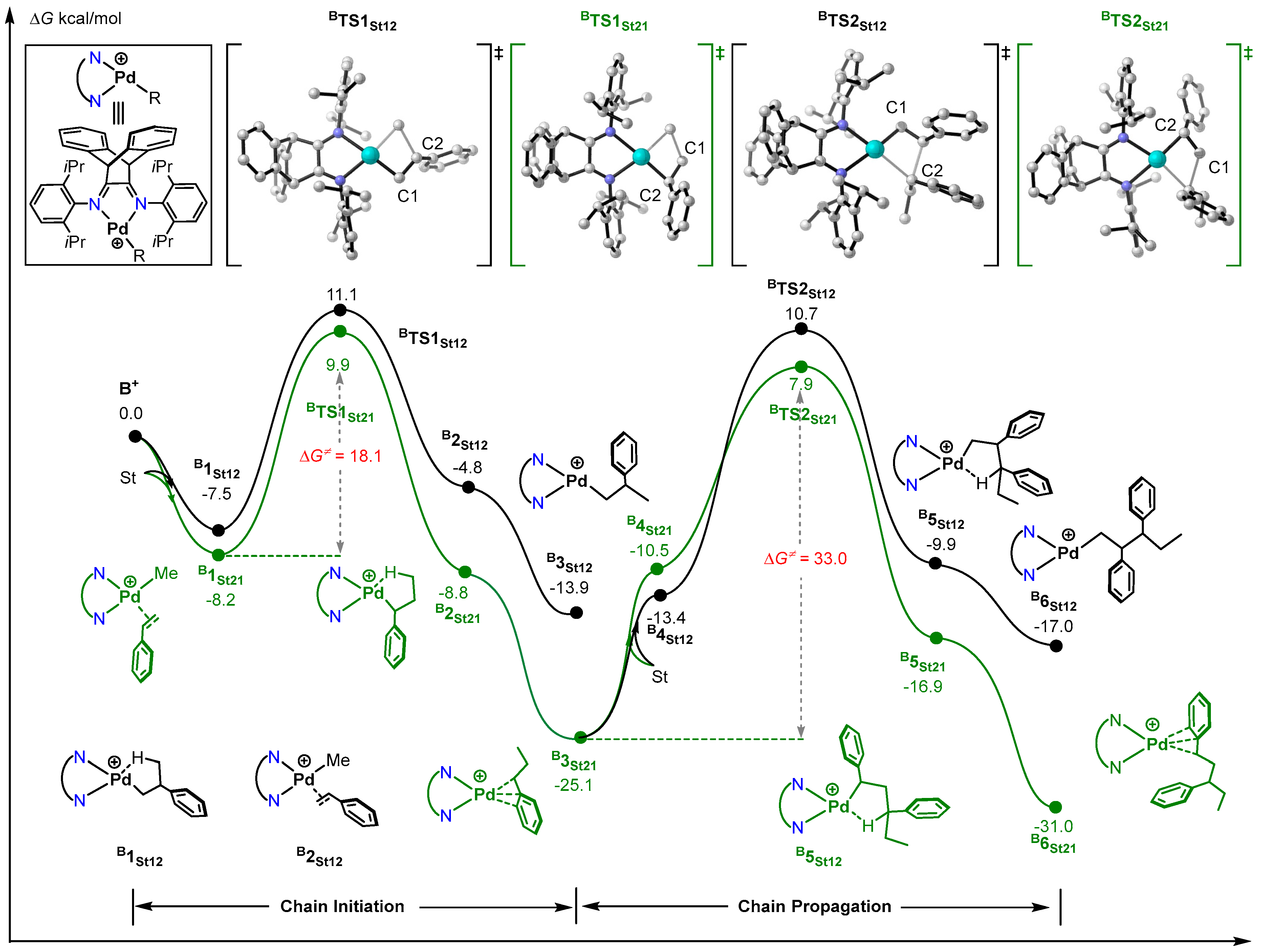
2.2. Mechanism of pMOS Polymerization by Cationic Species B+

Unlike the class α-diimine palladium catalyst A+, where only a trace amount of polymer was observed, the dibenzobarrelene-based α-diimine complex B+ demonstrated high activity in pMOS polymerization. To elucidate this intriguing reactivity difference, detailed mechanistic studies were undertaken. As with species A+, the chain initiation stage for pMOS polymerization based on complex B+ was calculated for both 2,1-insertion and 1,2-insertion pathways. As illustrated in Figure 2, the 2,1-insertion pathway (B1pMOS21→BTS1pMOS21→B2pMOS21→B3pMOS21) involves an energy barrier of 21.3 kcal/mol and is accompanied by an exergonic release of 28.0 kcal/mol. Conversely, the 1,2-insertion pathway (B1pMOS12→BTS1pMOS12→B2pMOS12→B3pMOS12) presents a relative free energy barrier of 20.9 kcal/mol and an exergonic release of 15.1 kcal/mol. Notably, the energy barrier gap (ΔΔG (1,2–2,1)) between the 1,2- and 2,1-insertions shifted from 2.8 to −0.4 kcal/mol compared to A⁺. It is significant to note that the formation of intermediate B3pMOS12 is exergonic by 15.1 kcal/mol, whereas intermediate B3pMOS21 is exergonic by 28.0 kcal/mol, which is 12.9 kcal/mol more exergonic than the 1,2-insertion.
Given that the two pathways are kinetically competitive and that the 2,1-insertion is thermodynamically more favorable, further calculations were performed on the chain propagation process based on B3pMOS21. These calculations indicated that the 2,1-insertion pathway (B3pMOS21→B4pMOS21→BTS2pMOS21→B5pMOS21→B6pMOS21) encounters lower energy barriers compared to the 1,2-insertion pathway (B3pMOS12→B4pMOS12→BTS2pMOS12→B5pMOS12→B6pMOS12), thus making it more advantageous. Nevertheless, the energy barriers for these pathways, at 34.1 and 37.3 kcal/mol, respectively, are prohibitively high, challenging the explanation of catalytic reactivity. This contradiction leads to a further analysis that the activation energies for both insertion reactions are similar, with the 1,2-insertion being marginally favored by 0.4 kcal/mol. The Eyring equation further elucidates the relationship between the kinetic constants for the two reactions, k12 and k21. Calculated at T = 303 K, the ratio k12/k21 = exp((ΔG12≠ − ΔG21≠)/RT) reveals a value of k12/k21 = 1.94, suggesting that the 1,2-insertion reaction is kinetically favored. Quantification of the pMOS insertion products showed a predominant formation of the 1,2-insertion product B3pMOS12 (66% yield), alongside a lesser amount of the 2,1-insertion product B3pMOS21 (34%). Consequently, the chain propagation process based on B3pMOS12, following the 1,2-insertion, was evaluated. As depicted in Figure 3 (right), the calculations indicate that the 1,2-insertion reaction, proceeding through B3pMOS12→B4’pMOS12→BTS2’pMOS12→B5’pMOS12→B6’pMOS12, requires overcoming an energy barrier of only 19.9 kcal/mol, which is lower than that for 2,1-insertion (B3pMOS12→B4’pMOS21→BTS2’pMOS21→B5’pMOS21→B6’pMOS21) by 1.38 kcal/mol. Thus, it is plausible to conclude that for the dibenzobarrelene-based α-diimine complex B+, the chain initiation stage should predominantly follow the 1,2-insertion, potentially a kinetically controlled process.
To further explore the feasibility of the polymerization reaction, the chain termination process following the chain initiation via 1,2-insertion was examined (Figure 3, left). The chain termination mechanism initiates with β−H elimination (BTS3’pMOS12BHE), leading to the intermediate B8’pMOS12BHE with an activation barrier of 3.9 kcal/mol. Subsequently, two chain transfer pathways were considered: dissociative and associative chain transfer. The dissociative chain transfer pathway proceeds through the Pd−H intermediate B10diss, with an activation barrier of 21.7 kcal/mol (6.6–(−15.1)), and the associative chain transfer, facilitated by pMOS via BTS6’pMOS12ass, presents a comparable activation barrier of 21.5 kcal/mol (6.4–(−15.1)). Based on B3pMOS12, chain propagation is kinetically more favorable than the chain transfer processes (19.9 vs. 21.9, 21.4 kcal/mol). This kinetic preference aligns with experimental observations indicating a high 1,2-regioselectivity polymer.
Comparative analysis revealed that the barrier to chain propagation is significantly large, attributable to the varying thermodynamic stabilities of products from the 1,2- and 2,1-insertion chain initiation modes. Consequently, a detailed examination of B3pMOS12 and B3pMOS21 is conducted, focusing on their structural characteristics and charge distributions (refer to the top of Figure 4). Charge dispersion is known to contribute to structural stability. In the chain initiation products, the four-membered units comprising Pd, C1, C2, and C3 are critical for chemical reactivity. To clarify the reasons for the stability of B3pMOS12 and B3pMOS21, natural bond orbital (NBO) analyses were employed. Then, the unsigned average charges (|Q|) and square errors (S) of the atoms in intermediates B3pMOS12 and B3pMOS21 were calculated to estimate charge dispersion. The |Q| value was defined for the Pd, C1, C2, and C3 atoms as |Q| = ∑|Qx|)/n, where n = 4 and Qx denotes the individual atomic charges. The average charges for B3pMOS12 and B3pMOS21 are 0.31 and 0.22, respectively. The S value defined for the four atoms as S = ∑(|Qx| − |Q|)2/n, where n = 4, serves as an indicator of structural stability. A lower S value indicates higher stability. The S value in B3pMOS21 is 0.009, which is smaller than B3pMOS12 (0.016), thus suggesting greater stability and a deeper potential well for B3pMOS21. Additionally, Hirshfeld partition analysis [23,24] demonstrated stronger van der Waals interactions in B3pMOS21 (darker blue in the middle of Figure 4) compared to B3pMOS12. Extended transition state-natural orbitals for chemical valence analysis [24,25] (refer to the bottom of Figure 4) further confirmed stronger donation (1.629 vs. 1.595) and back-donation (0.374 vs. 0.362) in B3pMOS21 compared to B3pMOS12. This analysis supports the identification of η3-π-benzyl intermediate B3pMOS21 as a stable resting state which impedes further chain propagation.
By comparing the computational results of catalysts A+ and B+, it is evident that adjusting the steric hindrance of the auxiliary ligand significantly influences the chain initiation insertion mode, thereby affecting activity and regioselectivity. To further explore this effect, a series of complexes with increased steric hindrance were designed and calculated. As illustrated in Figure 5, the isopropyl groups in the N-aryl moieties were replaced with a phenyl group (catalyst C+), a methyl-phenyl group (catalyst D+), and a phenyl-phenyl group (catalyst E+). The computational results of the chain initiation process are summarized in Table 1 and the figure including the full Gibbs free energy and geometries has been show in the Supplementary Materials (Figures S1–S3). These calculations indicate that an increase in the van der Waals volume [26] of the auxiliary ligand leads to a reduced energy barrier gap for 1,2- and 2,1-insertion (ΔΔG (1,2–2,1) changing from 2.8 to −0.4 to 0.2 to −2.4 to −3.3 to −5.2 kcal/mol), making the 1,2-insertion pathway increasingly favorable. A linear relationship was established between ΔΔG (1,2–2,1) and the van der Waals volume of the catalyst (Figure 5), demonstrating a strong negative correlation (R2 = 0.95). A larger van der Waals volume corresponds to a lower barrier gap ΔΔG (1,2–2,1), which enhances the propensity for 1,2-insertion. This trend suggests that while the barrier for 1,2-insertion is minimally affected by increasing steric hindrance (from 19.5 to 20.9 kcal/mol), the barrier for 2,1-insertion is significantly raised (from 18.0 to 25.0 kcal/mol). Consequently, this alteration leads to a more negative difference in the energy barriers between the two pathways, thereby enhancing the selectivity for 1,2-insertion.

2.3. Mechanism of Styrene Polymerization by Cationic Species B+

Concurrently, the dibenzobarrelene-based α-diimine catalyst B+ demonstrates high activity in catalyzing the polymerization of pMOS yet shows no activity in styrene polymerization. This discrepancy prompts an investigation into the factors influencing its activity, which could elucidate the catalyst’s regioselectivity for different monomers. Accordingly, the styrene polymerization mechanism using catalyst B+ was computationally analyzed (Figure 6). The 2,1-insertion barrier for styrene at the chain initiation stage is calculated to be 18.1 kcal/mol, which is kinetically 1.2 kcal/mol more favorable than the 1,2-insertion. The η3 intermediate, B3St21, formed by 2,1-insertion, is also thermodynamically more stable than the 1,2-insertion product, B3St12 (−25.1 vs. −13.9 kcal/mol). The ratio of kinetic constants, estimated according to the Eyring equation k₁₂/k₂₁ = exp((ΔG12≠ − ΔG21≠)/RT) at T = 303 K, yields a calculated reactivity ratio (k12/k21 = 0.14), indicating that 1,2-insertion of styrene into the Pd−Me complex B1St21 is less favorable compared to 2,1-insertion. Quantification of the styrene insertion products revealed that 88% yield was of the 2,1-insertion product B3St21, with only a trace amount (12%) of the 1,2-insertion product B3St12. Thus, subsequent chain propagation is predominantly based on the 2,1-insertion product B3St21. Starting from B3St21, chain propagation of styrene through the transition state BTS2St21 requires overcoming an activation energy of 33.0 kcal/mol. This substantial barrier underscores the challenges in the chain propagation process during styrene polymerization, aligning with experimental observations that no polymers are formed.

3. Computational Details

Theoretical calculations were performed using Gaussian 16 [27]. All structures were optimized in the gas phase using the B3LYP-D3 functional [28,29,30] combined with the Lanl2DZ [31,32] basis set for Pd and the 6-31G(d,p) basis set for other atoms. Polarization functions for Pd were included with ζf = 1.472 [33]. Frequency analysis was calculated to confirm the optimized structures as transition states (only one imaginary frequency) or minima (no imaginary frequencies). Intrinsic reaction coordinate (IRC) calculations were performed to link every transition state to correct reactants and products. IRC were carried out for twenty steps from the TS (both in the forward and reverse directions). The ensuing structures were fully optimized to identify the minima [34]. Based on the optimized gas-phase geometries, single-point calculations were performed in dichloromethane using the SMD solvent model [35,36,37], with the B3LYP-D3 functional employing a mixed basis set (SDD for Pd [38,39,40,41,42] and 6-311+G(d,p) for other atoms). Structures in this study were visualized using CYLview [43]. Thermodynamic corrections to Gibbs free energy were applied using solution-phase single-point energies plus 1.9 kcal/mol [44,45] (to adjust for the standard state change from 1 atm to 1 mol/L at 298.15 K), thus calculating the solution-phase Gibbs free energies for subsequent discussions. Tools such as Multiwfn [24] and VMD [46] were utilized to analyze non-covalent interactions (using the independent gradient model based on the Hirshfeld partition method) [24] and to perform extended transition state and natural orbitals for chemical valence analyses [25]. To verify the feasibility of the computational results, the ωB97XD method and the optimization using the SMD model for key steps in the chain initiation were also tested and showed similar performance to that from SMD(dichloromethane)-B3LYP-D3/SDD/6-311+G(d,p)//B3LYP-D3/Lanl2DZ/6-31G(d,p) (Figures S4 and S5, in the Supplementary Materials).

4. Conclusions

DFT studies have analyzed the activity and regioselectivity differences in para-alkoxystyrene polymerization catalyzed by cationic α-diimine palladium complexes alkyl species [{(2,6-iPr2C6H3)-N=C(R)-C(R)=N-2,6-iPr2C6H3)}PdMe]⁺ (A+, R = Me; B+, R = dibenzobarrelene) with varying auxiliary ligands. The limited polymer formation observed experimentally with species A+ in para-methoxystyrene polymerization is attributed to the formation of a stable η3-benzyl chelate dormant state, resulting from a 2,1-insertion during the chain initiation process. In contrast, species B+, demonstrating a high 1,2-regioselectivity in the polymerization process, favors a continuous 1,2/1,2 insertion mode. The 2,1-insertion and 1,2-insertion pathways are dynamically competitive, reflected by similar energy barriers at the chain initiation. The 2,1-insertion intermediate displays enhanced thermodynamic stability due to a smaller average charge |Q| and square errors S of Pd, C1, C2, and C3 units, thus favoring a dormant state. Conversely, the 1,2-insertion intermediate is more likely to continue coordination and insertion of the subsequent para-methoxystyrene monomer. Both dissociative and associative chain transfer pathways have been calculated and considered improbable. Improvements in the catalytic 1,2-regioselectivity of para-methoxystyrene polymerization may be achieved by enlarging the substituents on the N-aryl moieties. A series of sterically hindered catalysts were computationally designed to assess the impact of steric effects on the chain initiation step. The results confirm a negative correlation between the energy barrier gap ∆∆G (1,2–2,1) and the van der Waals volume of the catalysts, with a correlation coefficient R2 of 0.95. A larger van der Waals volume indicates a lower barrier gap ∆∆G (1,2–2,1), which facilitates the occurrence of 1,2-insertion in para-methoxystyrene polymerization. Unlike para-methoxystyrene polymerization, which is not similarly inhibited and allows subsequent chain propagation, the polymerization of styrene predominantly forms a stable η3-structured intermediate due to a slightly more favorable 2,1-insertion. These findings are expected to provide valuable insights into the development of cationic α-diimine palladium alkyl species for para-alkoxystyrene polymerization.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics12120315/s1, Figure S1: Calculated Gibbs free energy profiles for insertion of pMOS based on C+ at the chain initiation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively, Figure S2: Calculated Gibbs free energy profiles for insertion of pMOS based on D+ at the chain initiation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively, Figure S3: Calculated Gibbs free energy profiles for insertion of pMOS based on E+ at the chain initiation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively, Figure S4: Gibbs energy profile at the B3LYP-D3/ Lanl2DZ/ 6-31G(d,p) level of theory with the SMD solvation model in dichloromethane for insertion of pMOS based on A+ at the chain initiation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively, Figure S5: Calculated relative Gibbs free energies by ωB97XD/SDD/6-311+G(d,p) /SMD(toluene)//B3LYP-D3/Lanl2DZ/6-31G(d,p) (in kcal/mol). The relative energies of ATS1pMOS21 were set to be 0.0 kcal/mol, Table S1: Calculated thermodynamic corrections for Gibbs free energies (ΔGcor in Hartrees), solution-phase single-point energies (ΔEsol in Hartrees) and solution-phase Gibbs free energies (ΔGsol in Hartrees). DFT geometries are also collected in a separate .xyz file.

Author Contributions

Conceptualization, L.Z., G.Z. and Y.L.; methodology, L.Z., G.Z. and Y.L.; software, X.W.; formal analysis, X.W.; investigation, L.Z.; data curation, L.Z., G.Z. and Y.L.; writing—original draft, L.Z.; writing—review and editing, L.Z., X.W., W.Z., G.Z. and Y.L.; supervision, W.Z., G.Z. and Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the NSFC (Nos. 22071015) and the Open Funding Project of Key Laboratory of Functional Polymer Materials, Ministry of Education, Nankai University (KLFPM202301).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Zou, C.; Chen, C.L. Polar-functionalized, crosslinkable, self-healing and photoresponsive polyolefins. Angew. Chem. Int. Ed. 2020, 59, 395–402. [Google Scholar] [CrossRef] [PubMed]
  2. Tan, C.; Zou, C.; Chen, C. Material properties of functional polyethylenes from transition-metal-catalyzed ethylene–polar monomer copolymerization. Macromolecules 2022, 55, 1910–1922. [Google Scholar] [CrossRef]
  3. Mu, H.; Zhou, G.; Hu, X.; Jian, Z. Recent advances in nickel mediated copolymerization of olefin with polar monomers. Coord. Chem. Rev. 2021, 435, 213802–213818. [Google Scholar] [CrossRef]
  4. De, P.; Faust, R. Living carbocationic polymerization of p-methoxystyrene using p-methoxystyrene hydrochloride/SnBr4 initiating system: Determination of the absolute rate constant of propagation for ion pairs. Macromolecules 2004, 37, 7930–7937. [Google Scholar] [CrossRef]
  5. Kojima, K.; Sawamoto, M.; Higashimura, T. Living cationic polymerization of p-methoxystyrene by the hydrogen iodide/zinc iodide and hydrogen iodide/iodine initiating systems: Effects of tetrabutylammonium halides in a polar solvent. Macromolecules 1990, 23, 948–953. [Google Scholar] [CrossRef]
  6. Kawamura, T.; Uryu, T.; Matsuzaki, K. Stereoregularity of polystyrene derivatives, 1. poly(methylstyrene)s and poly-(methoxystyrene)s obtained with ziegler catalyst, cationic catalyst, or radical initiators. Makromol. Chem. 1982, 183, 125–141. [Google Scholar] [CrossRef]
  7. Iio, K.; Kobayashi, K.; Matsunaga, M. Radical polymerization of allyl alcohol and allyl acetate. Polym. Adv. Technol. 2007, 18, 953–958. [Google Scholar] [CrossRef]
  8. Chen, M.; Chen, C.L. Direct and tandem routes for the copolymerization of ethylene with polar functionalized internal olefins. Angew. Chem., Int. Ed. 2020, 59, 1206–1210. [Google Scholar] [CrossRef]
  9. Mitsushige, Y.; Yasuda, H.; Carrow, B.P.; Ito, S.; Kobayashi, M.; Tayano, T.; Watanabe, Y.; Okuno, Y.; Hayashi, S.; Kuroda, J.; et al. Methylene-bridged bisphosphine monoxide ligands for palladium-catalyzed copolymerization of ethylene and polar monomers. ACS Macro Lett. 2018, 7, 305–311. [Google Scholar] [CrossRef]
  10. Ota, Y.; Ito, S.; Kobayashi, M.; Kitade, S.; Sakata, K.; Tayano, T.; Nozaki, K. Crystalline isotactic polar polypropylene from the palladium-catalyzed copolymerization of propylene and polar monomers. Angew. Chem. Int. Ed. 2016, 55, 7505–7509. [Google Scholar] [CrossRef]
  11. Zhang, Y.; Wang, C.; Mecking, S.; Jian, Z. Ultrahigh branching of main-chain-functionalized polyethylenes by inverted insertion selectivity. Angew. Chem. Int. Ed. 2020, 59, 14296–14302. [Google Scholar] [CrossRef]
  12. Chen, J.; Gao, Y.; Marks, T.J. Early transition metal catalysis for olefin-polar monomer copolymerization. Angew. Chem. Int. Ed. 2020, 59, 14726–14735. [Google Scholar] [CrossRef] [PubMed]
  13. Keyes, A.; Basbug Alhan, H.E.; Ordonez, E.; Ha, U.; Beezer, D.B.; Dau, H.; Liu, Y.S.; Tsogtgerel, E.; Jones, G.R.; Harth, E. Olefins and vinyl polar monomers: Bridging the gap for next generation materials. Angew. Chem. Int. Ed. 2019, 58, 12370–12391. [Google Scholar] [CrossRef] [PubMed]
  14. Yuan, S.F.; Yan, Y.; Solan, G.A.; Ma, Y.; Sun, W.H. Recent advancements in N-ligated group 4 molecular catalysts for the (co)polymerization of ethylene. Coord. Chem. Rev. 2020, 411, 213254. [Google Scholar] [CrossRef]
  15. Wang, Y.; Lai, J.; Gao, R.; Gou, Q.; Li, B.; Zheng, G.; Guo, Z. Recent advances in nickel catalysts with industrial exploitability for copolymerization of ethylene with polar monomers. Polymers 2024, 16, 1676. [Google Scholar] [CrossRef] [PubMed]
  16. Xiao, X.; Zheng, H.; Gao, H.; Cheng, Z.; Feng, C.; Yang, J.; Gao, H. Recent advances in synthesis of non-alternating polyketone generated by copolymerization of carbon monoxide and ethylene. Int. J. Mol. Sci. 2024, 25, 1348. [Google Scholar] [CrossRef]
  17. Xu, M.; Yu, F.; Li, P.; Xu, G.; Zhang, S.; Wang, F. Enhancing chain initiation efficiency in the cationic allyl-nickel catalyzed (co)polymerization of ethylene and methyl acrylate. Inorg. Chem. 2020, 59, 4475–4482. [Google Scholar] [CrossRef]
  18. Wu, Q.; Wang, W.; Xu, G.; Pang, W.; Li, Y.; Tan, C.; Wang, F. Bulky iminophosphine-based nickel and palladium catalysts bearing 2,6-dibenzhydryl groups for ethylene oligo-/polymerization. Appl. Organomet. Chem. 2020, 34, 5428. [Google Scholar] [CrossRef]
  19. Guironnet, D.; Roesle, P.; Runzi, T.; Gottker Schnetmann, I.; Mecking, S. Insertion polymerization of acrylate. J. Am. Chem. Soc. 2009, 131, 422–423. [Google Scholar] [CrossRef]
  20. Jian, Z.; Mecking, S. Insertion homo- and copolymerization of diallyl ether. Angew. Chem. Int. Ed. 2015, 54, 15845–15849. [Google Scholar] [CrossRef]
  21. Saki, Z.; D’Auria, I.; Dall’anese, A.; Milani, B.; Pellecchia, C. Copolymerization of ethylene and methyl acrylate by pyridylimino Ni(II) catalysts affording hyperbranched poly(ethylene-co-methyl acrylate)s with tunable structures of the ester groups. Macromolecules 2020, 53, 9294–9305. [Google Scholar] [CrossRef]
  22. Liao, G.; Xiao, Z.; Chen, X.; Du, C.; Zhong, L.; Cheung, C.S.; Gao, H. Fast and regioselective polymerization of para-alkoxystyrene by palladium catalysts for precision production of high-molecular weight polystyrene derivatives. Macromolecules 2020, 53, 256–266. [Google Scholar] [CrossRef]
  23. Lu, T.; Chen, Q. Independent gradient model based on hirshfeld partition: A new method for visual study of interactions in chemical systems. J. Comput. Chem. 2022, 43, 539–555. [Google Scholar] [CrossRef] [PubMed]
  24. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  25. Mitoraj, M.P.; Michalak, A.; Ziegler, T. A combined charge and energy decomposition scheme for bond analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
  26. Bondi, A. Van der waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
  27. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  28. Lee, C.; Yang, W.; Parr, R.G. Development of the colle salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter Mater. Phys. 1988, 37, 785–789. [Google Scholar] [CrossRef]
  29. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and accurate Ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  30. Huang, W.; Xi, Y.; Pan, D.; Fan, L.; Fang, K.; Huang, G.; Chen, Y. Palladium-catalyzed enantioselective multicomponent cross-coupling of trisubstituted olefins. J. Am. Chem. Soc. 2024, 146, 16892–16901. [Google Scholar] [CrossRef]
  31. Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
  32. Uchikura, T.; Kato, S.; Makino, Y.; Fujikawa, M.J.; Yamanaka, M.; Akiyama, T. Chiral phosphoric acid-palladium(II) complex catalyzed asymmetric desymmetrization of biaryl compounds by C(sp3)-H activation. J. Am. Chem. Soc. 2023, 145, 15906–15911. [Google Scholar] [CrossRef] [PubMed]
  33. Ehlers, A.W.; Böhme, M.; Dapprich, S.; Gobbi, A.; Höllwarth, A.; Jonas, V.; Köhler, K.F.; Stegmann, R.; Veldkamp, A.; Frenking, G. A set of f-polarization functions for pseudo-potential basis sets of the transition metals Sc-Cu, Y-Ag and La-Au. Chem. Phys. Lett. 1993, 208, 111–114. [Google Scholar] [CrossRef]
  34. Fukui, K. The path of chemical reactions-the IRC approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
  35. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B. 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
  36. Ni, H.Q.; Karunananda, M.K.; Zeng, T.; Yang, S.; Liu, Z.; Houk, K.N.; Liu, P.; Engle, K.M. Redox-paired alkene difunctionalization enables skeletally divergent synthesis. J. Am.Chem. Soc. 2023, 145, 12351–12359. [Google Scholar] [CrossRef]
  37. Ni, H.Q.; Alturaifi, T.M.; Rodphon, W.; Scherschel, N.F.; Yang, S.; Wang, F.; Engle, K.M. Anti-selective cyclopropanation of nonconjugated alkenes with diverse pronucleophiles via directed nucleopalladation. J. Am. Chem. Soc. 2024, 146, 24503–24514. [Google Scholar] [CrossRef]
  38. Andrae, D.; Haüβermann, U.; Dolg, M.; Stoll, H.; Preuβ, H. Energy-adjusted ab initio pseudopotentials for the 2nd and 3rd row transition-elements. Theor. Chim. Acta. 1990, 77, 123–141. [Google Scholar] [CrossRef]
  39. Zhang, P.; Guo, C.Q.; Yao, W.; Lu, C.J.; Li, Y.Z.; Paton, R.S.; Liu, R.R. Pd-catalyzed asymmetric amination of enamines: Expedient synthesis of structurally diverse N-C atropisomers. ACS Catal. 2023, 13, 7680–7690. [Google Scholar] [CrossRef]
  40. Biosca, M.; Saltó, J.; Magre, M.; Norrby, P.-O.; Pàmies, O.; Diéguez, M. An Improved Class of Phosphite-Oxazoline Ligands forPd-Catalyzed Allylic Substitution Reactions. ACS Catal. 2019, 9, 6033–6048. [Google Scholar] [CrossRef]
  41. Yan, M.; Kang, X.; Li, S.; Xu, X.; Luo, Y.; He, S.; Chen, C. Mechanistic Studies on Nickel-Catalyzed Ethylene Polymerization: Ligand Effects and Quantitative Structure–Activity Relationship Model. Organometallics 2022, 41, 3212–3218. [Google Scholar] [CrossRef]
  42. Seo, S.; Shin, T.; Choi, I.; Kim, H. Origin of Stereoselectivity in Pd-Catalyzed Asymmetric Allylic Substitutions with Trost-Type Mixed Bidentate Phosphorus Ligands. ACS Catal. 2024, 14, 11113–11120. [Google Scholar] [CrossRef]
  43. Legault, C.Y. CYLView, Version 1.0b; Université de Sherbrooke: Sherbrooke, QC, Canada, 2020. Available online: http://www.cylview.org (accessed on 11 April 2023).
  44. Liu, C.; Qin, Z.X.; Ji, C.L.; Hong, X.; Szostak, M. Highly-chemoselective step-down reduction of carboxylic acids to aromatic hydrocarbons via palladium catalysis. Chem. Sci. 2019, 10, 5736–5742. [Google Scholar] [CrossRef] [PubMed]
  45. Fan, H.; Kang, X.; Dai, S. Stable ultrahighly branched polyethylene synthesis via externally robust chain-walking polymerization. ACS Catal. 2024, 14, 13531–13541. [Google Scholar] [CrossRef]
  46. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
Inorganics 12 00315 sch001
Scheme 1. Polymerization of para-methoxystyrene/styrene catalyzed by palladium complexes.
Scheme 1. Polymerization of para-methoxystyrene/styrene catalyzed by palladium complexes.
Inorganics 12 00315 sch001
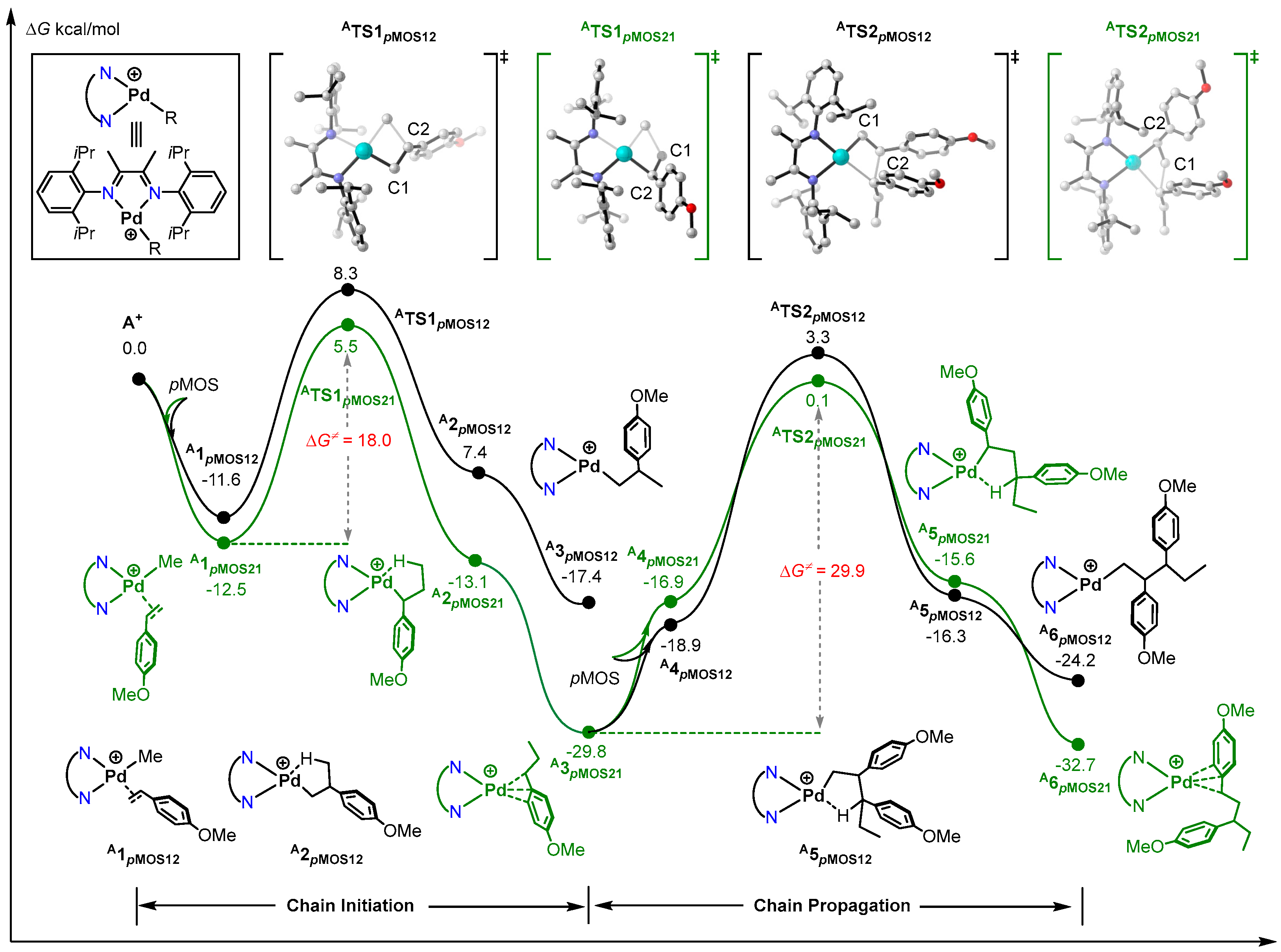
Inorganics 12 00315 g001
Figure 1. Calculated Gibbs free energy profiles for insertion of pMOS based on A+ at the chain initiation and chain propagation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively. The transition state structures were denoted by (≠).
Figure 1. Calculated Gibbs free energy profiles for insertion of pMOS based on A+ at the chain initiation and chain propagation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively. The transition state structures were denoted by (≠).
Inorganics 12 00315 g001
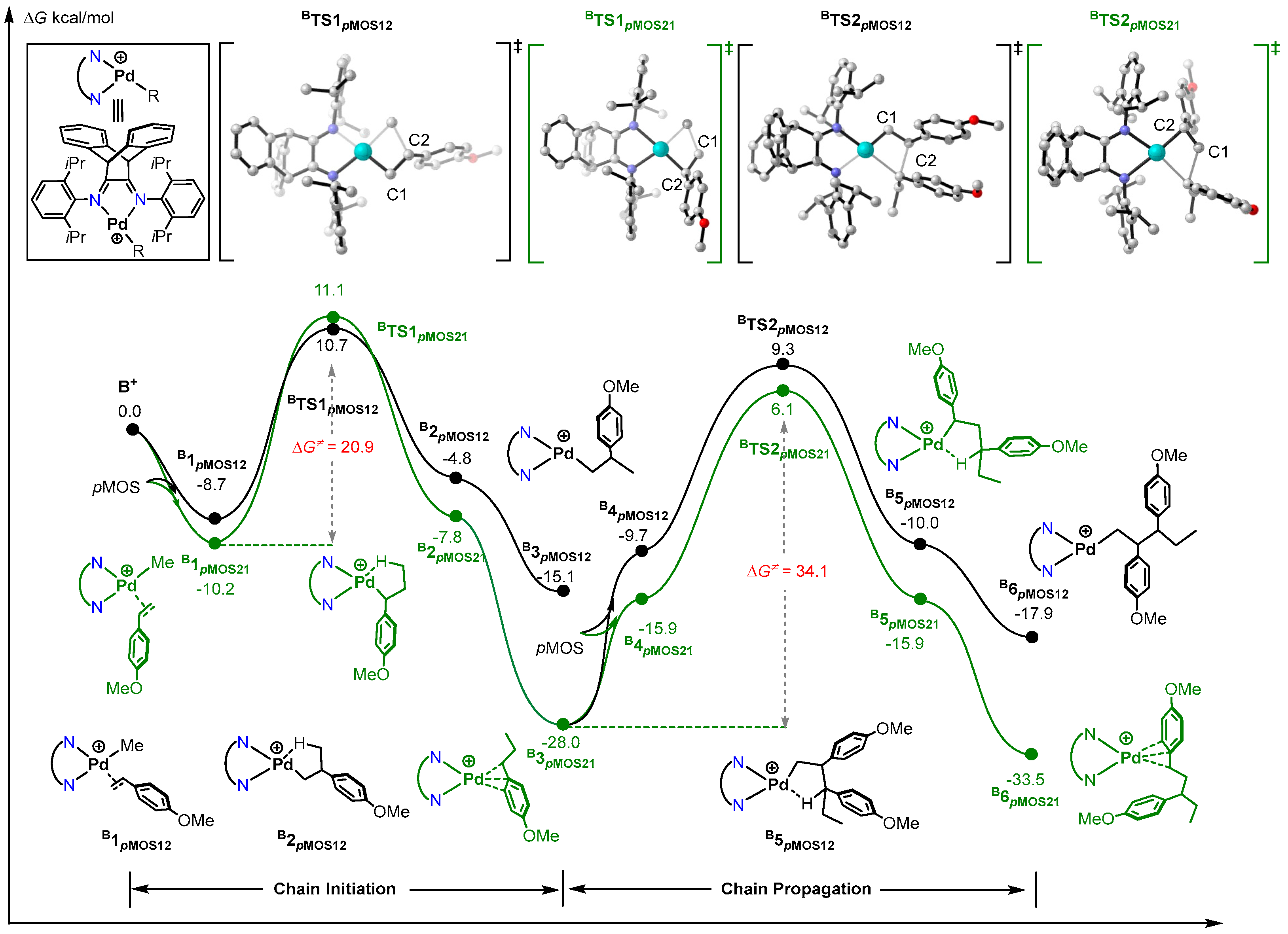
Inorganics 12 00315 g002
Figure 2. Calculated Gibbs free energy profiles for insertion of pMOS based on B+ at the chain initiation and chain propagation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively. The transition state structures were denoted by (≠).
Figure 2. Calculated Gibbs free energy profiles for insertion of pMOS based on B+ at the chain initiation and chain propagation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively. The transition state structures were denoted by (≠).
Inorganics 12 00315 g002
Inorganics 12 00315 g003
Figure 3. Calculated Gibbs free energy profiles for the B+ mediated competitive pathways for the chain propagation and the chain transfer of pMOS based on B3pMOS12 (in kcal/mol). The 1,2- and 2,1-insertion pathways in the chain propagation are in black and green, respectively. The dissociative associative and associative pathways in the chain transfer are in gray and orange, respectively. The transition state structures were denoted by (≠).
Figure 3. Calculated Gibbs free energy profiles for the B+ mediated competitive pathways for the chain propagation and the chain transfer of pMOS based on B3pMOS12 (in kcal/mol). The 1,2- and 2,1-insertion pathways in the chain propagation are in black and green, respectively. The dissociative associative and associative pathways in the chain transfer are in gray and orange, respectively. The transition state structures were denoted by (≠).
Inorganics 12 00315 g003
Inorganics 12 00315 g004
Figure 4. The structures, independent gradient model based on Hirshfeld partition, and Extended Transition State-Natural Orbitals for Chemical Valence analysis for (a) B3pMOS12 and (b) B3pMOS21. Distances, NBO atomic charges, and the |Q|/S values are shown in black, blue, and red, respectively. (distances in Å).
Figure 4. The structures, independent gradient model based on Hirshfeld partition, and Extended Transition State-Natural Orbitals for Chemical Valence analysis for (a) B3pMOS12 and (b) B3pMOS21. Distances, NBO atomic charges, and the |Q|/S values are shown in black, blue, and red, respectively. (distances in Å).
Inorganics 12 00315 g004
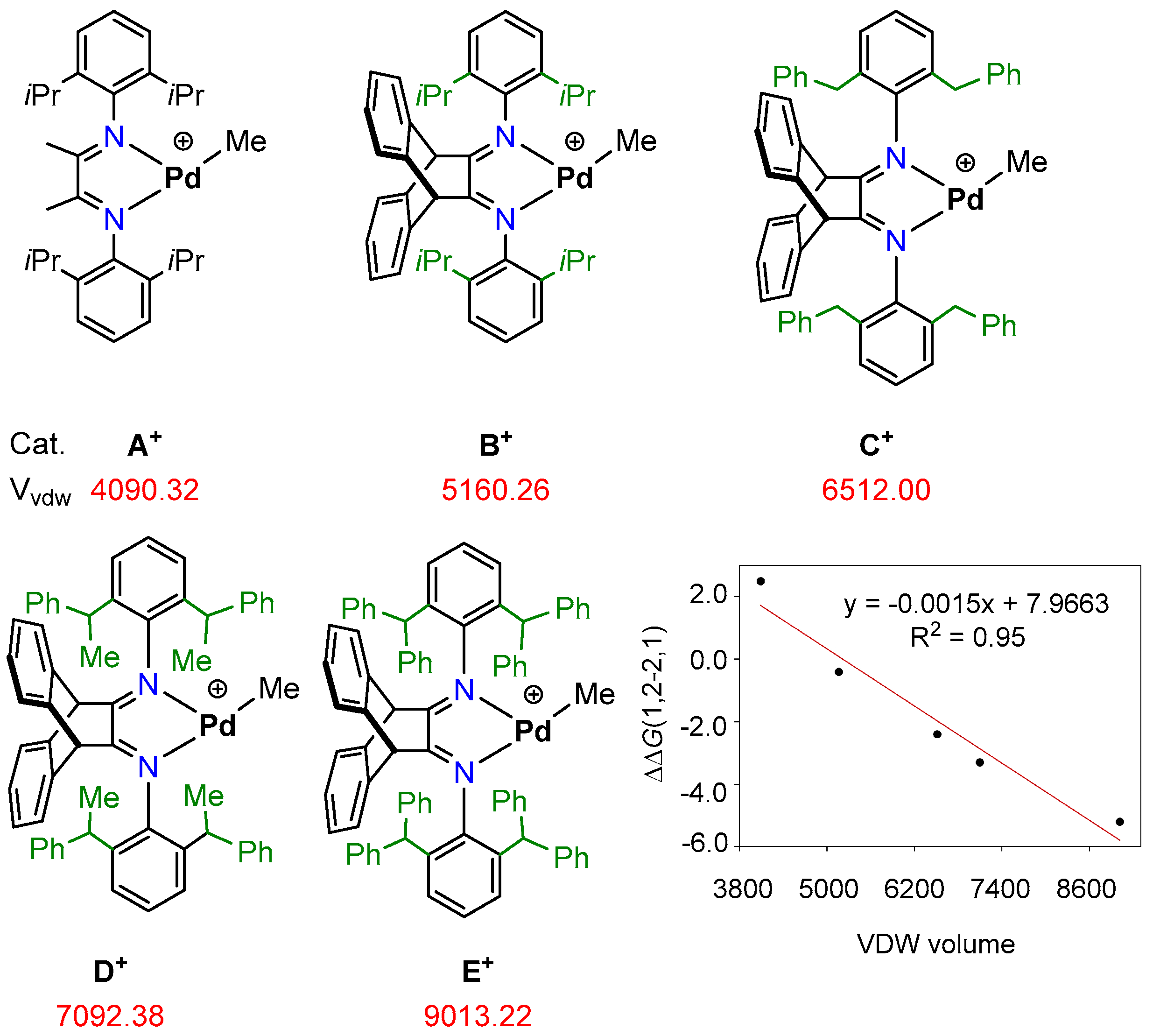
Inorganics 12 00315 g005
Figure 5. The new designed catalysts; the VDW volumes are given in Bohr3(red). The R2 values between the VDW volume (Bohr3) of catalysts A+, B+, or C+–E+ and their corresponding insertion energy gaps (kcal/mol).
Figure 5. The new designed catalysts; the VDW volumes are given in Bohr3(red). The R2 values between the VDW volume (Bohr3) of catalysts A+, B+, or C+–E+ and their corresponding insertion energy gaps (kcal/mol).
Inorganics 12 00315 g005
Inorganics 12 00315 g006
Figure 6. Calculated Gibbs free energy profiles for insertion of styrene based on B+ at the chain initiation and chain propagation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively. The transition state structures were denoted by (≠).
Figure 6. Calculated Gibbs free energy profiles for insertion of styrene based on B+ at the chain initiation and chain propagation stage (in kcal/mol). The 1,2- and 2,1-insertion pathways are in black and green, respectively. The transition state structures were denoted by (≠).
Inorganics 12 00315 g006
Table 1. Gibbs free energies (kcal/mol) for reactions of pMOS insertion for catalysts A+, B+, and C+–E+ at the chain initiation stage.
Table 1. Gibbs free energies (kcal/mol) for reactions of pMOS insertion for catalysts A+, B+, and C+–E+ at the chain initiation stage.
Catalysts1pMOS21TS1pMOS12 (TS1pMOS21)P12 (P21)∆∆P∆G (1,2-)∆G (2,1-)∆∆G (1,2–2,1)
A+−12.58.3 (5.5)−17.4 (−29.8)12.420.518.02.5
B+−10.210.7 (11.1)−15.1 (−28.0)12.920.921.3−0.4
C+−15.44.5 (6.9)−20.6 (−30.5)9.919.922.3−2.4
D+−6.213.3 (16.7)−10.3 (−17.1)6.819.522.8−3.3
E+−8.511.3 (16.5)−14.4 (−22.8)8.319.825.0−5.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhu, L.; Luo, Y.; Wen, X.; Zhang, W.; Zhou, G. Theoretical Investigations of Para-Methoxystyrene/Styrene Polymerization Catalyzed by Cationic Methyl- and Dibenzobarrelene-Based α-Diimine Palladium Complexes. Inorganics 2024, 12, 315. https://doi.org/10.3390/inorganics12120315

AMA Style

Zhu L, Luo Y, Wen X, Zhang W, Zhou G. Theoretical Investigations of Para-Methoxystyrene/Styrene Polymerization Catalyzed by Cationic Methyl- and Dibenzobarrelene-Based α-Diimine Palladium Complexes. Inorganics. 2024; 12(12):315. https://doi.org/10.3390/inorganics12120315

Chicago/Turabian Style

Zhu, Ling, Yi Luo, Xin Wen, Wenzhen Zhang, and Guangli Zhou. 2024. "Theoretical Investigations of Para-Methoxystyrene/Styrene Polymerization Catalyzed by Cationic Methyl- and Dibenzobarrelene-Based α-Diimine Palladium Complexes" Inorganics 12, no. 12: 315. https://doi.org/10.3390/inorganics12120315

APA Style

Zhu, L., Luo, Y., Wen, X., Zhang, W., & Zhou, G. (2024). Theoretical Investigations of Para-Methoxystyrene/Styrene Polymerization Catalyzed by Cationic Methyl- and Dibenzobarrelene-Based α-Diimine Palladium Complexes. Inorganics, 12(12), 315. https://doi.org/10.3390/inorganics12120315

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop