Phase Relations in the Pseudo-Binary BiFeO3–EuFeO3 System in the Subsolidus Region Derived from X-Ray Diffraction Data—A Machine Learning Approach
Abstract
1. Introduction
- (i)
- In the (left-hand side) composition region having 50 mol% Fe2O3 or less, and temperatures between 1000 and 1450 °C, crystallization of a mixture of B-type Eu2O3 and perovskite-type EuFeO3 occurs;
- (ii)
- The region delimited by 50 and 62.5 mol% Fe2O3 and temperatures between 1000 and 1450 °C is characterized by the crystallization of a mixture of perovskite-type EuFeO3 and garnet type Eu3Fe5O12;
- (iii)
- In the region delimited by 62.5 and 100 mol% Fe2O3, at temperatures between 1000 and 1400 °C, the crystallization of garnet type Eu3Fe5O12 and corundum-type phase (α) can be observed; at higher temperatures for the same composition range, the corundum-type phase suffers a polymorphic transition to the spinel structure.
2. Materials and Methods
2.1. Materials Processing
2.2. X-Ray Diffraction Characterization
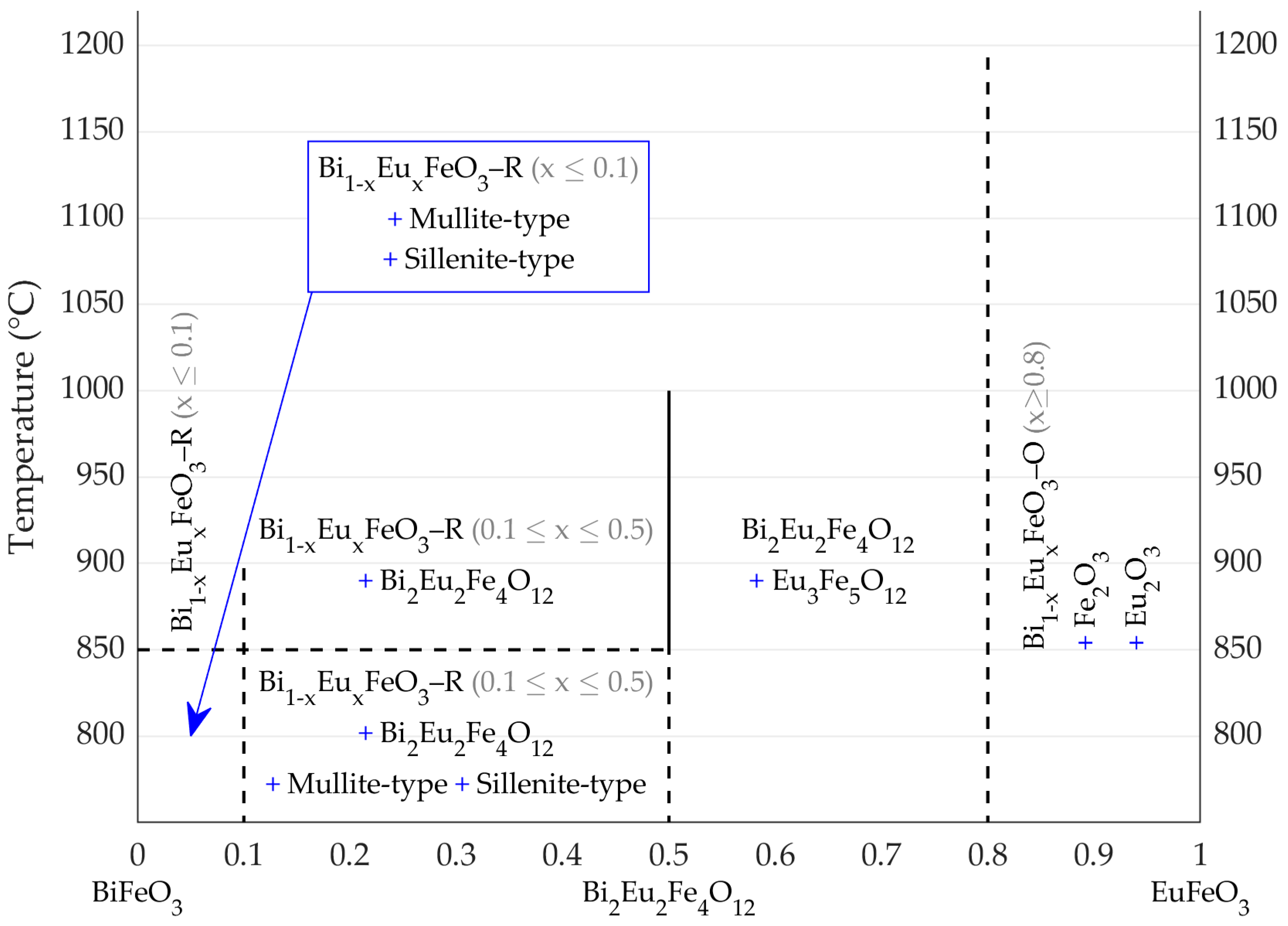
3. Results and Discussion
3.1. Automated Approach: Unsupervised Machine Learning (Clustering)
3.2. Traditional Approach
- (1)
- Bi1−xEuxFeO3–R (x < 0.1) + Mullite-type + Sillenite-type;
- (2)
- Bi1−xEuxFeO3–R (x < 0.1);
- (3)
- Bi1−xEuxFeO3–R (0.1 < x < 0.5) + Bi2Eu2Fe4O12 + Mullite-type + Sillenite-type;
- (4)
- Bi1−xEuxFeO3–R (0.1 < x < 0.5) + Bi2Eu2Fe4O12;
- (5)
- Bi2Eu2Fe4O12 + Eu3Fe5O12;
- (6)
- Bi1−xEuxFeO3–O (x ≥ 0.8) + Fe2O3 + Eu2O3.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cano, A.; Meier, D.; Trassin, M. Multiferroics: Fundamentals and Applications; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2021; ISBN 3110582139. [Google Scholar]
- Meier, D.G.; Lottermoser, T. A Short History of Multiferroics. 2020. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/2726206 (accessed on 20 October 2024).
- Grosso, B.F. New Structures and Functionalities in Multiferroic Bismuth Ferrite: First-Principles–Based Studies. 2021. Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/513311 (accessed on 20 October 2024).
- Bayaraa, T. Interplay Between the Lattice and Spin Degrees of Freedom in Magnetoelectric and Magnetic Materials; University of Arkansas: Fayetteville, AR, USA, 2021; ISBN 9798790661075. [Google Scholar]
- Bimashofer, G. Electrochemically Induced Magnetic Phase Transitions in Rare-Earth Manganese Oxides: A Case Study on LaxSryLizMnO3. Doctoral Dissertation, ETH Zurich, Zurich, Switzerland, 2021. [Google Scholar]
- Chattopadhyay, S.; Balédent, V.; Panda, S.K.; Yamamoto, S.; Duc, F.; Herrmannsdörfer, T.; Uhlarz, M.; Gottschall, T.; Mathon, O.; Wang, Z. 4 f spin driven ferroelectric-ferromagnetic multiferroicity in PrMn2O5 under a magnetic field. Phys. Rev. B 2020, 102, 94408. [Google Scholar] [CrossRef]
- Ferret, R.M. Magnetodielectric Effect and Conduction Mechanism in BFO-REMO Multiferroics. Doctoral Dissertation, University of Puerto Rico, San Juan, PR, USA, 2021. [Google Scholar]
- Smolenskii, G.A.; Bokov, V.A. Coexistence of magnetic and electric ordering in crystals. J. Appl. Phys. 1964, 35, 915–918. [Google Scholar] [CrossRef]
- Aizu, K. Possible species of “ferroelastic” crystals and of simultaneously ferroelectric and ferroelastic crystals. J. Phys. Soc. Jpn. 1969, 27, 387–396. [Google Scholar] [CrossRef]
- Schmid, H. Multi-ferroic magnetoelectrics. Ferroelectrics 1994, 162, 317–338. [Google Scholar] [CrossRef]
- Khan, H.; Ahmad, T. Perspectives and Scope of ABO3 Type Multiferroic Rare-Earth Perovskites. Chin. J. Phys. 2024, 91, 199–219. [Google Scholar] [CrossRef]
- Zhang, M.; Koval, V.; Shi, Y.; Yue, Y.; Jia, C.; Wu, J.; Viola, G.; Yan, H. Magnetoelectric coupling at microwave frequencies observed in bismuth ferrite-based multiferroics at room temperature. J. Mater. Sci. Technol. 2023, 137, 100–103. [Google Scholar] [CrossRef]
- Gupta, R.; Kotnala, R.K. A review on current status and mechanisms of room-temperature magnetoelectric coupling in multiferroics for device applications. J. Mater. Sci. 2022, 57, 12710–12737. [Google Scholar] [CrossRef]
- Haykal, A.; Fischer, J.; Akhtar, W.; Chauleau, J.-Y.; Sando, D.; Finco, A.; Godel, F.; Birkhölzer, Y.A.; Carrétéro, C.; Jaouen, N. Antiferromagnetic textures in BiFeO3 controlled by strain and electric field. Nat. Commun. 2020, 11, 1704. [Google Scholar] [CrossRef]
- NV, S.; Vinayakumar, K.B.; Nagaraja, K.K. Magnetoelectric coupling in bismuth ferrite—Challenges and perspectives. Coatings 2020, 10, 1221. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Ma, J.; Li, S.; Pan, H.; Nan, C.-W.; Lin, Y.-H. Controllable electrical, magnetoelectric and optical properties of BiFeO3 via domain engineering. Prog. Mater. Sci. 2022, 127, 100943. [Google Scholar] [CrossRef]
- Lee, J.H.; Fina, I.; Marti, X.; Kim, Y.H.; Hesse, D.; Alexe, M. Spintronic functionality of BiFeO3 domain walls. Adv. Mater. 2014, 26, 7078–7082. [Google Scholar] [CrossRef] [PubMed]
- Sando, D.; Agbelele, A.; Rahmedov, D.; Liu, J.; Rovillain, P.; Toulouse, C.; Infante, I.C.; Pyatakov, A.P.; Fusil, S.; Jacquet, E. Crafting the magnonic and spintronic response of BiFeO3 films by epitaxial strain. Nat. Mater. 2013, 12, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Yakout, S.M. Spintronics and innovative memory devices: A review on advances in magnetoelectric BiFeO3. J. Supercond. Nov. Magn. 2021, 34, 317–338. [Google Scholar] [CrossRef]
- Deka, B.; Cho, K.-H. BiFeO3-based relaxor ferroelectrics for energy storage: Progress and prospects. Materials 2021, 14, 7188. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, P.; Qiu, F.; Tang, J.; Tan, G. The role of samarium (Sm) dopant on structural, magnetic and ferroelectric properties of BiFeO3 for magnetic data storage. J. Magn. Magn. Mater. 2022, 564, 170148. [Google Scholar] [CrossRef]
- Khan, A.R.; Mustafa, G.M.; Abbas, S.K.; Atiq, S.; Saleem, M.; Ramay, S.M.; Naseem, S. Flexible ferroelectric and magnetic orders in BiFeO3/MnFe2O4 nanocomposites to steer wide range energy and data storage capability. Results Phys. 2020, 16, 102956. [Google Scholar] [CrossRef]
- Blázquez Martínez, A.; Grysan, P.; Girod, S.; Glinsek, S.; Aruchamy, N.; Biswas, P.; Guennou, M.; Granzow, T. Strain engineering of the electro-optic effect in polycrystalline BiFeO3 films. Opt. Mater. Express 2023, 13, 2061–2070. [Google Scholar] [CrossRef]
- Sando, D.; Hermet, P.; Allibe, J.; Bourderionnet, J.; Fusil, S.; Carrétéro, C.; Jacquet, E.; Mage, J.-C.; Dolfi, D.; Barthélémy, A. Linear electro-optic effect in multiferroic BiFeO3 thin films. Phys. Rev. B 2014, 89, 195106. [Google Scholar] [CrossRef]
- Ghosh, S.; Roy, S.K.; Acharya, S.; Chakrabarti, P.K.; Zurowska, M.; Dabrowski, R. Effect of multiferroic BiFeO3 nanoparticles on electro-optical and dielectric properties of a partially fluorinated orthoconic antiferroelectric liquid crystal mixture. Europhys. Lett. 2011, 96, 47003. [Google Scholar] [CrossRef]
- He, C.; Ma, Z.-J.; Sun, B.-Z.; Sa, R.-J.; Wu, K. The electronic, optical and ferroelectric properties of BiFeO3 during polarization reversal: A first principle study. J. Alloys Compd. 2015, 623, 393–400. [Google Scholar] [CrossRef]
- Zhao, J.-J.; Zhang, J.-S.; Zhang, F.; Wang, W.; He, H.-R.; Cai, W.-Y.; Wang, J. Electro-optical dual modulation on resistive switching behavior in BaTiO3/BiFeO3/TiO2 heterojunction. Chin. Phys. B 2019, 28, 126801. [Google Scholar] [CrossRef]
- Speranskaya, E.I.; Skorikov, V.M.; Rode, E.Y.; Terekhova, V.A. The phase diagram of the system bismuth oxide-ferric oxide. Bull. Acad. Sci. USSR Div. Chem. Sci. 1965, 14, 873–874. [Google Scholar] [CrossRef]
- Skinner, S. Magnetically Ordered Ferroelectric Materials. IEEE Trans. Parts Mater. Packag. 1970, 6, 68–90. [Google Scholar] [CrossRef]
- Selbach, S.M.; Einarsrud, M.A.; Grande, T. On the thermodynamic stability of BiFeO3. Chem. Mater. 2009, 21, 169–173. [Google Scholar] [CrossRef]
- Silva, J.; Reyes, A.; Esparza, H.; Camacho, H.; Fuentes, L. BiFeO3: A review on synthesis, doping and crystal structure. Integr. Ferroelectr. 2011, 126, 47–59. [Google Scholar] [CrossRef]
- Surdu, V.-A.; Trușcă, R.D.; Vasile, B.Ș.; Oprea, O.C.; Tanasă, E.; Diamandescu, L.; Andronescu, E.; Ianculescu, A.C. Bi1−xEuxFeO3 Powders: Synthesis, Characterization, Magnetic and Photoluminescence Properties. Nanomaterials 2019, 9, 1465. [Google Scholar] [CrossRef]
- Castillo, M.E.; Shvartsman, V.V.; Gobeljic, D.; Gao, Y.; Landers, J.; Wende, H.; Lupascu, D.C. Effect of particle size on ferroelectric and magnetic properties of BiFeO3 nanopowders. Nanotechnology 2013, 24, 355701. [Google Scholar] [CrossRef] [PubMed]
- Dhir, G.; Uniyal, P.; Verma, N.K. Effect of particle size on magnetic and dielectric properties of nanoscale Dy-doped BiFeO3. J. Supercond. Nov. Magn. 2014, 27, 1569–1577. [Google Scholar] [CrossRef]
- Yotburut, B.; Thongbai, P.; Yamwong, T.; Maensiri, S. Synthesis and characterization of multiferroic Sm-doped BiFeO3 nanopowders and their bulk dielectric properties. J. Magn. Magn. Mater. 2017, 437, 51–61. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.F.; Wu, P.; Hai, X.; Wang, S.Y.; Liu, G.Y.; Rao, G.H. Unusual magnetic behaviors and electrical properties of Nd-doped BiFeO 3 nanoparticles calcined at different temperatures. J. Nanopart. Res. 2014, 16, 2205. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Qi, J.; Tian, Y.; Zhang, J.; Wei, M.; Liu, Y.; Yang, J. Structural, magnetic and impedance spectroscopy properties of Ho3+ modified BiFeO3 multiferroic thin film. J. Mater. Sci. Mater. Electron. 2019, 30, 2942–2952. [Google Scholar] [CrossRef]
- Freitas, V.F.; Grande, H.L.C.; de Medeiros, S.N.; Santos, I.A.; Cótica, L.F.; Coelho, A.A. Structural, microstructural and magnetic investigations in high-energy ball milled BiFeO3 and Bi0.95Eu0.05FeO3 powders. J. Alloys Compd. 2008, 461, 48–52. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Z.; Yin, X.; Wang, F.; Gu, W.; Fu, Z.; Lu, Y. Enhanced magnetism and light absorption of Eu-doped BiFeO3. J. Mater. Sci. Mater. Electron. 2016, 27, 7079–7083. [Google Scholar] [CrossRef]
- Liu, J.; Fang, L.; Zheng, F.; Ju, S.; Shen, M. Enhancement of magnetization in Eu doped BiFeO3 nanoparticles. Appl. Phys. Lett. 2009, 95, 2–5. [Google Scholar] [CrossRef]
- Muneeswaran, M.; Lee, S.H.; Kim, D.H.; Jung, B.S.; Chang, S.H.; Jang, J.-W.; Choi, B.C.; Jeong, J.H.; Giridharan, N.V.; Venkateswaran, C. Structural, vibrational, and enhanced magneto-electric coupling in Ho-substituted BiFeO3. J. Alloys Compd. 2018, 750, 276–285. [Google Scholar] [CrossRef]
- Reddy, B.P.; Sekhar, M.C.; Prakash, B.P.; Suh, Y.; Park, S.-H. Photocatalytic, magnetic, and electrochemical properties of La doped BiFeO3 nanoparticles. Ceram. Int. 2018, 44, 19512–19521. [Google Scholar] [CrossRef]
- Reshak, A.H.; Tlemçani, T.S.; El Bahraoui, T.; Taibi, M.; Plucinski, K.J.; Belayachi, A.; Abd-Lefdil, M.; Lis, M.; Alahmed, Z.A.; Kamarudin, H. Characterization of multiferroic Bi0.8RE0.2FeO3 powders (RE = Nd3+, Eu3+) grown by the sol–gel method. Mater. Lett. 2015, 139, 104–107. [Google Scholar] [CrossRef]
- Vijayasundaram, S.V.; Suresh, G.; Mondal, R.A.; Kanagadurai, R. Composition-driven enhanced magnetic properties and magnetoelectric coupling in Gd substituted BiFeO3 nanoparticles. J. Magn. Magn. Mater. 2016, 418, 30–36. [Google Scholar] [CrossRef]
- Xu, X.; Guoqiang, T.; Huijun, R.; Ao, X. Structural, electric and multiferroic properties of Sm-doped BiFeO3 thin films prepared by the sol–gelprocess. Ceram. Int. 2013, 39, 6223–6228. [Google Scholar] [CrossRef]
- Karpinsky, D.V.; Troyanchuk, I.O.; Mantytskaja, O.S.; Chobot, G.M.; Sikolenko, V.V.; Efimov, V.; Tovar, M. Magnetic and piezoelectric properties of the Bi1−xLaxFeO3 system near the transition from the polar to antipolar phase. Phys. Solid State 2014, 56, 701–706. [Google Scholar] [CrossRef]
- Rusakov, D.A.; Abakumov, A.M.; Yamaura, K.; Belik, A.A.; Van Tendeloo, G.; Takayama-Muromachi, E. Structural evolution of the BiFeO3−LaFeO3 system. Chem. Mater. 2011, 23, 285–292. [Google Scholar] [CrossRef]
- Karpinsky, D.V.; Troyanchuk, I.O.; Tovar, M.; Sikolenko, V.; Efimov, V.; Kholkin, A.L. Evolution of crystal structure and ferroic properties of La-doped BiFeO3 ceramics near the rhombohedral-orthorhombic phase boundary. J. Alloys Compd. 2013, 555, 101–107. [Google Scholar] [CrossRef]
- Troyanchuk, I.O.; Bushinsky, M.V.; Karpinsky, D.V.; Mantytskaya, O.S.; Fedotova, V.V.; Prochnenko, O.I. Structural transformations and magnetic properties of Bi1−xLnxFeO3 (Ln = La, Nd, Eu) multiferroics. Phys. Status Solidi Basic Res. 2009, 246, 1901–1907. [Google Scholar] [CrossRef]
- Al-Haj, M. X-ray diffraction and magnetization studies of BiFeO3 multiferroic compounds substituted by Sm3+, Gd3+, Ca2+. Cryst. Res. Technol. J. Exp. Ind. Crystallogr. 2010, 45, 89–93. [Google Scholar] [CrossRef]
- Khomchenko, V.A.; Kiselev, D.A.; Bdikin, I.K.; Shvartsman, V.V.; Borisov, P.; Kleemann, W.; Vieira, J.M.; Kholkin, A.L. Crystal structure and multiferroic properties of Gd-substituted BiFeO3. Appl. Phys. Lett. 2008, 93, 262905. [Google Scholar] [CrossRef]
- Xu, J.M.; Wang, G.M.; Wang, H.X.; Ding, D.F.; He, Y. Synthesis and weak ferromagnetism of Dy-doped BiFeO3 powders. Mater. Lett. 2009, 63, 855–857. [Google Scholar] [CrossRef]
- Pattanayak, S.; Choudhary, R.N.P.; Das, P.R.; Shannigrahi, S.R. Effect of Dy-substitution on structural, electrical and magnetic properties of multiferroic BiFeO3 ceramics. Ceram. Int. 2014, 40, 7983–7991. [Google Scholar] [CrossRef]
- Arnold, D.C. Composition-driven structural phase transitions in rare-earth-doped BiFeO3 ceramics: A review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 62–82. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Deng, S.; Liu, H.; Li, T.; Song, Y.; Bai, H.; Zhu, T.; Wang, J.; Wang, H. Significantly Enhanced Room-Temperature Ferromagnetism in Multiferroic EuFeO3−δ Thin Films. Nano Lett. 2023, 23, 1273–1279. [Google Scholar] [CrossRef]
- Pilo, J.; Arévalo-López, E.P.; Cervantes, J.M.; Escamilla, R.; Romero, M. DFT + U study of the structural, electronic and magnetic properties in the EuCoO3, EuFeO3, and EuCo0.5Fe0.5O3 type perovskite compounds. J. Magn. Magn. Mater. 2024, 589, 171543. [Google Scholar] [CrossRef]
- Schneider, S.J.; Roth, R.S.; Waring, J.L. Solid state reactions involving oxides of trivalent cations. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1961, 65, 345. [Google Scholar] [CrossRef] [PubMed]
- EL-Bey, A.; Dinia, S.; El Bahraoui, T.; Boudad, L.; Taibi, M.; Belayachi, A.; Abd-Lefdil, M. Phase transitions in multiferroic Bi1−xEuxFeO3 synthesized by sol-gel method. Phys. Scr. 2023, 98, 025015. [Google Scholar] [CrossRef]
- Dai, H.; Li, T.; Xue, R.; Chen, Z.; Xue, Y. Effects of europium substitution on the microstructure and electric properties of bismuth ferrite ceramics. J. Supercond. Nov. Magn. 2012, 25, 109–115. [Google Scholar] [CrossRef]
- Sati, P.C.; Kumar, M.; Chhoker, S.; Jewariya, M. Influence of Eu substitution on structural, magnetic, optical and dielectric properties of BiFeO3 multiferroic ceramics. Ceram. Int. 2015, 41, 2389–2398. [Google Scholar] [CrossRef]
- Cuervo-Farfán, J.A.; Vargas, C.A.P.; Viana, D.S.F.; Milton, F.P.; Garcia, D.; Téllez, D.A.L.; Roa-Rojas, J. Structural, magnetic, dielectric and optical properties of the Eu2Bi2Fe4O12 bismuth-based low-temperature biferroic. J. Mater. Sci. Mater. Electron. 2018, 29, 20942–20951. [Google Scholar] [CrossRef]
- Uniyal, P.; Yadav, K.L. Room temperature multiferroic properties of Eu doped BiFeO3. J. Appl. Phys. 2009, 105, 3–6. [Google Scholar] [CrossRef]
- Durga Rao, T.; Ranjith, R.; Asthana, S. Enhanced magnetization and improved insulating character in Eu substituted BiFeO3. J. Appl. Phys. 2014, 115, 124110. [Google Scholar] [CrossRef]
- Zhang, X.; Sui, Y.; Wang, X.; Wang, Y.; Wang, Z. Effect of Eu substitution on the crystal structure and multiferroic properties of BiFeO3. J. Alloys Compd. 2010, 507, 157–161. [Google Scholar] [CrossRef]
- Surdu, V.-A.; Győrgy, R. X-ray diffraction data analysis by machine learning methods—A review. Appl. Sci. 2023, 13, 9992. [Google Scholar] [CrossRef]
- Rachinger, W.A. A Correction for the α1 α2 Doublet in the Measurement of Widths of X-ray Diffraction Lines. J. Sci. Instrum. 1948, 25, 254. [Google Scholar] [CrossRef]
- Kelley, L.A.; Gardner, S.P.; Sutcliffe, M.J. An automated approach for clustering an ensemble of NMR-derived protein structures into conformationally related subfamilies. Protein Eng. Des. Sel. 1996, 9, 1063–1065. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Rebaza, A.V.G.; Toro, C.E.D.; Chanduví, H.H.M.; Téllez, D.A.L.; Roa-Rojas, J. Thermodynamic evidence of the ferroelectric Berry phase in europium-based ferrobismuthite Eu2Bi2Fe4O12. J. Alloys Compd. 2021, 884, 161114. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Die gesetze der krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
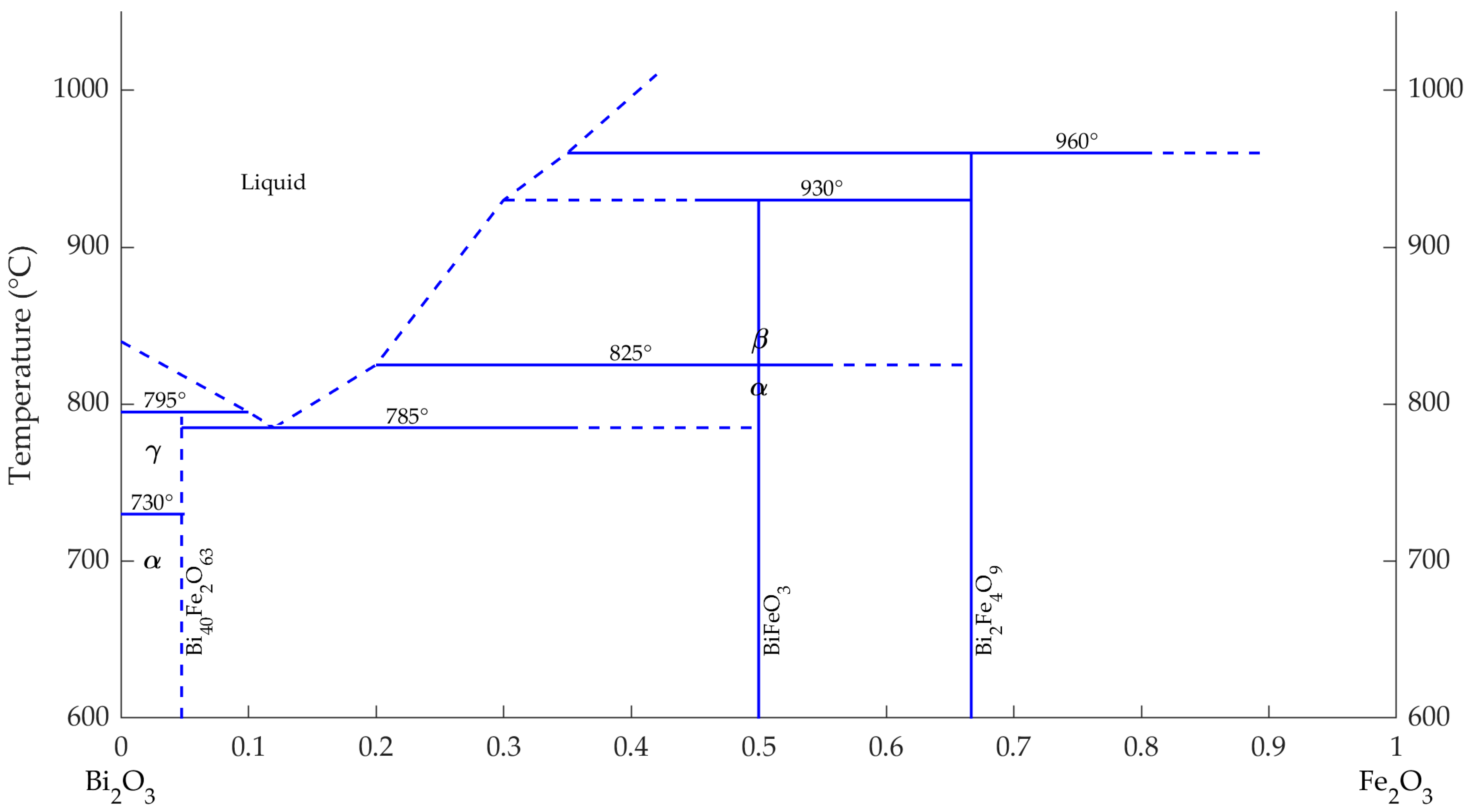
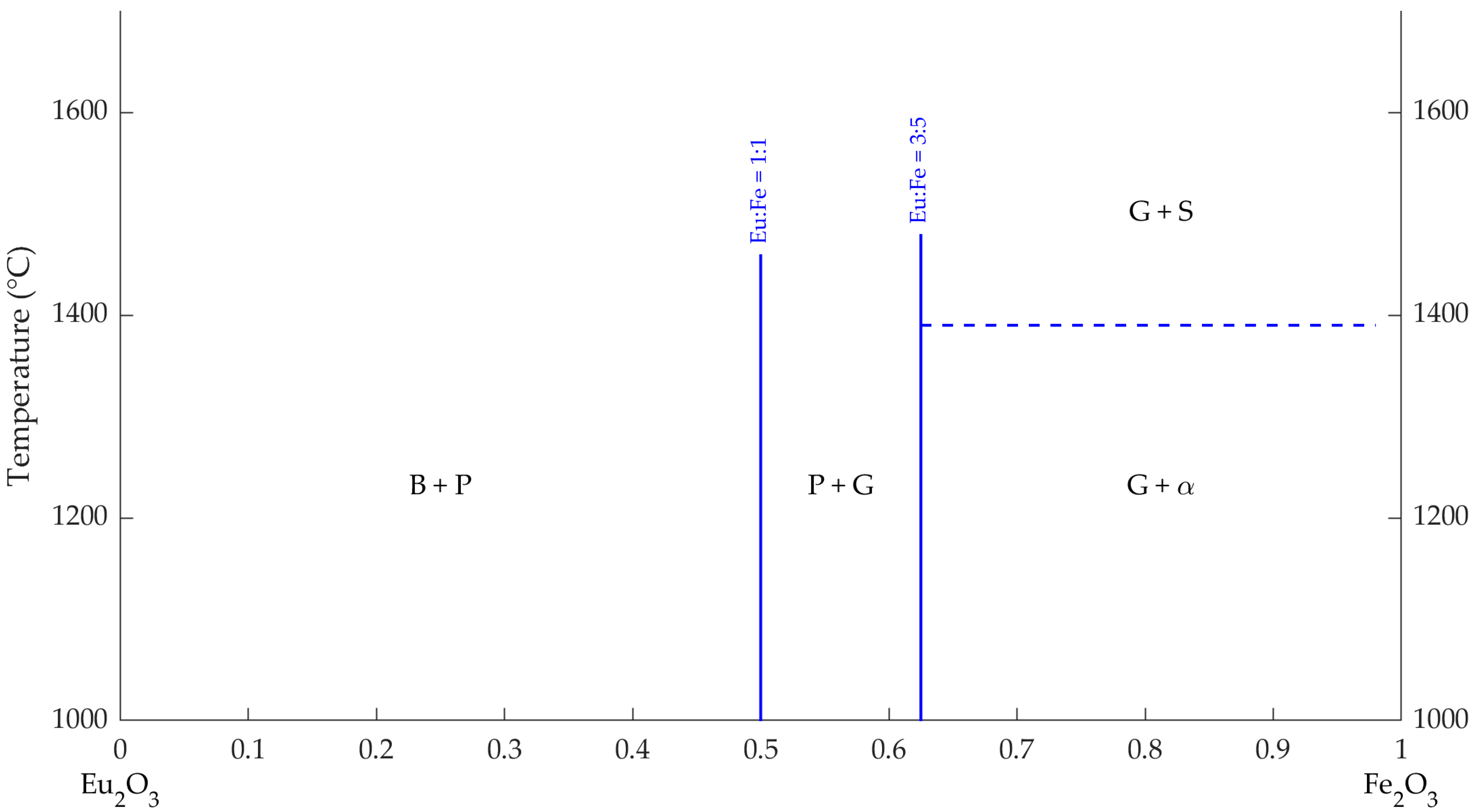
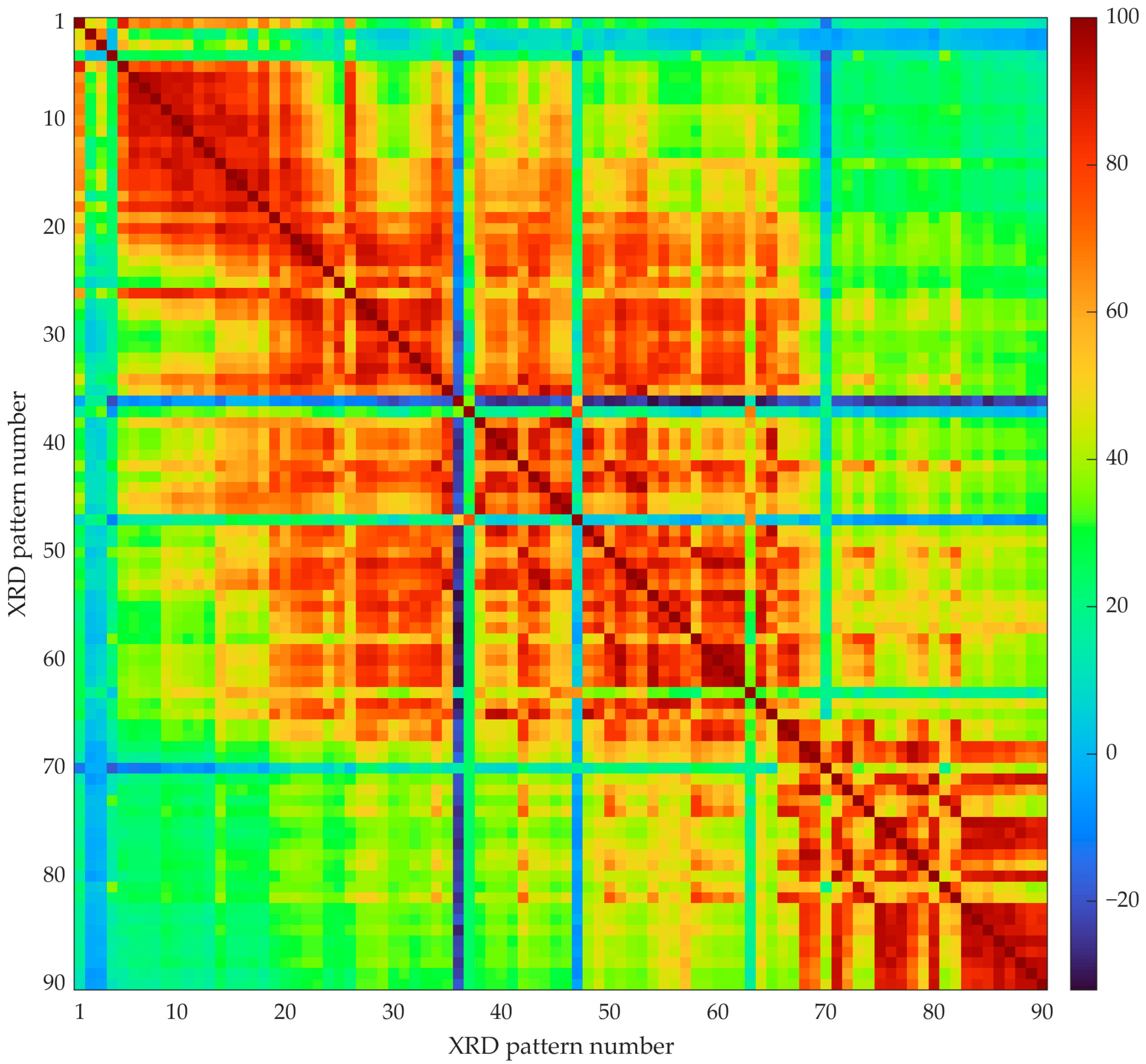


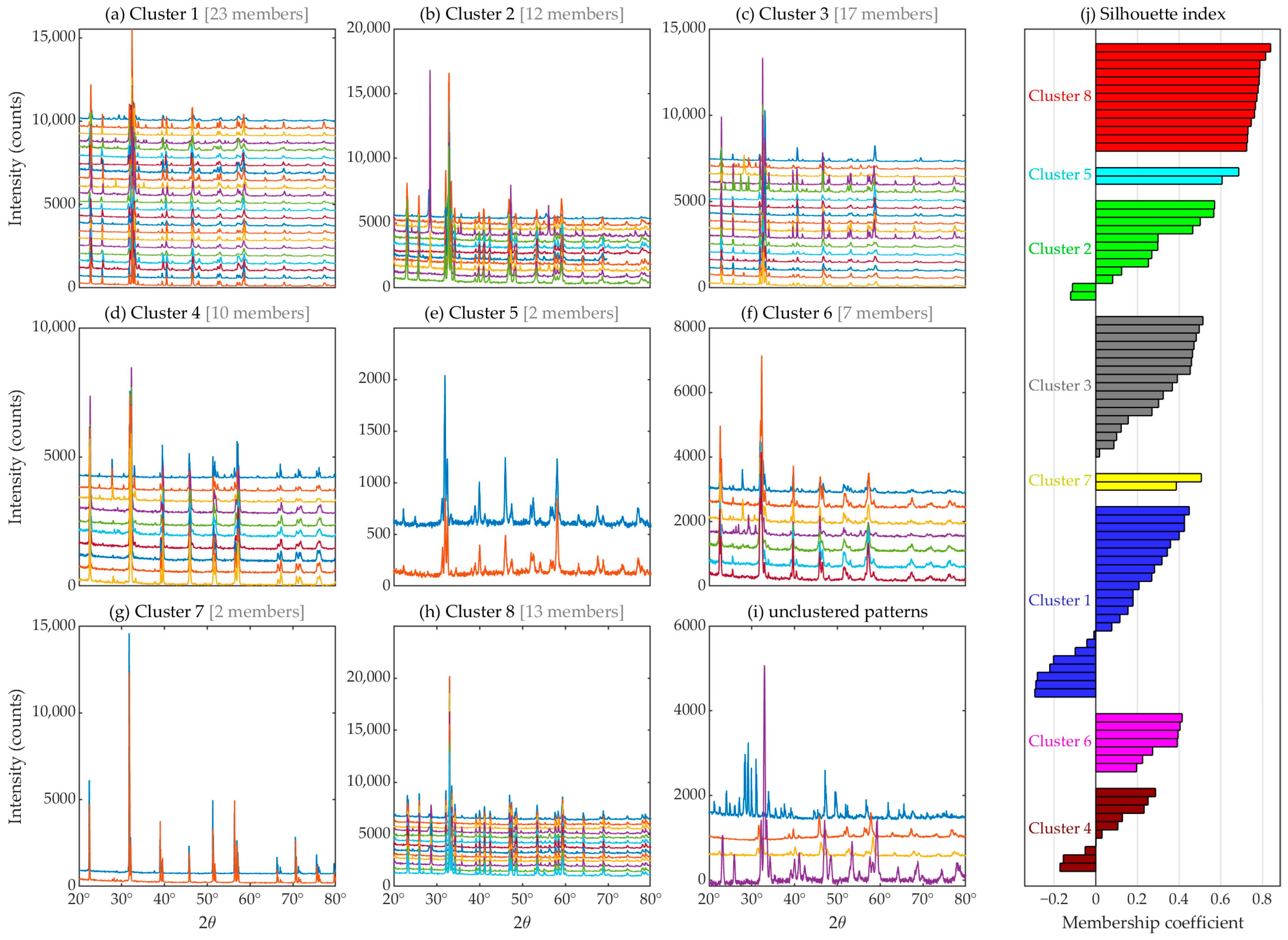

| Composition | Bi2O3 Content (g) | Eu2O3 Content (g) | Fe2O3 Content (g) |
|---|---|---|---|
| BiFeO3 | 11.6490 | 0 | 3.9922 |
| Bi0.95Eu0.05FeO3 | 11.0665 | 0.4399 | 3.9922 |
| Bi0.90Eu0.10FeO3 | 10.4841 | 0.8798 | 3.9922 |
| Bi0.85Eu0.15FeO3 | 9.9016 | 1.3197 | 3.9922 |
| Bi0.80Eu0.20FeO3 | 9.3192 | 1.7596 | 3.9922 |
| Bi0.70Eu0.30FeO3 | 8.1543 | 2.6394 | 3.9922 |
| Bi0.60Eu0.40FeO3 | 6.9894 | 3.5193 | 3.9922 |
| Bi0.50Eu0.50FeO3 | 5.8245 | 4.3991 | 3.9922 |
| Bi0.40Eu0.60FeO3 | 4.6596 | 5.2789 | 3.9922 |
| Bi0.30Eu0.70FeO3 | 3.4947 | 6.1587 | 3.9922 |
| Bi0.20Eu0.80FeO3 | 2.3298 | 7.0385 | 3.9922 |
| Bi0.10Eu0.90FeO3 | 1.1649 | 7.9183 | 3.9922 |
| EuFeO3 | 0 | 8.7982 | 3.9922 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Surdu, V.-A.; Győrgy, R. Phase Relations in the Pseudo-Binary BiFeO3–EuFeO3 System in the Subsolidus Region Derived from X-Ray Diffraction Data—A Machine Learning Approach. Inorganics 2024, 12, 314. https://doi.org/10.3390/inorganics12120314
Surdu V-A, Győrgy R. Phase Relations in the Pseudo-Binary BiFeO3–EuFeO3 System in the Subsolidus Region Derived from X-Ray Diffraction Data—A Machine Learning Approach. Inorganics. 2024; 12(12):314. https://doi.org/10.3390/inorganics12120314
Chicago/Turabian StyleSurdu, Vasile-Adrian, and Romuald Győrgy. 2024. "Phase Relations in the Pseudo-Binary BiFeO3–EuFeO3 System in the Subsolidus Region Derived from X-Ray Diffraction Data—A Machine Learning Approach" Inorganics 12, no. 12: 314. https://doi.org/10.3390/inorganics12120314
APA StyleSurdu, V.-A., & Győrgy, R. (2024). Phase Relations in the Pseudo-Binary BiFeO3–EuFeO3 System in the Subsolidus Region Derived from X-Ray Diffraction Data—A Machine Learning Approach. Inorganics, 12(12), 314. https://doi.org/10.3390/inorganics12120314







