Abstract
Band-structure calculations were performed using the spin-polarized relativistic Korringa–Kohn–Rostoker (SPR-KKR) band-structure method, determining intrinsic magnetic properties, such as magnetic moments, magnetocrystalline anisotropy energy (MAE), and Curie temperatures, of Fe5−x−yCoxMySiB2 (M = Re, W) alloys. The general gradient approximation (GGA) for the exchange–correlation potential and the atomic sphere approximation (ASA) were used in the calculations. Previous studies have shown that for Fe5SiB2, the easy magnetization direction is in-plane, but it turns axial for Co-doping in the range 1 < x ≤ 2.5 (y = 0). Furthermore, studies have shown that 5d-doping enhances the MAE by enabling the strong spin–orbit coupling of Fe–3d and M–5d states. The aim of the present theoretical calculations was to find the dependence of the anisotropy constant K1 for combined Co- and M-doping, building a two-dimensional (2D) map of K1 for 0 ≤ x ≤ 2 and 0 ≤ y ≤ 1. Similar theoretical 2D maps for magnetization and Curie temperature vs. Co and M content (M = W and Re) were built, allowing for the selection of alloy compositions with enhanced values of uniaxial anisotropy, magnetization, and Curie temperature. The magnetic properties of the Fe4.1W0.9SiB2 alloy that meet the selection criteria for axial anisotropy K1 > 0.2 meV/f.u., Curie temperature Tc > 800 K determined by the mean-field approach, and magnetization µ0Ms > 1 T are discussed.
1. Introduction
Magnetic materials are crucial for technological development in many sectors, such as electric motors, transformers, power generators, and recording media. High-performance permanent magnets with a large saturation magnetization, high Curie temperature, and large uniaxial magnetic anisotropy are necessary, with these requirements currently being fulfilled by rare-earth permanent magnets such as Sm–Co and Nd–Fe–B [1]. The volatile prices and restricted accessibility to rare-earth resources raised a strategic issue, directing the research efforts in the last two decades to the search for new magnetic materials with close performance to Sm–Co and Nd–Fe–B magnets but with lower rare-earth content. Also, the search for new permanent magnets without rare-earth elements has aroused research interest in magnetic materials [2,3,4]. Due to their reduced costs and small supply risks, their use in less demanding applications can be efficient. This research direction is motivated by the large gap in the price–performance diagram between the hard ferrite/alnico magnets and the high-performance RE, which could be filled by new rare-earth-free permanent magnets. In this last category, the Fe compounds with an anisotropic crystal structure are important candidates for functional rare-earth-free permanent magnets due to their lower price, standardized preparation procedure, and good mechanical properties. One such compound is Fe5SiB2, discovered in the 1960s by Aronsson et al. [5], which crystallizes in the Cr5B3 structure type (I4/mcm space group). According to recent research, a saturation magnetization Ms = 9.2 µB/f.u. (1.34 MA/m) was theoretically predicted for this compound [6]. The magnetic measurements at 10 K show a considerably lower value of Ms of 1.1 MA/m, while large values of spin magnetic moments on both Fe crystal sites (2.31 µB for Fe on the 4c site and 2.10 µB for Fe on the 16l site) were determined by neutron diffraction at 16 K [7]. Several investigations reported Curie temperatures over 800 K for this compound [7,8]. Also, a magnetic anisotropy constant |K1|of 0.25 MJ/m3 was estimated from the term of magnetization M vs. magnetic field H dependence [6]. The spin orientation was revealed by the Mössbauer spectroscopy of Ericsson et al. [9] and the neutron diffraction experiments of Cedervall et al. [7]. The Fe5SiB2 alloy is a simple ferromagnet with in-plane spins at low temperatures and spins parallel to the c-axis for temperatures between ~140 K and the Curie temperature [9]. Despite the large values of saturation magnetization and Curie temperature of the Fe5SiB2 alloy, due to its in-plane anisotropy and spin reorientation [7], this compound is considered inefficient for the development of permanent magnets (PMs). Further research found that the Co for Fe substitution in (Fe,Co)5SiB2 can turn the sign of MAE from negative to positive, enabling an axial easy magnetization direction for the corresponding alloys. Also, the spin-reorientation transition temperature is decreased by Co-doping to the lowest temperature [10]. Other studies report a moderate improvement of magnetic anisotropy by Ge and P for Si substitutions in the Fe5SiB2 alloy, respectively [11,12,13], along with the decrease in the spin-reorientation temperature to 60 K [11] and 10 K [13].
On the other hand, previous studies showed that doping with 5d elements (M) builds stronger uniaxial anisotropy in Fe alloys, due to the stronger spin–orbit coupling of Fe–3d and M–5d states [14,15]. The earlier research of Thakur et al. on Fe5PB2 doped with W [16] showed that the anisotropy constant K1 increases from 0.152 MJ/m3 in Fe5PB2 to 1.135 MJ/m3 in Fe4WPB2, and this enhancement is attributed to the strong spin–orbit coupling of Fe–3d states and W–5d states. Still, the magnetization and the Curie temperature are decreased by 5d-doping in Fe alloys, substituting Fe with a nonmagnetic element. In this case, the doping amount has to be optimized to keep the intrinsic magnetic properties at values compatible with functional applications. Our previous theoretical investigations showed for the Fe4WSiB2 alloy an anisotropy constant of 0.218 meV/f.u. In this case, W-doping in Fe5SiB2 improves the anisotropy at the cost of the magnetization reduction (to 7.97 µB/f.u.) and the Curie temperature decrease (747 K) [17].
Also, other 5d elements could be effective for magnetic anisotropy tailoring. For instance, 5d-doping in an Fe2B alloy showed larger efficiency for Re-doping (K1 = 1.5 MJ/m3, magnetization µ0Ms = 1.22 T and an estimated Curie temperature of 595 K for Fe1.52Re0.48B), whilst the W-doping effects on anisotropy are much weaker [18].
In this study, we present the magnetic anisotropy behavior of 5d-doping in Fe5−x−yCoxMySiB2 alloys (M = W and Re) in the range 0 ≤ x ≤ 2 and 0 ≤ y ≤ 1. The Co- and M-doping ranges were chosen accounting for the substitution effects on MAE, Curie temperatures, and magnetization in (Fe,Co)5SiB2 alloys. The balance between the benefit of doping for the anisotropy and its detrimental influence on the magnetization and Curie temperature restricted the x and y choice. The Co-doping needed to change the sign of MAE (x > 1) was reported, while for x > 2, the Curie temperatures Tc of the (Fe,Co)5SiB2 alloys are less appropriate for permanent magnet applications (Tc < 500 K) [6,8]. A similar expected decrease in magnetization and Curie temperatures by a nonmagnetic 5d element, M, for Fe substitution limits the y-doping in our study to y = 1.
Two-dimensional maps of the anisotropy constant were built, allowing for the selection of the composition range for compounds with large uniaxial anisotropies. Further investigations on the magnetization and Curie temperature behavior vs. Co and M content (M = W and Re) enable a detailed view of the intrinsic magnetic properties of these alloys. Fully relativistic theoretical calculations in the framework of density functional theory (DFT) using the exchange–correlation potential under general gradient approximation were employed for the current investigations. The torque method for magnetic anisotropy energy calculations was used. The Curie temperatures were evaluated using the Heisenberg exchange interaction parameters extracted from DFT results and used as inputs for the mean field approach calculations.
2. Results and Discussion
2.1. Crystal Structure
The crystal structure of the Fe5−x−yCoxMySiB2 alloys (Figure 1) consists of a body-centered tetragonal unit cell (space group I4/mcm, no. 140), with Fe atoms on two different sites (4c and 16l) and B atoms on 8h sites, whilst Si atoms occupy the 4a crystallographic sites. The lattice parameters determined by X-ray diffraction are a = 5.5541 Å and c = 10.3429 Å [7].
Electronic band-structure calculations for the Fe5−x−yCoxMySiB2 alloys (for 0 ≤ x ≤ 2 and 0 ≤ y ≤ 1) in the tetragonal structure (space group I4/mcm) using the experimental lattice parameters [2,19] were performed. The experimental free parameters of 8h and 16l crystallographic sites, determined by Cedervall et al. for Fe5SiB2, were considered [7]. The lattice constants of the W- and Re-doped alloys were evaluated using the lattice constants of Re5SiB2, W5SiB2, and Co5SiB2 [7,19], considering their linear dependence via doping. The low effect of the structural relaxation on MAE in Fe compounds evidenced by Lawrence et al. [20], as well as the low effect of pressure on the magnetization and Curie temperature of Fe5SiB2 [21], allowed us to rely on this estimated lattice constants. The occupation of Co atoms on 16l crystal sites was considered, according to our previous investigations [8]. A similar preferential occupation was obtained for Re atoms, whilst a random occupation of the 4c and 16l sites was derived for W atoms by total energy calculations.
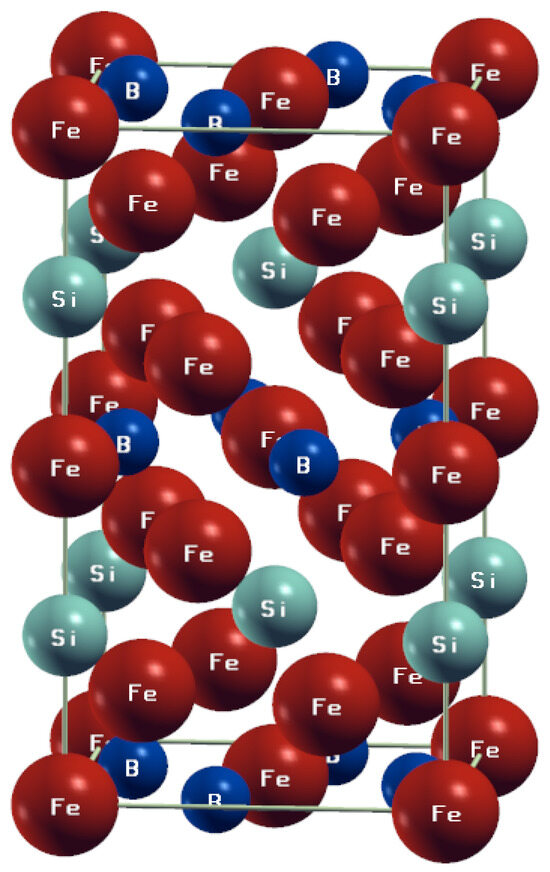
Figure 1.
The body-centered tetragonal unit cell (space group I4/mcm, no. 140) of Fe5SiB2 alloy, with Fe atoms on two different sites (4c and 16l), the B atoms on 8h sites, and Si atoms on 4a crystallographic sites. The graphic program XCrySDen [22] was used.
2.2. Magnetic Moments
Band-structure calculations for the Fe5SiB2 alloy were performed using different exchange and correlation parametrizations (local density approximation (LDA) and general gradient approximation (GGA)) with atomic sphere approximation as well as the full-potential approach. The results of the calculations are listed in Table 1, together with the results of experimental measurements [7] and other theoretical results based on the full-potential local orbital minimum-basis method (FPLO) [6].

Table 1.
Total magnetic moments and site-dependent spin and orbital magnetic moments for the Fe5SiB2 alloy, determined by different exchange–correlation approaches in the ASA and full-potential mode. Present calculations based on the spin-polarized relativistic Korringa–Kohn–Rostoker method (SPR-KKR) [23] (details in Section 3) are compared with theoretical full-potential local orbital minimum-basis method (FPLO) results [6]. The experimental values for saturation magnetization and neutron diffraction [6,7] are also shown.
According to our calculations, the Fe5SiB2 alloy is ferromagnetic, with a total magnetic moment between 8.46 and 9.41 µB/f.u., depending significantly on the exchange–correlation potential and the potential symmetry (spherical in ASA and no shape approximation in the full-potential approach). As can be seen in Table 1, the VWN-ASA approach gives an underestimated total magnetic moment compared with the experimental data. Better agreement is obtained by the use of the GGA approach, with a total magnetic moment of 9.34 µB/f.u. (GGA-ASA) and 9.41 µB/f.u. (GGA-FP). Also, the SPR-KKR shows similar values of individual magnetic moments with FPLO calculations with only minor deviations, determined most probably by the lattice constants used for calculations. The Fe magnetic moments show higher values for Fe 4c, but the ratio between Fe 4c/16l moments depends on the calculation approach.
Based on these results, the GGA-ASA calculation mode was chosen to deal with the combined Co- and M (M = Re, W)-doping. Moreover, the GGA-ASA calculated value of µ0Ms (1.36 T) is close to the value determined experimentally by McGuire et al. (1.31 T) [10].
The total magnetic moments calculated for the Fe5−x−yCoxMySiB2 alloys for 0 ≤ x ≤ 2 and 0 ≤ y ≤ 1 were used to build a two-dimensional map of magnetization vs. Co and M content (x,y), shown in Figure 2. According to the contour maps for several selected values of total magnetic moment, the Re- and W-doping have a similar effect in combination with Co-doping on the magnetization of the Fe5−x−yCoxMySiB2 alloys. The values of magnetization are decreased by both combined doping types (Co and Re; Co and W, respectively) from 9.34 µB/f.u. to values lower than 5 µB/f.u. The decrease in magnetization has already been evidenced for doping with Co [6,8]. Still, the use of combined doping (Co + Re; Co + W) can enhance this tendency, as shown in Figure 2. If the desired values of magnetization are set to values over 6 µB/f.u., the corresponding alloys have Co content x ≤ 1.5 and M content y ≤ 0.6.
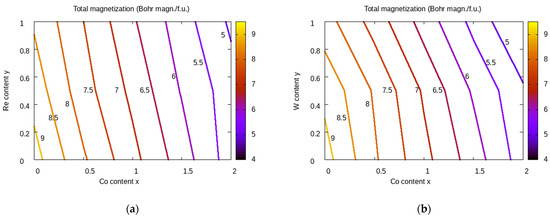
Figure 2.
The calculated total magnetization for the Fe5−x−yCoxMySiB2 alloys for M = Re (a) and M = W (b) is represented as 2D maps of Co vs. M content (x, y). The isolines for discrete values of magnetization (in µB/f.u.) are shown. The preferential occupation by Co+M-doping was accounted for in the total energy calculations (Co and Re on 16l site, random occupation on 4c and 16l sites for W).
2.3. Magnetic Anisotropy
The earlier reports show that the anisotropy constant of (Fe,Co)5SiB2 alloys changes the sign for a certain range of Co amount [6,8]. This effect is accounted for in the present study, as easy-axis anisotropy is obtained by Co-doping, followed by expected anisotropy enhancement by further doping with 5d elements. The validity of this mechanism is discussed below, using the representation of the anisotropy constants K1 calculated for Fe5−x−yCoxMySiB2 alloys. The K1 values obtained for both M = Re and W in a 5 × 3 grid for 0 ≤ x ≤ 2 and 0 ≤ y ≤ 1 (Δx = Δy = 0.5) were used to build the K1(x,y) 2D maps. The K1 isolines between −0.3 meV/f.u and 0.25 meV/f.u. are shown in Figure 3. As can be seen, significantly different K1 2D maps were obtained by Re-/W-doping in Fe5−x−yCoxMySiB2 alloys. In the case of Re, values of K1 over 0.25 meV/f.u. can be obtained for a combination of Co-doping with approx. x ≥ 1.8 and Re-doping with y ≥ 0.7. The disadvantage of the Re-doping is made visible by overlapping the Ms 2D map (Figure 2) and K1 2D map (Figure 3). The (x,y) areas with large K1 values almost overlap with the areas with low magnetization values, as Ms < 5 µB/f.u. for x ≥ 1.5. This behavior of magnetocrystalline anisotropy is opposite to that evidenced in the Fe2B alloy, where Re-doping promoted large axial anisotropy [18].
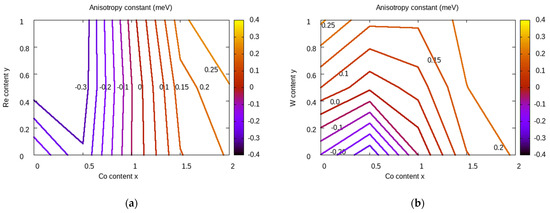
Figure 3.
The calculated anisotropy constants for the Fe5−x−yCoxMySiB2 alloys for (a) M = Re and (b) M = W are represented as 2D maps of Co vs. M content (x, y). The isolines for discrete values of K1 (in meV) are shown. The preferential occupation by Co+M-doping was accounted for in the total energy calculations (Co and Re on 16l site, random occupation on 4c and 16l sites for W).
On the other hand, W-doping can increase the anisotropy of the Fe5SiB2 alloy, with values of K1 ≥ 0.2 meV/f.u. being obtained for x = 0 and y > 0.8. Also, values of K1 ≥ 0.25 meV/f.u. are seen for x = 0 and y~1. By overlapping the 2D maps of Ms and K1 in the case of M = W, one can find magnetization values between 8 and 8.5 µB/f.u. It is interesting to note that in the case of Re-doping, the area (x = 0, y > 0.9) corresponds to the largest value of in-plane magnetocrystalline anisotropy, whilst W-doping alone can switch the anisotropy to easy-axis anisotropy without additional Co-doping.
2.4. Curie Temperatures and Exchange-Coupling Parameters
The Curie temperatures (Tc) were determined by the mean field approach (MFA) using the procedure described in Section 3. The grid data for Tc were used to build isolines with constant values of Tc, which are represented in Figure 4. According to our calculations, the Fe5SiB2 alloy is ferromagnetic with a Curie temperature of 1162 K, calculated with the mean field approach. As the mean field method is known to overestimate the Curie temperature values by ~20%, the estimated Tc would be comparable with the experimental value of 850 K [8].
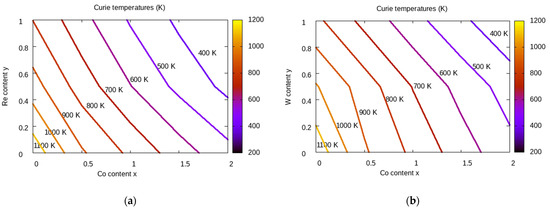
Figure 4.
The calculated Curie temperatures for the Fe5−x−yCoxMySiB2 alloys for (a) M = Re and (b) M = W are represented as 2D maps of Co vs. M content (x, y). The isolines for discrete values of Tc (in K) are shown. The preferential occupation by Co+M-doping was accounted for in the total energy calculations (Co and Re on 16l site, random occupation on 4c and 16l sites for W).
From the Tc representation in Figure 4, it is obvious that the combined Co + M-doping will decrease the Curie temperatures for both M = Re and W. This decrease is slightly steeper in the case of Co + Re. For Re-doped alloys, by overlapping the areas where K1 ≥ 0.2 meV/f.u. on the K1 2D map with the Curie temperature map, the corresponding alloys have Tc values under 400 K, which makes the Re-doping rather unsuitable for PM applications.
On the other hand, the expected Tc values of the W-doped alloys with anisotropy constant K1 ≥ 0.2 meV/f.u. (obtained for x = 0 and y > 0.8) are between 850 and 900 K, compatible with PM applications.
Due to the promising intrinsic properties of Fe1−yWySiB2 alloys in the doping range y > 0.8, we investigated in more detail the magnetic properties of such W-doped alloys. We used a complementary approach by considering particular microscopic models, making use of magnetic interaction based on the classical Heisenberg Hamiltonian described in Section 3. Using this approach, the Fe–Fe exchange-coupling parameters are obtained and represented as a function of distance (in units of lattice constant a). The Fe–Fe exchange interactions for Fe5SiB2 and Fe4.1W0.9SiB2 alloys are presented in Figure 5. As can be seen in Figure 5, the dominant exchange interactions are positive, favoring ferromagnetic ordering. Negative exchange interactions are also seen, mostly between Fe 16l spins at distances of between 0.6a and 0.9a. The largest exchange interactions are between Fe 4c–Fe 16l nearest neighbors. These exchange interactions are affected by the W-doping, and a decrease in the exchange-coupling parameters between nearest neighbors in Fe4.1W0.9SiB2 compared with Fe5SiB2 can be seen. Also, a decrease in the exchange-coupling parameter values by W-doping is observed for the interactions between the Fe 4c–Fe 4c spins. The exchange interactions between nearest Fe 4c–Fe 4c spins are much smaller, as their interatomic distance is considerably larger than those of the other pairs. The Curie temperature is mostly determined by the Fe 16l–Fe 16l and Fe 4c–Fe 16l exchange interactions.
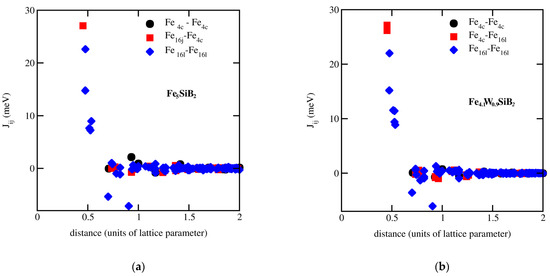
Figure 5.
The Fe–Fe exchange-coupling parameters for (a) Fe5SiB2 and (b) Fe4.1W0.9SiB2 alloys plotted as a function of the distance between Fe spins. The preferential occupation by W-doping was accounted for in the total energy calculations (random occupation on 4c and 16l sites for W).
The spin and orbital magnetic moments, magnetization µ0Ms, anisotropy constant K1, Curie temperature, and hardness parameter for the Fe4.1W0.9SiB2 alloy are listed in Table 2. In particular, the spin and orbital moments on Fe sites (2.43 µB and 0.07 µB for Fe 4c; 1.95 µB and 0.06 µB for Fe 16l) are higher compared with the corresponding values in Fe5SiB2 (see Table 1), but the weight of the magnetic atoms decreases by about 18%, resulting in a magnetization decrease (8.37 µB/f.u.) by W-doping, which corresponds to a µ0Ms value of 1.17 T.

Table 2.
Spin and orbital magnetic moments and magnetization µ0Ms, together with the magnetocrystalline anisotropy constant K1 and Curie temperature for the Fe4.1W0.9SiB2 alloy.
The results from Table 2 show that Fe4.1W0.9SiB2 alloy is a semi-hard permanent magnet, with µ0Ms > 1T and a magnetic anisotropy energy of 0.46 MJ/m3, close to the values in Sr ferrite [4]. The magnetic hardness parameter captures the potential of the present alloy, with adequate magnetization µ0Ms (1.17 T), to be developed into a compact permanent magnet. The value obtained according to the formula is 0.65, corresponding to a semi-hard magnetic material. The Curie temperature is expected to be overestimated by MFA, but a value over 680 K is still expected for the Fe4.1W0.9SiB2 alloy. The high value of the Curie temperature allows for the use of these alloys in relatively high-temperature applications.
3. Materials and Methods
Spin-polarized fully relativistic band-structure calculations based on the Korringa–Kohn–Rostoker (SPRKKR) method were used for theoretical calculations [23]. This calculation method is based on the KKR–Green function formalism that makes use of the multiple scattering theory. Within this approach, the so-called t-scattering matrices describing the scattering properties of each scattering center (atom) are determined. In the second step, the multiple scattering matrices of all atoms in the lattice are calculated accounting for the fact that the incident wave at each atom is the sum of the outgoing waves from all other atoms. The central role in the KKR–Green function method is played by the crystal Green’s function, which is efficiently related to Green’s function of free space via the Dyson equation. The SPR-KKR calculation method supplies all the information about the electronic structure, similar to other band-structure methods that use energy eigenvalues and eigenfunctions to represent the electronic structure. In addition, the SPR-KKR band-structure method has an important advantage in dealing with chemical disorder, as the coherent potential approximation (CPA) [24] was efficiently integrated by defining Green’s function of the average crystal medium, which is determined self-consistently through the condition that the concentration average of the various atom types should not produce any additional scattering in this medium [24]. In this way, the SPR-KKR is a more efficient and reliable alternative to more laborious supercell techniques, requiring enlarged unit cells and atomic-configuration averaging in the supercells to describe the alloy’s properties. The 7.7 version of the Munich SPR-KKR band-structure program was used for the present investigations [25]. More details about the SPR-KKR method are extensively described elsewhere [23,25].
Local spin-density approximation (LSDA) [26] and generalized gradient approximation with the parametrization of Perdew et al. (GGA-PBE) [27] were used to account for the exchange and correlation effects. The k-space integration was performed using the special points method [28]. The study of magnetic anisotropy was performed with magnetic torque calculations. The magnetic torque acting on the magnetic moment of the atomic site I, oriented along the magnetization direction , generates a component:
with respect to the axis , where θ and φ are the polar angles [29,30]. The magnetic anisotropy energy, defined as the energy difference between the in-plane and out-of-plane magnetization directions, is related to the magnetic torque by a special geometry. By setting the polar angles to θ = π/4 and φ = 0, the calculated magnetic torque is [30]. The total energy for the tetragonal symmetry by first-order approximation of the magnetic anisotropy energy is given by the expression , where and are the anisotropic constants and is the polar angle between the magnetization direction and the easy axis. In the case of the Fe5SiB2 alloy, [7,13], and the magnetic anisotropy energy is described by The easy-plane anisotropy corresponds to negative values of . A dense k-mesh of 25 × 25 × 25 k-points in the Brillouin zone was used for magnetic torque calculations.
The magnetic behavior of Fe5−x−yCoxMySiB2 alloys was investigated using a complementary approach based on the classical Heisenberg Hamiltonian described by the expression:
where the summation is performed on all lattice sites i and j, and and are the unit vectors of magnetic moments on sites i and j, respectively. The total energy difference due to an infinitesimal change in angle between the magnetic moments of the (i, j) spin pair was calculated in scalar-relativistic mode and expressed to the lowest order with respect to the orientation angle between and . Using the expression derived by Liechtenstein [29] based on the magnetic force theorem, a one-to-one mapping between the exchange-coupling energy and the Heisenberg Hamiltonian is obtained, allowing for the determination of the Jij exchange-coupling parameters. The Jij exchange-coupling parameters were calculated for all magnetic atoms as a function of distance up to 15 Å around each lattice site. The mean field approach (MFA) was used to derive the Curie temperatures using the calculated Jij exchange-coupling parameters, according to the expression [29,31]:
where is the exchange-coupling parameter on ith site, and the sum runs over all coordination shells.
4. Conclusions
The aim of the present research was to identify the M 5d-doping elements and the doping amount able to switch to easy-axis anisotropy and enhance it by enabling strong spin–orbit coupling between the Fe–3d and M–5d states. Theoretical studies on the Fe5−x−yCoyWxSiB2 alloys show a decrease in the total magnetic moment and Curie temperatures of the alloys by increasing W and Re content x. Also, the theoretically calculated anisotropy constant turns from planar for the Fe5SiB2 alloy to axial for Fe5−x−yCoyWxSiB2 in different zones of the 2D map, showing the opposite impact of Re-/W-doping on the magnetocrystalline anisotropy behavior in these alloys. The superposition of the 2D maps for magnetization, MAE, and Curie temperatures allowed us to conclude that W-doping is favorable for the development of intrinsic properties compatible with PM applications, even without Co-doping. In the case of Re + Co-doping, such a concentration range was not found due to the reversed effects of combined doping on the magnetization and Curie temperature on one side and magnetocrystalline anisotropy on the other side. Despite its strong spin–orbit coupling with Fe–3d states, Re-doping determined large anisotropy constants for the alloys with low Curie temperatures and magnetizations, incompatible with PM applications. On the other hand, the W-doped Fe5SiB2 alloys can be optimized to allow for their use as semi-hard magnets in nanocomposite magnetic materials.
Funding
This research was funded by the Romanian Ministry of Education and the Romanian Ministry of Research and Innovation, CCCDI-UEFISCDI grant PN-III-P2-2.1-PED-2019-3484.
Data Availability Statement
Data are available on request.
Conflicts of Interest
The author declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Coey, J.M.D. Perspective and Prospects for Rare Earth Permanent Magnets. Engineering 2020, 6, 119–131. [Google Scholar] [CrossRef]
- Mohapatra, J.; Liu, J.P. Rare-Earth-Free Permanent Magnets: The Past and Future. In Handbook of Magnetic Materials; Elsevier: Amsterdam, The Netherlands, 2018; Volume 27, pp. 1–57. [Google Scholar] [CrossRef]
- Skokov, K.P.; Gutfleisch, O. Heavy rare earth free, free rare earth and rare earth free magnets—Vision and reality. Scr. Mater. 2018, 154, 289–294. [Google Scholar] [CrossRef]
- Cui, J.; Kramer, M.; Zhou, L.; Liu, F.; Gabay, A.; Hadjipanayis, G.; Sellmyer, D. Current progress and future challenges in rare-earth-free permanent magnets. Acta Mater. 2018, 158, 118–137. [Google Scholar] [CrossRef]
- Aronsson, B.; Engström, I. X-ray Investigations on Me-Si-B Systems (Me = Mn, Fe, Co). Acta Chem. Scand 1960, 14, 1403. [Google Scholar] [CrossRef]
- Werwiński, M.; Kontos, S.; Gunnarsson, K.; Svedlindh, P.; Cedervall, J.; Höglin, V.; Sahlberg, M.; Edström, A.; Eriksson, O.; Rusz, J. Magnetic properties of Fe5SiB2 and its alloys with P, S, and Co. Phys. Rev. B 2016, 93, 174412. [Google Scholar] [CrossRef]
- Cedervall, J.; Kontos, S.; Hansen, T.C.; Balmes, O.; Martinez-Casado, F.J.; Matej, Z.; Beran, P.; Svedlindh, P.; Gunnarsson, K.; Sahlberg, M. Magnetostructural transition in Fe5SiB2 observed with neutron diffraction. J. Solid State Chem. 2016, 235, 113–118. [Google Scholar] [CrossRef]
- Hirian, R.; Isnard, O.; Pop, V.; Benea, D. Investigations on the magnetic properties of the Fe5−xCoxSiB2 alloys by experimental and band structure calculation methods. J. Magn. Magn. Mater. 2020, 505, 166748. [Google Scholar] [CrossRef]
- Ericsson, T.; Häggström, L.; Wäppling, R. Spin rotation in Fe5SiB2. Phys. Scr. 1978, 17, 83–86. [Google Scholar] [CrossRef]
- McGuire, M.A.; Parker, D.S. Magnetic and structural properties of ferromagnetic Fe5PB2 and Fe5SiB2 and effects of Co and Mn substitutions. J. Appl. Phys. 2015, 118, 163903. [Google Scholar] [CrossRef]
- Lejeune, B.T.; Barua, R.; McDonald, I.J.; Gabay, A.M.; Lewis, L.H.; Hadjipanayis, G.C. Synthesis and processing effects on magnetic properties in the Fe5SiB2 system. J. Alloys Compd. 2018, 731, 995–1000. [Google Scholar] [CrossRef]
- Clulow, R.; Hedlund, D.; Vishina, A.; Svedlindh, P.; Sahlberg, M. Magnetic and structural properties of the Fe5Si1−xGexB2 system. J. Solid State Chem. 2022, 316, 123576. [Google Scholar] [CrossRef]
- Hedlund, D.; Cedervall, J.; Edström, A.; Werwiński, M.; Kontos, S.; Eriksson, O.; Rusz, J.; Svedlindh, P.; Sahlberg, M.; Gunnarsson, K.J. Magnetic properties of the Fe5SiB2−Fe5PB2 system. Phys. Rev. B 2017, 96, 094433. [Google Scholar] [CrossRef]
- Edström, A.; Werwiński, M.; Rusz, J.; Eriksson, O.; Skokov, K.P.; Radulov, I.A.; Ener, S.; Kuz’min, M.D.; Hong, J.; Fries, M.; et al. Effect of doping by 5d elements on magnetic properties of alloys, Magnetic properties of (Fe1−xCox)2B alloys and the effect of doping by 5d elements. Phys. Rev. B 2015, 92, 174413. [Google Scholar] [CrossRef]
- Khan, I.; Hong, J. Site dependent enhancement of magnetic anisotropy in 4d and 5d impurity doped α-Fe16N2: A first principles study. Curr. Appl. Phys. 2018, 18, 526–533. [Google Scholar] [CrossRef]
- Thakur, J.; Rani, P.; Tomar, M.; Gupta, V.; Kashyap, M.K. Enhancement of magnetic anisotropy of Fe5PB2 with W substitution: Ab-initio study. AIP Conf. Proc. 2019, 2093, 020012. [Google Scholar] [CrossRef]
- Hirian, R.; Pop, V.; Isnard, O.; Benea, D. Magnetic properties of the (Fe,Co)5SiB2 alloys by W doping. Stud. UBB Phys. 2022, 67, 1. [Google Scholar] [CrossRef]
- Benea, D.; Pop, V. Magnetic Properties of the Fe2B Alloy Doped with Transition Metal Elements. Magnetochemistry 2023, 9, 109. [Google Scholar] [CrossRef]
- Lawrence, R.A.; Donaldson, S.J.; Probert, M.I. Magnetic Transition State Searching: Beyond the Static Ion Approximation. Magnetochemistry 2023, 9, 42. [Google Scholar] [CrossRef]
- Kaštil, J.; Hirian, R.; Isnard, O. Effect of pressure on the magnetic and structural properties of Fe5SiB2 compound. Intermetallics 2019, 110, 106484. [Google Scholar] [CrossRef]
- Pan, Y.; Guan, W.M. Exploring the structural stability and mechanical properties of TM5SiB2 ternary silicides. Ceram. Int. 2018, 44, 9893. [Google Scholar] [CrossRef]
- Kokalj, A. XCrySDen—A new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 1999, 17, 176–179. [Google Scholar] [CrossRef] [PubMed]
- Ebert, H.; Ködderitzsch, D.; Minar, J. Calculating condensed matter properties using the KKR-Green’s function method—Recent developments and applications. Rep. Prog. Phys. 2011, 74, 096501. [Google Scholar] [CrossRef]
- Faulkner, J.S.; Stocks, G.M. Calculating properties with the coherent-potential approximation. Phys. Rev. B 1980, 21, 3222. [Google Scholar] [CrossRef]
- Munich SPRKKR Band Structure Program Package. Available online: https://www.ebert.cup.uni-muenchen.de/index.php/de/software/13-sprkkr (accessed on 8 December 2023).
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.; Pack, J. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Liechtenstein, A.I.; Katsnelson, M.I.; Antropov, V.P.; Gubanov, V.A. Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mater. 1987, 67, 65–74. [Google Scholar] [CrossRef]
- Mankovsky, S.; Polesya, S.; Minar, J.; Hoffmann, F.; Back, D.H.; Ebert, H. Spin-orbit coupling effect in (Ga, Mn) As films: Anisotropic exchange interactions and magnetocrystalline anisotropy. Phys. Rev. B 2011, 84, 201201. [Google Scholar] [CrossRef]
- Nieves, P.; Arapan, S.; Maudes-Raedo, J.; Marticorena-Sánchez, R.; Del Brío, N.L.; Kovacs, A.; Echevarria-Bonet, C.; Salazar, D.; Weischenberg, J.; Zhang, H.; et al. Database of novel magnetic materials for high-performance permanent magnet development. Comput. Mat. Sci. 2019, 168, 188–202. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).