Pr@C82 Metallofullerene: Calculated Isomeric Populations
Abstract
1. Introduction
2. Calculations
3. Results and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Ding, J.; Yang, S.; Li, X.-Y. Electrochemical Properties of 4f-block metallofullerenes. In Fullerenes. Recent Advances in the Chemistry and Physics of Fullerenes and Related Materials; Kadish, K.M., Ruoff, R.S., Eds.; Electrochemical Society: Pennington, Australia, 1997; Volume 4, pp. 417–428. [Google Scholar]
- Sun, D.Y.; Huang, H.J.; Yang, S.H.; Liu, Z.Y.; Liu, S.Y. Synthesis and characterization of a water-soluble endohedral metallofullerol. Chem. Mater. 1999, 11, 1003–1006. [Google Scholar] [CrossRef]
- Akasaka, T.; Okubo, S.; Wakahara, T.; Yamamoto, K.; Kato, T.; Suzuki, T.; Nagase, S.; Kobayashi, K. Isolation and characterization of a Pr@C82 isomer. In Recent Advances in the Chemistry and Physics of Fullerenes and Related Materials; Kamat, P.V., Guldi, D.M., Kadish, K.M., Eds.; Electrochemical Society: Pennington, Australia, 1999; Volume 7, pp. 771–778. [Google Scholar]
- Akasaka, T.; Okubo, S.; Kondo, M.; Maeda, Y.; Wakahara, T.; Kato, T.; Suzuki, T.; Yamamoto, K.; Kobayashi, K.; Nagase, S. Isolation and characterization of two Pr@C82 isomers. Chem. Phys. Lett. 2000, 319, 153–156. [Google Scholar] [CrossRef]
- Wakahara, T.; Okubo, S.; Kondo, M.; Maeda, Y.; Akasaka, T.; Waelchli, M.; Kako, M.; Kobayashi, K.; Nagase, S.; Kato, T.; et al. Ionization and structural determination of the major isomer of Pr@C82. Chem. Phys. Lett. 2002, 360, 235–239. [Google Scholar] [CrossRef]
- Hosokawa, T.; Fujiki, S.; Kuwahara, E.; Kubozono, Y.; Kitagawa, H.; Fujiwara, A.; Takenobu, T.; Iwasa, Y. Electronic properties for the C2v and Cs isomers of Pr@C82 studied by Raman, resistivity and scanning tunneling microscopy/spectroscopy. Chem. Phys. Lett. 2004, 395, 78–81. [Google Scholar] [CrossRef]
- Nagano, T.; Kuwahara, E.; Takayanagi, T.; Kubozono, Y.; Fujiwara, A. Fabrication and characterization of field-effect transistor device with C2v isomer of Pr@C82. Chem. Phys. Lett. 2005, 409, 187–191. [Google Scholar] [CrossRef]
- Katayanagi, H.; Kafle, B.P.; Kou, J.; Mori, T.; Mitsuke, K.; Takabayashi, Y.; Kuwahara, E.; Kubozono, Y.J. The 4d-4f dipole resonance of the Pr atom in an endohedral metallofullerene, Pr@C82. J. Quant. Spectrosc. Rad. Trans. 2008, 109, 1590–1598. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Feng, L.; Adamowicz, L. Calculated relative populations of Sm@C82 isomers. Fullerenes Nanotub. Carbon Nanostruct. 2018, 26, 233–238. [Google Scholar] [CrossRef]
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Slanina, Z.; Lee, S.-L.; Kobayashi, K.; Nagase, S. AM1 computed thermal effects within the nine isolated-pentagon-rule isomers of C82. J. Mol. Struct. 1995, 339, 89–93. [Google Scholar] [CrossRef]
- Slanina, Z.; Kobayashi, K.; Nagase, S. Ca@C82 isomers: Computed temperature dependency of relative concentrations. J. Chem. Phys. 2004, 120, 3397–3400. [Google Scholar] [CrossRef]
- Slanina, Z.; Kobayashi, K.; Nagase, S. Computed temperature development of the relative stabilities of La@C82 isomers. Chem. Phys. Lett. 2004, 388, 74–78. [Google Scholar] [CrossRef]
- Suzuki, M.; Slanina, Z.; Mizorogi, N.; Lu, X.; Nagase, S.; Olmstead, M.M.; Balch, A.L.; Akasaka, T. Single-crystal X-ray diffraction study of three Yb@C-82 isomers cocrystallized with Ni-II(octaethylporphyrin). J. Am. Chem. Soc. 2012, 134, 18772–18778. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Suzuki, M.; Lu, X.; Mizorogi, N.; Nagase, S.; Akasaka, T. Calculated temperature development of the relative stabilities of Yb@C82 isomers. Fullerenes Nanotub. Carbon Nanostruct 2014, 22, 147–154. [Google Scholar] [CrossRef]
- Hu, Z.; Hao, Y.; Slanina, Z.; Gu, Z.; Shi, Z.; Uhlík, F.; Zhao, Y.; Feng, L. Popular C82 fullerene cage encapsulating a divalent metal ion Sm2+: Structure and electrochemistry. Inorg. Chem. 2015, 54, 2103–2108. [Google Scholar] [CrossRef]
- Slanina, Z.; Lee, S.-L.; Adamowicz, L. C80, C86, C88: Semiempirical and ab initio SCF calculations. Int. J. Quantum. Chem. 1997, 63, 529–535. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F. Temperature dependence of the Gibbs energy ordering of isomers of Cl2O2. J. Phys. Chem. 1991, 95, 5432–5434. [Google Scholar] [CrossRef]
- Slanina, Z.; Zhao, X.; Lee, S.-L.; Ōsawa, E. C90-Temperature effects on relative stabilities of the IPR isomers. Chem. Phys. 1997, 219, 193–200. [Google Scholar] [CrossRef]
- Uhlík, F.; Slanina, Z.; Ōsawa, E. C78 IPR fullerenes: Computed B3LYP/6-31G*//HF/3-21G temperature-dependent relative concentrations. Eur. Phys. J. D 2001, 16, 349–352. [Google Scholar] [CrossRef]
- Slanina, Z.; Zhao, X.; Uhlík, F.; Lee, S.-L.; Adamowicz, L. Computing enthalpy-entropy interplay for isomeric fullerenes. Int. J. Quantum Chem. 2004, 99, 640–653. [Google Scholar] [CrossRef]
- Slanina, Z.; Lee, S.-L.; Adamowicz, L.; Uhlík, F.; Nagase, S. Computed structure and energetics of La@C60. Int. J. Quantum Chem. 2005, 104, 272–277. [Google Scholar] [CrossRef]
- Slanina, Z.; Lee, S.-L.; Uhlík, F.; Adamowicz, L.; Nagase, S. Computing relative stabilities of metallofullerenes by Gibbs energy treatments. Theor. Chem. Acc. 2007, 117, 315–322. [Google Scholar] [CrossRef]
- Wang, Y.; Morales-Martínez, R.; Zhang, X.; Yang, W.; Wang, Y.; Rodríguez-Fortea, A.; Poblet, J.M.; Feng, L.; Wang, S.; Chen, N. Unique four-electron metal-to-cage charge transfer of Th to a C82 fullerene cage: Complete structural characterization of Th@C3v(8)-C82. J. Am. Chem. Soc. 2017, 139, 5110–5116. [Google Scholar] [CrossRef] [PubMed]
- Slanina, Z.; Uhlík, F.; Nagase, S.; Akasaka, T.; Adamowicz, L.; Lu, X. Eu@C72: Computed comparable populations of two non-IPR isomers. Molecules 2017, 22, 1053. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Zhao, R.; Zhao, P.; Yuan, K.; Li, Q.; Zhao, X. Unmasking the optimal isomers of Ti2C84: Ti2C2@C82 Instead of Ti2C84. J. Phys. Chem. C. 2018, 122, 13148–13155. [Google Scholar] [CrossRef]
- Binkley, J.S.; Pople, J.A.; Hehre, W.J. Self-consistent molecular orbital methods. 21. Small split-valence basis sets for first-row elements. J. Am. Chem. Soc. 1980, 102, 939–947. [Google Scholar] [CrossRef]
- Cao, X.Y.; Dolg, M. Segmented contraction scheme for small-core lanthanide pseudopotential basis sets. J. Mol. Struct. 2002, 581, 139–147. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-consistent molecular orbital methods. 12. Further extensions of Gaussian-type basis sets for use in molecular-orbital studies of organic-molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Schlegel, H.B.; McDouall, J.J.W. Do you have SCF stability and convergence problems? In Computational Advances in Organic Chemistry; Ögretir, C., Csizmadia, I.G., Eds.; Kluwer: Dordrecht, The Netherlands, 1991; pp. 167–185. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Adamowicz, L. Computations of model narrow nanotubes closed by fragments of smaller fullerenes and quasi-fullerenes. J. Mol. Graph. Mod. 2003, 21, 517–522. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Rev. C.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Slanina, Z. Equilibrium isomeric mixtures: Potential energy hypersurfaces as originators of the description of the overall thermodynamics and kinetics. Int. Rev. Phys. Chem. 1987, 6, 251–267. [Google Scholar] [CrossRef]
- Slanina, Z. A Program for determination of composition and thermodynamics of the ideal gas-phase equilibrium isomeric mixtures. Comput. Chem. 1989, 13, 305–311. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Zerner, M.C. C5 isomeric structures: Relative stabilities at high temperatures. Rev. Roum. Chim. 1991, 36, 965–974. [Google Scholar]
- Slanina, Z.; Adamowicz, L. On relative stabilities of dodecahedron-shaped and bowl-shaped structures of C20. Thermochim. Acta 1992, 205, 299–306. [Google Scholar] [CrossRef]
- Cross, R.J.; Saunders, M. Transmutation of fullerenes. J. Am. Chem. Soc. 2005, 127, 3044–3047. [Google Scholar] [CrossRef]
- Slanina, Z.; Adamowicz, L.; Kobayashi, K.; Nagase, S. Gibbs energy-based treatment of metallofullerenes: Ca@C72, Ca@C74, Ca@C82, and La@C82. Mol. Simul. 2005, 31, 71–77. [Google Scholar] [CrossRef]
- Akasaka, T.; Nagase, S.; Kobayashi, K.; Walchli, M.; Yamamoto, K.; Funasaka, H.; Kako, M.; Hoshino, T.; Erata, T. 13C and 139La NMR studies of La2@C80: First evidence for circular motion of metal atoms in endohedral dimetallofullerenes. Angew. Chem. Int. Ed. 1997, 36, 1643–1645. [Google Scholar] [CrossRef]
- Kobayashi, K.; Nagase, S.; Maeda, Y.; Wakahara, T.; Akasaka, T. La2@C80: Is the circular motion of two La atoms controllable by exohedral addition? Chem. Phys. Lett. 2003, 374, 562–566. [Google Scholar] [CrossRef]
- Slanina, Z. Contemporary Theory of Chemical Isomerism; Academia: Prague, Czech Republic; D. Reidel Publ. Comp.: Dordrecht, The Netherlands, 1986; pp. 21–23. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Bao, L.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculated relative populations for the Eu@C82 isomers. Chem. Phys. Lett. 2019, 726, 29–33. [Google Scholar] [CrossRef]
- Takata, M.; Nishibori, E.; Sakata, M.; Shinohara, H. Charge density level structures of endohedral metallofullerenes determined by synchrotron radiation powder method. New Diam. Front. Carb. Technol. 2002, 12, 271–286. [Google Scholar]
- Hehre, W.J. A Guide to Molecular Mechanics and Quantum Chemical Calculations; Wavefunction: Irvine, CA, USA, 2003; p. 435. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry; Wiley: Chichester, UK, 2017; p. 319. [Google Scholar]
- Campanera, J.M.; Bo, C.; Poblet, J.M. General rule for the stabilization of fullerene cages encapsulating trimetallic nitride templates. Angew. Chem. Int. Ed. 2005, 44, 7230–7233. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Pan, C.; Akasaka, T.; Lu, X.; Adamowicz, L. Computed stabilization for a giant fullerene endohedral: Y2C2@C1(1660)-C108. Chem. Phys. Lett. 2018, 710, 147–149. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Nagase, S. Structural and bonding features of Z@C82 (Z = Al, Sc, Y, La) endohedrals. J. Comput. Meth. Sci. Engn. 2010, 10, 569–574. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Shen, W.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculations of the relative populations of Lu@C82 isomers. Nanotub. Carbon Nanostruct. 2019, 27, 710–714. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculated relative thermodynamic stabilities of the Gd@C82 isomers. ECS J. Solid State Sci. Technol. 2021, 10, 071013-1–071013-4. [Google Scholar] [CrossRef]
- Meng, Q.Y.; Morales-Martínez, R.; Zhuang, J.X.; Yao, Y.R.; Wang, Y.F.; Feng, L.; Poblet, J.M.; Rodríguez-Fortea, A.; Chen, N. Synthesis and characterization of two isomers of Th@C82: Th@C2v(9)-C82 and Th@C2(5)-C82. Inorg. Chem. 2021, 60, 11496–11502. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Feng, L.; Adamowicz, L. Ho@C82 metallofullerene: Calculated isomeric composition. ECS J. Solid State Sci. Technol. 2022, 11, 053018-1–053018-4. [Google Scholar] [CrossRef]
- Andreoni, W.; Curioni, A. Freedom and constraints of a metal atom encapsulated in fullerene cages. Phys. Rev. Lett. 1996, 77, 834–837. [Google Scholar] [CrossRef]
- Popov, A.A.; Dunsch, L. Bonding in endohedral metallofullerenes as studied by quantum theory of atoms in molecules. Chem. Eur. J. 2009, 15, 9707–9729. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Akasaka, T.; Nagase, S. Computed stabilities in metallofullerene series: Al@C82, Sc@C82, Y@C82, and La@C82. Int. J. Quant. Chem. 2011, 111, 2712–2718. [Google Scholar] [CrossRef]
- Rodríguez-Fortea, A.; Balch, A.L.; Poblet, J.M. Endohedral metallofullerenes: A unique host-guest association. Chem. Soc. Rev. 2011, 40, 3551–3563. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef]
- Yang, H.; Yu, M.; Jin, H.; Liu, Z.; Yao, M.; Liu, B.; Olmstead, M.M.; Balch, A.L. Isolation of three isomers of Sm@C84 and X-ray crystallographic characterization of Sm@D3d(19)-84 and Sm@C2(13)-C84. J. Am. Chem. Soc. 2012, 134, 5331. [Google Scholar] [CrossRef]
- Slanina, Z.; Zhao, X.; Uhlík, F.; Ozawa, M.; Osawa, E. Computational modelling of the metal and other elemental catalysis in the Stone-Wales fullerene rearrangements. J. Organomet. Chem. 2000, 599, 57–61. [Google Scholar] [CrossRef]
- Hao, Y.; Feng, L.; Xu, W.; Gu, Z.; Hu, Z.; Shi, Z.; Slanina, Z.; Uhlík, F. Sm@C2v(19138)-C76: A Non-IPR Cage Stabilized by a Divalent Metal Ion. Inorg. Chem. 2015, 54, 4243–4248. [Google Scholar] [CrossRef]
- Hao, Y.; Tang, Q.; Li, X.; Zhang, M.; Wan, Y.; Feng, L.; Chen, N.; Slanina, Z.; Adamowicz, L.; Uhlík, F. Isomeric Sc2O@C78 related by a single-step Stone–Wales. transformation: Key links in an unprecedented fullerene formation pathway. Inorg. Chem. 2016, 55, 11354–11361. [Google Scholar] [CrossRef]
- Jehlička, J.; Svatoš, A.; Frank, O.; Uhlík, F. Evidence for fullerenes in solid bitumen from pillow lavas of proterozoic age from Mítov (Bohemian Massif, Czech Republic) Geochem. Cosmochem. Acta 2003, 67, 1495–1506. [Google Scholar] [CrossRef]
- Lian, Y.; Shi, Z.; Zhou, X.; Gu, Z. Different extraction behaviors between divalent and trivalent endohedral metallofullerenes. Chem. Mater. 2004, 16, 1704–1714. [Google Scholar] [CrossRef]
- Maeda, Y.; Tsuchiya, T.; Kikuchi, T.; Nikawa, H.; Yang, T.; Zhao, X.; Slanina, Z.; Suzuki, M.; Yamada, M.; Lian, Y.; et al. Effective derivatization and extraction of insoluble missing lanthanum metallofullerenes La@C2n (n = 36–38) with iodobenzene. Carbon 2016, 98, 67–73. [Google Scholar] [CrossRef]
- An, D.-Y.; Su, J.-G.; Li, C.-H.; Li, J.-Y. Computational studies on the interactions of nanomaterials with proteins and their impacts. Chin. Phys. B 2015, 24, 120504-1–120504-8. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Tahuilan-Anguiano, D.E. Complexation of free-base and 3d transition metal(II) phthalocyanines. with endohedral fullerene Sc3N@C80. Chem. Phys. Lett. 2019, 722, 146–152. [Google Scholar] [CrossRef]
- Tahuilan-Anguiano, D.E.; Basiuk, V.A. Complexation of free-base and 3d transition metal(II) phthalocyanines with endohedral fullerenes H@C60, H2@C60 and He@C60: The effect of encapsulated species. Diam. Rel. Mat. 2021, 118, 108510-1–108510-5. [Google Scholar] [CrossRef]
- Li, M.; Zhao, R.; Dang, J.; Zhao, X. Theoretical study on the stabilities, electronic structures, and reaction and formation mechanisms of fullerenes and endohedral metallofullerenes. Coor. Chem. Rev. 2022, 471, 214762-1–214762-12. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Adamowicz, L. Theoretical predictions of fullerene stabilities. In Handbook of Fullerene Science and Technology; Lu, X., Akasaka, T., Slanina, Z., Eds.; Springer: Singapore, 2022; pp. 111–179. [Google Scholar]
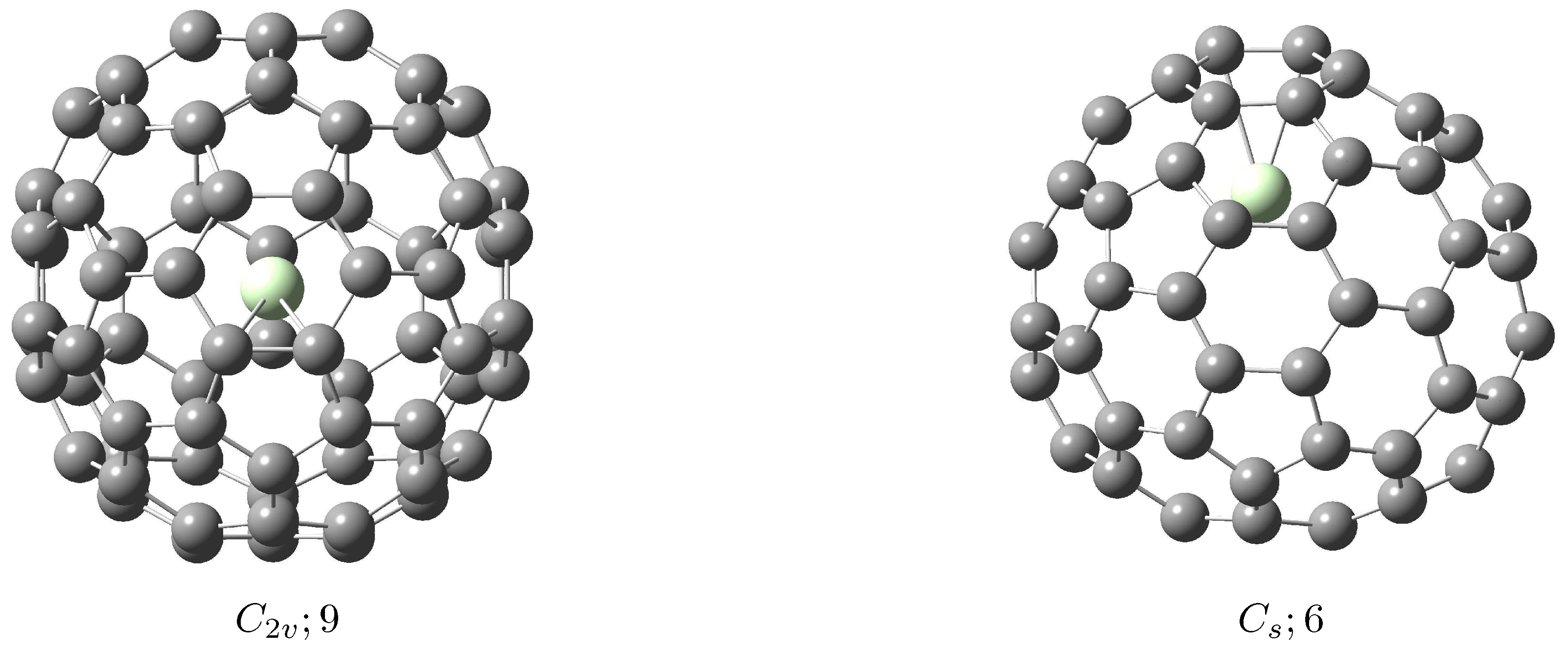
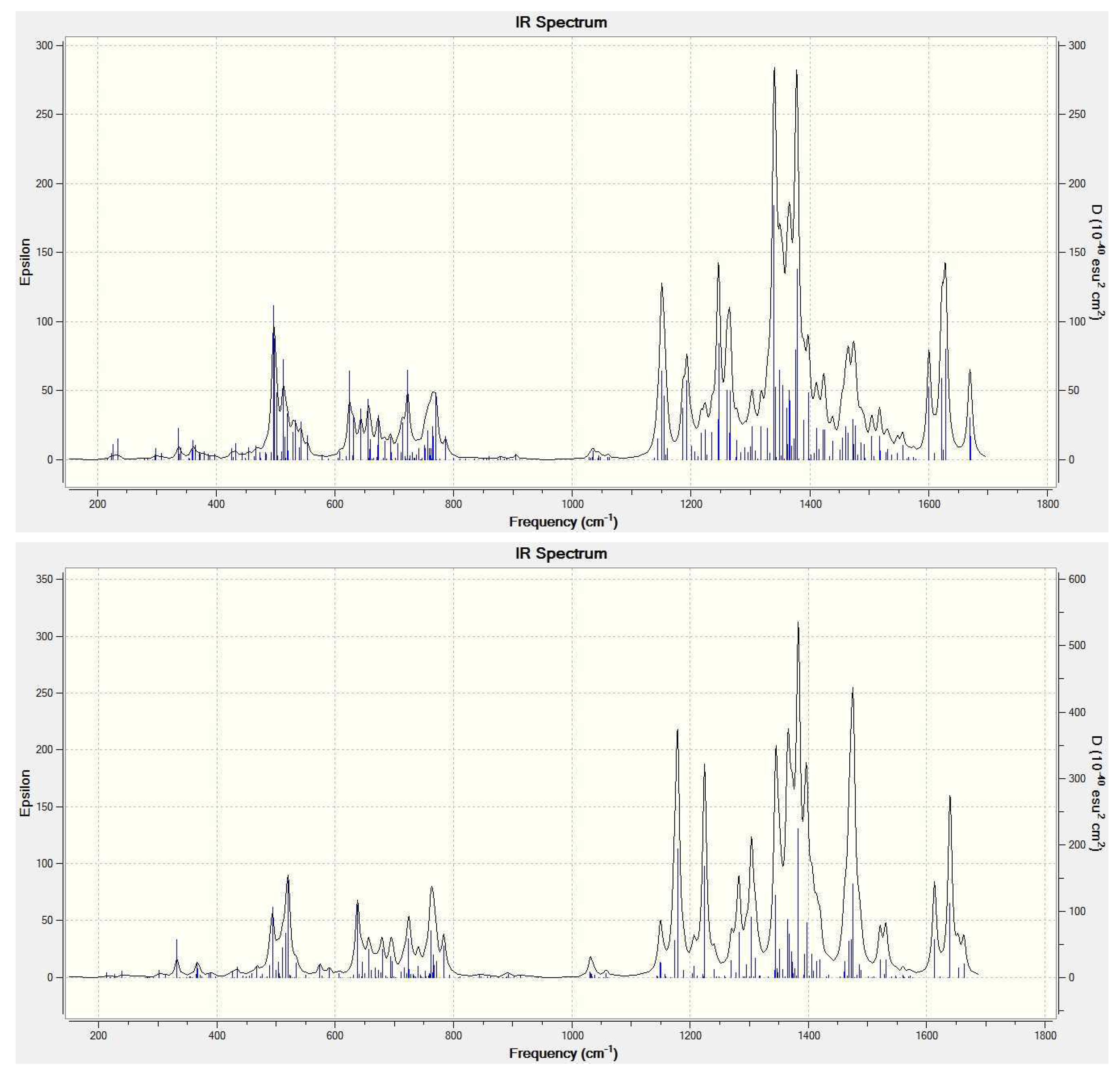
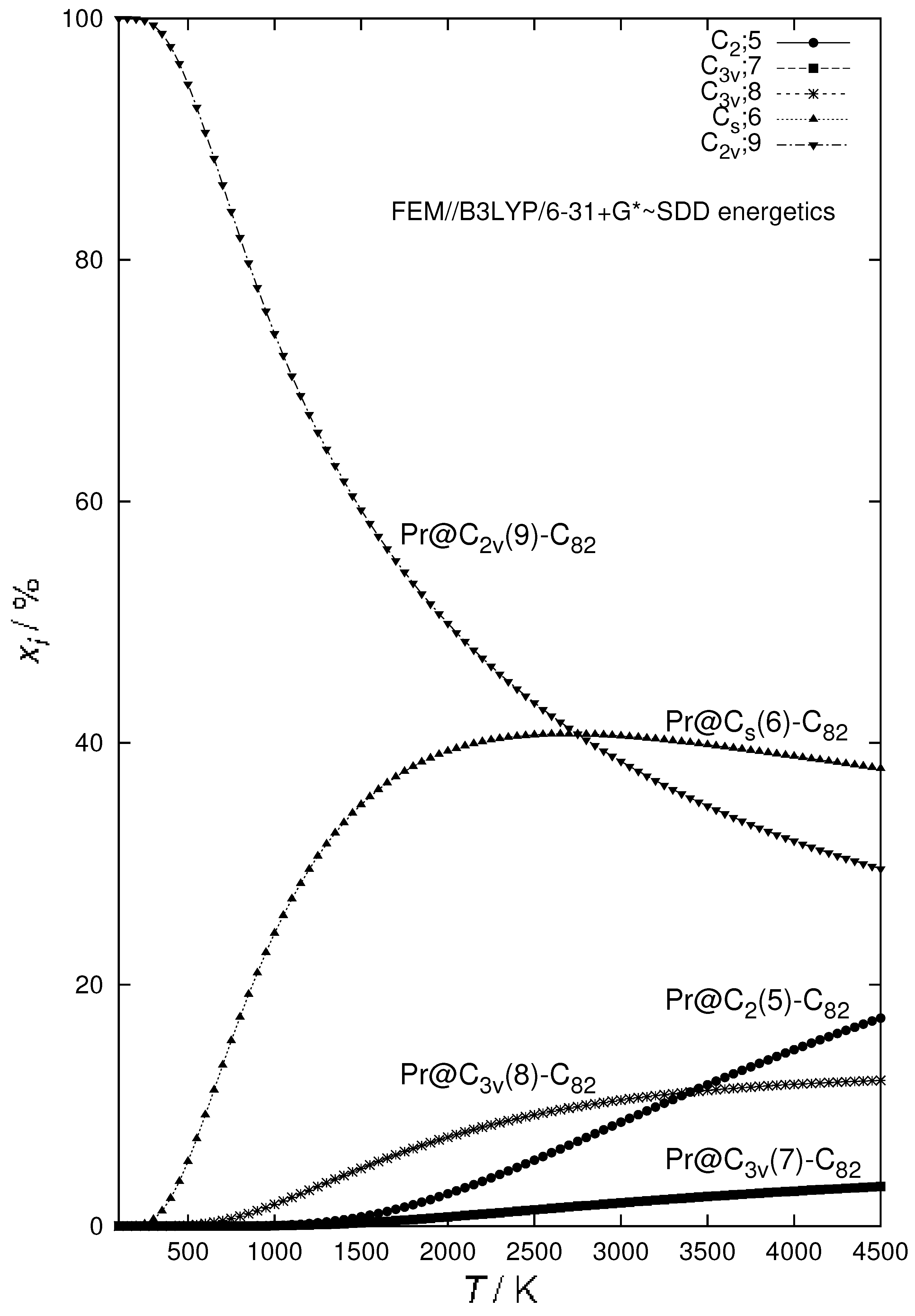
| Species | /kcal mol B3LYP/6-31G∼SDD | B3LYP/6-31+G∼SDD |
|---|---|---|
| 17.9 | 17.3 | |
| 13.0 | 14.2 | |
| 7.54 | 7.37 | |
| 3.46 | 3.47 | |
| 0.0 | 0.0 |
| Species | /Å | / cm | |
|---|---|---|---|
| 2.512 | 2.449 | 39.3 | |
| 2.516 | 2.293 | 17.6 | |
| 2.476 | 2.462 | 22.3 | |
| 2.500 | 2.337 | 20.5 | |
| 2.549 | 2.364 | 15.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Pr@C82 Metallofullerene: Calculated Isomeric Populations. Inorganics 2023, 11, 313. https://doi.org/10.3390/inorganics11070313
Slanina Z, Uhlík F, Akasaka T, Lu X, Adamowicz L. Pr@C82 Metallofullerene: Calculated Isomeric Populations. Inorganics. 2023; 11(7):313. https://doi.org/10.3390/inorganics11070313
Chicago/Turabian StyleSlanina, Zdeněk, Filip Uhlík, Takeshi Akasaka, Xing Lu, and Ludwik Adamowicz. 2023. "Pr@C82 Metallofullerene: Calculated Isomeric Populations" Inorganics 11, no. 7: 313. https://doi.org/10.3390/inorganics11070313
APA StyleSlanina, Z., Uhlík, F., Akasaka, T., Lu, X., & Adamowicz, L. (2023). Pr@C82 Metallofullerene: Calculated Isomeric Populations. Inorganics, 11(7), 313. https://doi.org/10.3390/inorganics11070313









