Defect Structure of Nanocrystalline NiO Oxide Stabilized by SiO2
Abstract
1. Introduction
2. Results and Discussion
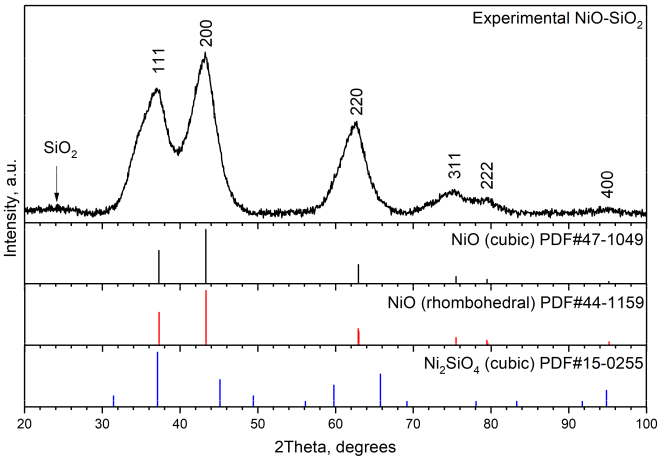
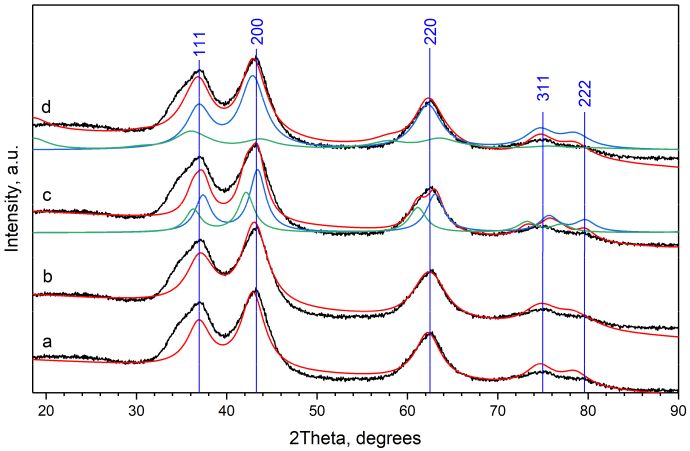
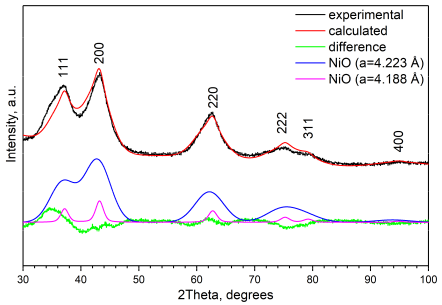
2.1. Rietveld Analysis
2.2. HRTEM Characterization
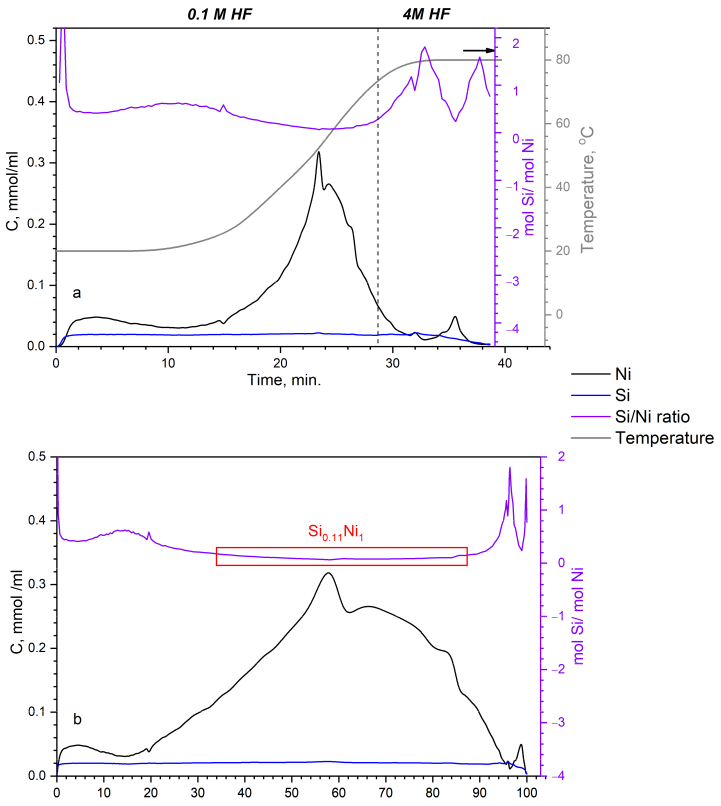
2.3. Differential Dissolution
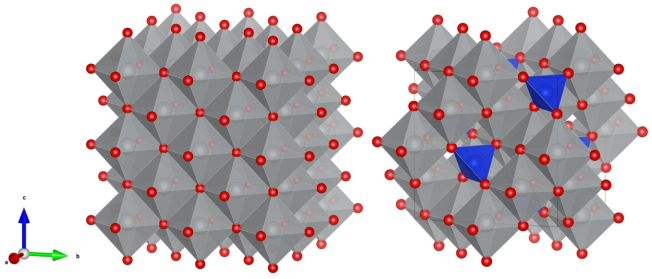
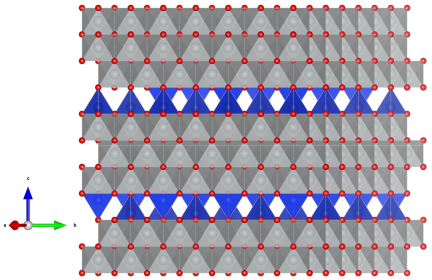
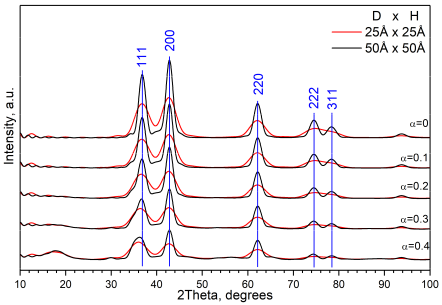
2.4. Simulation of SiO2 Incorporation into the NiO Structure
2.5. Rietveld Analysis by Two Cubic Phases
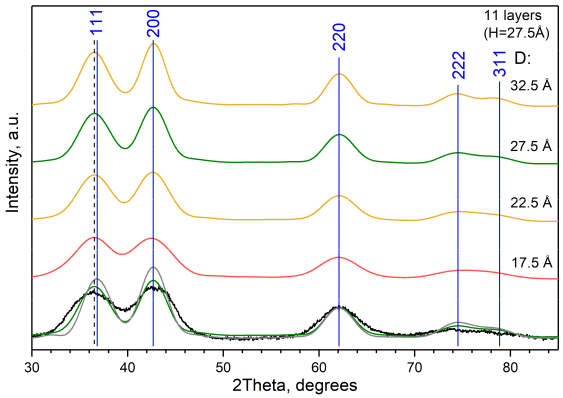
2.6. Optimization of the Model of Cylindrical Particles Consisting of Ni4O4 and Si2O4 Layers
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Meloni, E.; Martino, M.; Palma, V. A short review on Ni based catalysts and related engineering issues for methane steam reforming. Catalysts 2020, 10, 352. [Google Scholar] [CrossRef]
- Pastor-Pérez, L.; Saché, E.L.; Jones, C.; Gu, S.; Arellano-Garcia, H.; Reina, T.R. Synthetic natural gas production from CO2 over Ni-x/CeO2-ZrO2 (x = Fe, Co) catalysts: Influence of promoters and space velocity. Catal. Today 2018, 317, 108–113. [Google Scholar] [CrossRef]
- Mo, W.; Ma, F.; Ma, Y.; Fan, X. The optimization of Ni–Al2O3 catalyst with the addition of La2O3 for CO2–CH4 reforming to produce syngas. Int. J. Hydrog. Energy 2019, 44, 24510–24524. [Google Scholar] [CrossRef]
- Sánchez, J.; Tallafigo, M.F.; Gilarranz, M.A.; Rodríguez, F. Refining Heavy Neutral Oil Paraffin by Catalytic Hydrotreatment over Ni−W/Al2O3 Catalysts. Energy Fuels 2006, 20, 245–249. [Google Scholar] [CrossRef]
- Srinivas, D.; Satyanarayana, C.V.V.; Potdar, H.S.; Ratnasamy, P. Structural studies on NiO-CeO2-ZrO2 catalysts for steam reforming of ethanol. Appl. Catal. A Gen. 2003, 246, 323–334. [Google Scholar] [CrossRef]
- Xu, S.; Yan, X.; Wang, X. Catalytic performances of NiO–CeO2 for the reforming of methane with CO2 and O2. Fuel 2006, 85, 2243–2247. [Google Scholar] [CrossRef]
- Mohd Ridzuan, N.D.; Shaharun, M.S.; Anawar, M.A.; Ud-Din, I. Ni-Based Catalyst for Carbon Dioxide Methanation: A Review on Performance and Progress. Catalysts 2022, 12, 469. [Google Scholar] [CrossRef]
- Laurent, E.; Delmon, B. Deactivation of a Sulfided NiMo/γ-Al2O3 during the Hydrodeoxygenation of Bio-Oils: Influence of a High Water Pressure. Stud. Surf. Sci. Catal. 1994, 88, 459–466. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, L.; Xin, H.; Wang, G.; Li, D.; Hu, C. The production of diesel-like hydrocarbons from palmitic acid over HZSM-22 supported nickel phosphide catalysts. Appl. Catal. B Environ. 2015, 174–175, 504–514. [Google Scholar] [CrossRef]
- Kirumakki, S.R.; Shpeizer, B.G.; Sagar, G.V.; Chary, K.V.R.; Clearfield, A. Hydrogenation of Naphthalene over NiO/SiO2–Al2O3 catalysts: Structure–activity correlation. J. Catal. 2006, 242, 319–331. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Horiguchi, J.; Kobayashi, S.; Yamazaki, Y.; Omata, K.; Nagao, D.; Konno, M.; Yamada, M. Effect of NiO content in mesoporous NiO–Al2O3 catalysts for high pressure partial oxidation of methane to syngas. Appl. Catal. A Gen. 2011, 395, 129–137. [Google Scholar] [CrossRef]
- Parmaliana, A.; Arena, F.; Frusteri, F.; Giordano, N. Temperature-programmed reduction study of NiO-MgO interactions in magnesia-supported Ni catalysts and NiO-MgO physical mixture. J. Chem. Soc. Faraday Trans. 1990, 86, 2663–2669. [Google Scholar] [CrossRef]
- Smirnov, A.A.; Khromova, S.A.; Ermakov, D.Y.; Bulavchenko, O.A.; Saraev, A.A.; Aleksandrov, P.V.; Kaichev, V.V.; Yakovlev, V.A. The composition of Ni-Mo phases obtained by NiMoOx-SiO2 reduction and their catalytic properties in anisole hydrogenation. Appl. Catal. A Gen. 2016, 514, 224–234. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, J.; Chen, Y. Studies of surface NiO species in NiO/SiO2 catalysts using temperature-programmed reduction and X-ray diffraction. J. Chem. Soc. Faraday Trans. 1992, 88, 2075–2078. [Google Scholar] [CrossRef]
- Thalinger, R.; Gocyla, M.; Heggen, M.; Dunin-Borkowski, R.; Grünbacher, M.; Stöger-Pollach, M.; Schmidmair, D.; Klötzer, B.; Penner, S. Ni–perovskite interaction and its structural and catalytic consequences in methane steam reforming and methanation reactions. J. Catal. 2016, 337, 26–35. [Google Scholar] [CrossRef]
- Aghayan, M.; Potemkin, D.; Rubio-Marcos, F.; Uskov, S.; Snytnikov, P.; Hussainova, I. Template-assisted wet-combustion synthesis of fibrous nickel-based catalyst for carbon dioxide methanation and methane steam reforming. ACS Appl. Mater. Interfaces 2017, 9, 43553–43562. [Google Scholar] [CrossRef]
- Pakharukova, V.P.; Potemkin, D.I.; Rogozhnikov, V.N.; Stonkus, O.A.; Gorlova, A.M.; Nikitina, N.A.; Suprun, E.A.; Brayko, A.S.; Rogov, V.A.; Snytnikov, P.V. Effect of Ce/Zr Composition on Structure and Properties of Ce1-xZrxO2 Oxides and Related Ni/Ce1-xZrxO2 Catalysts for CO2 Methanation. Nanomaterials 2022, 12, 3207. [Google Scholar] [CrossRef]
- Alekseeva, M.V.; Rekhtina, M.A.; Lebedev, M.Y.; Zavarukhin, S.G.; Kaichev, V.V.; Venderbosch, R.H.; Yakovlev, V.A. Hydrotreatment of 2-Methoxyphenol over High Ni-Loaded Sol-Gel Catalysts: The Influence of Mo on Catalyst Activity and Reaction Pathways. ChemistrySelect 2018, 3, 5153–5164. [Google Scholar] [CrossRef]
- Fornasiero, P.; Balducci, G.; Di Monte, R.; Kašpar, J.; Sergo, V.; Gubitosa, G.; Ferrero, A.; Graziani, M. Modification of the redox behaviour of CeO2 induced by structural doping with ZrO2. J. Catal. 1996, 164, 173–183. [Google Scholar] [CrossRef]
- Lázaro, M.J.; Echegoyen, Y.; Alegre, C.; Suelves, I.; Moliner, R.; Palacios, J.M. TiO2 as textural promoter on high loaded Ni catalysts for methane decomposition. Int. J. Hydrog. Energy 2008, 33, 3320–3329. [Google Scholar] [CrossRef]
- Kukushkin, R.G.; Eletskii, P.M.; Bulavchenko, O.A.; Saraev, A.A.; Yakovlev, V.A. Studying the Effect of Promotion with Copper on the Activity of the Ni/Al2O3 Catalyst in the Process of Ester Hydrotreatment. Catal. Ind. 2019, 11, 198–207. [Google Scholar] [CrossRef]
- Philippov, A.A.; Nesterov, N.N.; Pakharukova, V.P.; Martyanov, O.N. High-loaded Ni-based catalysts obtained via supercritical antisolvent coprecipitation in transfer hydrogenation of anisole: Influence of the support. Appl. Catal. A Gen. 2022, 643, 118792. [Google Scholar] [CrossRef]
- Ermakova, M.; Ermakov, D.Y.; Kuvshinov, G.; Plyasova, L. New nickel catalysts for the formation of filamentous carbon in the reaction of methane decomposition. J. Catal. 1999, 187, 77–84. [Google Scholar] [CrossRef]
- Bykova, M.; Bulavchenko, O.; Ermakov, D.Y.; Lebedev, M.Y.; Yakovlev, V.; Parmon, V. Guaiacol hydrodeoxygenation in the presence of Ni-containing catalysts. Catal. Ind. 2011, 3, 15–22. [Google Scholar] [CrossRef]
- Bykova, M.; Ermakov, D.Y.; Kaichev, V.; Bulavchenko, O.; Saraev, A.; Lebedev, M.Y.; Yakovlev, V. Ni-based sol–gel catalysts as promising systems for crude bio-oil upgrading: Guaiacol hydrodeoxygenation study. Appl. Catal. B Environ. 2012, 113, 296–307. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Kukushkin, R.G.; Yeletsky, P.M.; Bulavchenko, O.A.; Chesalov, Y.A.; Yakovlev, V.A. Temperature-programmed reduction of model CuO, NiO and mixed CuO–NiO catalysts with hydrogen. J. Alloys Compd. 2020, 844, 156135. [Google Scholar] [CrossRef]
- Cherepanova, S.V. X-ray scattering on one-dimensional disordered structures. J. Struct. Chem. 2012, 53, 109–132. [Google Scholar] [CrossRef]
- Cherepanova, S.; Tsybulya, S. Peculiarities of the X-ray diffraction of oxygen-deficient perovskite-related materials with partial vacancy ordering. Z. Fur Krist. Suppl. 2008, 27, 5–12. [Google Scholar] [CrossRef]
- Cherepanova, S.V.; Leont’eva, N.N.; Arbuzov, A.B.; Drozdov, V.A.; Belskaya, O.B.; Antonicheva, N.V. Structure of oxides prepared by decomposition of layered double Mg–Al and Ni–Al hydroxides. J. Solid State Chem. 2015, 225, 417–426. [Google Scholar] [CrossRef]
- Leont’eva, N.; Cherepanova, S.; Drozdov, V.; Bel’skaya, O.; Tsybulya, S.; Stepanova, L. Influence of the Mg and Al ratio on the restructuring of hydrotalcite. Theor. Exp. Chem. 2012, 48, 278–282. [Google Scholar] [CrossRef]
- Leont’eva, N.N.; Cherepanova, S.V.; Stepanova, L.N.; Drozdov, V.A.; Lavrenov, A.V. Structural Aspects of “Memory Effect” for MgGa LDHs: New Data Obtained by Simulation of XRD Patterns for 1D Disordered Crystals. Crystals 2022, 12, 629. [Google Scholar] [CrossRef]

| Model | Phase | Space Group | wt% | Lattice Constants, Å | D, Å | Rwp, % |
|---|---|---|---|---|---|---|
| a | NiO-cubic | Fm3m | 100 | a = 4.209(3) | 20 | 37 |
| b | NiO-rhombohedral | R-3m | 100 | a = 3.005(4), c = 7.193(2) | 20 | 24 |
| c | NiO-cubic | Fm3m | 61(1) | a = 4.169(5) | 25 | 36 |
| NiO-cubic | Fm3m | 39(1) | a = 4.288(7) | 25 | ||
| d | NiO-cubic | Fm3m | 66(1) | a = 4.218(2) | 20 | 21 |
| Ni2SiO4. | Fd3m | 34(1) | a = 8.28(2) | 15 |
| Ni4O4 | Si2O4 | ||||||
|---|---|---|---|---|---|---|---|
| Atom | x | y | z | Atom | x | y | z |
| O | 1/6 | 5/6 | 0 | O | 1/6 | 5/6 | 0 |
| 1/6 | 1/3 | 0 | 1/6 | 1/3 | 0 | ||
| 2/3 | 5/6 | 0 | 2/3 | 5/6 | 0 | ||
| 2/3 | 1/3 | 0 | 2/3 | 1/3 | 0 | ||
| Ni | 0 | 0 | 0.5 | Si | 1/3 | 2/3 | 0.25 |
| 0.5 | 0 | 0.5 | 2/3 | 1/3 | 0.75 | ||
| 0 | 0.5 | 0.5 | |||||
| 0.5 | 0.5 | 0.5 | |||||
| D, Å | ||||||||
|---|---|---|---|---|---|---|---|---|
| H, Å | 17.5 | 20 | 22.5 | 25 | 27.5 | 30 | 32.5 | 35 |
| 27.5 | 0.141 | 0.110 | 0.067 | 0.033 | 0.007 | 0.017 | 0.035 | 0.051 |
| 25 | 0.135 | 0.103 | 0.067 | 0.037 | 0.012 | 0.006 | 0.020 | 0.033 |
| 22.5 | x | 0.114 | 0.083 | 0.057 | 0.037 | 0.024 | 0.013 | 0.004 |
| 20 | x | x | 0.111 | 0.090 | 0.076 | 0.065 | 0.058 | 0.105 |
| 17.5 | x | x | x | 0.098 | 0.117 | 0.111 | 0.108 | 0.105 |
| 15 | x | x | x | x | 0.179 | 0.177 | 0.178 | 0.177 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikhnenko, M.D.; Cherepanova, S.V.; Gerasimov, E.Y.; Pochtar, A.A.; Alekseeva, M.V.; Kukushkin, R.G.; Yakovlev, V.A.; Bulavchenko, O.A. Defect Structure of Nanocrystalline NiO Oxide Stabilized by SiO2. Inorganics 2023, 11, 97. https://doi.org/10.3390/inorganics11030097
Mikhnenko MD, Cherepanova SV, Gerasimov EY, Pochtar AA, Alekseeva MV, Kukushkin RG, Yakovlev VA, Bulavchenko OA. Defect Structure of Nanocrystalline NiO Oxide Stabilized by SiO2. Inorganics. 2023; 11(3):97. https://doi.org/10.3390/inorganics11030097
Chicago/Turabian StyleMikhnenko, Maxim D., Svetlana V. Cherepanova, Evgeny Yu Gerasimov, Alena A. Pochtar, Maria V. Alekseeva (Bykova), Roman G. Kukushkin, Vadim A. Yakovlev, and Olga A. Bulavchenko. 2023. "Defect Structure of Nanocrystalline NiO Oxide Stabilized by SiO2" Inorganics 11, no. 3: 97. https://doi.org/10.3390/inorganics11030097
APA StyleMikhnenko, M. D., Cherepanova, S. V., Gerasimov, E. Y., Pochtar, A. A., Alekseeva, M. V., Kukushkin, R. G., Yakovlev, V. A., & Bulavchenko, O. A. (2023). Defect Structure of Nanocrystalline NiO Oxide Stabilized by SiO2. Inorganics, 11(3), 97. https://doi.org/10.3390/inorganics11030097









