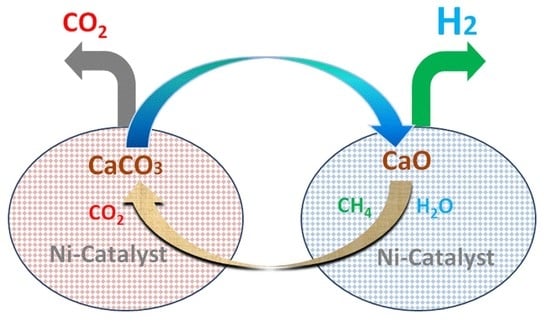
Simulation of Sorption-Enhanced Steam Methane Reforming over Ni-Based Catalyst in a Pressurized Dual Fluidized Bed Reactor
Abstract
1. Introduction
2. Results and Discussion
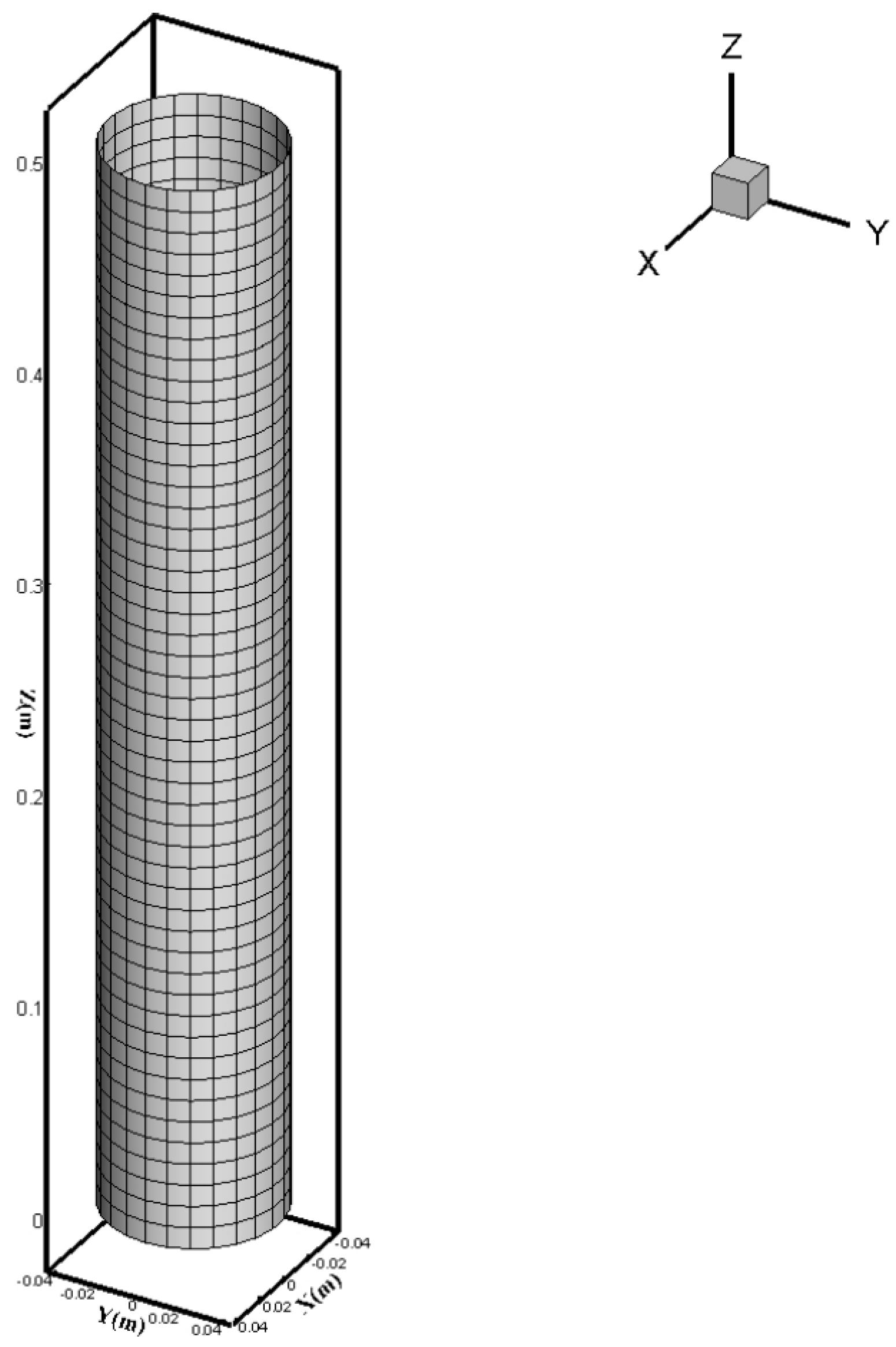
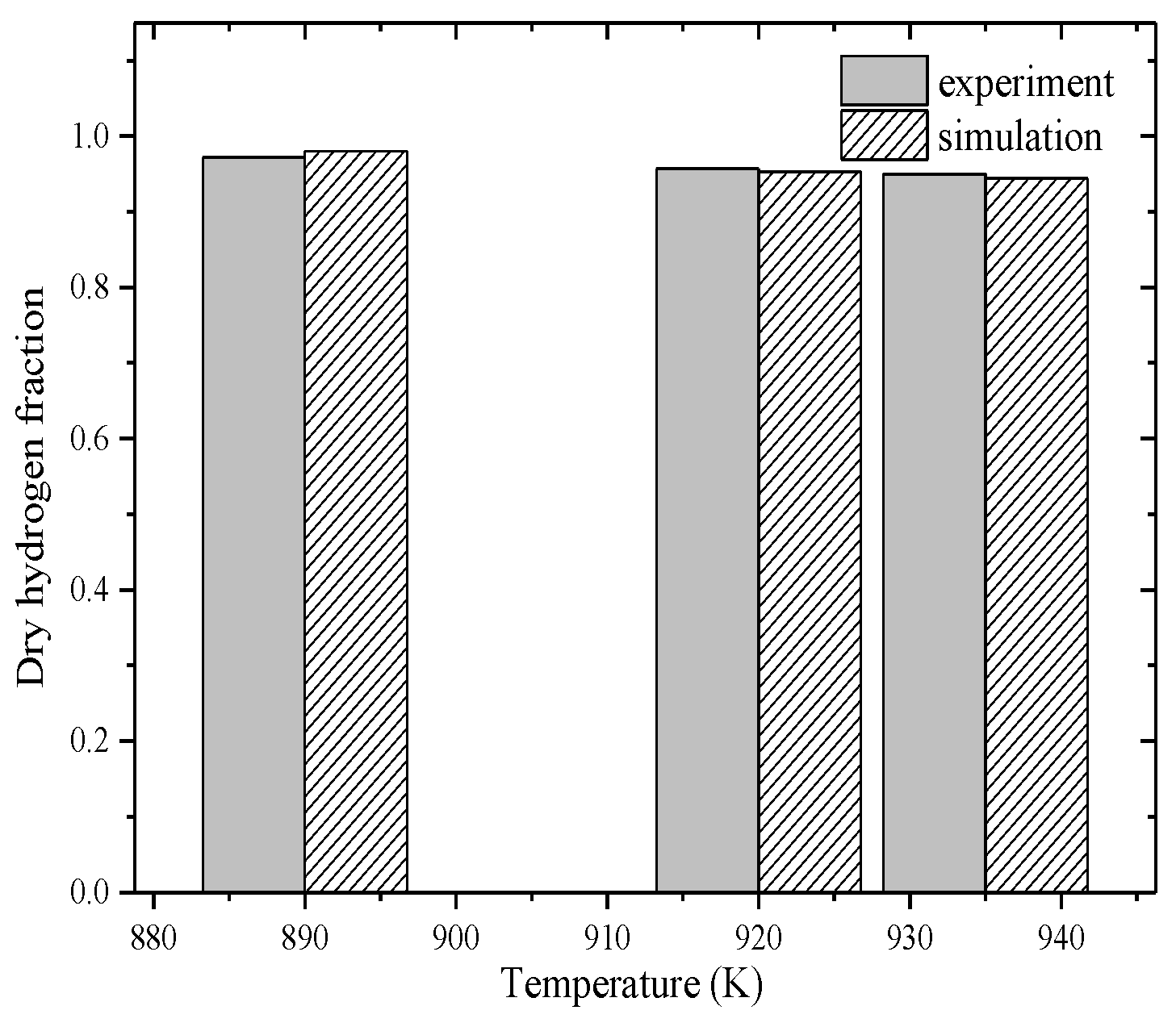
2.1. Model Validation
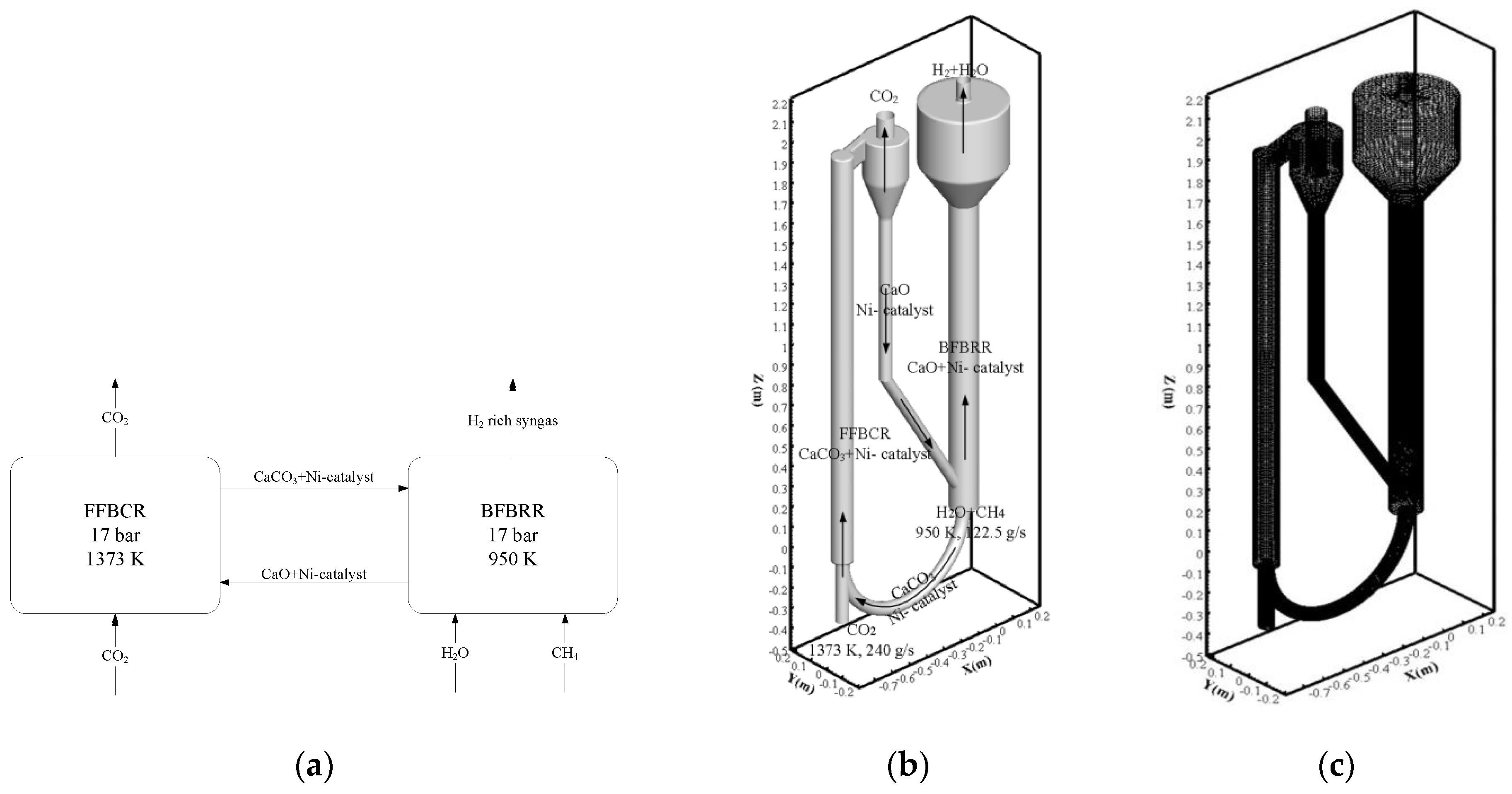
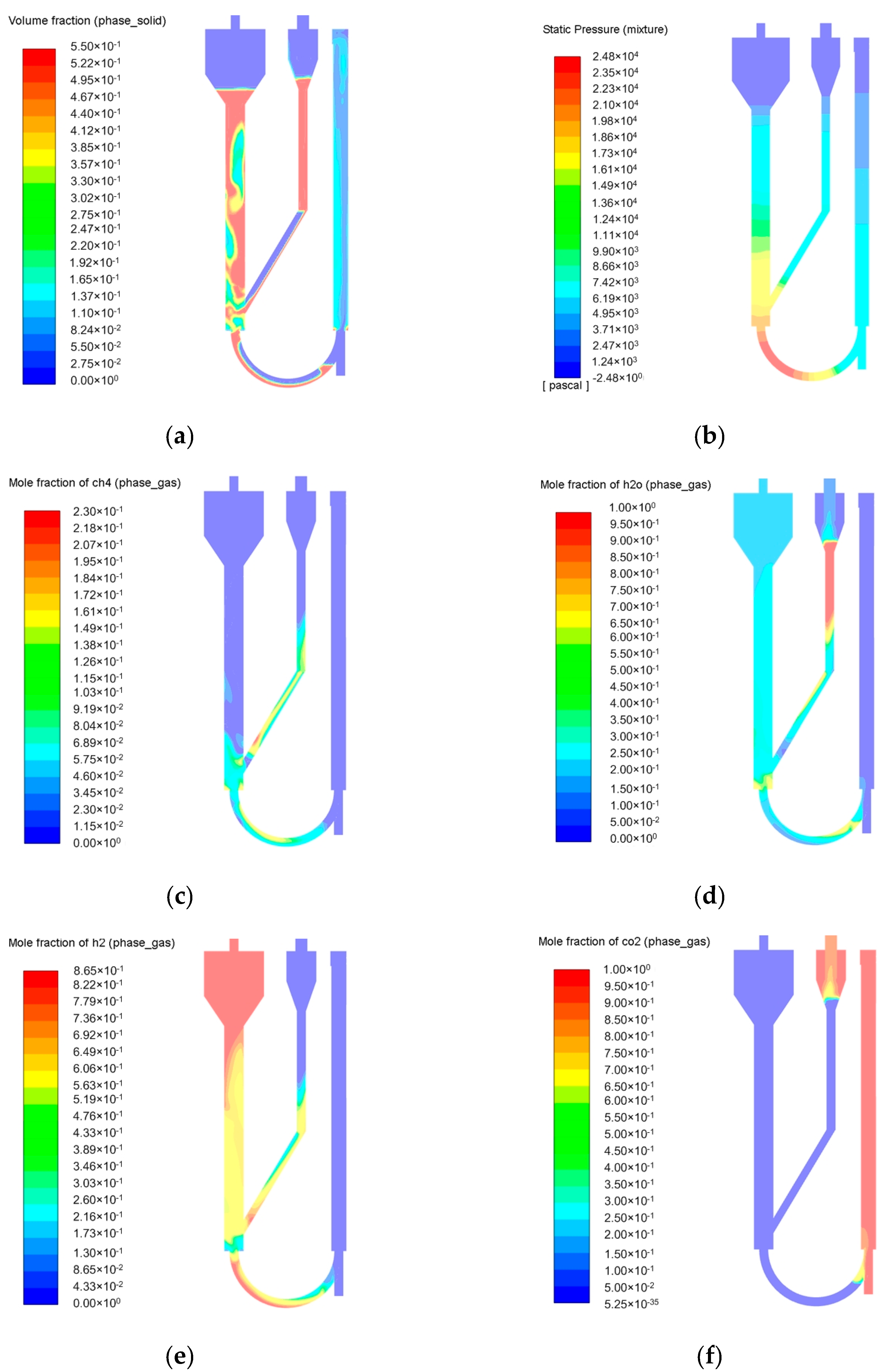
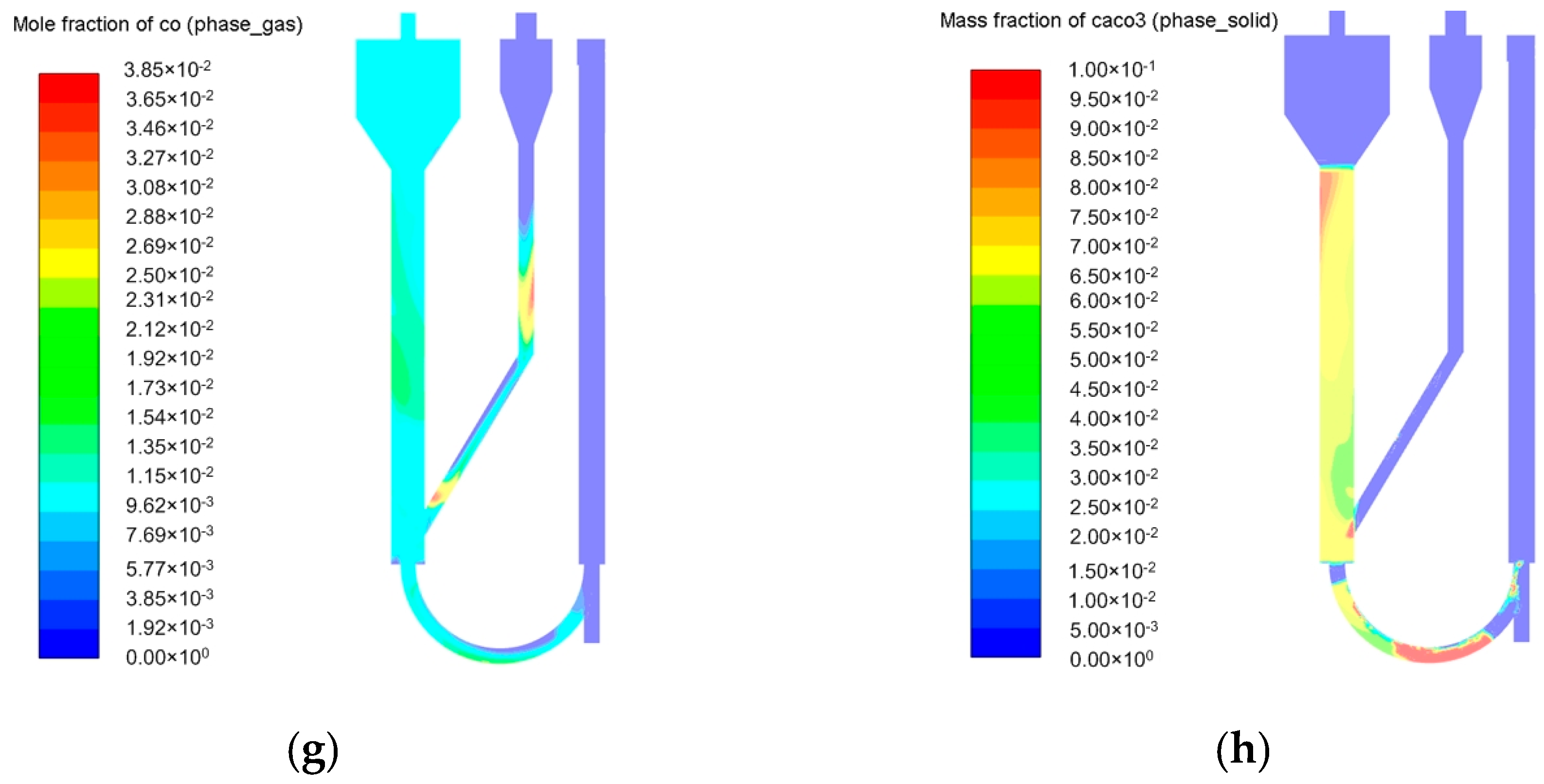
2.2. Simulation of the Pressurized Dual Fluidized Bed Reactor
3. Materials and Methods
3.1. Computational Fluid Dynamics Model
3.2. The Reaction Kinetics
3.3. Solution Methods
4. Conclusions
- (1)
- The numerical simulation model for the sorption-enhanced SRM is solid and can be used to predict similar processes;
- (2)
- The dual fluidized bed designed for the SMR process operates stably and can be used for H2 production by sorption-enhanced SMR technology;
- (3)
- The methane conversion in the dual fluidized bed reactor at the given operating condition is close to 100%. The H2 mole fraction in the dry syngas is about 98.8%. The CO2 capture ratio is about 96.4%. The cold-gas efficiency of the reactor is 98.5%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamshybayeva, G.K.; Kossalbayev, B.D.; Sadvakasova, A.K.; Kakimova, A.B.; Bauenova, M.O.; Zayadan, B.K.; Lan, C.-W.; Alwasel, S.; Tomo, T.; Chang, J.-S.; et al. Genetic engineering contribution to developing cyanobacteria-based hydrogen energy to reduce carbon emissions and establish a hydrogen economy. Int. J. Hydrogen Energy 2023. [Google Scholar] [CrossRef]
- Kalamaras, C.M.; Efstathiou, A.M. Hydrogen production technologies: Current state and future developments. Conf. Pap. Energy 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Ogden, J.M.; Steinbugler, M.M.; Kreutz, T.G. Cmparison of hydrogen, methanol and gasoline as fuels for fuel cell vehicles: Implications for vehicle design and infrastructure development. J. Power Sources 1999, 79, 143–168. [Google Scholar] [CrossRef]
- Hohn, K.L.; Schmidt, L.D. Partial oxidation of methane to syngas at high space velocities over Rh-coated spheres. Appl. Catal. A 2001, 211, 53–68. [Google Scholar] [CrossRef]
- Joensen, F.; Rostrup-Nielsen, J.R. Conversion of hydrocarbons and alcohols for fuel cells. J. Power Sources 2002, 105, 195–201. [Google Scholar] [CrossRef]
- Bromberg, L.; Cohn, D.R.; Rabinovich, A. Plasma reformer-fuel cell system for decentralized power applications. Int. J. Hydrogen Energy 1997, 22, 83–94. [Google Scholar] [CrossRef]
- Demirbas, M.F. Hydrogen from various biomass species via pyrolysis and steam gasification processes. Energy Sources 2006, 28, 245–252. [Google Scholar] [CrossRef]
- Demirbaş, A. Recovery of chemicals and gasoline-range fuels from plastic wastes via pyrolysis. Energy Sources 2005, 27, 1313–1319. [Google Scholar] [CrossRef]
- Davda, R.R.; Shabaker, J.W.; Huber, G.W.; Cortright, R.D.; Dumesic, J.A. Aqueous-phase reforming of ethylene glycol on silica-supported metal catalysts. Appl. Catal. B 2003, 43, 13–26. [Google Scholar] [CrossRef]
- Turner, J.; Sverdrup, G.; Mann, M.K.; Maness, P.C.; Kroposki, B.; Ghirardi, M.; Evans, R.J.; Blake, D. Renewable hydrogen production. Int. J. Energy Res. 2008, 32, 379–407. [Google Scholar] [CrossRef]
- Hamelinck, C.N.; Faaij, A.P.C. Future prospects for production of methanol and hydrogen from biomass. J. Power Sources 2002, 111, 1–22. [Google Scholar] [CrossRef]
- Steinfeld, A. Solar thermochemical production of hydrogen—A review. Sol. Energy 2005, 78, 603–615. [Google Scholar] [CrossRef]
- Oh, K.; Kim, D.; Lim, K.; Ju, H. Multidimensional modeling of steam methane reforming based fuel processor for hydrogen production. Fusion Sci. Technol. 2020, 76, 415–423. [Google Scholar] [CrossRef]
- Cherif, A.; Nebbali, R.; Sen, F.; Sheffeld, J.W.; Doner, N.; Nasser, L. Modeling and simulation of steam methane reforming and methane combustion over continuous and segmented catalyst beds in autothermal reactor. Int. J. Hydrogen Energy 2022, 47, 9127–9138. [Google Scholar] [CrossRef]
- Sadeghi, M.T.; Molaei, M. CFD simulation of a methane steam reforming reactor. Int. J. Chem. React. Eng. 2008, 6, 1–12. [Google Scholar] [CrossRef]
- Wang, H.; Yang, G.G.; Li, S.; Shen, Q.W.; Li, Z.; Chen, B.J. Numerical study on the effect of discrete catalytic layer arrangement on methane steam reforming performance. RSC Adv. 2021, 11, 2958–2967. [Google Scholar] [CrossRef]
- Chen, K.; Zhao, Y.; Zhang, W.; Feng, D.; Sun, S. The intrinsic kinetics of methane steam reforming over a nickel-based catalyst in a micro fluidized bed reaction system. Int. J. Hydrogen Energy 2019, 43, 1615–1628. [Google Scholar] [CrossRef]
- Cownden, R.; Mullen, D.; Lucquiaud, M. Towards net-zero compatible hydrogen from steam reformation—Techno-economic analysis of process design options. Int. J. Hydrogen Energy 2023. [Google Scholar] [CrossRef]
- Wu, W.; Tungpanututh, C. Optimization of a methane autothermal reforming-based hydrogen production system with low CO2 emissions. IFAC Proc. Vol. 2012, 15, 661–666. [Google Scholar] [CrossRef]
- Vanga, G.; Gattia, D.M.; Stendardo, S.; Scaccia, S. Novel synthesis of combined CaO-Ca12Al14O33-Ni sorbent-catalyst material for sorption enhanced steam reforming processes. Ceram. Int. 2019, 45, 7594–7605. [Google Scholar] [CrossRef]
- Menikpura, S.N.M.; Basnayake, B.F.A. New applications of ‘Hess Law’ and comparisons with models for determining calorific values of municipal solid wastes in the Sri Lankan context. Renew. Energy 2009, 6, 1587–1594. [Google Scholar] [CrossRef]
- George, W.R. Chemical Reactions and Chemical Reactors; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Powell, J.; Wongsakulphasatch, S.; Kokoo, R.; Noppakun, N.; Prapainainar, C.; Aziz, M.A.A.; Assabumrungrat, S. Optimisation of a sorption-enhanced chemical looping steam methane reforming process. Chem. Eng. Res. Des. 2021, 173, 183–192. [Google Scholar] [CrossRef]
- Carlo, A.D.; Bocci, E.; Zuccari, F.; Dell’Era, A. Numerical investigation of sorption enhanced steam methane reforming process using computational fluid dynamics Eulerian-Eulerian Code. Ind. Eng. Chem. Res. 2010, 49, 1561–1576. [Google Scholar] [CrossRef]
- Fernandez, J.R.; Abanades, J.C.; Grasa, G. Modeling of sorption enhanced steam methane reforming-Part II: Simulation within a novel Ca/Cu chemical loop process for hydrogen production. Chem. Eng. Sci. 2012, 84, 12–20. [Google Scholar] [CrossRef]
- Giuliano, A.D.; Gin, J.; Massacesi, R.; Gallucci, K.; Courson, C. Sorption enhanced steam methane reforming by Ni-CaO materials supported on mayenite. Int. J. Hydrogen Energy 2017, 19, 13661–13680. [Google Scholar] [CrossRef]
- Nardo, A.D.; Calchetti, G.; Carlo, A.; Stendardo, S. Sorption enhanced steam methane reforming in a bubbling fluidized bed reactor: Simulation and analysis by the CPFD method. Comput. Chem. Eng. 2023, 169, 108080. [Google Scholar] [CrossRef]
- Solsvik, J.; Chao, Z.; Sánchez, R.A.; Jakobsen, H.A. Numerical investigation of steam methane reforming with CO2-capture in bubbling fluidized bed reactors. Fuel Process. Technol. 2014, 125, 290–300. [Google Scholar] [CrossRef]
- Yan, L.; Cao, Y.; Zhou, H.; He, B. Investigation on biomass steam gasification in a dual fluidized bed reactor with the granular kinetic theory. Bioresour. Technol. 2018, 269, 384–392. [Google Scholar] [CrossRef]
- Bokkers, G.A.; Annaland, M.S.; Kuipers, J.A.M. Mixing and segregation in a bi-disperse gas-solid fluidised bed: A numerical and experimental study. Powder Technol. 2004, 140, 176–186. [Google Scholar] [CrossRef]
- Gerber, S.; Oevermann, M. A two dimensional Euler–Lagrangian model of wood gasification in a charcoal bed—Part I: Model description and base scenario. Fuel 2014, 115, 385–400. [Google Scholar] [CrossRef]
- Yan, L.; Lim, C.J.; Yue, G.; He, B.; Grace, J.R. Simulation of biomass-steam gasification in fluidized bed reactors: Model setup, comparisons and preliminary predictions. Bioresour. Technol. 2016, 221, 625–635. [Google Scholar] [CrossRef]
- Li, T.; Mahecha-Botero, A.; Grace, J.R. Computational Fluid Dynamic Investigation of Change of Volumetric Flow in Fluidized-Bed Reactors. Ind. Eng. Chem. Res. 2010, 45, 6780–6789. [Google Scholar] [CrossRef]
- Lu, H.L.; Gidaspow, D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures. Chem. Eng. Sci. 2003, 58, 3777–3792. [Google Scholar]
- ANSYS FLUENT User’s Guide; Version 19.0; ANSYS Inc.: Canonsburg, PA, USA, 2018.
- Xu, J.; Froment, G.F. Methane Steam Reforming, Methanation and Water-Gas Shift: 1. Intrinsic Kinetics. AIChE J. 1989, 35, 88–96. [Google Scholar] [CrossRef]
- Morf, P.; Hasler, P.; Nussbaumer, T. Mechanisms and kinetics of homogeneous secondary reactions of tar from continuous pyrolysis of wood chips. Fuel 2002, 81, 843–853. [Google Scholar] [CrossRef]
- Yan, L.; Cao, Y.; Li, X.; He, B. On a carbon-negative energy production scheme via a quadruple fluidized bed gasifier. Energy Convers. Manag. 2018, 171, 326–338. [Google Scholar] [CrossRef]

| The mass-conservation equations | |
| (1a) | |
| (1b) | |
| The momentum-conservation equations | |
| (2a) | |
| (2b) | |
| The energy-conservation equations | |
| (3a) | |
| (3b) | |
| The species-transportation equation | |
| (4a) | |
| (4b) | |
| The turbulence equations | |
| (5a) | |
| (5b) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Li, K.; Sui, H.; He, B.; Geng, C.; Fang, B. Simulation of Sorption-Enhanced Steam Methane Reforming over Ni-Based Catalyst in a Pressurized Dual Fluidized Bed Reactor. Inorganics 2023, 11, 107. https://doi.org/10.3390/inorganics11030107
Yan L, Li K, Sui H, He B, Geng C, Fang B. Simulation of Sorption-Enhanced Steam Methane Reforming over Ni-Based Catalyst in a Pressurized Dual Fluidized Bed Reactor. Inorganics. 2023; 11(3):107. https://doi.org/10.3390/inorganics11030107
Chicago/Turabian StyleYan, Linbo, Kexin Li, Hongyang Sui, Boshu He, Cong Geng, and Baizeng Fang. 2023. "Simulation of Sorption-Enhanced Steam Methane Reforming over Ni-Based Catalyst in a Pressurized Dual Fluidized Bed Reactor" Inorganics 11, no. 3: 107. https://doi.org/10.3390/inorganics11030107
APA StyleYan, L., Li, K., Sui, H., He, B., Geng, C., & Fang, B. (2023). Simulation of Sorption-Enhanced Steam Methane Reforming over Ni-Based Catalyst in a Pressurized Dual Fluidized Bed Reactor. Inorganics, 11(3), 107. https://doi.org/10.3390/inorganics11030107