Abstract
This study looked at the thermal conductivity of translucent (Y1−xGdx)2O3 (where 0 ≤ x ≤ 1) solid solution ceramics in the temperature range from 50 K to 300 K. The samples were obtained by hot pressing from high-purity nanopowders at 1600 °C, no sintering additives were used. Compositions with cubic syngony (x ≤ 0.7) and a monoclinic one (x ≥ 0.9) were investigated. Furthermore, a dense sample of cubic Gd2O3 with a LiF sintering additive was obtained and its thermal conductivity was determined (k = 11.7 W/(m K) at 300 K). It was shown that in the range of solid solution ceramic compositions 0.2 ≤ x ≤ 0.7, the thermal conductivity was practically unchanged and close to the value k ≈ 5 W/(m K) at 300 K.
1. Introduction
Solid solutions of yttrium and gadolinium oxides are widely used in the form of optical ceramics doped with europium ions as a scintillation medium for detecting high-energy radiation, for example, in computer tomography apparatus [1]. Eu3+ ions have a high light output, and their emission line (λ = 610 nm) coincides with the maximum sensitivity of the most common CCDs. Gadolinium oxide, due to its high effective atomic number, has a good absorption ability of gamma- and X-ray radiation, and as a matrix component provides a more intense photoluminescence of Eu3+ ions compared to other REM oxides and an improved time response of scintillation. Yttrium oxide is introduced into the matrix primarily as a process additive. To achieve the optical transparency of ceramics, an almost complete removal of pores is required, which is achieved with free sintering in a vacuum or hydrogen atmosphere at temperatures in the order of 1800–1900 °C [2]. As the transformation of Gd2O3 from cubic to monoclinic modification occurs at ~1200–1250 °C [3], the introduction of 50–70% Y2O3 is necessary to increase the phase transition temperature and, accordingly, the possibility of sintering without cracking samples and the appearance of secondary scattering phases in ceramics. A concomitant purpose of introducing yttrium oxide into the ceramic composition is to reduce the absorption ability of the scintillator, for example, so that it is consistent with the corresponding characteristics of bone tissue.
Recently, optical ceramics of REM oxides of mixed composition are of increasing interest for the creation of active media for lasers [4,5,6,7,8]. Just like scintillators, they have in their composition an active ion, in the levels at which the emission transitions occur, but the composition of the matrix is selected for other reasons. The main idea in this case is the formation of a structure in which the active ions are in a different environment (with a different strength of crystal field), which affects the level splitting. This provides a broadening of the luminescence spectrum, which, in particular, is necessary to increase the laser tuning range or to obtain pulses of ultra-short duration (in particular, femtosecond pulses).
However, as is known, solid solutions always have a thermal conductivity lower than at least one of the individual components. This is due to the disordering of the crystal lattice of solid solutions and, consequently, increased phonon scattering. In traditional scintillation applications, the radiation power density is usually negligible, and thus the thermal conductivity of the material does not affect the performance of the device. The situation is completely different in the case of laser applications of optical ceramics. Thermal-induced effects are one of the key factors limiting achievable laser power [9]. Solid solutions of yttrium and gadolinium oxides are of particular interest for radiation generation in the 2 μm region and beyond, for example, when doped with thulium or erbium ions. The high quantum defect in these ions (λpumping ~800 nm and ~980 nm; λgeneration ~1940 nm and ~2800 nm for Tm3+ and Er3+ ions, respectively [5,10]) means that more than half of the pump energy is converted into the vibrations of the crystal lattice due to nonradiative transitions. This creates a high thermal load on the element, and in order to create an effective laser in the 2–3 μm range, the issue of thermal conductivity of the active medium is a priority.
Since the main purpose of determining the thermal conductivity of (Y1−xGdx)2O3 solid solution ceramics is their promising laser applications, thus, the main requirement for the samples for this study was their maximum density. In the present work, we used hot pressing of nanopowders, which was previously successfully used to obtain optical (including laser) ceramics of rare-earth metal oxides [11,12,13,14]. In these works, nanopowders were obtained by self-propagating high-temperature synthesis (SHS); the flame spray pyrolysis (FSP) method used in this work is essentially a development of it. The composition of the FSP precursor was the same as in SHS, but a flame was used to initiate the reaction. This avoided (or significantly reduced) the formation of relatively coarse agglomerates compared to SHS. The dissipation of reaction heat by massive (relative to the mass of the powder) flask walls in SHS leads to the extinguishing of precursor combustion in the adjacent layer. A lack of flame led to ineffective foaming of the precursor, thus, in this layer a fragile foam is not formed but rather rigid coral-like powders up to several microns in size. Such particles are inevitably the source of micron pores in ceramics. During FSP, all precursor droplets are in more homogeneous conditions, and thus despite some dispersion of the resulting powder in size, we did not find particles in the photographs from the scanning electron microscope that could be classified as rigid agglomerates. After the hot pressing of such powders and subsequent annealing in the air, the obtained ceramics were translucent, which we attribute to their almost full density.
This work gives an overview of the dependence of the thermal conductivity of Y2O3-Gd2O3 solid solutions on the composition in the temperature range from cryogenic to 300 K, which is most important for the operation of the active media of solid-state lasers.
2. Results and Discussion
The results of measurements of the thermal conductivity of solid solutions (Y1−xGdx)2O3 in the form of plots of the temperature dependence k(T) are shown in Figure 1. The numerical values of the thermal conductivity coefficient for several temperatures are shown in Table 1.
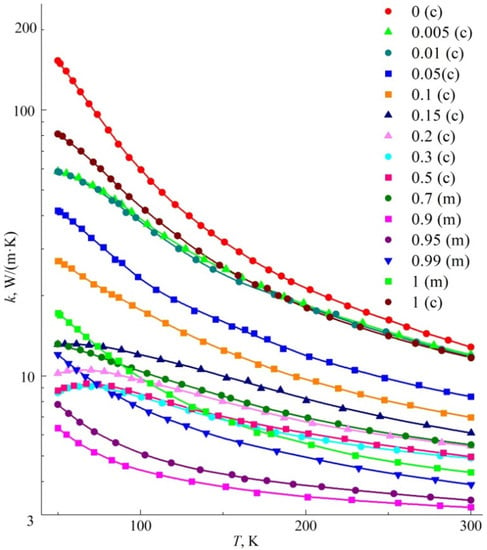
Figure 1.
Temperature dependence of thermal conductivity of ceramic samples of solid solution (Y1−xGdx)2O3. In the legend, the numbers denotes x; (c) refers to the cubic phase of the solid solution; (m) refers to the monoclinic one.

Table 1.
The thermal conductivity of solid solutions (Y1−xGdx)2O3 at different temperatures.
It can be seen that monotonically decreasing dependences k(T) were mainly observed. The rate of change of dk/dT decreased as the temperature grew and the concentration of the solid solution moved away from the bound values of x = 0 and x = 1. This behavior is quite typical for solid solutions with isovalent ionic substitution [15]. The results obtained for Y2O3 ceramics (x = 0) are in good agreement with the high-temperature data of the authors [16,17]. In the case of another bound composition—Gd2O3 (x = 1)—the values of thermal conductivity of both cubic and monoclinic ceramics determined at room temperature were significantly higher than the corresponding values obtained by the authors [18] for the same ceramics with a density of 85.7% (taking into account the recalculation to the density of 100%) and the two-phase structure. This is obviously due to the greater scattering of phonons in two-phase ceramics than in single-phase ones.
The k(T) curves of the samples with 15, 20, 30, and 50 mol% Gd2O3 differed from the others in the violation of monotonicity: as the temperatures lowered to sub nitrogen, the thermal conductivity of these samples decreased. The density of such samples also differs significantly from that calculated by the XRD method for “ideal” defect-free crystal (see Figure 2). Phonon scattering in the case of ceramic materials based on these solid solutions mainly occurs in crystalline grains at substitutional defects due to differences in the masses and sizes of Y3+ and Gd3+ ions and at grain boundaries. The presence of pores can also be an important factor limiting the heat transfer. The magnitude of this effect can be estimated using the Maxwell–Aiken expression [19]: , where kP is the experimental (“effective”) value of the thermal conductivity of ceramics with porosity P, determined through the ratio ρrel of real density to theoretical as , k0 is the thermal conductivity of ceramics with zero porosity (). The value of the parameter β depends on the shape and orientation of the pores [19] and we took it to be equal to ½. The ratios are about 0.95 or more, which corresponds to the limits of the experimental error in determining the thermal conductivity coefficient. Given the translucency of the samples, which is usually associated with high density, we can assume that the residual pores are not a decisive factor in the studied ceramics for deviations either in thermal conductivity or in density. Thus, structural defects of another nature are formed in (Y1−xGdx)2O3 solid solutions. In samples with a monoclinic structure (0.9 ≤ x ≤ 1), the deviation from the theoretical density was even more pronounced, probably due to the addition of stresses caused by the “frozen” phase transition.
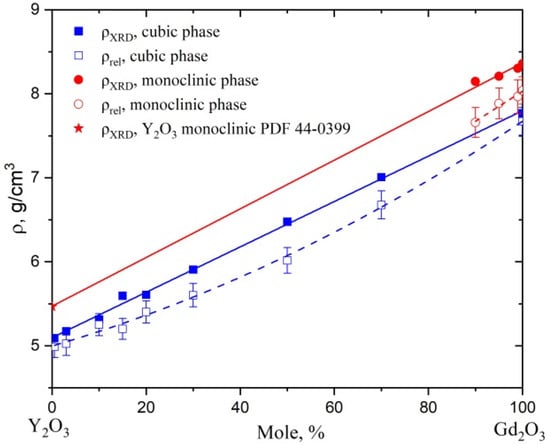
Figure 2.
The experimental and theoretical XRD densities of solid solutions (Y1−xGdx)2O3.
Figure 3 shows a plot of the concentration dependence of thermal conductivity k(x) of the studied solid solution (Y1−xGdx)2O3 at the temperature T = 300 K. The experimental points of k(x) of the cubic solid solution ceramics barely deviate from the approximating curve. The concentration dependence of the specific heat resistance w(x) = 1/k(x) is described satisfactorily (R2 = 0.9924) by the polynomial of the third degree (x is mol.%). However, this equation has no obvious physical foundation. It can be stated that the almost flat “bottom of the pit” of the concentration dependence of the thermal conductivity k(x) of (Y1−xGdx)2O3 solid solution is at about 5 W/(m K). The minimum value of thermal conductivity in the composition with x = 0.3 seems to be due to the proximity to the composition with an equal volume ratio of oxides (x ≈ 0.34).
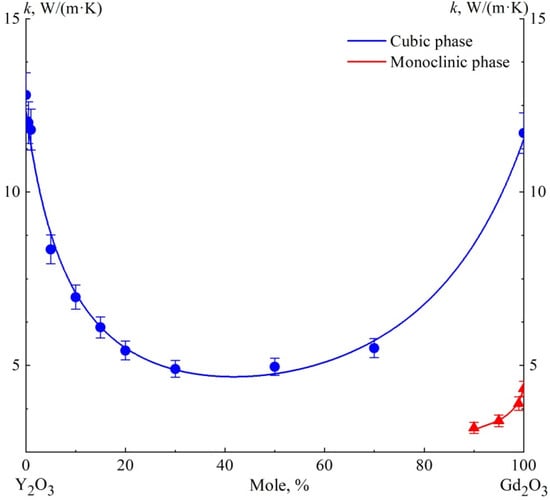
Figure 3.
Dependence of thermal conductivity at 300 K of solid solution ceramics (Y1−xGdx)2O3 on the composition.
Solid solution ceramics with monoclinic syngony (x ≥ 0.9) have almost three times lower thermal conductivity compared to cubic ones. We did not plot the data on two-phase ceramics, which are formed in the region of compositions 0.7 < x < 0.9 under the production modes used. As discussed above, their thermal conductivity is lower than that of single-phase ceramics, and its value depends not only on the composition, but also on the phase ratio.
The theoretical value of thermal conductivity for cubic Gd2O3 can be estimated by comparison with Y2O3 based on the well-known Debye expression , where is the heat capacity of the unit crystal volume, is the average propagation velocity of phonons (sound), and is the phonon mean free path. From the calorimetric data [20,21] it follows that at T = 300 K the ratio is a value equal to 1.055. The speed of sound is proportional to , where E is the Young’s modulus, and ρ is the density of the material. The value of the expression is close to 1.23. We did not find any information about the Young’s modulus value for cubic Gd2O3. However, the very close sizes of the lattice cells of Gd2O3 and Y2O3 allowed us to assume that the values of this elastic characteristic were also close. Therefore, the ratio can be estimated by a value . Significantly larger differences in the masses of cations and anions in Gd2O3 with respect to Y2O3 also suggest a more intense phonon-phonon scattering and, accordingly, smaller values of the phonons mean a free path in Gd2O3. The paramagnetic properties of Gd3+ ions, which manifest themselves in anomalies in the thermophysical properties of gadolinia in the range of helium temperatures [22], did not significantly affect the results in the temperature range studied by us. In view of the above reasoning, the estimated value k for cubic Gd2O3 ceramics is ≈10 W/(m K) at 300 K. This is slightly less than the experimentally measured value (k = 11.7 W/(m K) at 300 K), but shows that the thermal conductivity of cubic gadolinia is near the expected value and naturally lower than that of yttria.
It is well known that for laser applications, the lutetia-based optical elements are preferable to yttria- and especially scandia-based ones at high doping levels [23]. This is related to the fact that due to differences in the atomic masses and ionic radii of the matrix and the dopant cations, the thermal conductivity of REE3+:Y2O3 and REE3+:Sc2O3 decreases several times compared to undoped ones, whereas in REE3+:Lu2O3, its decrease is smoother. The experimentally measured thermal conductivity of cubic gadolinia within the measurement error was the same as the value for lutetia ceramics (12.2 W/(m K) at 300 K [24]). However, both the atomic masses and the ionic radii of common dopant ions, such as Dy3+, Ho3+, and especially Nd3+, are noticeably closer to Gd3+ than to Lu3+. Potentially, this means that cubic gadolinia can be used to create the most efficient laser media (such as highly doped Nd3+:Gd2O3) in terms of reducing undesirable thermal effects. Thus, the task of developing laser-quality cubic gadolinia-based media, although challenging, is very promising.
3. Materials and Methods
3.1. Synthesis of Ceramics
The nanopowder preparation of yttria, gadolinia and their solid solution was carried out by flame spray pyrolysis (FSP) then consolidated into a dense ceramic by hot pressing. The materials used for the synthesis of precursors were yttria (99.999% Polirit, Russia), gadolinia (99.99% Polirit, Russia), nitric acid (99.9999%, Khimreaktiv, Russia) and glycine NH2CH2COOH (99.9%, Khimreaktiv, Russia).
First, yttrium and gadolinium nitrates were prepared by dissolving 10 g of the corresponding oxides in a stoichiometric amount of the nitric acid upon heating. A concentration of the solutions was determined by a thermogravimetric method after calcining the dry residue at 1200 °C. The nitrates were mixed in a proportion depending on the desired composition of the (Y1−xGdx)2O3. The glycine was added to the solution of the metal nitrates in a molar ratio of 1:1. The concentration of the resulting water solution used for FSP was 0.8 mol/L.
FSP was carried out on a liquid nozzle with an internal diameter of 0.5 mm and pneumatic atomization. A propane-air mixture at a pressure of 0.3 MPa was used as a spraying gas. Metal nitrate-glycine solution was fed to the nozzle at a constant flow rate of 2 mL/min using a 3D-printed syringe pump with a stepper motor and microprocessor control. The flame temperature was maintained no higher than 800 °C (by adding excess air) to avoid sintering and agglomeration of the forming oxide nanopowders. The combustion products were mixed with air to reduce their temperature and directed to a cylindrical electrostatic precipitator (Uspec = 10 kV/cm), where nanopowders were collected. The yield of the finished product was about 50% by mass. Then, for complete oxidation of possible residual organic intermediates, the nanopowders were annealed in air at 900 °C for 5 h. The specific surface area of the nanopowders after annealing was about 20 g/cm3, which approximately corresponds to the equivalent particle diameter of 40…60 nm, and was almost independent of the composition of the solid solution.
The powders were precompacted in a stainless-steel mold at a pressure of about 10 MPa. Then the compacts were isolated using a graphite paper, placed in a graphite mold (Ø20 mm) and consolidated by hot pressing in vacuum at a heating rate of 10 °C/min, a maximum temperature of 1600 °C, a holding time 1 h, and uniaxial pressure of 30 MPa using a home-made equipment. The heating was carried out by graphite heaters; the residual pressure in the chamber was about 10 Pa. Then the ceramics were calcined in air at 1000 °C for 5 h to decrease the oxygen vacancies formed in the highly reduced atmosphere of the hot press. The resulting ceramic disks were ground to rectangular parallelepipeds about 19.5 × 4.5 × 4.5 mm in size, and then polished with a diamond suspension. Cubic gadolinia was produced in a similar way, but the hot pressing temperature was 1150 °C, the holding time was 5 h, and a sintering additive of 0.1% wt. lithium fluoride was used.
3.2. Experimental
The X-ray diffraction analysis of powdered ceramics was performed on a Shimadzu LabX XRD-6000 diffractometer (Shimadzu, Japan) with Cu (Kα1,2 λ = 1542 Å) radiation in the range of angles 2θ = 15–50° in 0.02° increments and 2°/min scanning speed. Qualitative and quantitative analysis of diffractograms was performed using software pack PhasanX 2.0 and UnitCell. The theoretical density of solid solutions was calculated based on the unit cell volume using the formula , where is the number of formula units in the unit cell (4), is the molar mass of the solid solution, is the unit cell volume and is the Avagadro number.
The mass of the samples was measured on a laboratory analytical electronic balance KERN EW420-3NM (Kern & Sohn GmbH, Balingen, Germany) with an accuracy of ±0.5 mg. The density of the hot pressed samples was determined by the Archimedes method using weighing in distilled water. The accuracy of the density measurement was no worse than 0.1% of the theoretical density of the solid solutions.
The experimental determination of thermal conductivity in the temperature range of 50–300 K was carried out by the absolute stationary method of longitudinal heat flux. To provide a flat profile of the heating front, a heater was glued to the end surface of the sample. The temperature difference along the sample (ΔT) created by the heater did not exceed 1 K and was measured with a chromel (copper + iron) thermocouple. The values of the thermal conductivity coefficient k(T) were calculated using the Fourier equation. The measurement error in determining of k(T) was ±5%. The instrumentation and measurement technique are described in detail in [25].
4. Conclusions
Nanopowders of solid solutions (Y1−xGdx)2O3 were obtained by flame-spray pyrolysis from aqueous glycine-nitrate precursors (where 0 ≤ x ≤ 1). By hot pressing at a temperature of 1600 °C for 1 h, these powders were consolidated into high density translucent ceramics. The absolute stationary method of the longitudinal heat flux method was used to measure the thermal conductivity of the obtained ceramics in the temperature range from 50 K to 300 K. The highest thermal conductivity is in neat Y2O3 ceramics (k = 12.8 W/(m K) at 300 K and k = 153 W/(m K) at 50 K), with an increase in the content of gadolinia, both the thermal conductivity of solid solutions and its growth as the temperature goes down significantly decrease.
In the used production modes, compositions with 0.7 < x < 0.9 have a two-phase structure of (Y1−xGdx)2O3 solid solution with cubic and monoclinic syngony, which leads to a significant decrease in the thermal conductivity of ceramics. The monoclinic Gd2O3 ceramics has a thermal conductivity of k = 4.3 W/(m K) at 300 K and k = 17.2 W/(m K) at 50 K.
Almost the same thermal conductivity of (Y1−xGdx)2O3 solid solutions (k ≈ 5 W/(m K) at 300 K) in the x range from 0.2 to 0.7 makes it possible not to take into account its change when optimizing the composition of optical ceramics, but to proceed from other functional or technological properties.
A dense, cubic Gd2O3 ceramic was made; it has high thermal conductivity both at room and cryogenic temperatures (k = 11.7 W/(m K) at 300 K and k = 81.0 W/(m K) at 50 K). The closeness of the atomic masses and ionic radii of Gd3+ cations and many common dopant rare-earth ions indicates that gadolinia with a cubic structure may be the most preferable laser matrix for them in terms of reducing the undesirable thermal effects.
Author Contributions
Investigation, S.B., T.E., D.P., O.P., A.P. and P.P.; writing—original draft preparation, S.B. and P.P.; writing—review and editing, S.B., T.E. and P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the RUSSIAN SCIENCE FOUNDATION, grant number 21-13-00397 https://rscf.ru/en/project/21-13-00397/ (accessed on 25 May 2022).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Duclos, S.J.; Greskovich, C.D.; Lyons, R.J.; Vartuli, J.S.; Hoffman, D.M.; Riedner, R.J.; Lynch, M.J. Development of the HiLightTM scintillator for computed tomography medical imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 505, 68–71. [Google Scholar] [CrossRef]
- Greskovich, C.; Duclos, S. Ceramic scintillators. Annu. Rev. Mater. Sci. 1997, 27, 69–88. [Google Scholar] [CrossRef]
- Permin, D.A.; Boldin, M.S.; Belyaev, A.V.; Balabanov, S.S.; Koshkin, V.A.; Murashov, A.A.; Ladenkov, I.V.; Lantsev, E.A.; Smetanina, K.E.; Khamaletdinova, N.M. IR-transparent MgO-Gd2O3 composite ceramics produced by self-propagating high-temperature synthesis and spark plasma sintering. J. Adv. Ceram. 2021, 10, 237–246. [Google Scholar] [CrossRef]
- Chaika, M.; Balabanov, S.; Permin, D. Spectral characteristics of “mixed” sesquioxide Yb:(Gd,Lu)2O3 transparent ceramics. Opt. Mater. X 2022, 13, 100123. [Google Scholar] [CrossRef]
- Basyrova, L.; Loiko, P.; Jing, W.; Wang, Y.; Huang, H.; Dunina, E.; Kornienko, A.; Fomicheva, L.; Viana, B.; Griebner, U.; et al. Spectroscopy and efficient laser operation around 2.8 μm of Er:(Lu,Sc)2O3 sesquioxide ceramics. J. Lumin. 2021, 240, 118373. [Google Scholar] [CrossRef]
- Permin, D.A.; Kurashkin, S.V.; Novikova, A.V.; Savikin, A.P.; Gavrishchuk, E.M.; Balabanov, S.S.; Khamaletdinova, N.M. Synthesis and luminescence properties of Yb-doped Y2O3, Sc2O3 and Lu2O3 solid solutions nanopowders. Opt. Mater. 2018, 77, 240–245. [Google Scholar] [CrossRef]
- Basyrova, L.; Balabanov, S.; Koshkin, V.; Permin, D.; Baranov, M.; Loiko, P. Synthesis, Structure and Luminescence of Transparent «Mixed» Ceramics Dy3+:(Lu,Y,La)2O3. In Proceedings of the 2020 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 2–6 November 2020. [Google Scholar]
- Pirri, A.; Maksimov, R.N.; Li, J.; Vannini, M.; Toci, G. Achievements and Future Perspectives of the Trivalent Thulium-Ion-Doped Mixed-Sesquioxide Ceramics for Laser Applications. Materials 2022, 15, 2084. [Google Scholar] [CrossRef] [PubMed]
- Palashov, O.V.; Starobor, A.V.; Perevezentsev, E.A.; Snetkov, I.L.; Mironov, E.A.; Yakovlev, A.I.; Balabanov, S.S.; Permin, D.A.; Belyaev, A.V. Thermo-Optical Studies of Laser Ceramics. Materials 2021, 14, 3944. [Google Scholar] [CrossRef]
- Antipov, O.L.; Getmanovskiy, Y.A.; Balabanov, S.S.; Larin, S.V.; Sharkov, V.V. 1940 nm, 1966 nm and 2066 nm multi-wavelength CW and passively-Q-switched operation of L-shaped Tm3+:Lu2O3 ceramic laser in-band fiber-laser pumped at 1670 nm. Laser Phys. Lett. 2021, 18, 055001. [Google Scholar] [CrossRef]
- Balabanov, S.; Filofeev, S.; Kaygorodov, A.; Khrustov, V.; Kuznetsov, D.; Novikova, A.; Permin, D.; Popov, P.; Ivanov, M. Hot pressing of Ho2O3 and Dy2O3 based magneto-optical ceramics. Opt. Mater. X 2022, 13, 100125. [Google Scholar] [CrossRef]
- Balabanov, S.; Permin, D.; Evstropov, T.; Andreev, P.; Basyrova, L.; Camy, P.; Baranov, M.; Mateos, X.; Loiko, P. Hot pressing of Yb:Y2O3 laser ceramics with LiF sintering aid. Opt. Mater. 2021, 119, 111349. [Google Scholar] [CrossRef]
- Balabanov, S.S.; Permin, D.A.; Rostokina, E.Y.; Palashov, O.V.; Snetkov, I.L. Characterizations of REE:Tb2O3 Magneto-Optical Ceramics. Phys. Status Solidi Basic Res. 2020, 257, 1900474. [Google Scholar] [CrossRef]
- Permin, D.A.; Balabanov, S.S.; Snetkov, I.L.; Palashov, O.V.; Novikova, A.V.; Klyusik, O.N.; Ladenkov, I.V. Hot pressing of Yb:Sc2O3 laser ceramics with LiF sintering aid. Opt. Mater. 2020, 100, 109701. [Google Scholar] [CrossRef]
- Berman, R.; Klemens, P.G. Thermal Conduction in Solids. Phys. Today 1978, 31, 56–57. [Google Scholar] [CrossRef]
- Harris, D.C.; Cambrea, L.R.; Johnson, L.F.; Seaver, R.T.; Baronowski, M.; Gentilman, R.; Scott Nordahl, C.; Gattuso, T.; Silberstein, S.; Rogan, P.; et al. Properties of an Infrared-Transparent MgO:Y2O3 Nanocomposite. J. Am. Ceram. Soc. 2013, 96, 3828–3835. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, Q.; Zhu, Q.; Jiang, B.; Feng, M.; Zhang, L. Fabrication of fine-grained undoped Y2O3 transparent ceramic using nitrate pyrogenation synthesized nanopowders. Ceram. Int. 2019, 45, 5339–5345. [Google Scholar] [CrossRef]
- Mistarihi, Q.; Sweidan, F.B.; Ryu, H.J. Thermo-physical properties of bulk Gd2O3 for fuel performance analysis of a lumped burnable absorber fuel design. In Proceedings of the Transactions of the Korean Nuclear Society Autumn Meeting Gyeongju, Gyeongju, Korea, 26–27 October 2017. [Google Scholar]
- Maxwell, J. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1892. [Google Scholar]
- Goldstein, H.W.; Neilson, E.F.; Walsh, P.N. David White: The Heat Capacities Yttrium Oxide(Y2O3) Lanthanum Oxide (La2O3), and Neodymium Oxide (Nd2O3) from 16 to 300°K. J. Phys. Chem. 1959, 63, 1445–1449. [Google Scholar] [CrossRef]
- Justice, B.H.; Westrum, E.F. Thermophysical properties of the lanthanide oxides. II. Heat capacities, thermodynamic properties, and some energy levels of samarium(III), gadolinium(III), and ytterbium(III) oxides from 10 to 350°K. J. Phys. Chem. 1963, 67, 345–351. [Google Scholar] [CrossRef]
- Stewart, G.R.; Barclay, J.A.; Steyert, W.A. The specific heat of C-phase Gd2O3. Solid State Commun. 1979, 29, 17–19. [Google Scholar] [CrossRef]
- Chaika, M.; Balabanov, S.; Permin, D. Optical spectra and gain properties of Er3+:Lu2O3 ceramics for eye-safe 1.5-μm lasers. Opt. Mater. 2021, 112, 110785. [Google Scholar] [CrossRef]
- Peters, R.; Kränkel, C.; Petermann, K.; Huber, G. Broadly tunable high-power Yb:Lu2O3 thin disk laser with 80% slope efficiency. Opt. Express 2007, 15, 7075. [Google Scholar] [CrossRef] [PubMed]
- Popov, P.A.; Sidorov, A.A.; Kul’chenkov, E.A.; Anishchenko, A.M.; Avetissov, I.C.; Sorokin, N.I.; Fedorov, P.P. Thermal conductivity and expansion of PbF2 single crystals. Ionics 2017, 23, 233–239. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).