Three-Dimensional Force Sensor Based on Fiber Bragg Grating for Medical Puncture Robot
Abstract
:1. Introduction
2. FBG Force Sensor Principle
3. Design of Force Sensors
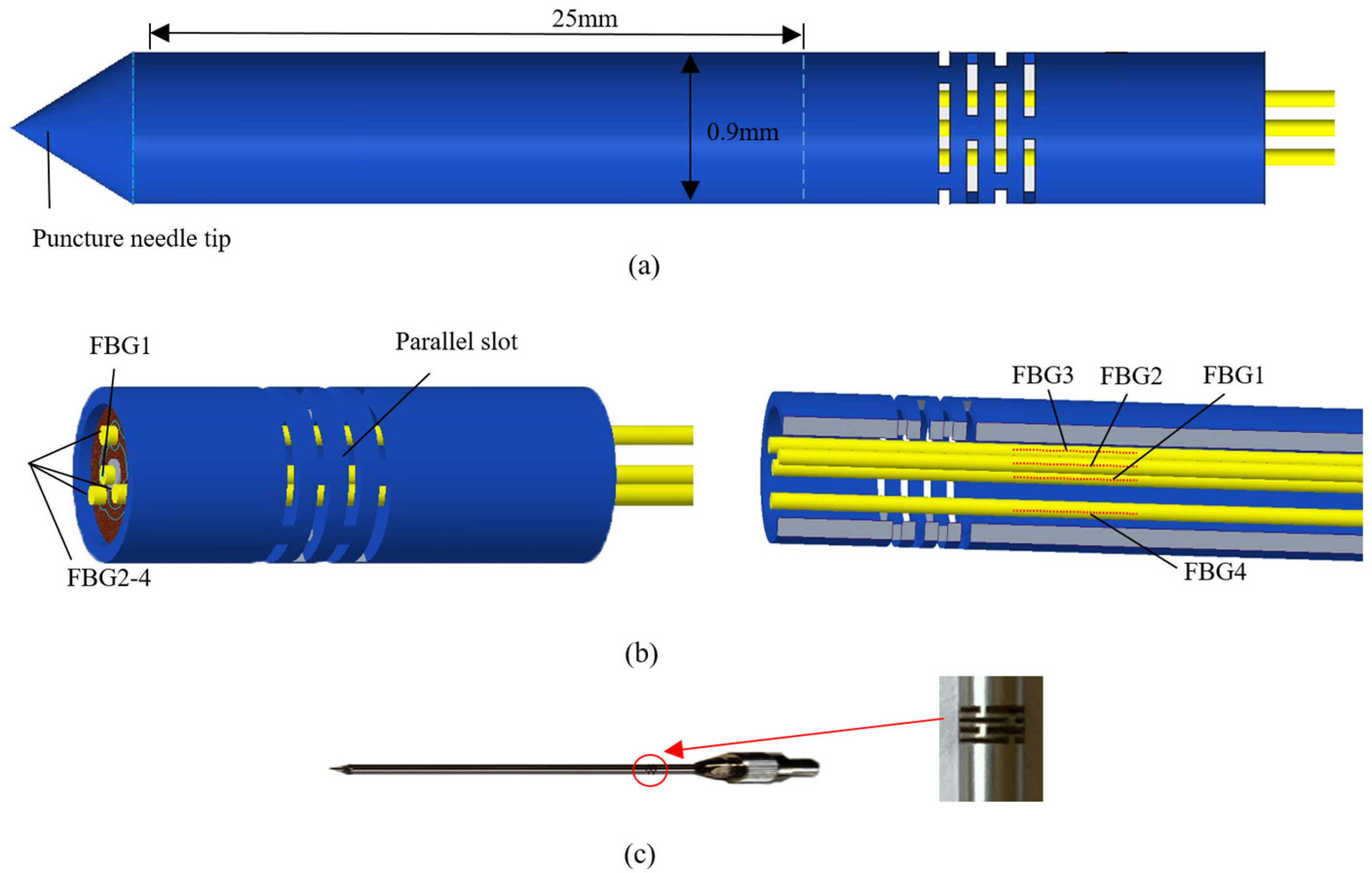
3.1. Structure of the Sensor
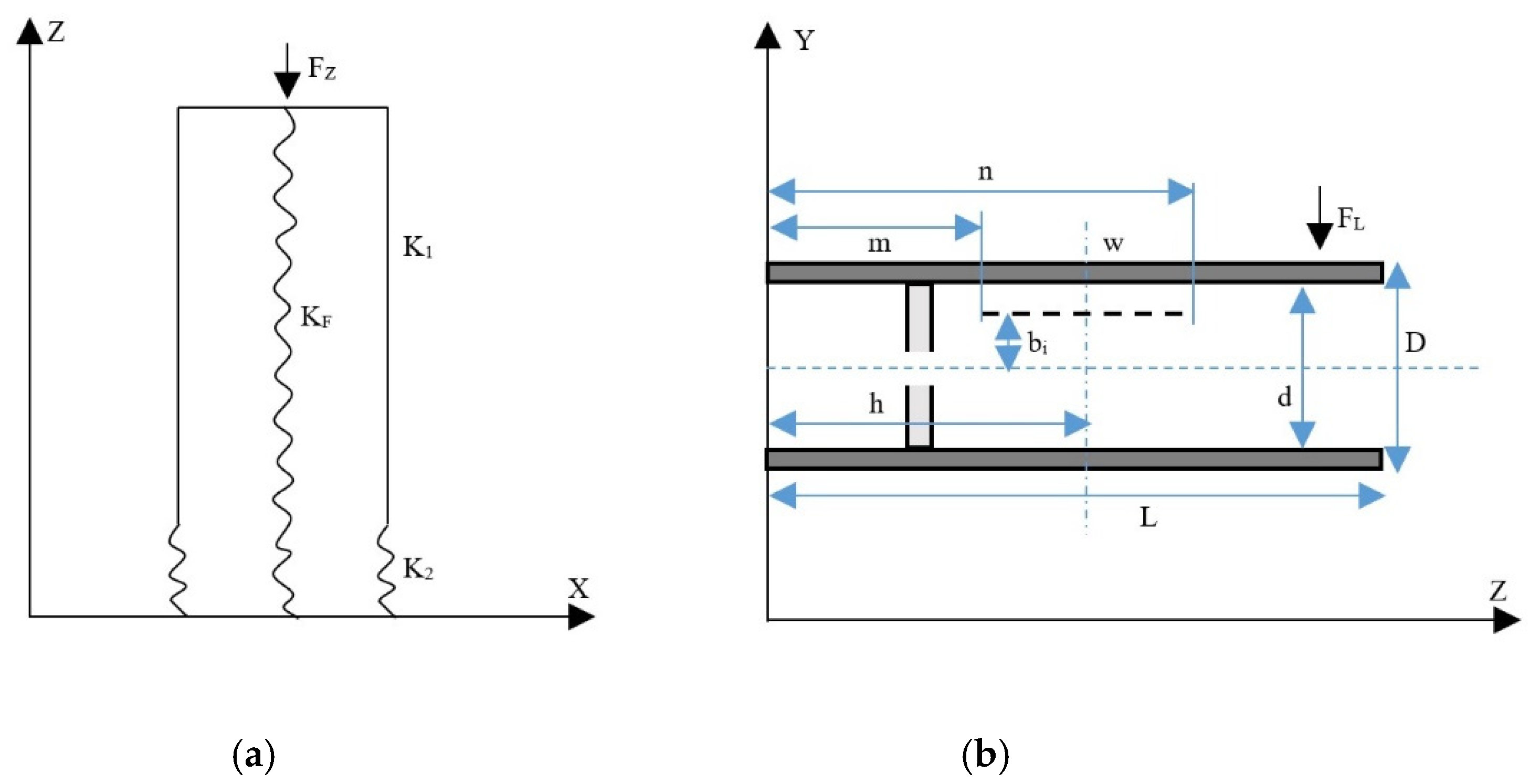
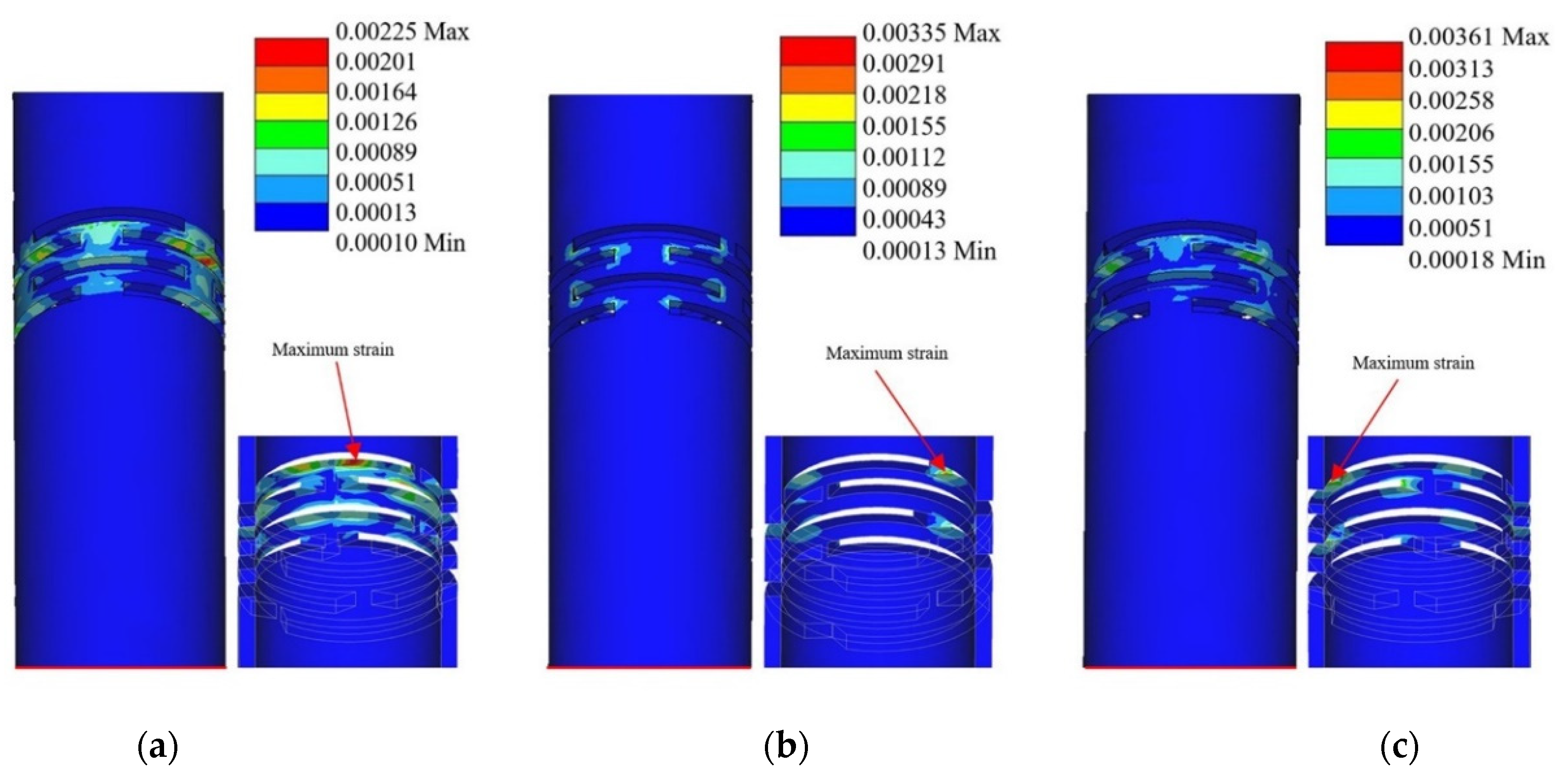
3.2. Force Model Analysis of Sensor
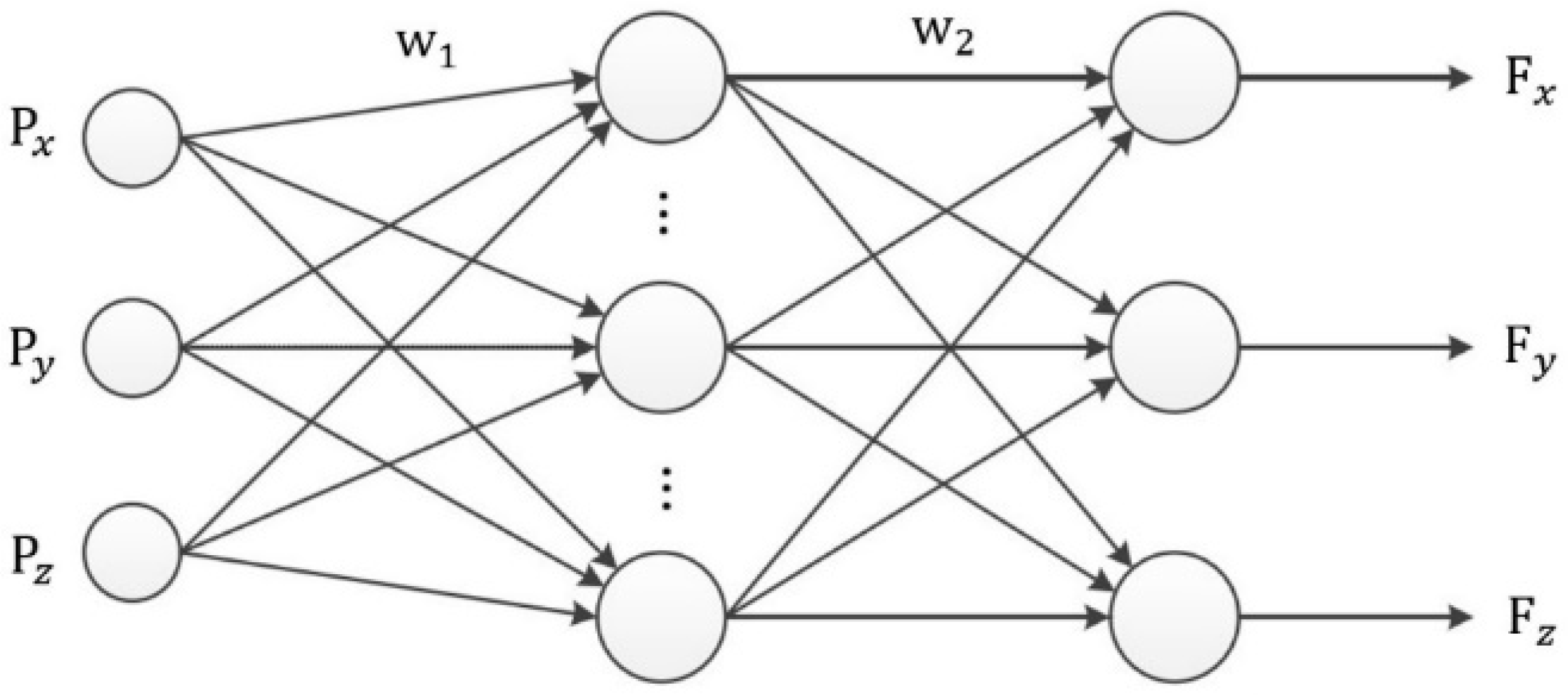
3.3. Decoupling Algorithm
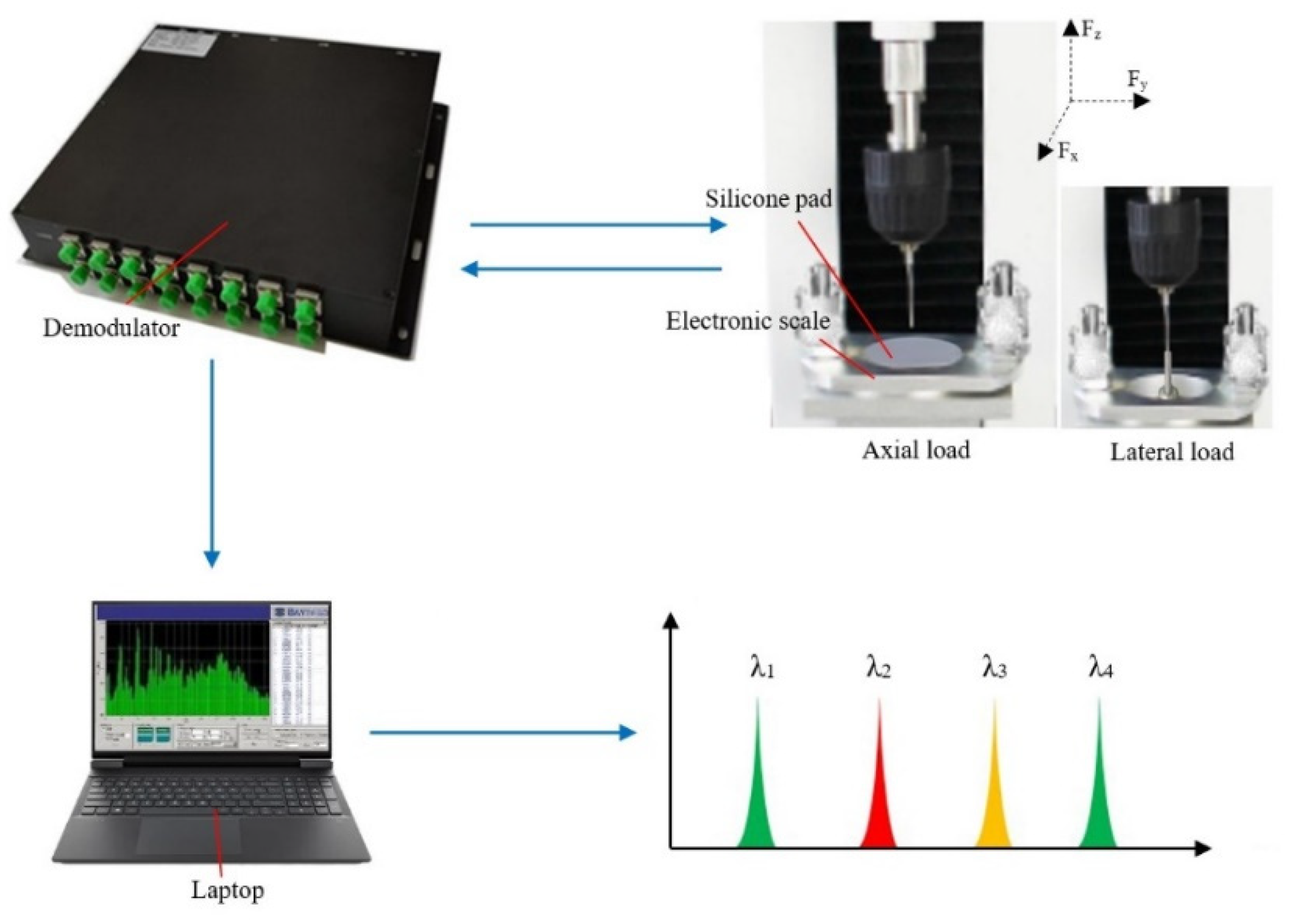
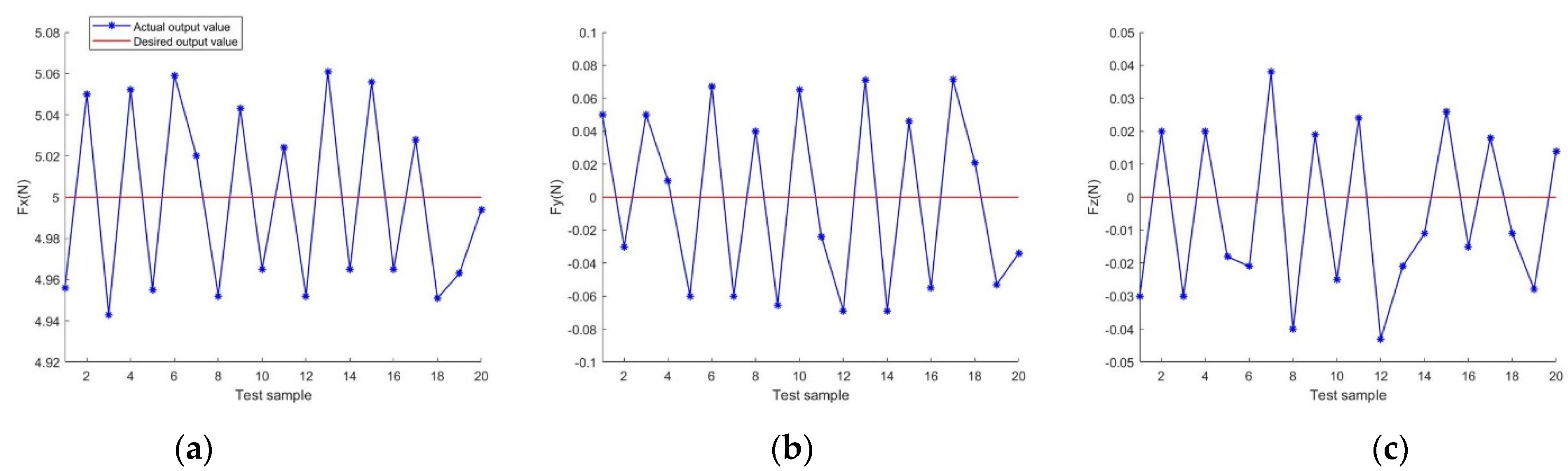
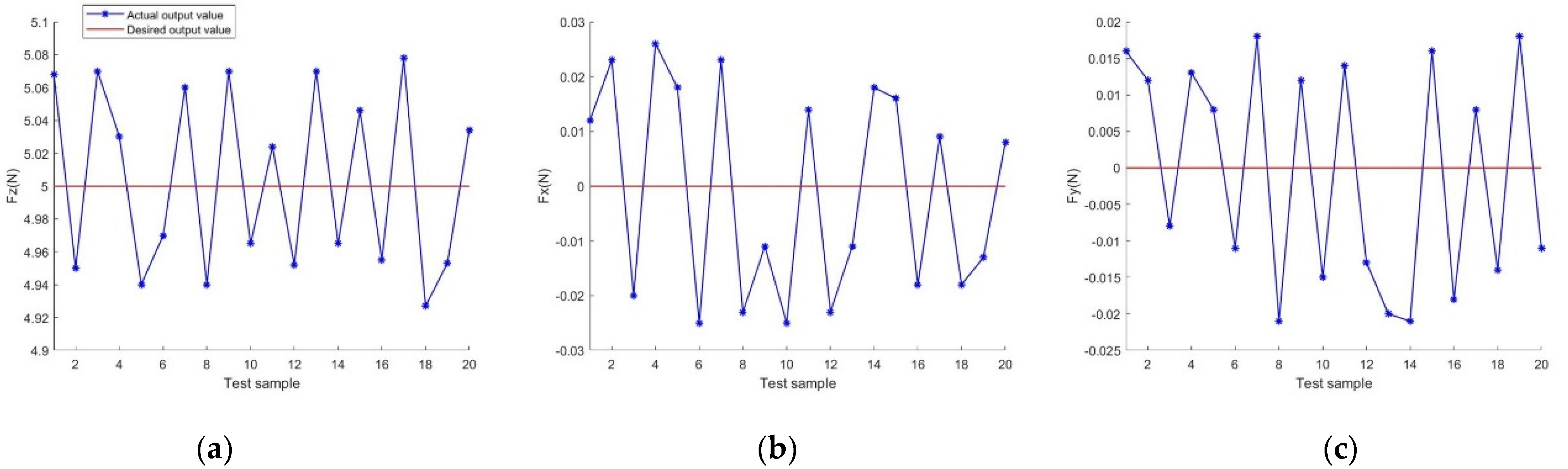
4. Experimental Results
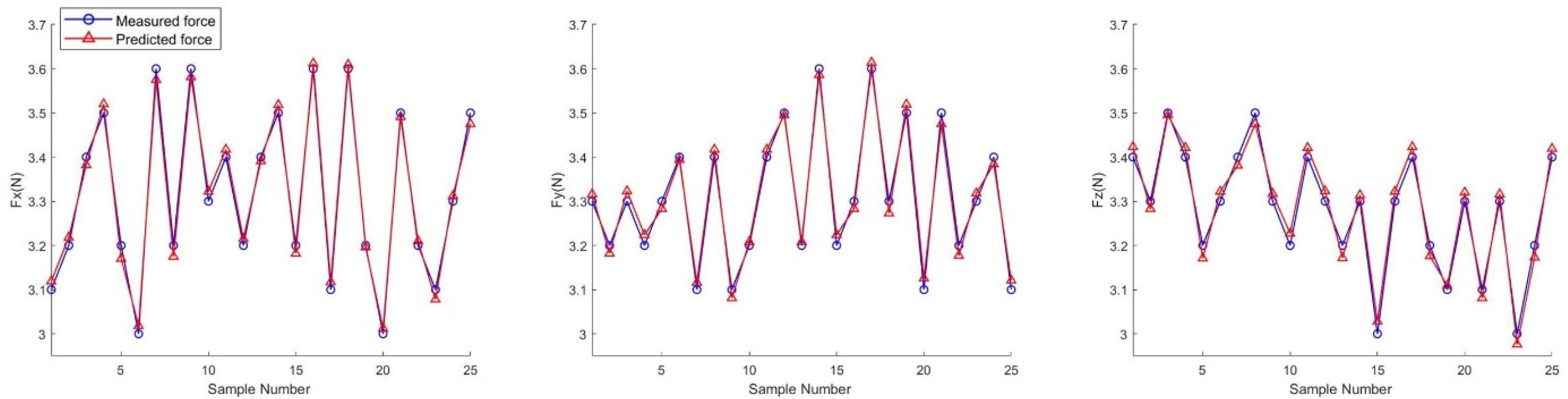
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okamura, A.M. Haptics in robot-assisted minimally invasive surgery. In The Encyclopedia of Medical Robotics. Volume 1: Minimally Invasive Surgical Robotics; World Scientific: Singapore, 2019; pp. 317–339. [Google Scholar]
- Ranzani, T.; Gerboni, G.; Cianchetti, M.; Menciassi, A. A bioinspired soft manipulator for minimally invasive surgery. Bioinspir. Biomim. 2015, 10, 035008. [Google Scholar] [CrossRef]
- Chen, S.; Wang, F.; Lin, Y.; Shi, Q.; Wang, Y. Ultrasound-guided needle insertion robotic system for percutaneous puncture. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 475–484. [Google Scholar] [CrossRef]
- Zhang, W.; Bao, K.; Zheng, L.; Cai, L.; Yan, B.; Yang, R. A robotic puncture system with optical and mechanical feedback under respiratory motion. Int. J. Med. Robot. Comput. Assist. Surg. 2022, 18, e2403. [Google Scholar] [CrossRef]
- Guo, S.; Wang, Y.; Xiao, N.; Li, Y.; Jiang, Y. Study on real-time force feedback for a master–slave interventional surgical robotic system. Biomed. Microdev. 2018, 20, 37. [Google Scholar] [CrossRef]
- Yu, H.; Wang, H.; Chang, J.; Niu, J.; Wang, F.; Yan, Y.; Tian, H.; Fang, J.; Lu, H. A novel vascular intervention surgical robot based on force feedback and flexible clamping. Appl. Sci. 2021, 11, 611. [Google Scholar] [CrossRef]
- Yoon, S.M.; Kim, W.J.; Lee, M.C. Design of bilateral control for force feedback in surgical robot. Int. J. Control Autom. Syst. 2015, 13, 916–925. [Google Scholar] [CrossRef]
- Li, K.; Pan, B.; Gao, W.-P.; Feng, H.-B.; Fu, Y.-L.; Wang, S.-G. Miniature 6-axis force/torque sensor for force feedback in robot-assisted minimally invasive surgery. J. Central South Univ. 2015, 22, 4566–4577. [Google Scholar] [CrossRef]
- Overtoom, E.M.; Horeman, T.; Jansen, F.W.; Dankelman, J.; Schreuder, H.W. Haptic feedback, force feedback, and force-sensing in simulation training for laparoscopy: A systematic overview. J. Surg. Educ. 2019, 76, 242–261. [Google Scholar] [CrossRef]
- Kim, U.; Lee, D.H.; Yoon, W.J.; Hannaford, B.; Choi, H.R. Force sensor integrated surgical forceps for minimally invasive robotic surgery. IEEE Trans. Robot. 2015, 31, 1214–1224. [Google Scholar] [CrossRef]
- Bao, X.; Guo, S.; Xiao, N.; Li, Y.; Shi, L. Compensatory force measurement and multimodal force feedback for remote-controlled vascular interventional robot. Biomed. Microdev. 2018, 20, 74. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Marques, C.; Ribeiro, M.R.N.; Pontes, M.J.; Frizera, A. FBG-embedded 3-D printed ABS sensing pads: The impact of infill density on sensitivity and dynamic range in force sensors. IEEE Sens. J. 2018, 18, 8381–8388. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Biazi, V.; Marques, C.; Frizera, A. Force-displacement analysis in diaphragm-embedded fiber bragg grating sensors. Sensors 2022, 22, 5355. [Google Scholar] [CrossRef] [PubMed]
- Marques, C.A.; Bilro, L.B.; Alberto, N.J.; Webb, D.J.; Nogueira, R.N. Narrow bandwidth Bragg gratings imprinted in polymer optical fibers for different spectral windows. Opt. Commun. 2013, 307, 57–61. [Google Scholar] [CrossRef]
- Woyessa, G.; Theodosiou, A.; Markos, C.; Kalli, K.; Bang, O. Single peak fiber Bragg grating sensors in tapered multimode polymer optical fibers. J. Light. Technol. 2021, 39, 6934–6941. [Google Scholar] [CrossRef]
- Ourak, M.; Smits, J.; Esteveny, L.; Borghesan, G.; Gijbels, A.; Schoevaerdts, L.; Douven, Y.; Scholtes, J.; Lankenau, E.; Eixmann, T.; et al. Combined OCT distance and FBG force sensing cannulation needle for retinal vein cannulation: In vivo animal validation. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 301–309. [Google Scholar] [CrossRef]
- Liang, Q.; Zou, K.; Long, J.; Jin, J.; Zhang, D.; Coppola, G.; Sun, W.; Wang, Y.; Ge, Y. Multi-component FBG-based force sensing systems by comparison with other sensing technologies: A review. IEEE Sens. J. 2018, 18, 7345–7357. [Google Scholar] [CrossRef]
- Sun, K.; Li, M.; Wang, S.; Zhang, G.; Liu, H.; Shi, C. Development of a fiber Bragg grating-enabled clamping force sensor integrated on a grasper for laparoscopic surgery. IEEE Sens. J. 2021, 21, 16681–16690. [Google Scholar] [CrossRef]
- Lai, W.; Cao, L.; Liu, J.; Tjin, S.C.; Phee, S.J. A three-axial force sensor based on fiber Bragg gratings for surgical robots. IEEE/ASME Trans. Mechatr. 2021, 27, 777–789. [Google Scholar] [CrossRef]
- Lv, C.; Wang, S.; Shi, C. A high-precision and miniature fiber Bragg grating-based force sensor for tissue palpation during minimally invasive surgery. Ann. Biomed. Eng. 2020, 48, 669–681. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, B.; Zuo, S. A novel 3-DOF force sensing microneedle with integrated fiber Bragg grating for microsurgery. IEEE Trans. Ind. Electron. 2021, 69, 940–949. [Google Scholar] [CrossRef]
- Shi, C.; Tang, Z.; Wang, S. Design and experimental validation of a fiber Bragg grating-enabled force sensor with an ortho-planar spring-based flexure for surgical needle insertion. IEEE Trans. Med. Robot. Bionics 2021, 3, 362–371. [Google Scholar] [CrossRef]
- Deng, Y.; Yang, T.; Dai, S.; Song, G. A miniature triaxial fiber optic force sensor for flexible ureteroscopy. IEEE Trans. Biomed. Eng. 2020, 68, 2339–2347. [Google Scholar] [CrossRef]
- Chen, W.; Yang, S.; Hu, Q.; Song, A. Design of a wireless six-axis wrist force sensor for teleoperation robots. In Proceedings of the International Conference on Intelligent Robotics and Applications, Macau, China, 4–8 November 2019; Springer: Cham, Switzerland, 2019; pp. 702–713. [Google Scholar]
- Xiong, L.; Guo, Y.; Jiang, G.; Zhou, X.; Liu, H. An FBG-based 2-DOF force sensing intraocular lens positioning hook for cataract surgery. IEEE Photon. Technol. Lett. 2019, 31, 1674–1677. [Google Scholar] [CrossRef]
- Aiguo, S.; Liyue, F.U. Multi-dimensional force sensor for haptic interaction: A review. Virtual Real. Intell. Hardw. 2019, 1, 121–135. [Google Scholar]
- Cappelleri, D.J.; Krishnan, G.; Kim, C.; Kumar, V.; Kota, S. Toward the design of a decoupled, two-dimensional, vision-based μN force sensor. J. Mech. Robot. 2010, 2, 021010. [Google Scholar] [CrossRef]
- Zhou, S.; Sun, J.; Chen, W.; Li, W.; Gao, F. Method of designing a six-axis force sensor for stiffness decoupling based on Stewart platform. Measurement 2019, 148, 106966. [Google Scholar] [CrossRef]
- Kang, M.K.; Lee, S.; Kim, J.H. Shape optimization of a mechanically decoupled six-axis force/torque sensor. Sens. Actuator A Phys. 2014, 209, 41–51. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiao, L.; Weng, D.; Zhang, D.; Zheng, R. Decoupling principle analysis and development of a parallel three-dimensional force sensor. Sensors 2016, 16, 1506. [Google Scholar] [CrossRef]
- Liu, Q.; Li, D.; Ge, S.S.; Ji, R.; Ouyang, Z.; Tee, K.P. Adaptive bias RBF neural network control for a robotic manipulator. Neurocomputing 2021, 447, 213–223. [Google Scholar] [CrossRef]
- Ma, J.; Song, A.; Xiao, J. A robust static decoupling algorithm for 3-axis force sensors based on coupling error model and ε-SVR. Sensors 2012, 12, 14537–14555. [Google Scholar] [CrossRef]
- Liang, Q.; Wu, W.; Coppola, G.; Zhang, D.; Sun, W.; Ge, Y.; Wang, Y. Calibration and decoupling of multi-axis robotic force/moment sensors. Robot. Comput.-Integr. Manuf. 2018, 49, 301–308. [Google Scholar] [CrossRef]
- Sahota, J.K.; Gupta, N.; Dhawan, D. Fiber Bragg grating sensors for monitoring of physical parameters: A comprehensive review. Opt. Eng. 2020, 59, 060901. [Google Scholar] [CrossRef]
- Broadway, C.; Min, R.; Leal-Junior, A.G.; Marques, C.; Caucheteur, C. Toward commercial polymer fiber Bragg grating sensors: Review and applications. J. Light. Technol. 2019, 37, 2605–2615. [Google Scholar] [CrossRef]
- Li, J.; Wang, C.; Mao, Z.; Liu, Y.; Wang, Z.; Liu, H. A compact FBG-based triaxial force sensor with parallel helical beams for robotic-assisted surgery. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]




| Decoupling Method | Fx | Fy | Fz | TC |
|---|---|---|---|---|
| Before decoupling | 3.62 | 3.27 | 4.15 | 0 ms |
| BP | 1.54 | 1.41 | 1.73 | 1.87 ms |
| BRFNN | 1.42 | 1.43 | 1.69 | 2.63 ms |
| SVR | 1.51 | 1.38 | 1.74 | 2.08 ms |
| ELM | 1.37 | 1.24 | 1.54 | 2.45 ms |
| GOFF-BP | 1.25 | 1.18 | 1.56 | 2.26 ms |
| Decoupling Method | Fx | Fy | Fz | TC |
|---|---|---|---|---|
| Before decoupling | 6.71 | 7.24 | 2.55 | 0 ms |
| BP | 1.84 | 1.92 | 1.53 | 1.87 ms |
| BRFNN | 1.46 | 1.54 | 1.17 | 2.63 ms |
| SVR | 1.57 | 1.59 | 1.24 | 2.08 ms |
| ELM | 1.42 | 1.51 | 1.03 | 2.45 ms |
| GOFF-BP | 1.38 | 1.47 | 0.94 | 2.26 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Lin, J.; Pang, Y.; Yang, D.; Zhong, L.; Li, Z. Three-Dimensional Force Sensor Based on Fiber Bragg Grating for Medical Puncture Robot. Photonics 2022, 9, 630. https://doi.org/10.3390/photonics9090630
Li X, Lin J, Pang Y, Yang D, Zhong L, Li Z. Three-Dimensional Force Sensor Based on Fiber Bragg Grating for Medical Puncture Robot. Photonics. 2022; 9(9):630. https://doi.org/10.3390/photonics9090630
Chicago/Turabian StyleLi, Xi, Jinzhao Lin, Yu Pang, Dewei Yang, Lisha Zhong, and Zhangyong Li. 2022. "Three-Dimensional Force Sensor Based on Fiber Bragg Grating for Medical Puncture Robot" Photonics 9, no. 9: 630. https://doi.org/10.3390/photonics9090630
APA StyleLi, X., Lin, J., Pang, Y., Yang, D., Zhong, L., & Li, Z. (2022). Three-Dimensional Force Sensor Based on Fiber Bragg Grating for Medical Puncture Robot. Photonics, 9(9), 630. https://doi.org/10.3390/photonics9090630





