Orbital and Spin Dynamics of Electron’s States Transition in Hydrogen Atom Driven by Electric Field

Abstract

State transition in the multiple-levels system has the great potential applications in the quantum technology. In this article we employ a deterministic approach in complex space to analyze the dynamics of the 1s–2p electron transition in the hydrogen atom. The electron’s spin motion is embodied in the framework of quantum Hamilton mechanics that allows us to examine the transition dynamics more precisely. The transition is driven by an oscillating electric field in the z-direction. The electron’s transition process can be visualized by monitoring its motion in the complex space. The quantum potential and the total energy proposed in this paper provide new indices to observe the dynamic changes of electrons in the transition process.

1. Introduction

The multiple-level system has widely applications in different scientific fields, such as the atomic clock, information storage, quantum computing, and so on [1,2,3,4,5]. Quantum transitions in multiple-level states have been studied in different systems with some studies focusing on the excitation resources and the theoretical methods [6,7,8,9,10,11,12,13,14,15,16,17]. The hydrogen atom is one of the basic system considered in the level-energy transition problem. In the trajectory interpretation of quantum mechanics, Bohmian mechanics is one of the most used theories to model the quantum systems. However, Bohmian mechanics is developed on the basis of the Schrödinger equation which has no spin counterpart. Therefore, the original Bohm’s guidance law is not adapted to the system with spin particles. To include the spin effect, a modified guidance law was proposed [18] to study spin-dependent Bohm trajectories associated with an electronic transition in hydrogen. This modified guidance laws provides a trajectory-based platform for researchers to study the electron’s energy-level transitions [19,20,21,22,23].

In addition to the modified Bohmian guidance law, many studies deal with the complex-extended quantum systems, such as complex energy [24,25], complex time [26,27,28], complex space [29,30,31], complex photonic lattices [32], and so on. After the weak value method has been proposed, the eigenvalues of the measured quantity are not constrained to the real numbers [33,34,35,36]. Corresponding to the experimental concept, the weak measurement is able to observe a quantum system in a minimum interfering condition so that it allows scientists to acquire the classical-counterpart physical quantities of the quantum system with the complex eigenvalues. The quantum trajectory has been observed in different systems by means of the weak measurement [37,38,39,40,41,42,43,44]. The features of the non-Hermitian system and parity time have been detected by using the weak value method [45,46,47,48]. In 2021, two experiments revealed that the imaginary number in quantum mechanics has the physical meaning in reality [49,50]. According to these experimental results, the complex number appeared in the Schrödinger equation is not merely a mathematical tool but has an actual physical meaning [51,52].

Quantum Hamilton mechanics (QHM) is one of the trajectory interpretation of quantum mechanics. It is established on the foundation of the complex-space structure within which all physical quantities are complex-valued [53]. The quantum operators, quantization rules, uncertainty principle, correspondence principle, quantum probability, spin, and all other fundamental properties of quantum mechanics can have their corresponding trajectory-based descriptions underlying the framework of QHM in the complex domain [54,55,56,57]. It is found that the spin motion of the electron in the hydrogen atom is independent of the wavefunction, and is determined solely by the geometrical property of the complex- space structure [58,59]. The combined orbital and spin motion in the hydrogen atom can therefore be precisely described in detail under the framework of QHM. It provides us the most finery model to discuss the electron’s transition in the hydrogen energy levels.

In this article, we apply an oscillating electric field with strength $E=8.8\times {10}^8 \mathrm{V}/\mathrm{m}$ and frequncy $\mathsf{\omega }=1.548750 1/\mathrm{s}$ to the hydrogen electron to analyze its transition dynamics by means of QHM. The transition trajectory, the time evolution of the electron’s total energy, and the time responses of the transition process are presented in addition to the occupation probability, which is the only information that quantum mechanics can provide. The paper is organized as follows. QHM as the main framework will be briefly introduced in Section 2, where the dynamics and the trajectories of the hydrogen electron in the complex spherical coordinate are analyzed to reveal the forces and the quantum potential acting on the electron. Section 3 will derive the spin dynamics from the Schrödinger equation and the wavefunction-independent feature of the spin dynamics will be demonstrated by means of the hydrogen electron in the ground state. With the established orbital and spin dynamics, the 1s–2p transition dynamics in the hydrogen atom will be considered in Section 4. Section 5 discusses how QHM differs from probability-based quantum mechanics, and shows how QHM outperforms other trajectory-based interpretations of quantum mechanics. Conclusions are given in Section 6.

2. Quantum Hamilton Mechanics

2.1. Quantum Hamilton-Jacobi Equation

In this section we will introduce the quantum Hamilton mechanics (QHM) [54] to analyze the quantum motion of the electron in hydrogen atom. The derivation of QHM starts from its classical counterpart:

$$\frac{\partial S_c\left(t,q\right)}{\partial t}+{\left.H_c\left(t,q,p\right)\right|}_{p=\nabla S_c}=0,$$

(1)

where $S_c$ is classical action function, $H_c=p^2/2m+V\left(q\right)$ is the classical Hamiltonian of a particle with mass $m$ moving under the action of the potential $V\left(q\right)$, and $\left(q,p\right)$ are the canonical coordinate and momentum. The Schrödinger equation can be transformed into a form similar to the classical Hamilton-Jacobi Equation (1) by the following transformation

$$\mathsf{\Psi }\left(t,q\right)=\exp \left(iS\left(t,q\right)/\hslash \right),$$

(2)

where $\mathsf{\Psi }\left(t,q\right)$ is the wavefunction and $S\left(t,q\right)$ is the quantum action function. In Equation (2), the wavefunction $\mathsf{\Psi }\left(t,q\right)$ has been normalized to a dimensionless form, and the action function $S\left(t,q\right)$ has the same unit of angular momentum as $\hslash$. The substitution of Equation (2) into the Schrödinger equation

$$i\hslash \frac{\partial \mathsf{\Psi }\left(t,q\right)}{\partial t}=-\frac{{\hslash }^2}{2m}{\nabla }^2\mathsf{\Psi }\left(t,q\right)+V\mathsf{\Psi }\left(t,q\right)=0$$

(3)

leads to the quantum Hamilton-Jacobi equation

$$\frac{\partial S\left(t,q\right)}{\partial t}+{\left.H\left(t,q,p\right)\right|}_{p=\nabla S}=\frac{\partial S\left(t,q\right)}{\partial t}+{\left[\frac{1}{2m}{p}^2+V-\frac{i\hslash }{2m}\nabla ·p\right]}_{p=\nabla S}=0,$$

(4)

where the canonical momentum $p$ is related to the quantum action function $S\left(t,q\right)$ via

$$p=\nabla S=-i\hslash \nabla \ln \mathsf{\Psi }\left(t,q\right)\in ℂ.$$

(5)

In comparison with the classical Hamiltonian $H_c\left(t,q,p\right)=p^2/2m+V\left(q\right)$, the quantum Hamiltonian $H\left(t,q,p\right)$ appeared in Equation (4) has an additional term called quantum potential,

$$Q={\left.\frac{i\hslash }{2m}\nabla ·p\right|}_{p=\nabla S}=-\frac{i\hslash }{2m}{\nabla }^{2}S=-\frac{{\hslash }^2}{2m}{\nabla }^2\mathsf{\Psi }\left(t,q\right),$$

(6)

which is uniquely determined by the wavefunction $\mathsf{\Psi }\left(t,q\right)$. When the applied potential is independent of time, i.e., $V=V\left(q\right)$, a general solution to the Schrödinger Equation (3) can be separated as

$$\mathsf{\Psi }\left(t,q\right)=\psi \left(q\right)\exp \left(-iEt/\hslash \right),$$

(7)

where $E$ is the conserved total energy of the system and $\psi \left(q\right)$ satisfies the time-independent Schrödinger equation,

$$\frac{{\hslash }^2}{2m}{\nabla }^2\psi \left(q\right)+\left(E-V\left(q\right)\right)\psi \left(q\right)=0.$$

(8)

The associated quantum action function defined by Equation (2) becomes

$$S\left(t,q\right)=-i\hslash \ln \mathsf{\Psi }\left(t,q\right)=-i\hslash \ln \psi \left(q\right)-Et.$$

(9)

For a conservative system, the quantum Hamilton-Jacobi Equation (4) then reads

$$H\left(t,q,p\right)=\frac{1}{2m}{p}^2+V+Q=-\frac{\partial S\left(t,q\right)}{\partial t}=E.$$

(10)

This is the energy conservation law in QHM, manifesting that the total energy in QHM comprises three terms: kinetic energy $p^2/2m$, external potential energy $V\left(q\right)$, and intrinsic potential energy $-\left(i\hslash /2m\right)\nabla ·p$. The equivalence between Equations (8) and (10) can be verified by substituting $p=\nabla S\left(t,q\right)=-i\hslash \nabla \ln \psi \left(q\right)$ into Equation (10). The physical meaning underlying this equivalence is that the time-independent Schrödinger equation is just the energy conservation law in QHM.

For a conservative system, further simplification of the total potential $V+Q$ can be made by Equation (10):

$$V_{\mathrm{Total}}=V+Q=E-\frac{p^2}{2m}=E-\frac{1}{2m}{\left(\nabla S\right)}^2=E+\frac{{\hslash }^2}{2m}{\left(\nabla \ln \psi \right)}^2,$$

(11)

from which a relationship between the probability density function ${\left|\psi \right|}^2={\psi }^{*}\psi$ and the total potential can be established as

$$\left|V_{\mathrm{Total}}-E\right|=\frac{{\hslash }^2}{2m}\frac{{\left|\nabla \psi \right|}^2}{{\psi }^{*}\psi },$$

(12)

which shows that the magnitude of $V_{\mathrm{Total}}$ with respect to $E$ is inversely proportional to the probability density function ${\psi }^{*}\psi$.

2.2. Quantum Equation of Motion in Central Force Field

Now we apply the quantum Hamiltonian $H\left(t,q,p\right)=p^2/2m+V+Q$ defined in Equation (4) to the spherical coordinate $q=\left(r,\theta ,\varphi \right)$ and obtain

$$H=\frac{1}{2m}\left[p_r^2+\frac{p_{\theta }^2}{r^2}+\frac{p_{\varphi }^2}{r^2{\sin }^2\theta }\right]-\frac{i\hslash }{2m}\left[\frac{2}{r}{p}_r+\frac{p_{\theta }\cot \theta }{r^2}+\frac{\hslash }{i}\left(\frac{{\partial }^2\ln \psi }{\partial r^2}+\frac{1}{r^2}\frac{{\partial }^2\ln \psi }{\partial {\theta }^2}+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^2\ln \psi }{\partial {\varphi }^2}\right)\right]+V\left(r,\theta ,\varphi \right),$$

(13)

where the terms in the first bracket comprise the kinetic energy and the terms in the second bracket comprise the quantum potential $Q$ expressed in the spherical coordinates. The canonical momentum $p=\left(p_r,p_{\theta },p_{\varphi }\right)$ is related to the wavefunction $\psi \left(r,\theta ,\varphi \right)$ via

$$p_r=\frac{\hslash }{i}\frac{\partial \ln \psi }{\partial r}\in ℂ, p_{\theta }=\frac{\hslash }{i}\frac{\partial \ln \psi }{\partial \theta }\in ℂ, p_{\varphi }=\frac{\hslash }{i}\frac{\partial \ln \psi }{\partial \varphi }\in ℂ.$$

(14)

Due to the appearance of the imaginary number $i=\sqrt{-1}$, the canonical momentum $p$ has to be defined in the complex domain. The quantum Hamiltonian (13) can be used to derive the Hamilton equations of motion of the particle as follows,

$$\dot{r}=\frac{\partial H}{\partial p_r}=\frac{p_r}{m}+\frac{\hslash }{i}\frac{1}{mr}=\frac{\hslash }{im}\frac{1}{\psi }\frac{\partial \psi }{\partial r}+\frac{\hslash }{i}\frac{1}{mr}, r\in ℂ,$$

(15a)

$$\dot{\theta }=\frac{\partial H}{\partial p_{\theta }}=\frac{p_{\theta }}{m{r}^2}+\frac{\hslash }{i}\frac{\cot \theta }{2m{r}^2}=\frac{\hslash }{im{r}^2}\frac{1}{\psi }\frac{\partial \psi }{\partial \theta }+\frac{\hslash }{i}\frac{\cot \theta }{2m{r}^2}, \theta \in ℂ,$$

(15b)

$$\dot{\varphi }=\frac{\partial H}{\partial p_{\varphi }}=\frac{p_{\varphi }}{m{r}^2{\sin }^2\theta }=\frac{\hslash }{im{r}^2{\sin }^2\theta }\frac{1}{\psi }\frac{\partial \psi }{\partial \varphi }, \varphi \in ℂ,$$

(15c)

where we note that the quantum trajectory $\left(r\left(t\right),\theta \left(t\right),\varphi \left(t\right)\right)$ solved from Equation (15) is generally defined in the complex domain due to the appearance of the imaginary number $i$. In terms of $\left(\dot{r},\dot{\theta },\dot{\varphi }\right)$, the quantum Hamiltonian $H$ defined in Equation (13) can be rewritten in a classical-like form:

$$H=\frac{m}{2}\left[{\dot{r}}^2+{\left(r\dot{\theta }\right)}^2+{\left(r\dot{\varphi }\sin \theta \right)}^2\right]+V_{\mathrm{Total}},$$

(16)

in which the terms in the bracket constitute the classical counterpart of the kinetic energy, and $V_{\mathrm{Total}}=Q+V$ represents the total potential which contains the quantum potential $Q$ and the external potential $V\left(r,\theta ,\varphi \right)$:

$$V_{\mathrm{Total}}=\left\{\frac{{\hslash }^2}{8m{r}^2}\left(4+{\cot }^2\theta \right)-\frac{{\hslash }^2}{2m}\left[\frac{{\partial }^2\ln \psi }{\partial r^2}+\frac{1}{r^2}\frac{{\partial }^2\ln \psi }{\partial {\theta }^2}+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^2\ln \psi }{\partial {\varphi }^2}\right]\right\}+V\left(r,\theta ,\varphi \right).$$

(17)

In Bohr’s atomic model, the dominant potential is the Coulomb potential $V\left(r\right)$ which attracts the electron to the nucleus so that the electron eventually will fall on the nucleus; however, it never happens in reality. Equation (17) proposes an explanation of how atom can keep balance between the quantum potential $Q$ and the Coulomb potential $V\left(r\right)$. The quantum potential $Q$, which is responsible for all the quantum effects, can be recognized as the potential barrier to stop the electron crashing on the nucleus.

2.3. Orbital Dynamics of Electron in Hydrogen Atom

The central-force field in the hydrogen atom is specified by the Coulomb potential:

$$V=V\left(r\right)=\frac{-e^2}{4\pi {\epsilon }_{0}r},$$

(18)

where $r$ is the distance between the electron and the nucleus. The solution of the Schrödinger Equation (8) with $V=V\left(r\right)$ is separable as

$${\psi }_{nl{m}_l}\left(r,\theta ,\varphi \right)=C{R}_{nl}\left(r\right){\Theta }_{l{m}_l}\left(\theta \right){\mathsf{Ф}}_{m_l}\left(\varphi \right),$$

(19)

where $l$ and $m_l$ denote the orbital quantum number and the magnetic quantum number, respectively, and the constant $C$ is determined so that ${\psi }_{nl{m}_l}$ is normalized to a dimensionless form. The three separated functions in Equation (19) are related to the Laguerre polynomial $L_{n-l-1}^{2l+1}\left(r\right)$, associated Legendre polynomial $P_l^{m_l}\left(\cos \theta \right)$, and the exponential function as follows:

$$R_{nl}\left(\rho \right)={\left(2\rho /n\right)}^l{e}^{-\rho /n}{L}_{n-l-1}^{2l+1}\left(2\rho /n\right), n=1, 2, 3, \cdots ,$$

(20a)

$${\Theta }_{l{m}_l}\left(\theta \right)=P_l^{m_l}\left(\cos \theta \right), l=0,1,2,\cdots ,n-1,$$

(20b)

$${\mathsf{Ф}}_{m_l}\left(\varphi \right)=e^{i{m}_l\varphi }, m_l=0, \pm 1, \pm 2,\cdots ,\pm l.$$

(20c)

The energy level $E_n$ is related to the principal quantum number $n$ as

$$E_n=-\left(\frac{{\hslash }^2}{2m{a}_0}\right)\frac{1}{n^2},$$

(21)

where $\rho =r/a_0$ is the dimensionless radius and $a_0$ is the Bohr radius. By inserting the wavefunction (19) into Equation (15), we obtain the equations of motion for the electron moving in the eigenstate ${\psi }_{nl{m}_l}$:

$$\frac{d\rho }{d\tau }=\frac{2}{i}\frac{d}{d\rho }\ln \left(\rho R_{nl}\left(\rho \right)\right), \rho \in ℂ$$

(22a)

$$\frac{d{z}_{\theta }}{d\tau }=\frac{1}{i{\rho }^2}\left[2\left(1-z_{\theta }^2\right)\frac{d}{d{z}_{\theta }}\ln \left({\Theta }_{l{m}_l}\left(z_{\theta }\right)\right)-z_{\theta }\right], z_{\theta }=\cos \theta \in ℂ,$$

(22b)

$$\frac{d\varphi }{d\tau }=\frac{2m_l}{{\rho }^2\left(1-z_{\theta }^2\right)}, \varphi \in ℂ$$

(22c)

where we define the dimensionless time $\tau =t\hslash /\left(2m{a}_0^2\right)$.

The total potential that the electron encounters in the hydrogen atom can be obtained by inserting the wavefunction (19) to Equation (17),

$${\overline{V}}_{nl{m}_l}=\overline{V}+\overline{Q}=-\frac{2}{\rho }+\left[\frac{\left(4+{\cot }^2\theta \right)}{4{\rho }^2}-\frac{d^2\ln R_{nl}\left(\rho \right)}{d{\rho }^2}-\frac{1}{{\rho }^2}\frac{d^2\ln {\Theta }_{l{m}_l}\left(\theta \right)}{d{\theta }^2}\right],$$

(23)

where the terms with bar denote the dimensionless form. The terms within the bracket constitute the quantum potential $\overline{Q}$ and form the shell structures in the hydrogen atom. Differentiating $V_{nl{m}_l}$ with respect to $\rho$, $\theta$, and $\varphi$ give the total forces acting on the electron in the three directions:

$${\overline{f}}_{nl{m}_l}^{\rho }=-\frac{2}{{\rho }^2}+\frac{1}{2{\rho }^3}\left(4+{\cot }^2\theta \right)-\frac{d^3\ln R_{nl}\left(\rho \right)}{d{\rho }^3}-\frac{2}{{\rho }^2}\frac{d^2\ln {\Theta }_{l{m}_l}\left(\theta \right)}{d{\theta }^2},$$

(24a)

$${\overline{f}}_{nl{m}_l}^{\theta }=\frac{1}{{\rho }^2}\frac{d^3\ln {\Theta }_{l{m}_l}\left(\theta \right)}{d{\theta }^3}+\frac{1}{2{\rho }^2}\frac{\cos \theta }{{\sin }^3\theta },$$

(24b)

$${\overline{f}}_{nl{m}_l}^{\varphi }=\frac{1}{{\rho }^2{\sin }^2\theta }\frac{d^3\ln {\mathsf{Ф}}_{m_l}\left(\varphi \right)}{d{\varphi }^3}=0.$$

(24c)

2.4. Electronic Quantum Motion in Eigenstates

One can picturize how the electron moves in a specific eigenstate by analyzing the total forces acting on it. Taking the 1s state with $\left(n, l, m_l\right)=\left(1,0,0\right)$ as an example, the total force can be acquired from Equation (24) with the ground-state wavefunction, $R_{10}\left(\rho \right)=e^{-\rho }$ and ${\Theta }_{00}\left(\theta \right)={\mathsf{Ф}}_0\left(\varphi \right)=1$,

$${\overline{f}}_{100}^{\rho }=-\frac{2}{{\rho }^2}+\frac{1}{2{\rho }^3}\left(4+{\cot }^2\theta \right), {\overline{f}}_{100}^{\theta }=\frac{1}{2{\rho }^2}\frac{\cos \theta }{{\sin }^3\theta }, f_{100}^{\varphi }=0.$$

(25)

The position satisfying ${\overline{f}}_{100}^{\rho }={\overline{f}}_{100}^{\theta }={\overline{f}}_{100}^{\varphi }=0$ is called the equilibrium position and is found as

$${\rho }_{\mathrm{eq}}=1, {\theta }_{\mathrm{eq}}=\pi /2.$$

(26)

The electron has the tendency to stay at the equilibrium position since it is the most stable place in a dynamic sense. The tendency of being at ${\rho }_{\mathrm{eq}}=1$ (or equivalently, $r_{\mathrm{eq}}=a_0)$, is compatible with the probability distribution $P_{10}\left(\rho \right)=4\pi {\rho }^2{e}^{-2\rho }$, which achieves its maximum at the Bohr radius $a_0$, i.e., at the equilibrium position ${\rho }_{\mathrm{eq}}=1$. The correspondence between the particle dynamic and the wave probability is one of the significant features of the hydrogen electron revealed by QHM. Another feature shows that the electron mostly lies on the x-y plane since ${\theta }_{\mathrm{eq}}=\pi /2$. The electron cloud may have the brightest (most intense) part focused on a ring with radius $a_0$ on the x-y plane if combining the two features together. The radial force at ${\theta }_{\mathrm{eq}}=\pi /2$ is

$${\overline{f}}_{100}^{\rho }\left(\rho ,\pi /2\right)={\overline{f}}_V^{\rho }\left(\rho \right)+{\overline{f}}_Q^{\rho }\left(\rho \right)=-\frac{2}{{\rho }^2}+\frac{2}{{\rho }^3},$$

(27)

where the subscripts $V$ and $Q$ denote the Coulomb force and the quantum force, respectively. Obviously, the quantum force is much greater than the Coulomb force when $\rho <1$, which means that the quantum force forbids the electron from colliding with the nucleus. This is the third remarkable feature of the hydrogen electron revealed by QHM. The motion of the electron in the ground state can be obtained from Equation (22):

$$\frac{d\rho }{d\tau }=\frac{2}{i}\frac{1-\rho }{\rho }, \frac{d\theta }{d\tau }=\frac{\cot \theta }{i{\rho }^2}, \frac{d\varphi }{d\tau }=0.$$

(28)

Figure 1a displays some complex trajectories projected on the real x-z plane ($\varphi =0$), which are solved from Equation (28) with different initial positions. The electron moving periodically can be observed in Figure 1b. In particular, the electron almost stays at the equilibrium radius ${\rho }_{\mathrm{eq}}=1$ if its initial position is on it, as Figure 1c shows. It is clear to see from Figure 1d that the oscillating trajectory has a period of $2\pi$. The periodic trajectory is the fourth feature of the hydrogen electron, which represents a remarkable property of energy conversation systems. Please note that the electron’s motion can happen in any value of $\varphi$ between $0$ and $2\pi$since the wavefunction is spherically symmetric and $\dot{\varphi }=0$.

Figure 2a illustrates the complex trajectories of the electron in the $2s$ state projected on the real x-z plane. The equations of motion for the $2s$ state read,

$$\frac{d\rho }{d\tau }=i\frac{{\rho }^2-6\rho +4}{\rho \left(\rho -2\right)}, \frac{d\theta }{d\tau }=\frac{\cot \theta }{i{\rho }^2}, \frac{d\varphi }{d\tau }=0.$$

(29)

We notice that there are two equilibrium positions in the radial direction and one in the azimuthal direction,

$${\rho }_{\mathrm{eq}}=3\pm \sqrt{5}, {\theta }_{\mathrm{eq}}=\pi /2.$$

(30)

Two equilibrium positions in the radial direction reflect that there are two shell structures of the electron cloud (probability distribution) separated by the boundary at $\rho =2$. The electron is allowed to move either in the first shell $0<\rho <2$or the second shell $\rho >2$. The trajectories illustrated in Figure 2a can be divided into two groups. The inner group corresponds to the motions in the first shell and the outer group corresponds to the motion in the second shell. The shell structure is formed by the spatial distribution of the total potential,

$${\overline{V}}_{200}=\overline{V}+\overline{Q}=-\frac{2}{\rho }+\left[-\frac{2}{{\left(2-\rho \right)}^3}+\frac{1}{2{\rho }^2}\left(4+{\cot }^2\theta \right)\right].$$

(31)

In fact, the quantum potential contributes the most part of the shell structure as represented by Equation (31). Figure 2b illustrates the total potential in the radial direction. The two equilibrium positions ${\rho }_{\mathrm{eq}}=3\pm \sqrt{5}$ are at the lowest points in the two shells of ${\overline{V}}_{200}$.

3. Spin Dynamics of Electron in Hydrogen Atom

The eigenstate of the hydrogen electron with zero orbital angular momentum $\left(l=0\right)$ is spherically symmetric and decays more or less exponentially with increasing distance from the origin. It is noted that the electron in the state with zero orbital angular momentum, such as $1s$ or $2s$ state, still has nonzero probability distribution in the azimuthal direction. However, the motion with zero orbital angular momentum could happen only if the electron is oscillating along the straight line connecting the electron and the nucleus in a classical sense. In QHM this contrary observation between the quantum perspective and classical perspective about the zero angular momentum can be explained. From Equation (28) and Equation (29) we can see that the electron is not only moving in the radial direction but also in the azimuthal direction in both 1s and 2s states. This azimuthal motion is caused by a special term $\left(4+{\cot }^2\theta \right)/4{\rho }^2$ in the total potential, which in turn generates a force component $\cos \theta /2{\rho }^2{\sin }^3\theta$ in the $\theta$-direction, as can be seen in Equation (24b). Thus, the electron moves in the azimuthal direction even if the orbital angular momentum is zero. This is the most significant feature of the electron and is recognized as the spin motion

The combined orbital and spin motion of the electron is described by (15b),

$$m{r}^2\dot{\theta }=p_{\theta }+p_s=\frac{\hslash }{i}\frac{d\ln {\Theta }_{l{m}_l}\left(\theta \right)}{d\theta }+\frac{\hslash }{2i}\cot \theta ,$$

(32)

where $p_{\theta }$ and $p_s$ denote the orbital angular momentum and the spin angular momentum, respectively. The spin angular momentum $p_s$ is responsible for the angular motion when the orbital angular momentum $p_{\theta }$ is zero:

$$m{r}^2\dot{\theta }=p_s=\frac{\hslash }{2i}\cot \theta .$$

(33)

Spin is a unique quantum feature that has no classical counterpart. However, in the framework of QHM, spin motion can be demonstrated in a classical manner. What makes QHM so special that it can describe explicitly the electron’s spin motion? The answer is hidden in the extension of the space dimension. The spin angular momentum can never be shown by Equation (33) if the extension to complex space is not considered. Besides the spin-up and spin-down motions, Equation (33) reveals a still-unknown electron spin motion, spinless motion.

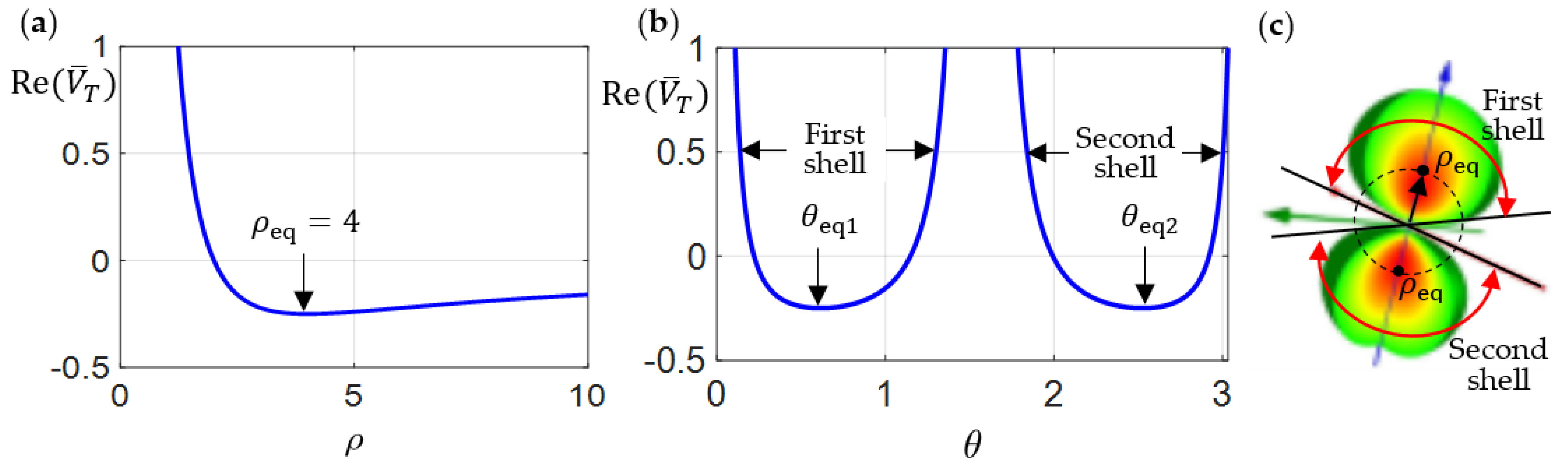
3.1. Spinless Dynamics

The same spin dynamics represented by Equation (33) appears in both Equation (28) and Equation (29) for the 1s and 2s states, since their orbital angular momentum $p_{\theta }$ is zero. In the following, we will reveal the spinless, spin-up, and spin-down dynamics existing in the 1s state. It is surprising to see that the electron is actually spinless, when the electron is near its equilibrium position. Recall that the radial force acting on the electron in the 1s state is given by Equation (24a):

$${\overline{f}}_{100}^{\rho }=-\frac{2}{{\rho }^2}+\frac{1}{2{\rho }^3}\left(4+{\cot }^2\theta \right)={\overline{f}}_C^{\rho }+{\overline{f}}_Q^{\rho },$$

(34)

which is composed of the attractive Coulomb force ${\overline{f}}_C^{\rho }$ and repulsive quantum force ${\overline{f}}_Q^{\rho }$. There is no radial force acting on the electron when it is at the equilibrium position ${\rho }_{\mathrm{eq}}=1, {\theta }_{\mathrm{eq}}=\pi /2$ according to Equation (34). When the electron deviates from the equilibrium position, ${\overline{f}}_C^{\rho }$ and ${\overline{f}}_Q^{\rho }$ become unequal,

$${\overline{f}}_C^{\rho }<{\overline{f}}_Q^{\rho }, \rho <1,$$

(35a)

$${\overline{f}}_C^{\rho }>{\overline{f}}_Q^{\rho }, \rho >1.$$

(35b)

In either case, there is a force driving the electron to return to the equilibrium position. Similarly, the total tangential force ${\overline{f}}_{100}^{\theta }=0$ at ${\theta }_{\mathrm{eq}}=\pi /2$ can be obtained according to Equation (24b). Therefore, the electron has a stable oscillation motion around the equilibrium point, which can be described mathematically by

$$\rho \left(\tau \right)=1+\mathrm{Lambert}W\left(e^{2i\tau +c_0}\right),$$

(36a)

$$\cos \left(\theta \left(\tau \right)\right)=\frac{c_1{e}^{i\tau +c_0}}{\sqrt{e^{\mathrm{Lambert}W\left(e^{2i\tau +c_0}\right)}+e^{2i\tau +c_0}}},$$

(36b)

where the special function $y=\mathrm{Lambert}W\left(x\right)$ is defined as the solution to $y{e}^y=x$. The oscillatory motion has the zero-mean property,

$$\langle \frac{d\rho }{d\tau }\rangle =\langle \frac{d\theta }{d\tau }\rangle =0,$$

(37)

which leads to the zero angular momentum,

$$\langle m{r}^2\frac{d\theta }{dt}\rangle =\frac{\hslash }{2}\langle {\rho }^2\frac{d\theta }{d\tau }\rangle =0.$$

(38)

This significant result reveals that the electron has no spin motion in the neighborhood of the equilibrium position $\left({\rho }_{\mathrm{eq}},{\theta }_{\mathrm{eq}}\right)$ in the $l=0$ state. The electron in such a situation is said to be in a spinless mode. Figure 3a illustrates the electron’s motion near its equilibrium position in the complex $\theta$-plane. The zero-mean property of $d\theta /d\tau$ in spinless mode can be observed in Figure 3b.

3.2. Spin-Up and Spin-Own Dynamics

How can the electron have no spin motion if spin is its intrinsic feature? If it is the fact, then how could scientists never observe the spinless electron? The answer is that there is only a small region in the complex space, within which the electron has no spin motion. The spinless motion only happens in the neighborhood of the equilibrium position, $\left({\theta }_R,{\theta }_I\right)=\left(\pi /2,0\right)$. As shown in Figure 3a, the equilibrium position $\left({\theta }_R,{\theta }_I\right)=\left(\pi /2,0\right)$ is a center surrounded by closed phase-lane trajectories. Even the circling motion with greater radius has larger ${\rho }^{2}d\theta /d\tau$ as indicated by Figure 3b, the average value of ${\rho }^{2}d\theta /d\tau$ is still zero around the closed trajectories. When the initial position $\left({\theta }_R\left(0\right),{\theta }_I\left(0\right)\right)$ is not in the neighborhood of the equilibrium position, for example, $\left({\theta }_R\left(0\right),{\theta }_I\left(0\right)\right)=\left(0,0.5\right)$, the electron’s motion in the complex $\theta$-plane does not follow a closed path but a oscillatory open trajectory forwarding to the negative ${\theta }_R$ direction, as the dotted green line illustrates in Figure 3c. This oscillatory trajectory has a nonzero mean value of ${\rho }^{2}d\theta /d\tau$ and equals to $-1$, as Figure 3d shows. This oscillating motion in the complex $\theta$-plane leads to the following result:

$$\langle m{r}^2\frac{d\theta }{dt}\rangle =\frac{\hslash }{2}\langle {\rho }^2\frac{d\theta }{d\tau }\rangle =-\frac{\hslash }{2},$$

(39)

which can be recognized as the spin angular momentum with negative sign, i.e., the spin-down angular momentum.

Similarly, the angular momentum of the spin-up motion can be observed in the lower half region of the complex $\theta$-plane. For instance, the oscillating trajectory forwarding to the positive ${\theta }_R$direction is observed with $\left({\theta }_R\left(0\right),{\theta }_I\left(0\right)\right)=\left(0,-0.5\right)$, as the dotted green line displays in Figure 3e. The corresponding average value of ${\rho }^{2}d\theta /d\tau$ is equal to 1, as displayed in Figure 3f. Hence, we have

$$\langle m{r}^2\frac{d\theta }{dt}\rangle =\frac{\hslash }{2}\langle {\rho }^2\frac{d\theta }{d\tau }\rangle =\frac{\hslash }{2},$$

(40)

which is the spin-up angular momentum.

The boundary separating the three spin modes can be established by solving Equation (28) for $\theta \left(\tau \right)$ at $\rho ={\rho }_{\mathrm{eq}}=1$:

$$\cos \theta \left(\tau \right)=\left(\cos {\theta }_0\right)e^{i\tau }, {\theta }_0\in ℂ,$$

(41)

which has the property,

$$\left|\cos \theta \left(\tau \right)\right|=\left|\cos {\theta }_0\right|=\mathrm{constant}.$$

(42)

with the substitution $\theta ={\theta }_R+i{\theta }_I$ into solution (42), the trajectory in the complex $\theta$-plane can be obtained as follows,

$${\cos \mathrm{h}}^2{\theta }_I={\left|\cos {\theta }_0\right|}^2+1-{\cos }^2{\theta }_R\ge 1.$$

(43)

It can be seen that $\left|\cos {\theta }_0\right|=1$ is the bifurcation curve in that the ${\theta }_R$ dynamics is bounded as in the spinless mode, if $\left|\cos {\theta }_0\right|<1$, and is unbounded as in the spin-up and spin-down mode, if $\left|\cos {\theta }_0\right|\ge 1$. Hence, the trajectory corresponds to the three spin modes can be divided by the boundary curve:

$$\left|\cos \theta \right|=1\leftrightarrow \left|\sin \mathrm{h}{\theta }_I\right|=\left|\sin {\theta }_R\right|.$$

(44)

Along the boundary curve (44), the three spin regions can be defined as follows:

• Spin-down region $S_{\downarrow }\triangleq \left\{\left.\left({\theta }_R,{\theta }_I\right)\right|\sin \mathrm{h}{\theta }_I\ge \left|\sin {\theta }_R\right|\right\}$
• Spinless region $S_0\triangleq \left\{(\left.{\theta }_R,{\theta }_I)\right|\sin \mathrm{h}{\theta }_I<\left|\sin {\theta }_R\right|\right\},$
• Spin-up region $S_{\uparrow }\triangleq \left\{(\left.{\theta }_R,{\theta }_I)\right|\sin \mathrm{h}{\theta }_I\le -\left|\sin {\theta }_R\right|\right\}.$

and the corresponding angular momentum reads

$$\langle m{r}^2\frac{d\theta }{dt}\rangle =\frac{\hslash }{2}\langle {\rho }^2\frac{d\theta }{d\tau }\rangle =\left\{\begin{array}{ll}-\hslash /2, & \forall {\theta }_R\left(\tau \right)\in S_{\downarrow }\\ 0,& \forall {\theta }_R\left(\tau \right)\in S_0\\ \hslash /2,& \forall {\theta }_R\left(\tau \right)\in S_{\uparrow }\end{array}\right..$$

(45)

The electron is found to have no spin in a very small region in the complex space around the equilibrium point. Out of the nearby region of the equilibrium point, the electron has the spin motion. The spin motions can be distinguished as spin up and spin down according to whether the trajectory in the complex $\theta$-plane is forwarding to the positive or negative ${\theta }_R$ direction.

Although the observed spin angular momentum is a time-averaged result, there are special situations where the electron’s spin angular momentum is truly constant. In the region $S_0$, the ideal spinless motion is achieved when the electron enters the equilibrium position $\left(r_{\mathrm{eq}}, {\theta }_{\mathrm{eq}}\right)=\left(a_0, \pi /2\right)$ at which the spin angular momentum is zero exactly. In the regions of $S_{\uparrow }$ and $S_{\downarrow }$, the constant spin angular momentum $\pm \hslash /2$ can be achieved by noting

$$\cos \theta =\cos {\theta }_R\cosh {\theta }_I-i\sin {\theta }_R\sinh {\theta }_I=e^{\left|{\theta }_I\right|}\left(\cos {\theta }_R\mp i\sin {\theta }_R\right)/2, \left|{\theta }_I\right|\gg 0,$$

(46a)

$$\sin \theta =\sin {\theta }_R\cosh {\theta }_I+i\cos {\theta }_R\sinh {\theta }_I=e^{\left|{\theta }_I\right|}\left(\sin {\theta }_R\pm i\cos {\theta }_R\right)/2, \left|{\theta }_I\right|\gg 0,$$

(46b)

and thus from Equation (33)

$$m{r}^2\dot{\theta }=\frac{\hslash }{2i}\frac{\cos \theta }{\sin \theta }\approx \left\{\begin{array}{cc}\frac{\hslash }{2i}\frac{\cos {\theta }_R-i\sin {\theta }_R}{\sin {\theta }_R+i\cos {\theta }_R}=\frac{\hslash }{2},& {\theta }_I\gg 0\\ \frac{\hslash }{2i}\frac{\cos {\theta }_R+i\sin {\theta }_R}{\sin {\theta }_R-i\cos {\theta }_R}=-\frac{\hslash }{2},& {\theta }_I\ll 0\end{array}\right..$$

(47)

Therefore, in the region with large $\left|{\theta }_I\right|$, the spin angular momentum $\pm \hslash /2$ is attained precisely without any perturbation.

It has to be pointed out that the commonly known spin angular momentum $\pm \hslash /2$ is referred to the mean value $\langle m{r}^2\dot{\theta }\rangle$, but not to the instantaneous value of $m{r}^2\dot{\theta }$. Indeed, ${\rho }^{2}d\theta /d\tau$ is oscillating with time, as illustrated in Figure 3d,f. The oscillation period of ${\rho }^{2}d\theta /d\tau$ is $2\pi$ whose corresponding physical time period is $T=2\pi \left(2m{a}_0^2/\hslash \right)=3.0385\times {10}^{-16} \mathrm{s}$. This very short oscillation period of the spin angular momentum can only be observed with a time resolution finer than $3.0385\times {10}^{-16} \mathrm{s}$. The experimental verification of this spin angular momentum perturbation would be the most remarkable discovery ever since the fundamental characteristics of the electron were proposed.

3.3. Deriving Spin Dynamics from Schrödinger Equation

In quantum mechanics, spin can only be revealed in the Dirac equation in which the relativity effect of the electron is considered. The reason that the spin dynamic cannot be exposed in the Schrödinger equation is the definition of the angular momentum in quantum mechanics, not because of the lack of consideration of the relativity effect. Let us inspect the expression of the angular momentum in complex space firstly. The quantum Hamiltonian (13) derived from the Schrödinger equation can be expressed in terms of the action function $S=-i\hslash \ln \psi$ as

$$H=\left[\frac{1}{2m}{\left(\frac{\partial S}{\partial r}\right)}^2+\frac{\hslash }{2mi}\left(\frac{2}{r}\frac{\partial S}{\partial r}+\frac{{\partial }^{2}S}{\partial r^2}\right)\right]+\frac{L^2}{2m{r}^2}+V\left(r,\theta ,\varphi \right).$$

(48)

The terms within the bracket comprise the energy related to the radial motion, and $L^2/2m{r}^2$ comprises the energy related to the angular motion defined as:

$$L^2={\left(\frac{\partial S}{\partial \theta }\right)}^2+\frac{\hslash }{i}\cot \theta \frac{\partial S}{\partial \theta }+\frac{\hslash }{i}\frac{{\partial }^{2}S}{\partial {\theta }^2}+\frac{L_z^2}{{\sin }^2\theta }, L_z^2={\left(\frac{\partial S}{\partial \varphi }\right)}^2+\frac{\hslash }{i}\frac{{\partial }^{2}S}{\partial {\varphi }^2},$$

(49)

where $L$ can be identified as the orbital angular momentum and $L_z$ is the $z-$component angular momentum in the complex domain. Using $S=-i\hslash \ln \psi$, it can be shown easily that $L^2$ and $L_z$ are the functional representations of their corresponding quantum operators ${\widehat{L}}^2$ and ${\widehat{L}}_z$ as

$${\widehat{L}}^2\psi =L^2\psi , {\widehat{L}}_z\psi =L_z\psi$$

(50)

where

$${\widehat{L}}^2=-{\hslash }^2\left(\frac{{\partial }^2}{\partial {\theta }^2}+\cot \theta \frac{\partial }{\partial \theta }+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2}{\partial {\varphi }^2}\right), {\widehat{L}}_z=\frac{\hslash }{i}\frac{\partial }{\partial \varphi }.$$

(51)

The squared orbital angular momentum operator ${\widehat{L}}^2$ gives rise to the quantization of the squared orbital angular momentum, which is described by the orbital quantum number $l\left(l+1\right){\hslash }^2$. On the other hand, the quantization of ${\widehat{L}}_z$ is described by the magnetic quantum number $m_l\hslash$. Let us consider the $2p$ state with $\left(n,l,m_l\right)=\left(2,1,1\right)$, as an example to show that $L^2$ and $L_z$ can give exactly the same quantization result. Substituting the wave function ${\psi }_{211}$ into Equation (50), we have

$$L^2=\frac{{\hslash }^2}{4}\left[{\left(-3i\cot \theta \right)}^2+{\left(\frac{\pm 2}{\sin \theta }\right)}^2+{\cot }^2\theta -4\left(-{\csc }^2\theta \right)\right]=2{\hslash }^2, L_z=\hslash ,$$

(52)

which is identical to the result given by the quantum numbers $l=1$ and $m_l=1$. The orbital angular momentum operator ${\widehat{L}}^2$ roots from the convergence requirement of the Legendre polynomials. The admissible solutions ${\psi }_{nl{m}_l}$ turn out to be the eigenfunctions of ${\widehat{L}}^2$ with eigenvalues $l\left(l+1\right){\hslash }^2$, i.e., ${\widehat{L}}^2{\psi }_{nl{m}_l}=l\left(l+1\right){\hslash }^2{\psi }_{nl{m}_l}$. This operator formulism is just the origin that excludes the spin angular momentum from ${\widehat{L}}^2$. However, underlying the framework of QHM, we still can extract the spin angular momentum from $L^2$, i.e., the functional representation of ${\widehat{L}}^2$.

The functional representation of ${\widehat{L}}^2$ is given by Equation (49), which can be rewritten with the help of Equation (15) as

$$L^2=\left[{\left(m{r}^2\dot{\theta }\right)}^2+{\left(m{r}^2\dot{\varphi }\sin \theta \right)}^2\right]+\left[\frac{{\hslash }^2}{4}{\cot }^2\theta -{\hslash }^2\left(\frac{{\partial }^2\ln \psi }{\partial {\theta }^2}+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2\ln \psi }{\partial {\varphi }^2}\right)\right],$$

(53)

in which the first bracket is the classical counterpart of the angular momentum and the second bracket is the quantum correction. When the electron is in the state with $l=m_l=0$, we have $L^2=0$, $\dot{\varphi }=0$ and all the $\psi -$related terms are equal to zero. Then the remaining terms of Equation (53) satisfy the following relation:

$${\left(m{r}^2\dot{\theta }\right)}^2=-\frac{{\hslash }^2}{4}{\cot }^2\theta .$$

(54)

Solving for $m{r}^2\dot{\theta }$ then gives

$$m{r}^2\dot{\theta }=\frac{\hslash }{2i}\cot \theta ,$$

(55)

which is identical to Equation (33), the spin angular momentum.

4. Dynamics of Electron’s States Transitions

4.1. Energy Level Differences and Electric Field

The state transition problem is very similar to the orbit transfer problem in space engineering. The satellite needs the thrust to transfer from a lower-altitude orbit to a higher-altitude orbit. The required energy is needed to escape the gravitational attraction of Earth, which is analog to the transition energy that the electron needs to overcome the electrical attraction of the nucleus. However, there are two differences between two problems in different scales: (1) There is an additional force, the quantum force, acting on the electron; and (2) the states transition in the hydrogen atom takes place in a complex space.

The time-dependent wavefunction describing the two-level energy transition is given by the superposing the two eigen-state wavefunctions:

$$\Psi =C_1\left(t\right){\psi }_1{e}^{-i{E}_{1}t}+C_2\left(t\right){\psi }_2{e}^{-i{E}_{2}t},$$

(56)

where the subscripts $1$ and $2$ stand for the initial state and the final state, respectively. The time-dependent coefficients $C_1\left(t\right)$ and $C_2\left(t\right)$ are determined by the initial and final states according to the following relations

$$\frac{d{C}_1\left(t\right)}{dt}=-\frac{i{V}_{12}}{2\hslash }{e}^{-i\left({\omega }_0-\omega \right)t}{C}_2\left(t\right),$$

(57a)

$$\frac{d{C}_2\left(t\right)}{dt}=-\frac{i{V}_{21}}{2\hslash }{e}^{i\left({\omega }_0-\omega \right)t}{C}_1\left(t\right),$$

(57b)

where $V_{ij}=\int {\psi }_i^{*}{V}_{\mathrm{ext}}{\psi }_{j}dz$ and ${\omega }_0=\left(E_2-E_1\right)/\hslash$. The external potential energy $V_{\mathrm{ext}}$ is provided by the electric field oscillating z-direction,

$$V_{\mathrm{ext}}=-\frac{ezE}{2}{e}^{-i\omega t},$$

(58)

where $E$ and $\omega$ represent the strength and frequency of the electric field, respectively. The coefficients in Equation (56) determine the occupation probability of the initial state and the final state,

$$P_1={\left|C_1\left(t\right)\right|}^2, P_2={\left|C_2\left(t\right)\right|}^2.$$

(59)

The time history of $P_1$ and $P_2$ can be used to monitor the transition process.

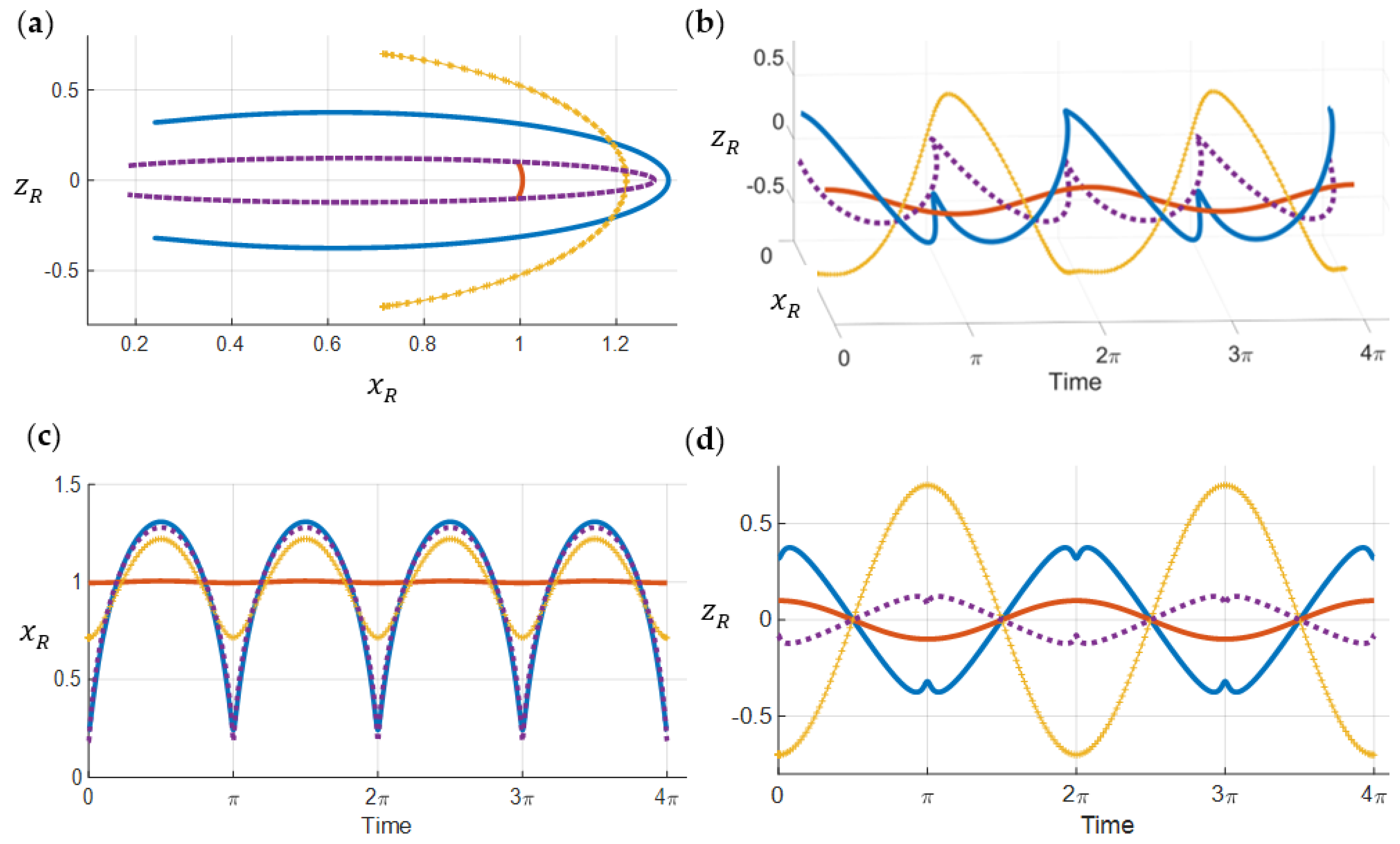
4.2. 1s–2p State Transition

Unlike the traditional probability description, here we will demonstrate the 1s–2p transition process in terms of the electron’s orbital and spin dynamics. Only the non-degenerate 1s and 2p states are considered here to emphasize the dynamic aspect of the transition process; however, transition trajectories between degenerate 1s and 2p states may make deviation from the non-degenerate case discussed below. The 2p state ${\psi }_{210}=\rho e^{-\rho /2}\cos \theta$ has two shell structures in the total potential

$${\overline{V}}_{210}=\overline{V}+\overline{Q}=-\frac{2}{\rho }+\frac{1}{4{\rho }^2}\left(8+\mathrm{c}\mathrm{o}{\mathrm{t}}^2\theta +4\mathrm{s}\mathrm{e}{\mathrm{c}}^2\theta \right),$$

(60)

as shown in Figure 4. The equations of motion of the electron under the action of ${\overline{V}}_{210}$ is given by Equation (22):

$$\frac{d\rho }{d\tau }=\frac{4-\rho }{i\rho }, \frac{d{z}_{\theta }}{d\tau }=\frac{2-3z_{\theta }^2}{i{\rho }^2{z}_{\theta }}, \frac{d\varphi }{d\tau }=0.$$

(61)

The two shell structures can be distinguished by the equilibrium points, which are located at ${\rho }_{\mathrm{eq}}=4$ and ${\theta }_{\mathrm{eq}}={\cos }^{-1}\left(\pm \sqrt{2/3}\right)$. Therefore, there are two spherical shells in the upper and lower real x-y plane along the $\theta$ direction, as the electron cloud exhibited in Figure 4c. By solving Equation (61), one can obtain the electron’s trajectory in the 2p state. Figure 5 displays the electron’s trajectories starting from the initial positions $\left(\rho \left(0\right),\theta \left(0\right)\right)=\left(4,\pi /3\right)\in S_0$ and $\left(\rho \left(0\right),\theta \left(0\right)\right)=\left(4,\pi /3\pm i\right)\in S_{\downarrow }\left(S_{\uparrow }\right)$, which are illustrated by the solid-blue line and dashed-red line, respectively. It is clear to see that the electron with ${\theta }_I\left(0\right)=0$ travels in a smaller region in the real x-z plane; while the electron with ${\theta }_I\left(0\right)=\pm i$ contains the spin motion and travels farther than the one with no spin motion. It is the spin motion that makes the difference between the two trajectories. Figure 5b illustrates the electron’s motion in the complex $\theta$-plane. The closed trajectory circling the ${\theta }_{\mathrm{eq}}={\cos }^{-1}\left(-\sqrt{2/3}\right)$ represents the spinless motion, and the open trajectories correspond to spin down and spin up motion. The electron’s spin motion is coupled with the orbital motion in the 2p state, however, the basic feature of spinless and spin modes are still apparent. The analysis of the interaction between orbital and spin dynamics refers to [60].

The wavefunction describes the 1s–2p state transition can be obtained according to Equation (56),

$$\Psi =C_1\left(\tau \right){\psi }_{100}{e}^{-i{\overline{E}}_1\tau }+C_2\left(\tau \right){\psi }_{210}{e}^{-i{\overline{E}}_2\tau },$$

(62)

where ${\overline{E}}_1=-1$ and ${\overline{E}}_2=-0.25$ are the energy levels of the 1s state and 2p state, respectively. By inserting ${\psi }_{100}$ and ${\psi }_{210}$ into Equation (62), we have the following expression:

$$\Psi =C_1\left(\tau \right)e^{-\rho }{e}^{-i{\overline{E}}_1\tau }+C_2\left(\tau \right)\rho e^{-\rho /2}\cos \theta e^{-i{\overline{E}}_2\tau },$$

(63)

in which the amplitude coefficients are determined by the following equations:

$${\dot{C}}_1\left(\tau \right)=\rho \left(\tau \right)\cos \theta \left(\tau \right)\overline{E}{e}^{-i∆\overline{\omega }\tau }{C}_2\left(\tau \right)/2,$$

(64a)

$${\dot{C}}_2\left(\tau \right)=\rho \left(\tau \right)\cos \theta \left(\tau \right)\overline{E}{e}^{i∆\overline{\omega }\tau }{C}_1\left(\tau \right)/2,$$

(64b)

where $∆\overline{\omega }={\omega }_0-\omega$. The state transition in hydrogen atom which is driven by electric field can be represented by the control block diagram as shown in Figure 6, where the wave function (62) and the quantum dynamics (15) constitute the system model, and the applied electric field plays the role of the controller. The control procedures are stated as follows. (1) Input the time-dependent amplitude coefficients, $C_1\left(\tau \right)$ and $C_2\left(\tau \right)$, to the system model and the system model outputs the electron’s transition trajectories, $\rho \left(\tau \right)$ and $\theta \left(\tau \right)$. (2) The system outputs are then measured by sensors and sent back to the controller as the feedback signals. (3) The controller computes the error between the target state and the output state, and then adjusts the amplitude coefficients, $C_1\left(\tau \right)$ and $C_2\left(\tau \right)$, according to Equation (64) based on the received feedback signals $\rho \left(\tau \right)$ and $\theta \left(\tau \right)$.

Next we will perform a computational simulation of the above control block diagram, where the electron is launched at the initial position $\left(\rho \left(0\right),\theta \left(0\right)\right)=\left(4.2,\pi /3\right)$ in the 1s state and the transition to the target 2p state is driven by the electric field with strength $E=8.8\times {10}^8 V/m$ and frequency $\omega =1.548750 1/s$. The transition trajectory can be obtained by solving the equations of motion (13) with the wavefunction $\Psi$ given by Equation (62), and the result is illustrated in Figure 7. The transition trajectory is observed to transit repeatedly between the 1s and 2p state, which is caused by the periodic change of the applied electric potential, as shown in Figure 8a. The electron arrives at the 2p state when $P_1={\left|C_1\right|}^2=0$ and $P_2={\left|C_2\right|}^2=1$, at time $\tau =1328$ (see Figure 8c), where the electric field reaches its maximum value. After the electron reaches the furthest point from the initial position, the applied electric field starts to decrease to its initial value and the electron returns to the 1s state when $P_1=1$ and $P_2=0$. In addition to the action of the electric field, the electron’s spin dynamics also participates in the transition process. From Figure 7 we can see that the time response of ${\theta }_R$ is monotonically increasing or decreasing in the transition process and the same phenomenon can be observed in the spin dynamics as shown in Figure 5a.

It is worth noting that the maximum external electric potential ${\overline{V}}_{\mathrm{ext}}$ is less than $0.05$ (see Figure 8a), but the energy gap between the 1s state and 2p state is $∆\overline{E}={\overline{E}}_2-{\overline{E}}_1=-0.25+1=0.75$. How can the electron accomplish the transition with the applied electric energy smaller than the energy gap? The answer lies in the quantum potential $\overline{Q}$. Let us have a closer inspection of the total energy in the transition,

$${\overline{E}}_{\mathrm{Total}}=\overline{V}+\overline{Q}+{\overline{V}}_{\mathrm{ext}}+E_k.$$

(65)

as depicted in Figure 8b. The quantum potential $\overline{Q}$ during the transition process can be expressed by

$$\begin{gathered} \overline{Q}=\frac{\left(4+\mathrm{c}\mathrm{o}{\mathrm{t}}^2\theta \right)}{4{\rho }^2}+\frac{1}{4}\left[\frac{C_2\cos \theta \left(C_1\left(\rho +4\right)e^{-i\left({\overline{E}}_1+{\overline{E}}_2\right)\tau -\rho /2}-4C_2\cos \theta e^{-2i{\overline{E}}_2\tau }\right)}{2C_1{C}_2\rho \cos \theta e^{-i\left({\overline{E}}_1+{\overline{E}}_2\right)\tau -\rho /2}+{\left(C_2\rho \cos \theta e^{-i{\overline{E}}_2\tau }\right)}^2+C_1^2{e}^{-2i{\overline{E}}_2\tau -\rho }}\right] \\ -\frac{1}{{\rho }^2}\left[\frac{C_2\rho \cos \theta e^{-\rho /2}{e}^{-i{\overline{E}}_2\tau }}{C_1{e}^{-\rho }{e}^{-i{\overline{E}}_1\tau }+C_2\rho \cos \theta e^{-\rho /2}{e}^{-i{\overline{E}}_2\tau }}+\frac{{\left(C_2\rho \sin \theta e^{-\rho }{e}^{-i{\overline{E}}_2\tau }\right)}^2}{{\left(C_1{e}^{-\rho }{e}^{-i{\overline{E}}_1\tau }+C_2\rho \cos \theta e^{-\rho /2}{e}^{-i{\overline{E}}_2\tau }\right)}^2}\right], \end{gathered}$$

(66)

It can be seen from Figure 8b that ${\overline{E}}_{\mathrm{Total}}$ can change from its minimum value ${\overline{E}}_1=-1$ at 1s state to its maximum value $-0.25$, with the range of change far beyond the magnitude of electric potential ${\overline{V}}_{\mathrm{ext}}=0.05$ (see Figure 8a). Apparently, it is the quantum potential $\overline{Q}$ that complements the lack of the transition energy and provides the quantum force outward from the nucleus that leads the electron to reach the outside 2p shell. A similar quantum phenomenon happens in the tunneling process, where the particle’s kinetic energy is found to be insufficient to overcome the potential barrier, and it is impossible from the viewpoint of classical mechanics to have any probability of finding the particle outside the potential barrier. However, the particle does appear outside the potential barrier. It is again the quantum potential that complement the required energy to the particle for overcoming the potential barrier. For more details on the classical interpretation of quantum effects by QHM, please refer to [61].

5. Discussions

When compared with the standard quantum mechanics, QHM adopts different approaches to handling state transition in the hydrogen atom:

• Through the equivalence of the Schrödinger equation and the Hamilton-Jacobi equation, the electron transition behavior, which was originally described by the quantum probability, can now be described by the dynamic trajectories of the combined orbital and spin motions.
• By extending motion domain from the real space to the complex space, the physical observables, which were originally represented by abstract quantum operators, can now be represented by complex variables or complex functions.
• Spin motion, which was originally described by relativistic quantum mechanics, can now be described by the Schrödinger equation defined in the complex domain.
• Quantum phenomena, which were inexplicable by classical mechanics and can only be predicted by the quantum probability, can now be understood intuitively by the action of the quantum potential $Q$.

QHM considers quantum motion in the complex space so that spin motion becomes an intrinsic property of QHM and forms an inseparable whole with orbital motion. By contrast, Bohmian mechanics (BM) [18], which considers quantum motion in real space, i.e., $\left(r, \theta ,\varphi \right)\in {ℝ}^3$ and $\left(p_r, p_{\theta },p_{\varphi }\right)\in {ℝ}^3$, has to add externally the spin motion to the orbital motion. Like Equation (5), the orbital motion of BM is given by ${\mathit{p}}_{\mathit{B}}=\nabla S_B$, where the subscript B refers to BM. To include the spin effect, an additional term is added to $\nabla S_B$ to form a combined momentum [19,20,21]:

$${\mathit{p}}_{\mathit{B}}=\nabla S_B+\nabla \ln {\rho }_B\times \mathit{S},$$

(67)

where ${\rho }_B\left(r, \theta ,\varphi \right)=\psi {\psi }^{*}$ is the probability density function with $\left(r, \theta ,\varphi \right)\in {ℝ}^3$, and $\mathit{S}=\left(\hslash /2\right){\overrightarrow{e}}_k$ is the spin vector. To evaluate $p_B$ explicitly, we consider motion in the ground state whose dynamics is described by the wavefunction ${\psi }_{100}=e^{-r/a_0}$. The spin momentum given by Equation (67) can be calculated by crossing

$$\nabla \ln {\rho }_B=\left(-2/a_0\right){\overrightarrow{e}}_r,$$

(68)

with

$$\mathit{S}=\hslash \left(\cos \theta {\overrightarrow{e}}_r-\sin \theta {\overrightarrow{e}}_{\theta }\right)/2,$$

(69)

to obtain

$$\nabla \ln {\rho }_B\times \mathit{S}=\frac{\hslash }{a_0}\sin \theta {\overrightarrow{\mathit{e}}}_{\varphi }.$$

(70)

This added spin momentum does not lead to the expected result, $\hslash /2$. However, we can still find its connection to the complex action function $S$ defined by Equation (2). We show this connection by expressing the wave function as

$$\psi \left(r, \theta ,\varphi \right)=e^{iS/\hslash }=e^{i\left(S_R+i{S}_I\right)/\hslash }=e^{-S_I/\hslash }{e}^{i{S}_R/\hslash },$$

(71)

where $S_R$ and $S_I$ are the real and imaginary parts of $S$. By treating $\left(r, \theta ,\varphi \right)$ as real variables in Equation (71), the probability density ${\rho }_B=\psi {\psi }^{*}$ in BM can be expressed by

$${\rho }_B=\psi {\psi }^{*}=e^{-2S_I/\hslash },$$

(72)

which then leads to

$$\nabla \ln {\rho }_B=-\frac{2}{\hslash }\nabla S_I.$$

(73)

This relation shows that the additional spin term added to Equation (67) actually originates from the imaginary part of the complex action function $S$. As mentioned earlier, the spin motion can only be revealed in the complex space. The spin momentum externally added into BM somewhat reflects this point from a different approach.

6. Conclusions

The electron 1s–2p transition in the hydrogen atom driven by electric field is demonstrated. In the framework of QHM, the system model provides a perfect platform to analyze the electron’s transition dynamics. Combining the orbital and spin dynamics together in the model, the transition trajectory is oscillating between two states under the influence of the oscillating electric field. The electron’s total energy varies between two eigen-energies with the same period as the transition trajectory. It shows that the electron has ${\overline{E}}_1=-1$ at the 1s state and has the average energy of ${\overline{E}}_1=-0.25$, when the 2p state is reached. The other interesting finding is that the electric potential energy in the transition process has the maximum value 0.04, which is much less than the energy difference $∆\overline{E}={\overline{E}}_2-{\overline{E}}_1=-0.25+1=0.75$. It is the quantum potential that fills this energy gap and allows the electron to finish the transition.

The electron’s spin angular momentum has been regarded a constant and is one of the fundamental constants in quantum mechanics. As an electron’s intrinsic feature, the spin motion has not yet been analyzed in detail in a classical dynamics way. In this paper, we have discussed the spin dynamics underlying the framework of QHM. The spin motion can only be revealed in the complex space as discussed in Section 3. When the orbital angular momentum is zero, the electron has an intrinsic spin angular momentum with values of $\pm \hslash /2$, which represent the spin up and spin down motions, respectively. A significant finding is that the electron’s spin angular momentum is not a constant, but has a small periodic perturbation with period $T=3.0385\times {10}^{-16} \mathrm{s}$ with the small periodic perturbation. It will be the remarkable finding of the electron’s fundamental property if this small perturbation can be measured experimentally. According to the recent experiments of the electron spin [62,63], and the latest time precision improvement for the weak measurement to the order of ${10}^{-18} \mathrm{s}$ [64], we believe that the progress of detecting the spin properties will soon beyond the human’s conventional knowledge about the spin.