One-Dimensional Photonic Crystals with Different Termination Layer Thicknesses and Very Narrow Bloch Surface Wave and Guided Wave Based Resonances for Sensing Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structures under Study
2.2. Experiment
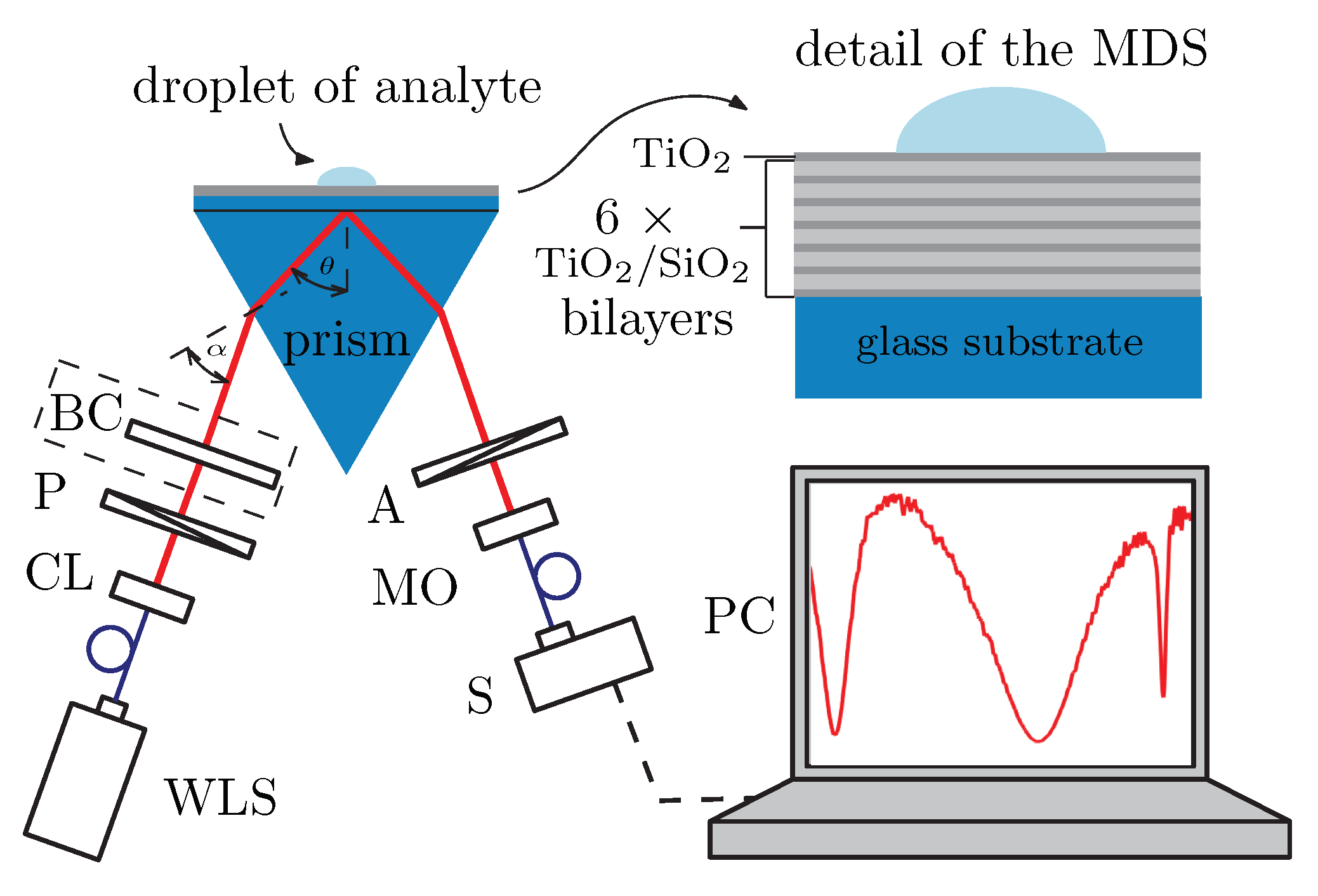
2.2.1. Experimental Setup
2.2.2. Analytes
2.3. Theoretical Analysis
3. Results
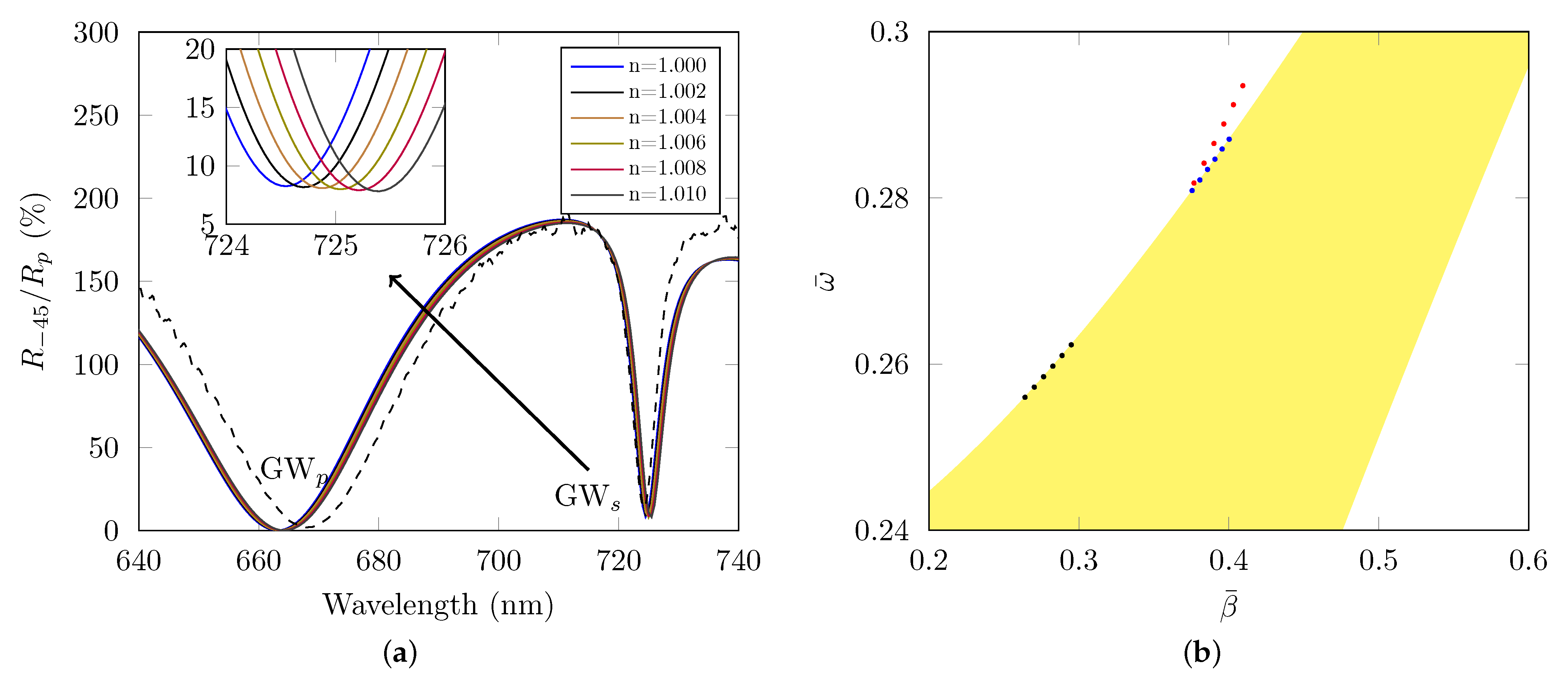
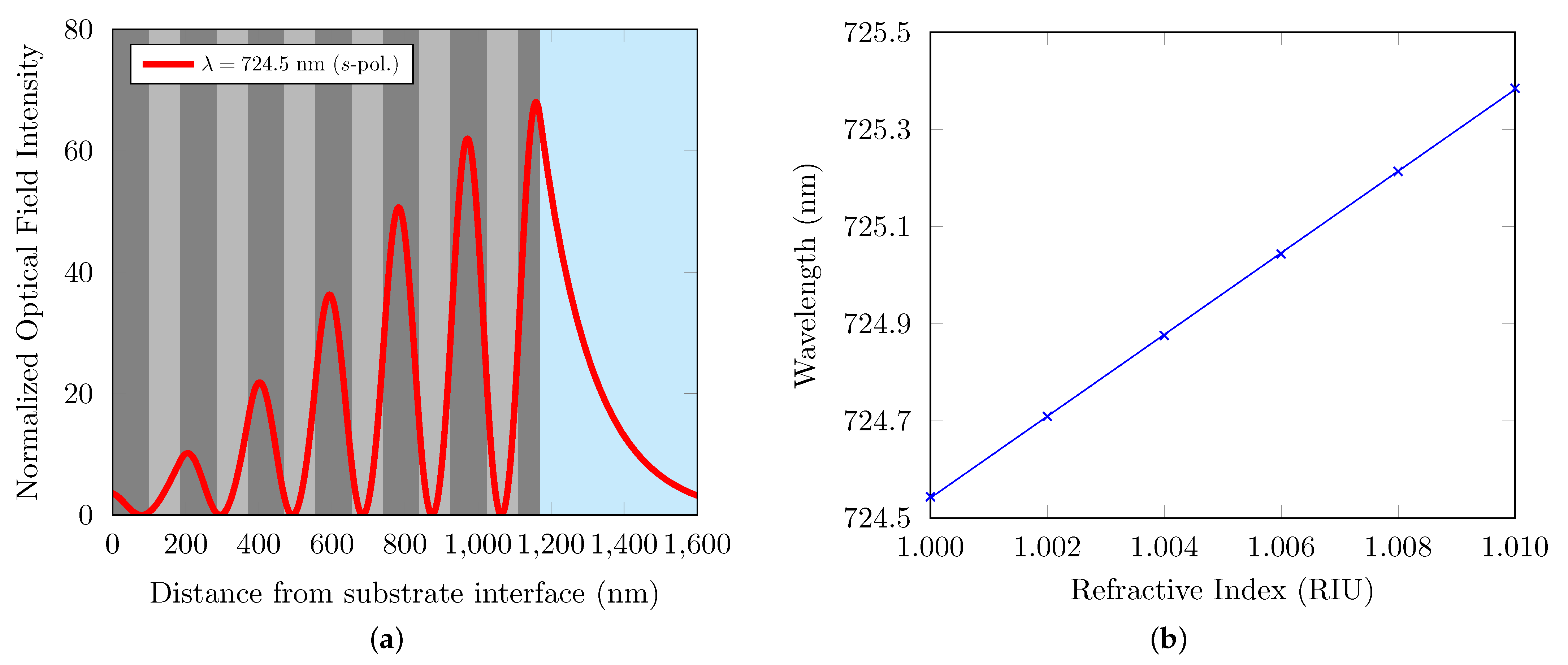
3.1. Reflectances for Air and Water
3.2. Water and Aqueous Analytes
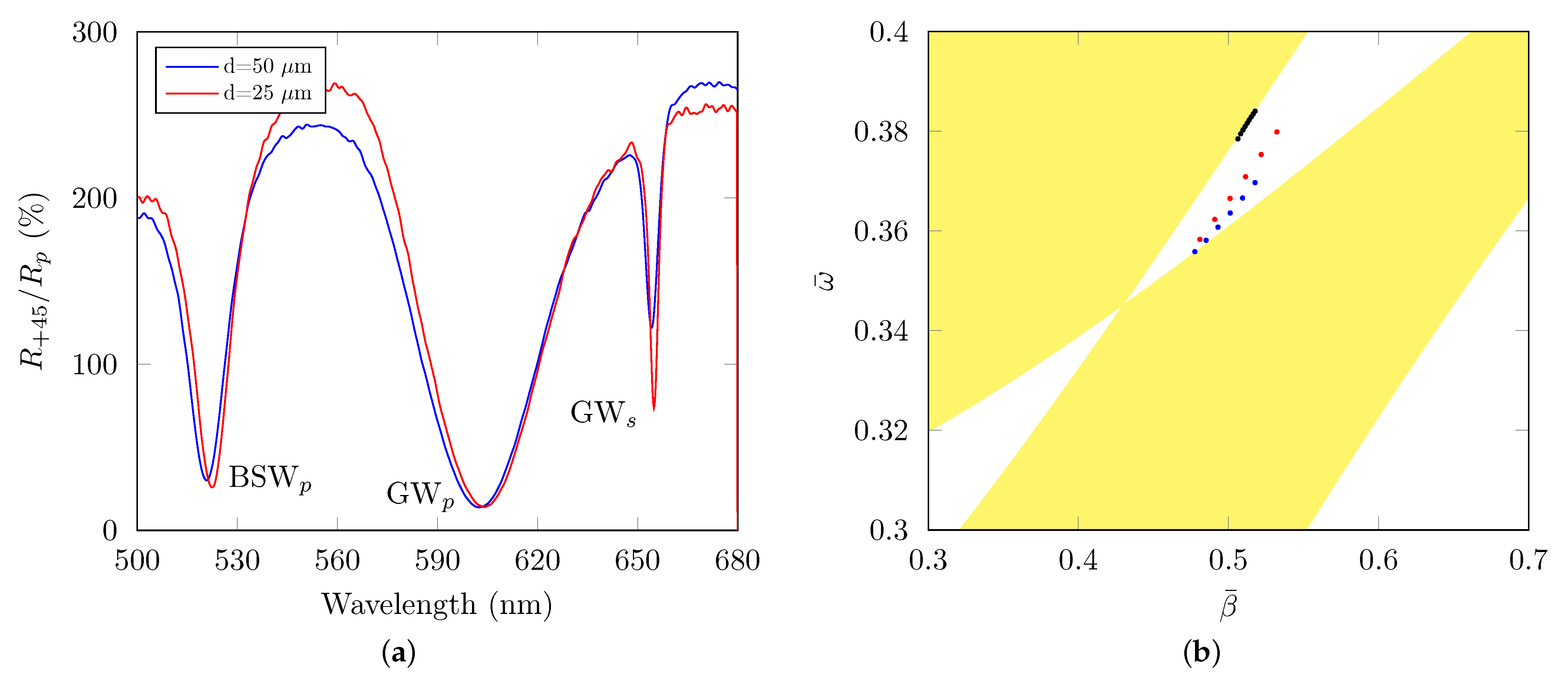
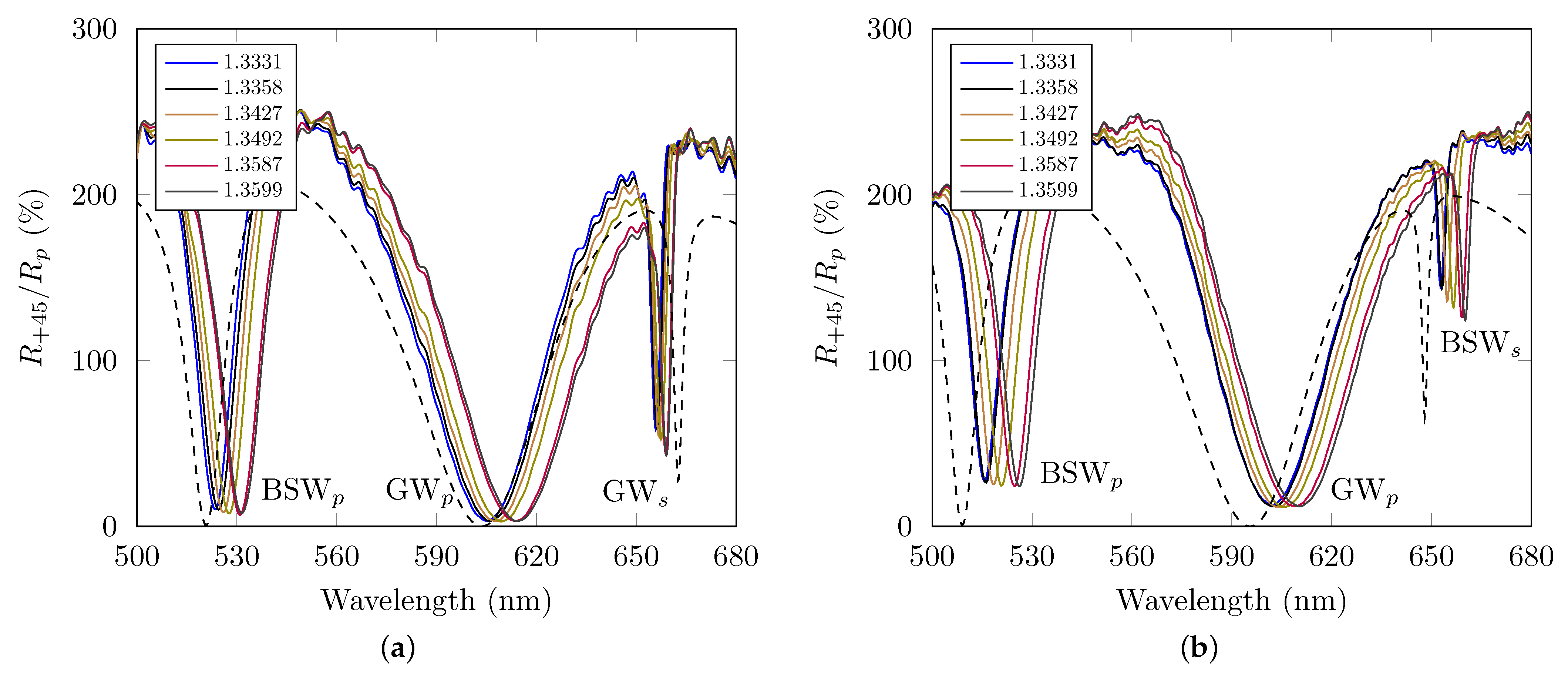
3.3. Termination Layers with Thicknesses of 60 nm and 50 nm
3.4. Phase Responses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yeh, P. Optical Waves in Layered Media; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer: New York, NY, USA, 1988. [Google Scholar]
- Wu, F.; Lyu, K.; Hu, S.; Yao, M.; Xiao, S. Ultra-large omnidirectional photonic band gaps in one-dimensional ternary photonic crystals composed of plasma, dielectric and hyperbolic metamaterial. Opt. Mater. 2021, 111, 110680. [Google Scholar] [CrossRef]
- Giorgis, F.; Descrovi, E.; Summonte, C.; Dominici, L.; Michelotti, F. Experimental determination of the sensitivity of Bloch Surface Waves based sensors. Opt. Express 2010, 18, 8087–8093. [Google Scholar] [CrossRef] [PubMed]
- Farmer, A.; Friedli, A.C.; Wright, S.M.; Robertson, W.M. Biosensing using surface electromagnetic waves in photonic band gap multilayers. Sens. Actuators B Chem. 2012, 173, 79–84. [Google Scholar] [CrossRef]
- Kong, W.; Zheng, Z.; Wan, Y.; Li, S.; Liu, J. High-sensitivity sensing based on intensity-interrogated Bloch surface wave sensors. Sens. Actuators B Chem. 2014, 193, 467–471. [Google Scholar] [CrossRef]
- Deng, C.Z.; Ho, Y.L.; Lee, Y.C.; Wang, Z.; Tai, Y.H.; Zyskowski, M.; Daiguji, H.; Delaunay, J.J. Two-pair multilayer Bloch surface wave platform in the near- and mid-infrared regions. Appl. Phys. Lett. 2019, 115, 091102. [Google Scholar] [CrossRef]
- Gan, S.; Wang, H.; Liang, J.; Dai, X.; Xiang, Y. Ultra-Sensitive Refractive Index Sensors Based on Bloch Surface Waves with Transition Metal Dichalcogenides. IEEE Sens. J. 2019, 19, 8675–8680. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Hlubina, P. Sensing concept based on Bloch surface waves and wavelength interrogation. Opt. Lett. 2020, 45, 1096–1099. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Hlubina, P. Bloch surface wave resonance based sensors as an alternative to surface plasmon resonance sensors. Sensors 2020, 20, 5119. [Google Scholar] [CrossRef]
- Goyal, A.K.; Pal, S. Design analysis of Bloch surface wave based sensor for haemoglobin concentration measurement. Appl. Nanosci. 2020, 10, 3639–3647. [Google Scholar] [CrossRef]
- Guillermain, E.; Lysenko, V.; Orobtchouk, R.; Benyattou, T.; Roux, S.; Pillonnet, A.; Perriat, P. Bragg surface wave device based on porous silicon and its application for sensing. Appl. Phys. Lett. 2007, 90, 241116. [Google Scholar] [CrossRef]
- Kang, X.B.; Wen, L.; Wang, Z.G. Design of guided Bloch surface wave resonance bio-sensors with high sensitivity. Opt. Commun. 2017, 383, 531–536. [Google Scholar] [CrossRef]
- Kovalevich, T.; Belharet, D.; Robert, L.; Ulliac, G.; Kim, M.S.; Herzig, H.P.; Grosjean, T.; Bernal, M.P. Bloch surface waves at the telecommunicationwavelength with Lithium Niobate as top layer for integrated optics. Appl. Opt. 2019, 58, 1757–1762. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sinibaldi, A.; Rizzo, R.; Figliozzi, G.; Descrovi, E.; Danz, N.; Munzert, P.; Anopchenko, A.; Michelotti, F. A full ellipsometric approach to optical sensing with Bloch surface waves on photonic crystals. Opt. Express 2013, 21, 23331–23344. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yang, T.; Song, S.; Pang, Z.; Du, G. Phase properties of Bloch surface waves and their sensing applications. Appl. Phys. Lett. 2013, 103, 041116. [Google Scholar] [CrossRef]
- Li, Y.; Yang, T.; Pang, Z.; Du, G.; Song, S. Phase-sensitive Bloch surface wave sensor based on variable angle spectroscopic ellipsometry. Opt. Express 2014, 22, 21403–21410. [Google Scholar] [CrossRef]
- Kaňok, R.; Hlubina, P.; Gembalová, L.; Ciprian, D. Efficient Optical Sensing Based on Phase Shift of Waves Supported by a One-Dimensional Photonic Crystal. Sensors 2021, 21, 6535. [Google Scholar] [CrossRef]
- Hlubina, P.; Gryga, M.; Ciprian, D.; Pokorny, P.; Gembalova, L.; Sobota, J. High performance liquid analyte sensing based on Bloch surface wave resonances in the spectral domain. Opt. Laser Technol. 2022, 145, 107492. [Google Scholar] [CrossRef]
- Chen, Y.H.; Shi, W.H.; Feng, L.; Xu, X.Y.; Shang-Guan, M.Y. Study on simultaneous sensing of gas concentration and temperature in one-dimensional photonic crystal. Superlattices Microstruct. 2019, 131, 53–58. [Google Scholar] [CrossRef]
- Goyal, A.K.; Kumar, A.; Massoud, Y. Thermal Stability Analysis of Surface Wave Assisted Bio-Photonic Sensor. Photonics 2022, 9, 324. [Google Scholar] [CrossRef]
- Pettersson, L.A.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Daimon, M.; Masumura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. [Google Scholar] [CrossRef] [PubMed]
- Polyanskiy, M.N. Refractive Index Database. Available online: http://refractiveindex.info (accessed on 1 July 2022).
- Sinibaldi, A.; Descrovi, E.; Giorgis, F.; Dominici, L.; Ballarini, M.; Mandracci, P.; Danz, N.; Michelotti, F. Hydrogenated amorphous silicon nitride photonic crystals for improved-performance surface electromagnetic wave biosensors. Biomed. Opt. Express 2012, 3, 2405–2410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hlubina, P. Dispersive spectral-domain two-beam interference analysed by a fibre-optic spectrometer. J. Mod. Opt. 2004, 51, 537–547. [Google Scholar] [CrossRef]
- Dubey, R.; Barakat, E.; Häyrinen, M.; Roussey, M.; Honkanen, S.K.; Kuittinen, M.; Herzig, H.P. Experimental investigation of the propagation properties of bloch surface waves on dielectric multilayer platforms. J. Eur. Opt. Soc. 2017, 13, 5. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Ye, J.Y.; Divin, C.; Huang, B.; Thomas, T.P.; Baker, J.R.; Norris, T.B. Real-time biomolecular binding detection using a sensitive photonic crystal biosensor. Anal. Chem. 2010, 82, 211–5218. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Valencia, E.; Herrera, R.A.; Torres, P. Bloch surface wave resonance in photonic crystal fibers: Towards ultra-wide range refractive index sensors. Opt. Express 2019, 27, 8236–8545. [Google Scholar] [CrossRef]
- Gonzalez-Valencia, E.; Villar, I.D.; Torres, P. Novel Bloch wave excitation platform based on few-layer photonic crystal deposited on D-shaped optical fiber. Sci. Rep. 2021, 11, 11266. [Google Scholar] [CrossRef]
- Wan, X.Y.D.; Yan, Z. Simulation and analysis of surface plasmon resonance biosensor based on phase detection. Sens. Actuators B Chem. 2003, 91, 285–290. [Google Scholar]
- Zhang, C.; Wang, R.; Min, C.; Zhu, S.; Yuan, X.C. Experimental approach to the microscopic phase-sensitive surface plasmon resonance biosensor. Appl. Phys. Lett. 2013, 102, 011114. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Wu, F.; Liu, D.; Li, Y.; Li, H. Ultra-sensitive refractive index sensing enabled by a dramatic ellipsometric phase change at the band edge in a one-dimensional photonic crystal. Opt. Express 2022, 30, 29030–29043. [Google Scholar] [CrossRef]





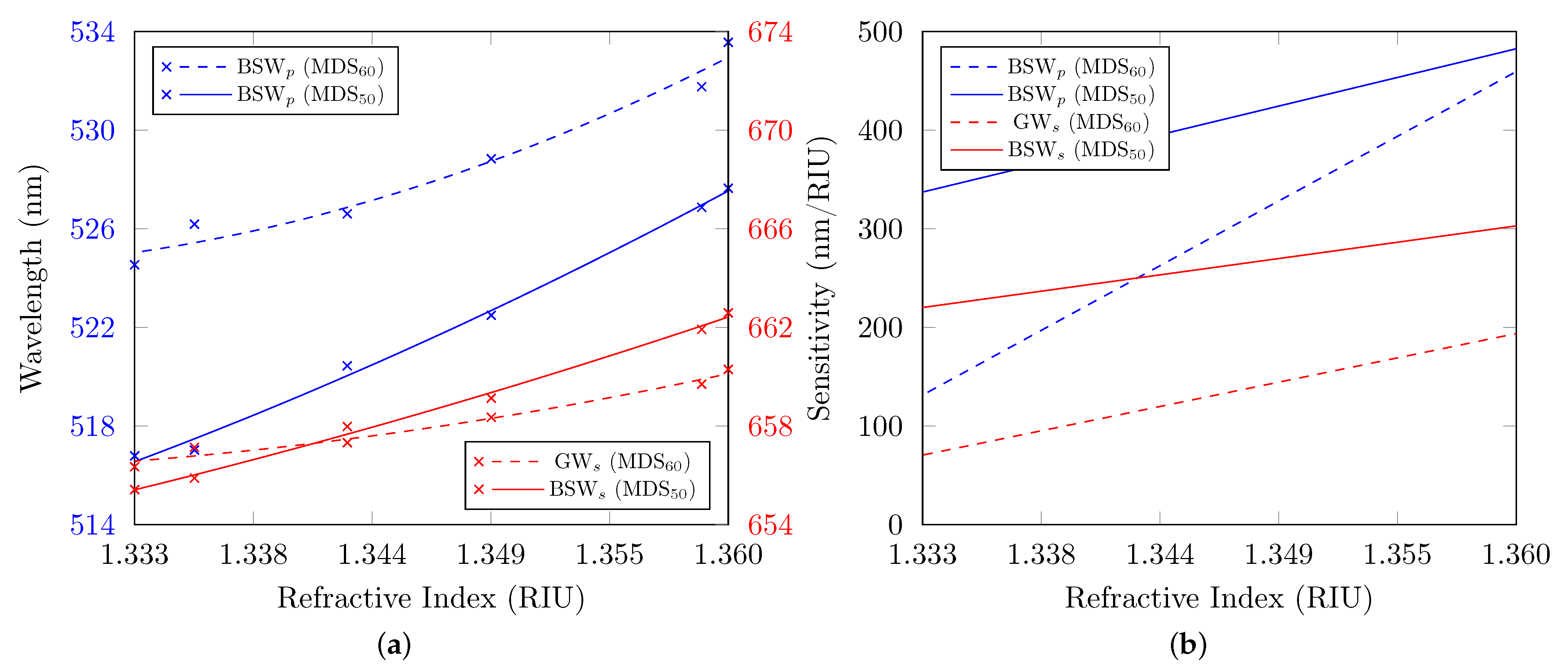
| Sensor Parameters for Aqueous Analytes | ||||
|---|---|---|---|---|
| Structure | MDS | MDS | ||
| Wave | BSW | GW | BSW | BSW |
| S (nm/RIU) | 203.8–370.2 | 70.3–161.7 | 295.5–544.3 | 180.7–371.4 |
| (nm) | 13.3 | 2.7 | 10 | 2 |
| D | 0.96 | 0.78 | 0.96 | 0.44 |
| (RIU) | 9.2–26.7 | 20.3–52.1 | 28.4–52.3 | 39.8–81.7 |
| Sensor Parameters for Aqueous Analytes | ||||
|---|---|---|---|---|
| Structure | MDS | MDS | ||
| Wave | BSW | GW | BSW | BSW |
| S (nm/RIU) | 131.4–459.0 | 70.5–193.7 | 337.2–482.5 | 220.1–302.9 |
| (nm) | 4 | 1 | 12 | 1–2.1 |
| (RIU) | 32.85–114.75 | 75.5–193.7 | 28.0–40.2 | 104.8–302.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fort, T.; Kanok, R.; Hlubina, P.; Pokorny, P.; Sobota, J. One-Dimensional Photonic Crystals with Different Termination Layer Thicknesses and Very Narrow Bloch Surface Wave and Guided Wave Based Resonances for Sensing Applications. Photonics 2022, 9, 561. https://doi.org/10.3390/photonics9080561
Fort T, Kanok R, Hlubina P, Pokorny P, Sobota J. One-Dimensional Photonic Crystals with Different Termination Layer Thicknesses and Very Narrow Bloch Surface Wave and Guided Wave Based Resonances for Sensing Applications. Photonics. 2022; 9(8):561. https://doi.org/10.3390/photonics9080561
Chicago/Turabian StyleFort, Tomas, Roman Kanok, Petr Hlubina, Pavel Pokorny, and Jaroslav Sobota. 2022. "One-Dimensional Photonic Crystals with Different Termination Layer Thicknesses and Very Narrow Bloch Surface Wave and Guided Wave Based Resonances for Sensing Applications" Photonics 9, no. 8: 561. https://doi.org/10.3390/photonics9080561
APA StyleFort, T., Kanok, R., Hlubina, P., Pokorny, P., & Sobota, J. (2022). One-Dimensional Photonic Crystals with Different Termination Layer Thicknesses and Very Narrow Bloch Surface Wave and Guided Wave Based Resonances for Sensing Applications. Photonics, 9(8), 561. https://doi.org/10.3390/photonics9080561





