Novel Inversion Algorithm for the Atmospheric Aerosol Extinction Coefficient Based on an Improved Genetic Algorithm

Abstract

As an important atmospheric component, aerosols play a very important role in the radiation budget balance of the earth–atmosphere system. To study the optical characteristics of aerosols, it is necessary to use an inversion algorithm to process the lidar return signal to obtain both the aerosol extinction coefficient and the backscattering coefficient. However, the lidar return power equation is ill-conditioned and contains two unknown parameters, meaning that traditional inversion algorithms must be solved by adopting certain assumptions (e.g., a uniform atmosphere and the lidar ratio), which to a certain extent can seriously affect the inversion accuracy. Here, to improve the accuracy of the aerosol extinction coefficient inversion, an inversion method based on an improved genetic algorithm is proposed. Using the U.S. Standard Atmosphere model and the return power equation, the aerosol extinction coefficient and the backscattering coefficient are independent variables that randomly provide initial values to simulate the theoretical lidar power. Then, the genetic algorithm is used to approximate the theoretical lidar power to the measured lidar return power with height; when the two are infinitely close, the values of the corresponding two independent variables (i.e., the extinction and backscattering coefficients) are inverted. Experiments performed to compare the different effects between a simple genetic algorithm and the improved genetic algorithm showed the proposed method capable of inverting the aerosol extinction coefficient without reliance on traditional inversion methods, representing a novel approach to the inversion of the aerosol extinction coefficient and the backscattering coefficient.

1. Introduction

With the rapid development of human society and industrial progress, the emissions associated with everyday life and industrial production pose great threats to the atmospheric environment and human health [1]. Therefore, monitoring the atmospheric environment to inform air pollution prevention strategies and support the implementation of effective control measures has long been the focus of environmental protection departments, and the study of atmospheric aerosols is extremely important [2,3]. Atmospheric aerosols, formed by dispersion in the atmosphere of solid or liquid particles with a diameter of approximately 0.001–100 μm, have a small but extremely important role [4,5,6]. Aerosols can be divided into primary and secondary aerosols according to their source. Primary aerosols exist in the form of particles derived directly from their source, e.g., desert dust. As the name suggests, secondary aerosols are formed by transforming primary aerosols through some physical and/or chemical processes. There are many sources of primary aerosols, but they can be classified broadly into two groups: natural sources, such as pollen or seeds of plants, desert dust, and foam evaporation, and anthropogenic sources that include the emissions of everyday life and industrial production [7].

Aerosols play a role in various atmospheric processes. Solar radiation is affected by absorption and scattering by aerosols, and thus aerosols can affect the budget and expenditure of the earth–air system to a certain extent [8]. Aerosols also play an important role as cloud condensation nuclei, which means that the physical properties of clouds can be affected by aerosols [9]. Additionally, aerosols can also participate directly in chemical reactions in the atmosphere, which can affect the concentrations of ozone and other atmospheric components that can have a detrimental impact on human health and everyday life [10]. Therefore, studying atmospheric aerosols is of great importance [11]. However, despite the considerable amount of earlier research on this topic, the current understanding of aerosols remains insufficient, and further extensive and in-depth research on aerosols is necessary [12].

To study the optical characteristics of aerosols, it is necessary to use an inversion algorithm to process lidar return signals to obtain both the aerosol extinction coefficient and the backscattering coefficient [13]. The aerosol extinction coefficient mainly reflects the degree of absorption and scattering of light by aerosols, while the backscattering coefficient mainly reflects its scattering characteristics in the backward direction. A study of the aerosol extinction coefficient can indirectly predict the content of particulate matter in the atmosphere, and the particulate matter content in the atmosphere reflects the air quality to a certain extent. Therefore, a study of the aerosol extinction coefficient can indirectly lead to a prediction of air quality. Moreover, accurate inversion of the extinction coefficient can also support the study of atmospheric visibility and particle size, which is also very important [14]. However, for Mie-scattering lidar, the lidar return equation contains two unknowns, i.e., the aerosol extinction coefficient and the backscattering coefficient; therefore, it is impossible to obtain the inversion results directly. The traditional inversion method is performed on the basis of many assumptions, but these assumptions have a considerable impact on inversion accuracy [15,16].

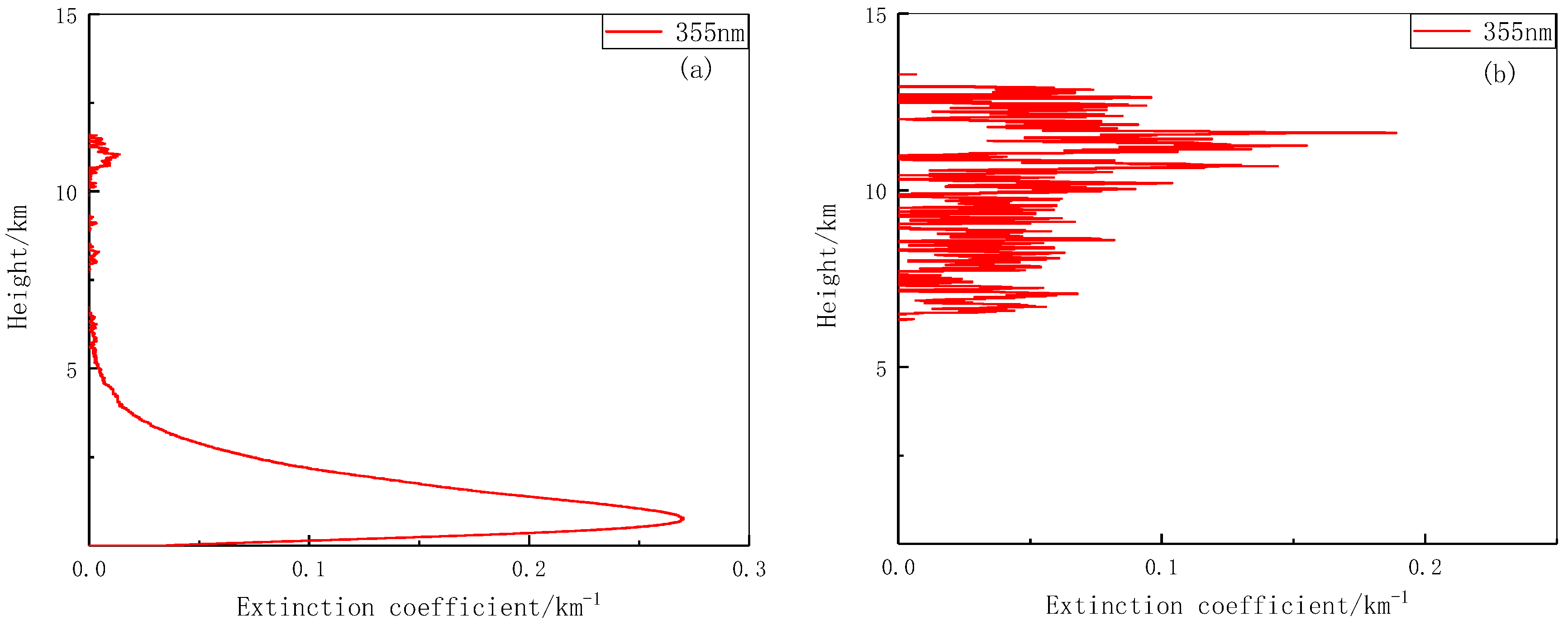
Taking the widely used Klett method as an example, the inverted aerosol extinction coefficient profile often contains many negative values attributable to improper selection of the extinction boundary value and the lidar ratio, which cause the profile to be discontinuous or displayed on the negative half of the axis. Figure 1 shows the extinction coefficient profile of a return signal at the wavelength of 355 nm inverted using the Klett method, as detected by a small Mie-scattering lidar developed at North Minzu University, China.

In Figure 1a, owing to improper selection of the lidar ratio, which was set to 50, the extinction coefficient profile appears with an obvious discontinuity at the height of 7–10 km. In Figure 1b, owing to improper selection of the boundary value of the extinction coefficient, a large number of negative values appear at heights below 7 km and are present in the negative half of the axis. Therefore, to improve inversion accuracy, it is of great importance to develop an inversion algorithm without assumptions and with strong adaptive characteristics.

In recent years, many studies have been conducted to improve the inversion accuracy of the aerosol extinction coefficient. However, most were based on traditional inversion methods, such as the Klett and Fernald method, which seek to select a more suitable lidar ratio or a more accurate extinction coefficient boundary value to improve the inversion accuracy. In 2003, from the perspective of selecting the extinction coefficient boundary value, Tian et al. [17] proposed a method based on the existing algorithm to determine the extinction coefficient boundary value more accurately and proved its rationality through experiment. In 2016, from the perspective of choosing a lidar ratio, Song et al. [18] used a new method for determining the lidar ratio more accurately for low-level aerosols and demonstrated improvement in the inversion accuracy. In 2019, Dou et al. [19] proposed a method to obtain a more accurate extinction coefficient boundary value and select an appropriate lidar ratio based on the Klett backward integral model. The former was obtained through the construction of nonlinear equations and Steffensen iteration. The latter cleverly utilized differential absorption lidar and was derived from its function model to obtain a more accurate aerosol extinction coefficient profile.

Some studies have applied the neural network method to the inversion algorithm and developed adaptive inversion methods based on neural networks to obtain more accurate inversion results. However, because most of such approaches used supervised learning methods, the determination of the tutor signal remained connected to the traditional inversion method. In 2007, Han et al. [20] used the Madaline neural network to develop an adaptive inversion algorithm model, which trains the input-to-output mapping in terms of solving nonlinear equations by building a neural network, and uses the trained network to invert the aerosol extinction coefficient; however, the tutor signal that they used was the average of multiple sets of extinction coefficients inverted using the Klett method. In 2017, Li et al. [21] applied the chord interception method to determine both the extinction coefficient boundary value and the lidar ratio, used the radial basis function neural network to invert the extinction coefficient, and established a feedback radial basis network model to correct the network output using optical thickness measured by a sun photometer. In that case, the tutor signal used to construct the network was obtained using the Fernald method. In 2019, Wang et al. [22] considered solving nonlinear functions to solve the Mie-scattering lidar equation using the backpropagation neural network. They performed different optimizations to obtain more accurate inversion results without assumptions. However, the network output also used an extinction coefficient obtained using the Klett method.

The Raman-scattering lidar was developed to invert the aerosol extinction coefficient using the relatively stable properties of nitrogen in the air [23,24,25,26]. When using Raman lidar to detect and invert the aerosol extinction coefficient, there is no need to assume certain parameters such as the lidar ratio and the boundary value, which overcomes the limitation of Mie-scattering lidar to a certain extent. However, the cross-section of Raman scattering is much smaller than that of Mie scattering. Therefore, when using Raman-scattering lidar for actual detection, the return signal is weak with serious noise interference, which introduces serious errors and uncertainties into the inversion. Consequently, it is necessary to develop an adaptive inversion method based on the existing Mie-scattering lidar hardware system that does not require multiple assumptions.

Here, a novel inversion algorithm is proposed for the atmospheric aerosol extinction coefficient based on an improved genetic algorithm. The genetic algorithm, first proposed by Professor J. Holland in the United States in 1975 [27], is a random global search and optimization algorithm formed by simulating the genetic mechanism of nature and the biological evolution theory of the “survival of the fittest” [28,29]. It can be used to solve many problems, such as parameter optimization for neural networks and Proportion Integration Differentiation controllers [30,31], and the improved genetic algorithms are designed to help us solve problems better. The core idea of the inversion algorithm based on the genetic algorithm is to fit the theoretical return power with the actual measured lidar return power. The aerosol extinction coefficient and the backscattering coefficient are taken as variables and randomly assigned initial values to calculate the theoretical return power. The values of the two independent variables are constantly updated using the genetic algorithm during the fitting process of the theoretical return power and the measured lidar return power. When the theoretical return power is infinitely close to the measured return signal, the corresponding optimal solution of the two variables can be obtained, thereby completing the inversion process.

2. Methodology

Traditional inversion methods that include the Collis slope method [32], Klett method [33], and Fernald method [34] all require assumptions to invert the extinction coefficient, such as assuming that the atmosphere is uniform and assuming the lidar ratio, before the lidar return equation can be solved, thereby severely limiting the inversion accuracy.

For Mie-scattering lidar systems, the return signal can be described as follows:

$$P\left(r\right)=k\cdot E_0\cdot R_{freq}\cdot \frac{c\tau }{2}\cdot \frac{Ar}{R^2}\cdot Y\cdot \beta \left(r\right)\cdot e^{-2{\displaystyle {\int }_0^{r^{\prime }}\alpha \left(r\right)dr}}$$

(1)

where $P\left(r\right)$ is the received lidar return signal power at distance r, k is the optical loss parameter, E₀ is the laser emitting power, R_freq is the pulse frequency, c is the speed of light, τ is the pulse width, A_r is the receiving area of the telescope, R is the detection height, Y is a geometric coincidence factor, $\beta \left(r\right)$ denotes the backscattering coefficient, and $\alpha \left(r\right)$ denotes the extinction coefficient.

Both $\beta \left(r\right)$ and $\alpha \left(r\right)$ are unknown quantities. Generally, it is impossible to solve an equation with two unknowns. Therefore, it is necessary to assume the ratio of the aerosol extinction coefficient to the backscattering coefficient (i.e., the lidar ratio) for inversion of the aerosol extinction coefficient when using traditional algorithms.

2.1. Traditional Inversion Methods

2.1.1. Klett Method

The Collis slope method inverts the aerosol extinction coefficient by assuming that the atmosphere is uniform over a certain spatial range; however, in practical application, the atmosphere is usually nonuniform [35], which means that the Collis slope method is inapplicable in many cases. In the Klett method, the following relationship is presumed between the aerosol extinction coefficient and the backscattering coefficient:

$$\beta =H\cdot {\alpha }^k$$

(2)

where H is a constant, and k is usually set to 1. The aerosol extinction coefficient can be obtained according to the lidar equation, which is expressed as follows:

$$\alpha \left(r\right)=\frac{\exp \left[\frac{S\left(r\right)-S\left(r_m\right)}{k}\right]}{\frac{1}{{\alpha }_m}+\frac{2}{k}{\displaystyle {\int }_r^{r_m}\exp \left[\frac{S\left(r\right)-\mathrm{S}\left(r_m\right)}{k}\right]dr}}$$

(3)

where r_m is the reference height, which represents the furthest detection distance. $S(r)=\ln \left[P(r)r^2\right]$, which represents the distance square log correction signal. The extinction coefficient value of this height ${\alpha }_m$ is unknown, and how best to select its value is the problem to be resolved, which is a limitation of the Klett method [36].

2.1.2. Fernald Method

The Fernald inversion method is an improvement of the Klett method that considers the contribution of atmospheric molecules. The Fernald method divides the extinction coefficient into atmospheric molecular and aerosol parts. Thus, the extinction coefficient $\alpha \left(r\right)$ and the backscattering coefficient $\beta \left(r\right)$ can be expressed as follows:

$$\alpha \left(r\right)={\alpha }_a\left(r\right)+{\alpha }_m\left(r\right)$$

(4)

$$\beta \left(r\right)={\beta }_a\left(r\right)+{\beta }_m\left(r\right)$$

(5)

where ${\alpha }_a\left(r\right)$ is the aerosol extinction coefficient, ${\alpha }_m\left(r\right)$ is the atmospheric molecular extinction coefficient, ${\beta }_a\left(r\right)$ is the aerosol backscattering coefficient, and ${\beta }_m\left(r\right)$ is the atmospheric molecular backscattering coefficient. First, with the help of the U.S. Standard Atmosphere model of 1978, atmospheric molecular extinction coefficients and aerosol extinction coefficients can be expressed as follows:

$${\alpha }_a=S_1{\beta }_a$$

(6)

$${\alpha }_m=S_2{\beta }_m$$

(7)

where S₁ is the extinction-to-backscatter ratio of atmospheric aerosols (i.e., the lidar ratio), and S₂ is the extinction-to-backscatter ratio of atmospheric molecules, which can be derived from Rayleigh scattering theory that shows that $S_2=8\pi /3$. If we let $Q\left(r\right)=r^{2}P\left(r\right)$, which represents the distance squared correction signal, the aerosol extinction coefficient above reference height $r_m$ can be expressed as follows:

$${\alpha }_a\left(r\right)=-\frac{S_1}{S_2}{\alpha }_m\left(r\right)+\frac{Q\left(r\right)\exp \left[2\left(1-\frac{S_1}{S_2}\right){\displaystyle {\int }_{r_m}^r{\alpha }_m\left(r^{\prime }\right)dr}\right]}{\frac{Q\left(r_m\right)}{{\alpha }_a\left(r_m\right)+\frac{S_1}{S_2}{\alpha }_m\left(r_m\right)}-2{\displaystyle {\int }_{r_m}^{r}Q\left(r\right)\exp \left[2\left(1-\frac{S_1}{S_2}\right){\displaystyle {\int }_{r_m}^r{\alpha }_m\left(r^{\prime }\right)d{r}^{\prime }}\right]}dr}$$

(8)

2.2. Genetic Algorithms

The genetic algorithm is a method with high efficiency, parallel processing, and strong global search capability [37]. It can automatically acquire and accumulate knowledge about a search space during the search process and adaptively control the search process to obtain the optimal solution [38,39]. In a genetic algorithm, the initial solution to the required problem is usually generated by a random process. The solution to the problem is encoded into the chromosome using a specific coding method [40], thereby forming population individuals. Then, an appropriate function is used to calculate the fitness of each individual, the adaptability of the individual to the environment is evaluated by its fitness, and the process of survival of the fittest is performed. Individuals with low fitness are eliminated, while those with high fitness are selected for genetic operations of selection, crossover, and variation. For the population after the genetic operations, the law of survival of the fittest is also used to select the most adaptable individual set to form the next generation of the new population. Then, the sub-population undergoes similar repeat genetic operations until a certain termination condition is reached.

In comparison with traditional optimization algorithms, the advantage of a genetic algorithm [41,42] is that it deals with the code of the problem to be solved rather than the value of the problem itself, i.e., it introduces concepts such as chromosomes and genes, which are common in biology, into the optimization algorithm to optimize the problem through calculation of the code. It also uses the degree of fitness rather than the objective function in the traditional algorithms as the search information [43]. From practical experience, the search value is much more efficient than the search function. Therefore, a greater search scope can be determined using the fitness value for the search operation, and search efficiency can be improved. Genetic algorithms use probabilistic searching to replace the deterministic rules of the traditional algorithms, and the selection, crossover, mutation, and other operations are performed in a probabilistic manner. In searching, parallel processing is adopted to start the search process with the initial population that might be composed of many individuals, which gives the algorithm high flexibility and efficiency. However, it is sometimes a time-consuming process that might result in local optimality, so some optimizations are performed for the simple genetic algorithm to improve the global searching capability and help us solve problems better. The following is a detailed introduction to the principles and corresponding rules of three genetic operations.

2.2.1. Selection Operation

Selection refers to choosing excellent individuals from the population according to certain rules for subsequent calculation. Such rules are usually based on the degree of adaptation of individuals to the environment. To obtain greater numbers of excellent individuals, the selection operation is used to choose relatively excellent individuals in the population for subsequent crossover and mutation operations. Then, according to the theory of biological evolution, the stronger the ability of an individual to adapt to the environment, the easier it is for that individual to survive, and the greater the probability of such an individual being selected. Commonly, the roulette selection method is used to select individuals, where the size of the area on the roulette wheel is determined according to the proportion of the fitness value. It is not difficult to appreciate from experience that the larger the area on the roulette wheel, the easier it would be to be selected [44]. The selection probability of individual n can be expressed as follows:

$$f_n=\frac{k}{F_n}$$

(9)

$$p_n=\frac{f_n}{{\displaystyle {\sum }_{i=1}^N{f}_i}}$$

(10)

where $F_n$ represents the fitness value of individual n, k is the coefficient (usually in the range of [0, 1]), and N is the number of individuals in the population.

2.2.2. Crossover Operation

Crossover refers to the exchange of two selected chromosomes with a certain probability, i.e., a random position is selected in the chromosome. The genes behind this position are exchanged with genes in the same position on another chromosome to obtain two new chromosomes. New individuals obtained through the crossover operation are not all retained in the next generation but are selected again according to the survival of the fittest rule, and only those who become better are eligible to be retained as individuals in the new population. If the m-th chromosome $a_{mi}$ and the n-th chromosome $a_{ni}$ are crossed at position i, then their rules can be expressed as follows:

$$\begin{array}{l}{a}_{mi}=a_{mi}(1-b)+a_{ni}b\\ a_{ni}=a_{ni}(1-b)+a_{mi}b\end{array}$$

(11)

where b is a random number in the range of [0, 1].

2.2.3. Mutation Operation

Mutation refers to the process of genetic mutation of new individuals generated by the crossover operation and retained according to a certain probability [45]. Generally, a new individual obtained by the crossover operation is randomly assigned a location, and genetic mutations are performed according to probability to produce new individuals. As with crossover mutation, only those individuals who become better can be saved. The rules for mutation operations can be expressed as follows:

$$\begin{array}{l}{a}_{mn}=\left\{\begin{array}{l}{a}_{mn}+(a_{mn}-a_{\max })\times \epsilon {(1-\frac{g}{G_{\max }})}^2,r>0.5\\ a_{mn}+(a_{\min }-a_{mn})\times \epsilon {(1-\frac{g}{G_{\max }})}^2,r\le 0.5\end{array}\right.\\ \end{array}$$

(12)

where $a_{mn}$ represents the n-th gene of the m-th individual, $a_{\max }$ represents the upper bound of gene $a_{mn}$, $a_{\min }$ represents the lower bound of gene $a_{mn}$, $\epsilon$ is a random number (usually in the range of [0, 1]), g denotes the current number of iterations, and $G_{\max }$ is the maximum number of set evolutions. A flowchart of a simple genetic algorithm is shown in Figure 2.

2.3. Aerosol Extinction Coefficient Inversion Based on a Genetic Algorithm

As mentioned above, the Klett method assumes that when the aerosol concentration is large, the influence of atmospheric molecule interaction with the laser is relatively small and could be ignored. Therefore, solving the lidar equation by assuming that the aerosol extinction coefficient and the backscattering coefficient meet a certain relationship is a very good inversion method, but it ignores the influence of atmospheric molecules. The Fernald method considers the influence of atmospheric molecules using the Standard Atmosphere model to obtain the extinction coefficient backscattering ratio of atmospheric molecules, and it also assumes the lidar ratio of aerosols, which has a certain impact on the inversion accuracy. Therefore, in the method proposed in this paper, instead of using the Klett method and the Fernald method, the lidar equation, and the Standard Atmosphere model are used to design an adaptive inversion method that does not require assumptions. The inversion of the aerosol extinction coefficient is realized with the help of a genetic algorithm that has strong adaptability and global search capability.

Figure 3 shows a block diagram of the inversion algorithm. First, with the help of the U.S. Standard Atmosphere model and the lidar equation, the aerosol extinction coefficient and the backscattering coefficient are taken as variables that affect the theoretical return power, and the theoretical return power is simulated randomly with an initial value. Then, the theoretical power is fitted with the practically measured power at the starting height, and the genetic algorithm is used to search for the optimal solution and update the values of both variables. Iterations continue until the theoretical power and the measured power are infinitely close. The values of these two variables are the optimal solution, and the inversion results at the starting height can be obtained. At the next height, similar processing is performed, and the process repeats until the inversion results of all heights are calculated. To obtain an optimal result that accords with reality, these two variables are usually given a limited empirical range to improve the feasibility and accuracy of the algorithm.

2.3.1. Theoretical Return Power Calculation

The theoretical return power can be calculated according to Equation (1), and the optical loss is in the range of [0, 1]; here, it was set to 0.5. Laser emission power is measured using a power meter in the actual detection, while the pulse frequency, pulse bandwidth, and telescope receiving area are known. Because the overlap factor is not considered, the blind area is removed manually when the detection height is selected. The atmospheric molecular backscattering coefficient and the extinction coefficient can be obtained according to the U.S. Standard Atmosphere model, and the calculation expression is as follows:

$${\beta }_m\left(r\right)=1.54\times {10}^{-6}\cdot e^{-\frac{r\cos \theta }{7000}}$$

(13)

$${\alpha }_m\left(r\right)=\frac{8\pi }{3}{\beta }_m\left(r\right)$$

(14)

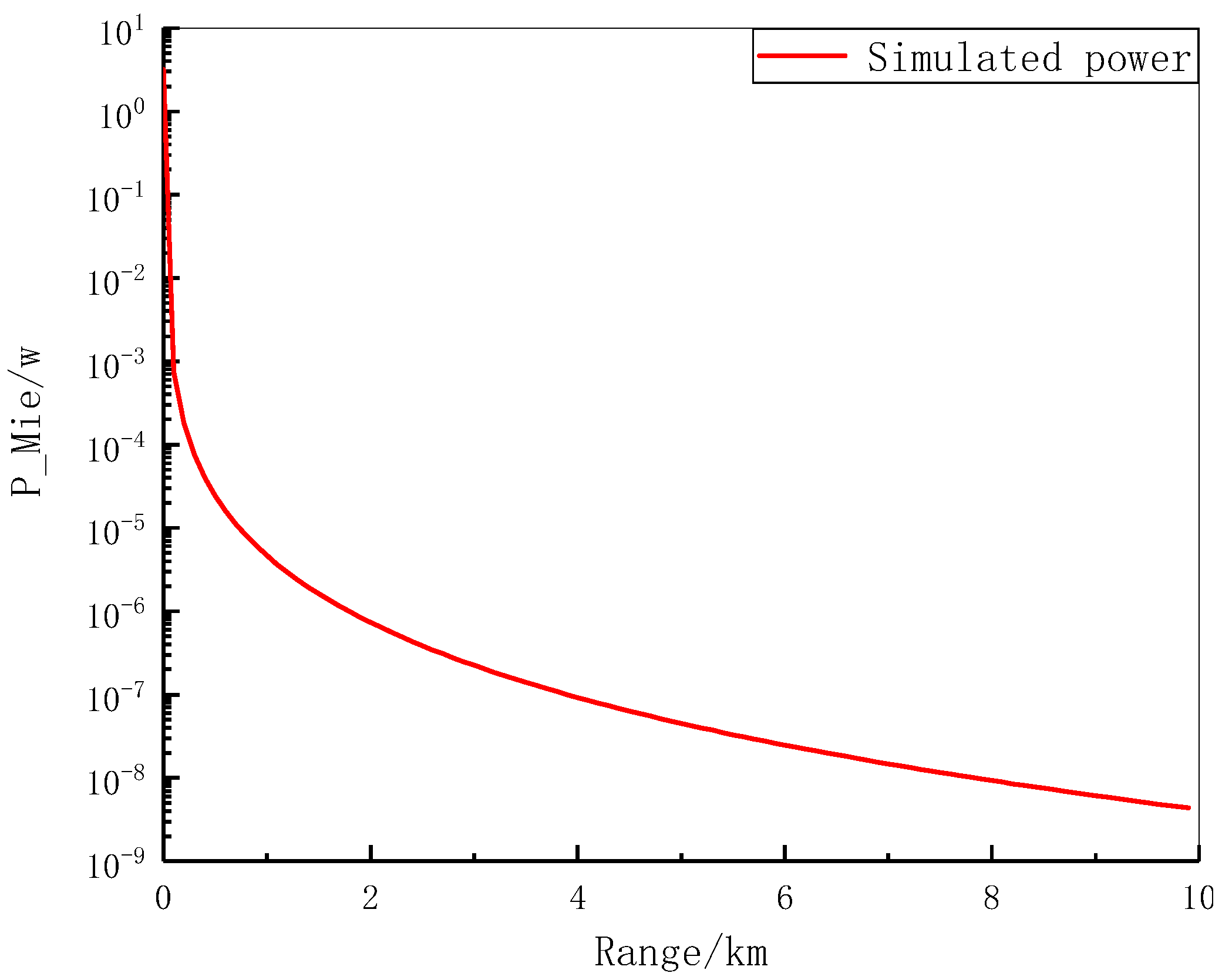
The aerosol extinction coefficient and the backscattering coefficient are used as the unknown optimization objects, and the initial values are randomly given and continuously updated during the iteration process. Figure 4 shows the theoretical return power profile of a Mie-scattering lidar.

2.3.2. Objective Function

The error function is obtained by minimizing the difference between the theoretical return power and the practically measured return power with height. The minimum error function can be used as the optimization target. The error function is expressed as follows:

$$error(r)=\frac{1}{2}{\left(P_s\left(r\right)-P_l\left(r\right)\right)}^2$$

(15)

where $P_s(r)$ is the measured lidar return power at height r, and $P_l(r)$ is the theoretical return power at height r.

2.3.3. Aerosol Extinction Coefficient Inversion Using the Improved Genetic Algorithm

Generally, a simple genetic algorithm might fall into local optimization. Therefore, some optimizations are performed for the simple genetic algorithm to improve the global searching capability, mainly for the selection algorithm of crossover and mutation probability. According to the actual problem, if the probability of crossover and mutation could be selected adaptively according to the actual situation in a more suitable manner, it would be very beneficial for solving the problem. Given that a simple genetic algorithm might fall into local optimization, this paper proposes using the following changes to the simple genetic algorithm.

(1)

Realize the adaptive selection of the crossover probability. The fixed crossover probability of a simple genetic algorithm is improved such that the improved algorithm can adjust the corresponding crossover probability according to the fitness value of the individual. The adjusted algorithm is expressed as follows:

$$P_c=\left\{\begin{array}{l}w1\left(f_{\max }-f_c\right)/\left(f_{\max }-f_{\min }\right),f_c\ne f_{\max },f_{\min }\\ w2,f_c=f_{\max }\\ w3,f_c=f_{\min }\end{array}\right.$$

(16)

where P_c is the crossover probability, f_c is the more adaptable one of the first two parents before the crossover operation, f_max and f_min represent the maximum and minimum values of fitness in the population, respectively, and w1, w2, and w3 are constants in the range of [0, 1] and w2 < w3. The improved algorithm can adjust the crossover probability adaptively according to the fitness value. For example, for the individuals with maximum and minimum fitness, different crossover probabilities are used for the crossover operation to obtain better individuals.

(2)

Realize the adaptive selection of the mutation probability. The improved algorithm can adjust the corresponding mutation probability according to the fitness value of the individual. The adjusted algorithm is expressed as follows:

$$P_m=\left\{\begin{array}{l}w4\left(f_{\max }-f_c\right)/\left(f_{\max }-f_{\min }\right),f_c\ne f_{\max },f_{\min }\\ w5,f_c=f_{\max }\\ w6,f_c=f_{\min }\end{array}\right.$$

(17)

where P_m is the mutation probability, f_c is the more adaptable one of the first two parents before the mutation operation, f_max and f_min represent the maximum and minimum value of fitness in the population, respectively, and w4, w5, and w6 are constants in the range of [0, 1] and w5 < w6. The improved algorithm can adjust the mutation probability adaptively according to the fitness value. For example, for the individuals with maximum and minimum fitness, different mutation probabilities are used for the mutation operation to obtain better individuals.

After improving the adaptive selection of crossover and mutation probability, the specific steps of realization of the aerosol extinction coefficient inversion method based on the improved genetic algorithm are as follows (taking a point at a certain height as an example).

(1)

The aerosol extinction coefficient and the backscattering coefficient at a certain height are encoded to generate the initial population, and the number of populations and the maximum number of iterations are set.

(2)

The error between the theoretical return power and the measured return power at this height is selected to evaluate the fitness of the individuals in the population. The objective is to make the two infinitely close, i.e., to minimize the error.

(3)

According to the roulette selection method, individuals with stronger adaptability to the environment are selected to enter the next step of the crossover operation. Individuals with high fitness are more likely to be retained.

(4)

According to the adaptive crossover probability, the selected individuals undergo crossover manipulation, and the individuals who become better are selected to form a new population.

(5)

According to the adaptive mutation probability, the gene mutation operation is performed on the individuals obtained through the crossover operation. The individuals who become better are retained as individuals in the new population after screening.

(6)

Steps (2)–(5) are repeated until the algorithm reaches a stop condition, i.e., the difference between the theoretical return power and the measured return power tends toward zero, thereby completing the optimization at the specified height.

(7)

Decode the final result and restore the solution to the problem. The operational steps are the same for other heights. After repeating the above process, the solutions of the aerosol extinction coefficient and the backscattering coefficient can be obtained by integrating the results for all heights.

3. Experiment Results and Analysis

To verify the feasibility of the proposed algorithm, some actual signals detected by a small Mie-scattering lidar developed at North Minzu University, China (38°29′ N, 106°06′ E) at the wavelength of 532 nm under different weather conditions were employed. The system parameters of the Mie-scattering lidar are shown in

Table 1. System parameters of the Mie-scattering lidar.

Parameters	Parameters Index
Laser	Nd:YAG laser
Wavelength	1064 nm, 532 nm, 355 nm
Single pulse energy	350 mJ@1064 nm, 170 mJ@532 nm, 80 mJ@355 nm
Impulse frequency	1–10 Hz
Pulse width	≤10 ns@1064 nm
Beam diameter	~9 mm@1064 nm
Divergence angle	≤0.5 mrad@1064 nm
Telescope	Schmidt-Cassegrain type
Diameter	300 mm
Field of view angle	0.4 mrad
Horizontal angle	0–360°
Pitching angle	0–90°
Detection range	100–13,000 m (Night), 100–10,000 m (Daytime)

.

A simple genetic algorithm was used to invert the data under sunny and cloudy conditions. The results were compared with the inversion results obtained using the Klett method (here, when using the Klett method for inversion, the lidar ratio was set to 50). Based on the feasibility verification, an improvement was made to the simple genetic algorithm. Its processing results were compared with the inversion results obtained using the Klett method, which further verified the reliability and accuracy of the improved inversion algorithm. Moreover, for calculating the same aerosol extinction coefficient profile, when the computer CPU is Intel Core 9 and the memory is 8 G, the simple genetic algorithm usually takes about 5 min, and the improved genetic algorithm takes about 4 min. The Klett method takes about 4 s, and the Fernald method takes about 6 s. Of course, the algorithm proposed mainly provides a new idea for aerosol extinction coefficient inversion. The advantage of the Genetic algorithm is mainly reflected in parameter optimization, which can realize the inversion of aerosol extinction coefficient and backscattering coefficient without prior assumptions. Namely, it is not necessary to assume a lidar ratio for inversion for the Klett and Fernald method.

For a genetic algorithm, the initial population is usually in the range of [20, 200], and it was set to 100 here. The objective function to be optimized using the genetic algorithm is obtained by minimizing the difference between the theoretical return power and the practically measured return power at different heights, see Equation (15). The binary encoding form was used here, and each parameter was a 10-bit unsigned binary number. There were two parameters to be optimized, and therefore the chromosome code length was set to 20. The fixed crossover/mutation probability and adaptive crossover/mutation probability were adopted. The genetic algorithm parameters are listed in

Table 2. Parameters of the genetic algorithm.

Serial Number	Parameter Name	Parameter Value
1	Population size	100
2	Chromosome coding length	20
3	Crossover probability	Fixed or adaptive
4	Mutation probability	Fixed or adaptive

.

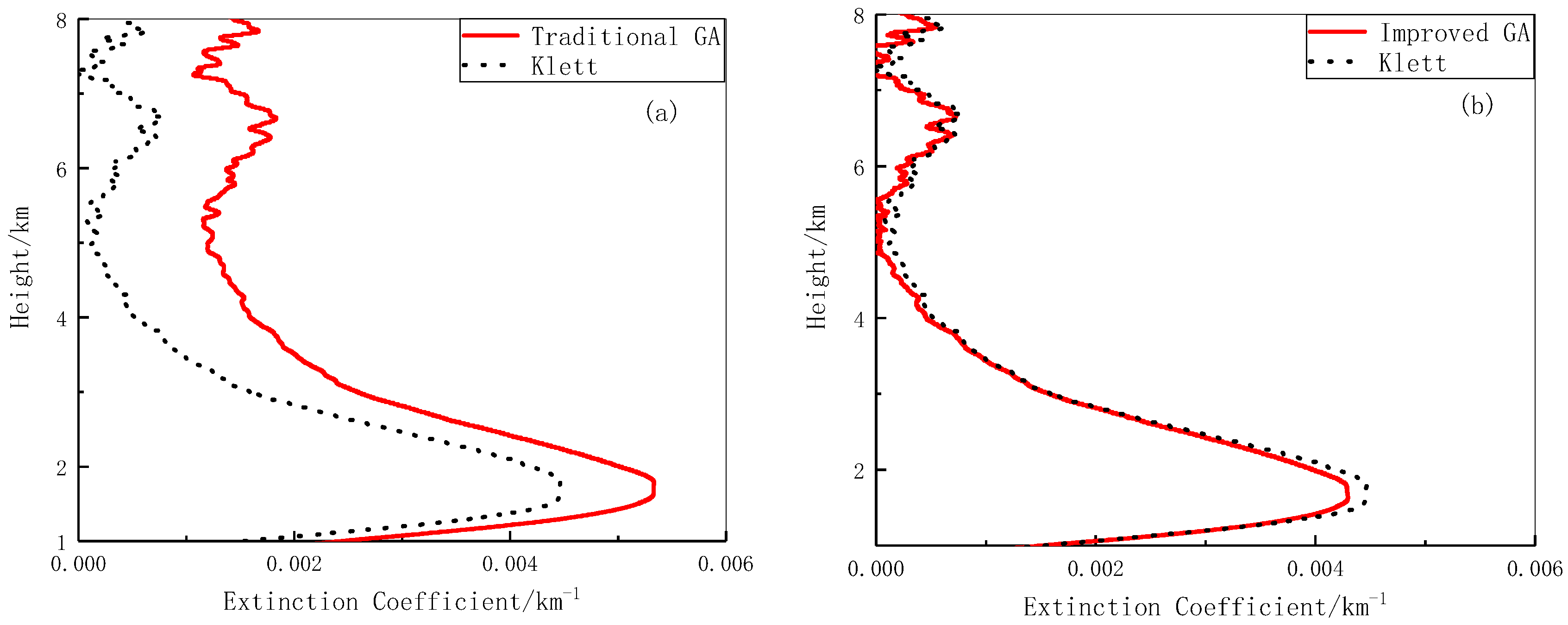
Figure 5 shows the inversion results obtained under sunny conditions. Figure 5a shows the inversion results obtained using the simple genetic algorithm and the Klett method. The calculation of the theoretical return power does not consider the overlap factor, but there is a blind area in the actual detection process. Therefore, manual operation to remove the blind area was adopted, i.e., the calculation began for heights above 1 km. It can be seen that the aerosol extinction coefficient profiles obtained by the two inversion methods have the same general trend, but there is a certain difference between the values. Nevertheless, the feasibility of the algorithm is preliminarily proved.

Figure 5b shows the inversion results obtained using the improved genetic algorithm and the Klett method. It can be seen that the inversion results obtained by the two methods are very close in terms of both trend and value below 4 km. Although there is a slight difference between the values above 4 km, the trend is consistent. Compared to the results shown in Figure 5a, the improved genetic algorithm produces a better inversion effect.

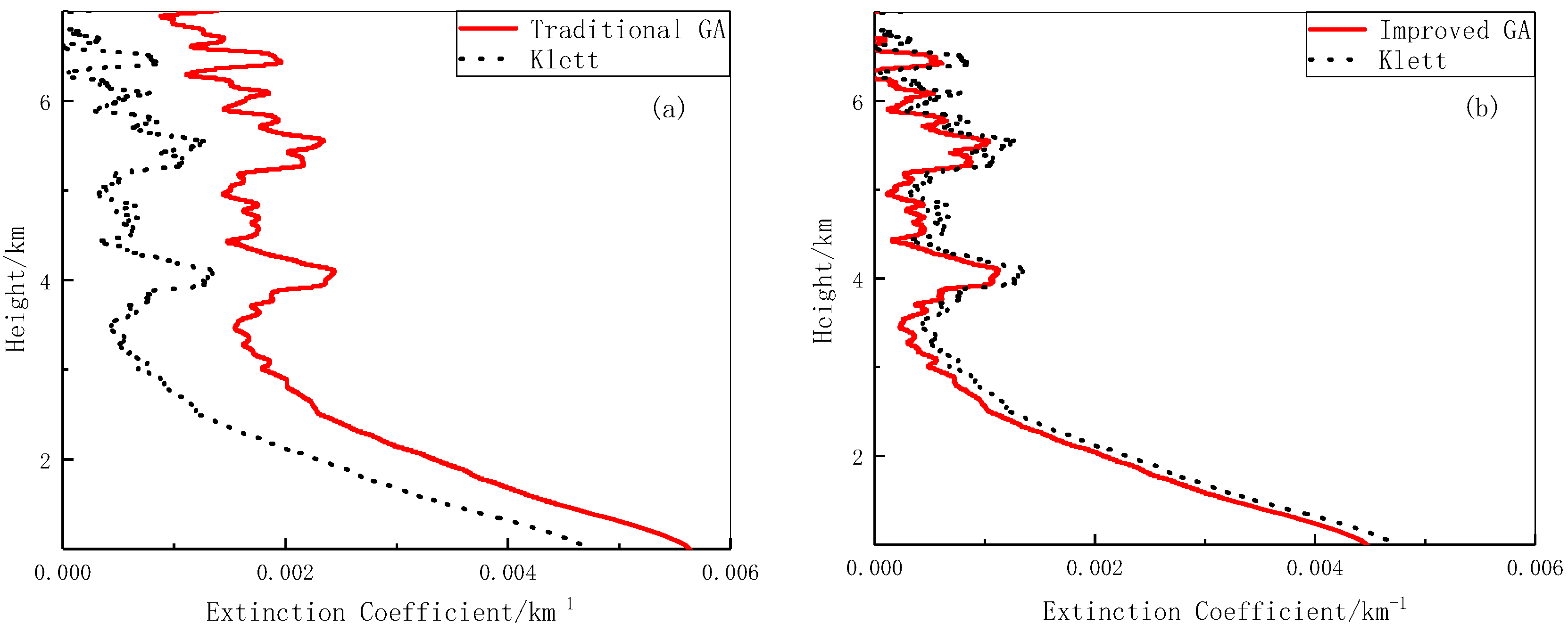
Figure 6 shows the inversion results obtained under conditions of thin cloud. Figure 6a shows the inversion results obtained using the simple genetic algorithm and the Klett method. It can be seen that the main difference between these data and those shown in Figure 5 lies in the signal characteristics between 5 and 7 km. The trend of the inversion results of the two methods are broadly similar, but there is a large difference in the values, indicating that the inversion results obtained using the genetic algorithm alone are not particularly accurate. Generally, the values of the aerosol extinction coefficient have been increased to a certain extent. Figure 6b shows the inversion results obtained using the improved genetic algorithm and the Klett method. It is apparent from the figure that the aerosol extinction coefficient profile obtained using the improved algorithm has a better inversion effect.

Figure 7 shows the inversion results obtained on a day with more obvious cloud features. Figure 7a shows the inversion results obtained using the simple genetic algorithm and the Klett method. As can be seen, there is obvious variation in the air mass between the heights of 3 and 6 km, producing distinct characteristics in the signal. Despite the large difference in values between the two inversion methods, the trends of the profiles are similar. Figure 7b shows the inversion results obtained using the improved genetic algorithm and the Klett method. Compared with Figure 7a, the inversion results obtained using the improved genetic algorithm are proven more accurate and reliable.

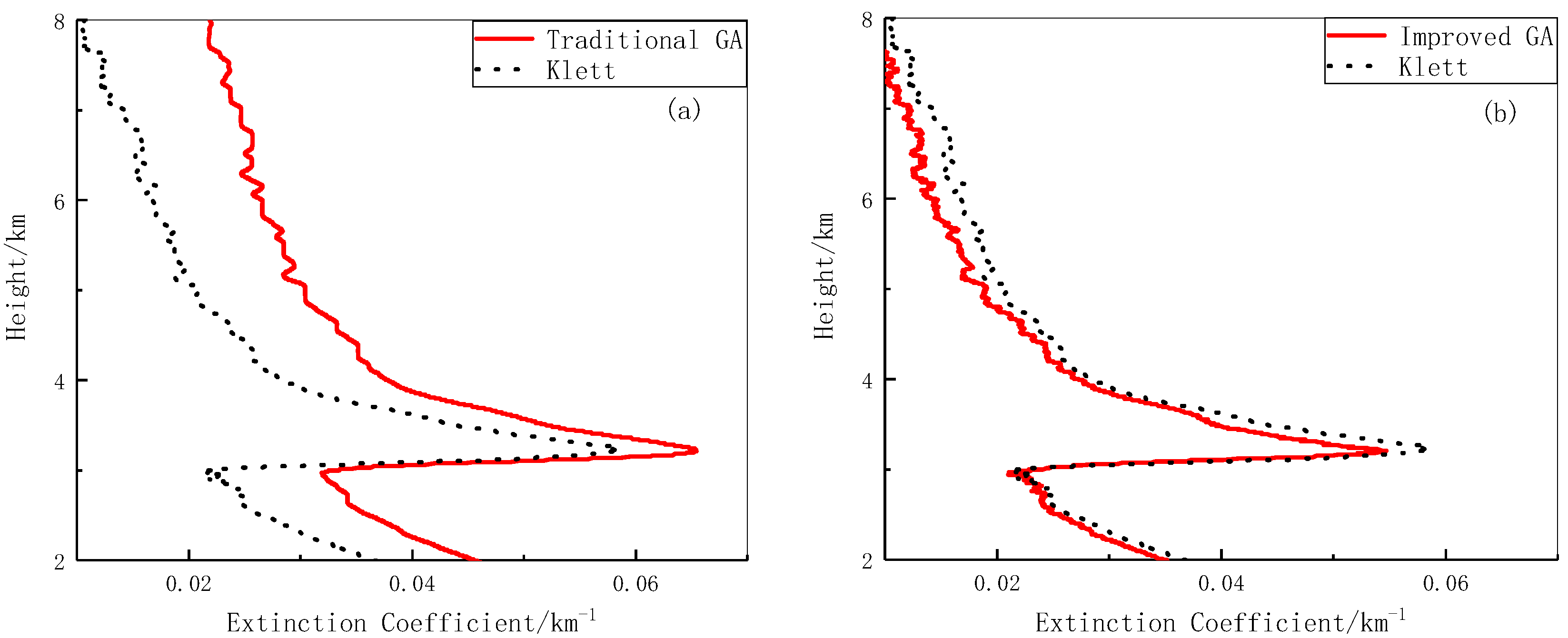
To evaluate the feasibility and effectiveness of the improved algorithm, it was used to perform inversion under cloudy weather. Figure 8a shows the inversion results obtained using the simple genetic algorithm and the Klett method with one obvious layer of low cloud. The difference between the results of the two algorithms is obvious regarding the numerical values. Figure 8b shows the inversion results obtained using the improved genetic algorithm and the Klett method for the same data shown in Figure 8a. Although the inversion results of the two algorithms are slightly different, the overall trends are similar. In comparison with Figure 8a, it can be seen that the inversion effect obtained using the improved genetic algorithm is much better, thereby confirming its applicability to the inversion of data under cloudy conditions.

To further verify the effectiveness of the improved algorithm, it was used to perform inversion under conditions with two layers of cloud. Figure 9a shows the inversion results for data containing two layers of cloud obtained using the simple genetic algorithm and the Klett method. It is evident that all the cloud features can be inverted, but there is still a certain gap in terms of the numerical values. Figure 9b shows the inversion results obtained using the improved genetic algorithm and the Klett method for the same data shown in Figure 9a. It can be seen that the characteristics of the clouds and the values of the aerosol extinction coefficient can be well inverted using the improved genetic algorithm.

4. Conclusions

Aerosols are a very important component of the atmosphere. Although their concentration might be small, they play important roles in atmospheric processes. In this paper, an aerosol extinction coefficient inversion algorithm based on the genetic algorithm is proposed. It uses the U.S. Standard Atmosphere model and the lidar equation to simulate the return power. The theoretical return power and the measured return power are fitted according to height, and the genetic algorithm with its strong global search capability and adaptive capability is used to optimize the process. When the theoretical return power is infinitely close to the measured return power, the values of the two independent variables, i.e., the aerosol extinction coefficient and the backscattering coefficient, can be obtained for a specific height, and other heights can be inverted in the same manner. The method proposed in this paper can obtain results similar to those derived using the traditional Klett method without requiring similar assumptions, and has a strong adaptive capability. The feasibility of the proposed algorithm was proven using inversion results obtained on sunny and cloudy days. The proposed algorithm represents a novel approach for the inversion of the aerosol extinction coefficient. The effect is similar to the Klett method according to the preliminary results, and optimizing the algorithm to get more accurate inversion results will be our next research goal. Moreover, the Genetic algorithm proposed in this paper provides a good solution for retrieving aerosol extinction coefficient and backscattering coefficient, but it is not limited to using a genetic algorithm. Using other intelligent optimization algorithms to obtain better results is also the research direction in the future.