Multicore Photonic Complex-Valued Neural Network with Transformation Layer
Abstract
:1. Introduction
- Using the multicore PCNN architecture to improve computing capability;
- Proposing the transformation layer, which can be implemented by the designed PCNN chip for improving performance of the PCNN;
- Analyzing the effect of phase noise on the multicore PCNN.
2. Multicore Photonic Complex-Valued Neural Network
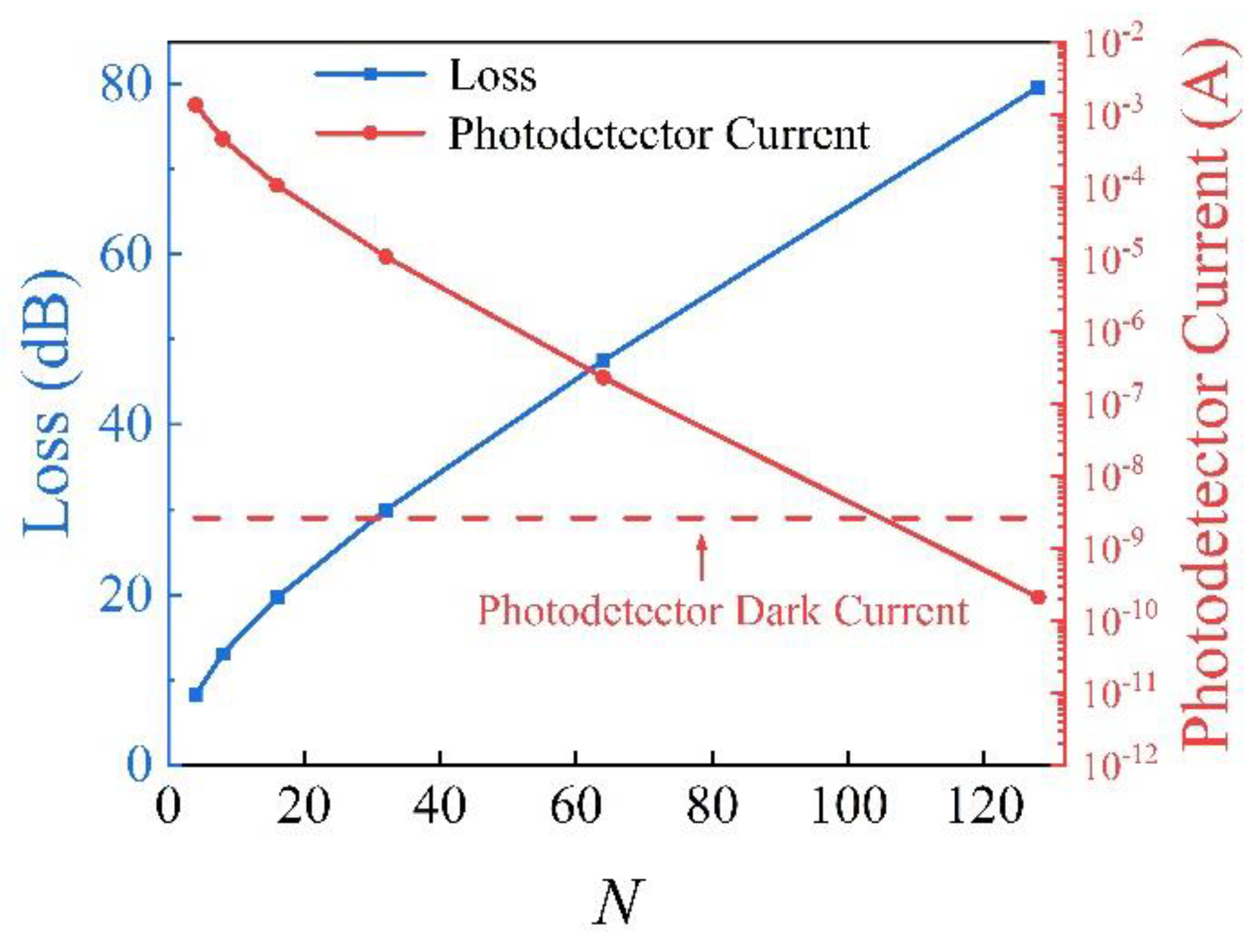
2.1. Photonic Complex-Valued Neural Network Chip
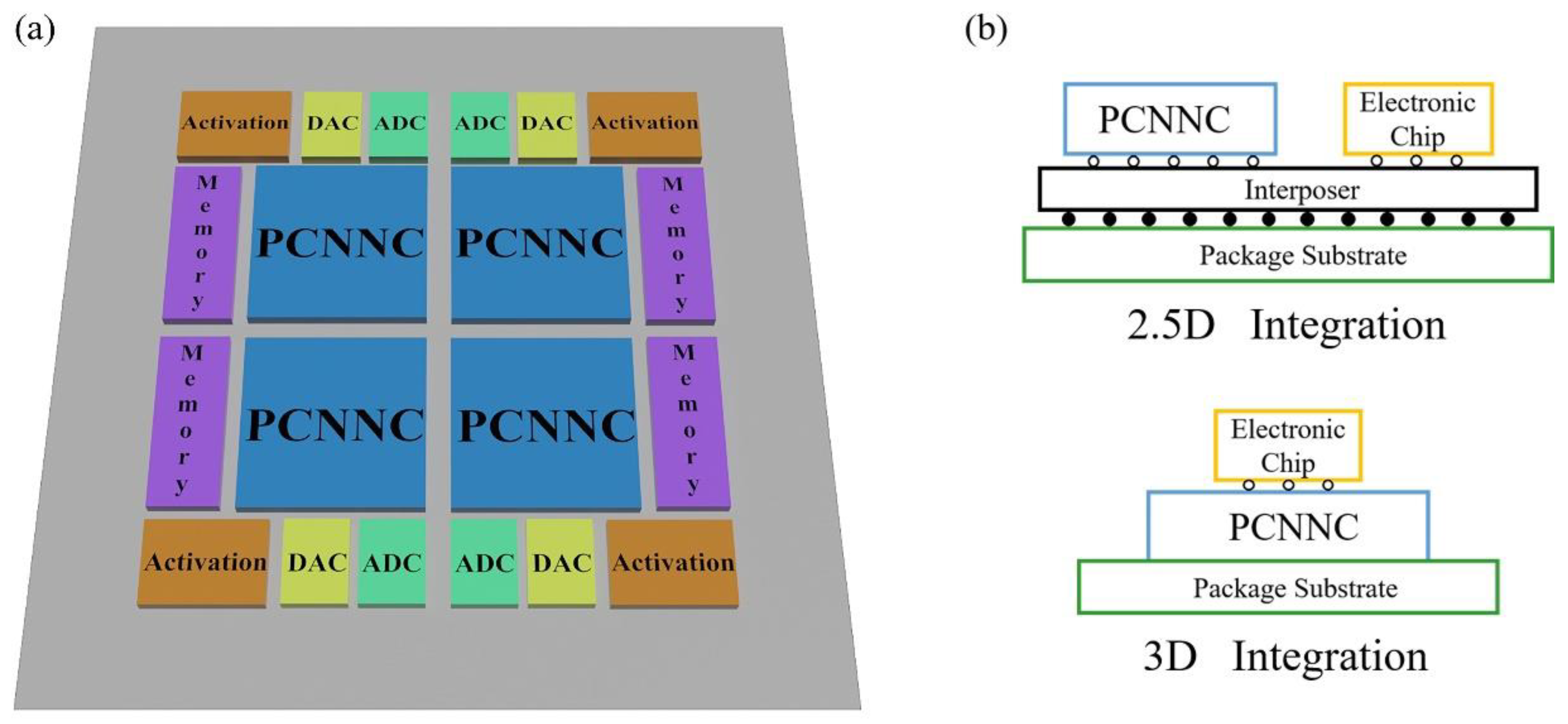
2.2. Multicore Architecture of Photonic Chip
2.3. Multicore Photonic Complex-Valued Neural Network
3. Results
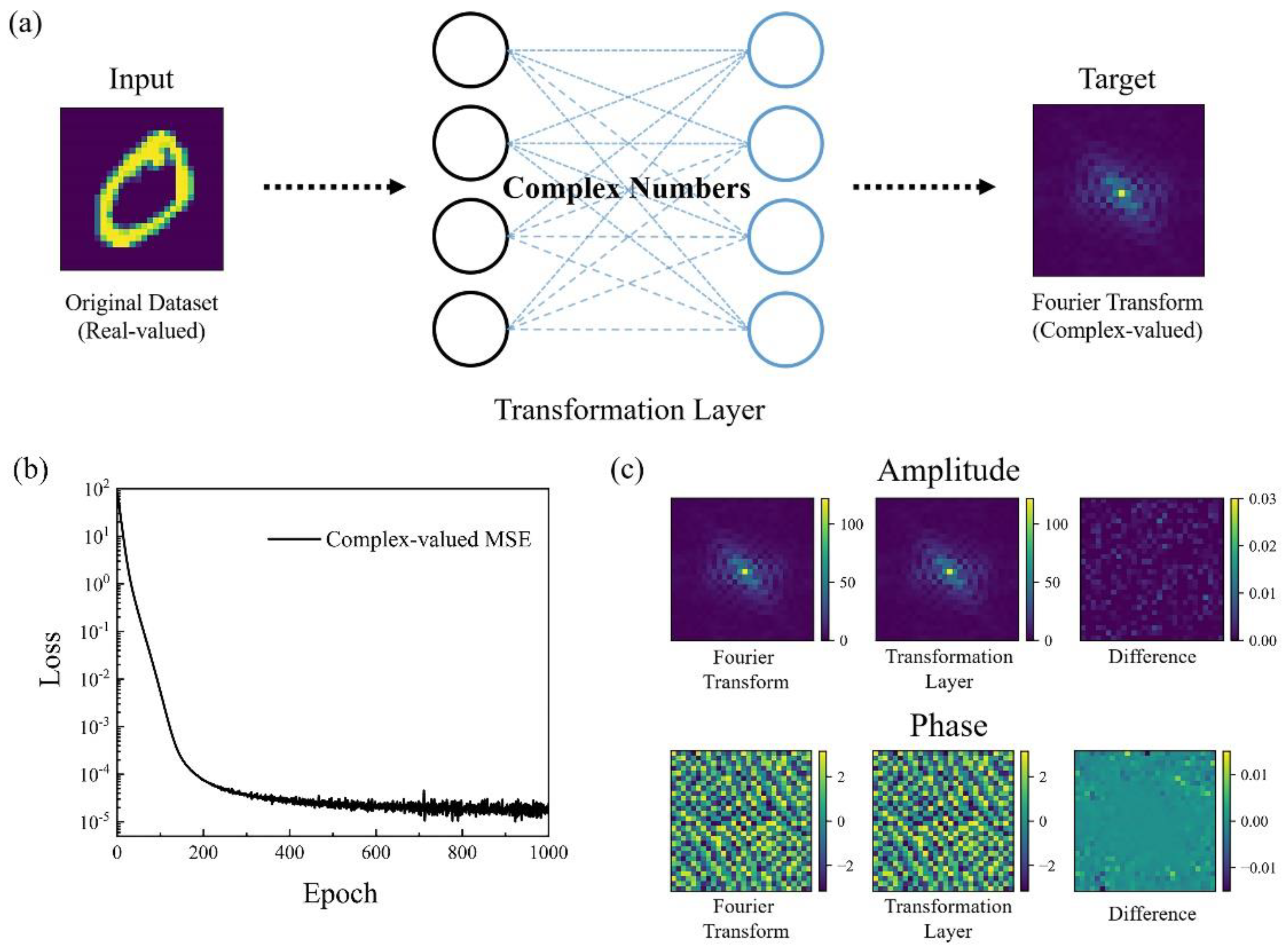
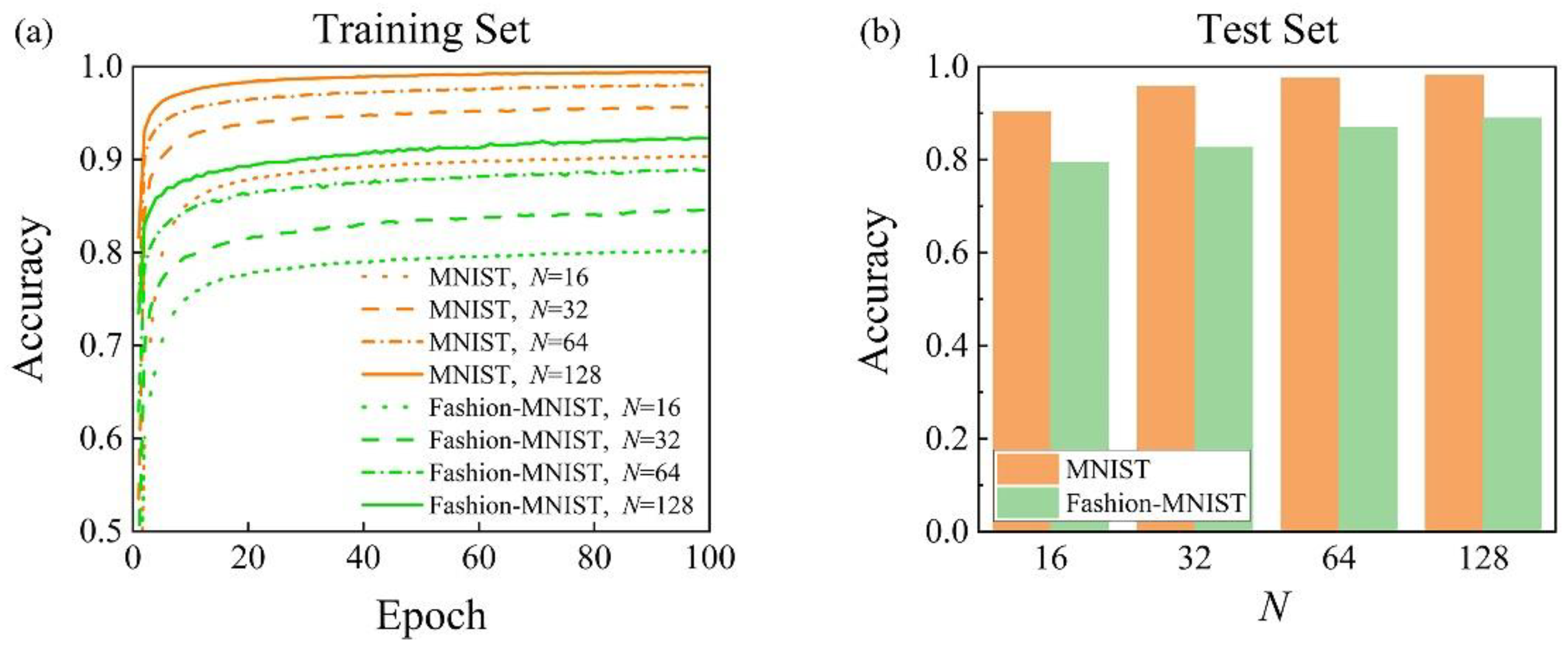
3.1. Photonic Complex-Valued Neural Network with Transformation Layer
3.2. Multicore Architecture Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sciuto, G.L.; Capizzi, G.; Coco, S.; Shikler, R. Geometric shape optimization of organic solar cells for efficiency enhancement by neural networks. In Advances on Mechanics, Design Engineering and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 789–796. [Google Scholar]
- Gostimirovic, D.; Winnie, N.Y. An open-source artificial neural network model for polarization-insensitive silicon-on-insulator subwavelength grating couplers. IEEE J. Sel. Top. Quantum Electron. 2018, 25, 8200205. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; Larochelle, H.; Englund, D. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Tait, A.N.; De Lima, T.F.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 2017, 7, 7430. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Wang, J.; Shu, H.; Zhang, Z.; Yi, S.; Bai, B.; Wang, X.; Liu, J.; Zou, W. Optical coherent dot-product chip for sophisticated deep learning regression. arXiv 2021, arXiv:2105.12122. [Google Scholar] [CrossRef] [PubMed]
- On, M.B.; Lu, H.; Chen, H.; Proietti, R.; Yoo, S.B. Wavelength-space domain high-throughput artificial neural networks by parallel photoelectric matrix multiplier. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Trabelsi, C.; Bilaniuk, O.; Zhang, Y.; Serdyuk, D.; Subramanian, S.; Santos, J.F.; Mehri, S.; Rostamzadeh, N.; Bengio, Y.; Pal, C.J. Deep complex networks. arXiv 2017, arXiv:1705.09792. [Google Scholar]
- Zhang, H.; Gu, M.; Jiang, X.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457. [Google Scholar] [CrossRef]
- Popa, C.-A. Complex-valued convolutional neural networks for real-valued image classification. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 816–822. [Google Scholar]
- Popa, C.-A.; Cernăzanu-Glăvan, C. Fourier transform-based image classification using complex-valued convolutional neural networks. In Proceedings of the International Symposium on Neural Networks, Minsk, Belarus, 25–28 June 2018; pp. 300–309. [Google Scholar]
- Williamson, I.A.; Hughes, T.W.; Minkov, M.; Bartlett, B.; Pai, S.; Fan, S. Reprogrammable electro-optic nonlinear activation functions for optical neural networks. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 7700412. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Miscuglio, M.; George, J.; Alkabani, Y.; El Gazhawi, T.; Sorger, V.J. Highly-parallel optical fourier intensity convolution filter for image classification. In Proceedings of the Frontiers in Optics, Washington, DC, USA, 15–19 September 2019; p. JW4A. 101. [Google Scholar]
- Ahmed, M.; Al-Hadeethi, Y.; Bakry, A.; Dalir, H.; Sorger, V.J. Integrated photonic FFT for photonic tensor operations towards efficient and high-speed neural networks. Nanophotonics 2020, 9, 4097–4108. [Google Scholar] [CrossRef]
- Clements, W.R.; Humphreys, P.C.; Metcalf, B.J.; Kolthammer, W.S.; Walmsley, I.A. Optimal design for universal multiport interferometers. Optica 2016, 3, 1460–1465. [Google Scholar] [CrossRef]
- Ramey, C. Silicon photonics for artificial intelligence acceleration: HotChips 32. In Proceedings of the 2020 IEEE Hot Chips 32 symposium (HCS), Palo Alto, CA, USA, 16–18 August 2020; pp. 1–26. [Google Scholar]
- Abrams, N.C.; Cheng, Q.; Glick, M.; Jezzini, M.; Morrissey, P.; O’Brien, P.; Bergman, K. Silicon photonic 2.5 D multi-chip module transceiver for high-performance data centers. J. Lightwave Technol. 2020, 38, 3346–3357. [Google Scholar] [CrossRef]
- Pai, S.; Williamson, I.A.; Hughes, T.W.; Minkov, M.; Solgaard, O.; Fan, S.; Miller, D.A. Parallel programming of an arbitrary feedforward photonic network. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 6100813. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Al-Qadasi, M.; Chrostowski, L.; Shastri, B.; Shekhar, S. Scaling up silicon photonic-based accelerators: Challenges and opportunities. APL Photonics 2022, 7, 020902. [Google Scholar] [CrossRef]
- Jacques, M.; Samani, A.; El-Fiky, E.; Patel, D.; Xing, Z.; Plant, D.V. Optimization of thermo-optic phase-shifter design and mitigation of thermal crosstalk on the SOI platform. Opt. Express 2019, 27, 10456–10471. [Google Scholar] [CrossRef] [PubMed]
- Chrostowski, L.; Shoman, H.; Hammood, M.; Yun, H.; Jhoja, J.; Luan, E.; Lin, S.; Mistry, A.; Witt, D.; Jaeger, N.A. Silicon photonic circuit design using rapid prototyping foundry process design kits. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 8201326. [Google Scholar] [CrossRef]
- Sia, J.X.B.; Li, X.; Wang, J.; Wang, W.; Qiao, Z.; Guo, X.; Lee, C.W.; Sasidharan, A.; Gunasagar, S.; Littlejohns, C.G. Wafer-Scale Demonstration of Low-Loss (~0.43 dB/cm), High-Bandwidth (>38 GHz), Silicon Photonics Platform Operating at the C-Band. IEEE Photonics J. 2022, 14, 6628609. [Google Scholar] [CrossRef]
- Dumais, P.; Wei, Y.; Li, M.; Zhao, F.; Tu, X.; Jiang, J.; Celo, D.; Goodwill, D.J.; Fu, H.; Geng, D. 2 × 2 multimode interference coupler with low loss using 248 nm photolithography. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–24 March 2016; p. W2A.19. [Google Scholar]
- Zhang, D.; Zhang, Y.; Zhang, Y.; Su, Y.; Yi, J.; Wang, P.; Wang, R.; Luo, G.; Zhou, X.; Pan, J. Training and Inference of Optical Neural Networks with Noise and Low-Bits Control. Appl. Sci. 2021, 11, 3692. [Google Scholar] [CrossRef]
- Pai, S.; Bartlett, B.; Solgaard, O.; Miller, D.A. Matrix optimization on universal unitary photonic devices. Phys. Rev. Appl. 2019, 11, 064044. [Google Scholar] [CrossRef] [Green Version]
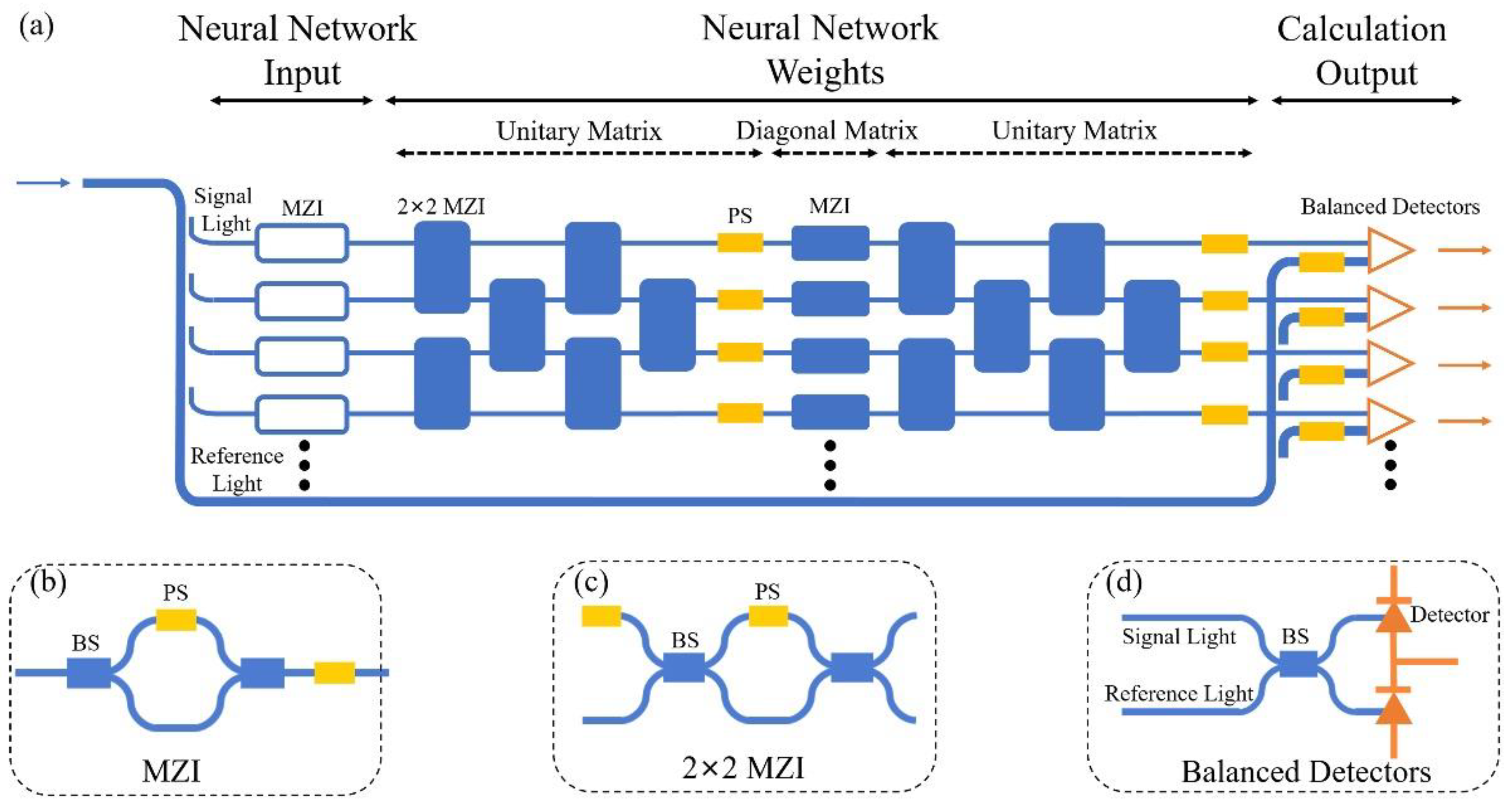



| Part of PCNN Chip | Variable | Description |
|---|---|---|
| Neural network weights | Complex-valued matrix | |
| Unitary matrix | ||
| Diagonal matrix | ||
| Unitary transformation of 2 × 2 MZI | ||
| Inner phase shift value of 2 × 2 MZI | ||
| outer phase shift value of 2 × 2 MZI | ||
| Calculation output | ) | Signal light(Reference light) |
| ) | Amplitude of signal light(reference light) | |
| ) | Phases of signal light(reference light) | |
| Frequency of signal light and reference light | ||
| Output photocurrent of balanced detectors |
| Device Parameter | Variable | Value | Refs |
|---|---|---|---|
| Input splitter insertion loss | 10log10N | ||
| Input splitter excess loss | 0.1 dB | [22] | |
| Waveguide loss | 0.43 dB/cm | [23] | |
| MZI length | 640 μm | [21] | |
| Weights splitter excess loss | 0.1 dB | [24] | |
| Laser power | 10 dBm | ||
| Photodetector responsivity | 0.835 A/W | [23] | |
| Photodetector dark current | 2.58 nA |
| Size of Photonic Complex-Valued Neural Network | Classification Accuracy | ||
|---|---|---|---|
| MNIST | Fashion-MNIST | ||
| Single-core | 32 × 32 | 95.76% | 82.60% |
| 64 × 64 | 97.51% | 87.01% | |
| 128 × 128 | 98.12% | 88.95% | |
| Multicore | 4-core, 64 × 64/core | 98.07% | 88.96% |
| 16-core, 32 × 32/core | 97.95% | 88.96% | |
| This Work | [9] | [18] | ||||
|---|---|---|---|---|---|---|
| Neural Network | PCNN | Multicore PCNN | PCNN | PUNN | ||
| Size | 64 × 64 | 4-core, 64 × 64/core | 8 × 8 | 36 × 36 | ||
| Dataset | MNIST | MNIST | MNIST | MNIST | ||
| Preprocessing | Original dataset | Transformation layer | Transformation layer | Real encoding | Complex encoding | Fourier transform |
| Classification Accuracy | 93.14% | 97.51% | 98.07% | 91.00% | 93.50% | 96.60% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Wang, P.; Lyu, C.; Luo, G.; Yu, H.; Zhou, X.; Zhang, Y.; Pan, J. Multicore Photonic Complex-Valued Neural Network with Transformation Layer. Photonics 2022, 9, 384. https://doi.org/10.3390/photonics9060384
Wang R, Wang P, Lyu C, Luo G, Yu H, Zhou X, Zhang Y, Pan J. Multicore Photonic Complex-Valued Neural Network with Transformation Layer. Photonics. 2022; 9(6):384. https://doi.org/10.3390/photonics9060384
Chicago/Turabian StyleWang, Ruiting, Pengfei Wang, Chen Lyu, Guangzhen Luo, Hongyan Yu, Xuliang Zhou, Yejin Zhang, and Jiaoqing Pan. 2022. "Multicore Photonic Complex-Valued Neural Network with Transformation Layer" Photonics 9, no. 6: 384. https://doi.org/10.3390/photonics9060384
APA StyleWang, R., Wang, P., Lyu, C., Luo, G., Yu, H., Zhou, X., Zhang, Y., & Pan, J. (2022). Multicore Photonic Complex-Valued Neural Network with Transformation Layer. Photonics, 9(6), 384. https://doi.org/10.3390/photonics9060384





