Influence of Radiative and Non-Radiative Recombination Lifetimes and Feedback Strength on the States and Relative Intensity Noise of Laser Diode
Abstract
:1. Introduction
2. Theoretical Model
3. Numerical Calculations Process
4. Simulation Results Analysis, and Discussions
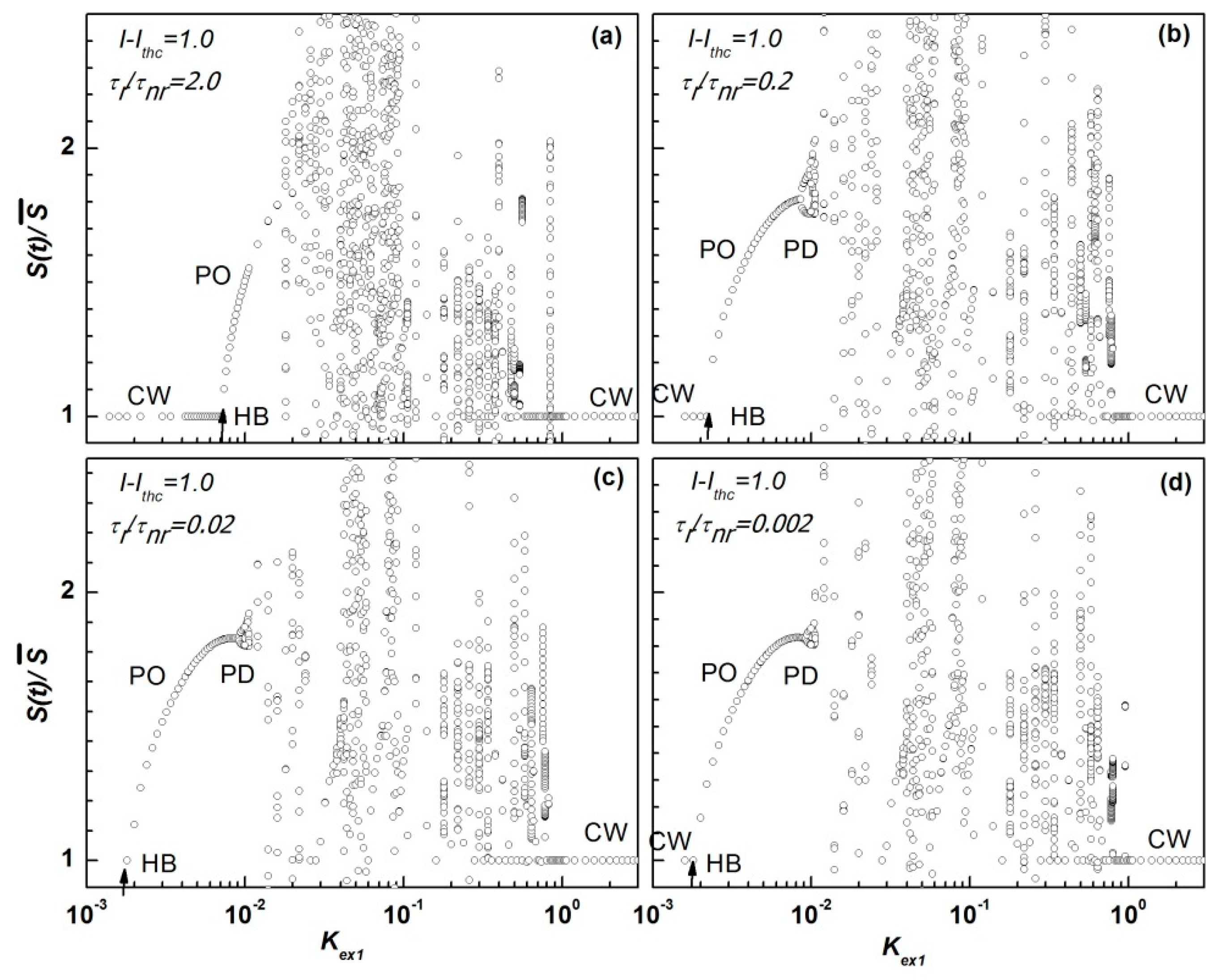
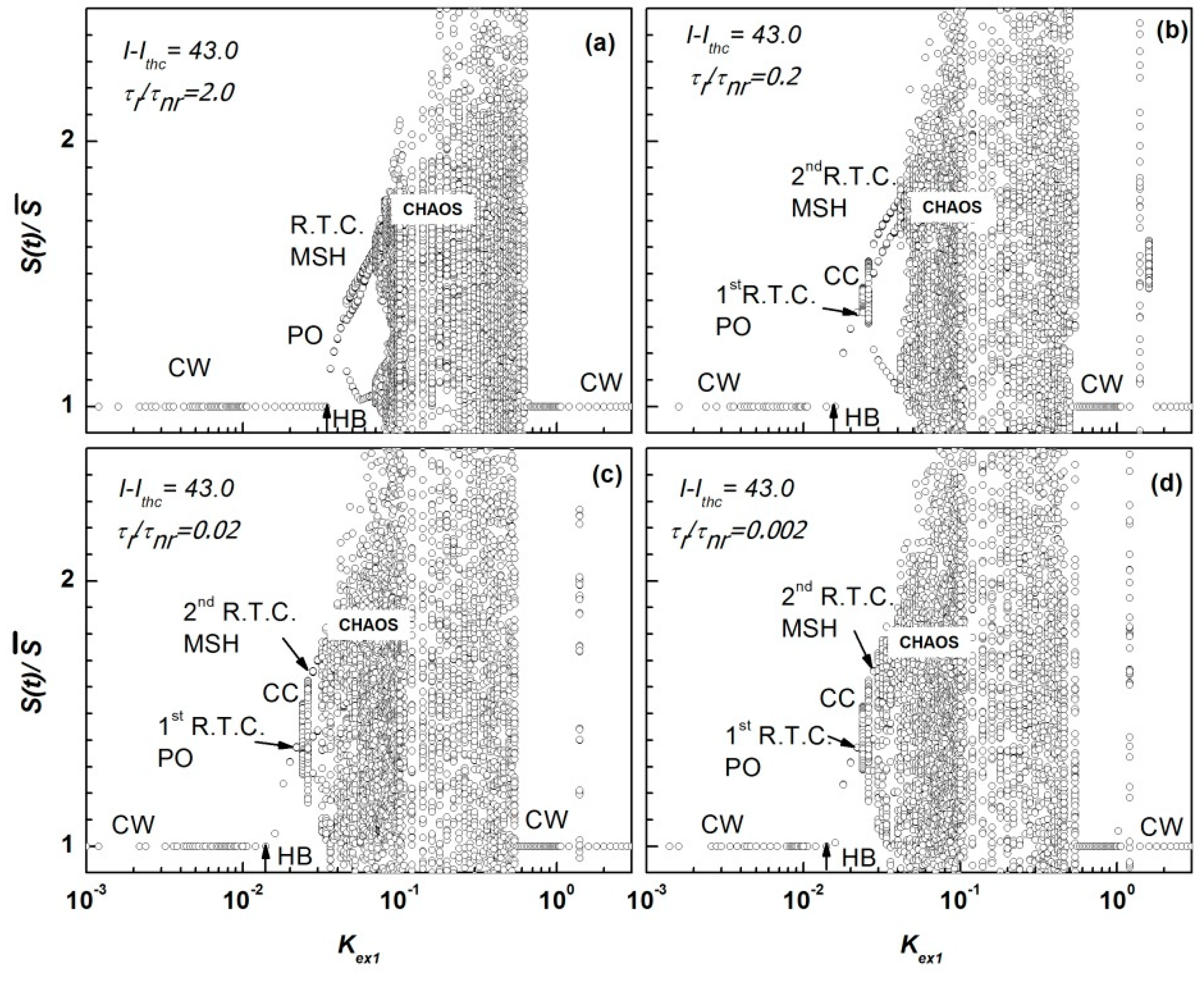
4.1. Bifurcation Diagrams with OFB Strength
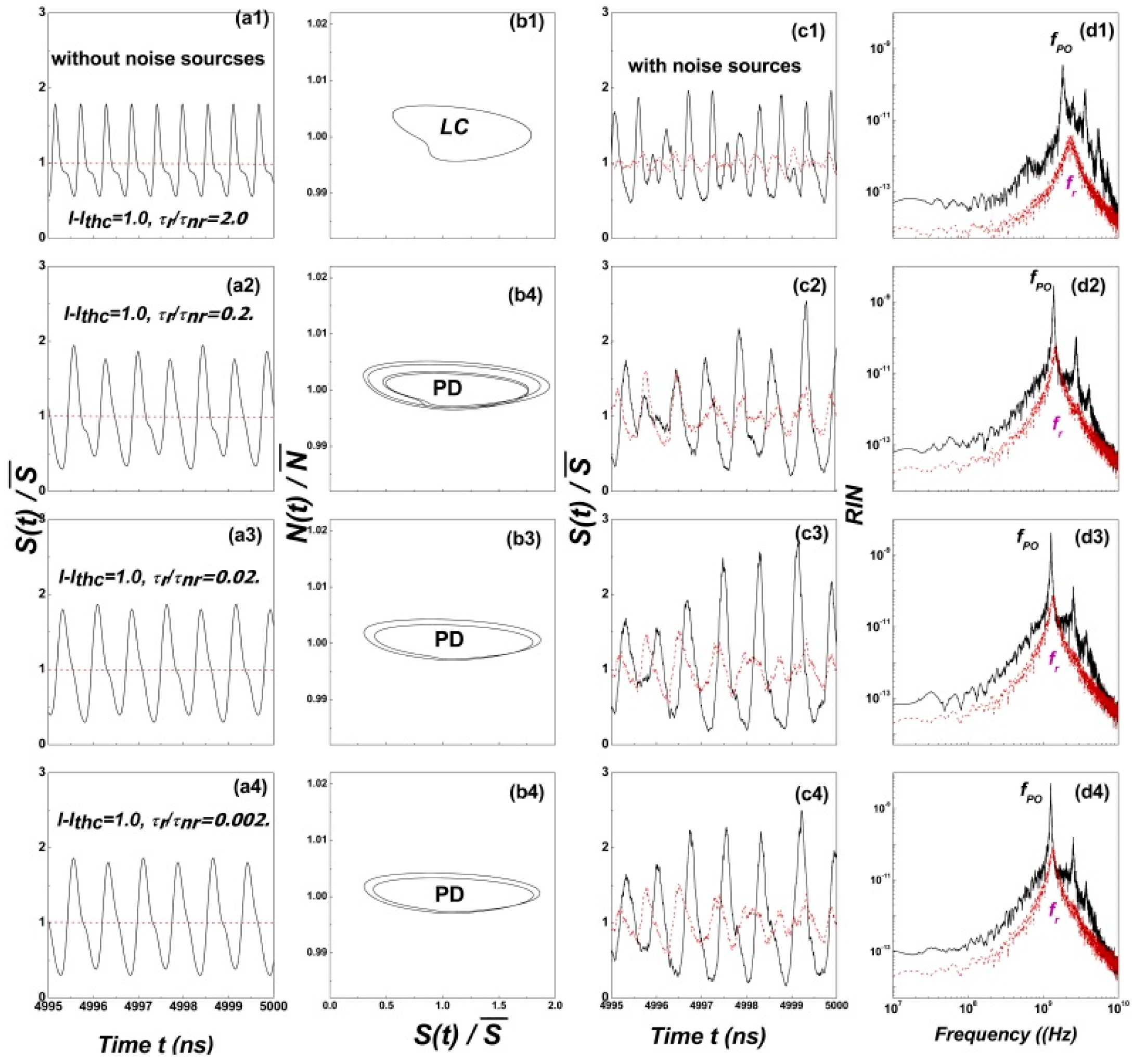
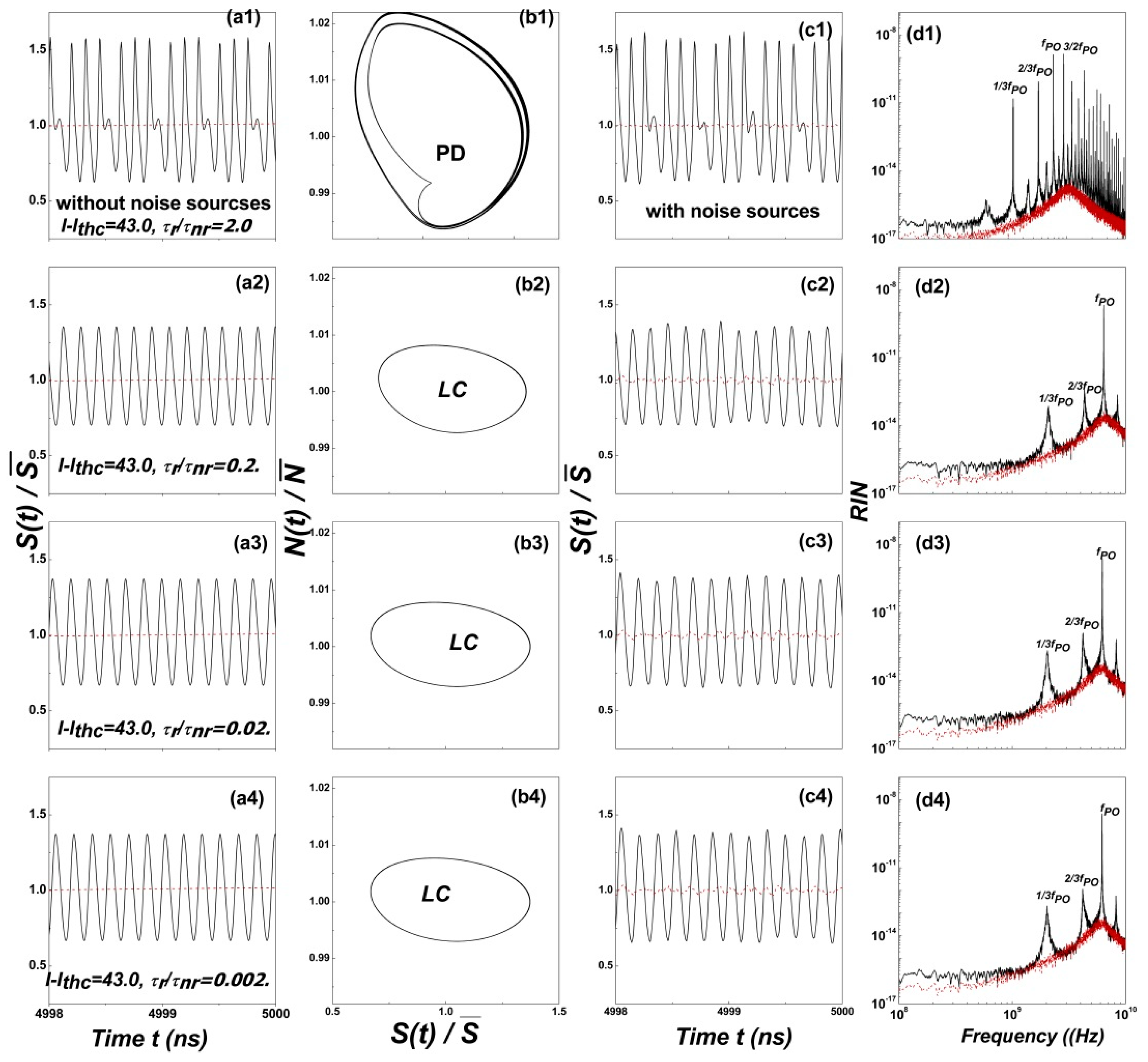
4.2. Time Variation, Phase Portrait, and RIN of S(t)/ at Route to Chaos
4.3. Influence of OFB and the Ratio τr/τnr on the Low-Frequency RIN
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agrawal, G.P.; Dutta, N.K. Semiconductor Lasers, 2nd ed.; Van Nostrand: New York, NY, USA, 1993. [Google Scholar]
- Mork, J.; Tromborg, B.; Mark, J. Chaos in semiconductor lasers with optical feedback: Theory and experiment. IEEE J. Quantum Electron. 1992, 28, 93–108. [Google Scholar] [CrossRef]
- Hess, O.; Kuhn, T. Maxwell-Bloch equations for spatially inhomogeneous semiconductor lasers. I. Theoretical formulation. Phys. Rev. A 1996, 54, 3347. [Google Scholar] [CrossRef]
- Münkel, M.; Kaiser, F.; Hess, O. Stabilization of spatiotemporally chaotic semiconductor laser arrays by means of delayed optical feedback. Phys. Rev. E 1997, 56, 3868–3875. [Google Scholar] [CrossRef]
- Lenstra, D.; Verbeek, B.H.; den Boef, A.J. Coherence collapse in single-mode semiconductor lasers due to optical feed-back. IEEE J. Quantum Electron. 1985, 21, 674–679. [Google Scholar] [CrossRef]
- Agrawal, G.P. Optical Fiber Communication Systems, Chapter 6; Van Nostrand Reinhold: New York, NY, USA, 2012. [Google Scholar]
- Kitaoka, Y.; Sato, H.; Mizuuchi, K.; Yamamoto, K.; Kato, M. Intensity noise of laser diodes with optical feedback. IEEE J. Quantum Electron. 1996, 32, 822–828. [Google Scholar] [CrossRef]
- Kallimani, K.; O’Mahony, M. Relative intensity noise for laser diodes with arbitrary amounts of optical feedback. IEEE J. Quantum Electron. 1998, 34, 1438–1446. [Google Scholar] [CrossRef]
- Safwat, W.Z.; Moustafa, A.M.; Hassan, A.M.A. Comprehensive large-signal analysis of RF modulation of vertical cavity surface emitting lasers. Opt. Laser Technol. 2013, 45, 406–413. [Google Scholar]
- Harrison, J.; Mooradian, A. Linewidth and offset frequency locking of external cavity GaAlAs lasers. IEEE J. Quantum Electron. 1989, 25, 1152–1155. [Google Scholar] [CrossRef]
- Kahn, M.; Burrus, C.A.; Raybon, G. High-stability 1.5 m external-cavity semiconductor lasers for phase lock applications. IEEE Photon. Technol. Lett. 1989, 1, 159–161. [Google Scholar] [CrossRef]
- Wenke, G.; Gross, R.; Meissner, P.; Patzak, E. Characteristics of a compact three cavity laser configuration. J. Light. Technol. 1987, 5, 608–615. [Google Scholar] [CrossRef]
- Agrawal, G.; Henry, C. Modulation performance of a semiconductor laser coupled to an external high-Q resonator. IEEE J. Quantum Electron. 1988, 24, 134–142. [Google Scholar] [CrossRef]
- Fouad, N.; Mohamed, T.; Mahmoud, A. Impact of linewidth enhancement factor and gain suppression on chirp characteristics of high-speed laser diode and performance of 40 Gbps optical fiber links. Appl. Phys. A 2022, 128, 45. [Google Scholar] [CrossRef]
- Cho, Y.; Umeda, T. Observation of chaos in a semiconductor laser with delayed feedback. Opt. Commun. 1986, 59, 131–136. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Ahmed, M.; Okamoto, T.; Ishimori, W.; Yamada, M. An improved analysis of semiconductor laser dynamics under strong optical feedback. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1265–1274. [Google Scholar] [CrossRef]
- Moustafa, A.; Minoru, Y.; Salah, A. Numerical modeling of the route-to-chaos of semiconductor lasers under optical feedback and its dependence on the external cavity length. Int. J. Numer. Model. Electron. Netw. Devices Fields 2009, 22, 434–445. [Google Scholar]
- Abdulrhmann, S. The Nonlinear Gain and the Route to Chaos in Semiconductor Laser with Optical Feedback. Int. J. Phys. Res. 2013, 3, 83–90. [Google Scholar]
- Koryukin, I.V.; Mandel, P. Dynamics of semiconductor lasers with optical feedback: Comparison of multimode models in the low-frequency fluctuation regime. Phys. Rev. A 2004, 70, 53819. [Google Scholar] [CrossRef] [Green Version]
- Bauer, S.; Brox, O.; Kreissl, J.; Sartorius, B.; Radziunas, M.; Sieber, J.; Wünsche, H.-J.; Henneberger, F. Nonlinear dynamics of semiconductor lasers with active optical feedback. Phys. Rev. E 2004, 69, 16206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toomey, J.P.; Kane, D.M.; Lee, M.W.; Shore, K.A. Nonlinear dynamics of semiconductor lasers with feedback and modulation. Opt. Express 2010, 18, 16955–16972. [Google Scholar] [CrossRef]
- Meneghini, M.; Trivellin, N.; Orita, K.; Takigawa, S.; Yuri, M.; Tanaka, T.; Ueda, D.; Zanoni, E.; Meneghesso, G. Degradation of InGaN-based laser diodes related to nonradiative recombination. IEEE Electron Device Lett. 2009, 30, 356–358. [Google Scholar] [CrossRef]
- Olshansky, R.; Su, C.; Manning, J.; Powazinik, W. Measurment of radiative and nonradiative Recombination rates in InGaAs light sources. IEEE J. Quantum Electron. 1984, 20, 838–854. [Google Scholar] [CrossRef]
- Hisham, H.; Mahdiraji, G.A.; Abas, A.F.; Mahdi, M.A.; Adikan, F.R.M. Characterization of Turn-On Time Delay in a Fiber Grating Fabry–Perot Lasers. IEEE Photon. J. 2012, 4, 1662–1678. [Google Scholar] [CrossRef] [Green Version]
- Abdulrhmann, S.; Ahmed, M.; Yamada, M. Influence of Nonlinear Gain and Nonradiative Recombination on the Quantum Noise in InGaAsP Semiconductor Lasers. Opt. Rev. 2002, 9, 260–268. [Google Scholar] [CrossRef]
- Ahmed, M.; Yamada, M. An infinite-order approach to gain calculation in injection semiconductor lasers. J. Appl. Phys. 1998, 84, 3004–3015. [Google Scholar] [CrossRef]
- Petermann, K. Laser Diode Modulation and Noise; Kluwer Academic: Dordrecht, Germany, 1988. [Google Scholar] [CrossRef]
- Ahmed, M.; Mahmoud, S.W.Z.; Yamada, M. Numerical analysis of optical feedback phenomenon and intensity noise of fibre-grating semiconductor lasers. Int. J. Numer. Model. Electron. Netw. Devices Fields 2007, 20, 117–132. [Google Scholar] [CrossRef] [Green Version]
- Mørk, J.; Mark, J.; Tromborg, B. Route to chaos and competition between relaxation oscillations for a semiconductor laser with optical feedback. Phys. Rev. Lett. 1990, 65, 1999–2002. [Google Scholar] [CrossRef]
- Kao, Y.H.; Wang, N.M.; Chen, H.M. Mode description of routes to chaos in external-cavity coupled semiconductor lasers. IEEE J. Quantum Electron. 1994, 30, 1732–1739. [Google Scholar] [CrossRef] [Green Version]
- Ryan, A.T.; Agrawal, G.P.; Gray, G.R.; Gage, E.C. Optical-feedback-induced chaos and its control in multimode semi-conductor lasers. IEEE J. Quantum Electron. 1994, 30, 668–679. [Google Scholar] [CrossRef]
- Asada, M.; Suematsu, Y. The effects of loss and nonradiative recombination on the temperature dependence of threshold current in 1.5–1.6 µm GalnAsP/InP lasers. IEEE J. Quantum Electron. 1983, 1, 917–923. [Google Scholar] [CrossRef]





| Parameter | Value | Unit |
|---|---|---|
| External cavity refractive index nex | 1.0 | --- |
| Gain tangential coefficient a | 7.9 × 10−12 | m3s−1 |
| Carrier number at transparency Ng | 1.33 × 108 | --- |
| Active region refractive index nD | 3.513 | --- |
| Active region length LD | 300 | μm |
| Active region volume V | 150 | μm3 |
| Field confinement factor ξ | 0.2 | --- |
| Front-facet reflectivity Rf | 0.3 | -- |
| Back-facet reflectivity Rb | 0.8 | -- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulrhmann, S.; Altowyan, A.S.; Hakami, J. Influence of Radiative and Non-Radiative Recombination Lifetimes and Feedback Strength on the States and Relative Intensity Noise of Laser Diode. Photonics 2022, 9, 541. https://doi.org/10.3390/photonics9080541
Abdulrhmann S, Altowyan AS, Hakami J. Influence of Radiative and Non-Radiative Recombination Lifetimes and Feedback Strength on the States and Relative Intensity Noise of Laser Diode. Photonics. 2022; 9(8):541. https://doi.org/10.3390/photonics9080541
Chicago/Turabian StyleAbdulrhmann, Salah, Abeer S. Altowyan, and Jabir Hakami. 2022. "Influence of Radiative and Non-Radiative Recombination Lifetimes and Feedback Strength on the States and Relative Intensity Noise of Laser Diode" Photonics 9, no. 8: 541. https://doi.org/10.3390/photonics9080541
APA StyleAbdulrhmann, S., Altowyan, A. S., & Hakami, J. (2022). Influence of Radiative and Non-Radiative Recombination Lifetimes and Feedback Strength on the States and Relative Intensity Noise of Laser Diode. Photonics, 9(8), 541. https://doi.org/10.3390/photonics9080541






