Abstract
Compared with state-of-the-art radio frequency accelerators, the gradient of laser wakefield accelerators is 3–4 orders of magnitude higher. This is of great significance in the development of miniaturized particle accelerators and radiation sources. Higher requirements have been proposed for the quality of electron beams, owing to the increasing application requirements of tabletop radiation sources, specifically with the rapid development of free-electron laser devices. This review briefly examines the electron beam quality optimization scheme based on laser wakefield acceleration and presents some representative studies. In addition, manipulation of the electron beam phase space by means of injection, plasma profile distribution, and laser evolution is described. This review of studies is beneficial for further promoting the application of laser wakefield accelerators.
1. Introduction
In 1979, Tajima and Dawson [1] proposed the concept of laser wakefield acceleration (LWFA) [2]. When a strong laser is incident on the plasma, the ponderomotive force dislodges the electrons in the background plasma and then excites a wakefield to accelerate the particles. Without the breakdown voltage limitation in the plasma, the acceleration gradient of the LWFA can reach 100 GV/m, which is three orders of magnitude higher than that of the conventional radio frequency accelerator. Therefore, it is of great significance for the development of miniaturized particle accelerators. The nonlinear wakefield, called the bubble, has a microstructure, and the accelerated electrons usually have only an fs-level pulse length and a μm-level transverse size. In addition to being affected by the longitudinal acceleration field, the electron beam also oscillates transversely in the wakefield, which generates betatron radiation covering the ultraviolet to X-ray wave bands, whose frequencies are related to the plasma frequency and electron energy. Gamma rays can also be generated by inverse Compton scattering, caused by the interaction of the electron beam with the laser beam. When the electron beam quality meets the high-gain free-electron laser (FEL) conditions, it can be applied to the FEL [3,4,5]. These features make LWFA a potential tabletop accelerator and radiation source.
LWFA has high requirements for laser intensity (~25 fs pulse length, 1018 W/cm2 power density). It was impossible to experimentally obtain a monoenergetic electron beam for a long time, owing to the lack of a strong driving laser. In 1985, the introduction of chirped pulse amplification (CPA) [6] led to the rapid development of ultra-intense and ultra-short laser devices, providing a driving light source with relativistic intensity for the excitation of the laser wakefield. In 2004, Faure et al., Geddes et al. and Mangles et al. experimentally obtained 100 MeV level quasi-mono-energetic electron beams for the first time experimentally, which were reported on the cover of Nature with the title “Dream Beam” [7,8,9]. LWFA ushered in a milestone breakthrough, marking the beginning of miniaturized particle accelerators. An increasing number of groups have devoted themselves to electron acceleration research based on LWFA. This research has entered a period of rapid development concentrated on energy gain improvements [10], acceleration stability [11], and electron beam quality optimization [12].
As a typical example, the group led by Leemans has carried out a lot of important work in the promotion of electron beam energy and also enhanced the electron beam energy multiple times [13,14,15]. The acceleration distance can be extended, and the maximum acceleration energy can be increased by optimizing laser guidance [16]. In 2019, they used a 20-cm-long capillary [17] to guide the laser to maintain good focus and electron beams with energy peaks up to 7.8 GeV [15]. These are the highest LWFA-based energy electrons that have been reported internationally. In terms of electron beam stability, Osterhoff et al. [18] used a cylindrical gas box 15 mm long and 250 μm in diameter as a gas pool structure to create a stable plasma profile distribution in 2008. An electron beam with a divergence angle of ~2.1 mrad was obtained by continuous collection. The RMS (root mean square) energy jitter from shot to shot was less than 2.5%, and the pointing jitter was less than 1.4 mrad, which was the best result for stability reported at the time. In 2020, Maier et al. conducted further experiments on the stability of LWFA [11]. They accurately measured the electron beam energy drift and jitter with a combination of diagnostic methods, which provided a basis for obtaining electron beam acceleration feedback and active control. According to the correlation between the laser and electron parameters, the electron beam quality is parameterized to enable loop feedback and fine-tuning of the accelerator, resulting in a reproducible electron beam [19,20]. The continuous acquisition of 100,000 high-stability electron beams within 24 h has realized the long-term stable operation of LWFA.
Methods for electron injection and electron phase-space manipulation have been continuously proposed and improved, with the intent of boosting the quality of electron beams based on LWFA. In 2006, Faure et al. first experimentally verified the colliding laser pulse injection proposed in the early theory [21]. They also realized a flexible adjustment of the electron beam peak energy by changing the collision position of the two pulses. Thus, the electron beam was further optimized. The phase-space volume of the injected particles can be controlled by adjusting the optical injection parameters, thereby controlling the electron beam charge and energy spread. An electron beam with 200 MeV, 10 pC, and 1% relative energy spread was experimentally obtained [22]. Along with the theory of ionization injection, in 2007, Oz et al. [23] took the lead in performing LWFA based on ionization injection in experiments. In 2014, Xu et al. and Yu et al. [24,25] conducted research on obtaining low-emittance electron beams based on two-color laser ionization injection. Zeng et al. proposed an ionization implantation scheme, in which a triple-frequency injection laser propagates co-linearly with the driving laser to obtain a low-energy spread electron beam [26].
As mentioned above, it is difficult to describe the overall quality of an electron beam using a single parameter. Drawing on conventional accelerators, we introduce the six-dimensional phase-space brightness in units of A/m2/0.1% [12,27,28] to characterize the comprehensive quality of the electron beam, which can be defined as the total bunch charge divided by the product of the rms horizontal, vertical and longitudinal normalized emittances be expressed as
where represents the peak current; and represent the horizontal and vertical transverse emittance, respectively; and represents the RMS relative energy spread. High brightness in the 6D phase space requires the electron beam to have a low energy spread, low emittance, and high current, which results in high quality and provides guidance for optimizing the electron beam.
In this review, we briefly examine an electron beam quality optimization scheme based on LWFA. The analysis of the influencing factors indicates the direction of electron beam parameter optimization. The effects of the injection method, phase-space manipulation, and improvements of electron beam parameters at different stages are discussed. In addition, this review briefly discusses a portion of the outstanding work of related research teams on LWFA and provides guidance for future electron beam quality optimization.
2. Emittance
Emittance, which is the area of transverse phase space occupied by a beam of particles, as shown in Figure 1a, characterizes the transverse quality of the beam. It is necessary to control the electron beam injection and acceleration in the wakefield by controlling the profile of the plasma density and evolution of the laser pulse to obtain an electron beam with low emittance. An increase in the electron beam emittance was suppressed, and high-quality electron beams with low emittance were finally obtained by controlling the evolution of the phase space to match the parameters of the wakefield.
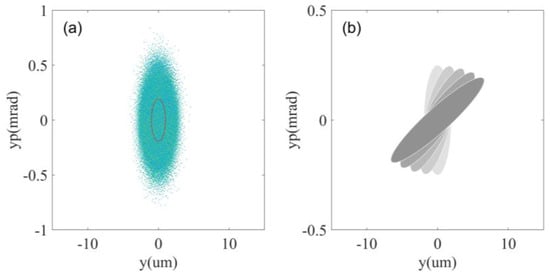
Figure 1.
Transverse phase space distribution of electron beam: (a) definition of emittance, area (red line) = emittance × π; (b) phase space distribution of electron beam with different phase.
Beam density remains constant in the phase space according to the Liouville theorem. Therefore, when particle beam density remains unchanged, the volume occupied by the particle beam in the phase space remains unchanged during motion. The injected emittance determines the lower limit of the final emittance for a mono-energetic electron beam, while neglecting collective effects, such as space charge. The transverse wave breaking threshold will be lower than the traditional one-dimensional wave breaking threshold in two-dimensional or three-dimensional structures [29], which promotes the transverse injection of the electron beam. The off-axis injected electrons maintain betatron oscillation inside the bubble, under the influence of the transverse field. Collision ionization injection reduces the influence of the transverse force. Two oppositely propagating ultrashort laser beams with the same parameters were injected transversely, and the lasers were controlled to collide precisely on the axis. The two trigger lasers were linearly polarized along the z-axis, which reduced the transverse modulation of the electrons injected from the trigger laser. The electron beam injection phase is controlled so that it enters the accelerated focusing field quickly after injection to reduce the transverse divergence, and finally, electrons with an emittance of nm rad level are obtained.
During acceleration in the wakefield, the injected electron beam is not only affected by the longitudinal acceleration field, but also by the transverse focusing and defocusing field. Matching the particle beam to the focusing and defocusing field of the plasma accelerator is critical for maintaining beam quality. While accelerated in the longitudinal direction, the electron beam also oscillates continuously in the transverse direction, and its oscillation frequency is related to the energy and longitudinal phase of the electron beam. Therefore, a strong coupling exists between the longitudinal and transverse directions of the electron beam during wakefield acceleration. This strong coupling causes the oscillation phase of the electron to change with the longitudinal position, eventually leading to complete decoherence. Phase decoherence is an important factor leading to an increase in electron beam emittance during the acceleration process. Generally, these effects are caused by a non-zero energy spread or non-zero pulse length. It is necessary to construct a specific plasma profile distribution and control the evolution of the laser pulse to control the electron beam motion in the wakefield, such that the electron beam phase space matches the wakefield and suppresses the electron beam emittance growth [30].
According to the Mathieu–Hill equation and the relationship between the Courant–Snyder parameter states, the evolution of the beta function in a line-focusing system follows a function. For a narrow electron beam () in LWFA, the electrons can be approximately subjected to a linear transverse force [31,32,33], as follows:
where e and m represent the charge and mass of the electron, respectively. represents the Lorentz factor, c represents the speed of light in a vacuum, and represents the transverse electric field. For a given K, the evolution of the beta function can be expressed as [30]
where denotes the initial beta function. The formula shows that the beta function of the electron beam in the normally focused channel oscillates between and . When the initial beta function value is K−1/2, the electron beam maintains the transverse size, which can be called a matched electron beam. Similarly, for a given electron beam envelope parameter, K can be tuned to match the electron beam by constructing a specific plasma density profile. Matching the electron beam to the mean parameter K slows the betatron oscillations, which also provides guidance for controlling emittance growth. When the single stage is extended to multiple stages, the electron beam parameters can be adjusted to match the channel and effectively avoid the increase in emittance caused by the nonlinear coupling of lateral and longitudinal motions. In both theory and simulation [30,34,35,36,37], the matched parameters can control the increase in electron beam emittance at the level of several percent.
Similar to bubbles, the energy spread also results in an increase in the electron beam emittance in the free space. When an electron beam passes through a magnet and is subjected to a magnetic field with the same gradient, electrons with different energies are focused and defocused. The energy spread causes a phase difference in the electron beam transverse phase space, as shown in Figure 1b, which is also the main reason that the projected emittance is greater than the slice emittance. Increasing the transport distance or electron beam energy spread exacerbates the increase in emittance until saturation. Therefore, it is necessary to design a compact beam transport line and strictly compress the electron beam energy spread [38,39,40]. The scheme of controlling electrons to achieve a low energy spread is described below.
3. Energy Spread
The final energy spread of the electron beam is affected by the initial energy spread and inhomogeneous acceleration, which originate from the inhomogeneity of the longitudinal acceleration field, beam loading, and phase slippage caused by the betatron oscillations. The electrons injected at different times are affected by the acceleration field for different durations, which means that the electrons in the head (those injected first) have higher energy. Therefore, the electron beam initially appears as a negative chirp. Continuous electron beam injection results in increased initial energy spread. Figure 2 shows a snapshot of a bubble and the on-axis longitudinal field (white line) in the PIC simulation. During the acceleration process, owing to the nonuniform longitudinal acceleration field, the energy gain of the electrons in the tail of the beam gradually becomes higher than that at the head, and the negative chirp evolves into a positive chirp. Therefore, energy spread compression is achieved by reducing the injection duration, as well as weakening the inhomogeneity of the acceleration field and chirp compensation in the injection and acceleration stages, respectively. The injection process plays an important role in the electron beam quality. Several methods, including ionization [41,42], density gradient, and collision, are used to trigger injection. There are also some improved injection methods, such as utilizing Tesla-scale magnetic fields to control self-injection and an evolved electron beam to drive plasma waves to achieve injection control. The following discussion will take an example and examine its influence on the electron beam energy spread during the injection process.
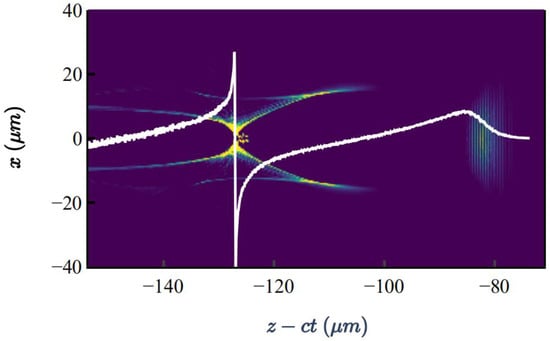
Figure 2.
Snapshot of a bubble and the on-axis longitudinal field lineouts (white line) in the PIC simulation.
Density gradient injection is a controllable injection scheme that was first proposed by Bulanov [43]. He studied the wave breaking phenomenon generated in the region of a slow-varying plasma density down ramp and then explored the conditions of the injection. Subsequently, Suk et al. [44] conducted a theoretical study of the case of discontinuously varying densities. The phase velocity of the wakefield decreased as the wavelength of the plasma wave in this area increased. The magnitude of the reduction was proportional to the distance of the wakefield from the driving laser and the gradient of the density-down ramp. Electrons are injected when the wakefield phase velocity is smaller than the electron velocity.
In 2008, Geddes et al. [45] obtained low-energy electron beams with only 0.17 MeV energy spread based on density gradient injection. In 2010, Faure et al. also conducted experiments on density-gradient injection [46]. They used an inclined auxiliary laser beam to generate a plasma channel at an angle of 135° corresponding to the axis. The inclined channel generates a relatively large density gradient, and the wakefield continues to accelerate the injected electrons after the wave breaks. In 2013, Wang et al. adopted a cascade acceleration scheme based on gradient injection [47]. Active control of the density gradient is achieved by changing the distance between the two gas cells or the back-pressure difference of the gas. The absolute energy spread introduced by the injection stage can be effectively controlled in the experiment by changing the plasma density of the second stage to lower than the conditions required for electron injection. As the plasma density of the accelerating stage is further reduced, the size of the bubble becomes significantly larger, causing the electrons initially injected in the second bubble to slip into the first bubble. Through density control, the electron beam can be slipped to a better matched phase in the first bubble and finally accelerated to 0.5 GeV, resulting in a significantly reduced energy spread of approximately 3%.
The previously discussed methods are used to construct density gradients artificially, by means of auxiliary lasers or the injection of gases with different back pressures. However, these approaches make it difficult to construct plasma distributions with high-density gradients. During the interaction between the laser and gas, the evolution of the normalized intensity of the laser also affects the size of the bubble and phase velocity of the wakefield, owing to the effects of self-focusing and defocusing. When the plasma profile density gradient was small, the wavelength change in the plasma wave was less affected by the density. Compared to the influence of the evolution of the laser, the influence of the density gradient on the wakefield phase velocity is not dominant. Therefore, it is difficult to achieve low energy spread and high stability injection by relying only on the density gradient constructed in this manner.
To improve the controllability of the electron quality, several research groups have successively improved the method to construct specific plasma distributions. When supersonic gas was sprayed on a target, a shock wave with a density gradient was formed in the local area. Based on this principle, different structural targets, such as blades, capillaries, and steel wires [48,49,50,51], were used as nozzles to construct matching density distributions. Similarly, the dual-nozzle structure [52] can also be used to construct a plasma density falling edge. The upper and lower nozzles were used for gas injection. A high-density area with an adjustable width can be generated by adjusting the relative horizontal positions of the two nozzles. The second self-injection of the electron beam was suppressed by the density peak, and the injection cut-off was effectively realized. In addition, the electron beam passes through a wakefield with a negative energy chirp slope at the density down ramp, that is, the low-energy electrons at the tail of the beam obtain a higher energy gain, and the high-energy electrons at the head obtain a lower energy gain. This is beneficial for the energy-spread compression of the electron beam in the bubble. In 2016, Wang et al. used a double-nozzle structure to obtain a 530–580 MeV electron beam with an energy spread of less than 1% [12]. It can be found that the energy spread of the electron beam obtained by LWFA based on gradient injection is mostly at the level of several percent, which cannot meet the relative energy spread at the level of several thousandths required by the tabletop FEL. In the final analysis, the density gradient injection was still a wave break injection [29,53,54], but the injection threshold reduction was controlled. Therefore, the density gradient injection still has the disadvantage of wave-breaking injection, which depends on the nonlinear effect of the wakefield.
As mentioned previously, an electron beam with an energy spread of ~1% can be experimentally obtained using the cascade acceleration scheme. Furthermore, the construction of a multistage plasma distribution system to achieve further compression of the energy spread through electron beam length compression has also been proposed. However, cascade acceleration is usually complex to operate and requires high stability of each part; thus, it is challenging to stably generate electron beams with ultra-low energy spread. The increase in the energy spread in the acceleration stage was mainly affected by the inhomogeneity of the longitudinal acceleration field (usually a positive chirp). We can construct an appropriate non-uniform acceleration field (usually a negative chirp) to compress the electron energy spread and solve this problem. In recent years, researchers of conventional accelerators have designed special dechirp devices to remove energy chirps [55,56]. Such devices can make the electron beam energy spread to a level of a few thousandths. However, the dechirp devices used in conventional accelerators have a low intensity, which is not suitable for high-energy chirped electron beams generated in LWFA.
Drawing on the chirp compensation mechanism of conventional accelerators, the concept of plasma dechirp device was first proposed in 2017. The basic principle is to use the wakefield generated by an electron beam in the plasma (particle wakefield acceleration, PWFA) to remove the energy chirp [57,58]. The longitudinal field excited in the plasma by a positive-energy chirp electron beam causes the tail to decelerate more than the head. After a suitable distance, the energy chirp of the electron beam is removed. In 2019, D’Arcy et al., Shpakov et al. and Wu et al. each experimentally verified the concept of a plasma dechirper [59,60,61].
In addition to the external plasma dechirp device in the beamline, the wakefield acceleration process uses a similar technology called energy chirp compensation [20]. The difference between them lies in the generation of the dechirp field and interaction process. Relativistic self-focusing plays an important role in the interaction between the laser and plasma. When the laser power is sufficiently high, there will be enough critical energy for the laser to self-focus. Usually, the laser self-focusing process can be used to extend the laser transport distance and control the electron beam injection; however, the laser defocusing process is rarely considered. Experiments and simulations have shown that the laser defocusing process can degenerate the wakefield from a strong nonlinear state to a weak nonlinear state under the matched parameters. In this process, the acceleration field at the position where the injected electrons are located changes from a positive slope to a negative slope, which effectively removes the positive chirp of the electron beam. By introducing a density spike at a suitable position, Dopp et al. [62] achieved electron beam energy spread compression from tens of percent to less than ten percent. In 2021, Ke et al. used shock injection to generate 780–840 MeV, 2.4‰–4.1‰ energy spread high-quality electron beams in the experiment [63], as shown in Table 1. A suitable plasma profile distribution was constructed by adjusting the relative positions of the nozzles, such that the electron beam could inject the bubble at an appropriate position before laser defocusing. When the laser is defocused, the electron beam can interact with the formed dechirping field and carry out an effective dechirping process. The effect of plasma density on laser self-focusing and defocusing was used to control the acceleration field, and a high-energy electron beam with ultralow energy spread was obtained.

Table 1.
Summary of parameters from different laboratories, as discussed in the text.
4. Current
Current, the ratio of electron beam charge to pulse length, is usually at the level of KA in LWFA (it deals with the peak current). From the definition, the electron beam current can be increased by increasing the electron beam charge or compressing the pulse length [64]. The number of injected electrons in the bubble is positively correlated with the laser intensity, according to the model established by Gordienko et al. [65,66]. However, realizing a large amount of charge does not only guarantee an electron beam with high current. More importantly, it increases the amount of charge injected per unit time. For the qualitative analysis of the injection process, the phase velocity of the plasma wave in the bubble can be expressed as [67]
where is the laser group velocity, is the longitudinal position in the co-moving coordinate system, and is the plasma density longitudinal distribution. The formula shows that when has a down ramp in the longitudinal direction, the relativistic factor of the plasma wave can be effectively reduced. The wave break threshold decreases as the plasma wave phase velocity decreases, making it easier for electrons to inject. With the further increase in the density gradient, the wave break threshold decreases more, which is beneficial to realize the high current of the electron beam. However, a decrease in plasma density means a decrease in the number of cardinality that can be injected with electrons, which suppresses the electron beam current. Therefore, it is necessary to quantitatively analyze [68,69] and optimize the density gradient to improve the electron beam current by particle-in-cell simulation.
In the experiments, the current is difficult to increase, since the charge scales with the pulse length under the same conditions. Continued injection results in a high-charge electron beam accompanied by an increase in the pulse length. This will result in a more significant difference in energy gain between the head and tail of the electron beam, which increases the beam energy spread. Focused adjustment of the electron beam quality is necessary for different radiation source requirements. As required for high-gain FELs, its Pierce parameter should be greater than the relative energy spread of the electron beam. Figure 3 shows the Pierce parameters for different currents and transverse sizes based on specific electron beam and undulator parameters. Taking the transverse size as 40 μm, when the current increases from 5 kA to 15 kA, the Pierce parameter (upper limit of relative energy spread) only increases from 0.4% to less than 0.6%, whose increase is significantly smaller than that of the current. Wang et al. presented an experimental demonstration of undulator radiation amplification in the exponential-gain regime [70]. The accelerated electron beam typically has a peak energy of ~490 MeV, with the energy spread of approximately 0.5%, an average integrated charge of around 30 pC, and r.m.s. divergence of approximately 0.2 mrad. Simulations show that the electron beam current is approximately 5 kA. Although no emphasis has been placed on optimizing the current, experimentally, the per-mille-level relative energy spread enables electrons to achieve 100-fold gain in the third undulator. Therefore, compared with high current, low energy spread plays a dominant role. For those with less demanding electron beam energy spread, such as betatron radiation, an increase in current intensity or charge is beneficial to obtain a higher photon number [71,72].
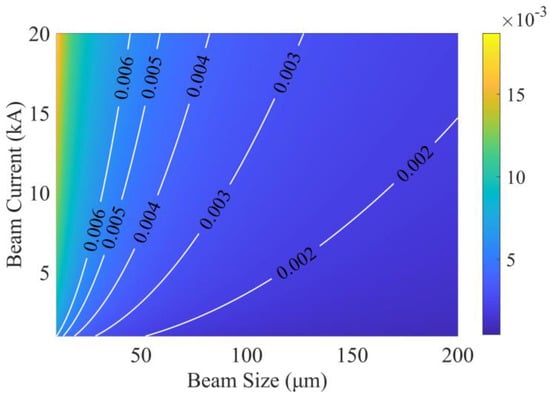
Figure 3.
The Pierce parameters for different currents and transverse sizes.
5. Conclusions
With the continuous efforts of various research teams, LWFA has developed rapidly in the past ten years, and the electron beam quality has gradually improved. The brightness of the electron beam and radiation source based on LWFA have also been improved [63,73,74,75,76]. The tabletop FEL [70,77,78] based on LWFA was verified experimentally. Such proof-of-principle experiments will expedite the development of future compact facilities with broad applications. However, owing to limited high-field laser technology developments, instability in laser and plasma interactions, and acceleration field inhomogeneities, the current electron beams cannot meet the application requirements in terms of performance and repetition frequency. More theoretical and experimental research is necessary, including the exploration of new injection methods, high-resolution diagnostic schemes, ultralong low-density plasma channel development, and machine learning to promote electron beam performance optimization. It is necessary to continuously optimize the electron beam quality to meet its application requirements for various tabletop radiation sources [74,79,80,81], so that the LWFA can be stably available and realize miniaturization acceleration. This review briefly examines recent LWFA-based electron beam quality optimization schemes, aiming to provide a complete and clear understanding of LWFA research, while promoting cooperation and exchanges in interdisciplinary fields.
Author Contributions
Conceptualization, K.J. and K.F.; Methodology, K.J., W.W. and K.F.; Validation, W.W.; Investigation, K.J.; Software, K.J. and K.F.; Funding acquisition, W.W. and R.L.; Writing—original draft preparation, K.J.; Writing—review and editing, W.W. and K.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant nos. 11991072 and 11875065), the State Key Laboratory Program of the Chinese Ministry of Science and Technology and CAS Youth Innovation Promotion Association (Y201952) and the National Natural Science Foundation of China (grant nos. 12105353).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tajima, T.; Dawson, J.M. Laser Electron Accelerator. Phys. Rev. Lett. 1979, 43, 267. [Google Scholar] [CrossRef]
- Tajima, T.; Nakajima, K.; Mourou, G. Laser acceleration. Riv. Nuovo Cim. 2017, 40, 33–133. [Google Scholar] [CrossRef]
- Emma, C.; Van Tilborg, J.; Assmann, R.; Barber, S.; Cianchi, A.; Corde, S.; Couprie, M.E.; D’Arcy, R.; Ferrario, M.; Habib, A.F.; et al. Free electron lasers driven by plasma accelerators: Status and near-term prospects. High Power Laser Sci. Eng. 2021, 9, e57. [Google Scholar] [CrossRef]
- Huang, Z.R.; Ding, Y.T.; Schroeder, C.B. Compact X-ray Free-Electron Laser from a Laser-Plasma Accelerator Using a Transverse-Gradient Undulator. Phys. Rev. Lett. 2012, 109, 204801. [Google Scholar] [CrossRef] [PubMed]
- Pellegrini, C.; Marinelli, A.; Reiche, S. The physics of X-ray free-electron lasers. Rev. Mod. Phys. 2016, 88, 55. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Faure, J.; Glinec, Y.; Pukhov, A.; Kiselev, S.; Gordienko, S.; Lefebvre, E.; Rousseau, J.P.; Burgy, F.; Malka, V. A laser-plasma accelerator producing monoenergetic electron beams. Nature 2004, 431, 541–544. [Google Scholar] [CrossRef]
- Geddes, C.G.R.; Toth, C.; van Tilborg, J.; Esarey, E.; Schroeder, C.B.; Bruhwiler, D.; Nieter, C.; Cary, J.; Leemans, W.P. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 2004, 431, 538–541. [Google Scholar] [CrossRef]
- Mangles, S.P.D.; Murphy, C.D.; Najmudin, Z.; Thomas, A.G.R.; Collier, J.L.; Dangor, A.E.; Divall, E.J.; Foster, P.S.; Gallacher, J.G.; Hooker, C.J.; et al. Monoenergetic beams of relativistic electrons from intense laser-plasma interactions. Nature 2004, 431, 535–538. [Google Scholar] [CrossRef]
- Nakajima, K.; Kim, H.T.; Jeong, T.M.; Nam, C.H. Scaling and design of high-energy laser plasma electron acceleration. High Power Laser Sci. Eng. 2015, 3, e10. [Google Scholar] [CrossRef][Green Version]
- Maier, A.R.; Delbos, N.M.; Eichner, T.; Hubner, L.; Jalas, S.; Jeppe, L.; Jolly, S.W.; Kirchen, M.; Leroux, V.; Messner, P.; et al. Decoding Sources of Energy Variability in a Laser-Plasma Accelerator. Phys. Rev. X 2020, 10, 031039. [Google Scholar] [CrossRef]
- Wang, W.T.; Li, W.T.; Liu, J.S.; Zhang, Z.J.; Qi, R.; Yu, C.H.; Liu, J.Q.; Fang, M.; Qin, Z.Y.; Wang, C.; et al. High-Brightness High-Energy Electron Beams from a Laser Wakefield Accelerator via Energy Chirp Control. Phys. Rev. Lett. 2016, 117, 124801. [Google Scholar] [CrossRef] [PubMed]
- Leemans, W.P.; Nagler, B.; Gonsalves, A.J.; Toth, C.; Nakamura, K.; Geddes, C.G.R.; Esarey, E.; Schroeder, C.B.; Hooker, S.M. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2006, 2, 696–699. [Google Scholar] [CrossRef]
- Leemans, W.P.; Gonsalves, A.J.; Mao, H.S.; Nakamura, K.; Benedetti, C.; Schroeder, C.B.; Toth, C.; Daniels, J.; Mittelberger, D.E.; Bulanov, S.S.; et al. Multi-GeV Electron Beams from Capillary-Discharge-Guided Subpetawatt Laser Pulses in the Self-Trapping Regime. Phys. Rev. Lett. 2014, 113, 245002. [Google Scholar] [CrossRef]
- Gonsalves, A.J.; Nakamura, K.; Daniels, J.; Benedetti, C.; Pieronek, C.; de Raadt, T.C.H.; Steinke, S.; Bin, J.H.; Bulanov, S.S.; van Tilborg, J.; et al. Petawatt Laser Guiding and Electron Beam Acceleration to 8 GeV in a Laser-Heated Capillary Discharge Waveguide. Phys. Rev. Lett. 2019, 122, 084801. [Google Scholar] [CrossRef] [PubMed]
- Oubrerie, K.; Leblanc, A.; Kononenko, O.; Lahaye, R.; Andriyash, I.A.; Gautier, J.; Goddet, J.P.; Martelli, L.; Tafzi, A.; Phuoc, K.T.; et al. Controlled acceleration of GeV electron beams in an all-optical plasma waveguide. Light-Sci. Appl. 2022, 11, 180. [Google Scholar] [CrossRef]
- Turner, M.; Gonsalves, A.J.; Bulanov, S.S.; Benedetti, C.; Bobrova, N.A.; Gasilov, V.A.; Sasorov, P.V.; Korn, G.; Nakamura, K.; van Tilborg, J.; et al. Radial density profile and stability of capillary discharge plasma waveguides of lengths up to 40 cm. High Power Laser Sci. Eng. 2021, 9, e17. [Google Scholar] [CrossRef]
- Osterhoff, J.; Popp, A.; Major, Z.; Marx, B.; Rowlands-Rees, T.P.; Fuchs, M.; Geissler, M.; Hoerlein, R.; Hidding, B.; Becker, S.; et al. Generation of stable, low-divergence electron beams by laser-wakefield acceleration in a steady-state-flow gas cell. Phys. Rev. Lett. 2008, 101, 085002. [Google Scholar] [CrossRef]
- Jalas, S.; Kirchen, M.; Messner, P.; Winkler, P.; Hubner, L.; Dirkwinkel, J.; Schnepp, M.; Lehe, R.; Maier, A.R. Bayesian Optimization of a Laser-Plasma Accelerator. Phys. Rev. Lett. 2021, 126, 104801. [Google Scholar] [CrossRef]
- Kirchen, M.; Jalas, S.; Messner, P.; Winkler, P.; Eichner, T.; Hubner, L.; Hulsenbusch, T.; Jeppe, L.; Parikh, T.; Schnepp, M.; et al. Optimal Beam Loading in a Laser-Plasma Accelerator. Phys. Rev. Lett. 2021, 126, 174801. [Google Scholar] [CrossRef]
- Faure, J.; Rechatin, C.; Norlin, A.; Lifschitz, A.; Glinec, Y.; Malka, V. Controlled injection and acceleration of electrons in plasma wakefields by colliding laser pulses. Nature 2006, 444, 737–739. [Google Scholar] [CrossRef]
- Rechatin, C.; Faure, J.; Ben-Ismail, A.; Lim, J.; Fitour, R.; Specka, A.; Videau, H.; Tafzi, A.; Burgy, F.; Malka, V. Controlling the Phase-Space Volume of Injected Electrons in a Laser-Plasma Accelerator. Phys. Rev. Lett. 2009, 102, 164801. [Google Scholar] [CrossRef]
- Oz, E.; Deng, S.; Katsouleas, T.; Muggli, P.; Barnes, C.D.; Blumenfeld, I.; Decker, F.J.; Emma, P.; Hogan, M.J.; Ischebeck, R.; et al. Ionization-induced electron trapping in ultrarelativistic plasma wakes. Phys. Rev. Lett. 2007, 98, 084801. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.L.; Wu, Y.P.; Zhang, C.J.; Li, F.; Wan, Y.; Hua, J.F.; Pai, C.H.; Lu, W.; Yu, P.; Joshi, C.; et al. Low emittance electron beam generation from a laser wakefield accelerator using two laser pulses with different wavelengths. Phys. Rev. Spec. Top.-Accel. Beams 2014, 17, 061301. [Google Scholar] [CrossRef]
- Yu, L.L.; Esarey, E.; Schroeder, C.B.; Vay, J.L.; Benedetti, C.; Geddes, C.G.R.; Chen, M.; Leemans, W.P. Two-Color Laser-Ionization Injection. Phys. Rev. Lett. 2014, 112, 125001. [Google Scholar] [CrossRef] [PubMed]
- Zeng, M.; Chen, M.; Yu, L.L.; Mori, W.B.; Sheng, Z.M.; Hidding, B.; Jaroszynski, D.A.; Zhang, J. Multichromatic Narrow-Energy-Spread Electron Bunches from Laser-Wakefield Acceleration with Dual-Color Lasers. Phys. Rev. Lett. 2015, 114, 084801. [Google Scholar] [CrossRef]
- Di Mitri, S.; Cornacchia, M. Electron beam brightness in linac drivers for free-electron-lasers. Phys. Rep.-Rev. Sec. Phys. Lett. 2014, 539, 1–48. [Google Scholar] [CrossRef]
- Manahan, G.G.; Habib, A.F.; Scherkl, P.; Delinikolas, P.; Beaton, A.; Knetsch, A.; Karger, O.; Wittig, G.; Heinemann, T.; Sheng, Z.M.; et al. Single-stage plasma-based correlated energy spread compensation for ultrahigh 6D brightness electron beams. Nat. Commun. 2017, 8, 15705. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Pegoraro, F.; Pukhov, A.M.; Sakharov, A.S. Transverse-wake wave breaking. Phys. Rev. Lett. 1997, 78, 4205–4208. [Google Scholar] [CrossRef]
- Mehrling, T.; Grebenyuk, J.; Tsung, F.S.; Floettmann, K.; Osterhoff, J. Transverse emittance growth in staged laser-wakefield acceleration. Phys. Rev. Spec. Top.-Accel. Beams 2012, 15, 111303. [Google Scholar] [CrossRef]
- Esarey, E.; Schroeder, C.B.; Leemans, W.P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229–1285. [Google Scholar] [CrossRef]
- Lu, W.; Huang, C.; Zhou, M.; Tzoufras, M.; Tsung, F.S.; Mori, W.B.; Katsouleas, T. A nonlinear theory for multidimensional relativistic plasma wave wakefields. Phys. Plasmas 2006, 13, 056709. [Google Scholar] [CrossRef]
- Rosenzweig, J.B.; Breizman, B.; Katsouleas, T.; Su, J.J. Acceleration and focusing of electrons in 2-dimensional nonlinear plasma wake fields. Phys. Rev. A 1991, 44, R6189–R6192. [Google Scholar] [CrossRef] [PubMed]
- Migliorati, M.; Bacci, A.; Benedetti, C.; Chiadroni, E.; Ferrario, M.; Mostacci, A.; Palumbo, L.; Rossi, A.R.; Serafini, L.; Antici, P. Intrinsic normalized emittance growth in laser-driven electron accelerators. Phys. Rev. Spec. Top.-Accel. Beams 2013, 16, 011302. [Google Scholar] [CrossRef]
- Li, X.K.; Chance, A.; Nghiem, P.A.P. Preserving emittance by matching out and matching in plasma wakefield acceleration stage. Phys. Rev. Accel. Beams 2019, 22, 021304. [Google Scholar] [CrossRef]
- Floettmann, K. Adiabatic matching section for plasma accelerated beams. Phys. Rev. Spec. Top.-Accel. Beams 2014, 17, 054402. [Google Scholar] [CrossRef]
- Dornmair, I.; Floettmann, K.; Maier, A.R. Emittance conservation by tailored focusing profiles in a plasma accelerator. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 041302. [Google Scholar] [CrossRef]
- Loulergue, A.; Labat, M.; Evain, C.; Benabderrahmane, C.; Malka, V.; Couprie, M.E. Beam manipulation for compact laser wakefield accelerator based free-electron lasers. New J. Phys. 2015, 17, 023028. [Google Scholar] [CrossRef]
- Pousa, A.F.; de la Ossa, A.M.; Brinkmann, R.; Assmann, R.W. Compact Multistage Plasma-Based Accelerator Design for Correlated Energy Spread Compensation. Phys. Rev. Lett. 2019, 123, 054801. [Google Scholar] [CrossRef]
- Van Tilborg, J.; Steinke, S.; Geddes, C.G.R.; Matlis, N.H.; Shaw, B.H.; Gonsalves, A.J.; Huijts, J.V.; Nakamura, K.; Daniels, J.; Schroeder, C.B.; et al. Active Plasma Lensing for Relativistic Laser-Plasma-Accelerated Electron Beams. Phys. Rev. Lett. 2015, 115, 184802. [Google Scholar] [CrossRef]
- Hafz, N.A.M.; Li, S.; Li, G.Y.; Mirzaie, M.; Zeng, M.; Zhang, J. Generation of high-quality electron beams by ionization injection in a single acceleration stage. High Power Laser Sci. Eng. 2016, 4, e24. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.F.; Wang, J.G.; Li, D.Z.; Zhu, C.Q.; Tan, J.H.; Geng, X.T.; Liu, F.; Chen, L.M. Optical control of transverse motion of ionization injected electrons in a laser plasma accelerator. High Power Laser Sci. Eng. 2021, 9, e5. [Google Scholar] [CrossRef]
- Bulanov, S.; Naumova, N.; Pegoraro, F.; Sakai, J. Particle injection into the wave acceleration phase due to nonlinear wake wave breaking. Phys. Rev. E 1998, 58, R5257–R5260. [Google Scholar] [CrossRef]
- Suk, H.; Barov, N.; Rosenzweig, J.B.; Esarey, E. Plasma electron trapping and acceleration in a plasma wake field using a density transition. Phys. Rev. Lett. 2001, 86, 1011–1014. [Google Scholar] [CrossRef] [PubMed]
- Geddes, C.G.R.; Nakamura, K.; Plateau, G.R.; Toth, C.; Cormier-Michel, E.; Esarey, E.; Schroeder, C.B.; Cary, J.R.; Leemans, W.P. Plasma-density-gradient injection of low absolute-momentum-spread electron bunches. Phys. Rev. Lett. 2008, 100, 215004. [Google Scholar] [CrossRef] [PubMed]
- Faure, J.; Rechatin, C.; Lundh, O.; Ammoura, L.; Malka, V. Injection and acceleration of quasimonoenergetic relativistic electron beams using density gradients at the edges of a plasma channel. Phys. Plasmas 2010, 17, 083107. [Google Scholar] [CrossRef]
- Wang, W.T.; Li, W.T.; Liu, J.S.; Wang, C.; Chen, Q.; Zhang, Z.J.; Qi, R.; Leng, Y.X.; Liang, X.Y.; Liu, Y.Q.; et al. Control of seeding phase for a cascaded laser wakefield accelerator with gradient injection. Appl. Phys. Lett. 2013, 103, 243501. [Google Scholar] [CrossRef]
- Schmid, K.; Buck, A.; Sears, C.M.S.; Mikhailova, J.M.; Tautz, R.; Herrmann, D.; Geissler, M.; Krausz, F.; Veisz, L. Density-transition based electron injector for laser driven wakefield accelerators. Phys. Rev. Spec. Top.-Accel. Beams 2010, 13, 091301. [Google Scholar] [CrossRef]
- Gonsalves, A.J.; Nakamura, K.; Lin, C.; Panasenko, D.; Shiraishi, S.; Sokollik, T.; Benedetti, C.; Schroeder, C.B.; Geddes, C.G.R.; van Tilborg, J.; et al. Tunable laser plasma accelerator based on longitudinal density tailoring. Nat. Phys. 2011, 7, 862–866. [Google Scholar] [CrossRef]
- Buck, A.; Wenz, J.; Xu, J.; Khrennikov, K.; Schmid, K.; Heigoldt, M.; Mikhailova, J.M.; Geissler, M.; Shen, B.; Krausz, F.; et al. Shock-Front Injector for High-Quality Laser-Plasma Acceleration. Phys. Rev. Lett. 2013, 110, 185006. [Google Scholar] [CrossRef]
- Burza, M.; Gonoskov, A.; Svensson, K.; Wojda, F.; Persson, A.; Hansson, M.; Genoud, G.; Marklund, M.; Wahlstrom, C.G.; Lundh, O. Laser wakefield acceleration using wire produced double density ramps. Phys. Rev. Spec. Top.-Accel. Beams 2013, 16, 011301. [Google Scholar] [CrossRef]
- Hansson, M.; Aurand, B.; Davoine, X.; Ekerfelt, H.; Svensson, K.; Persson, A.; Wahlstrom, C.G.; Lundh, O. Down-ramp injection and independently controlled acceleration of electrons in a tailored laser wakefield accelerator. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 071303. [Google Scholar] [CrossRef]
- Lu, W.; Huang, C.; Zhou, M.; Mori, W.B.; Katsouleas, T. Nonlinear theory for relativistic plasma wakefields in the blowout regime. Phys. Rev. Lett. 2006, 96, 165002. [Google Scholar] [CrossRef] [PubMed]
- Corde, S.; Thaury, C.; Lifschitz, A.; Lambert, G.; Phuoc, K.T.; Davoine, X.; Lehe, R.; Douillet, D.; Rousse, A.; Malka, V. Observation of longitudinal and transverse self-injections in laser-plasma accelerators. Nat. Commun. 2013, 4, 1501. [Google Scholar] [CrossRef] [PubMed]
- Antipov, S.; Baturin, S.; Jing, C.; Fedurin, M.; Kanareykin, A.; Swinson, C.; Schoessow, P.; Gai, W.; Zholents, A. Experimental Demonstration of Energy-Chirp Compensation by a Tunable Dielectric-Based Structure. Phys. Rev. Lett. 2014, 112, 114801. [Google Scholar] [CrossRef] [PubMed]
- Emma, P.; Venturini, M.; Bane, K.L.F.; Stupakov, G.; Kang, H.S.; Chae, M.S.; Hong, J.; Min, C.K.; Yang, H.; Ha, T.; et al. Experimental Demonstration of Energy-Chirp Control in Relativistic Electron Bunches Using a Corrugated Pipe. Phys. Rev. Lett. 2014, 112, 034801. [Google Scholar] [CrossRef]
- Chen, P.; Dawson, J.M.; Huff, R.W.; Katsouleas, T. Acceleration of electrons by the interaction of a bunched electron-beam with a plasma. Phys. Rev. Lett. 1985, 54, 693–696. [Google Scholar] [CrossRef]
- Litos, M.; Adli, E.; An, W.; Clarke, C.I.; Clayton, C.E.; Corde, S.; Delahaye, J.P.; England, R.J.; Fisher, A.S.; Frederico, J.; et al. High-efficiency acceleration of an electron beam in a plasma wakefield accelerator. Nature 2014, 515, 92–95. [Google Scholar] [CrossRef]
- D’Arcy, R.; Wesch, S.; Aschikhin, A.; Bohlen, S.; Behrens, C.; Garland, M.J.; Goldberg, L.; Gonzalez, P.; Knetsch, A.; Libov, V.; et al. Tunable Plasma-Based Energy Dechirper. Phys. Rev. Lett. 2019, 122, 034801. [Google Scholar] [CrossRef]
- Shpakov, V.; Anania, M.P.; Bellaveglia, M.; Biagioni, A.; Bisesto, F.; Cardelli, F.; Cesarini, M.; Chiadroni, E.; Cianchi, A.; Costa, G.; et al. Longitudinal Phase-Space Manipulation with Beam-Driven Plasma Wakefields. Phys. Rev. Lett. 2019, 122, 114801. [Google Scholar] [CrossRef]
- Wu, Y.P.; Hua, J.F.; Zhou, Z.; Zhang, J.; Liu, S.; Peng, B.; Fang, Y.; Nie, Z.; Ning, X.N.; Pai, C.H.; et al. Phase Space Dynamics of a Plasma Wakefield Dechirper for Energy Spread Reduction. Phys. Rev. Lett. 2019, 122, 204804. [Google Scholar] [CrossRef] [PubMed]
- Dopp, A.; Thaury, C.; Guillaume, E.; Massimo, F.; Lifschitz, A.; Andriyash, I.; Goddet, J.P.; Tazfi, A.; Phuoc, K.T.; Malka, V. Energy-Chirp Compensation in a Laser Wakefield Accelerator. Phys. Rev. Lett. 2018, 121, 074802. [Google Scholar] [CrossRef] [PubMed]
- Ke, L.T.; Feng, K.; Wang, W.T.; Qin, Z.Y.; Yu, C.H.; Wu, Y.; Chen, Y.; Qi, R.; Zhang, Z.J.; Xu, Y.; et al. Near-GeV Electron Beams at a Few Per-Mille Level from a Laser Wakefield Accelerator via Density-Tailored Plasma. Phys. Rev. Lett. 2021, 126, 214801. [Google Scholar] [CrossRef] [PubMed]
- Gotzfried, J.; Dopp, A.; Gilljohann, M.F.; Foerster, F.M.; Ding, H.; Schindler, S.; Schilling, G.; Buck, A.; Veisz, L.; Karsch, S. Physics of High-Charge Electron Beams in Laser-Plasma Wakefields. Phys. Rev. X 2020, 10, 041015. [Google Scholar] [CrossRef]
- Gordienko, S.; Pukhov, A. Scalings for ultrarelativistic laser plasmas and quasimonoenergetic electrons. Phys. Plasmas 2005, 12, 3109. [Google Scholar] [CrossRef]
- Lu, W.; Tzoufras, M.; Joshi, C.; Tsung, F.S.; Mori, W.B.; Vieira, J.; Fonseca, R.A.; Silva, L.O. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys. Rev. Spec. Top.-Accel. Beams 2007, 10, 061301. [Google Scholar] [CrossRef]
- Kuschel, S.; Schwab, M.B.; Yeung, M.; Hollatz, D.; Seidel, A.; Ziegler, W.; Savert, A.; Kaluza, M.C.; Zepf, M. Controlling the Self-Injection Threshold in Laser Wakefield Accelerators. Phys. Rev. Lett. 2018, 121, 154801. [Google Scholar] [CrossRef]
- Li, Y.F.; Li, D.Z.; Huang, K.; Tao, M.Z.; Li, M.H.; Zhao, J.R.; Ma, Y.; Guo, X.; Wang, J.G.; Chen, M.; et al. Generation of 20 kA electron beam from a laser wakefield accelerator. Phys. Plasmas 2017, 24, 023108. [Google Scholar] [CrossRef]
- Couperus, J.P.; Pausch, R.; Kohler, A.; Zarini, O.; Kramer, J.M.; Garten, M.; Huebl, A.; Gebhardt, R.; Helbig, U.; Bock, S.; et al. Demonstration of a beam loaded nanocoulombclass laser wakefield accelerator. Nat. Commun. 2017, 8, 487. [Google Scholar] [CrossRef]
- Wang, W.T.; Feng, K.; Ke, L.T.; Yu, C.H.; Xu, Y.; Qi, R.; Chen, Y.; Qin, Z.Y.; Zhang, Z.J.; Fang, M.; et al. Free-electron lasing at 27 nanometres based on a laser wakefield accelerator. Nature 2021, 595, 516–520. [Google Scholar] [CrossRef]
- Rousse, A.; Phuoc, K.T.; Shah, R.; Pukhov, A.; Lefebvre, E.; Malka, V.; Kiselev, S.; Burgy, F.; Rousseau, J.P.; Umstadter, D.; et al. Production of a keV X-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys. Rev. Lett. 2004, 93, 135005. [Google Scholar] [CrossRef] [PubMed]
- Corde, S.; Phuoc, K.T.; Lambert, G.; Fitour, R.; Malka, V.; Rousse, A.; Beck, A.; Lefebvre, E. Femtosecond X rays from laser-plasma accelerators. Rev. Mod. Phys. 2013, 85, 1–48. [Google Scholar] [CrossRef]
- Yu, C.H.; Qi, R.; Wang, W.T.; Liu, J.S.; Li, W.T.; Wang, C.; Zhang, Z.J.; Liu, J.Q.; Qin, Z.Y.; Fang, M.; et al. Ultrahigh brilliance quasi-monochromatic MeV gamma-rays based on self-synchronized all-optical Compton scattering. Sci. Rep. 2016, 6, 29518. [Google Scholar] [CrossRef] [PubMed]
- Phuoc, K.T.; Corde, S.; Thaury, C.; Malka, V.; Tafzi, A.; Goddet, J.P.; Shah, R.C.; Sebban, S.; Rousse, A. All-optical Compton gamma-ray source. Nat. Photonics 2012, 6, 308–311. [Google Scholar] [CrossRef]
- Dopp, A.; Mahieu, B.; Lifschitz, A.; Thaury, C.; Doche, A.; Guillaume, E.; Grittani, G.; Lundh, O.; Hansson, M.; Gautier, J.; et al. Stable femtosecond X-rays with tunable polarization from a laser-driven accelerator. Light-Sci. Appl. 2017, 6, e17086. [Google Scholar] [CrossRef]
- Wenz, J.; Dopp, A.; Khrennikov, K.; Schindler, S.; Gilljohann, M.F.; Ding, H.; Gotzfried, J.; Buck, A.; Xu, J.; Heigoldt, M.; et al. Dual-energy electron beams from a compact laser-driven accelerator. Nat. Photonics 2019, 13, 263–269. [Google Scholar] [CrossRef]
- Nalkajima, K. Towards a table-top free-electron laser. Nat. Phys. 2008, 4, 92–93. [Google Scholar] [CrossRef]
- Pompili, R.; Alesini, D.; Anania, M.P.; Arjmand, S.; Behtouei, M.; Bellaveglia, M.; Biagioni, A.; Buonomo, B.; Cardelli, F.; Carpanese, M.; et al. Free-electron lasing with compact beam-driven plasma wakefield accelerator. Nature 2022, 605, 659–662. [Google Scholar] [CrossRef]
- Sarri, G.; Corvan, D.J.; Schumaker, W.; Cole, J.M.; Di Piazza, A.; Ahmed, H.; Harvey, C.; Keitel, C.H.; Krushelnick, K.; Mangles, S.P.D.; et al. Ultrahigh Brilliance Multi-MeV gamma-Ray Beams from Nonlinear Relativistic Thomson Scattering. Phys. Rev. Lett. 2014, 113, 224801. [Google Scholar] [CrossRef]
- Schlenvoigt, H.P.; Haupt, K.; Debus, A.; Budde, F.; Jackel, O.; Pfotenhauer, S.; Schwoerer, H.; Rohwer, E.; Gallacher, J.G.; Brunetti, E.; et al. A compact synchrotron radiation source driven by a laser-plasma wakefield accelerator. Nat. Phys. 2008, 4, 130–133. [Google Scholar] [CrossRef]
- Svensson, J.B.; Guenot, D.; Ferri, J.; Ekerfelt, H.; Gonzalez, I.G.; Persson, A.; Svendsen, K.; Veisz, L.; Lundh, O. Low-divergence femtosecond X-ray pulses from a passive plasma lens. Nat. Phys. 2021, 17, 639–645. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).