Sensing by Dynamics of Lasers with External Optical Feedback: A Review
Abstract
1. Introduction
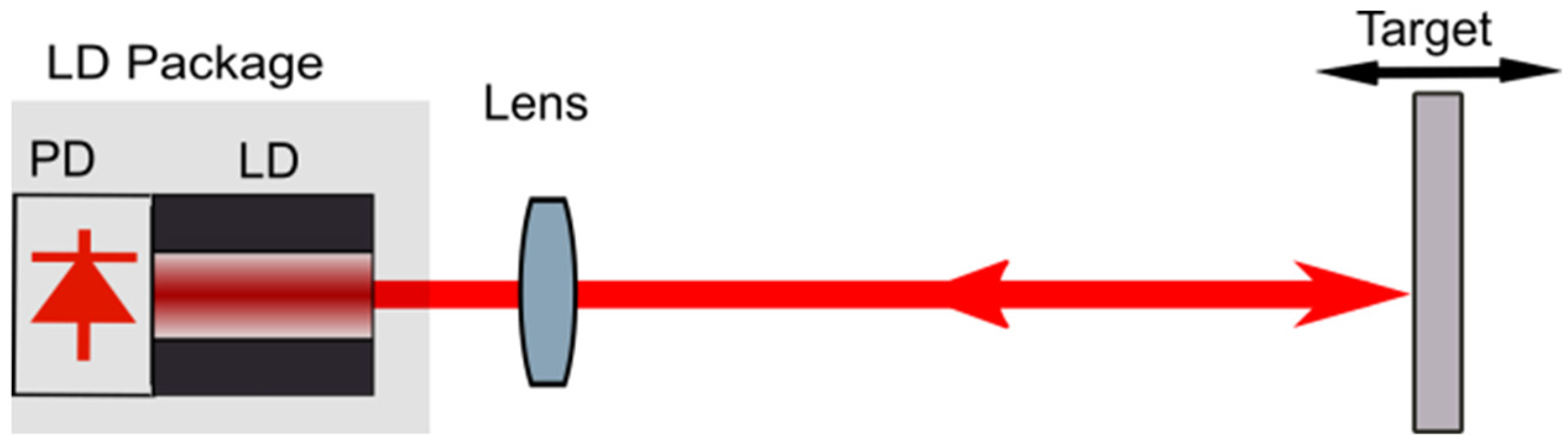
2. Operating Principle
3. Sensing by the Dynamics of Lasers with EOF
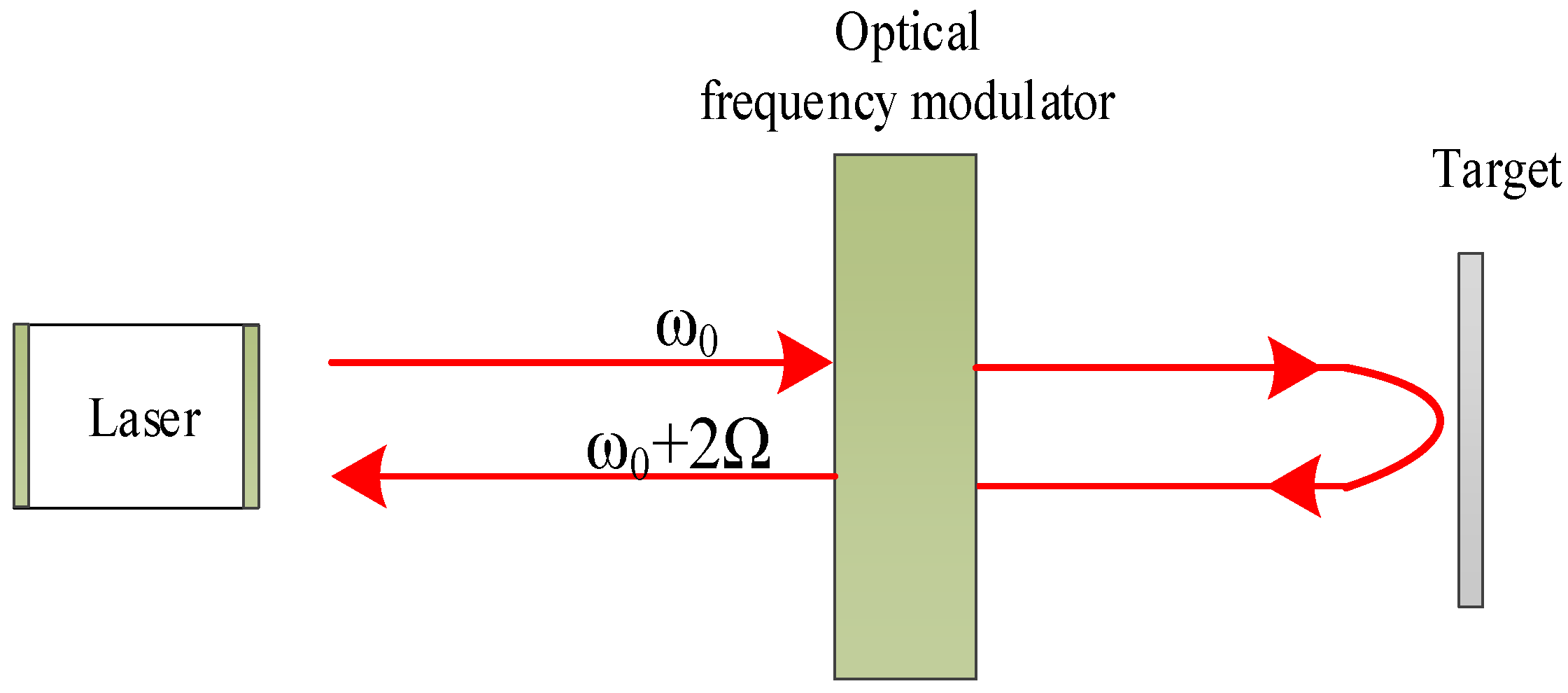
3.1. Sensing by Frequency-Shifted Optical Feedback
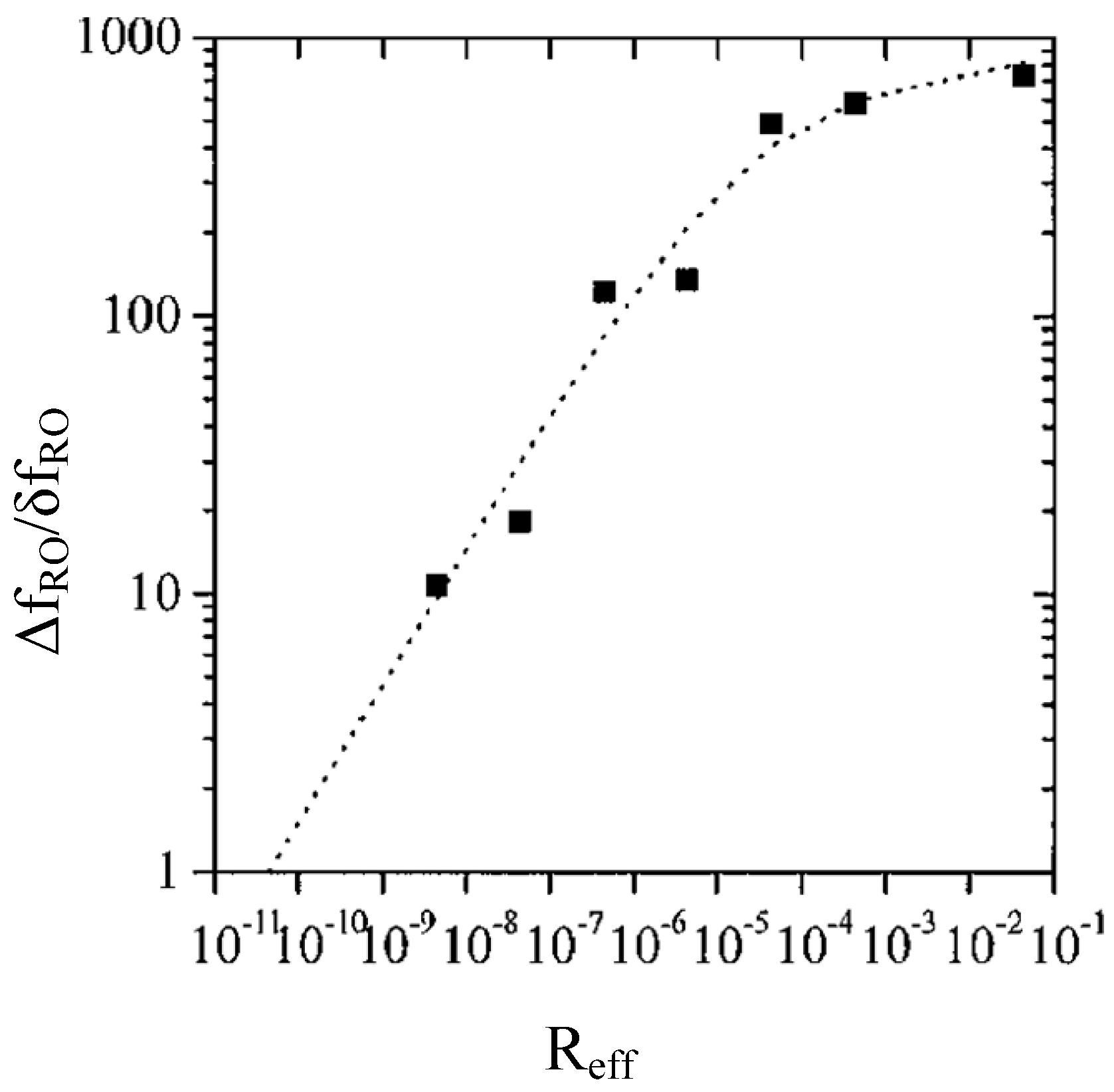
3.2. Sensing by Relaxation Oscillation Frequency
3.3. Sensing by Dynamics in SMI Signals
3.4. Sensing by Laser Optical Chaos
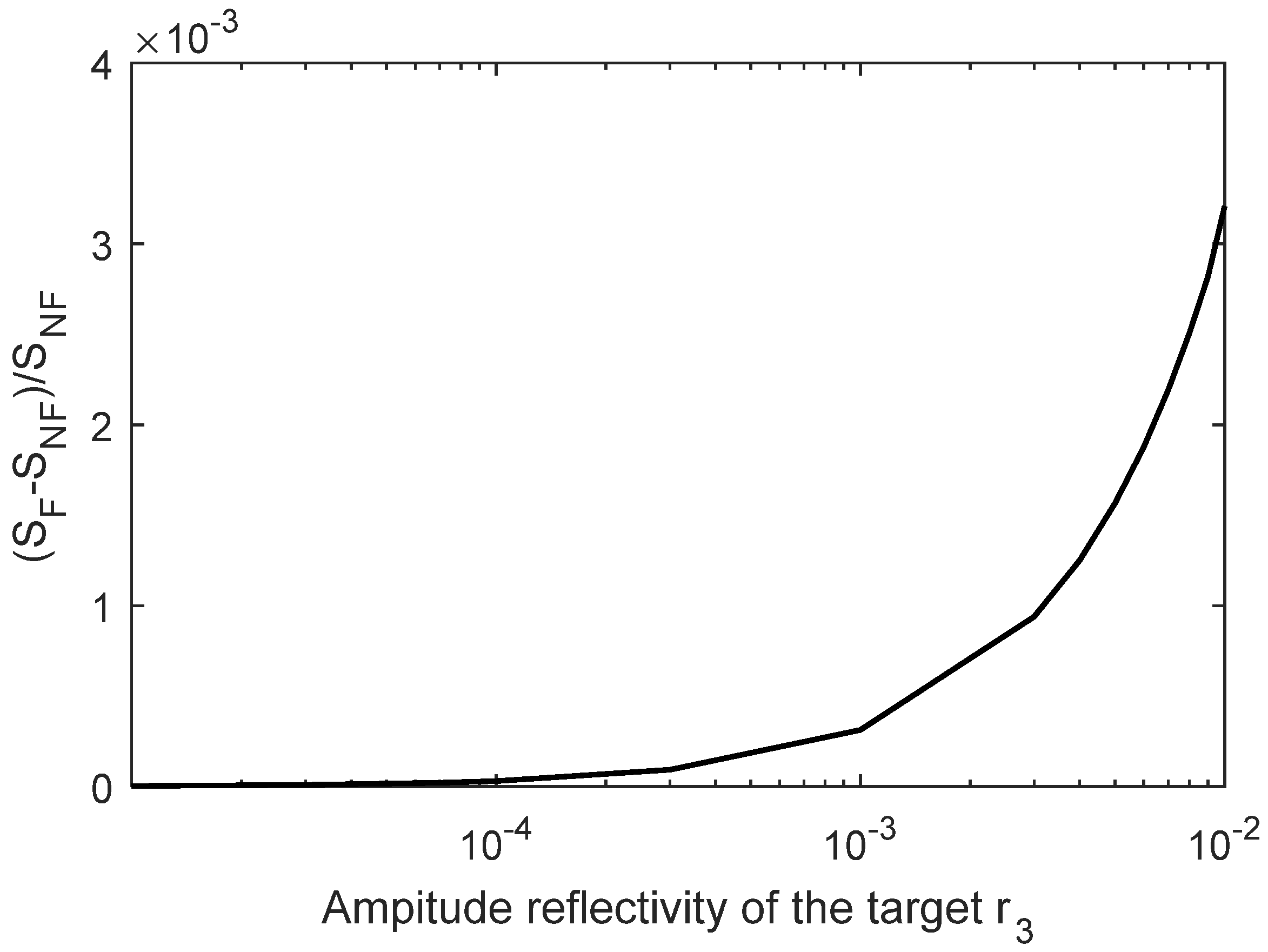
3.5. Transient Response of Lasers with EOF
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Kleinman, D.; Kisliuk, P. Discrimination Against Unwanted Orders in the Fabry-Perot Resonator. Bell Syst. Tech. J. 1962, 41, 453–462. [Google Scholar] [CrossRef]
- Rudd, M. A laser Doppler velocimeter employing the laser as a mixer-oscillator. J. Phys. E Sci. Instrum. 1968, 1, 723. [Google Scholar] [CrossRef]
- Yu, Y.; Xi, J.; Chicharo, J.F. Measuring the feedback parameter of a semiconductor laser with external optical feedback. Opt. Express 2011, 19, 9582–9593. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Xi, J.; Chicharo, J.F.; Bosch, T. Toward automatic measurement of the linewidth-enhancement factor using optical feedback self-mixing interferometry with weak optical feedback. IEEE J. Quantum Electron. 2007, 43, 527–534. [Google Scholar] [CrossRef]
- Yu, Y.; Xi, J.; Chicharo, J.F.; Bosch, T.M. Optical Feedback Self-Mixing Interferometry with a Large Feedback Factor C: Behavior Studies. IEEE J. Quantum Electron. 2009, 45, 840–848. [Google Scholar] [CrossRef]
- Lu, L.; Yang, J.; Zhai, L.; Wang, R.; Cao, Z.; Yu, B. Self-mixing interference measurement system of a fiber ring laser with ultra-narrow linewidth. Opt. Express 2012, 20, 8598–8607. [Google Scholar] [CrossRef]
- Wu, S.; Wang, D.; Xiang, R.; Zhou, J.; Ma, Y.; Gui, H.; Liu, J.; Wang, H.; Lu, L.; Yu, B. All-Fiber Configuration Laser Self-Mixing Doppler Velocimeter Based on Distributed Feedback Fiber Laser. Sensors 2016, 16, 1179. [Google Scholar] [CrossRef]
- Plantier, G.; Bes, C.; Bosch, T. Behavioral model of a self-mixing laser diode sensor. IEEE J. Quantum Electron. 2005, 41, 1157–1167. [Google Scholar] [CrossRef]
- Zhu, K.; Guo, B.; Lu, Y.; Zhang, S.; Tan, Y. Single-spot two-dimensional displacement measurement based on self-mixing interferometry. Optica 2017, 4, 729–735. [Google Scholar] [CrossRef]
- Khan, J.I.; Zabit, U. Sparsity Promoting Frequency Sampling Method for Estimation of Displacement and Self-Mixing Interferometry Parameters. IEEE Sens. J. 2021, 21, 10587–10594. [Google Scholar] [CrossRef]
- Norgia, M.; Giuliani, G.; Donati, S. Absolute distance measurement with improved accuracy using laser diode self-mixing interferometry in a closed loop. IEEE Trans. Instrum. Meas. 2007, 56, 1894–1900. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, C.; Zhao, Y.; Zhu, D.; Lu, L. An All-Fiber Self-Mixing Range Finder With Tunable Fiber Ring Cavity Laser Source. J. Lightwave Technol. 2021, 39, 4217–4224. [Google Scholar] [CrossRef]
- Guo, D.; Wang, M. Self-mixing interferometry based on a double-modulation technique for absolute distance measurement. Appl. Opt. 2007, 46, 1486–1491. [Google Scholar] [CrossRef] [PubMed]
- Guo, D.; Jiang, H.; Shi, L.; Wang, M. Laser self-mixing grating interferometer for MEMS accelerometer testing. IEEE Photon. J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, W.; Jiang, C.; Gao, B.; Chen, P. Velocity measurement based on multiple self-mixing interference. Appl. Opt. 2017, 56, 6709–6713. [Google Scholar] [CrossRef]
- Lin, K.; Yu, Y.; Xi, J.; Li, H.; Guo, Q.; Tong, J.; Su, L. A Fiber-Coupled Self-Mixing Laser Diode for the Measurement of Young’s Modulus. Sensors 2016, 16, 928. [Google Scholar] [CrossRef]
- Wang, B.; Liu, B.; An, L.; Tang, P.; Ji, H.; Mao, Y. Laser Self-Mixing Sensor for Simultaneous Measurement of Young’s Modulus and Internal Friction. Photonics 2021, 8, 550. [Google Scholar] [CrossRef]
- Yu, Y.; Giuliani, G.; Donati, S. Measurement of the linewidth enhancement factor of semiconductor lasers based on the optical feedback self-mixing effect. IEEE Photon. Technol. Lett. 2004, 16, 990–992. [Google Scholar] [CrossRef]
- Liu, B.; Ruan, Y.; Yu, Y.; Wang, B.; An, L. Influence of feedback optical phase on the relaxation oscillation frequency of a semiconductor laser and its application. Opt. Express 2021, 29, 3163–3172. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiang, R.; Huang, Z.; Chen, J.; Lu, L. Research on the Multi-longitudinal mode laser self-mixing static angle-measurement system using a right-angle prism. Measurement 2020, 162, 107906. [Google Scholar] [CrossRef]
- Wang, C.; Fan, X.; You, G.; Gui, H.; Wang, H.; Liu, J.; Yu, B.; Lu, L. Full-circle range and microradian resolution angle measurement using the orthogonal mirror self-mixing interferometry. Opt. Express 2018, 26, 10371–10381. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Ruan, Y.; Yu, Y. All-Fiber Laser-Self-Mixing Sensor for Acoustic Emission Measurement. J. Lightwave Technol. 2021, 39, 4062–4068. [Google Scholar] [CrossRef]
- Bertling, K.; Perchoux, J.; Taimre, T.; Malkin, R.; Robert, D.; Rakić, A.D.; Bosch, T. Imaging of acoustic fields using optical feedback interferometry. Opt. Express 2014, 22, 30346–30356. [Google Scholar] [CrossRef]
- Liu, B.; Ruan, Y.; Yu, Y.; Xi, J.; Guo, Q.; Tong, J.; Rajan, G. Laser self-mixing fiber Bragg grating sensor for acoustic emission measurement. Sensors 2018, 18, 1956. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, W.; Wei, Z.; Zhang, J.; An, T.; Wang, X.; Xu, H. Double-path acquisition of pulse wave transit time and heartbeat using self-mixing interferometry. Opt. Commun. 2017, 393, 178–184. [Google Scholar] [CrossRef]
- Arasanz, A.; Azcona, F.J.; Royo, S.; Jha, A.; Pladellorens, J. A new method for the acquisition of arterial pulse wave using self-mixing interferometry. Opt. Lasers Technol. 2014, 63, 98–104. [Google Scholar] [CrossRef]
- Norgia, M.; Pesatori, A.; Rovati, L. Self-mixing laser Doppler spectra of extracorporeal blood flow: A theoretical and experimental study. IEEE Sens. J. 2012, 12, 552–557. [Google Scholar] [CrossRef]
- Annovazzi-Lodi, V.; Merlo, S.; Norgia, M. Measurements on a micromachined silicon gyroscope by feedback interferometry. IEEE/ASME Trans. Mechatron. 2001, 6, 1–6. [Google Scholar] [CrossRef]
- Donadello, S.; Finazzi, V.; G Demir, A.; Previtali, B. Time-resolved quantification of plasma accumulation induced by multi-pulse laser ablation using self-mixing interferometry. J. Phys. D Appl. Phys. 2020, 53, 495201. [Google Scholar] [CrossRef]
- Donadello, S.; Demir, A.G.; Previtali, B. Probing multipulse laser ablation by means of self-mixing interferometry. Appl. Opt. 2018, 57, 7232–7241. [Google Scholar] [CrossRef] [PubMed]
- Lacot, E.; Day, R.; Stoeckel, F. Coherent laser detection by frequency-shifted optical feedback. Phys. Rev. A 2001, 64, 043815. [Google Scholar] [CrossRef]
- Giuliani, G.; Norgia, M.; Donati, S.; Bosch, T. Laser diode self-mixing technique for sensing applications. J. Opt. A Pure Appl. Opt. 2002, 4, S283. [Google Scholar] [CrossRef]
- Scalise, L.; Yu, Y.; Giuliani, G.; Plantier, G.; Bosch, T. Self-mixing laser diode velocimetry: Application to vibration and velocity measurement. IEEE Trans. Instrum. Meas. 2004, 53, 223–232. [Google Scholar] [CrossRef]
- Donati, S. Developing self-mixing interferometry for instrumentation and measurements. Laser Photonics Rev. 2012, 6, 393–417. [Google Scholar] [CrossRef]
- Taimre, T.; Nikolić, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakić, A.D. Laser feedback interferometry: A tutorial on the self-mixing effect for coherent sensing. Adv. Opt. Photonics 2015, 7, 570–631. [Google Scholar] [CrossRef]
- Yu, Y.; Fan, Y.; Liu, B. Self-Mixing Interferometry and Its Applications. In Optical Design and Testing VII; Wang, Y.T., Ed.; SPIE: Bellingham, WA, USA, 2016; Volume 10021. [Google Scholar]
- Li, J.; Niu, H.; Niu, Y.X. Laser feedback interferometry and applications: A review. Opt. Eng. 2017, 56, 050901. [Google Scholar] [CrossRef]
- Ohtsubo, J. Semiconductor Lasers: Stability, Instability and Chaos; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kallimani, K.I.; Mahony, M.J.O. Relative intensity noise for laser diodes with arbitrary amounts of optical feedback. IEEE J. Quantum Electron. 1998, 34, 1438–1446. [Google Scholar] [CrossRef]
- Ju, R.; Spencer, P.S.; Shore, K.A. The relative intensity noise of a semiconductor laser subject to strong coherent optical feedback. J. Opt. B Quantum Semiclass. Opt. 2004, 6, S775–S779. [Google Scholar] [CrossRef]
- Fan, Y.; Yu, Y.; Xi, J.; Guo, Q. Dynamic stability analysis for a self-mixing interferometry system. Opt. Express 2014, 22, 29260–29269. [Google Scholar] [CrossRef]
- Lacot, E.; Day, R.; Stoeckel, F. Laser optical feedback tomography. Opt. Lett. 1999, 24, 744–746. [Google Scholar] [CrossRef] [PubMed]
- Day, R.; Lacot, E.; Stoeckel, F.; Berge, B. Three-dimensional sensing based on a dynamically focused laser optical feedback imaging technique. Appl. Opt. 2001, 40, 1921–1924. [Google Scholar] [CrossRef]
- Liu, B.; Wang, B.; Ruan, Y.; Yu, Y. Suppression of undamped relaxation oscillation in a laser self-mixing interferometry sensing system. Opt. Express 2022, 30, 11254–11265. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.-B.; Wang, X.-G.; Zhang, J.; Wang, C. Relative intensity noise of a mid-infrared quantum cascade laser: Insensitivity to optical feedback. Opt. Express 2019, 27, 26639–26647. [Google Scholar] [CrossRef] [PubMed]
- Yanhua, H.; Paul, J.; Spencer, P.S.; Shore, K.A. The effects of polarization-resolved optical feedback on the relative intensity noise and polarization stability of vertical-cavity surface-emitting lasers. J. Lightwave Technol. 2006, 24, 3210–3216. [Google Scholar] [CrossRef]
- Petermann, K. External optical feedback phenomena in semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 1995, 1, 480–489. [Google Scholar] [CrossRef]
- Uchida, A. Optical Communication with Chaotic Lasers: Applications of Nonlinear Dynamics and Synchronization; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Donati, S.; Giuliani, G.; Merlo, S. Laser diode feedback interferometer for measurement of displacements without ambiguity. IEEE J. Quantum Electron. 1995, 31, 113–119. [Google Scholar] [CrossRef]
- Lacot, E.; Day, R.; Pinel, J.; Stoeckel, F. Laser relaxation-oscillation frequency imaging. Opt. Lett. 2001, 26, 1483–1485. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, Z.; Shen, X. A New Method for Measuring Refractive Index with a Laser Frequency-shifted Feedback Confocal Microscope. Curr. Opt. Photon. 2020, 4, 44–49. [Google Scholar]
- Mowla, A.; Du, B.W.; Taimre, T.; Be Rtling, K.; Rakić, A. Confocal laser feedback tomography for skin cancer detection. Biomed. Opt. Express 2017, 8, 4037. [Google Scholar] [CrossRef]
- Hugon, O.; Paun, I.; Ricard, C.; Van der Sanden, B.; Lacot, E.; Jacquin, O.; Witomski, A. Cell imaging by coherent backscattering microscopy using frequency-shifted optical feedback in a microchip laser. Ultramicroscopy 2008, 108, 523–528. [Google Scholar] [CrossRef] [PubMed]
- Girardeau, V.; Goloni, C.; Jacquin, O.; Hugon, O.; Inglebert, M.; Lacot, E. Nonlinear laser dynamics induced by frequency shifted optical feedback: Application to vibration measurements. Appl. Opt. 2016, 55, 9638–9647. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.; Wang, W.; Xu, C.; Zhang, S. Laser confocal feedback tomography and nano-step height measurement. Sci. Rep. 2013, 3, 2971. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.; Zhang, S.; Xu, C.; Zhao, S. Inspecting and locating foreign body in biological sample by laser confocal feedback technology. Appl. Phys. Lett. 2013, 103, 101909. [Google Scholar]
- Wang, W.; Zhang, S.; Li, Y. Surface microstructure profilometry based on laser confocal feedback. Rev. Sci. Instrum. 2015, 86, 103108. [Google Scholar] [CrossRef]
- Xu, C.; Tan, Y.; Zhang, S.; Zhao, S. The structure measurement of micro-electro-mechanical system devices by the optical feedback tomography technology. Appl. Phys. Lett. 2013, 102, 221902. [Google Scholar] [CrossRef]
- Tromborg, B.; Osmundsen, J.H.; Olesen, H. Stability analysis for a semiconductor laser in an external cavity. IEEE J. Quantum Electron. 1984, 20, 1023–1032. [Google Scholar] [CrossRef]
- Fan, Y.; Yu, Y.; Xi, J.; Guo, Q. Stability limit of a semiconductor laser with optical feedback. IEEE J. Quantum Electron. 2015, 51, 1–9. [Google Scholar] [CrossRef]
- Kane, D.M.; Toomey, J.P. Precision Threshold Current Measurement for Semiconductor Lasers Based on Relaxation Oscillation Frequency. J. Lightwave Technol. 2009, 27, 2949–2952. [Google Scholar] [CrossRef]
- Cohen, S.D.; Aragoneses, A.; Rontani, D.; Torrent, M.; Masoller, C.; Gauthier, D.J. Multidimensional subwavelength position sensing using a semiconductor laser with optical feedback. Opt. Lett. 2013, 38, 4331–4334. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Y.; Xi, J.; Guo, Q.; Tong, J.; Lewis, R.A. Displacement sensing using the relaxation oscillation frequency of a laser diode with optical feedback. Appl. Opt. 2017, 56, 6962–6966. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Y.; Liu, B.; Yu, Y.; Xi, J.; Guo, Q.; Tong, J. Measuring Linewidth Enhancement Factor by Relaxation Oscillation Frequency in a Laser with Optical Feedback. Sensors 2018, 18, 4004. [Google Scholar] [CrossRef] [PubMed]
- Teysseyre, R.; Bony, F.; Perchoux, J.; Bosch, T. Laser dynamics in sawtooth-like self-mixing signals. Opt. Lett. 2012, 37, 3771–3773. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Acket, G.A.; Lenstra, D.; Den Boef, A.; Verbeek, B. The influence of feedback intensity on longitudinal mode properties and optical noise in index-guided semiconductor lasers. IEEE J. Quantum Electron. 1984, 20, 1163–1169. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Y.; Xi, J.; Fan, Y.; Guo, Q.; Tong, J.; Lewis, R.A. Features of a self-mixing laser diode operating near relaxation oscillation. Sensors 2016, 16, 1546. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Ruan, Y.; Yu, Y.; Guo, Q.; Xi, J.; Tong, J. Modeling for optical feedback laser diode operating in period-one oscillation and its application. Opt. Express 2019, 27, 4090–4104. [Google Scholar] [CrossRef]
- Ruan, Y.; Liu, B.; Yu, Y.; Xi, J.; Guo, Q.; Tong, J. High sensitive sensing by a laser diode with dual optical feedback operating at period-one oscillation. Appl. Phys. Lett. 2019, 115, 011102. [Google Scholar] [CrossRef]
- Mørk, J.; Mark, J.; Tromborg, B. Route to chaos and competition between relaxation oscillations for a semiconductor laser with optical feedback. Phys. Rev. Lett. 1990, 65, 1999. [Google Scholar] [CrossRef]
- Donati, S.; Fathi, M.T. Transition from short-to-long cavity and from self-mixing to chaos in a delayed optical feedback laser. IEEE J. Quantum Electron. 2012, 48, 1352–1359. [Google Scholar] [CrossRef]
- Kanter, I.; Aviad, Y.; Reidler, I.; Cohen, E.; Rosenbluh, M. An optical ultrafast random bit generator. Nat. Phonton. 2010, 4, 58–61. [Google Scholar] [CrossRef]
- Chan, S.C.; Hwang, S.K.; Liu, J.M. Period-one oscillation for photonic microwave transmission using an optically injected semiconductor laser. Opt. Express 2007, 15, 14921–14935. [Google Scholar] [CrossRef]
- Chlouverakis, K.E.; Adams, M.J. Optoelectronic realisation of NOR logic gate using chaotic two-section lasers. Electron. Lett. 2005, 41, 359–360. [Google Scholar] [CrossRef]
- Sciamanna, M.; Shore, K.A. Physics and applications of laser diode chaos. Nat. Phonton. 2015, 9, 151–162. [Google Scholar] [CrossRef]
- Lin, F.-Y.; Liu, J.-M. Chaotic radar using nonlinear laser dynamics. IEEE J. Quantum Electron. 2004, 40, 815–820. [Google Scholar] [CrossRef]
- Lin, F.-Y.; Liu, J.-M. Chaotic lidar. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 991–997. [Google Scholar] [CrossRef]
- Myneni, K.; Barr, T.A.; Reed, B.R.; Pethel, S.D.; Corron, N.J. High-precision ranging using a chaotic laser pulse train. Appl. Phys. Lett. 2001, 78, 1496–1498. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Chen, C.-Y.; Chen, J.-D.; Pan, D.-K.; Ting, K.-T.; Lin, F.-Y. 3D pulsed chaos lidar system. Opt. Express 2018, 26, 12230–12241. [Google Scholar] [CrossRef]
- Feng, W.; Jiang, N.; Jin, J.; Zhao, A.; Zhang, Y.; Liu, S.; Qiu, K. High-Resolution Chaos Lidar Using Self-Phase-Modulated Feedback External-Cavity Semiconductor Laser-based Chaos Source. In Proceedings of 2021 19th International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 23–27 August 2021; pp. 1–3. [Google Scholar]
- Shen, Z.; Zhao, T.; Wang, Y.; Zheng, Y.; Shang, W.; Wang, B.; Li, J. Underwater target detection of chaotic pulse laser radar. Infrared Laser Eng. 2019, 48, 406004. [Google Scholar] [CrossRef]
- Wang, B.; Guo, Z.; Shen, Z.; Xu, H.; Li, J. Underwater 3D Imaging Utilizing 520 nm Chaotic Lidar. J. Russ. Laser Res. 2020, 41, 399–405. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, B.; Wang, A. Chaotic correlation optical time domain reflectometer utilizing laser diode. IEEE Photon. Technol. Lett. 2008, 20, 1636–1638. [Google Scholar] [CrossRef]
- Wang, A.; Wang, N.; Yang, Y.; Wang, B.; Zhang, M.; Wang, Y. Precise Fault Location in WDM-PON by Utilizing Wavelength Tunable Chaotic Laser. J. Lightwave Technol. 2012, 30, 3420–3426. [Google Scholar] [CrossRef]
- Dong, X.; Wang, A.; Zhang, J.G.; Hong, H.; Wang, Y. Combined Attenuation and High Resolution Fault Measurements Using Chaos-OTDR. IEEE Photon. J. 2015, 7, 1–6. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Zhang, J.; Zhang, M.; Qiao, L.; Wang, T. Long-Range and High-Precision Fault Measurement Based on Hybrid Integrated Chaotic Laser. Photonics Technol. Lett. IEEE 2019, 31, 1389–1392. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, B.; Wang, L.; Zhao, T.; Han, H.; Wang, Y.; Wang, A. Improving Spatial Resolution of Chaos OTDR Using Significant-Bit Correlation Detection. IEEE Photon. Technol. Lett. 2019, 31, 1029–1032. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Y.; Hu, X.; Guo, Y.; Zhang, J.; Qiao, L.; Wang, T.; Gao, S.; Zhang, M. Improvement of Strain Measurement Accuracy and Resolution by Dual-Slope-Assisted Chaotic Brillouin Optical Correlation Domain Analysis. J. Lightwave Technol. 2021, 39, 3312–3318. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zhang, M.; Zhang, Q.; Li, M.; Wu, C.; Qiao, L.; Wang, Y. Time-gated chaotic Brillouin optical correlation domain analysis. Opt. Express 2018, 26, 17597–17607. [Google Scholar] [CrossRef]





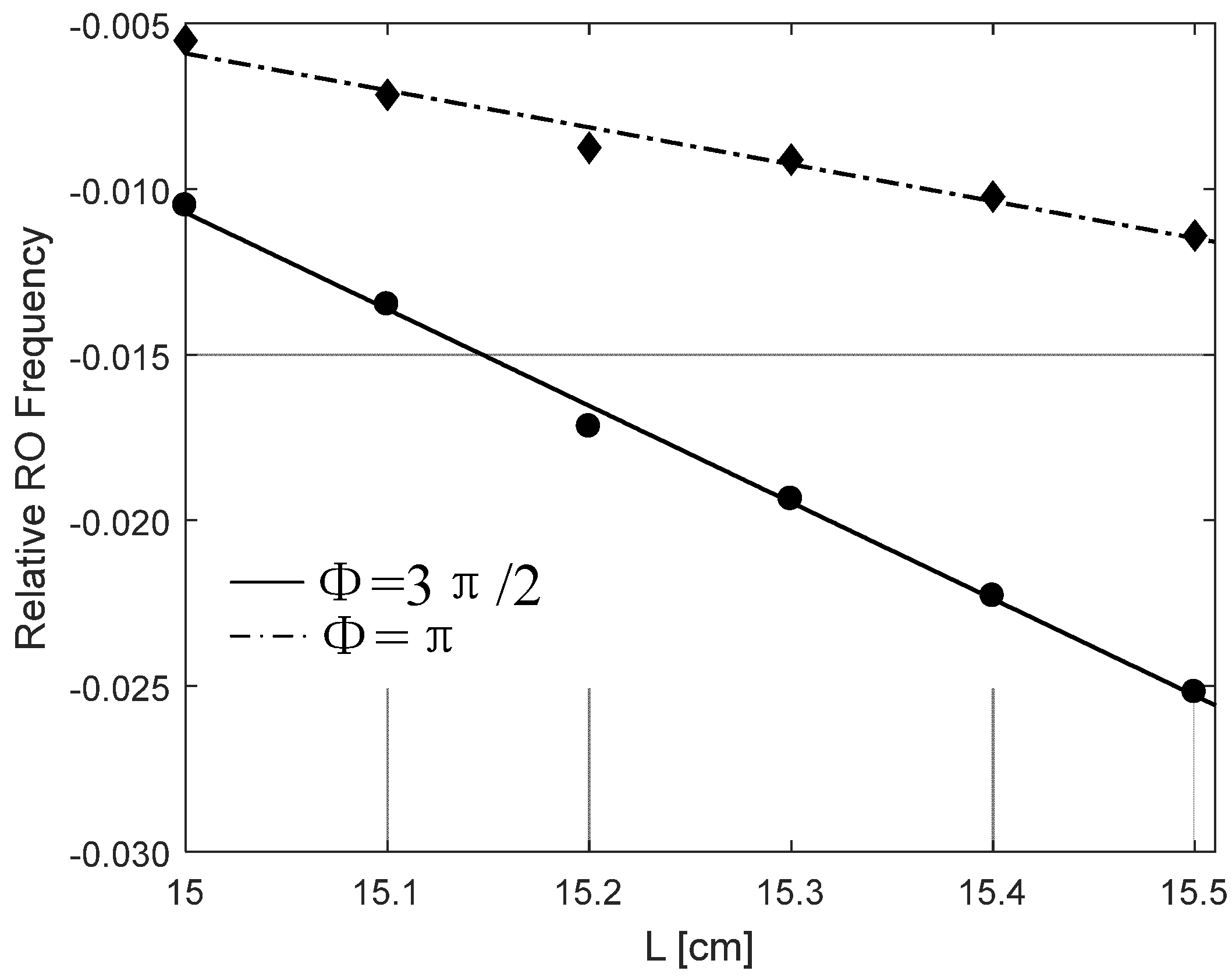
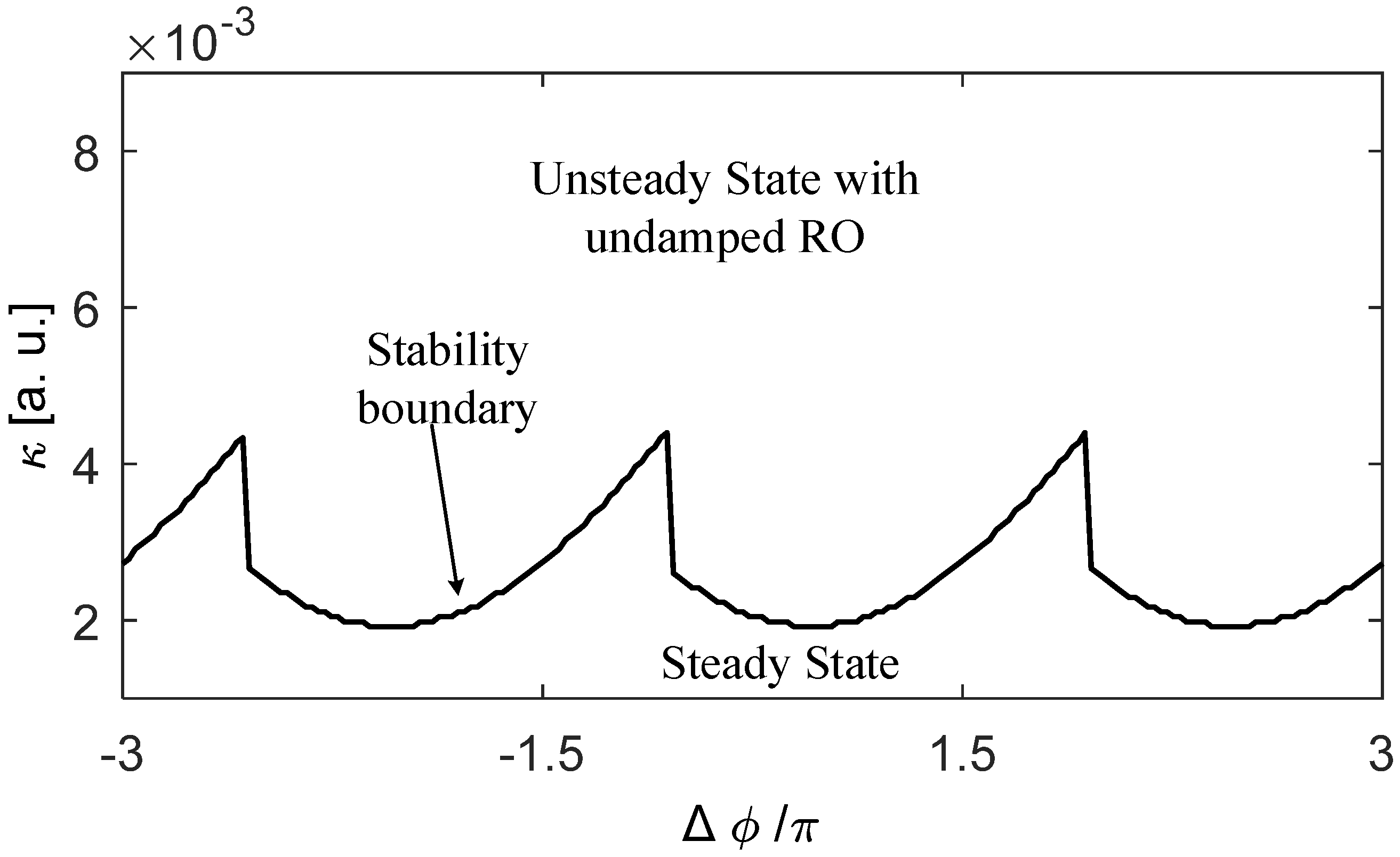
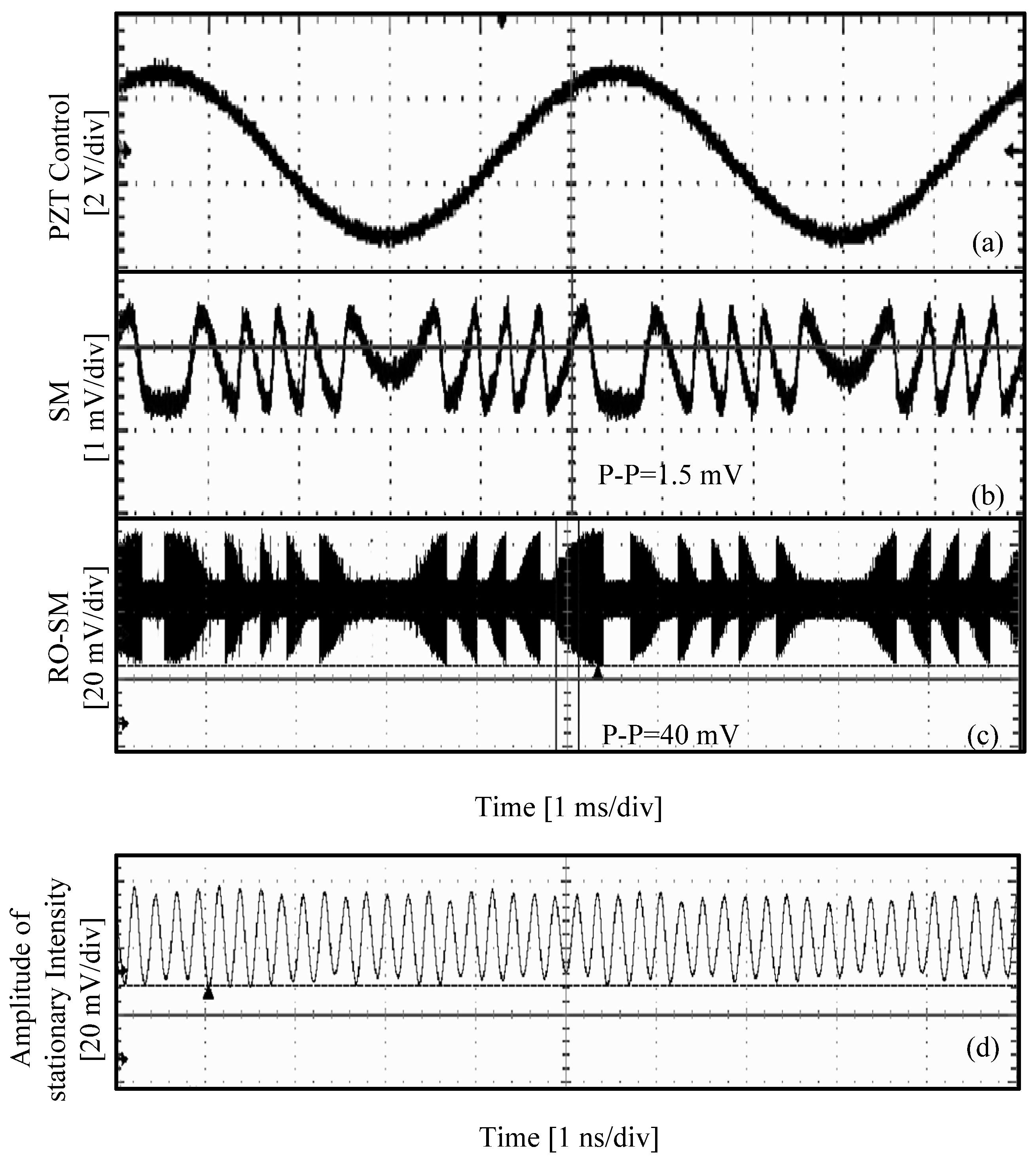
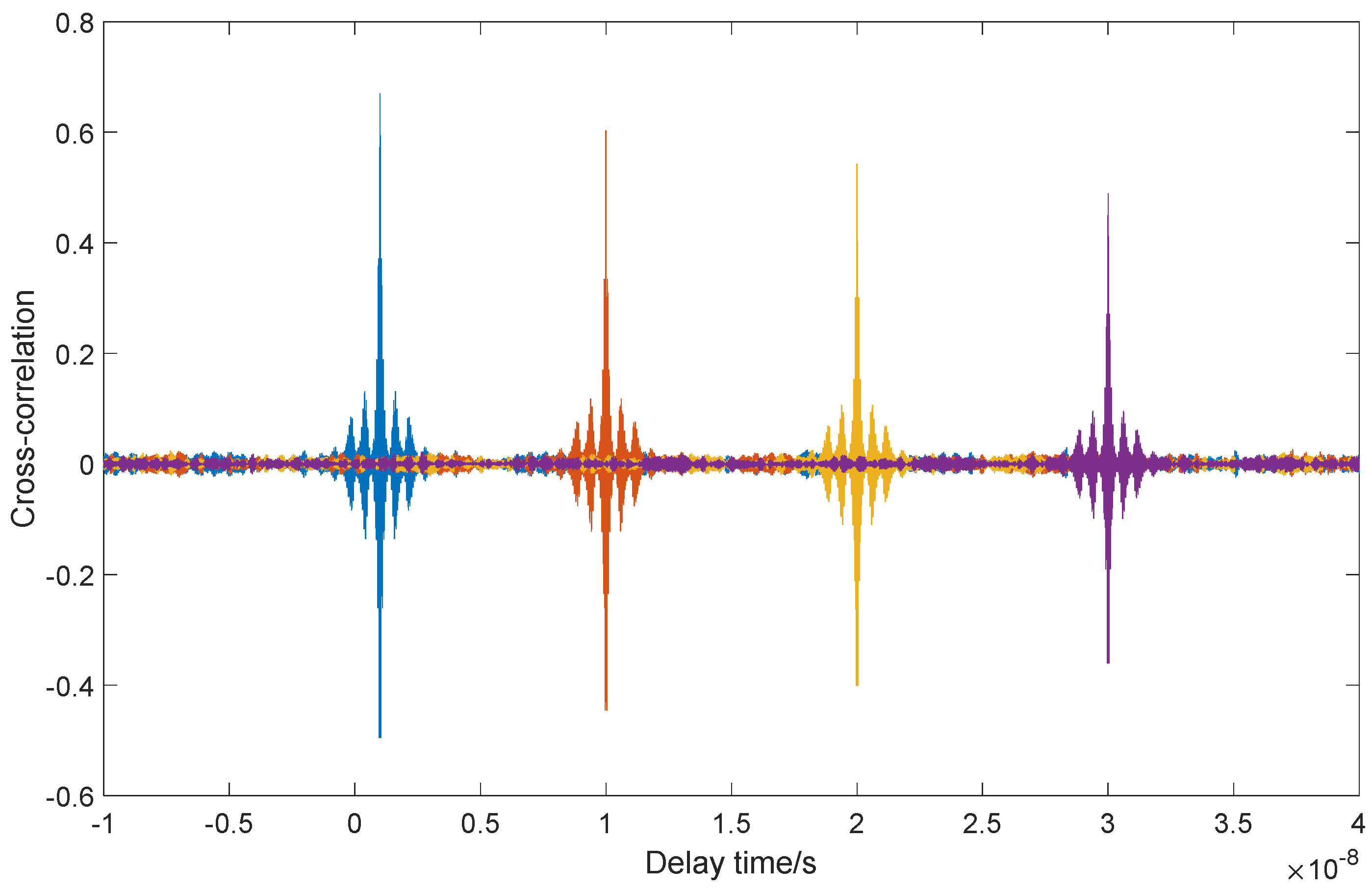

| Symbol | Physical Meaning | Value | |
|---|---|---|---|
| Fixed Parameters | modal gain coefficient | ||
| carrier density at transparency | |||
| nonlinear gain compression coefficient | |||
| confinement factor | |||
| photon life time | |||
| carrier life time | |||
| internal cavity round-trip time | |||
| linewidth enhancement factor | |||
| spontaneous emission factor | |||
| amplitude reflectivity | |||
| reinjection loss | |||
| e | elementary charge | ||
| V | volume of the active region | ||
| Controllable Parameters | amplitude reflectivity of the external target | ||
| injection current | |||
| external cavity length | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Jiang, Y.; Ji, H. Sensing by Dynamics of Lasers with External Optical Feedback: A Review. Photonics 2022, 9, 450. https://doi.org/10.3390/photonics9070450
Liu B, Jiang Y, Ji H. Sensing by Dynamics of Lasers with External Optical Feedback: A Review. Photonics. 2022; 9(7):450. https://doi.org/10.3390/photonics9070450
Chicago/Turabian StyleLiu, Bin, Yangfan Jiang, and Haining Ji. 2022. "Sensing by Dynamics of Lasers with External Optical Feedback: A Review" Photonics 9, no. 7: 450. https://doi.org/10.3390/photonics9070450
APA StyleLiu, B., Jiang, Y., & Ji, H. (2022). Sensing by Dynamics of Lasers with External Optical Feedback: A Review. Photonics, 9(7), 450. https://doi.org/10.3390/photonics9070450






