1. Introduction
The quantum degenerate gases prepared by laser cooling and evaporation cooling [
1] have proved to be fantastic systems in the investigations of quantum nonequilibrium dynamics and quantum for many body physical problems [
2,
3,
4]. They can be confined in a potential trap with high optical controllability, such as an optical lattice [
5] or an optical dipole trap (ODT). In an ultracold atomic ensemble, the most common application of parametric modulation is modulating power (trapping potential) for the ODT [
6]. The parametric modulation has been widely used in various ultracold atomic ensembles [
7,
8]. The parametric heating of bosons has been realized in a periodically-driven 2D lattice, in which exponential decay rates are observed [
9]. Direct condensation of thermal atoms in an optical lattice is also achieved using this technique [
10]. Furthermore, the creation of bosonic fractional quantum Hall states is expected in periodically-driven optical lattices [
11]. Note that parametric modulation can be used to selectively remove the high-temperature atoms, resulting in degenerate Fermi gases [
12]. Besides, it can be used to measure the trap frequency and the spring constant of an ODT, and to study the dynamical instability and the collisional processes of atoms in optical lattices [
13]. Parametric modulation-induced cooling has been accomplished for either bosonic atoms in a magnetic trap [
14] or fermionic atoms in a standing wave lattice [
15]. However, these experiments only study the parametric modulation effect of a sinusoidal signal. The best modulation type to measure trap frequency of the ODT through parametric heating has not been investigated. The different dynamic effects caused by different waveform modulations are still worthy of further study.
In this study, we have applied three common waveforms (sine, triangle, and square waves) to modulate the trapping potential of the ODT. The trap frequency is systematically measured for the different cases. We have investigated the evolution of the trapped atom populations at the modulation frequency = 2, where is the trap frequency (the principal circular frequency) of the unperturbed trapped atoms. The evolution of the trapped atom population at the frequency of 2 and the resonance loss spectra are also theoretically simulated. Theoretical studies correlate with the experimental results fairly well.
This paper is organized in four main sections.
Section 2 introduces the experimental setup and schemes. In
Section 3, we introduce the theoretical model simulations with parametric modulation.
Section 4 is the experimental results. Finally, the conclusion is presented in
Section 5.
2. Experimental Setup
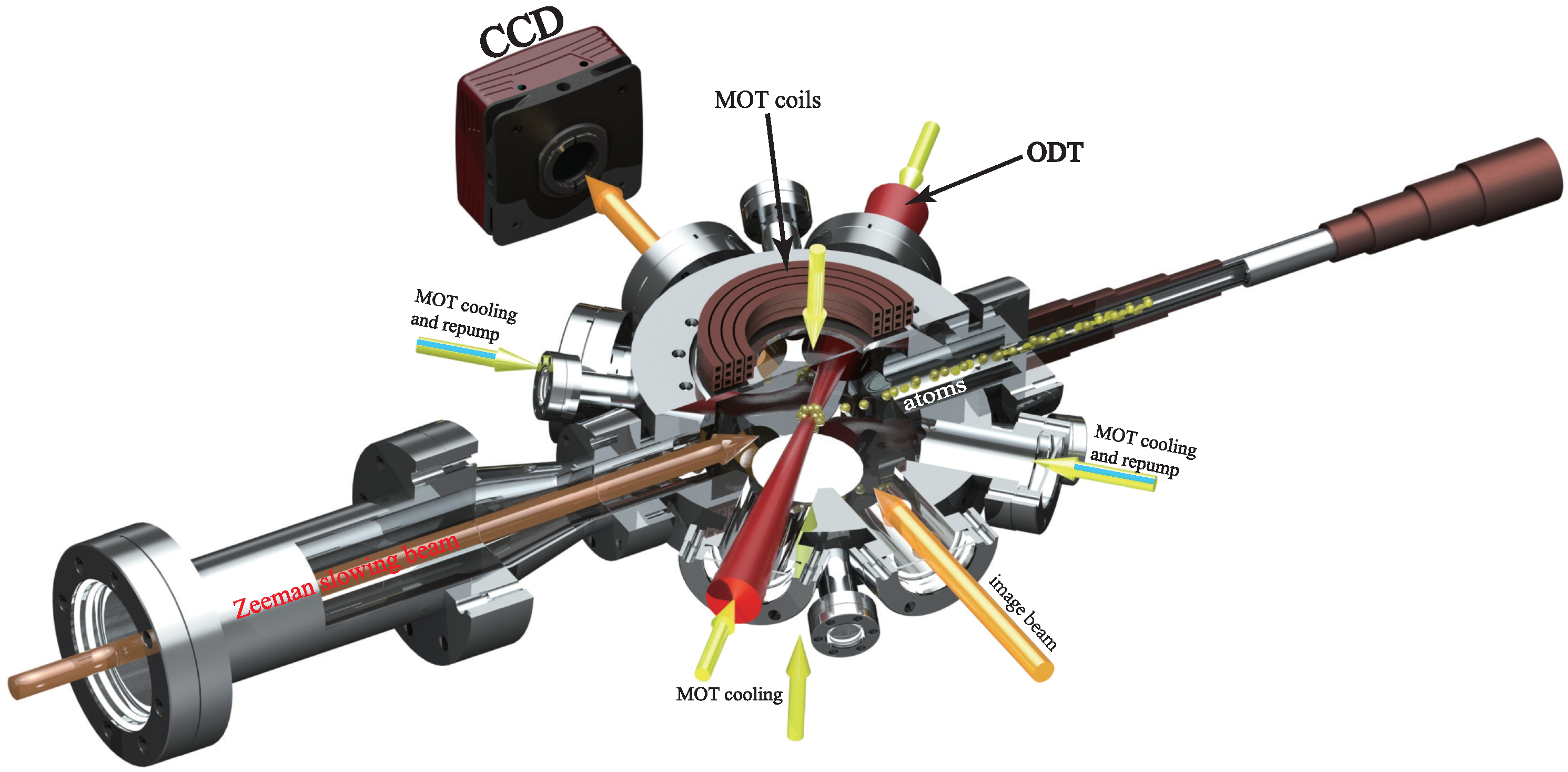
Figure 1 is a part of the experimental apparatus. The experimental apparatus has three parts: the oven chamber, the intermediate chamber, and the science chamber. The oven chamber contains 25 g sodium that is heated to 532 K. At this temperature, sodium has a vapor pressure of ∼6.7 ×
Torr. The intermediate chamber is a Zeeman slower which connects the oven and the science chamber. An ion pump (Agilent Star Cell, 150 L/s) and a Ti-sublimation pump are used to maintain the pressure at ∼2.3 ×
Torr in the science chamber. Sample preparation and manipulation are performed in the science chamber.
The Zeeman slower [
16] performs the first cooling step to slow down the atoms ejected from a pin hole in the oven chamber. A magneto-optical trap (MOT) [
17] is used to further cool and collect the atoms. The MOT is constructed with six cooling beams in three orthogonal directions, two repump beams, and a pair of 12-turn anti-Helmholtz coils (
Figure 1). The cooling and repump beams are provided by a frequency-doubled diode laser (TA-SHG pro, Toptica), of which the frequency is locked to the
Na atomic
transition line (
). The MOT cooling beams are detuned by
= −20 MHz from the cycling transition, have a power of 4.5 mW, and two of them combine with one 2.2 mW MOT repump beam. The magnetic field gradient is 10 G/cm. The frequency of MOT repump beams is nearly in resonance with the
transition. After 8 s of MOT loading, we collect 6 ×
sodium atoms. Next, the atoms are transferred to a compressed MOT (CMOT) and an optical molasses [
18] process efficiently cool 5 ×
atoms to 45
K (
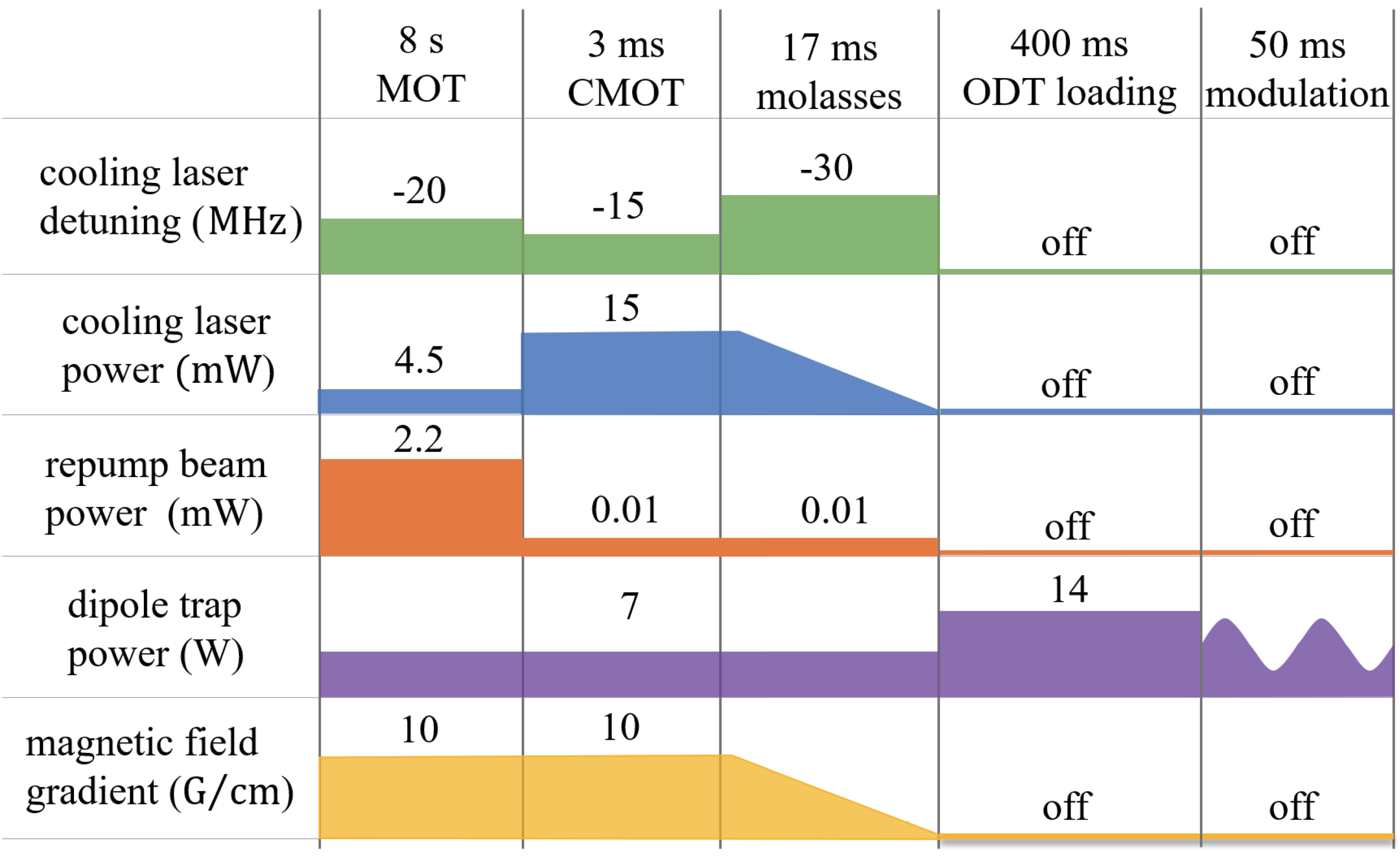
Figure 2). The atom gas is compressed by increasing the power of MOT cooling beams to 15 mW and reducing the power of MOT repump beams to 10
W as well as changing
to −15 MHz in 3 ms. In this CMOT stage, we kept the magnetic field gradient unchanged to keep the atoms stable. The optical molasses performs 17 ms, in which the frequency of MOT cooling beams are detuned to
= −30 MHz. Simultaneously, the power of the MOT cooling beams and the magnetic field gradient are linearly drops to 3.6 mW and 0.2 G/cm, respectively. The whole experimental sequence is shown in
Figure 2. To de-pump atoms into the
F = 1 hyperfine state, the repump beams are extinguished 1 ms before the MOT cooling beams, and the magnetic field gradient are turned off.
The next step is to load the pre-cooled atoms into the ODT. An ODT captures the atoms by the interaction of the induced dipole moment with the intensity gradient of the light field. For a far-off-resonance-detuned laser, the scattering rate
and the optical potential
for atoms are given by [
19]:
where
c is the speed of light,
ℏ is the reduced Planck constant,
is the resonant transition frequency,
is the detuning of the laser,
is the natural decay rate of the excited state in radians per second,
I is the intensity of the laser, and
r is the spatial coordinate. Equations (
1) and (
2) show that a large-detuned and high-intensity dipole trap can maintain low scattering rates for a certain potential depth.
In the experiment, a fiber-amplified laser (1070 nm, IPG-FLR-LP) with a power of 100 W is used to provide a large-detuned and high-intensity dipole trap laser. A dipole trap laser is focused to the atoms and has a waist of 32
m. As shown in
Figure 2, the power of the dipole trap laser is kept at half power (7 W) during the entire laser cooling process and is then jumped to the maximum (14 W). This process can effectively improve the ODT capture efficiency of atoms. [
20] After a 400 ms ODT loading, the ODT captures about 1 × 10
atoms at a temperature of ∼80
K. The phase space density is ∼0.3 × 10
. According to Equation (
1) and the parameters of our ODT, we have calculated that the trap frequency
is about 2.46 kHz.
Then we need to parametrically modulate the trapping potential that the atoms experience. An arbitrary function generator (Textronix AFG31153) is used to generate a modulation signal with an adjustable frequency, amplitude and waveform. The modulation signal and the analog signal are mixed by a summing amplifier (SRS SIM980). (The analog signal is used to control the power of the dipole trap laser. The power of the dipole trap laser can be modulated by the modulation signal.) The mixed signal is sent to a voltage-controlled oscillator (VCO) to generate a synthesized signal that can control the diffraction efficiency of the acousto-optic modulator (AOM). The synthesized signal is sent to the AOM through an amplifier to control and modulate the power of the first-order diffracted beam (the dipole trap laser). After the AOM, the diffracted beam is sent to the atoms through an optical fiber, which avoids the effects on the position change of the beam when the RF power of the AOM is modulated. Therefore, the trapping potential (the power of the dipole trap laser) can be modulated with an amplitude and a frequency . The modulation time T is set to 50 ms. Absorption imaging of the atoms for each experiment is performed after the dipole trap and the modulation were turned off.
Two trap frequencies in both radial and axial directions exist, and the trap frequency in the loosely confined axial direction is far less than the trap frequency in the closely confined radial direction. In our experiment, we predominantly consider the evolution of the atoms at the radial resonances.
The modulation induces the atoms to oscillations at the modulation frequency in the ODT. If the modulation frequency equals twice the axial or radial trap frequency, the parametric heating is most drastic and most atoms loss would happen. Regarding the lowest energetic atoms, the modulation energy is insufficient for them to escape from the trap, as it would happen for a harmonic potential. [
21] Conversely, atoms with high energy are easily heated out of the trap. The number of lost atoms will increase as the modulation amplitude (modulation depth) increases.
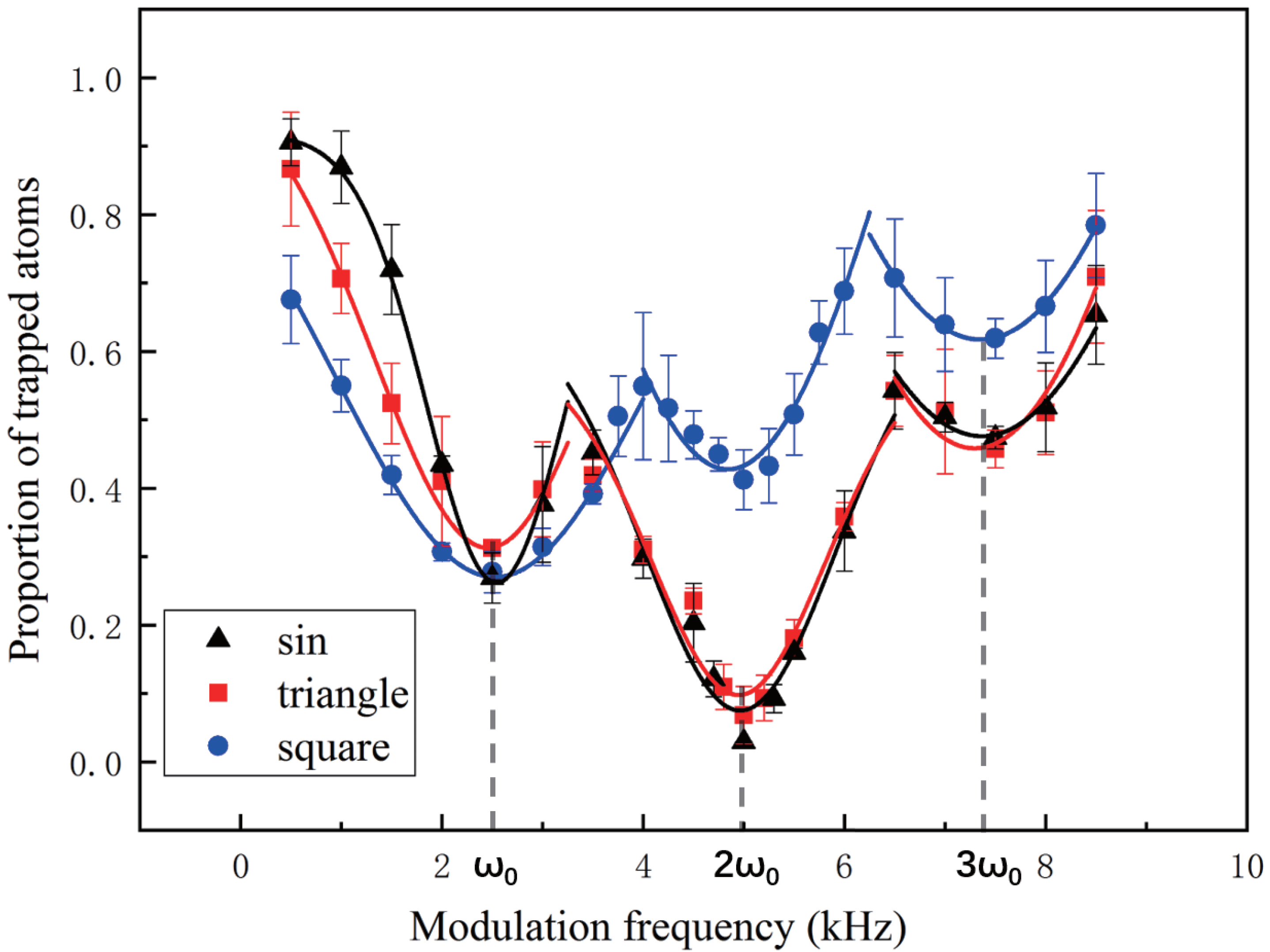
The relationship between the proportion of traped atoms and modulation frequency for three waveforms are shown in
Figure 3. The range of the modulation frequency is set to 0.5–8.5 kHz, which covers 1 to 3 times the theoretical value (2.46 kHz), and each data point is measured three times. In order to avoid distortion of the modulated signal, we slightly reduce the power of the ODT. The initial number of atoms is about 6 × 10
. We used the same modulation depth of 0.15 for the three wave forms to avoid the influence of the integral absolute intensities of the modulation signals. The modulation depth is the ratio of the effective amplitude to the total amplitude. In
Figure 3, we can clearly see the three resonances loss at ∼2.47 (±0.19) kHz, ∼4.89 (±0.15) kHz and ∼7.31 (±0.27) kHz in the loss spectra. The three resonances loss match the frequency of
,
, and
. By identifying three resonance frequencies and comparison with the theoretical value, the trap frequency
(±0.19) kHz. The measured trap frequency is equal to the calculated value and should be accurate for the atoms at low levels of the harmonic potential. The trap frequency measurements for three type modulation is precise, and each modulation type can be used to measure the trap frequency.
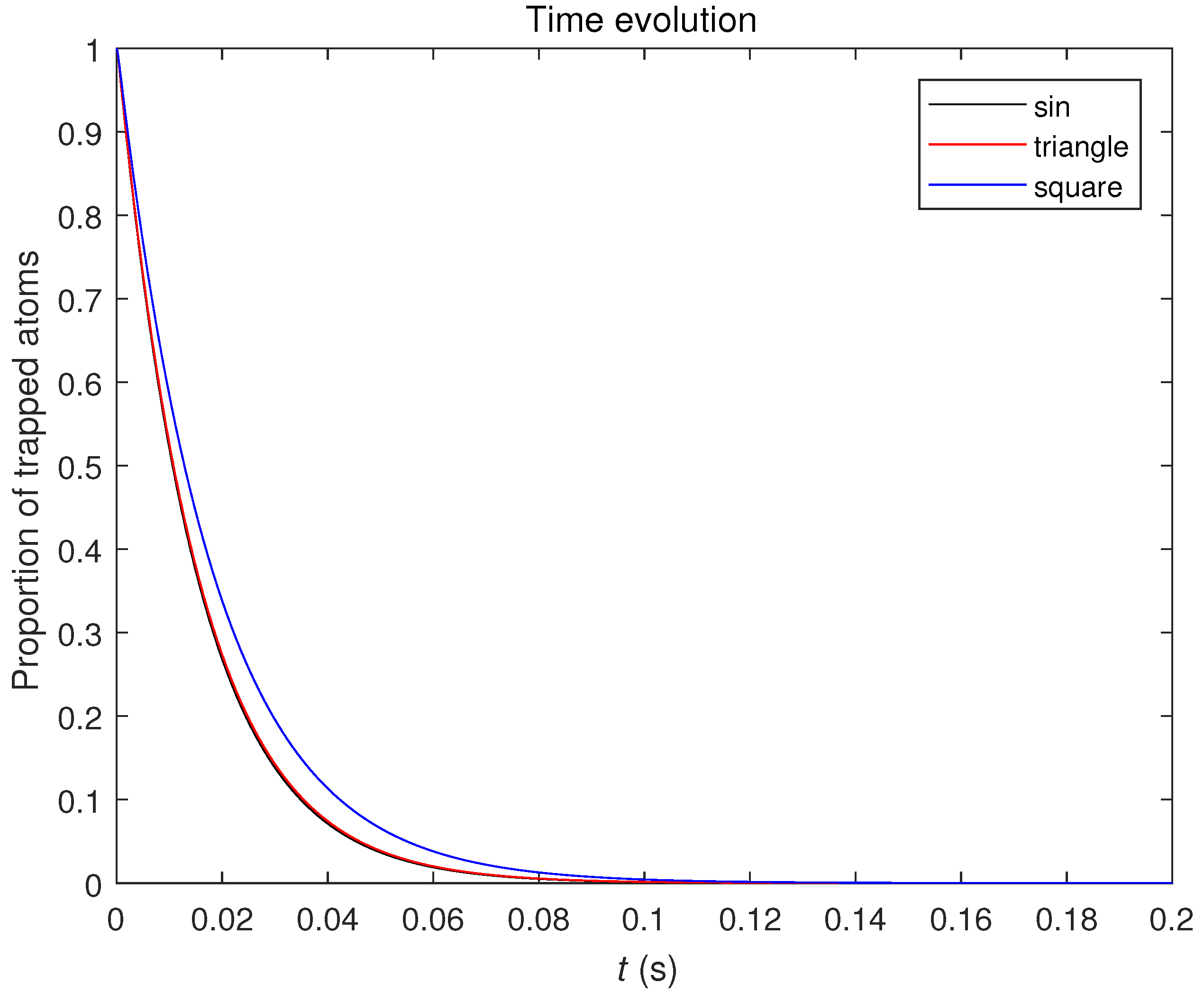
Figure 4 shows the results of the evolution of the trapped atoms population. As modulation time increases, the atom loss of sin and triangle wave modulation is faster than that of the square wave modulation. We also measured the lifetime of the atoms without modulation as 7.2 (±0.2) s (The data after 200 ms are not shown in the
Figure 4). The comparison of the evolution of the trapped population with and without modulation shows that modulation can cause intense trap losses in a brief time.
3. Theoretical Simulation
To simulate the parametrically modulate optical potentials, in many previous works (e.g., [
22] and references therein) the classical kinetic scheme with the transition probabilities computed in the first-order quantum mechanical perturbation theory for the model of the harmonic oscillator was employed. This approach implies a loss of the quantum coherence between transitions. However, the atomic ultracold ensembles are characterized by the long-living coherence. So, we apply a fully-coherent quantum mechanical calculation in the simulation.
The standard time-dependent Schrödinger equation is
where
t is the time,
is the Hamiltonian,
is the time-dependent potential function,
is the wavepacket of an atom in an ODT,
is the momentum,
x is the spatial coordinate,
M is the mass,
ℏ is the reduced Planck constant.
Assume that the potential function
takes the form
where
is a time–independent zero-th order potential,
is a contribution to the overall perturbation, which could arise from a distortion of the shape of the potential well during the modulation and can also effectively comprise an effect of the time-independent perturbations, keeping the zeroth-order potential as simple as possible, and
is some function of
t (modulation signal). Then,
is the spectrum of the zero-th order potential:
The quantities we are interested in are the time-dependent populations of the zero-th order states:
where
are the corresponding amplitudes. We assume that the number of atoms remained trapped by the instant
t can be approximated by
or, maybe, by a limited sum of few lowest
.
In principle, the set of equations above can be solved directly.
Using Equation (
3) with the substitution Equation (
4), we can derive an equation for the amplitudes Equation (
8)
Introducing the matrix notations
we can recast Equation (
9) into the matrix form
with all the multiplications understood in the matrix sense. The text-book time dependent perturbation theory results in its solution:
where
is the time-ordered exponent.
Within the model of Equation (
4), we have for the matrix elements of
W (Equation (
11)):
Hence, the first-order evolution operator in Equation (
13) between the time instants
and
can be written as:
for which we only have to compute relatively simple integrals
while the quantities
are time-independent and can be computed beforehand from a precomputed spectrum of the time-independent Schrödinger equation (Equation (
5)).
With a small enough time step
, the evolution of the amplitude vector
can be approximated by
Further on, we adopt the approximation of the harmonic oscillator:
where
is the vibrational quantum number. In this case the matrix elements of
W can be computed analytically.
In terms of the dimensionless coordinate,
where
a and
are the standard annihilation and creation operators, the recurrence relations
are valid, enabling a computation of the matrix elements
for all
k,
n,
m of interest starting with
(
is the Kronecker symbol). We also assume that the term
in the perturbation can be expressed as a power series in
:
with
measured in the units of the circular frequency
. This way, all the quantities
and
(Equation (
16)) as well as the entire matrix
W (Equation (
11)) are easily computed.
Let
be a periodic function with the period
so that
. For the simplest modulation signals of our interest, the integrals
(Equation (
15)) can be computed analytically, e.g., for the sinusoidal signal in a pure harmonic approximation:
However, such expressions contain indeterminate forms
at
, requiring special treatment. In practical computations, it is easier to estimate the integrals
(Equation (
15)) directly with some numerical algorithm. For the small enough time step
(
,
) the simple approximation can be appropriate:
however, in our computations we used a more elaborate integration procedure (see below).
Besides the sinusoidal signal, we consider the square modulation signals:
and the triangular modulation signal
where
is the modulo (remnant in division of
t by
T).
In the material above, we implied that a physical Hamiltonian is the Hermitian operator, resulting in the unitary evolution operator. In this case, the evolution remains conservative, so that no atoms escape the system, showing a kind of an oscillatory behavior of the individual levels’ populations. In order to simulate a possible escape from the ODT after every time step of the length
(with Equation (
17)), we first renormalized the vector
(it is necessary as the first-order evolution operator
is able to violate the norm conservation) and then multiplied the amplitudes
by a damping factor
with an adjustable parameter
for all levels starting with
(i.e., the lowest level
retained untouched).
In agreement with our experimental parameters, we performed test computations:
rad/s;
ms;
ms;
(the pure harmonic approximation) and
rad/s (the cubic perturbation);
; the computation included 11 (
) lowest levels of the harmonic potential well. The amplitude
C is set to
, and 0.15 for sin, triangle, and square wave modulations, respectively, to ensure the same effective amplitude. The time step was chosen
ms, the integrals
(Equation (
15)) were estimated with the rectangular rule using a net of 50 nodes within every
-interval.
Figure 5 shows the loss spectra at the terminal time
ms computed with the cubic perturbation
(see Equations (
4) and (
22)). The classical theory of the parametrically driven harmonic oscillator [
23] results in a conclusion that the resonance occurs at the modulation circular frequency of
with
being the principal circular frequency of the unperturbed harmonic oscillator. In our theoretical simulation, the majoring resonance at
and two other strong resonances at
and
appeared. Their origin is the transitions with
(m and n are vibrational quantum numbers) and
, allowed for in this more elaborate model. The extra resonances at
(
) [
24], clearly seen in
Figure 7, contribute noticeably to the square-wave case as well. The forms of the resonances in
Figure 5 resemble the ones observed experimentally, in spite of the relative simplicity of our computational model.
Figure 6 shows the time evolution of the lowest
level populations for the three modulation signals, computed within our model. The harmonic potential is completely bound, so the excited atoms would not leave its range. The real ODT potential is unbound; hence, the part of atoms with high enough energy would escape as soon as their energy reaches the ODT potential limit. We expect that this process goes on exponentially, [
25] resulting in an approximately exponential time dependence of the observed atomic losses. The experimental results (
Figure 4) under different waveforms correlate well with the theoretical analysis. As expected, they exhibit exponential-like behavior in
Figure 6. We consider the evolution of the population of atoms in the trap under different types of ODT modulation.
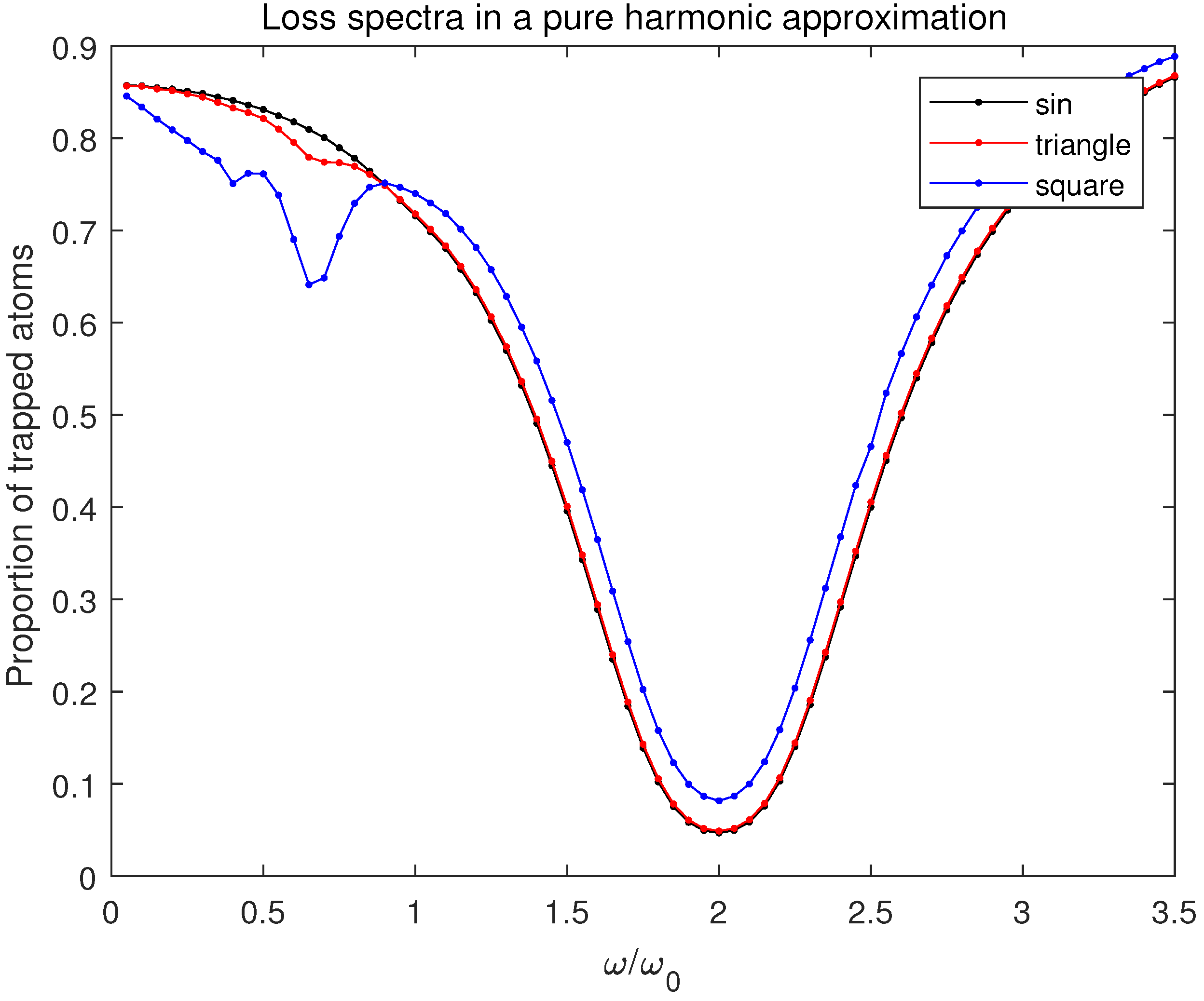
Figure 7 shows the loss spectra at the terminal time
ms computed within the pure harmonic approximation (
) for the three types of the modulation signal. All the spectra exhibit one strong resonance at the frequency of the modulation signal
, reflecting the fact that transitions between the levels separated by
with the uniform energy intervals
are only possible. The case of the square wave (and of the triangle one but much weaker) also exhibits extra resonances at the frequencies
with the odd integer
. These extra resonances occur due to the fact that the square- and triangular-wave signals with the frequencies
contain noticeable harmonics of the majoring resonance frequency
; the ones with even integer
k do not contribute because the corresponding integrals Equation (
15) over the full period
are zero for the kind of signals considered here.
In order to substantiate our approach, we estimated the average time between collisions of the gas kinetic theory as , with our measured values of the atomic spatial density and the mean velocity v, while for the radius R of the sodium atom we took a standard table value of 200 pm. The estimated time was close to 1 s, which is several orders of magnitude longer than the time scale of our experiments. This means that most atoms in the ODT do not experience collisions during the experiment and behave as independent quantum particles in the ODT potential. This justifies our pure quantum-mechanical treatment. On the other hand, we deal with a quite simple model of the ODT potential, so that both our quantum-mechanical and the kinetic approaches remain no more than phenomenological and are appropriate as long as they are able to explain the physics behind the observations. The theoretical model considered the three simple modulation types that can be easily extended to some complex waveform modulation.