Experimental Realization of Reconfigurable Photonic Lattices in Coherent Rydberg Atomic Vapors
Abstract
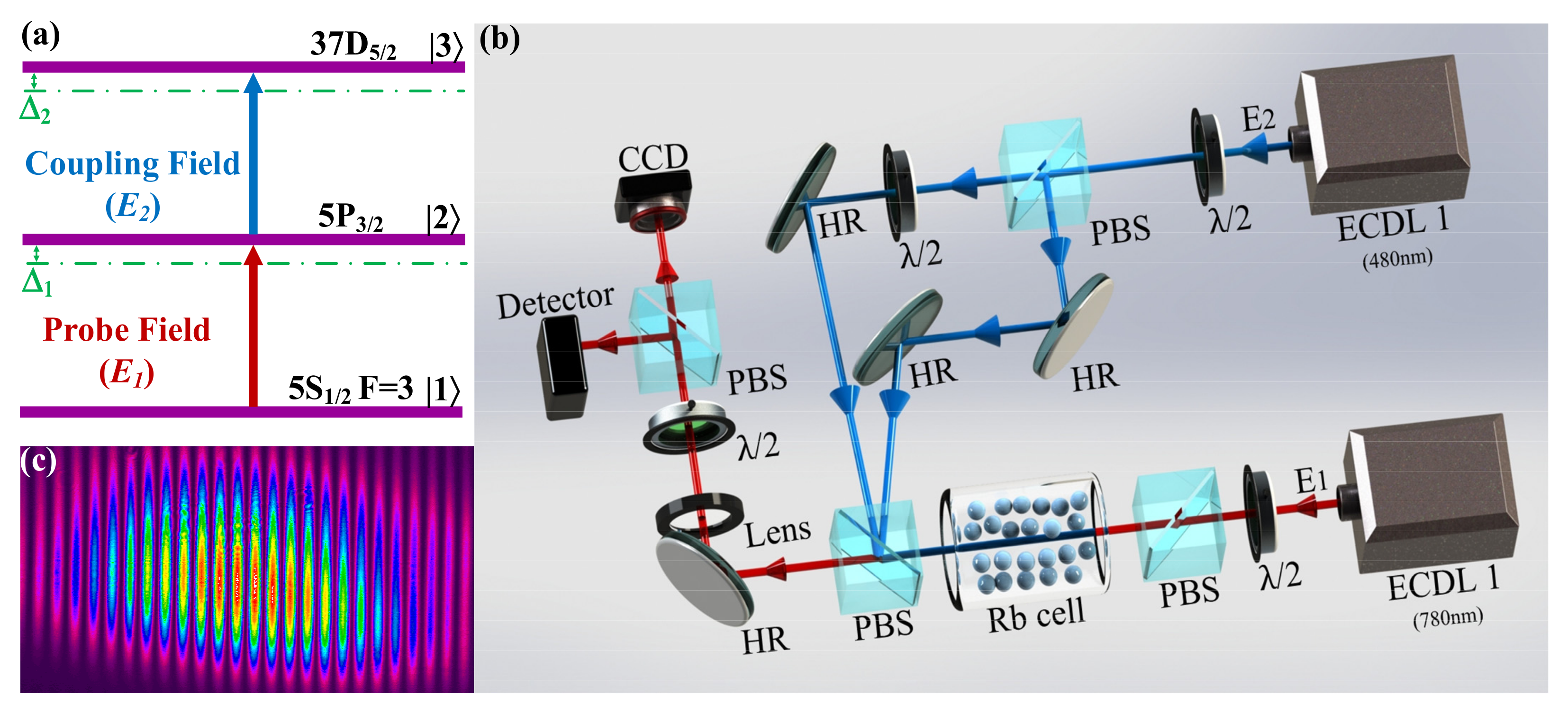
:1. Introduction
2. Experimental Scheme
3. Results
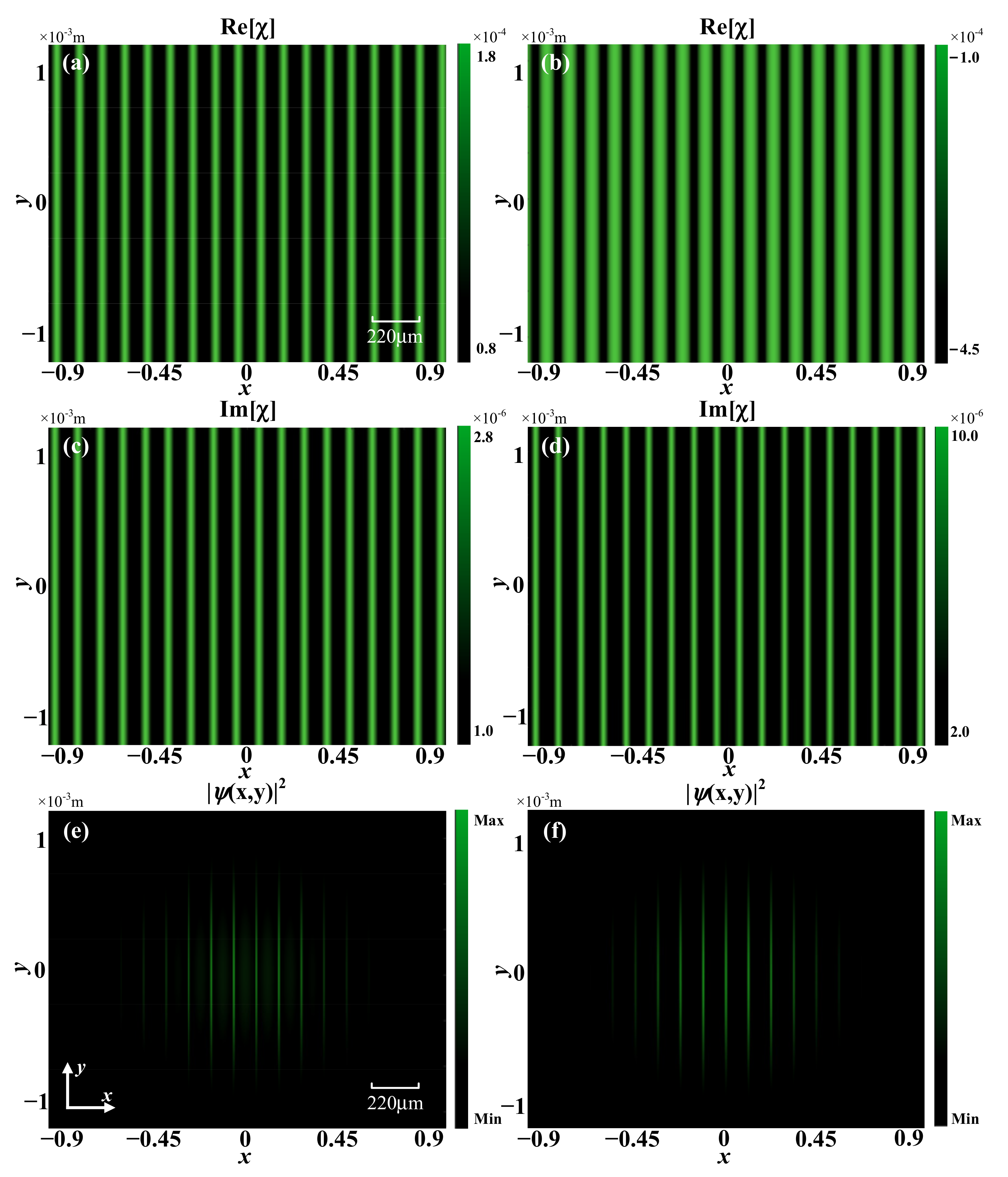
3.1. Theoretical Model
3.2. Experimental Results and Analysis on Manipulating Two-Photon Detuning
3.3. Experimental Results and Analysis on Manipulating Coupling Power
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lim, J.; Lee, H.; Ahn, J. Review of cold Rydberg atoms and their applications. J. Korean Phys. Soc. 2013, 63, 867–876. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, T.F. Rydberg Atoms; Cambridge University: Cambridge, UK, 1994. [Google Scholar]
- Shaffer, J.P.; Rittenhouse, S.T.; Sadeghpour, H.R. Ultracold Rydberg molecules. Nat. Commun. 2018, 9, 1965. [Google Scholar] [CrossRef] [PubMed]
- Dudin, Y.O.; Kuzmich, A. Strongly interacting Rydberg excitations of a cold atomic gas. Science 2012, 336, 887–889. [Google Scholar] [CrossRef] [PubMed]
- Huber, B.; Baluktsian, T.; Schlagmuller, M.; Kolle, A.; Kubler, H.; Low, R.; Pfau, T. GHz Rabi flopping to Rydberg states in hot atomic vapor cells. Phys. Rev. Lett. 2011, 107, 243001. [Google Scholar] [CrossRef] [Green Version]
- Browaeys, A.; Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
- Jing, M.; Hu, Y.; Ma, J.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, S. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 2020, 16, 911–915. [Google Scholar] [CrossRef]
- Gorshkov, A.V.; Otterbach, J.; Fleischhauer, M.; Pohl, T.; Lukin, M.D. Photon-photon interactions via Rydberg blockade. Phys. Rev. Lett. 2011, 107, 133602. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; He, B.; Wu, J.; Zhang, Z.; Xiao, M. Interacting photon pulses in a Rydberg medium. Optica 2016, 3, 1095–1103. [Google Scholar] [CrossRef] [Green Version]
- Spring, J.B.; Metcalf, B.J.; Humphreys, P.C.; Kolthammer, W.S.; Jin, X.; Barbieri, M.; Datta, A.; Thomas-Peter, N.; Langford, N.K.; Kundys, D.; et al. Boson sampling on a photonic chip. Science 2013, 339, 798–801. [Google Scholar] [CrossRef] [Green Version]
- Levine, H.; Keesling, A.; Omran, A.; Bernien, H.; Schwartz, S.; Zibrov, A.S.; Endres, M.; Greiner, M.; Vuletic, V.; Lukin, M.D. High-fidelity control and entanglement of Rydberg-atom qubits. Phys. Rev. Lett. 2018, 121, 123603. [Google Scholar] [CrossRef] [Green Version]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar] [CrossRef]
- Anderson, S.E.; Younge, K.C.; Raithe, G. Trapping Rydberg atoms in an optical lattice. Phys. Rev. Lett. 2011, 107, 263001. [Google Scholar] [CrossRef] [PubMed]
- Omran, A.; Levine, H.; Keesling, A.; Semeghini, G.; Wang, T.; Ebadi, S.; Bernien, H.; Zibrov, A.S.; Pichler, H.; Choi, S.; et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 2019, 365, 570–574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schachenmayer, J.; Lesanovsky, I.; Micheli, A.; Daley, A.J. Dynamical crystal creation with polar molecules or Rydberg atoms in optical lattices. New J. Phys. 2010, 12, 103044. [Google Scholar] [CrossRef]
- Zeiher, J.; Bijnen, R.; Schauss, P.; Hild, S.; Choi, J.Y.; Pohl, T.; Bloch, I.; Gross, C. Many-body interferometry of a Rydberg-dressed spin lattice. Nat. Phys. 2016, 12, 1095–1099. [Google Scholar] [CrossRef]
- De Léséleuc, S.; Lienhard, V.; Scholl, P.; Barredo, D.; Weber, S.; Lang, N.; Buchler, H.; Lahaye, T.; Browaeys, A. Observation of a symmetry-protected topological phase of interacting bosons with Rydberg atoms. Science 2019, 365, 775–780. [Google Scholar] [CrossRef] [Green Version]
- Kanungo, S.K.; Whalen, J.D.; Lu, Y.; Yuan, M.; Dasgupta, S.; Dunning, F.B.; Hazzard, K.R.A.; Killian, T.C. Realizing topological edge states with Rydberg-atom synthetic dimensions. Nat. Commun. 2022, 13, 972. [Google Scholar] [CrossRef]
- Xu, S.; Li, H.; Qin, Z.; Zhou, G.; Belic, M.; He, J.; Zhao, Y.; Zhao, D. Parity-time symmetry light bullets in a cold Rydberg atomic gas. Opt. Express 2020, 28, 16322–16332. [Google Scholar] [CrossRef]
- Hang, C.; Huang, G. Parity-time symmetry along with nonlocal optical solitons and their active controls in a Rydberg atomic gas. Phys. Rev. A 2018, 98, 043840. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Z.; Bienias, P.; Iadecola, T.; Gorshkov, A.V. Localization and criticality in antiblockaded two-dimensional Rydberg atom arrays. Phys. Rev. Lett. 2022, 128, 013603. [Google Scholar] [CrossRef]
- Moreno-Cardoner, M.; Goncalves, D.; Chang, D.E. Quantum nonlinear optics based on two-dimensional Rydberg atom arrays. Phys. Rev. Lett. 2021, 127, 263602. [Google Scholar] [CrossRef] [PubMed]
- Geabanacloche, J.; Li, Y.; Jin, S.; Xiao, M. Electromagnetically induced transparency in ladder-type inhomogeneously broadened media: Theory and experiment. Phys. Rev. A 1995, 51, 576. [Google Scholar] [CrossRef] [PubMed]
- Petrosyan, D.; Otterbach, J.; Fleischhauer, M. Electromagnetically induced transparency with Rydberg atoms. Phys. Rev. Lett. 2011, 107, 213601. [Google Scholar] [CrossRef] [PubMed]
- Ning, S.; Lu, J.; Liang, S.; Feng, Y.; Li, C.; Zhang, Z.; Zhang, Y. Talbot effect of an electromagnetically induced square photonic lattice assisted by a spatial light modulator. Opt. Lett. 2021, 46, 5035–5038. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, C.; Wang, L.; Chen, G.; Jia, S. Observation of diffraction pattern in two-dimensional optically induced atomic lattice. Opt. Lett. 2019, 44, 4123–4126. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, Y.; Ning, S.; Liang, S.; Feng, Y.; Li, C.; Zhang, Y.; Xiao, M. Transport of light in a moving photonic lattice via atomic coherence. Opt. Lett. 2021, 46, 4096–4099. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, X.; Zeng, J. Electromagnetically induced moiré optical lattices in a coherent atomic gas. Front. Phys. 2022, 17, 42508. [Google Scholar] [CrossRef]
- Sheng, J.; Wang, J.; Miri, M.A.; Christodoulides, D.N.; Xiao, M. Observation of discrete diffraction patterns in an optically induced lattice. Opt. Express 2015, 23, 19777–19782. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Yuan, J.; Dong, S.; Wu, C.; Wang, L. Observation of an electromagnetically induced grating in cold 85Rb atoms. Appl. Sci. 2020, 10, 5740. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, J.; Liu, X.; Sheng, J.; Zhang, Y.; Zhang, Y.; Xiao, M. Controllable photonic crystal with periodic Raman gain in a coherent atomic medium. Opt. Lett. 2018, 43, 919–922. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, R.; Zhang, Y.; Kartashov, Y.; Li, F.; Zhong, H.; Guan, H.; Gao, K.; Li, F.; Zhang, Y.; et al. Observation of Edge Solitons in Photonic Graphene. Nat. Commun. 2020, 11, 1902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, H.; Yuan, J.; Dong, S.; Wu, C.; Wang, L.; Xiao, L.; Jia, S. All-optical tunable high-order Gaussian beam splitter based on a periodic dielectric atomic structure. Opt. Express 2021, 29, 25439–25448. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Dong, S.; Zhang, H.; Wu, C.; Wang, L.; Xiao, L.; Jia, S. Efficient all-optical modulator based on a periodic dielectric atomic lattice. Opt. Express 2021, 29, 2712–2719. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, Y.; Ning, S.; Malpuech, G.; Solnyshkov, D.; Xu, Z.; Zhang, Y.; Xiao, M. Imaging lattice switching with Talbot effect in reconfigurable non-Hermitian photonic graphene. Photon. Res. 2022, 10, 958–964. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, S.; Li, F.; Ning, S.; Li, Y.; Guillaume, M.; Zhang, Y.; Xiao, M.; Solnyshkov, D. Spin-orbit coupling in photonic graphene. Optica 2020, 7, 455–462. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, F.; Malpuech, G.; Zhang, Y.; Bleu, O.; Koniakhin, S.; Li, C.; Zhang, Y.; Xiao, M.; Solnyshkov, D. Particle-like behavior of topological defects in linear wave packets in photonic graphene. Phys. Rev. Lett. 2019, 122, 233905. [Google Scholar] [CrossRef] [Green Version]
- Mohapatra, A.K.; Jackson, T.R.; Adams, C.S. Coherent optical detection of highly excited Rydberg states using electromagnetically induced transparency. Phys. Rev. Lett. 2007, 98, 113003. [Google Scholar] [CrossRef] [Green Version]
- Xiao, M.; Li, Y.; Jin, S.; Gea-Banacloche, J. Measurement of dispersive properties of electromagnetically induced transparency in rubidium atoms. Phys. Rev. Lett. 1995, 74, 666–669. [Google Scholar] [CrossRef]
- Yuan, J.; Dong, S.; Wu, C.; Wang, L.; Xiao, L.; Jia, S. Optically tunable grating in a V+Ξ configuration involving a Rydberg state. Opt. Express 2020, 28, 23820–23828. [Google Scholar] [CrossRef]
- Chen, C.; Yang, F.; Wu, X.; Shen, C.; Tey, M.K.; You, L. Two-color optical nonlinearity in an ultracold Rydberg atom gas mixture. Phys. Rev. A 2021, 103, 053303. [Google Scholar] [CrossRef]
- Hang, C.; Li, W.; Huang, G. Nonlinear light diffraction by electromagnetically induced gratings with PT symmetry in a Rydberg atomic gas. Phys. Rev. A 2019, 100, 043807. [Google Scholar] [CrossRef]
- Bai, Z.; Li, W.; Huang, G. Stable single light bullets and vortices and their active control in cold Rydberg gases. Optica 2019, 6, 309–317. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, Q.; Zhao, D.; Belic, M.; Zhao, Y. Spatiotemporal solitons in cold Rydberg atomic gases with Bessel optical lattices. Appl. Math. Lett. 2020, 106, 106230. [Google Scholar] [CrossRef]
- Walther, V.; Johne, R.; Pohl, T. Giant optical nonlinearities from Rydberg excitons in semiconductor microcavities. Nat. Commun. 2018, 9, 1309. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, S.; Yu, Q.; Lei, X.; Ning, S.; Li, C.; Zhang, Y.; Zhang, Z. Experimental Realization of Reconfigurable Photonic Lattices in Coherent Rydberg Atomic Vapors. Photonics 2022, 9, 422. https://doi.org/10.3390/photonics9060422
Liang S, Yu Q, Lei X, Ning S, Li C, Zhang Y, Zhang Z. Experimental Realization of Reconfigurable Photonic Lattices in Coherent Rydberg Atomic Vapors. Photonics. 2022; 9(6):422. https://doi.org/10.3390/photonics9060422
Chicago/Turabian StyleLiang, Shun, Qingsong Yu, Xing Lei, Shaohuan Ning, Changbiao Li, Yanpeng Zhang, and Zhaoyang Zhang. 2022. "Experimental Realization of Reconfigurable Photonic Lattices in Coherent Rydberg Atomic Vapors" Photonics 9, no. 6: 422. https://doi.org/10.3390/photonics9060422
APA StyleLiang, S., Yu, Q., Lei, X., Ning, S., Li, C., Zhang, Y., & Zhang, Z. (2022). Experimental Realization of Reconfigurable Photonic Lattices in Coherent Rydberg Atomic Vapors. Photonics, 9(6), 422. https://doi.org/10.3390/photonics9060422





