Refractive Bi-Conic Axicon (Volcone) for Polarization Conversion of Monochromatic Radiation
Abstract
:1. Introduction
2. Theory and Simulation
2.1. Theoretical Description of the Method for Calculating the Beam Path
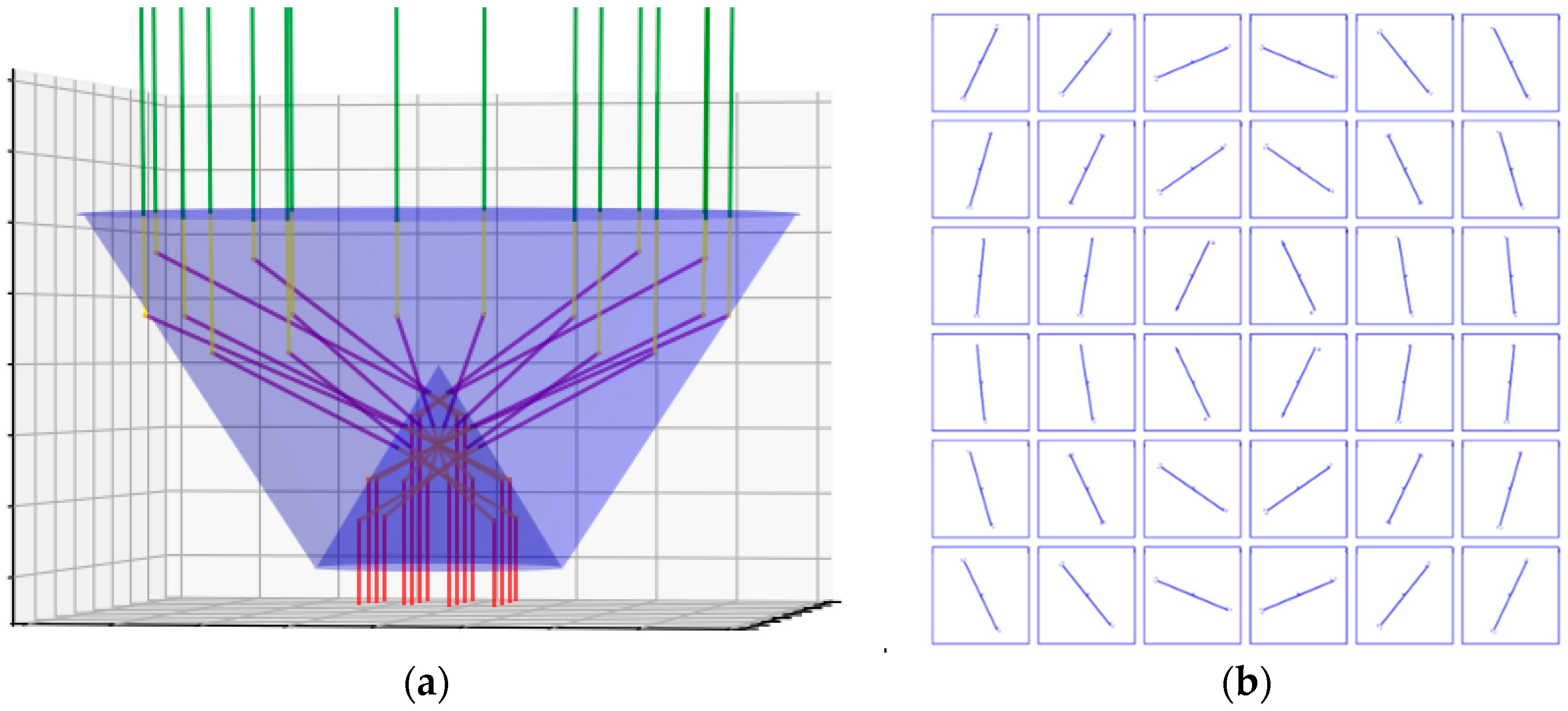
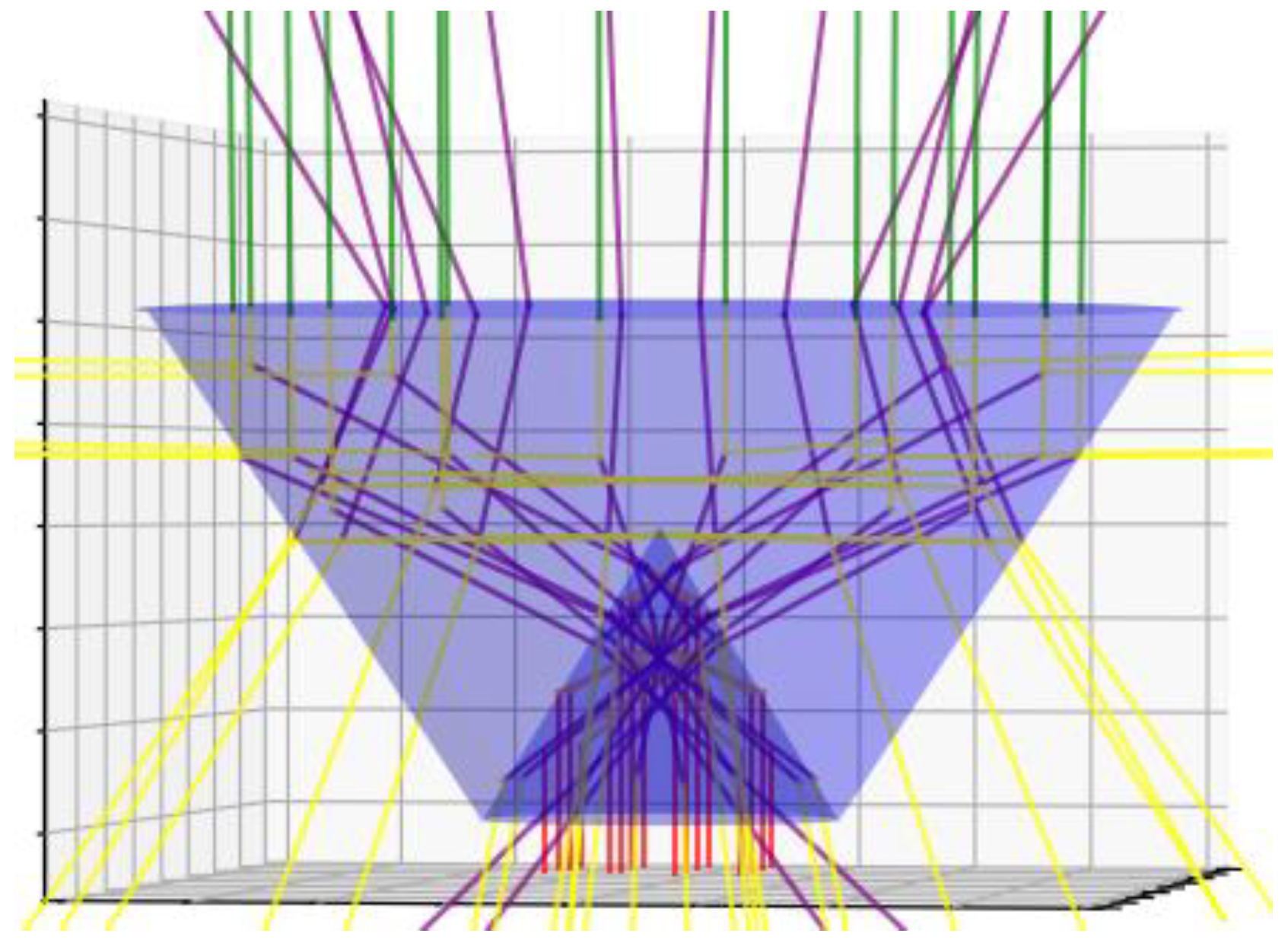
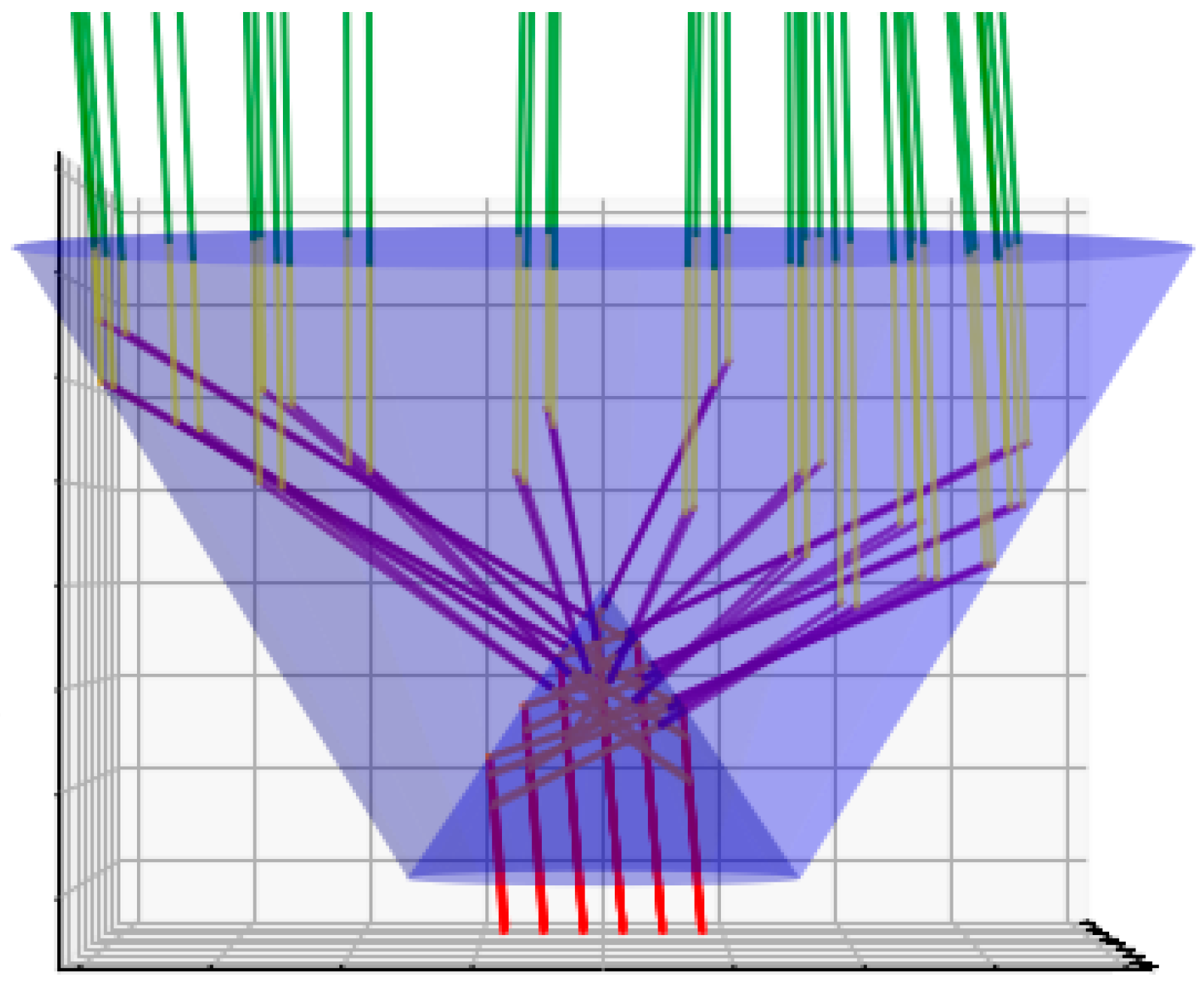
2.2. Calculation of the Path of the Beams through a Volcone
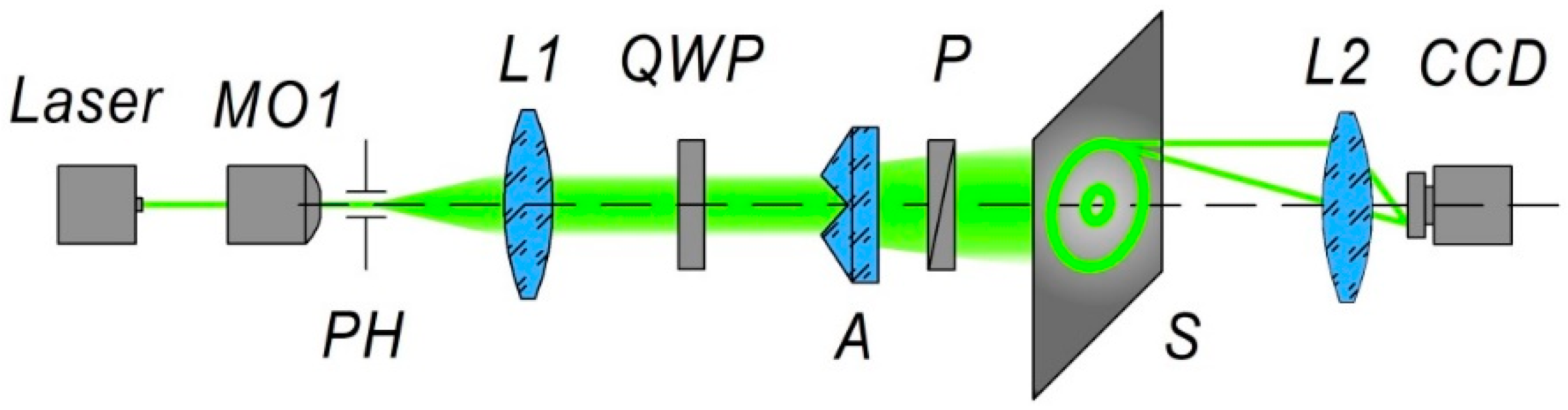
3. Materials and Methods
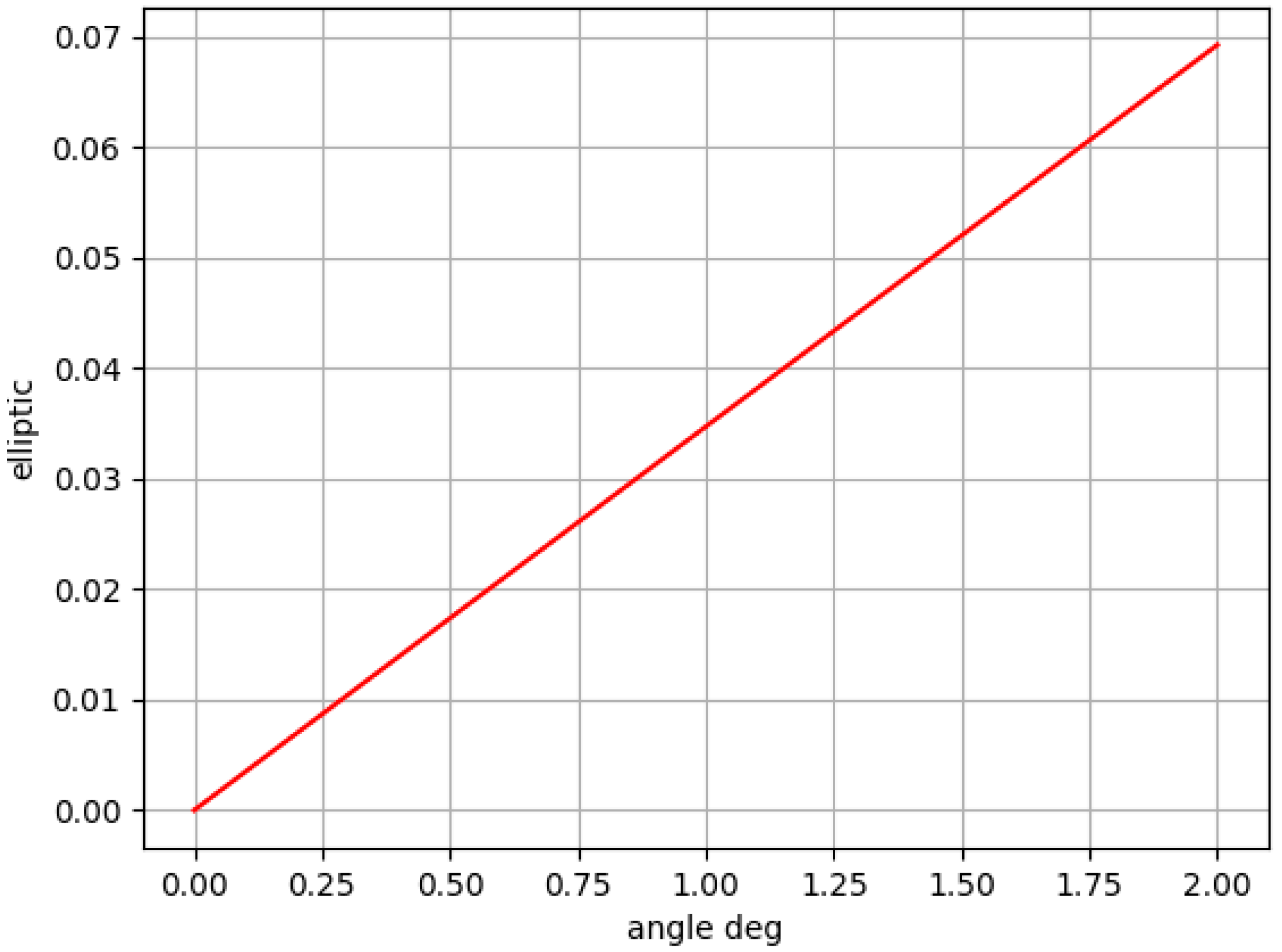
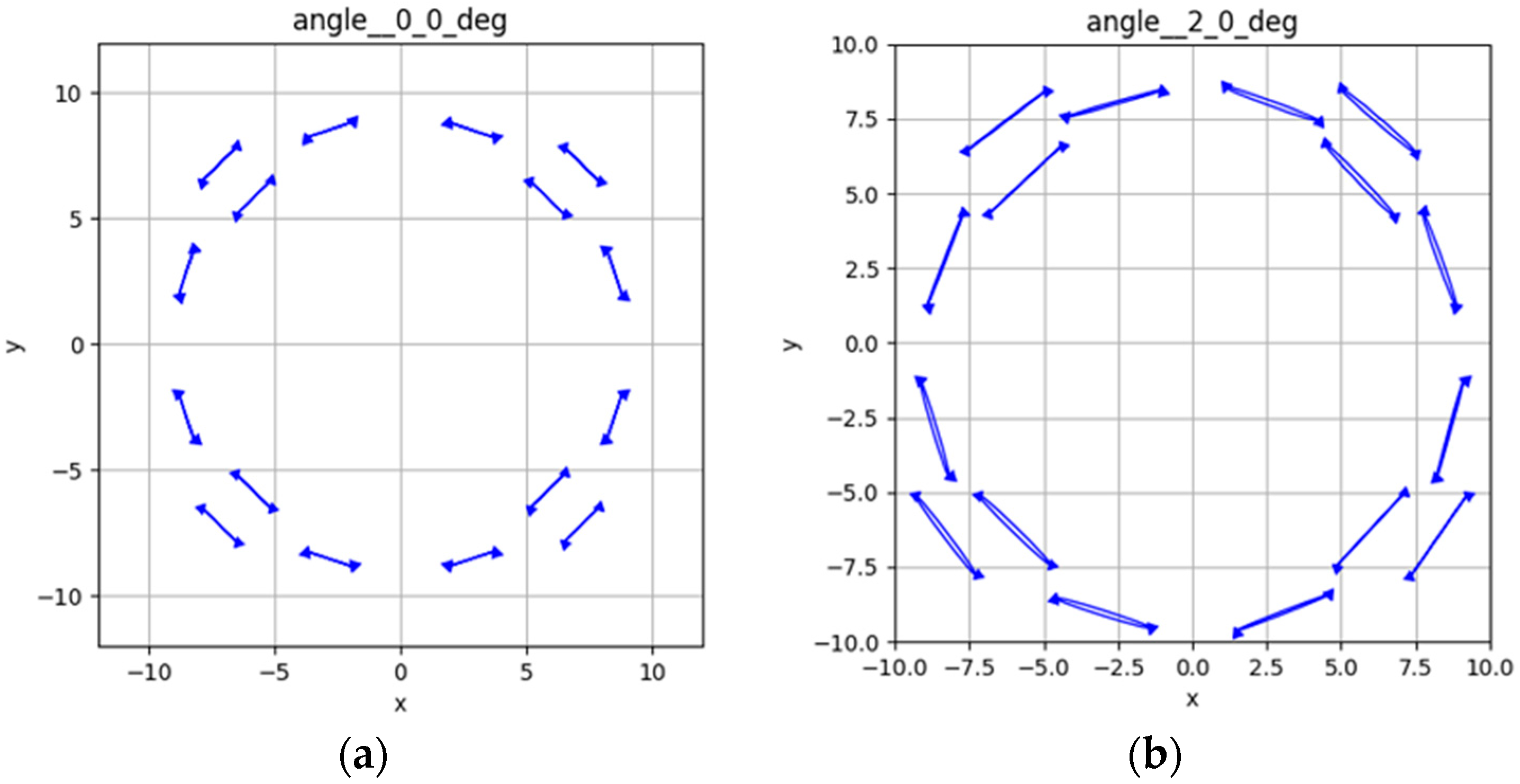
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Goldstein, D.H. Polarized Light; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Freund, I. Polarization flowers. Opt. Commun. 2001, 199, 47–63. [Google Scholar] [CrossRef]
- Maurer, C.; Jesacher, A.; Fürhapter, S.; Bernet, S.; RitschMarte, M. Tailoring of arbitrary optical vector beams. New J. Phys. 2007, 9, 78. [Google Scholar] [CrossRef]
- Wang, X.L.; Li, Y.; Chen, J.; Guo, C.S.; Ding, J.; Wang, H.T. A new type of vector fields with hybrid states of polarization. Opt. Express 2010, 18, 10786–10795. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Karpeev, S.V. Grating-based optical scheme for the universal generation of inhomogeneously polarized laser beams. Appl. Opt. 2010, 49, 1734–1738. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; She, W. Generation of tunable three-dimensional polarization in 4Pi focusing system. Opt. Express 2013, 21, 17265–17274. [Google Scholar] [CrossRef]
- Rong, Z.-Y.; Han, Y.-J.; Wang, S.-Z.; Guo, C.-S. Generation of arbitrary vector beams with cascaded liquid crystal spatial light modulators. Opt. Express 2014, 22, 1636–1644. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Ke, Y.; Liu, Y.; Shu, W.; Luo, H.; Wen, S. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere. Photon. Res. 2017, 5, 15–21. [Google Scholar] [CrossRef] [Green Version]
- Bauer, T.; Banzer, P.; Bouchard, F.; Orlov, S.; Marrucci, L.; Santamato, E.; Boyd, R.W.; Karimi, E.; Leuchs, G. Multi-twist polarization ribbon topologies in highly-confined optical fields. New J. Phys. 2019, 21, 053020. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Vector Lissajous laser beams. Opt. Lett. 2020, 45, 4112–4115. [Google Scholar] [CrossRef]
- Zhong, R.Y.; Zhu, Z.H.; Wu, H.J.; Rosales-Guzmán, C.; Song, S.W.; Shi, B.S. Gouy phase-mediated propagation variations and revivals of transverse structure in vectorially structured light. Phys. Rev. A 2021, 103, 053520. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P. Harnessing of inhomogeneously polarized Hermite–Gaussian vector beams to manage the 3D spin angular momentum density distribution. Nanophotonics 2022, 11, 697–712. [Google Scholar] [CrossRef]
- Milione, G.; Nguyen, T.A.; Leach, J.; Nolan, D.A.; Alfano, R.R. Using the nonseparability of vector beams to encode information for optical communication. Opt. Lett. 2015, 40, 4887–4890. [Google Scholar] [CrossRef] [PubMed]
- Akent’ev, A.S.; Sadovnikov, M.A.; Sokolov, A.L.; Simonov, G.V. Polarization analysis of the beam-steering device of quantum optical systems. Opt. Spectrosc. 2017, 122, 1008–1014. [Google Scholar] [CrossRef]
- Ndagano, B.; Nape, I.; Cox, M.A.; Rosales-Guzman, C.; Forbes, A. Creation and detection of vector vortex modes for classical and quantum communication. J. Lightwave Technol. 2018, 36, 292–301. [Google Scholar] [CrossRef] [Green Version]
- Karpeev, S.V.; Podlipnov, V.V.; Khonina, S.N.; Ivliev, N.A.; Ganchevskay, S.V. Free-space transmission and detection of variously polarized near-IR beams using standard communication systems with embedded singular phase structures. Sensors 2022, 22, 890–907. [Google Scholar] [CrossRef]
- Oron, D.; Tal, E.; Silberberg, Y. Depth-resolved multiphoton polarization microscopy by third-harmonic generation. Opt. Lett. 2003, 28, 2315–2317. [Google Scholar] [CrossRef]
- Serrels, K.; Ramsay, E.; Warburton, R.; Reid, D. Nanoscale optical microscopy in the vectorial focusing regime. Nat. Photonics 2008, 2, 311–314. [Google Scholar] [CrossRef]
- Kenny, F.; Lara, D.; Rodríguez-Herrera, O.; Dainty, C. Complete polarization and phase control for focus-shaping in high-NA microscopy. Opt. Express 2012, 20, 14015–14029. [Google Scholar] [CrossRef] [Green Version]
- Skelton, S.; Sergides, M.; Saija, R.; Iati, M.; Marago, O.; Jones, P. Trapping volume control in optical tweezers using cylindrical vector beams. Opt. Lett. 2013, 38, 28–30. [Google Scholar] [CrossRef]
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7, 041308. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Gorodetski, Y.; Niv, A.; Kleiner, V.; Hasman, E. Observation of the spin-based plasmonic effect in nanoscale structures. Phys. Rev. Lett. 2008, 101, 043903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beresna, M.; Gecevičius, M.; Kazansky, P.G.; Gertus, T. Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass. Appl. Phys. Lett. 2011, 98, 201101. [Google Scholar] [CrossRef]
- Mller, T.; Schumann, C.; Kraegeloh, A. STED Microscopy and its applications: New insights into cellular processes on the nanoscale. Chemphyschem 2012, 13, 1986–2000. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Golub, I. How low can STED go? Comparison of different write-erase beam combinations for stimulated emission depletion microscopy. J. Opt. Soc. Am. A 2012, 29, 2242–2246. [Google Scholar] [CrossRef]
- Varin, C.; Payeur, S.; Marceau, V.; Fourmaux, S.; April, A.; Schmidt, B.; Fortin, P.-L.; Thire, N.; Brabec, T.; Legare, F.; et al. Direct electron acceleration with radially polarized laser beams. Appl. Sci. 2013, 3, 70–93. [Google Scholar] [CrossRef] [Green Version]
- Ni, J.; Wang, C.; Zhang, C.; Hu, Y.; Yang, L.; Lao, Z.; Chu, J. Three-dimensional chiral microstructures fabricated by structured optical vortices in isotropic material. Light Sci. Appl. 2017, 6, e17011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Syubaev, S.A.; Zhizhchenko, A.Y.; Pavlov, D.V.; Gurbatov, S.O.; Pustovalov, E.V.; Porfirev, A.P.; Khonina, S.N.; Kulinich, S.A.; Rayappan, J.B.B.; Kudryashov, S.I.; et al. Plasmonic nanolenses produced by cylindrical vector beam printing for sensing applications. Sci. Rep. 2019, 9, 19750. [Google Scholar] [CrossRef] [Green Version]
- Porfirev, A.P.; Khonina, S.N.; Meshalkin, A.; Ivliev, N.A.; Achimova, E.; Abashkin, V.; Prisacar, A.; Podlipnov, V.V. Two-step maskless fabrication of compound fork-shaped gratings in nanomultilayer structures based on chalcogenide glasses. Opt. Lett. 2021, 46, 3037–3040. [Google Scholar] [CrossRef]
- Masuda, K.; Nakano, S.; Barada, D.; Kumakura, M.; Miyamoto, K.; Omatsu, T. Azo-polymer film twisted to form a helical surface relief by illumination with a circularly polarized Gaussian beam. Opt. Express 2017, 25, 12499–12507. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Volotovskiy, S.G.; Ivliev, N.A.; Podlipnov, V.V. Influence of optical forces induced by paraxial vortex Gaussian beams on the formation of a microrelief on carbazole-containing azopolymer films. Appl. Opt. 2020, 59, 9185–9194. [Google Scholar] [CrossRef] [PubMed]
- Kharintsev, S.S.; Fishman, A.I.; Kazarian, S.G.; Salakhov, M.K. Polarization of near-field light induced with a plasmonic nanoantenna. Phys. Rev. B 2015, 92, 115113. [Google Scholar] [CrossRef]
- Masuda, K.; Shinozaki, R.; Shiraishi, A.; Ichijo, M.; Yamane, K.; Miyamoto, K.; Omatsu, T. Picosecond optical vortex-induced chiral surface relief in an azo-polymer film. J. Nanophoton. 2020, 14, 016012. [Google Scholar] [CrossRef] [Green Version]
- Ferrer-Garcia, M.F.; Alvandi, Y.; Zhang, Y.; Karimi, E. Theoretical analysis on spatially structured beam induced mass transport in azo-polymer films. Opt. Express 2020, 28, 19954–19965. [Google Scholar] [CrossRef] [PubMed]
- Tidwell, S.C.; Ford, D.H.; Kimura, W.D. Generating radially polarized beams interferometrically. Appl. Opt. 1990, 29, 2234–2239. [Google Scholar] [CrossRef] [PubMed]
- Passilly, N.; de Saint, D.R.; Aït-Ameur, K.; Treussart, F.; Hierle, R.; Roch, J.-F. Simple interferometric technique for generation of a radially polarized light beam. J. Opt. Soc. Am. A 2005, 22, 984–991. [Google Scholar] [CrossRef]
- Liu, S.; Li, P.; Peng, T.; Zhao, J. Generation of arbitrary spatially variant polarization beams with a trapezoid Sagnac interferometer. Opt. Express 2012, 20, 21715–21721. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V. Generating inhomogeneously polarized higher-order laser beams by use of diffractive optical elements. J. Opt. Soc. Am. A 2011, 28, 2115–2123. [Google Scholar] [CrossRef]
- Sokolov, A.L.; Murashkin, V.V. Diffraction polarization optical elements with radial symmetry. Opt. Spectrosc. 2011, 111, 859–865. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Ustinov, A.V.; Khonina, S.N. Polarization conversion when focusing cylindrically polarized vortex beams. Sci. Rep. 2016, 6, 6. [Google Scholar] [CrossRef] [Green Version]
- Moreno, I.; Davis, J.A.; Hernandez, T.M.; Cottrell, D.M.; Sand, D. Complete polarization control of light from a liquid crystal spatial light modulator. Opt. Express 2012, 20, 364–376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karpeev, S.V.; Podlipnov, V.V.; Algubili, A.M. An interference scheme for generating inhomogeneously polarized laser radiation using a spatial light modulator. Comput. Opt. 2020, 44, 214–218. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Radially and azimuthally polarized beams generated by space-variant dielectric subwavelength gratings. Opt. Lett. 2002, 27, 285–287. [Google Scholar] [CrossRef] [PubMed]
- Lerman, G.M.; Levy, U. Generation of a radially polarized light beam using space-variant subwavelength gratings at 1064 nm. Opt. Lett. 2008, 33, 2782–2784. [Google Scholar] [CrossRef]
- Rubin, N.A.; Zaidi, A.; Juhl, M.; Li, R.P.; Mueller, J.B.; Devlin, R.C.; Leosson, K.; Capasso, F. Polarization state generation and measurement with a single metasurface. Opt. Express 2018, 26, 21455–21478. [Google Scholar] [CrossRef] [Green Version]
- Khonina, S.N.; Degtyarev, S.A.; Ustinov, A.V.; Porfirev, A.P. Metalenses for the generation of vector Lissajous beams with a complex Poynting vector density. Opt. Express 2021, 29, 18651–18662. [Google Scholar] [CrossRef]
- Machavariani, G.; Lumer, Y.; Moshe, I.; Meir, A.; Jackel, S.; Davidson, N. Birefringence-induced bifocusing for selection of radially or azimuthally polarized laser modes. Appl. Opt. 2007, 46, 3304–3310. [Google Scholar] [CrossRef]
- Karpeev, S.V.; Podlipnov, V.V.; Khonina, S.N.; Paranin, V.D.; Tukmakov, K.N. Anisotropic diffractive optical element for generating hybrid-polarized beams. Opt. Eng. 2019, 58, 082402. [Google Scholar]
- Loussert, C.; Brasselet, E. Efficient scalar and vectorial singular beam shaping using homogeneous anisotropic media. Opt. Lett. 2010, 35, 7–9. [Google Scholar] [CrossRef]
- Fadeyeva, T.A.; Shvedov, V.G.; Izdebskaya, Y.V.; Volyar, A.V.; Brasselet, E.; Neshev, D.N.; Desyatnikov, A.S.; Krolikowski, W.; Kivshar, Y.S. Spatially engineered polarization states and optical vortices in uniaxial crystals. Opt. Express 2010, 18, 10848–10863. [Google Scholar]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D.; Morozov, A.A. Polarization conversion under focusing of vortex laser beams along the axis of anisotropic crystals. Phys. Lett. A 2017, 381, 2444–2455. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Kazanskiy, N.L. Variable transformation of singular cylindrical vector beams using anisotropic crystals. Sci. Rep. 2020, 10, 5590. [Google Scholar] [CrossRef] [PubMed]
- Tovar, A.A. Production and propagation of cylindrically polarized Laguerre–Gaussian laser beams. J. Opt. Soc. Am. A 1998, 15, 2705–2711. [Google Scholar] [CrossRef]
- Kozawa, Y.; Sato, S. Generation of a radially polarized laser beam by use of a conical Brewster prism. Opt. Lett. 2005, 30, 3063–3065. [Google Scholar] [CrossRef] [PubMed]
- Radwell, N.; Hawley, R.D.; Gotte, J.B.; Franke-Arnold, S. Achromatic vector vortex beams from a glass cone. Nat. Commun. 2016, 7, 10654. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zeng, A.; Wang, Y.; Huang, H. A method for measuring the base angle of axicon lens based on chromatic dispersion. Opt. Commun. 2015, 346, 69–73. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, Q.; Ma, X.; Hu, J.; Zeng, A.; Huang, H. Measurement of base angle of an axicon lens based on autocollimation optical path. Opt. Commun. 2019, 434, 23–27. [Google Scholar] [CrossRef]
- Skidanov, R.V.; Morozov, A.A. Diffractive optical elements for forming radially polarized light, based on the use stack of Stoletov. Comput. Opt. 2014, 38, 614–618. [Google Scholar] [CrossRef]
- Karpeev, S.V.; Paranin, V.D.; Khonina, S.N. Generation of a controlled double-ring-shaped radially polarized spiral laser beam using a combination of a binary axicon with an interference polarizer. J. Opt. 2017, 19, 055701. [Google Scholar] [CrossRef]
- Khonina, S.N.; Tukmakov, K.N.; Degtyarev, S.A.; Reshetnikov, A.S.; Pavelyev, V.S.; Knyazev, B.A.; Choporova, Y.Y. Design, fabrication and investigation of a subwavelength axicon for terahertz beam polarization transforming. Comput. Opt. 2019, 43, 756–764. [Google Scholar] [CrossRef]
- Urbach, H.P.; Pereira, S.F. Field in Focus with a Maximum Longitudinal Electric Component. Phys. Rev. Lett. 2008, 100, 123904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khonina, S.N.; Savelyev, D.A. High-aperture binary axicons for the formation of the longitudinal electric field component on the optical axis for linear and circular polarizations of the illuminating beam. J. Exp. Theor. Phys. 2013, 117, 623–630. [Google Scholar] [CrossRef]
- Ustinov, A.V.; Khonina, S.N. Calculation of complex transmission function of refractive axicons. Comput. Opt. 2011, 35, 480–490. [Google Scholar]
- Khonina, S.N.; Degtyarev, S.A.; Savelyev, D.A.; Ustinov, A.V. Focused, evanescent, hollow, and collimated beams formed by microaxicons with different conical angles. Opt. Express 2017, 25, 19052–19064. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.-J.; Noh, H.; Hong, M.-H.; Noh, H.-R.; Arakawa, Y.; Jhe, W. Focusing characteristics of optical fiber axicon microlens for near-field spectroscopy: Dependence of tip apex angle. Opt. Commun. 2006, 267, 264–270. [Google Scholar] [CrossRef]
- Grosjean, T.; Saleh, S.S.; Suarez, M.A.; Ibrahim, I.A.; Piquerey, V.; Charraut, D.; Sandoz, P. Fiber microaxicons fabricated by a polishing technique for the generation of Bessel-like beams. Appl. Opt. 2007, 46, 8061–8067. [Google Scholar] [CrossRef]
- Žukauskas, A.; Malinauskas, M.; Brasselet, E. Monolithic generators of pseudo-nondiffracting optical vortex beams at the microscale. Appl. Phys. Lett. 2013, 103, 181122. [Google Scholar] [CrossRef] [Green Version]
- Chi, W.; George, N. Electronic imaging using a logarithmic sphere. Opt. Lett. 2001, 26, 875–877. [Google Scholar] [CrossRef]
- Golub, I.; Chebbi, B.; Shaw, D.; Nowacki, D. Characterization of a refractive logarithmic axicon. Opt. Lett. 2010, 35, 2828–2830. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V. Very compact focal spot in the near-field of the fractional axicon. Opt. Commun. 2017, 391, 24–29. [Google Scholar] [CrossRef]
- Gorelick, S.; Paganin, D.M.; de Marco, A. Axilenses: Refractive micro-optical elements with arbitrary exponential profiles. APL Photonics 2020, 5, 106110. [Google Scholar] [CrossRef]
- Sanchez-Padilla, B.; Žukauskas, A.; Aleksanyan, A.; Balčytis, A.; Malinauskas, M.; Juodkazis, S.; Brasselet, E. Wrinkled axicons: Shaping light from cusps. Opt. Express 2016, 24, 24075–24082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khonina, S.N.; Krasnov, S.V.; Ustinov, A.V.; Degtyarev, S.A.; Porfirev, A.P.; Kuchmizhak, A.; Kudryashov, S.I. Refractive twisted microaxicons. Opt. Lett. 2020, 45, 1334–1337. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Acuña, R.G.; Guitiérrez-Vega, J.C. Generalization of the axicon shape: The gaxicon. J. Opt. Soc. Am. A 2018, 35, 1915–1918. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Khorin, P.A.; Butt, M.A. Modern Types of Axicons: New Functions and Applications. Sensors 2021, 21, 6690. [Google Scholar] [CrossRef]
- Sokolov, A.L. Calculation of polarization aberrations by the method of polarization-wave matrices. Opt. Spectrosc. 2007, 103, 640–645. [Google Scholar] [CrossRef]
- Khonina, S.N. Vortex beams with high-order cylindrical polarization: Features of focal distributions. Appl. Phys. B 2019, 125, 100. [Google Scholar] [CrossRef]
- Kharitonov, S.I.; Khonina, S.N. Conversion of a conical wave with circular polarization into a vortex cylindrically polarized beam in a metal waveguide. Comput. Opt. 2018, 42, 197–211. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Degtyarev, S.A.; Karpeev, S.V.; Ivliev, N.A.; Strelkov, Y.S.; Podlipnov, V.V.; Khonina, S.N. Refractive Bi-Conic Axicon (Volcone) for Polarization Conversion of Monochromatic Radiation. Photonics 2022, 9, 421. https://doi.org/10.3390/photonics9060421
Degtyarev SA, Karpeev SV, Ivliev NA, Strelkov YS, Podlipnov VV, Khonina SN. Refractive Bi-Conic Axicon (Volcone) for Polarization Conversion of Monochromatic Radiation. Photonics. 2022; 9(6):421. https://doi.org/10.3390/photonics9060421
Chicago/Turabian StyleDegtyarev, Sergey A., Sergey V. Karpeev, Nikolay A. Ivliev, Yuriy S. Strelkov, Vladimir V. Podlipnov, and Svetlana N. Khonina. 2022. "Refractive Bi-Conic Axicon (Volcone) for Polarization Conversion of Monochromatic Radiation" Photonics 9, no. 6: 421. https://doi.org/10.3390/photonics9060421
APA StyleDegtyarev, S. A., Karpeev, S. V., Ivliev, N. A., Strelkov, Y. S., Podlipnov, V. V., & Khonina, S. N. (2022). Refractive Bi-Conic Axicon (Volcone) for Polarization Conversion of Monochromatic Radiation. Photonics, 9(6), 421. https://doi.org/10.3390/photonics9060421





