Two-Dimension Asymmetric Electromagnetically Induced Grating in Rydberg Atoms
Abstract
1. Introduction
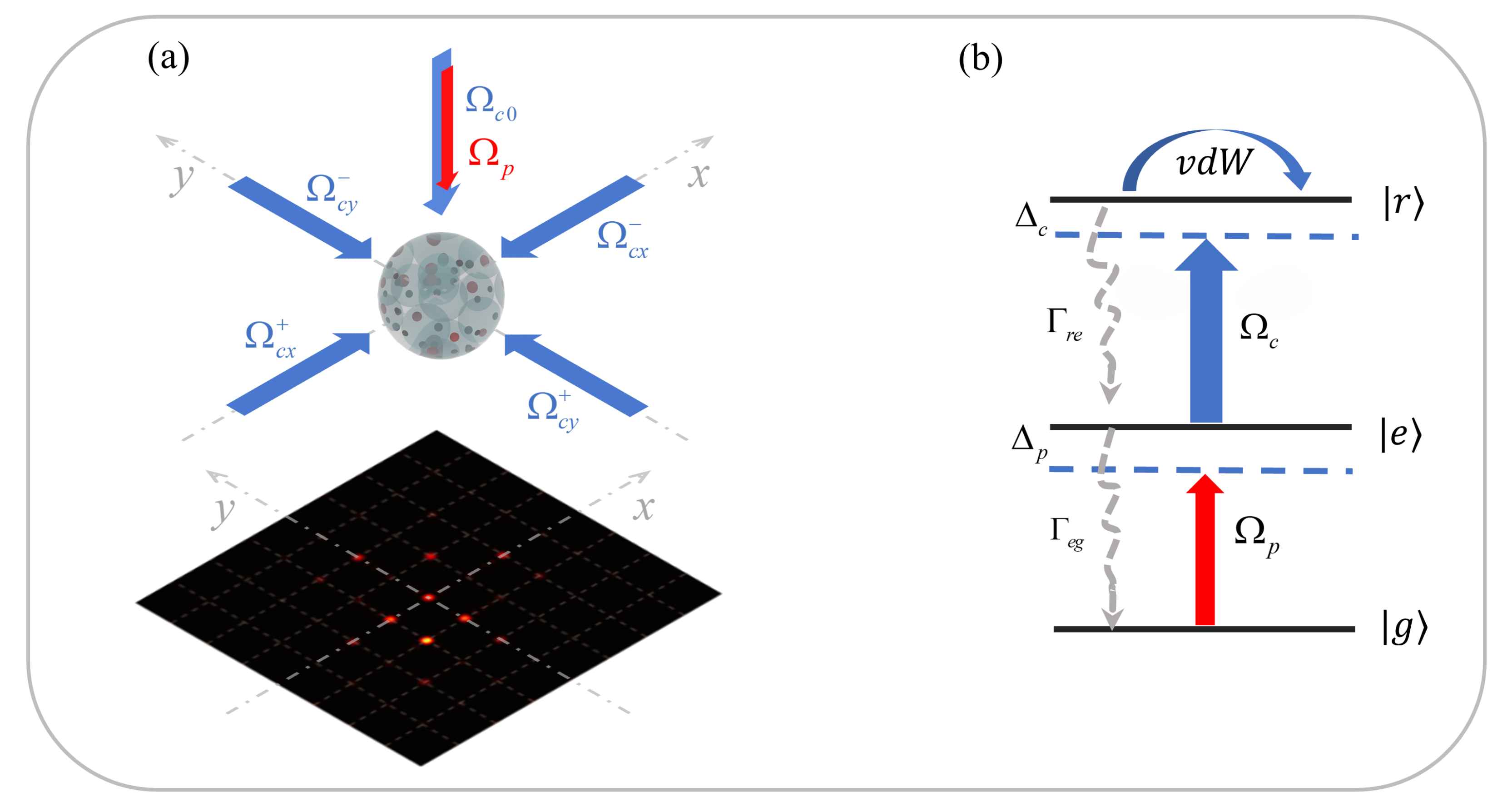
2. Model and Equations
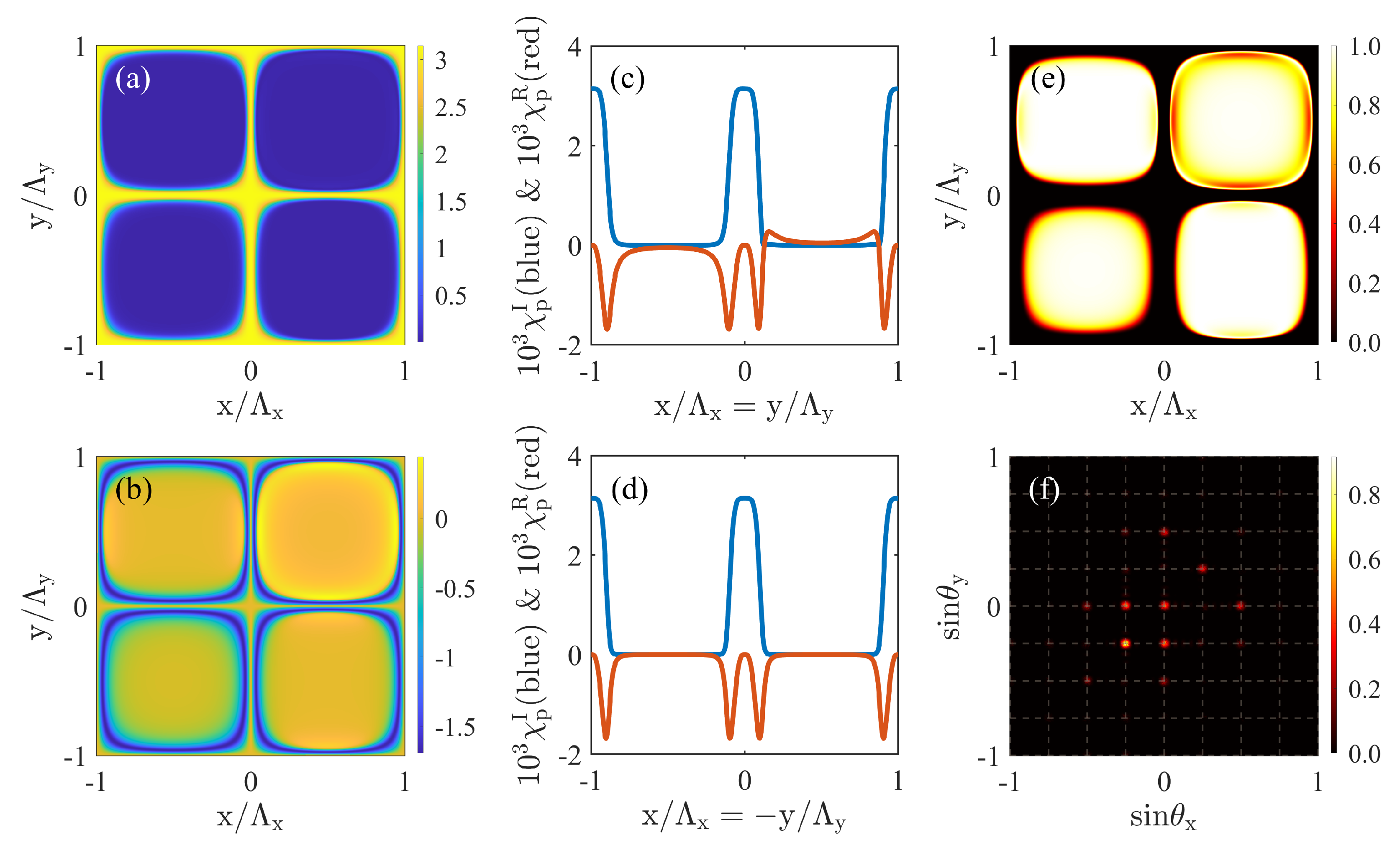
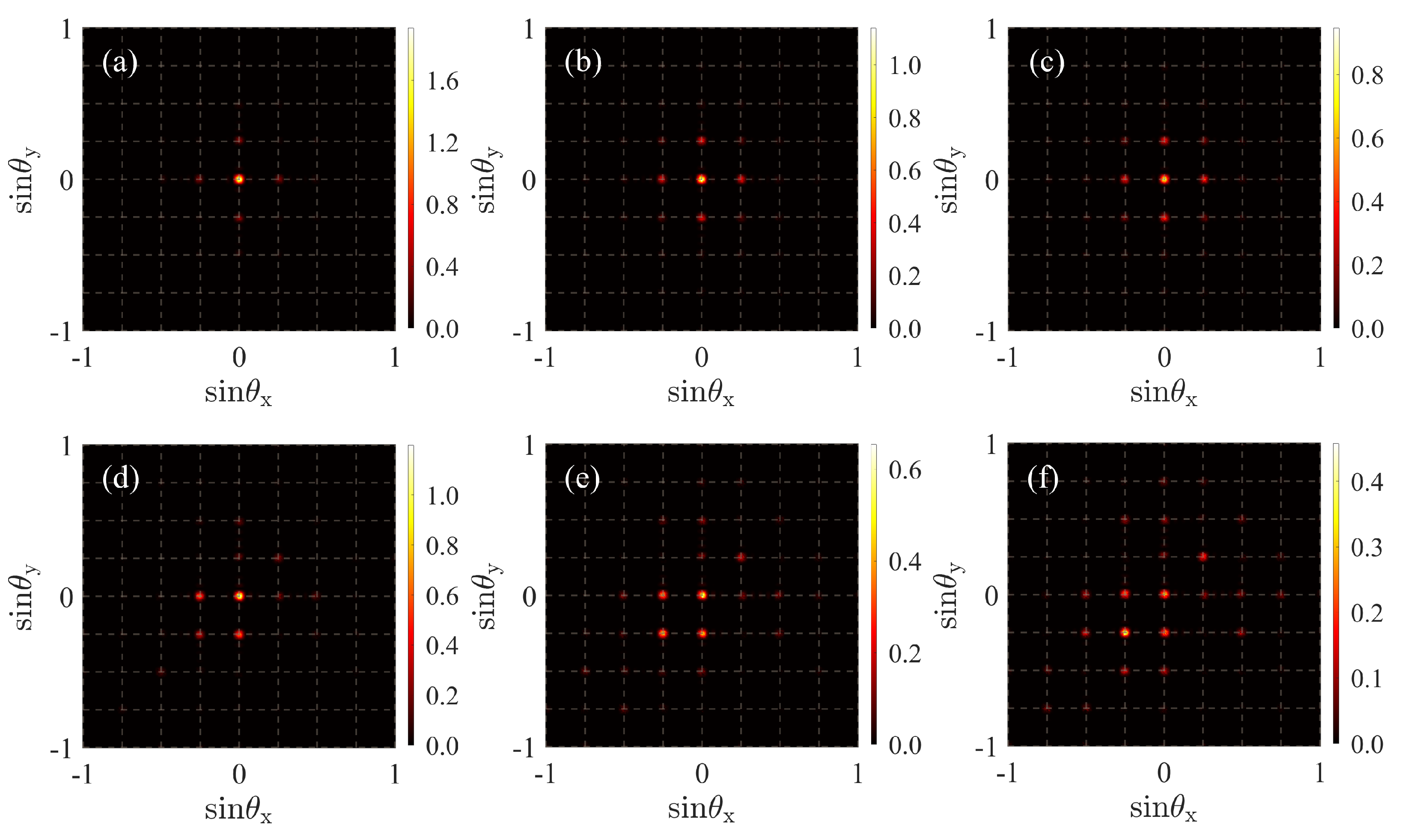
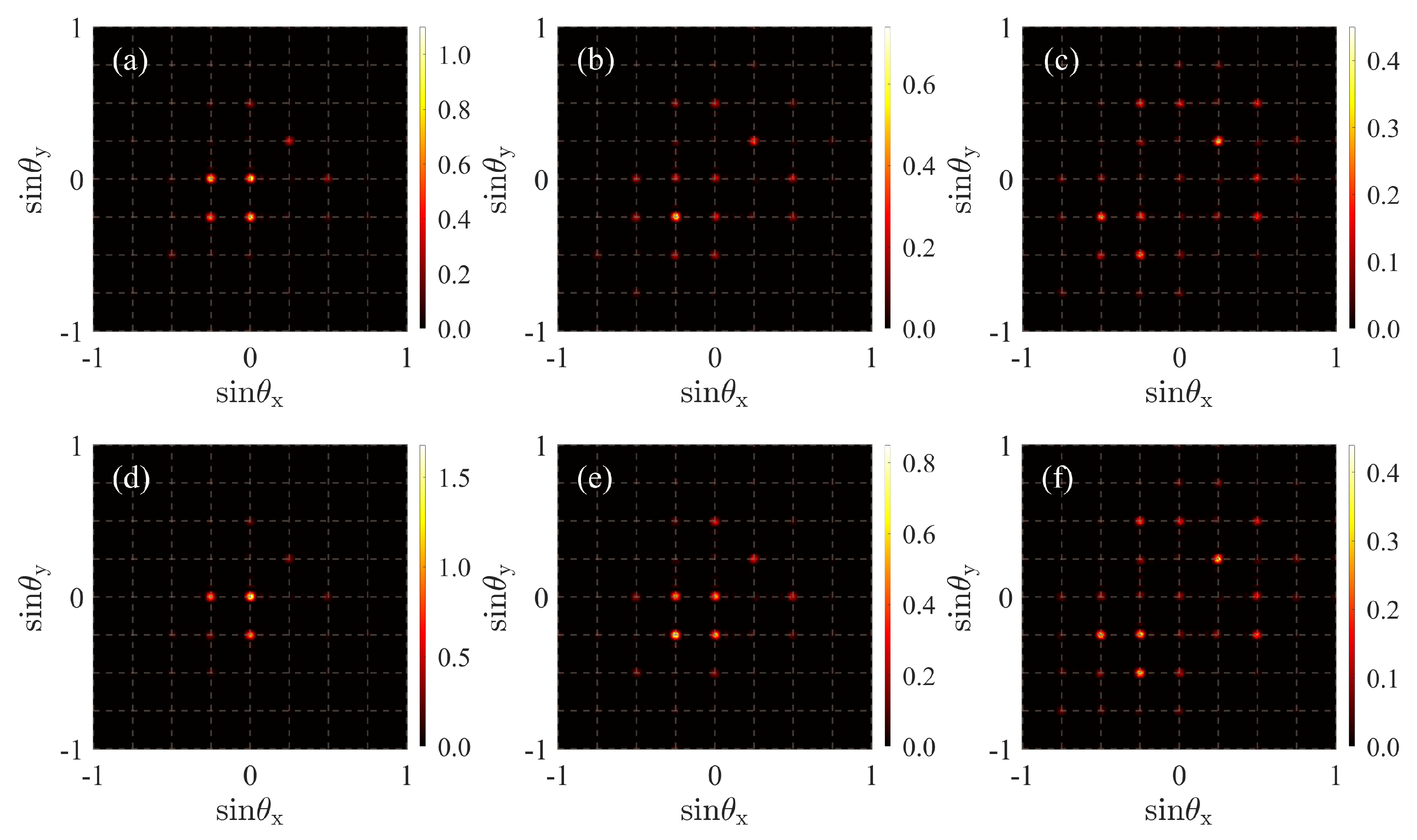
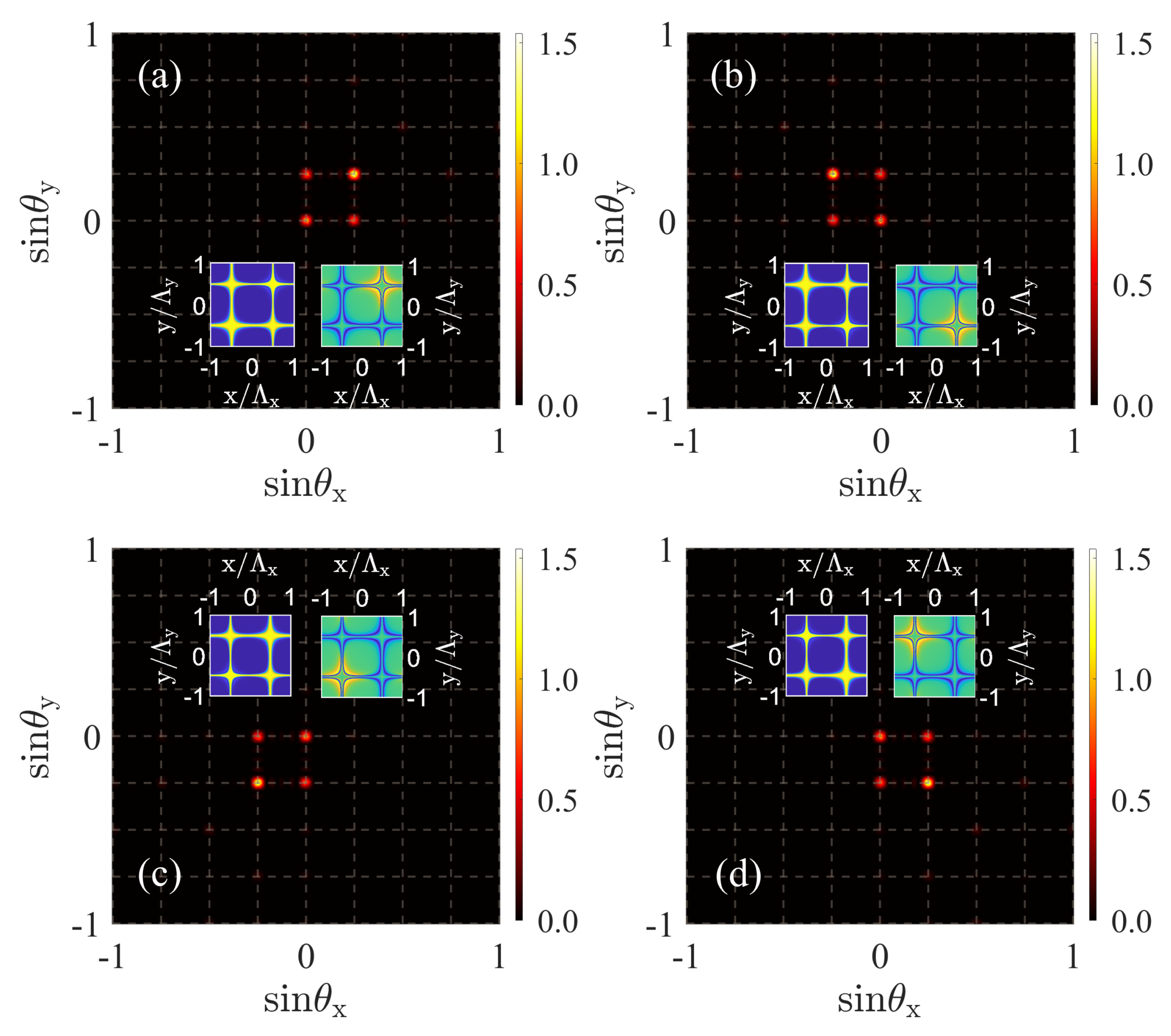
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef]
- Vanier, J.; Godone, A.; Levi, F. Coherent population trapping in cesium: Dark lines and coherent microwave emission. Phys. Rev. A 1998, 58, 2345–2358. [Google Scholar] [CrossRef]
- Harris, S.E. Lasers without inversion: Interference of lifetime-broadened resonances. Phys. Rev. Lett. 1989, 62, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Harris, S.E.; Field, J.E.; Imamoğlu, A. Nonlinear optical processes using electromagnetically induced transparency. Phys. Rev. Lett. 1990, 64, 1107–1110. [Google Scholar] [CrossRef]
- Harris, S.E. Electromagnetically Induced Transparency. Phys. Today 1997, 50, 36–42. [Google Scholar] [CrossRef]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Kash, M.M.; Sautenkov, V.A.; Zibrov, A.S.; Hollberg, L.; Welch, G.R.; Lukin, M.D.; Rostovtsev, Y.; Fry, E.S.; Scully, M.O. Ultraslow Group Velocity and Enhanced Nonlinear Optical Effects in a Coherently Driven Hot Atomic Gas. Phys. Rev. Lett. 1999, 82, 5229–5232. [Google Scholar] [CrossRef]
- Liu, C.; Dutton, Z.; Behroozi, C.H.; Hau, L.V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 2001, 409, 490–493. [Google Scholar] [CrossRef]
- Longdell, J.J.; Fraval, E.; Sellars, M.J.; Manson, N.B. Stopped Light with Storage Times Greater than One Second Using Electromagnetically Induced Transparency in a Solid. Phys. Rev. Lett. 2005, 95, 063601. [Google Scholar] [CrossRef]
- Harris, S.E.; Yamamoto, Y. Photon Switching by Quantum Interference. Phys. Rev. Lett. 1998, 81, 3611–3614. [Google Scholar] [CrossRef]
- Yan, M.; Rickey, E.G.; Zhu, Y. Nonlinear absorption by quantum interference in cold atoms. Opt. Lett. 2001, 26, 548–550. [Google Scholar] [CrossRef] [PubMed]
- Lukin, M.D.; Imamoğlu, A. Nonlinear Optics and Quantum Entanglement of Ultraslow Single Photons. Phys. Rev. Lett. 2000, 84, 1419–1422. [Google Scholar] [CrossRef] [PubMed]
- Lukin, M.D.; Imamoğlu, A. Controlling photons using electromagnetically induced transparency. Nature 2001, 413, 273–276. [Google Scholar] [CrossRef]
- Ling, H.Y.; Li, Y.Q.; Xiao, M. Electromagnetically induced grating: Homogeneously broadened medium. Phys. Rev. A 1998, 57, 1338–1344. [Google Scholar] [CrossRef]
- Mitsunaga, M.; Imoto, N. Observation of an electromagnetically induced grating in cold sodium atoms. Phys. Rev. A 1999, 59, 4773–4776. [Google Scholar] [CrossRef]
- de Araujo, L.E.E. Electromagnetically induced phase grating. Opt. Lett. 2010, 35, 977–979. [Google Scholar] [CrossRef]
- Carvalho, S.A.; de Araujo, L.E.E. Electromagnetically induced blazed grating at low light levels. Phys. Rev. A 2011, 83, 053825. [Google Scholar] [CrossRef]
- Liu, Y.M.; Gao, F.; Fan, C.H.; Wu, J.H. Asymmetric light diffraction of an atomic grating with PT symmetry. Opt. Lett. 2017, 42, 4283–4286. [Google Scholar] [CrossRef]
- Hang, C.; Li, W.; Huang, G. Nonlinear light diffraction by electromagnetically induced gratings with PT symmetry in a Rydberg atomic gas. Phys. Rev. A 2019, 100, 043807. [Google Scholar] [CrossRef]
- Zhou, F.; Qi, Y.; Sun, H.; Chen, D.; Yang, J.; Niu, Y.; Gong, S. Electromagnetically induced grating in asymmetric quantum wells via Fano interference. Opt. Express 2013, 21, 12249–12259. [Google Scholar] [CrossRef]
- Tian, S.C.; Wan, R.G.; Wang, L.J.; Shu, S.L.; Lu, H.Y.; Zhang, X.; Tong, C.Z.; Feng, J.L.; Xiao, M.; Wang, L.J. Asymmetric light diffraction of two-dimensional electromagnetically induced grating with PT symmetry in asymmetric double quantum wells. Opt. Express 2018, 26, 32918–32930. [Google Scholar] [CrossRef] [PubMed]
- Naseri, T. Electromagnetically induced grating with second field quantization in spherical semiconductor quantum dots. Opt. Quantum Electron. 2020, 52, 252. [Google Scholar] [CrossRef]
- Naseri, T. Optical properties and electromagnetically induced grating in a hybrid semiconductor quantum dot-metallic nanorod system. Phys. Lett. A 2020, 384, 126164. [Google Scholar] [CrossRef]
- Liu, Y.M.; Gao, F.; Wu, J.H.; Artoni, M.; La Rocca, G.C. Lopsided diffractions of distinct symmetries in two-dimensional non-Hermitian optical gratings. Phys. Rev. A 2019, 100, 043801. [Google Scholar] [CrossRef]
- Ma, D.; Yu, D.; Zhao, X.D.; Qian, J. Unidirectional and controllable higher-order diffraction by a Rydberg electromagnetically induced grating. Phys. Rev. A 2019, 99, 033826. [Google Scholar] [CrossRef]
- Wu, J.H.; Artoni, M.; La Rocca, G.C. Non-Hermitian Degeneracies and Unidirectional Reflectionless Atomic Lattices. Phys. Rev. Lett. 2014, 113, 123004. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Sheng, J.; Yang, L.; Miri, M.A.; Christodoulides, D.N.; He, B.; Zhang, Y.; Xiao, M. Observation of Parity-Time Symmetry in Optically Induced Atomic Lattices. Phys. Rev. Lett. 2016, 117, 123601. [Google Scholar] [CrossRef]
- Peng, P.; Cao, W.; Shen, C.; Qu, W.; Wen, J.; Jiang, L.; Xiao, Y. Anti-parity–time symmetry with flying atoms. Nat. Phys. 2016, 12, 1139–1145. [Google Scholar] [CrossRef]
- Lu, X.; Chen, N.; Zhang, B.; Yang, H.; Chen, Y.; Zhang, X.; Xu, J. Parity-Time Symmetry Enabled Band-Pass Filter Featuring High Bandwidth-Tunable Contrast Ratio. Photonics 2022, 9, 380. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, F.; Hu, P.; Niu, Y.; Gong, S. Two-dimensional electromagnetically induced cross-grating in a four-level tripod-type atomic system. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 225501. [Google Scholar] [CrossRef]
- Wu, J.C.; Hu, T.T. Two-dimensional electromagnetically induced gain-phase grating with an incoherent pump field. Laser Phys. Lett. 2018, 15, 065202. [Google Scholar] [CrossRef]
- Naseri, T. Two-dimensional induced grating in Rydberg atoms via microwave field. Eur. Phys. J. Plus 2019, 134, 530. [Google Scholar] [CrossRef]
- Asghar, S.; Ziauddin; Qamar, S.; Qamar, S. Electromagnetically induced grating with Rydberg atoms. Phys. Rev. A 2016, 94, 033823. [Google Scholar] [CrossRef]
- Liu, Y.M.; Tian, X.D.; Wang, X.; Yan, D.; Wu, J.H. Cooperative nonlinear grating sensitive to light intensity and photon correlation. Opt. Lett. 2016, 41, 408–411. [Google Scholar] [CrossRef]
- Gallagher, T.F. Rydberg Atoms; Cambridge Monographs on Atomic, Molecular and Chemical Physics, Cambridge University Press: Cambridge, UK, 1994. [Google Scholar] [CrossRef]
- Šibalić, N.; Adams, C.S. Rydberg Physics; IOP Publishing: London, UK, 2018; pp. 2399–2891. [Google Scholar] [CrossRef]
- Yan, D.; Bai, W.; Bai, J.; Chen, L.; Han, H.; Wu, J. Dynamical Collective Excitations and Entanglement of Two Strongly Correlated Rydberg Superatoms. Photonics 2022, 9, 242. [Google Scholar] [CrossRef]
- DeSalvo, B.J.; Aman, J.A.; Gaul, C.; Pohl, T.; Yoshida, S.; Burgdörfer, J.; Hazzard, K.R.A.; Dunning, F.B.; Killian, T.C. Rydberg-blockade effects in Autler-Townes spectra of ultracold strontium. Phys. Rev. A 2016, 93, 022709. [Google Scholar] [CrossRef]
- Han, J.; Vogt, T.; Li, W. Spectral shift and dephasing of electromagnetically induced transparency in an interacting Rydberg gas. Phys. Rev. A 2016, 94, 043806. [Google Scholar] [CrossRef]
- Weimer, H.; Löw, R.; Pfau, T.; Büchler, H.P. Quantum Critical Behavior in Strongly Interacting Rydberg Gases. Phys. Rev. Lett. 2008, 101, 250601. [Google Scholar] [CrossRef]
- Steck, D.A. Rubidium 87 D Line Data. Website. 2021. Available online: http://steck.us/alkalidata (accessed on 9 July 2021).
- Singer, K.; Stanojevic, J.; Weidemüller, M.; Côté, R. Long-range interactions between alkali Rydberg atom pairs correlated to the ns-ns, np-np and nd-nd asymptotes. J. Phys. B At. Mol. Opt. Phys. 2005, 38, S295–S307. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, J.; Dong, S.; Wu, C.; Wang, L. Observation of an Electromagnetically Induced Grating in Cold 85Rb Atoms. Appl. Sci. 2020, 10, 5740. [Google Scholar] [CrossRef]
- Gorniaczyk, H.; Tresp, C.; Bienias, P.; Paris-Mandoki, A.; Li, W.; Mirgorodskiy, I.; Büchler, H.P.; Lesanovsky, I.; Hofferberth, S. Enhancement of Rydberg-mediated single-photon nonlinearities by electrically tuned Förster resonances. Nat. Commun. 2016, 7, 12480. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, J.D.; Maxwell, D.; Gauguet, A.; Weatherill, K.J.; Jones, M.P.A.; Adams, C.S. Cooperative Atom-Light Interaction in a Blockaded Rydberg Ensemble. Phys. Rev. Lett. 2010, 105, 193603. [Google Scholar] [CrossRef] [PubMed]
- Liao, K.Y.; Tu, H.T.; Yang, S.Z.; Chen, C.J.; Liu, X.H.; Liang, J.; Zhang, X.D.; Yan, H.; Zhu, S.L. Microwave electrometry via electromagnetically induced absorption in cold Rydberg atoms. Phys. Rev. A 2020, 101, 053432. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Yan, D.; Liu, Y.; Wu, J. Two-Dimension Asymmetric Electromagnetically Induced Grating in Rydberg Atoms. Photonics 2022, 9, 674. https://doi.org/10.3390/photonics9100674
Wang B, Yan D, Liu Y, Wu J. Two-Dimension Asymmetric Electromagnetically Induced Grating in Rydberg Atoms. Photonics. 2022; 9(10):674. https://doi.org/10.3390/photonics9100674
Chicago/Turabian StyleWang, Binbin, Dong Yan, Yimou Liu, and Jinhui Wu. 2022. "Two-Dimension Asymmetric Electromagnetically Induced Grating in Rydberg Atoms" Photonics 9, no. 10: 674. https://doi.org/10.3390/photonics9100674
APA StyleWang, B., Yan, D., Liu, Y., & Wu, J. (2022). Two-Dimension Asymmetric Electromagnetically Induced Grating in Rydberg Atoms. Photonics, 9(10), 674. https://doi.org/10.3390/photonics9100674





