Control Scheme of Phase-Shifter for Photon Energy Scan

Abstract

Variable gap undulator widely used in X-ray free-electron laser (XFEL) enables the photon energy scan by changing its gap. A phase-shifter should be incorporated to compensate for the phase mismatch between the electron bunches and X-ray pulses arising while those traverse the drift space between undulator segments. The uncertainties in both the undulator parameter and the drift space distance introduce an error in calculating the optimum gap distance of the phase-shifter for the different undulator K. The phase-shifter gap needs to be set where the error is within the tolerable range. The control scheme we propose can maintain full FEL intensity over the scanned photon energies.

1. Introduction

The X-ray free-electron lasers introduced a new realm of coherent, high-intensity X-ray sources with full transverse coherence [1,2,3,4,5]. One can change the photon energy of XFEL by adjusting the undulator gap or by varying the electron energy. Variable gap undulator is useful even in the latter case because undulator tapering requires the undulator gap change. Therefore, almost all XFEL facilities use variable gap undulators, including CW XFELs under construction [6,7]. For the Pohang Accelerator Laboratory X-ray Free-Electron Laser (PAL-XFEL) undulators, the European-XFEL undulator design (5 m long variable gap, out-vacuum undulator) was adopted and modified [8,9,10].

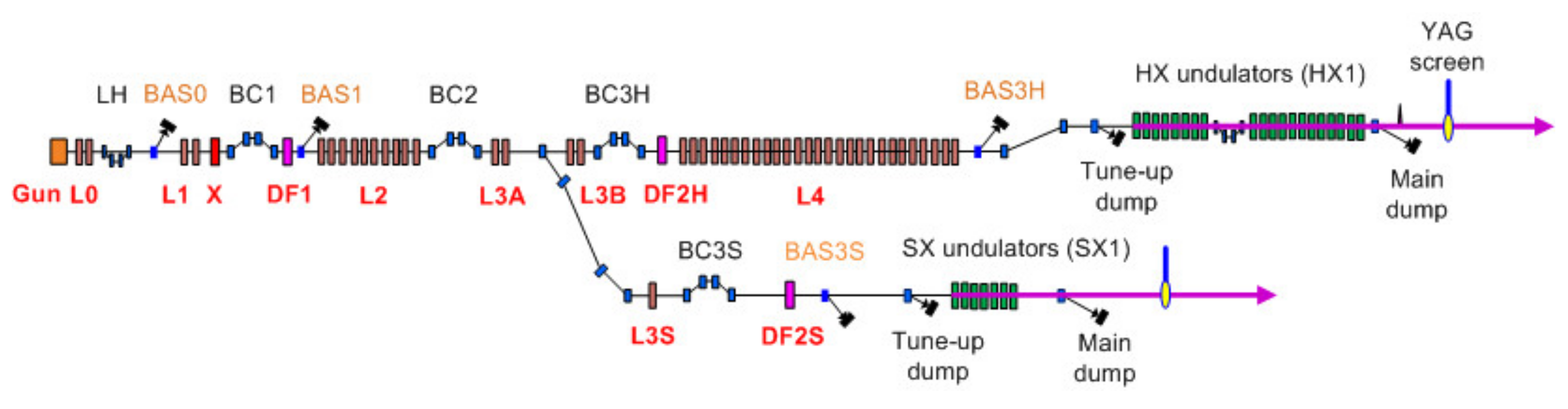
PAL-XFEL fully exploits the variable gap undulator system [11]. A hard X-ray FEL line (HX1) covers the photon energy of 2~20 keV by changing the e-beam energy (4~10.5 GeV) (see Figure 1). A soft X-ray FEL line (SX1) covers the photon energy of 0.39 to 1.25 keV by changing the undulator gap using the 3.0-GeV e-beam. The undulator K of HX1 is set to its maximum (~1.9) to get the highest gain for the 2~15 keV FEL. HX1 comprises twenty undulator segments, and SX1 consists of seven undulator segments. Nineteen and six phase-shifters are in use, respectively, for phase matching between undulator segments.

The FEL users want to change the photon energy at their convenience, freely use the photon energy scan, and incorporate it into their experiment procedure. The photon energy scan by changing the e-beam energy is pretty easy but limited in the photon energy scan range, which is typically below ±1.0% at PAL-XFEL. The larger the photon energy scan range, the more the e-beam energy change is required, making the e-beam deviate from the lattice matching condition to the undulator lattice. Therefore, if a significant photon energy change is necessary, a change in lattice matching for the new e-beam energy is needed to keep the FEL intensity at its highest.

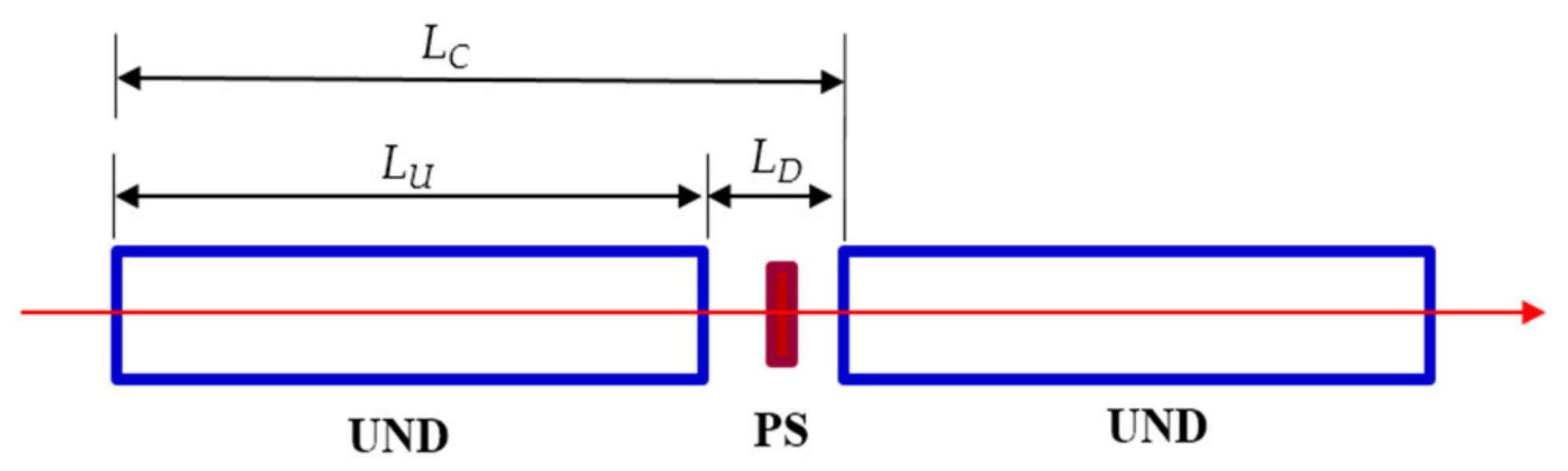
On the other hand, the photon energy scan by changing the undulator gap (thus its K value) allows users to use a larger photon energy scan range because the e-beam is not changed. This kind of photon energy scan is performed by changing the gaps of all undulators (and thus their K values) based on the measured K value data as a function of the undulator gap. When the undulator gap changes, the free-space phase slippage occurs while the electron bunches and X-ray pulses traverse the space between undulator segments. So, there should be a phase-shifter in the drift section between two undulator segments to compensate for the phase slippage, as shown in Figure 2 [12]. A 2π phase tunability is enough for this role of the phase shifter. This undulator segment gap-based photon energy scanning should maintain full FEL intensity over the scanned photon energies.

However, the larger the photon energy scan range is, the more the phase change of the phase-shifter is required. If a range of phase integral of a phase-shifter is not enough, an abrupt change of the phase-shifter gap happens. For example, at LCLS-II, the phase shifter phase integral is much smaller than the required phase integral to do the phase-matching [13]. Therefore, the phase shifter gap changes to cover a larger range shows a number of abrupt gap change, meaning the phase shifters require gap resets to cover the entire operational range [14]. An idea of phase jumps (adding phase 2π) was introduced to overcome that problem [13,15].

For European XFEL, an appropriately large tuning range for the phase integral was chosen to avoid this discontinuity over the wavelength range: the phase number ≥14 was chosen to scan K from 1.5 to 3.9 [16,17]. The PAL-XFEL adopted the European-XFEL phase-shifter design as well [18]. This large tuning range phase shifter allows a smooth change line of the phase-shifter gap enabling a wide range scan of photon energy (see Figure 8 in ref [17]). A phase-shifter with a relatively large phase integral allows at least a total slippage of 13 times the radiation wavelength at PAL-XFEL. As a result, at PAL-XFEL, users can control the photon energy of the soft X-ray FEL line in the range of 0.39 to 1.25 keV at their convenience [19,20].

Even though this scheme with the large tuning range phase shifter is very convenient for users’ experiments, it turned out that the uncertainties in both the undulator parameter and the drift space distance introduce an error in calculating the optimum gap distance of the phase-shifter for the different undulator K. We carried out the study to figure out the contribution of two uncertainties (the undulator parameter and the drift space distance) and to seek a proper method of photon energy scan.

The method should be different for the different photon energy scan methods: the undulator segment gap-based and the electron energy-based. We propose a way to find the phase shifter’s optimum gap with a large error tolerance, considering the uncertainties in the undulator parameter K_u and the drift length between undulator segments, L_D. As a result, we could successfully demonstrate the FEL output intensity stabilization during the photon energy scan.

2. Phase-Shifter to Compensate for the Slippage

Slippage (the path difference between the light and the electron) occurs due to the two contributions when the undulator gap changes: (1) slower electron speed compared to the light and (2) slowing down of the electron due to the wiggling motion. The slippage is defined as

$$s=ct-v_{z}t=\left(1-{\beta }_z\right)ct,$$

(1)

where c is the speed of light and $v_z$ is the electron velocity in the moving direction. ${\beta }_z$ can be written as ${\beta }_z=1-\frac{1}{2}\left({\beta }_x^2+\frac{1}{{\gamma }^2}\right)$, where γ is the relativistic factor of the electron, ${\beta }_x=\frac{dx}{dz}=x\prime$ is the deflection angle of wiggling motion due to the undulator magnetic field $B_y=B_0\cos \left(k_{u}z\right)$, where $k_u=2\pi /{\lambda }_u$ and ${\lambda }_u$ is the undulator period.

Differentiating Equation (1) yields $\mathrm{ds}=\frac{1}{2}\left(\frac{1}{{\gamma }^2}+{x\prime }^2\right)\mathrm{dz}$, and then slippage is expressed as

$$s=\frac{1}{2}\underset{-\infty }{\overset{z}{{\displaystyle \int }}}\left(\frac{1}{{\gamma }^2}+{x\prime }^2\right)dz$$

(2)

where the two contributions explicitly appear, and we only consider the slippage due to wiggling motion, $s_2=\frac{1}{2}{{\displaystyle \int }}_{-\infty }^z{x\prime }^{2}dz$.

The deflection angle of wiggling motion can be written as

$$x\prime \left(z\right)=\frac{e}{\gamma mc}{{\displaystyle \int }}_{-\infty }^z{B}_y\left(z^{\prime }\right)d{z}^{\prime }=\frac{e}{\gamma mc}{I}_1\left(z\right),$$

(3)

where e is the electron charge, m is the rest mass of the electron, and $I_1\left(z\right)={{\displaystyle \int }}_{-\infty }^z{B}_y\left(z^{\prime }\right)d{z}^{\prime }$. The slippage due to wiggling motion can be rewritten as

$$s_2=\frac{1}{2}{\left(\frac{e}{\gamma mc}\right)}^2{\displaystyle \int }{I}_1^2\left(z^{\prime }\right)d{z}^{\prime }=\frac{1}{2}{\left(\frac{e}{\gamma mc}\right)}^{2}PI\left(z\right),$$

(4)

where, $PI\left(z\right)=\int I_1^2\left(z^{\prime }\right)d{z}^{\prime }$ is so-called the phase integral. Rewriting Equation (2) yields

$$s=\frac{1}{2{\gamma }^2}\underset{-\infty }{\overset{z}{{\displaystyle \int }}}dz+\frac{1}{2}{\left(\frac{e}{\gamma mc}\right)}^{2}PI\left(z\right)$$

(5)

Introducing the phase period $T_0={\lambda }_u\left(1+\frac{K_u^2}{2}\right)/{\left(\frac{e}{mc}\right)}^2$, where $K_u$ is the undulator deflection parameter for a planar undulator ($K_u=\frac{e{B}_0}{mc{k}_u}$), and using the wavelength of the generated X-ray radiation ${\lambda }_R=\frac{{\lambda }_u}{2{\gamma }^2}\left(1+\frac{K_u^2}{2}\right)$, then

$$s=\left({\left(\frac{mc}{e}\right)}^2\frac{1}{T_0}\underset{-\infty }{\overset{z}{{\displaystyle \int }}}dz+\frac{1}{T_0}PI\right){\lambda }_R$$

(6)

The slippage along the undulator cell (L_C in Figure 2) should be an integer multiple of the radiation wavelength to keep phase-matching between the light and the micro-bunched e-beam [10]:

$$s\left(L_C\right)=\left({\left(\frac{mc}{e}\right)}^2\frac{1}{T_0}{L}_c+\frac{1}{T_0}(P{I}_u+P{I}_{ps})\right){\lambda }_R=n·{\lambda }_R,$$

(7)

where L_C is the length of the undulator cell (6.05m for PAL-XFEL), and n is the phase number representing the phase advance in multiples of 2π [17]. $P{I}_u$ and $P{I}_{ps}$ are the phase integral of the undulator and phase-shifter, respectively. Both can be calculated from the measured magnetic field. L_C is a fixed variable and $P{I}_u$ is an independent variable for the different K, while $P{I}_{ps}$ can be a practical control parameter easily controlled by changing the gap of the phase-shifter. The magnetic field measurement for the undulator and the phase-shifter was carried out at the field measurement lab, where the ambient temperature and earth magnetic field were controlled the same as that at the installation site in the undulator hall of PAL-XFEL [10,21]. Particularly, the ambient temperature variations should be better than ±0.1 °C to minimize the field variation of the magnetic block [21,22].

The phase slippage along the free space with a distance of L_D between undulator segments is [23]

$$\mathsf{\Delta }{\varphi }_{free space}=2\pi \frac{\mathsf{\Delta }s}{{\lambda }_R}=2\pi \frac{L_D}{{\lambda }_u\left(1+K_u^2/2\right)}=2\pi \frac{L_D}{L_{2\pi }},$$

(8)

where the slippage $\mathsf{\Delta }s=L_D/2{\gamma }^2$. The free space distance of 2π phase change is defined as $L_{2\pi }={\lambda }_u(1+K_u^2/2$). Additionally, the phase slippage along the undulator is $\mathsf{\Delta }{\varphi }_{und}=2\pi \mathsf{\Delta }s/{\lambda }_R=2\pi L_u/{\lambda }_u$. The phase slippage along the free space depends on the K values of the adjacent undulators, while the phase slippage along the undulator is only dependent on the constant undulator period length, λ_u. Therefore, when the undulator gap changes, the phase mismatch occurs while the electron bunches and X-ray pulses traverse the drift space between undulator segments.

Using the undulator parameter of the soft X-ray FEL line (λ_u = 35 mm and K_u = 3.48), T₀ = 717.5 T²·mm³ (see

Table 1. Undulator parameter.

	HX1	SX1
Undulator period, mm	26	35
Undulator length, m	5.0	5.0
Undulator parameter (max), K	1.94	3.48
Undulator type	Planar	Planar
Number of undulators	20	7
Drift space between undulator segments, m	1.05	1.05

). The phase integral of the SX1 undulator is 8.7 × 10⁴ T²·mm³ at maximum at the gap distance of 9 mm. The required phase integral of a phase-shifter to keep a phase-matched condition is at least T₀, allowing the phase number n $\ge 0$ in Equation (7). However, the maximum phase integral of the phase-shifter for PAL-XFEL was designed to have 9330 T² mm³ [18] as shown in Figure 3, allowing at least a total slippage of $13·{\lambda }_R$. This enables a continuous change of phase shift for a wide-range scan of photon energy.

3. Finding Phase-Matching Conditions with a Phase-Shifter

At the beginning of the hard X-ray FEL line (HX1) user service operation, we tried to set the phase shifter gap distance to the calculated value from Equation (7) for all phase-shifters. Then, we compared it with the scanning individual phase-shifter method by observing FEL intensity by a quadrant beam position monitor at the beamline. It turned out that the scanning individual phase-shifter gave rise to a better FEL intensity than the calculated. As shown in Figure 4a, there are differences in the optimum gap distances of the phase-shifters: the measurement and calculation. Our finding is that there are two uncertainties in the use of Equation (7): L_D (therefore, L_C) and K_u.

The uncertainties in undulator K are about the actual K the electron beam sees in the undulator. There should be a midplane offset in the undulator’s vertical direction, resulting in a slight increase in K [11]. We made the undulator mid-plane adjustment once a week for the undulators in the hard X-ray FEL line by measuring the undulator radiation measurement [11], which is absolutely necessary to compensate for the vertical motion of the undulator due to a slow ground motion. The other uncertainty in undulator K may come from an undulator tilt along the beam direction [11]. Additionally, another uncertainty in undulator K may come from the magnetic field measurement error at the field measurement lab. Those uncertainties in undulator K are almost impossible to clarify.

The uncertainties in L_D are actually concerned with the undulator’s actual length, which is 5 m in design, and the undulator’s position error in the undulator cell. The phase advance in the entrance and exit region differs significantly from segment to segment [17], meaning there should be uncertainty in the undulator location and, therefore, L_D. Additionally, the alignment tolerance of the undulator in the beam direction was not as strict as for quadrupole magnets.

The difference in the optimum gap distance of the phase-shifter is most significant in the self-seeding section where one undulator and a four-dipole chicane are placed, which is two times the length of the undulator cell (12.1 m for PAL-XFEL). We calculated the undulator cell distance, L_C, in Equation (7), making the calculated gap distance the same as the measured assumed with no error in K_u, shown in Figure 4b. The difference from the design value (6.05 m) is not negligible. In the self-seeding section, the undulator cell distance is 12.1 m, but the corrected one increases by 37 mm. Using the hard X-ray FEL line undulator parameters (λ_u = 26 mm and K_u = 1.87), the free space distance of 2π phase change, $L_{2\pi }$, is only 71 mm. The phase tolerance of 5 degrees, for example, gives a longitudinal position tolerance of 1 mm for the undulator.

Finding out the uncertainties mentioned above, we decided to use the scanning method to find the optimum gap position of the phase-shifter for increasing FEL intensity at the hard X-ray FEL line. Another reason to use the scanning method is that we change the e-beam energy for the different photon energy in the hard X-ray FEL line with the undulator K fixed at its proper value of tapering. The scanning starts from the beginning of the undulator line because undulator tapering should be set properly at the downstream undulators taking into account the electron energy decreases due to the FEL process.

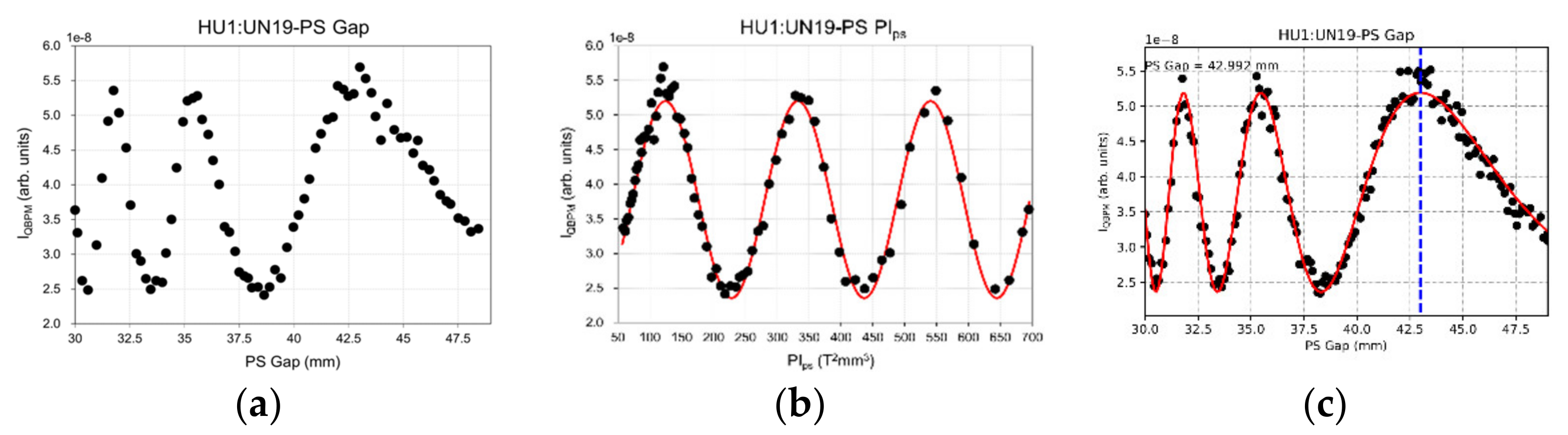
Figure 5 shows the measurement of FEL intensity as a function of the phase-shifter gap at the hard X-ray FEL line. A quadrant beam position monitor (QBPM) in the optical hutch of the beamline was used for intensity measurement [24,25]. The range of phase integral for the measurement was about 700 T²·mm³. Redrawing by changing the phase-shifter gap to phase integral (PI) clearly shows a periodically oscillating pattern (Figure 5b). Using the hard X-ray FEL line undulator parameters (λ_u = 26 mm and K_u = 1.87) and the phase period T₀ = 207.4 T²·mm³, a sine curve fitting was carried out using the fitting equation:

$$y=a·sin\left(\frac{2\pi }{T}x+b\right)+c,$$

(9)

where $x=P{I}_{ps}$, and a, b, and c are the fitting constants. Then, converting PI to the gap distance results in the fitting result as a function of the phase-shifter gap (Figure 5c). The optimal gap of the phase-shifter can be set to one of the gap distances where the FEL intensity is at maximum. However, the preferred gap is a large number (the dashed blue line in Figure 5c) because the setting error of the phase-shifter is well within the tolerable range.

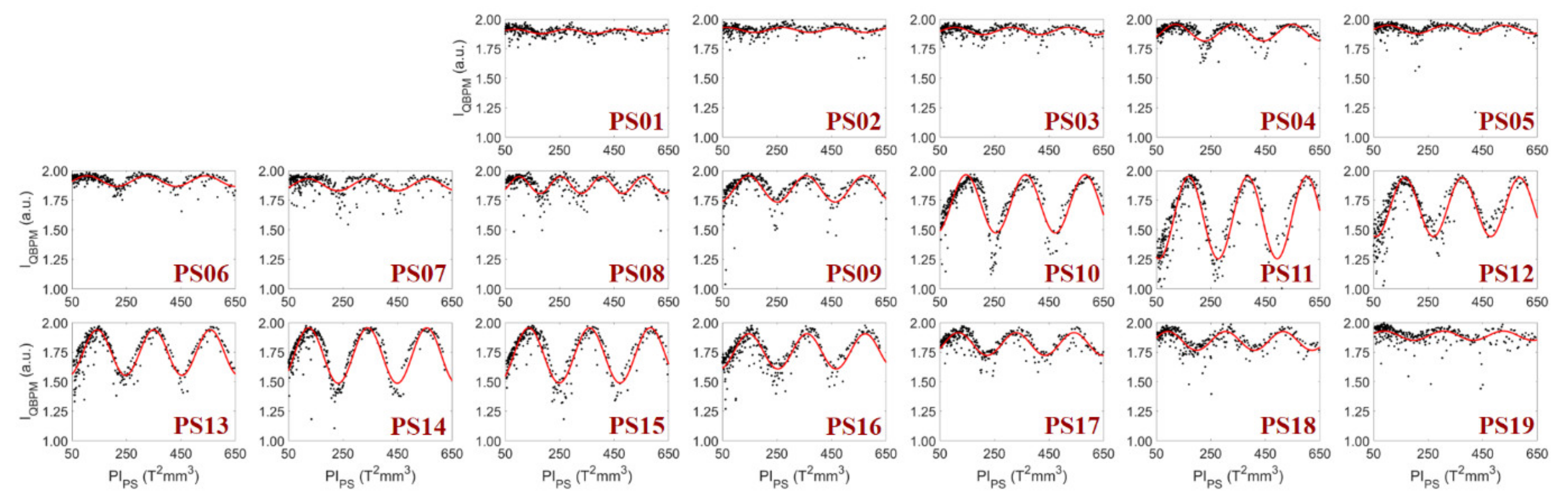
This kind of optimum gap finding for all phase-shifters helps to increase the FEL intensity in the hard X-ray FEL line. Figure 6 shows an example of the FEL intensity measurement with a QBPM as a function of $P{I}_{ps}$ and its sine curve fitting to find the gap distance for phase matching. The gap of the phase-shifter was scanned sequentially for all phase shifters starting from the beginning (PS01) to the end (PS19). In this sequential way, the optimum gap obtained through scanning is not dependent on other phase shifters. All show a periodically oscillating pattern as a function of $P{I}_{ps}$ with the same period (T₀ = 207.4 T²·mm³). Additionally, the oscillation amplitude of FEL intensity as a function of $P{I}_{ps}$ increases as the undulator number increases, and reaches its peak at PS11 (after the 12th undulator). It starts to decrease from PS12, and continues to decrease as the undulator number increases further. The XFEL gets saturated around the 12th undulator among 20, and this trend resembles the behavior of the e-beam bunching factor (see Figure 7 of ref. [12]).

4. Phase-Shifter Gap Control for a Photon Energy Scan

We change the undulator gap for the photon energy scan at the soft X-ray FEL line. The photon energy is adjustable from 0.39 to 1.25 keV by changing the undulator gap (K = 1.38~3.24) using the 3-GeV electron beam. The 0.25~0.39 keV photon energy is also available by changing the gap (K = 2.58~3.4) with a reduced beam energy of 2.5 GeV.

When all undulators (seven at SX1) change their gaps to vary the photon energy, all phase shifters should also change their gaps simultaneously to maintain the phase-matching condition between undulators. Since the undulator K changes for the photon energy scan, the scanning individual phase-shifter method is impossible to apply. Thus, setting the phase shifter phase integrals is only possible with the calculated values from Equation (7).

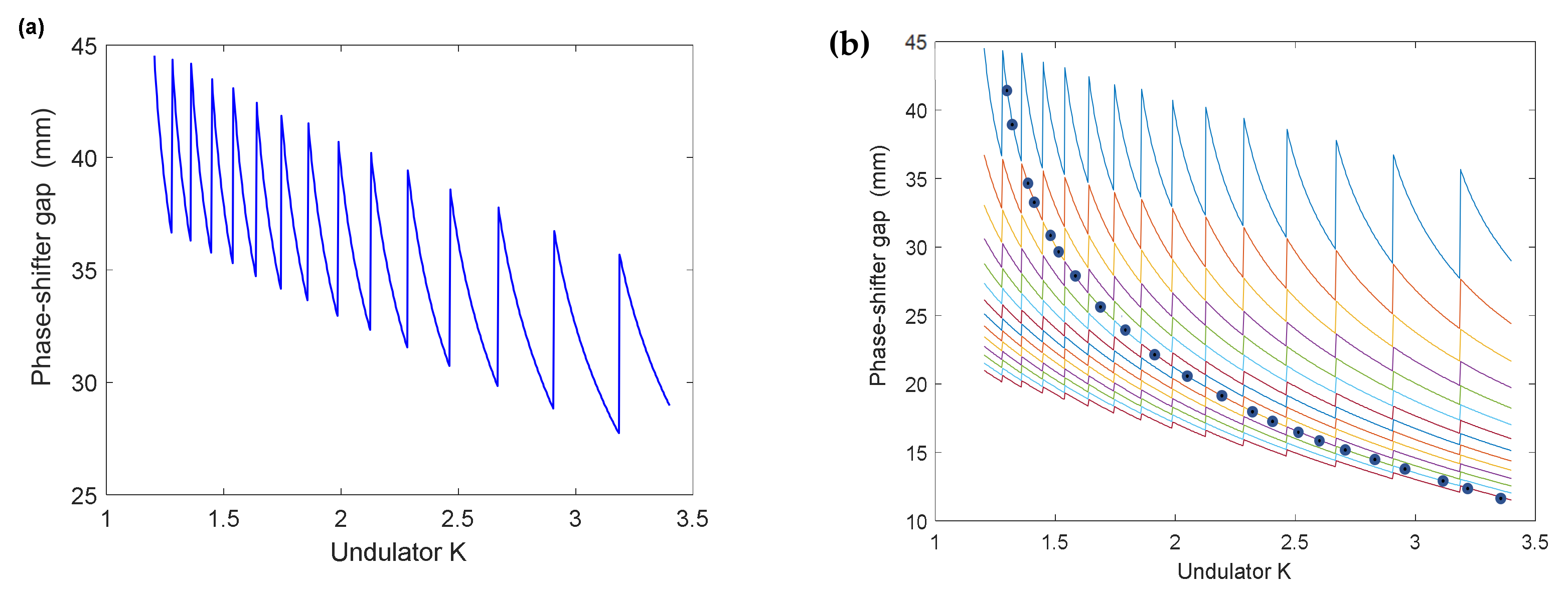
Figure 7 depicts the phase-shifter gap distance as a function of undulator K using Equation (7). The phase-shifter gap distance determined with n = 1 (Figure 7a) can be used to maintain the phase-matching condition between undulators. However, 14 cases of significant changes in gap position are shown in the figure, which may result in a drop in FEL intensity during those changes. Instead, a continuous curved line depicted in (b), consecutively connecting from n = 14 to n = 1 and marked by dots, allows us to change the gap smoothly, as explained in ref [17]. Looking at Equation (7), one can find $P{I}_{ps}$ connects consecutively as a function of K($P{I}_u$) with n changed stepwise. We chose this line as the phase-shifter gap control line for a broad photon energy control.

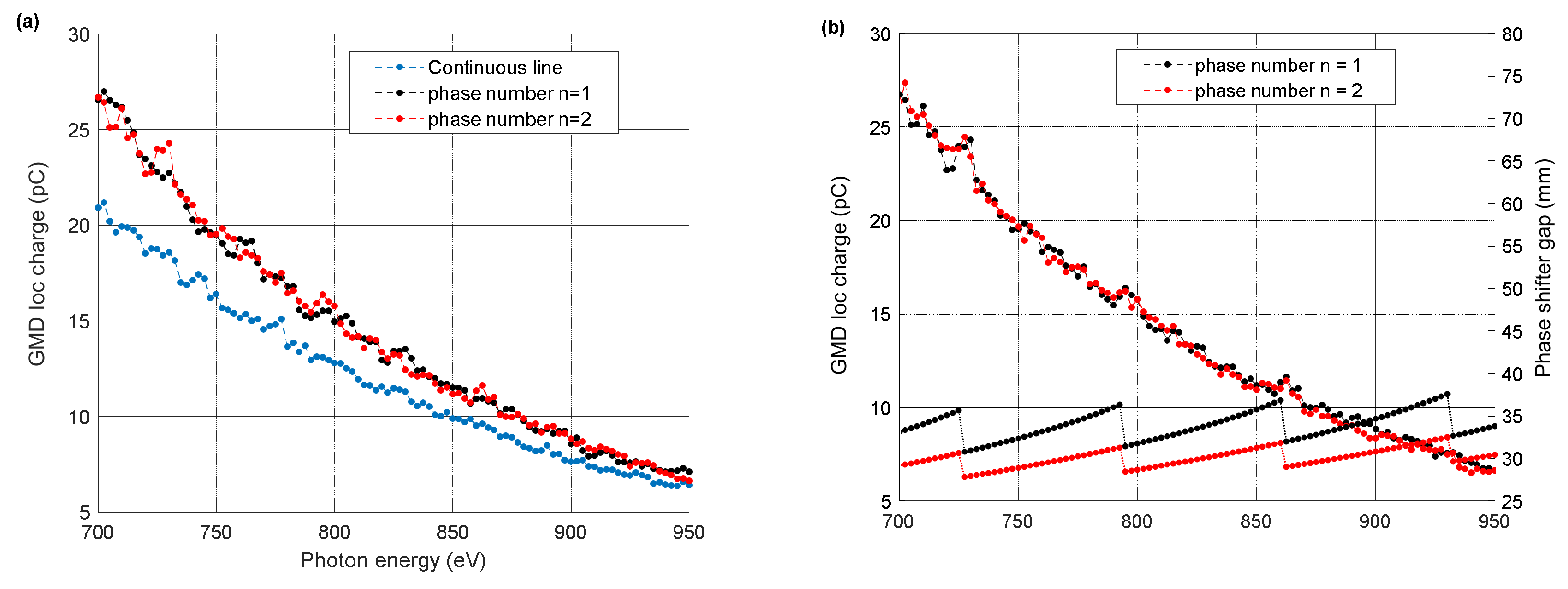
Figure 8 shows how well the phase-shifter gap control line works. In case the phase-shifter gap distance is unchanged (Figure 8a), the FEL intensity measured with a gas monitor detector (GMD) [26] shows a significant variation of the FEL intensity as the photon energy changes from 700 to 900 eV. A worst-case of a very low FEL intensity occurs at several photon energies. A sinusoidal variation of FEL intensity as a function of photon energy is clearly shown, and a phase-matching condition can be established at specific photon energies (five cases in the figure) even with the phase-shifter gap unchanged. On the other hand, if the phase-shifter gap varies according to the phase-shifter gap control line, the sinusoidal variation of FEL intensity disappears, as shown in Figure 8b. The GMD ion current shows a lower value at higher photon energy because of decreased photoionization cross-sections of gas molecules. With increasing photon energy, the photoabsorption and the photoionization cross-sections of matter generally decrease [27]. The GMD ion current decrease in Figure 8b represents only the trend of photoionization cross-sections of gas molecules. The FEL pulse energy measured by the electron energy loss scan [28] was 0.44 mJ at 700 eV and 0.4 mJ at 900 eV, meaning that the FEL intensity of Figure 8b is almost unchanged during the photon energy scan, and the phase-shifter gap control line helps keep the FEL intensity well during the photon energy scan. To keep the electron trajectory flat during the gap movement of undulators and phase-shifters, slow orbit feedback using correctors in drift space between undulators runs with a correction speed of 1 Hz for the 60-Hz beam rate. Actually, the slow orbit feedback covers the entire accelerator line from the injector end (L0 in Figure 1) to the end of the undulator line.

The peak FEL intensities at five specific photon energies in Figure 8a are higher than those with the calculated phase integrals for the phase-shifters (Figure 8b). The difference between the two is more significant at lower photon energy (~700 eV). It means that the calculated phase integrals for the phase-shifters are not optimum for phase matching, as we found in the hard X-ray FEL line. The two uncertainties (L_D and K_u) may play the same role in making the calculated phase integrals from Equation (7) deviate from the optimum.

We compared the phase-shifter gap calculated from Equation (7) at five specific Ks (1.5207, 1.7411, 1.8241, 2.1140, and 2.2529) with that obtained with the scanning method to assess the effect of the two uncertainties. Figure 9 shows the measured FEL intensity (GMD ion current) as a function of the phase-shifter gap with the undulator K of 2.2529. The intensity peaks are marked with a red circle and their corresponding phase number.

To find the exact contribution from each uncertainty (L_D and K_u) for each phase-shifter, we did the minimum error search by varying both Lc and K_u. The error between the calculated gap distance (g_n,cal) and the measured (g_n,meas) is calculated for the different phase numbers n:

$$\mathrm{Error}\left(K, L_c\right)={{\displaystyle \sum }}_{n=0}^N{\left(\frac{g_{n, cal}-g_{n, meas}}{g_{n, cal}}\right)}^2 /N.$$

(10)

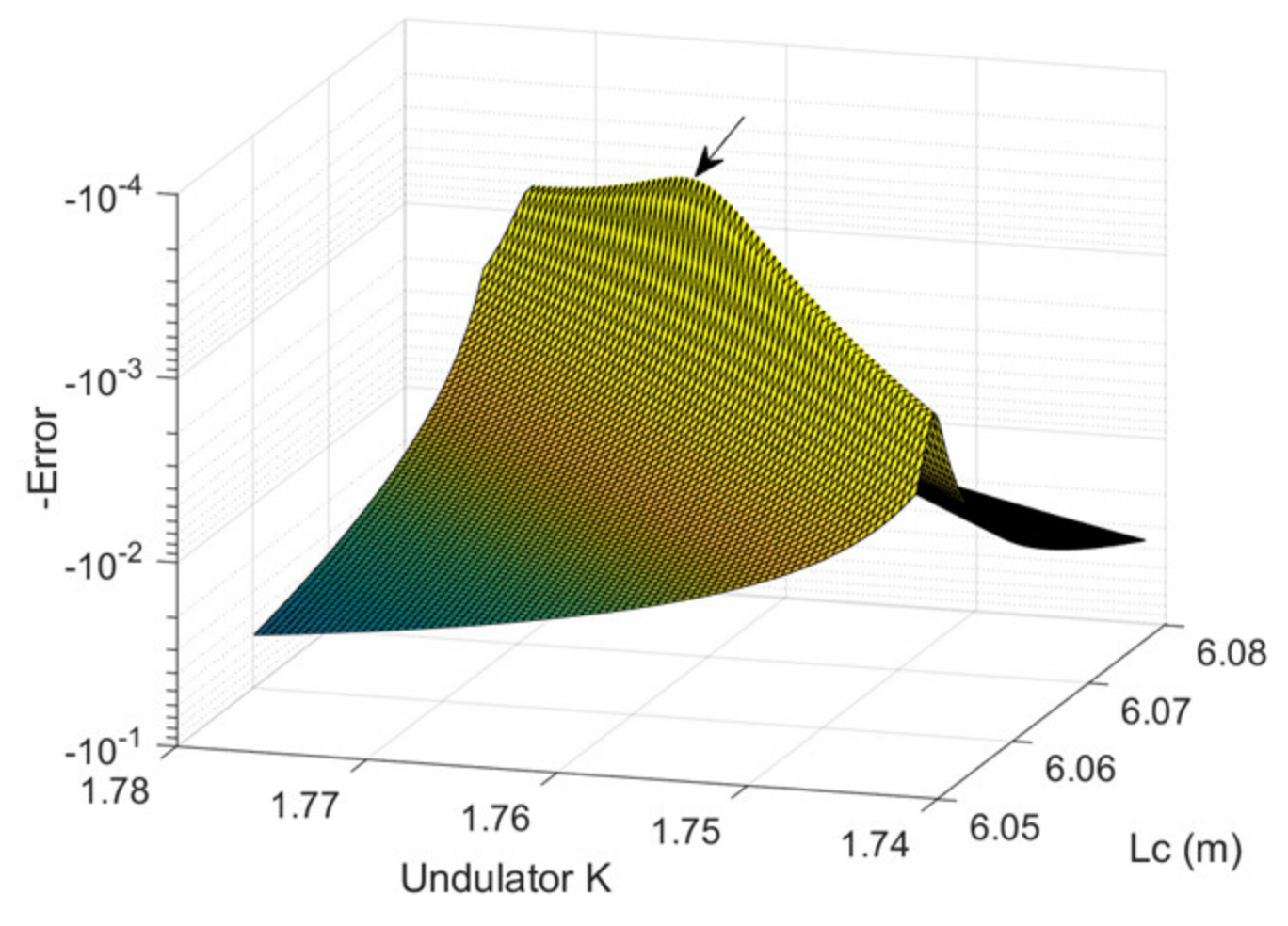
Figure 10 shows the minimum error search at K = 1.7411 for phase-shifter No. 5. The inverted surface shown in Figure 10 for the minimum search is a result of fitting to measurement data. The invert of the error is depicted to show the minimum clearly. The arrow indicates the minimum error point. The minimum error point is not predominant in the figure because of low statistics samples. Furthermore, the result at different Ks reveals an inconsistent value in Lc (Lc must be the same, independent from the undulator K). Thus, the minimum error search fails to give an exact number of Lc and K_u.

Even though we can not find the exact contribution from each uncertainty (L_D and K_u), we have to use Equation (7) for the photon energy scan if we change the undulator K. There should be an error in the calculation of phase-shifter gap distance because of those uncertainties. As we see in Figure 9, the error tolerance strongly depends on where the gap of the phase-shifter is moving. The preferred one is a larger gap because the calculation error of the phase-shifter is well within the tolerable range.

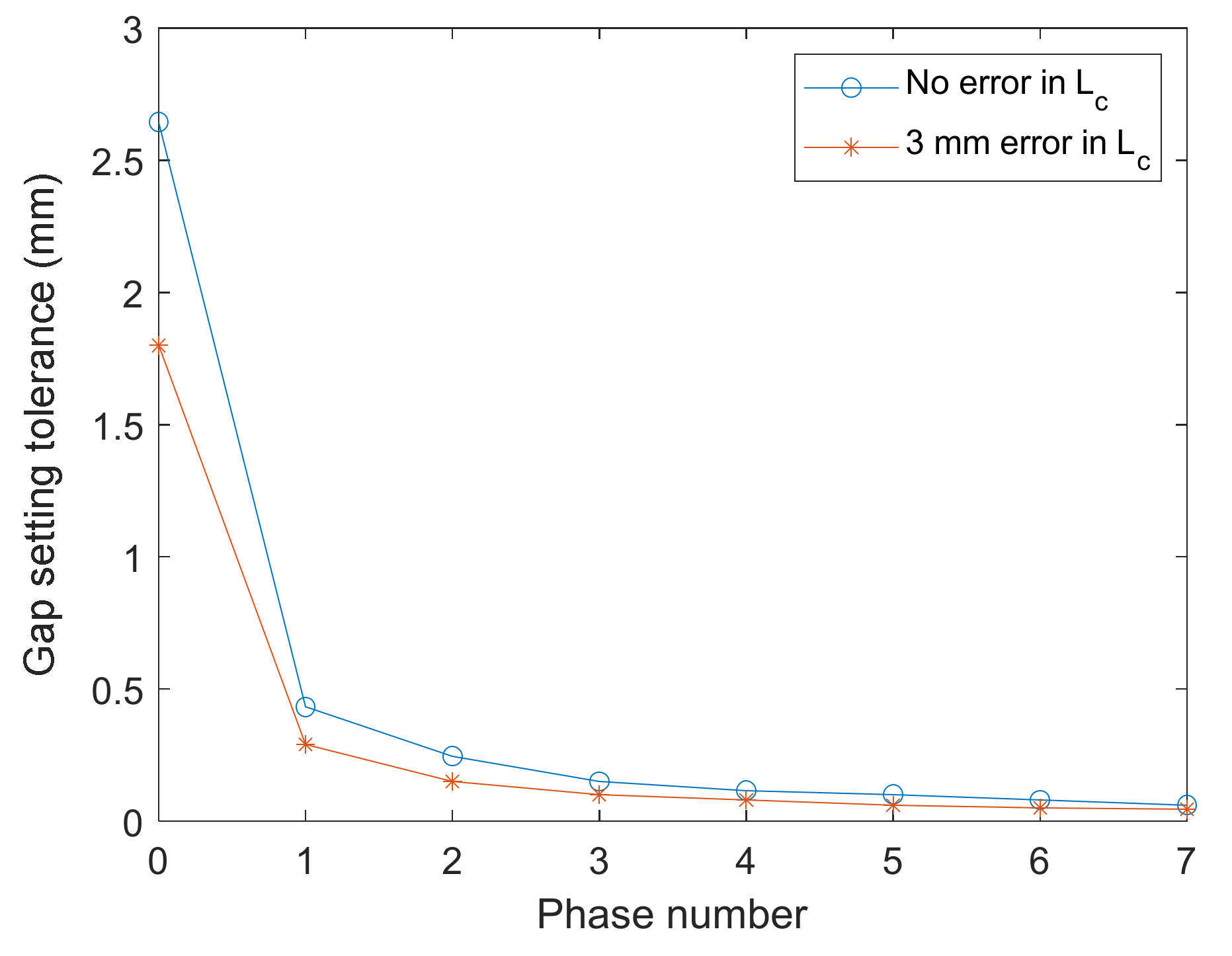
Figure 9 shows that the peak at n = 1 shows the largest tolerance of the phase-shifter gap setting while it decreases rapidly as the phase number increases. From Figure 9, the width of the phase integral for the decrease of 5% from the peak FEL intensity is 26 T²·mm³. Converting this width to the gap for n = 0 to 7 gives the gap tolerances allowing a 5% decrease in FEL intensity (see Figure 11). If an error in L_C is only considered, the error of 26 T²·mm³ in the phase integral corresponds to 8.9 mm in L_C. Supposing zero error in L_C, the gap tolerances are 2.65 mm for n = 0, 0.43 mm for n = 1, and 0.25 mm for n = 2. If the error in L_C is assumed 3 mm, the gap tolerances become worse, particularly for the phase number n > 2. Therefore, the acceptable phase number is n $\le$ 2, and the phase-shifter gap distance is over 25 mm (the phase integral <1300 T²·mm³), where the FEL intensity does not vary much even with the unknown calculation error of the phase-shifter gap.

Upon acknowledging the unknown calculation error of the phase-shifter gap from Equation (7), we have to choose the appropriate phase number for the photon energy scan to let the calculation error be within the tolerance range. From Figure 11, we can conclude that the phase number should be smaller than 3 (or the phase integral is below 1300 T²·mm³). This means that we cannot use the continuous operation line shown in Figure 7b. Instead, we have to use the phase number n = 0, 1, and 2 even though it intrudes an abrupt change of the phase-shifter gap.

Figure 12 shows the test results of the three different cases of the photon energy scan (the scan range is 700 to 950 eV): continuous line, n = 1, and n = 2. The continuous line case exhibits the worst performance, while others show no difference in FEL intensity. In the case of n = 1 and n = 2, the FEL intensity fluctuations appear at transition points of the phase-shifter gap, as shown in Figure 12b, which looks insignificant.

5. Discussion

Properly controlling phase-matching between undulator segments is essential in maintaining full FEL intensity over the scanned photon energies for the users’ experiment. The phase-shifter compensates for slippage between the light and the electron to keep phase-matching with an integer multiple of 2π. A method is proposed to find the phase shifter’s optimum gap, taking into account the uncertainties in the undulator parameter K_u and the drift length between undulator segments, L_D.

The FEL output intensity stabilization during the photon energy scan is successfully demonstrated at PAL-XFEL by appropriately tuning the gap of the phase shifters. The scanning individual phase-shifter method is adopted for the hard X-ray FEL line, where the undulator K is fixed at its proper value of tapering while the e-beam energy is adjusted for the photon energy scan. The largest tolerance of the phase-shifter gap could be found by measuring FEL intensity vs. the phase shifter gap, which can enable photon energy scan with high FEL intensities.

On the other hand, the undulator K should change for the photon energy scan at the soft X-ray FEL line. Therefore, the scanning individual phase-shifter method is impossible to apply. Instead, the calculated phase-shifter gap from the measured magnetic field data of the phase-shifter should be used for the different undulator K. The large phase integral phase-shifter was introduced to allow a continuous curved control line of the phase-shifter gap enabling a wide range scan of photon energy at the soft X-ray FEL line. However, to cover a wide range of photon energy along a single control line, the phase-shifter gap must drop below 20 mm at lower photon energy (higher undulator K), where the gap adjustment tolerance is very small.

We found that the width of the phase integral for the decrease of 5% from the peak FEL intensity is 26 T²·mm³. As the gap of the phase-shifter closes down, the magnet field amplitude goes up rapidly, and the change of phase integral per the gap change becomes steeper, as seen in Figure 3b, meaning that the error tolerance of the phase-shifter gap setting is shrinking further.

Furthermore, the calculation error of the phase-shifter gap from Equation (7) is not only nonnegligible but also unpredictable because of the two uncertainties (L_D and K_u). It is found that moving to the phase number over 3 puts the error out of the tolerable range to reduce the FEL intensity appreciably. Therefore, we propose a control scheme to use the phase numbers n = 0, 1, and 2, which entails an abrupt change of the phase-shifter gap. A test with those control lines shows that the FEL intensity fluctuation is insignificant during the gap changes.

Upon acknowledging the unknown calculation error of the phase-shifter gap from Equation (7), we have to choose the appropriate phase number for the photon energy scan to let the calculation error be within the tolerance range.

Conclusively, the acceptable phase number is n $\le$ 2, and the phase integral of the phase-shifter should be below 1300 T²·mm³, where the FEL intensity does not vary much with the unknown calculation error of the phase-shifter gap. Additionally, the maximum phase integral of the phase-shifter does not need to be as high as 9330 T² mm³; it is enough with 1500 T² mm³.

These novel procedures we propose will surely help the users of the XFEL facility to carry out successful experiments in many scientific fields.