Low-Rate Denial-of-Service Attack Detection: Defense Strategy Based on Spectral Estimation for CV-QKD

Abstract

Although continuous-variable quantum key distribution (CVQKD) systems have unconditional security in theory, there are still many cyber attacking strategies proposed that exploit the loopholes of hardware devices and algorithms. At present, few studies have focused on attacks using algorithm vulnerabilities. The low-rate denial-of-service (LDoS) attack is precisely an algorithm-loophole based hacking strategy, which attacks by manipulating a channel’s transmittance T. In this paper, we take advantage of the feature that the power spectral density (PSD) of LDoS attacks in low frequency band is higher than normal traffic’s to detect whether there are LDoS attacks. We put forward a detection method based on the Bartlett spectral estimation approach and discuss its feasibility from two aspects, the estimation consistency and the detection accuracy. Our experiment results demonstrate that the method can effectively detect LDoS attacks and maintain the consistency of estimation. In addition, compared with the traditional method based on the wavelet transform and Hurst index estimations, our method has higher detection accuracy and stronger pertinence. We anticipate our method may provide an insight into how to detect an LDoS attack in a CVQKD system.

1. Introduction

Humans have been giving great importance to cryptography since ancient times. With the development of computer technology, a massive amount of sensitive data called for more advanced encryption techniques to ensure security. Key distribution is the crucial issue of encryption techniques, and there have been many key distribution methods, such as RSA algorithms [1] of asymmetric encryption. However, all classical encryption techniques based on high computational complexity are decipherable and are unable to detect the disclosure of keys [2]. Thankfully, the progress of quantum key distribution (QKD) makes it possible for two remote communicating parties to share secure keys through an unsafe quantum channel controlled by an eavesdropper [3,4], since the Heisenberg uncertainty principle [5] and no-cloning theorem [6] of quantum mechanics guarantee QKD’s unconditional information security and the detectability of eavesdroppers. Compared with discrete-variable (DV)QKD, continuous-variable (CV)QKD has the merits of low-cost implementation for it is compatible with the current telecom networks and components such as homodyne and heterodyne detectors and has other advantages [7,8]. Specifically, the Gaussian-modulated coherent state (GMCS) protocol, the most developed CVQKD protocol, has been proven secure against collective attacks and coherent attacks theoratically [9,10,11,12,13].

By contrast, the imperfection of hardware devices and algorithms lead to security loopholes in CVQKD systems.

A great deal of research has put forward various practical attack strategies by exploiting hardware defects, and examples include the wavelength attack, the calibration attack, the local oscillator (LO) fluctuation attack and the saturation attack [14,15,16,17,18]. P. Huang et al. proposed an asynchronous countermeasure strategy without structural modifications of the conventional CVQKD scheme to defend against the above-mentioned attacks [19]. In stark contrast, there are few studies on the practical security analysis of the algorithms. Y. Li et al. proposed a denial-of-service (DoS) attack strategy aimed at the parameter estimation method in the communication process [20]. Under the DoS attack, eavesdroppers’ slight manipulation of the channel transmittance results in great underestimation of the secure transmittance distance, and subsequently the two sides of communication consider the channel insecure and thus terminate the communication process.

The low-rate denial-of-service (LDoS) attack is a more stealthy type of DoS attacks because it sends short-time but high-rate burst attack traffic periodically to maintain the average attack rate low, so as to escape from detection [21]. The LDoS attack, in the narrow sense, is TCP protocol oriented, while in GMCS protocol, the LDoS attack can be considered as short-time, high-rate and periodic burst attack on the parameter estimation. According to the periodicity of LDoS attacks and the characteristic differences between periodic signals and aperiodic signals in the frequency domain, the rule that the power spectral density (PSD) of the LDoS attack traffic in low frequency band is higher than normal is then obtained [22]. On the basis of this rule, the issue of LDoS attacks detection transforms into the spectral estimation of the stochastic sequence.

In this paper, to detect LDoS attacks and guarantee the consistency of spectral estimation, we proposed a detection method based on Bartlett’s spectral estimation approach (average periodogram). Spectral estimation is the issue of estimating the power spectrum of a stochastic process given partial data, usually only a finite number of samples of the autocorrelation function [23]. It detects whether the network traffic contains LDoS attack traffic by estimating the power spectral density in low frequency band. There are two broad categories of approaches in spectral estimation, the classical approaches (non-parametric approaches) and the modern approaches (parametric model-based approaches). The former consists mainly of the periodogram and its improved approaches, including data windowed periodogram, average periodogram, etc., and the typical models of the latter are autoregressive (AR), moving average (MA) and autoregressive moving average (ARMA) models [24,25,26]. The structure of the paper is as follows. Firstly, the strategy of LDoS attacks based on the GMCS protocol is briefly introduced. Secondly, we discuss three different spectral estimation approaches, autocorrelation estimation with rectangular window, periodogram with Bartlett window and the Bartlett approach (average periodogram), and then analyze their estimation results. Finally, we carry out the related experiences and it is demonstrated that the proposed method can effectively detect LDoS attacks.

2. System Description and Attack Detection

2.1. Attack Strategy against GMCS Protocol

In the GMCS protocol, Alice sends Bob a chain of coherent states $|x+\mathit{i}p⟩$ where the quadratures (x, p) are randomly chosen from a Gaussian distribution of mean zero and variance $V_A{N}_0$, where $N_0$ means the shot noise variance. Then, Bob randomly chooses to measure either x or p by homodyne detection and announces overtly to Alice which one he measured, so that she discards the irrelevant data. After several rounds of exchanges, Alice and Bob will share a set of correlated Gaussian variables, which are employed for further secret key extractions by way of post-processing procedures, including parameter estimation, reverse reconciliation and amplification. The above-mentioned process can be seen in Figure 1. To maintain consistency, the reconciliation protocol has to be unidirectional (from Bob to Alice) [27,28,29]. As LDoS attacks mainly aim at the process of parameter estimation, we will introduce the principle of parameter estimation methods of GMCS protocol at length in the following part.

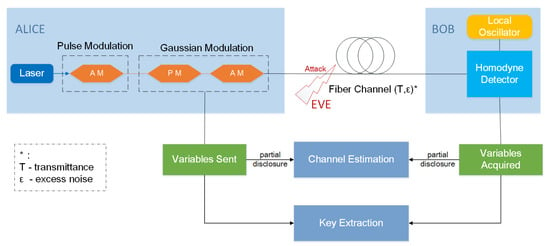
Figure 1. In the GMCS CVQKD protocol, Alice encodes the secret key information by modulating the quadratures x and p of coherent states with independent Gaussian distributions and sends them to Bob through an insecure channel controlled by Eve. Next, the homodyne detector on Bob’s end obtains the transmitted information. Then, some of the shared Gaussian variables are disclosed for channel estimation. Lastly, shared Gaussian variables are used to extract keys.

Some parameters in parameter estimation are determined by the instruments’ characteristic and measured beforehand. The detector efficiency $\eta$ and the electrical noise $V_{el}$ of Bob’s end are relatively stable in experimental repetition, thus we measure them in advance and treat them as constants during the communication. The shot noise can be expressed as $N_0=K_{N_0}{E}_{LO},$ where $K_{N_0}$ is a parameter that needs to be calibrated before communication, and $E_{LO}$ is the power of the local oscillator.

Others, including channel transmittance T and channel excess noise $\epsilon$, demand estimation in real time. Exploiting this loophole, Eve manipulates the parameters to cause estimation deviation till the communicating parties think the channel insecure and close it. In this way, an attack succeeds. In the GMCS protocol, some shared Gaussian variables are disclosed to estimate the channel transmittance and channel excess noise; others are used for key extraction and we generally estimate the above-mentioned parameters by means of statistical methods. In the classical parameter estimation method, Alice and Bob’s data are associated with each other through the linear model $y=tx+z,$ where $t=\sqrt{T}\in \mathbb{R}$ and z follows a centered normal distribution with unknown variance ${\sigma }^2=1+T\epsilon$.

According to the above linear model, adopting the maximum likelihood estimation method and neglecting the finite-size effect of limited data, we are able to estimate the value of the channel transmittance T and the channel excess noise $\epsilon$ as below

$$\widehat{t}=\frac{{\sum }_{i=1}^m{x}_i{y}_i}{{\sum }_{i=1}^m{x}_i^2}$$

(1)

$${\widehat{\sigma }}^2=\frac{1}{m}\sum _{i=1}^m{(y_i-\widehat{t}{x}_i)}^2,$$

(2)

where $\widehat{t}$ is the estimated value of $\sqrt{T}$, and ${\widehat{\sigma }}^2$ is the estimated value of $1+T\epsilon$. Furthermore, $\widehat{t}$ and ${\widehat{\sigma }}^2$ comply with the normal distribution and chi-square distribution, respectively,

$$\widehat{t}\sim \mathcal{N}(t,\frac{{\sigma }^2}{{\sum }_{i=1}^m{x}_i^2}){\widehat{\sigma }}^2\sim {\mathcal{X}}^2(m-1),$$

(3)

where t and ${\sigma }^2$ are the true values of the parameters $\sqrt{T}$ and $1+T\epsilon$, respectively.

Using Equations (1) and (2), we can estimate the value of T and $\epsilon$ convincingly. The authors of [30] proposed a method under the condition of considering the finite-size effect, while for the sake of simplicity, we do not consider the effect as it only degrades the precision of results. In the rest of this section, we will analyze the impact caused by Eve’s arbitrary manipulations in channel parameters under the framework of this parameter estimation method.

In the optical fiber transmission system, we generally treat the channel’s transmittance as a constant when making parameter estimations. Nonetheless, in consideration of Eve’s control of the channel, she can intentionally modify the characteristics of the channel, which will lead to deviations to parameter estimations. Such manipulation is a so-called denial-of-service attack, since it can make the actual secure channel perceived as insecure by two parties and lead to the communication discontinuance [20]. Now, we begin with Equations (1) and (2) to analyze the effects of DoS attacks.

As mentioned before, channel transmittance T and excess noise $\epsilon$ are the two parameters we lay stress on. We assume that Alice modulates X and Bob measures Y, where X is a cosine signal and Y is an X-distorted signal that is presented in the phase deviation and linear noise. Next, due to the phase compensation technique and the linear noise mean value of 0, the following formula can be obtained

$$\widehat{t}=E\left(\sqrt{T}\right),$$

(4)

where we highlight the conclusion. From Equation (4) we can draw the following conclusions: if the transmittance T is a constant, the estimated $\widehat{t}$ equals to the true value $\sqrt{T}$, while if not, there will be deviations in our estimation.

Similarly, by using the equivalent relations in Equation (4) and equation $V_A=E\left(X^2\right)$, we can rewrite Equation (2)

$${\widehat{\sigma }}^2=E\left(T\right)\epsilon +1+E\left(T\right)V_A-{\left(E\left(\sqrt{T}\right)\right)}^2{V}_A.$$

(5)

Likewise, if the transmittance T is a constant, the estimated ${\widehat{\sigma }}^2$ equals to the true value $1+T\epsilon$, while if not, $E\left(T\right)V_A\ne {\left(E\left(\sqrt{T}\right)\right)}^2{V}_A$ which will bring about inaccuracy in excess noise estimation.

Through the above brief analysis, Eve’s DoS attack strategy, namely making the parameter estimation deviates from the true value by manipulating the channel transmittance T, has been demonstrated. For the detailed derivation process, refer to Appendix A. As for the LDoS attack, it is one type of DoS attacks and conforms to their basic principles, characterized by the good quality of concealment.

2.2. Detection Principle of LDoS Attack by Spectral Estimation

Though Y. Li et al. suggested a countermeasure based on post-selection to suppress the DoS attack [20], there is still a vacancy in the detection of LDoS attacks. Y. Chen et al. analyzed the PSD distribution over the frequency domain to find that LDoS attacks are mainly distributed in the low-frequency band rather than broadband distribution of the normal traffic [22]. Hence, we can use such feature to effectively detect an LDoS attack and the flow chart of the detection method is shown in Figure 2.

Figure 2. The flow chart of LDoS attack detection. The Bartlett approach is used to obtain the PSD of traffic data, and then normalized cumulative power spectrum density (NCPSD) is gained after the normalization process. Judge whether there is an attack by analyzing the distribution of NCPSD in low frequency domain at last.

The power spectrum gives us an insight into the characteristics of the generalized stationary stochastic process in frequency domain, such as periodicity, peak position, frequency range, etc. The power spectrum of zero-mean generalized stationary stochastic process $\left\{x_n\right\}$ is defined as

$$S_x\left(e^{jw}\right)\equiv \sum _{m=-\infty }^{+\infty }{R}_x\left(m\right)e^{-jwm},$$

(6)

namely Wiener–Khinchin theorem, where the autocorrelation sequence $R_x\left(m\right)$ is defined as

$$\begin{array}{cc}\hfill R_x\left(m\right)& \equiv E\left[x\left(n\right)x^{*}(n+m)\right]\hfill \\ \hfill & \equiv \underset{N\to \infty }{lim}\frac{1}{2N+1}\sum _{n=-N}^{N}x\left(n\right)x^{*}(n+m),\hfill \end{array}$$

(7)

where N means the length of sample data. It is noteworthy that Equations (6) and (7) are only of theoretical significance for reasons as follows: first, there is no way to collect infinite data, and second, there is always noise mixed in our data. In any event, the spectral estimation of $\left\{x_n\right\}$ is then transformed into the estimation of its autocorrelation sequence $R_x\left(m\right)$. With regard to the stochastic process whose mean value is not equal to 0, its power spectrum will not change after eliminating the mean value, and thus only discussing the case where the mean value is 0 does not lose the conclusions’ generality [31]. In this section, we are going to compare three spectral estimation approaches from the perspective of consistency of estimations and discuss whether they are unbiased estimations.

2.2.1. Autocorrelation Estimation with Rectangular Window

Since it is impossible to get unlimited data, we can intercept a certain length of data by using the window function. Here, the rectangular window is our first consideration. We assume that $x\left(n\right)$ is a sampling sequence of stochastic process $\left\{x_n\right\}$ and we intercept a segment of $x\left(n\right)$ as

$$x_N\left(n\right)=w_R\left(n\right)x\left(n\right)=\left\{\begin{array}{ccc}\hfill x\left(n\right)& ,\hfill & \hfill 0\le n\le N-1\\ \hfill 0& ,\hfill & \hfill else,\end{array}\right.$$

(8)

where $w_R\left(n\right)$ is a rectangular window of length N

$$w_R\left(n\right)=\left\{\begin{array}{ccc}\hfill 1& ,\hfill & \hfill 0\le n\le N-1\\ \hfill 0& ,\hfill & \hfill else.\end{array}\right.$$

(9)

When the length of sample data is N, the autocorrelation $R_x\left(m\right)$ is estimated as

$${\widehat{R}}_x\left(m\right)=\left\{\begin{array}{cc}\hfill \sum _{n=-\infty }^{+\infty }& \frac{x_N\left(n\right)x_N^{*}(n+m)}{N-\mid m\mid },\mid m\mid \le N-1\hfill \\ \hfill & 0,else,\hfill \end{array}\right.$$

(10)

which can be simplified as

$${\widehat{R}}_x\left(m\right)=\left\{\begin{array}{cc}\hfill \sum _{n=0}^{N-1-\mid m\mid }& \frac{x\left(n\right)x^{*}(n+m)}{N-\mid m\mid },\mid m\mid \le N-1\hfill \\ \hfill & 0,else.\hfill \end{array}\right.$$

(11)

Next, we find the mathematical expectation of ${\widehat{R}}_x\left(m\right)$

$$\begin{array}{cc}\hfill E[{\widehat{R}}_x\left(m\right)]& =\sum _{n=0}^{N-1-\mid m\mid }\frac{E\left[x\left(n\right)x^{*}(n+m)\right]}{N-\mid m\mid }\hfill \\ \hfill & =\sum _{n=0}^{N-1-\mid m\mid }\frac{R_x\left(m\right)}{N-\mid m\mid }=R_x\left(m\right),\hfill \end{array}$$

(12)

which has values only if $\mid m\mid \le N-1$ and 0 in other cases. According to Equation (12), when ${\widehat{R}}_x\left(m\right)$ is used as the estimate of $R_x\left(m\right)$, estimation bias $B=R_x\left(m\right)-E[{\widehat{R}}_x\left(m\right)]=0$, namely ${\widehat{R}}_x\left(m\right)$ is the unbiased estimation. By the estimation of $R_x\left(m\right)$, the estimation of the power spectrum (${\widehat{P}}_x\left(\omega \right)$) can be obtained

$${\widehat{P}}_x\left(\omega \right)=\sum _{m=-(N-1)}^{N-1}{\widehat{R}}_x\left(m\right)e^{-jwm},$$

(13)

whose mathematical expectation is the convolution of frequency spectrum and rectangular window spectrum. When $N\to \infty$, the mean value is

$$\begin{array}{cc}\hfill \underset{N\to \infty }{lim}E[{\widehat{P}}_x\left(\omega \right)]& =\sum _{m=-\infty }^{+\infty }{w}_R\left(m\right)R_x\left(m\right)e^{-jwm}\hfill \\ \hfill & =\sum _{m=-\infty }^{+\infty }{R}_x\left(m\right)e^{-jwm}=P_x\left(\omega \right),\hfill \end{array}$$

(14)

from which $P_x\left(\omega \right)$ is the true value of power spectrum and we can see that ${\widehat{P}}_x\left(\omega \right)$ is the asymptotic unbiased estimation, as when $N\to \infty$, $w_R\left(m\right)\to 1$.

However, the Fourier transform of rectangular window function

$$\begin{array}{cc}\hfill W_R\left(e^{jw}\right)& =\sum _{n=-(N-1)}^{N-1}{w}_R\left(n\right)e^{-jwn}\hfill \\ \hfill & =\sum _{n=-(N-1)}^{N-1}{e}^{-jwn}=\frac{sin(\frac{w(2N-1)}{2})}{sin\left(\frac{w}{2}\right)}\hfill \end{array}$$

(15)

shows that it has values in negative number field which may lead to ${\widehat{P}}_x\left(\omega \right)$ less than zero subsequently. As there is no physics meaning if ${\widehat{P}}_x\left(\omega \right)<0$, the autocorrelation estimation with rectangular window is not used to estimate the power spectrum generally.

2.2.2. Periodogram with Bartlett Window

Due to the defects of rectangular window that some results are inconsistent with physics meaning and the estimation error is comparatively large when the value of $\mid m\mid$ is close to N, we consider using Bartlett window to optimize,

$$w_B\left(m\right)=\left\{\begin{array}{ccc}\hfill 1-\frac{\mid m\mid }{N}& ,\hfill & \hfill \mid m\mid \le N-1\\ \hfill 0& ,\hfill & \hfill else.\end{array}\right.$$

(16)

Thus, we get another estimate of $R_x\left(m\right)$

$${\widehat{R}}_x^{\prime }\left(m\right)=\left\{\begin{array}{cc}\hfill \sum _{n=0}^{N-1-\mid m\mid }& \frac{x\left(n\right)x^{*}(n+m)}{N},\mid m\mid \le N-1\hfill \\ \hfill & 0,else,\hfill \end{array}\right.$$

(17)

whose link with Equation (10) can be expressed as ${\widehat{R}}_x^{\prime }m=(N-\mid m\mid ){\widehat{R}}_x\left(m\right)/N$. Therefore, the mathematical expectation of ${\widehat{R}}_x^{\prime }\left(m\right)$ can be easily obtained

$$\begin{array}{cc}\hfill E[{\widehat{R}}_x^{\prime }\left(m\right)]& =E[\frac{N-\mid m\mid }{N}{\widehat{R}}_x\left(m\right)]\hfill \\ \hfill & =\frac{N-\mid m\mid }{N}{R}_x\left(m\right),\hfill \end{array}$$

(18)

which means ${\widehat{R}}_x^{\prime }\left(m\right)$ is the biased estimate of $R_x\left(m\right)$ because estimation bias $B=R_x\left(m\right)-{\widehat{R}}_x^{\prime }\left(m\right)=\mid m\mid R_x\left(m\right)/N$ is not equal to 0. While because of

$$\begin{array}{cc}\hfill \underset{N\to \infty }{lim}E\left[R_x^{\prime }\left(m\right)\right]& =\underset{N\to \infty }{lim}\frac{N-\mid m\mid }{N}{R}_x\left(m\right)\hfill \\ \hfill & =R_x\left(m\right),\hfill \end{array}$$

(19)

hence the autocorrelation estimation based on Bartlett window is the asymptotic unbiased estimation.

More importantly, the Fourier transform of Bartlett window can be regarded as the conjugated product of the rectangular window’s Fourier transform

$$\begin{array}{cc}\hfill W_B\left(e^{jw}\right)& =W_R\left(e^{jw}\right)W_R^{*}\left(e^{jw}\right)\hfill \\ \hfill & =\frac{1}{N}{\left(\frac{sin\left(\frac{wN}{2}\right)}{sin\left(\frac{w}{2}\right)}\right)}^2,\hfill \end{array}$$

(20)

which ensures the power spectrum estimation obtained later is greater than 0, thus being consistent with the physics meaning. Similarly, according to Equation (13), the mathematical expectation of power spectrum estimation can be deduced as

$$\begin{array}{cc}\hfill E[{\widehat{P}}_x\left(\omega \right)]& =E[\sum _{m=-\infty }^{+\infty }{\widehat{R}}_x\left(m\right)e^{-jwm}]\hfill \\ \hfill & =\sum _{m=-(N-1)}^{N-1}{w}_B\left(m\right)R_x\left(m\right)e^{-jwm}\hfill \\ \hfill & =\frac{1}{2\pi }{W}_B\left(\omega \right)\ast P_x\left(\omega \right)\hfill \\ \hfill & =\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{W}_B\left(\xi \right)P_x(\omega -\xi )d\xi ,\hfill \end{array}$$

(21)

which demonstrates its mean value is the convolution of frequency spectrum and Bartlett window spectrum. When $N\to \infty$, referring to Equation (14), it is not hard to draw that $E[{\widehat{P}}_x\left(\omega \right)]\to P_x\left(\omega \right)$.

Another indicator to measure estimation performance is estimate consistency, which can be represented by estimation variance

$$Var[{\widehat{P}}_x\left(\omega \right)]\approx P_x^2\left[1+{\left(\frac{sin\left(\omega N\right)}{Nsin\omega }\right)}^2\right],$$

(22)

from which we can find spectral estimation with Bartlett window is not a consistent estimation. Based on the above analyses, it is appropriate to make spectral estimations by using autocorrelation estimations with Bartlett window, though the results are not consistent.

Regrettably, the approach based on Equation (6) is still not simple enough, and then the so-called direct calculation approach of periodogram is proposed,

$$\begin{array}{c}{\widehat{P}}_x\left(\omega \right)=\sum _{m=-\infty }^{+\infty }{\widehat{R}}_x^{\prime }\left(m\right)e^{-jwm}\hfill \\ =\frac{1}{N}\sum _{m=-\infty }^{+\infty }\sum _{n=-\infty }^{+\infty }{x}_N(n+m)x_N^{*}\left(n\right)e^{-jwm}\hfill \\ \stackrel{n+m=k}{=}\frac{1}{N}\sum _{n=-\infty }^{+\infty }\sum _{k=-\infty }^{+\infty }{x}_N\left(k\right)e^{-jwk}{x}_N^{*}\left(n\right)e^{jwn}\hfill \\ =\frac{1}{N}{\left|\sum _{n=0}^{N-1}x\left(n\right)e^{-jwn}\right|}^2\hfill \\ =\frac{1}{N}{\left|X_N\left(e^{jw}\right)\right|}^2,\hfill \end{array}$$

(23)

where $X_N(e^{jw})={\sum }_{n=0}^{N-1}x\left(n\right)e^{-jwm}$. In this way, we no longer need to estimate the autocorrelation function, but obtain spectral estimation by directly Fourier transforming the sequence data and then squaring their modulus.

In a word, periodogram with Bartlett window guarantees the power spectrum greater than 0 and simultaneously the calculation is relatively simple, while the defect lies in the estimation inconsistency.

2.2.3. The Bartlett Approach

The result of periodogram is the asymptotic unbiased estimation, but not the consistent estimation of power spectrum. Inspired by Equation (14), if we could find the consistent estimation of $E[{\widehat{P}}_x\left(\omega \right)]$, and correspondingly the consistent estimation of $P_x\left(\omega \right)$ is then gained.

According to the statistic theory, the arithmetic mean of a set mutually independent data of a stochastic variable is the consistent estimation of this variable’s mathematical expectation. Consequently, we take several mutually independent sampling sequences of a stochastic process and average their periodogram results. The mean value so obtained would be the consistent spectral estimation of the stochastic process. Such approach is the so-called average periodogram, or the Bartlett approach.

Refer to the algorithm model in Figure 3, for data with N points, they are divided into L segments, each of which has M points, namely $N=L\times M$. For each segment, we perform periodogram with Bartlett window separately to estimate power spectrum

$${\widehat{P}}_i\left(\omega \right)=\sum _{m=-\infty }^{+\infty }{\widehat{R}}_i\left(m\right)e^{-jwm},(1\le i\le L)$$

(24)

and then average the total L segments’ estimation results

$$\begin{array}{cc}\hfill {\widehat{P}}_b\left(\omega \right)& =\frac{1}{L}\sum _{i=1}^L{\widehat{P}}_i\left(\omega \right)\hfill \\ \hfill & =\frac{1}{L}\sum _{i=1}^L\sum _{m=-\infty }^{+\infty }{\widehat{R}}_i\left(m\right)e^{-jwm}\hfill \\ \hfill & =\sum _{m=-\infty }^{+\infty }\left[\frac{1}{L}\sum _{i=1}^L{\widehat{R}}_i\left(m\right)\right]e^{-jwm},\hfill \end{array}$$

(25)

which means find out each segment’s autocorrelation function, calculate the average value and then conduct Fourier Transform.

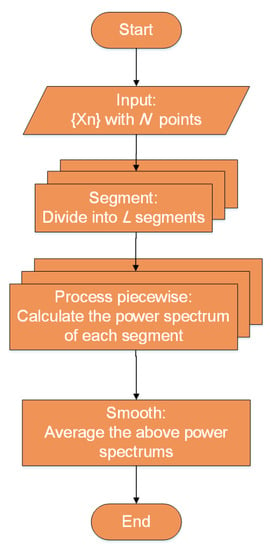
Figure 3. The algorithm model of the Bartlett approach.

$P_i\left(\omega \right)$ can be approximately regarded as mutually independent in the case of $M\gg 1$, hence the estimation variance of the Bartlett approach is

$$Var[{\widehat{P}}_b\left(\omega \right)]\approx \frac{1}{L^2}\sum _{i=0}^{L}Var[{\widehat{P}}_i\left(\omega \right)]=\frac{1}{L}Var[{\widehat{P}}_i\left(\omega \right)].$$

(26)

Considering the limiting case of $L\to \infty$, the variance $Var[{\widehat{P}}_b\left(\omega \right)]\to 0$, demonstrating the Bartlett approach is the consistent estimation.

3. Performance

3.1. Comparison with the Wavelet Approach

The detection principle of the traditional method, based on wavelet feature extraction and Hurst index estimation [32], is such that when the DoS attack occurs, the Hurst index of network traffic will decrease. The Hurst index of normal network traffic is roughly between 0.75 and 1, and the larger the Hurst index, the stronger the burst of traffic [33]. When the channel is completely blocked, the network traffic tends toward a Poisson distribution, and the Hurst index becomes 0.5. However, as the DDoS and LDos attack both are a type of DoS attack and will cause the drop of the Hurst index in the same way, it is unattainable to achieve the goal of distinguishing these two attacks. Moreover, the complexity of the wavelet transform is higher than that of the power spectrum estimation.

Based on a NS-2 simulation environment from Rice University, the performance of the wavelet approach and the Bartlett approach in LDoS attack detection accuracy is compared in Table 1. Only DDoS and LDoS attacks are set in the simulation environment. It can be seen from Table 1 that the wavelet approach has almost no ability to distinguish these two attacks.

Table 1. Detection accuracy of LDoS attack.

Method	Accuracy
The wavelet approach with Hurst estimation	53%
The Bartlett approach with NCPSD	88%

3.2. Estimation Consistency and Detection Effect

To verify the validity of our proposed detection approach, we initially compare the performance of estimation consistency, then detect the traffic containing LDoS attack streams by analyzing the distribution of normalized cumulative power spectrum density (NCPSD) in frequency band to test the authenticity of our approach. The authors of [20] conducted relevant simulation experiments to prove that a slight change in transmittance T will result in the keyrate-distance product decrease. A typical experiment in Ref. [20] shows that, in the channel where T obeys a two-point distribution, when p, which means the probability that the channel transmittance is non-zero, drops from 1 to 0.99, the channel’s secure transmission distance is reduced by more than half. Therefore, the LDoS attack stream in our experimental data mainly aims at tempering the transmittance T. As for the data used to test the estimation consistency, we adopt the filtered Gaussian white noise as the stochastic process sequence with a normalized center frequency (see Appendix B for definition) of 0.1 and a relative bandwidth (see Appendix B for definition) of 4%. Moreover, the sampling frequency is 100 Hz in the estimation consistency experiment.

As shown in Figure 4, our experiment data are filtered from Gaussian white noise by FIR filter with Blackman window and the data length is 1800 points. We carefully select the order of filter to balance the signal distortion and filtering effect. In accordance with a sampling frequency of 100 Hz, it can be calculated that the analog frequency corresponding to the normalized frequency of 0.1 should be $0.1\times 100$ Hz/2 = 5 Hz.

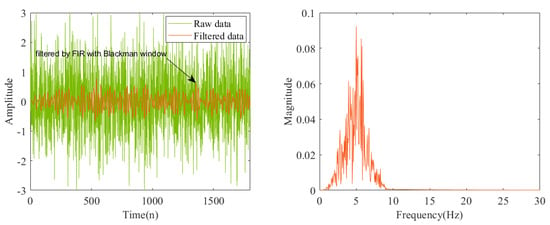
Figure 4. Data of estimation consistency experiment. Raw data is the Gaussian white noise with mean value of 0 and variance of 1. Filtered data is obtained by filtering the raw data with a high-order FIR filter. The figure on the right is the spectogram, distributed around 5 Hz, of filtered data.

After that, we successively used the periodogram with Bartlett window and the Bartlett approach to estimate the power spectrum of experiment data. In order to put stress on the estimation consistency, the power spectrum’s details in the vicinity of the center frequency are magnified in Figure 5. Both spectral estimation approaches estimate twice to analyze the consistency of the estimation.

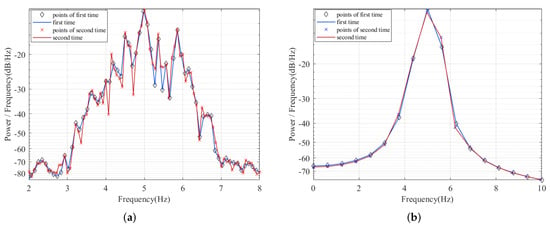
Figure 5. Comparison of estimation consistency. (a) Adopting the periodogram with Bartlett window for spectral estimation. (b) Adopting the Bartlett approach (average periodogram) for spectral estimation.

Comparing the two figures in Figure 5, except the discovery that the performance in consistency of the Bartlett approach outperforms the periodogram with Bartlett window, we can also find that the curve of the Bartlett approach is smoother and its center frequency peak is more distinct. Hence, the Bartlett approach’s estimation consistency has been strongly verified.

In the simulation experiment, the Bartlett approach is used for the spectral estimation. Using the NCPSD (see Appendix B for definition) calculation of the LDoS attack stream under different background traffic intensities, we test the feasibility of the proposed method to detect the LDoS attacks.

As shown in Figure 6a, the stream with the LDoS attacks has an energy distribution close to 70% of the total energy in the range of 0 to 50 Hz, while the normal stream has only 10% energy in this range. It, at the same time, proves that we can calculate the deviation of the NCPSD from the normal value to reflect whether the stream contains LDoS attacks.

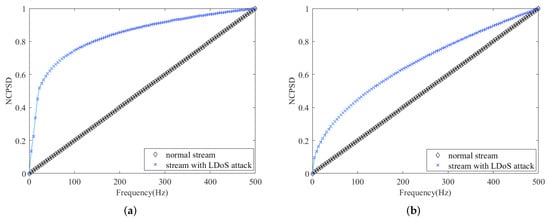
Figure 6. NCPSD under different background traffic intensity.(a) NCPSD of attack stream and normal stream under low background traffic. (b) NCPSD of attack stream and normal stream under high background traffic.

Figure 6b shows the NCPSD curves of stream with the LDoS attack and the normal one. In spite of the narrowed difference between the two curves, there is 30% of the total energy distributed within the range of 0 to 50 Hz, which is still quite deviated from 10% of the normal stream. That is to say, under the high intensity of background traffic, the detection effect has declined to some extent, but it can still detect whether the stream contains LDoS attacks.

4. Conclusions

In our paper, a method based on Bartlett’s approach of spectral estimation is proposed to detect LDoS attacks in the CVQKD communicating progress. The LDoS attack is an algorithm-aimed hacking strategy and related experiments have already demonstrated that a slight manipulation of a channel’s parameters can trigger the communication interruption. What we pay attention to is the channel’s transmittance T, as other parameters can be deduced from it. Taking advantage of the periodicity of LDoS attacks, we obtain the rule that the PSD of the LDoS attack stream is higher than normal in the low frequency domain, hence transforming the issue of the LDoS attack detection into the spectral estimation of stochastic sequence. Three of the spectral estimation approaches are discussed emphatically, including the autocorrelation estimation with rectangular window, periodogram with Bartlett window and the Bartlett approach, from the perspective of estimation consistency and estimation unbiasedness. Through mathematical deduction and experimental analysis, the Bartlett approach performs best among the three approaches. The simulation experiment results show that the Bartlett approach is consistent in its estimations and can effectively detect the LDos attacks.

Appendix B.1. NCPSD

The normalized cumulative power spectrum density is defined as

$$\varphi \left(f\right)=\sum _{i=1}^{f}PSD\left(i\right)/\sum _{i=1}^{f_{max}}PSD\left(i\right),$$

where $PSD\left(i\right)$ means the power spectral density of ith frequency component. The value range of NCPSD is 0 to 1, and NCPSD reflects the proportion of different frequency components in the whole signal.

Appendix B.2. Normalized Frequency

The normalized frequency is defined as

$$\omega =\frac{2\pi f}{f_s},$$

where f means the analog frequency and $f_s$ means the sampling frequency. It takes the sampling frequency as the reference value. In this way, a unified standard is achieved, which is conducive to comparing the distribution of various frequencies.

Appendix B.3. Relative Bandwidth

Relative bandwidth is defined as

$$f_{rb}=\frac{2(f_H-f_L)}{f_H+f_L},$$

where $f_H$ and $f_L$ are the upper and lower limit frequencies, respectively.