One-Pixel Attack for Continuous-Variable Quantum Key Distribution Systems

Abstract

Deep neural networks (DNNs) have been employed in continuous-variable quantum key distribution (CV-QKD) systems as attacking detection portions of defense countermeasures. However, the vulnerability of DNNs leaves security loopholes for hacking attacks, for example, adversarial attacks. In this paper, we propose to implement the one-pixel attack in CV-QKD attack detection networks and accomplish the misclassification on a minimum perturbation. This approach is based on the differential evolution, which makes our attack algorithm fool multiple DNNs with the minimal inner information of target networks. The simulation and experimental results show that, in four different CV-QKD detection networks, $52.8\%$, $26.4\%$, $21.2\%$, and $23.8\%$ of the input data can be perturbed to another class by modifying just one feature, the same as one pixel for an image. We carry out this success rate in the context of the original accuracy reaching up to nearly $99\%$ on average. Further, by enlarging the number of perturbed features, the success rate can be raised to a satisfactory higher level of about $80\%$. According to our experimental results, most of the CV-QKD detection networks can be deceived by launching one-pixel attacks.

1. Introduction

Quantum key distribution (QKD) [1] enables two remote correspondents, usually called Alice and Bob, to exchange secret keys in an information-theoretically secure way. According to the basic law of quantum mechanics, primarily the Heisenberg’s uncertainty principle [2] and the quantum no-cloning theorem [3], if there is an eavesdropper called Eve, the illegal measurements of Eve can be recognized by the legal receiver Bob and remove the leakage information. Taking the different implementation methods as the basis for classification, QKD can be divided into two categories: discrete-variable quantum key distribution (DV-QKD) [4,5] and continuous-variable quantum key distribution (CV-QKD) [6,7,8,9]. Previous researches have show that CV-QKD not only has a higher key rate but it is also easier to prepare and measure compared with DV-QKD. Additionally, CV-QKD is compatible with the existing optical networks, which provides it with an attractive future in a practical application. Here in this paper, our study is based on the CV-QKD system under its most practical protocol, a Gaussian-modulated coherent state (GMCS) protocol [10,11], which has been proven to be secure under collective attacks and coherent attacks in theory [12,13].

However, when it comes to an application in reality, the real CV-QKD system faces several security loopholes caused by the imperfection of realistic devices. The eavesdroppers in reality can break the security of the practical GMCS CV-QKD with attack strategies such as wavelength attacks [14,15], calibration attacks [16], local oscillator (LO) intensity attacks [17], saturation attacks [18], and homodyne-detector-blinding attacks [19]. To defend these practical attack strategies, diversified methods have been proposed. One type of defense method attempts to establish a new QKD protocol, such as device-independent QKD [20] and measurement device-independent QKD [21]. However, these protocols have shown a low key rate in previous practical research. Another typical defense method is to add security patches in the existing protocol, which probably leads to new loopholes by patching [22]. The other kind of countermeasure is to detect the timely parameter by adding relevant real-time monitoring modules on the system.

In recent years, with the swift development of artificial intelligence (AI) [23], many innovations based on the artificial neural network (ANN) has been proven to be effective. For example [24], Mao et al. [25] proposed an ANN model to classify their attack strategy, Luo et al. [26] proposed a semi-supervised deep learning method to detect known attacks and potential unknown attacks, and Du et al. [27] proposed an ANN model for multi-attacks detection. The main idea of these methods is to implement specific defense countermeasures based on the classification result from the ANN model. However, the defense countermeasures which depend on the ANN can also bring new potential security threats to the CV-QKD system. According to the theory of an adversarial attack [28], particular tiny perturbations on the input vector are capable of misclassifying the original input, which can be an enormous threat to this security-sensitive system.

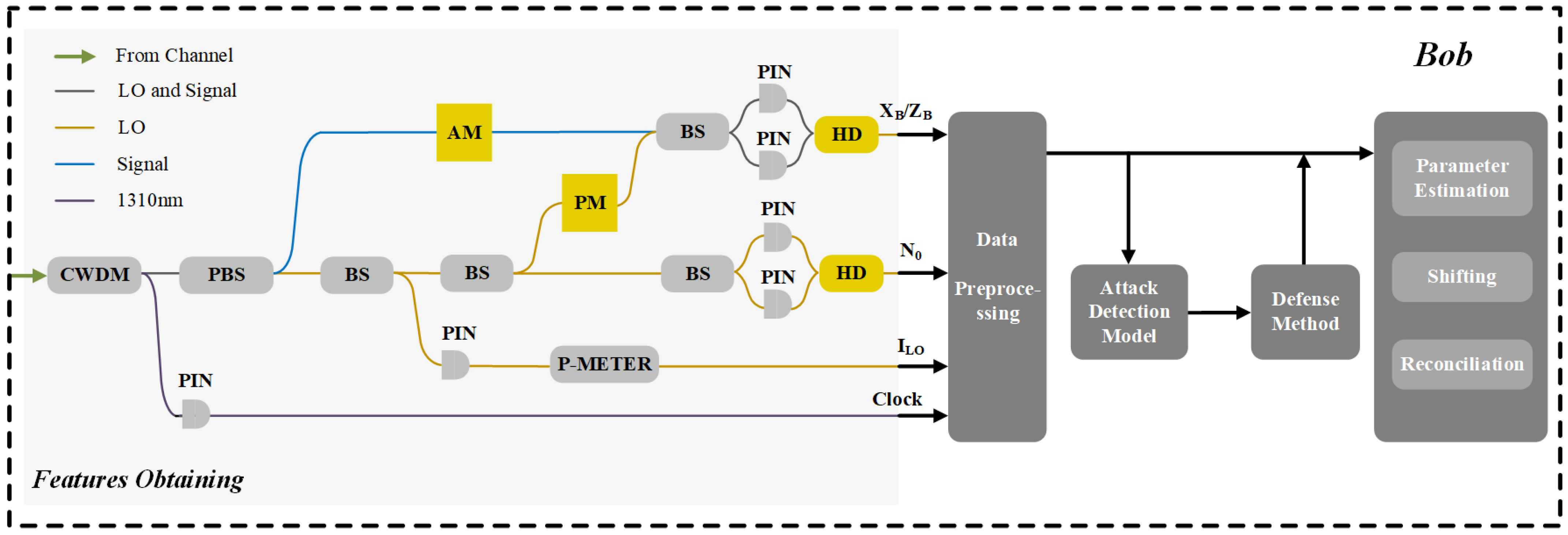
In this paper, we propose that a classical adversarial attack, the one-pixel attack [29], can be applied in the QKD field, directly against the CV-QKD defense countermeasures based on the DNNs classification. The schematic diagram of the CV-QKD systems that we attack is shown in Figure 1. In the experiment, we use a 1310 nm light source as our system independent clock. The pulse passes are split into the signal light source and the clock light source by a coarse wavelength-division multiplexing (CWDM) after reaching Bob. Then we take the separated 1310 nm light source as the system clock, which is used to monitor the real-time shot noise variance. The rest part of the pulses will pass a polarization beam splitter (PBS) after the CWDM to divide the signal pulses and the LO pulses. Next, the LO pulses are separated by a beam splitter (BS) to monitor the LO intensity and are sent to the next BS, respectively. The second BS will split the pulses into two parts for shot noise monitoring and homodyne detection with the signal being processed by an amplitude modulator. At last, those measurement results will come to the data preprocessing portion and be conducted as the original data which can be used in a neural network model for attack detection.

Considering the universality of the attacked models, we establish four representative DNNs, which are trained to distinguish the categories of attacks from three known attacks, one hybrid strategy attack, and the normal state as our attack targets. We migrate the method of the one-pixel attack, which is mostly based on a differential evolution (DE) algorithm [30], into these CV-QKD attack-detecting networks and investigate the prediction results of the perturbed data. Our experimental results have demonstrated that the one-pixel attack can be successfully removed from the image identification field to the CV-QKD attacking detection field. In addition, by slightly enlarging the number of perturbed pixels, we can significantly enhance the success rate of our attack. At last, we discuss the merit and demerit of our attacking strategy.

The paper is organized as follows. First, in Section 2, we introduce the dataset and methods used in our work, including the DNNs subjected to adversarial attacks and the algorithm details of the one-pixel attack. Then, we analyze the related simulation results of our attack strategy and discuss its merit and demerit in Section 3. Finally, we make a summary of our work in Section 4.

2. Materials and Methods

2.1. Datasets and Parameter Settings

In a CV-QKD system based on the GMCS protocol, Alice generates two continuous variable sets, x and p, which obey the Gaussian distribution with a zero average and variance $V_A{N}_0$. Then, by modulating weak coherent states $|x+ip>$, Alice encodes the key information and sends the encoded information to Bob through a strong $LO$ of intensity $I_{LO}$. On the receiving end, with the phase reference extracted from $LO$, Bob can measure one of the quadratures of the signal states by performing a homodyne detection. After repeating this procedure various times, Bob will receive the correlated data sequence $\overrightarrow{Y}=\left\{y_1,y_2,y_3...,y_n\right\}$. The mean and variance of a receiving sequence $\overrightarrow{Y}$ can be described by:

$$V_y=r\eta T\left(V_A{N}_0+\xi \right)+N_0+V_{el}$$

(1)

$$\overline{y}=0$$

(2)

where T and $\eta$ are the quantum channel transmittance and the efficiency of the homodyne detector, respectively. $V_{el}=v_{el}{N}_0$ is the detector’s electronic noise and $\xi =\epsilon N_0$ is the technical excess noise of the system.

To match with the existing classification networks of the CV-QKD attacks, our data consists of a normal condition, three kinds of common CV-QKD attacks: calibration attacks, local oscillator ($LO$) intensity attacks, and saturation attacks, and one hybrid attack strategy consisting of $LO$ intensity attacks and wavelength attacks. From another perspective, the classification network designed to distinguish the above-mentioned attack strategies is the most practical, since the individual wavelength attacks are only practicable in heterodyne detection CV-QKD systems. Here we obtain the labels of our dataset: $\left\{y_{normal},y_{LOI},y_{calib},y_{sat},y_{hyb}\right\}$.

According to Luo et al. and Mao et al. [25,26], there are some features that can be measured without disturbing the normal transmission between Alice and Bob. Among them, we select the intensity $I_{LO}$ of the $LO$, the shot noise variance $N_0$, the mean value $\overline{y}$, and the variance $V_y$ of Bob’s measurement as the features we use to distinguish diverse attack strategies. The value of these four features will change in a different degree after the CV-QKD process is attacked by different strategies. Therefore, we construct the vector $\overrightarrow{u}=\left\{\overline{y},V_y,I_{LO},N_0\right\}$ to describe the security status of the communication as our feature vector.

The steps of preparing our dataset contain four following parts. First of all, for each of the CV-QKD attack strategies, including the normal condition, we generate the original sampling dataset of $N=7.5\times {10}^7$ pulses in chronological order. Second, to acquire the statistical characteristics from the sampling characteristics, all $7.5\times {10}^7$ pulses in the original data are divided into M time boxes including $n={10}^5$ sets of sampling data in each box. Then we calculate the four statistical characteristics of each time box to obtain the feature vector $\overrightarrow{u}=\left\{\overline{y},V_y,I_{LO},N_0\right\}$. At last, in order to accommodate the universal ANN models in the image field and strengthen the stability of the input data as well, we combine 25 continuous feature vectors as an input matrix, which can be seen as a 25 × 4 image with one channel. The choice of this number refers the experiments of Luo et al. [26] and Du et al. [27]. The group generated here is the basic unit for our network to classify. At this point, we have five original datasets of each CV-QKD attack strategy. To build the rational training set and test set, 750 groups are randomly selected from each original dataset and divided into the training set and test set by a ratio of 2:1. Then we put all groups for training together to make a disrupted order and repeat this process to generate the test set. So far, the dataset for the model training and adversarial attack is well prepared. The rest of the details regarding the parameter setting and data perpetration are shown in Appendix A.

2.2. Models Architecture and Training Results

The significance of the CV-QKD attack detection models in our work can be mainly described in following two points. First of all, to conduct a one-pixel attack, we require numerous well-trained models as the scoring function. Second, the output labels of the models are the main metric to measure the effectiveness of our attack. According to the research of Jiawei Su et al. [29], which is the first to propose the one-pixel attack in the image field, this attack algorithm is effective in many deep neural networks, such as the all convolution network (AllConv), Network in Network (NiN) [31], Visual Geometry Group Network (VGG16) [32], and AlexNet. In our work, we select two classical models, AllConv and NiN, and additionally append two kinds of widely used DNNs, ResNet [33], and DenseNet [34] to validate our attack effect. The model training and attack simulation are programmed in Python with the help of its provided packages and some fundamental open source code; the dataset is generated in Matlab R2019b. The detailed structures of the AllConv and NiN network can be seen in Figure 2a,b, while the rest of the information is presented in Appendix B. Since the input matrix is relatively simpler than the initially designed input of the image information for the models, we predigest the structures slightly. Note that some dropout layers are added to our models compared with the original. We make these modifications in order to achieve a higher classification accuracy, which is proven to be effective by our tests. The standardized method is also used in data preprocessing in our work. In this way, the huge discrepancy between the measuring units of the different features can be mapped to a comparable range.

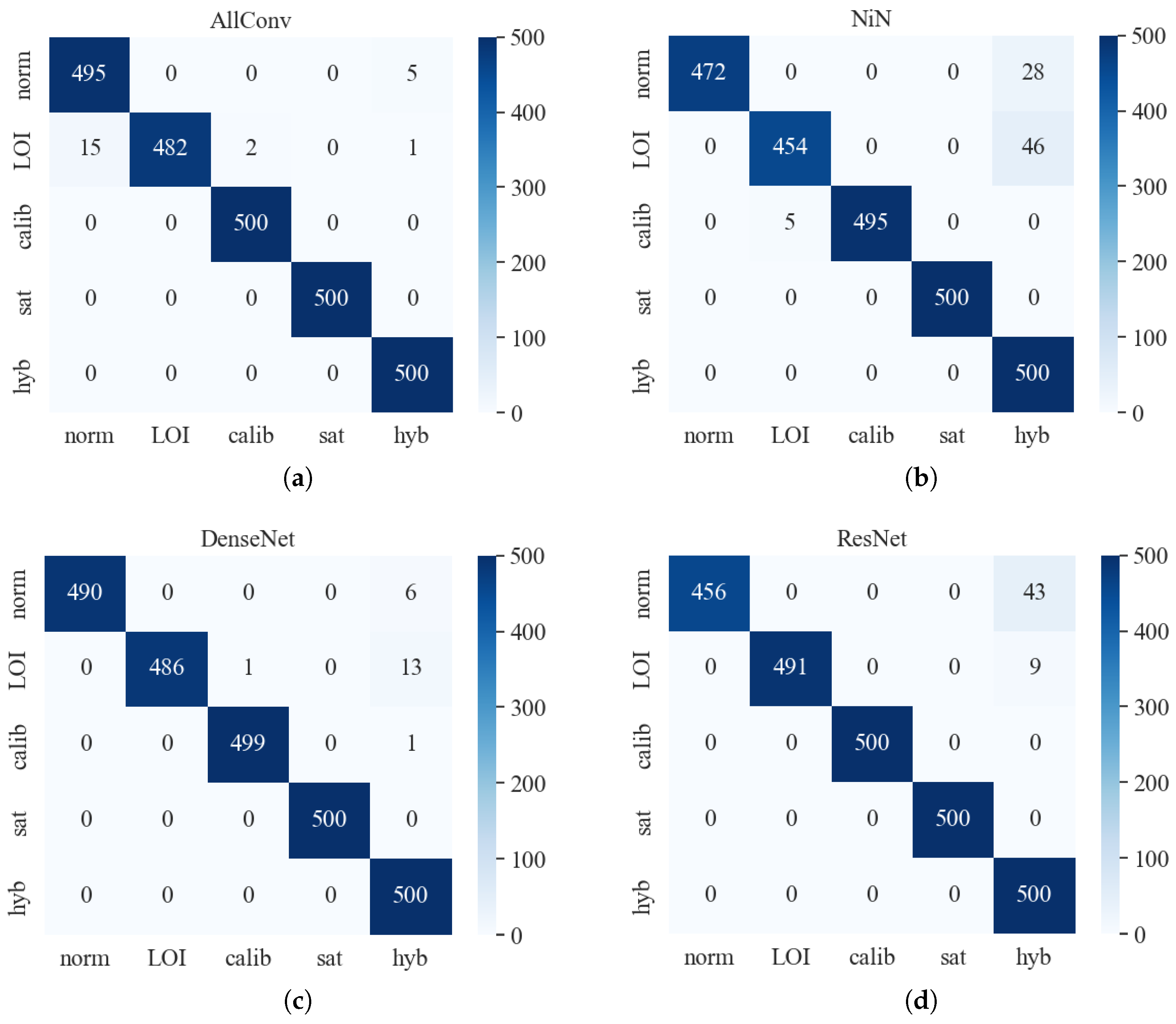
The performances of the trained models are shown in

Table 1. The optimal hyper-parameter setting and predicting performance of the four networks for CV-QKD attack detection. Epochs refer to the turn number of iterate over the dataset. Batch Size refers to the number of data we used in one iteration. AllConv: all convolution network. NiN: Network in Network.

	AllConv	NiN	ResNet	DenseNet
Epochs	30	50	50	50
Batch Size	64	32	32	32
Accuracy	97.88%	98.80%	96.84%	99.00%

and Figure 3. We select the most appropriate hyper-parameter value of epochs and batch size from $\left\{30,50,100\right\}$ and $\left\{16,32,64,128\right\}$ based on both the accuracy and efficiency. According to the consequence, the accuracy of the test set can reach a satisfactory result of $98.13\%$ on average. In Figure 3, most of the data fall on the diagonal of the confusion matrix, which visually shows the high accuracy of the four attack-detecting models.

2.3. Attacking Algorithm

As the research develops further, DNNs start to be applied to some safety-critical environments, for example, to the quantum communication. Therefore, the security of the DNNs draws the attention of numerous researchers. Amounts of previous studies suggest that DNNs are vulnerable to some specifically designed input samples which are similar to the original one; we call these adversarial examples. The one-pixel attack is a representative strategy to generate adversarial examples by only perturbing the input with a minimum of one pixel. Its approach can be described as the following formula:

$$\begin{array}{cc}\hfill & \underset{e{\left(\mathbf{x}\right)}^{*}}{maximize}{f}_{adv}(\mathbf{x}+e\left(\mathbf{x}\right))\hfill \\ \hfill & subjectto∥e{\left(\mathbf{x}\right)}_0∥\le d\hfill \end{array}$$

(3)

where $\mathbf{x}$ refers to the original input vector, $e\left(\mathbf{x}\right)$ refers to the perturbation, d is the number of perturbed pixels, and $f_{adv}(·)$ is the confidence of the target class.

The core advantages of the one-pixel attack can be concluded as three points below.

• First, it can execute an attack only relying on the probability labels of the target network without any inner information.
• Second, the attacking accuracy of the Kaggle CIFAR-10 dataset is regarded as high-efficiency. By only disturbing one pixel of a $32\times 32$ input image, it acquires a success rate above $60\%$.
• Third, it can be flexibly used on most of the DNNs according to its basic theory, differential evolution (DE).

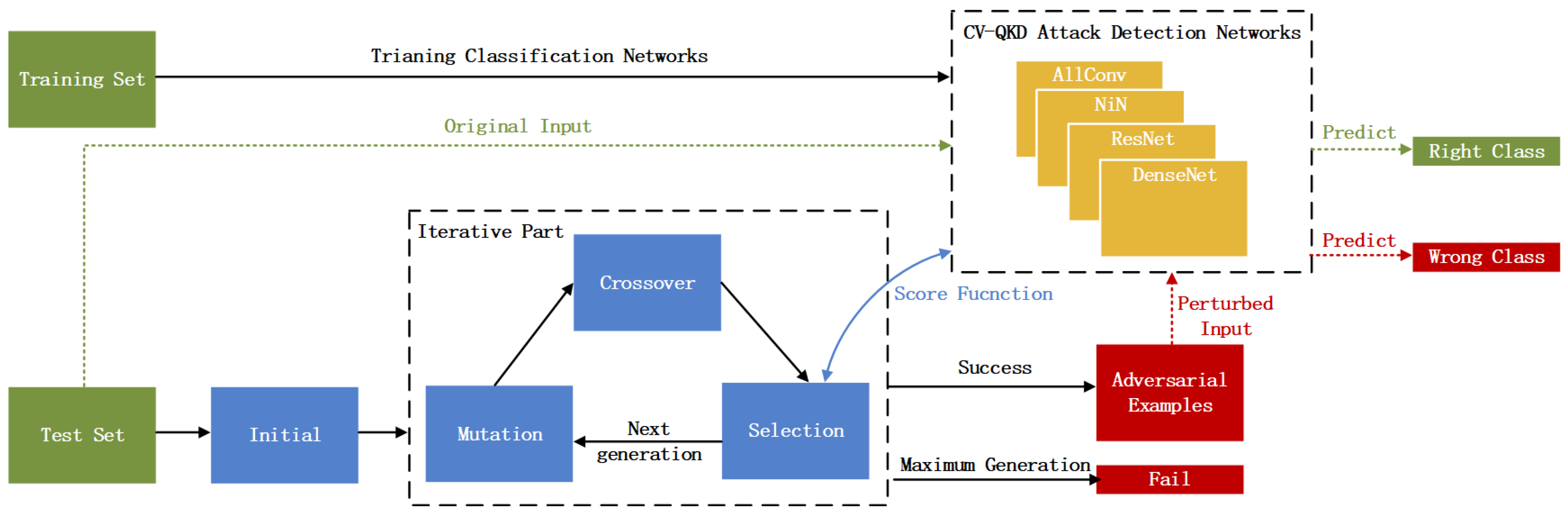
For a CV-QKD attacks detection network, the structure is generally designed as a DNN, which guarantees the feasibility of launching a one-pixel attack. Considering the compatibility, we rebuild the one-pixel attack on the basis of its original approach and DE algorithm. The frame of our attacking method is shown in Figure 4. The blue blocks in the frame are the four main parts of DE, which are used to find the most influential point to the classification result among an input matrix.

DE is a global optimization algorithm based on population-ecology theory. Generally, in each generation, primordial children will generate according to their parents. Then they will be used in a comparison with the parents, the results of which decide whether they can survive. The survivors will compose the new parents and give birth to the new generation to pass down their “genes”, what we call features in machine learning. By iteration, the last generation would be a convergent outcome, which is the most fraudulent perturbation we want to find.

To implement it specifically, the whole process can be divided into three main parts: the mutation, crossover, and selection. We assume the notation representing the ith individual in the population of $NP$ with D dimension:

$${\overrightarrow{X}}_i^t=\left[x_{1,i}^t,x_{2,i}^t,\dots ,x_{j,i}^t,\dots ,x_{D,i}^t\right]$$

(4)

where $j\in [0,D]$, $i\in [0,NP]$, $t\in [0,G]$.

First of all, the initial generation is created randomly by a certain distribution, usually a uniform distribution in the bounds in order to cover its range as much as we could. So, the first generation is initialized as:

$$x_{j,i}^0=x_{jmin}+ran{d}_{i,j}\left[1,0\right]\times \left(x_{jmax}-x_{jmin}\right)$$

(5)

where $x_{jmin}$ and $x_{jmax}$ describe the boundary of the output value.

Then the population starts to mutate depending on the following formula:

$${\overrightarrow{V}}_i=X_p^t+F\times \left(X_q^t-X_r^t\right),F\in [0,2]$$

(6)

where p, r, and q are integers randomly chosen from the range $[0,NP]$ and are different from each other at the same time. F is the mutation factor, which is settled as 0.5 usually.

A crossover step is carried out to enhance the diversity of the population. There are two ways to realize this goal:

$$Binomial:u_{j,i}^t=\left\{\begin{array}{c}{v}_{j,i},r_i\le C_r\hfill \\ x_{j,i}^t,otherwise\hfill \end{array}\right.$$

(7)

$$Exponential:u_{j,i}^t=\left\{\begin{array}{c}{v}_{j,i},forj\in [k,k-L+1]\hfill \\ x_{j,i}^t,otherwise\hfill \end{array}\right.$$

(8)

where $C_r$ is called the crossover rate.

In the last step of one iteration, we select the individual between the parents and children depending on their performance in the score function. The selecting principle can be described as:

$${\overrightarrow{X}}_i^{t+1}=\left\{\begin{array}{c}{\overrightarrow{U}}_i^t,iff({\overrightarrow{U}}_i^t)\le f({\overrightarrow{X}}_i^t)\hfill \\ {\overrightarrow{X}}_i^t,iff({\overrightarrow{U}}_i^t)>f({\overrightarrow{X}}_i^t)\hfill \end{array}\right.$$

(9)

where $f(·)$ represents the score function.

The steps mentioned above are the core method used in the one-pixel attack. According to this theory, we reset some parameters to adapt the dataset of the CV-QKD attack detection. Different from the RGB features of the images, the value of the input features $\left\{\overline{y},V_y,I_{LO},N_0\right\}$ is consecutive in their value domain. It means that there is infinite possible values for each feature, which forces us to augment the number of the population maximum $NP$. We have also attempted to enhance the attack by increasing the upper limit of the iterations. However, for the enormous amount of time consumed during the process, the slight change in the success rate is unworthy. As a result, we still use 100 as the limit superior to the iterations. In addition, the bounds of the different features are not unified. For the image input matrix, each RGB channel has the same boundary of [0, 255], whereas the four indicators of the CV-QKD attacks are in a different order of magnitude. To solve this problem, we add a normalization process as follows:

$$u_{i,pertub}=u_{i,min}+k_{pertub}\times \left(u_{i,max}-u_{i,min}\right),k_{pertub}\in [0,1]$$

(10)

where $k_{pertub}$ is the output of DE and $u_{i,pertub}$ is a perturbed feature (one pixel) in the input matrix.

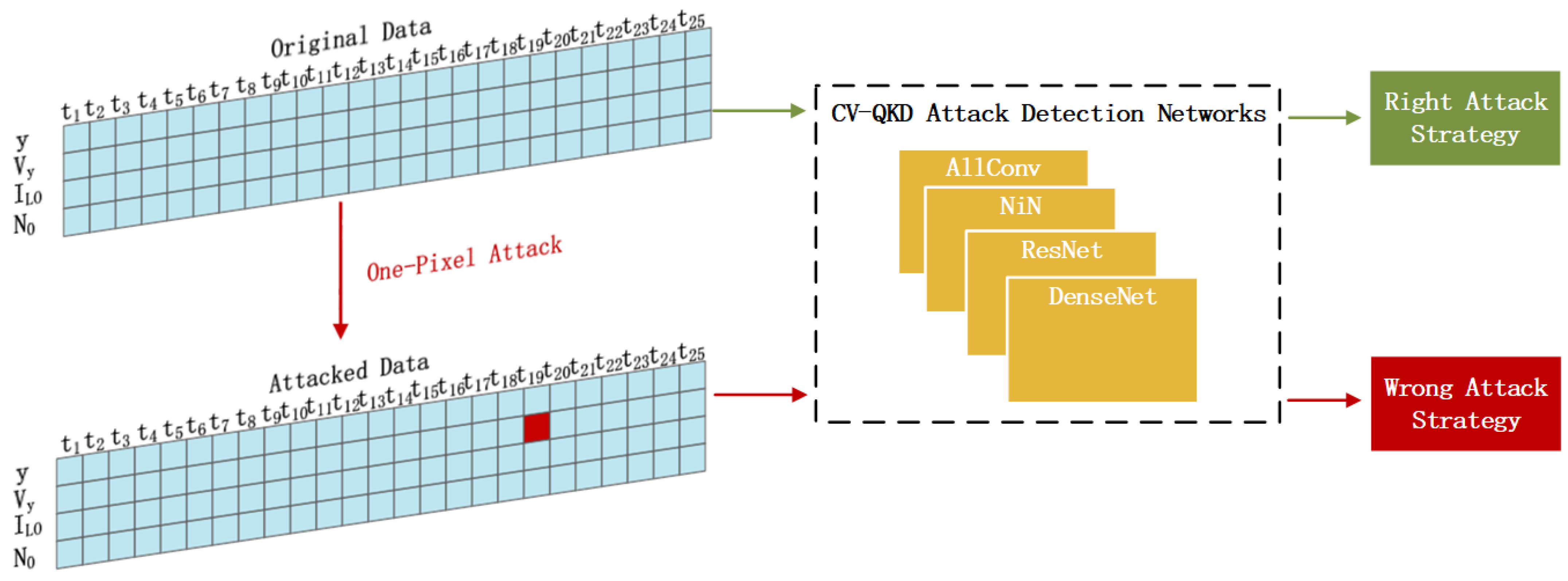
In this way, we generally finish the fundamental modification for the migration of the one-pixel attack into CV-QKD attacks detection. Using this method, an optimal perturbation for deceiving the CV-QKD attacks detection networks can be found, among each input matrix, shown in Figure 5. In the next section, we will display the performance of our work and draw a conclusion by analyzing the results.

3. Results

3.1. Evaluation Indicators

To verify the actual performance of our adversarial attack, we create a brand new set of data as the attacking objects. This objective dataset includes 500 groups of data randomly chosen from the test set, where the five attack strategies are almost mixed in the same proportion. Then, we carry out a four times targeted attack on the input data so that we are able to obtain 2000 attacking results for each model, which is shown in Figure 6b. Note that we only conduct the targeted attack, which is because the efficiency of the non-target attack can be calculated by the results of the targeted one. Therefore, the evaluation indicators for our adversarial attack are composed of the following:

• Success Rate:
  In the case of the targeted attack, we assume a successful attack only if the adversarial example can be classified into the target class. The denominator is defined as the number of all targeted attacks we launched. In the case of the non-targeted attack, we assume a successful attack when the adversarial data can be classified into any other classes except for itself. Correspondingly, the denominator is defined as the number of adversarial examples, which is equal to a quarter of the target attack times.
• Confidence Difference:
  We calculate the confidence difference for each successful perturbation by subtracting the confidence of the true label after the attack from the previous confidence of the true label. At last, we take the average confidence difference of all the successful target attacks as our evaluation indicator.
• Probability of Being Attacked:
  We introduce a false negative (FN) to estimate the probability of a CV-QKD attack strategy being misclassified.

  $$P_i^{attacked}=\frac{FN}{N_i^{non-tar}},i\in \left\{normal,LOI,calib,sat,hyb\right\}$$

  (11)

  where $FN$ denotes the number of examples that belong to an certain attack type but are not identified as such a type after a non-target attack, and $N_i$ denotes the number of examples with the true class of i.
• Probability of Being Mistaken:
  To estimate the probability of a CV-QKD attack strategy being mistaken, we introduce a false positive (FP), which denotes the number of examples that do not belong to a certain attack type but are identified as such a type after a target attack.

  $$P_i^{mistaken}=\frac{FP}{N_i^{tar}},i\in \left\{normal,LOI,calib,sat,hyb\right\}$$

  (12)

  where $N_i$ denotes the number of target attacks with the target of i.

3.2. Analysis

Based on the 2000 times of target one-pixel attacks launched in each network, the success rate of the target attacks mainly hovers around $7\%$, for AllConv $8.05\%$, DenseNet $6.25\%$, and ResNet $6.45\%$. The appearance of attacking the NiN network is more arresting with a success rate of $17.20\%$. As for the non-target attack, it shows that a success rate of attacking the NiN model reaches $52.80\%$, while the other three models are $26.40\%$, $21.20\%$, and $23.80\%$, respectively. In comparison with the original accuracy of the classification networks in Table 1, our perturbations successfully deceive all the four representative DNNs for CV-QKD attack detection.

Nevertheless, compared with the classical one-pixel attack in the image classification, it seems that the effect is not good enough. However, such a comparison is not reasonable. What is noteworthy is that, in the original CIFAR-10 test dataset, a more limited attack scenario, the original one-pixel attack also only gains $22.67\%$, $32.00\%$, and $30.33\%$ success rates. This result is more referential to judge the effect of our attack because our inputs have less practical noise, which obtains the target model with a higher classification accuracy. On the other hand, it also represents that our attack can achieve a better performance if the target model is trained by a more practical dataset with some real noise. The above result of our work suffices to prove the effectiveness of applying the one-pixel attack in CV-QKD attack detection networks. In the later work, we also try to increase the success rate on the basis of this scheme and successfully achieve our goal.

Table 2. Success rate, including target attack and non-target attack, and confidence difference of one-pixel attacks. AllConv: all convolution network. NiN: Network in Network. Non-tar Attack: non-target attack.

	AllConv	NiN	DenseNet	ResNet
Non-tar Attack	26.4%	52.8%	21.2%	23.80%
Target Attack	8.05%	17.20%	6.25%	6.45%
Difference	0.4015	0.6659	0.4942	0.5363

shows the confidence differences of each model on average, which are $0.6659$, $0.4015$, $0.4942$, and $0.5363$. It means each successful target attack can lead to a diminution of $0.5245$ in confidence, averagely. Since our strategy is to make the target network misclassify the perturbed data to a wrong class, the size of the numeric value does not matter, all that matters is if the attack succeeds. So, we can see that the value of confidence difference is not very high. It only represents the necessary decrement for misclassifying a CV-QKD attack.

The probability of being mistaken and attacked in each class can be seen in

Table 3. The probability of being mistaken under target attack (1 pixel). AllConv: all convolution network. NiN: Network in Network. Normal: the unattacked state. LOI: LO intensity attacks. Calib: calibration attacks. Sat: saturation attacks. Hyb: the hybrids attacks.

	AllConv	NiN	DenseNet	ResNet	Average
Normal	4.218%	1.241%	0%	0%	1.365%
LOI	3.659%	17.317%	6.585%	4.634%	8.049%
Calib	6.203%	0%	0.496%	0.248%	1.737%
Sat	4.145%	1.036%	0%	0%	1.295%
Hyb	22.111%	66.332 %	24.121%	27.387%	34.988%

and

Table 4. The probability of being attacked under non-target attack (1 pixel). AllConv: all convolution network. NiN: Network in Network. Normal: the unattacked state. LOI: LO intensity attacks. Calib: calibration attacks. Sat: saturation attacks. Hyb: the hybrids attacks.

	AllConv	NiN	DenseNet	ResNet	Average
Normal	69.07%	90.72%	52.58%	78.35%	72.68%
LOI	55.56%	87.78%	27.78%	36.67%	51.95%
Calib	0%	100%	18.56%	10.31%	32.22%
Sat	0%	0%	10.53%	0%	2.63%
Hyb	14.71%	0%	0%	0%	3.68%

. We can obviously see that the LO intensity attack strategy, calibration attack strategy, and normal condition have a high probability of being attacked, while the hybrid attack has the highest probability of being mistaken. Otherwise, the normal condition is much more vulnerable than others under one-pixel attacks. The hybrid attack is the easiest class to be disguised as. Otherwise, Figure 6a shows that the confusion matrix of each model is almost under the same distribution.

To make a further advance in the success rate, we enlarge the number of perturbed pixels from one to three and conduct the attack on the same dataset. The results can be seen in

Table 5. The probability of being mistaken under target attack (3 pixel). AllConv: all convolution network. NiN: Network in Network. Normal: the unattacked state. LOI: LO intensity attacks. Calib: calibration attacks. Sat: saturation attacks. Hyb: the hybrids attacks.

	AllConv	NiN	DenseNet	ResNet	Average
Normal	21.588%	17.122%	7.229%	14.458%	15.099%
LOI	45.122%	24.878%	50.617%	48.148%	42.191%
Calib	22.333%	5.211%	22.368%	17.105%	16.754%
Sat	23.057%	30.052%	0%	2.632%	13.935%
Hyb	100%	100%	100%	100%	100%
Total	42.45%	35.30%	34.10%	36.20%	37.01%

and

Table 6. The probability of being attacked under non-target attack (3 pixel). AllConv: all convolution network. NiN: Network in Network. Normal: the unattacked state. LOI: LO intensity attacks. Calib: calibration attacks. Sat: saturation attacks. Hyb: the hybrids attacks.

	AllConv	NiN	DenseNet	ResNet	Average
Normal	100%	100%	100%	100%	100%
LOI	100%	100%	100%	100%	100%
Calib	100%	98.97%	100%	100%	99.74%
Sat	100%	99.12%	100%	100%	99.78%
Hyb	87.25%	0%	0%	12.50%	24.94%
Total	97.40%	79.20%	79.60%	84.60%	85.20%

and Figure 6b. This modification gains a remarkable improvement, which enables the success rate to achieve up to $80\%$ success at least. Nonetheless, there is still an unattackable class for some of the models. We can see that the difference in the two possibly indicates that between difference models are smaller when carrying out a three-pixel attack. In a one-pixel attack, the difference in the train parameters and structure of the network led to the sensitivity of the minimum perturbation to have some diversity. Although, when we enlarge the perturbation, the difference between the models significantly decreases. Apart from that, the probability of being attacked can reach $100\%$, which means that our adversarial attack is effective for the CV-QKD attack conditions, except for the hybrid strategy, in all of our experiments.

3.3. Discussion

Obviously, the three advantages of the original one-pixel attack, the minimal perturbed point, semi-black box attack, and universal for most of the DNNs, can also be seen to be advantages of our migrated attack approach. To launch our adversarial attack, we only need the probability labels of the target network but not the inner parameters of a CV-QKD attack detection model. On the one hand, since we take DE as our optimization method, the problem led by calculating its gradient can be avoided. On the other hand, this optimization method allows us to apply our attack strategy in more DNNs instead of only these four networks validated by our work. Moreover, on account of modifying just one feature of the input in the same range of non-perturbed data, our adversarial examples are hard to be recognized as poisoned outlier data.

Nevertheless, as a low-cost and easy-implemented $L_0$ attack, it has a possibility of being detected by some adversarial perturbation detecting method. Many recent research projects put forward some countermeasures to defend against adversarial attacks, for example, the binary classifiers for distinguishing legitimate input and adversarial examples [35,36]. However, such detection layers also introduce the time delay into the CV-QKD attack detection network, which impairs the practicality to some degree. On the other hand, it is hard to show enough consideration to the intensity of the disturbance when considering the number of perturbed unites. As a result, there are some defense methods which are directly against a one-pixel attack. A patch selection denoiser [37], for example, has been proved to be efficient for a one-pixel attack, which can achieve a success rate of 98%. However, practical DNN models should take most adversarial attacks into consideration instead of just being aimed at one special attack. Such a targeted defense is not very economic. As a novel attempt at migrating adversarial attacks into the CV-QKD field, the meaning of our work is more about proving the possibility of the adversarial, not to propose a perfect attacking method. To guarantee the security of networks is a topic for a further investigation.

4. Conclusions

In this paper, we present that the one-pixel attack for deceiving the image classification network can be utilized via deceiving the CV-QKD attack detection networks. By carrying out a corresponding experimental demonstration in a simulated GMCS CV-QKD system, our results show that in four representative DNN models for CV-QKD attack detection, one-pixel attacks reach the highest success rate of $52.8\%$, while the three others are $26.4\%$, $21.2\%$, and $23.8\%$. In addition, we find an interesting appearance that the success rate of our attack can be elevated sharply up to $79.2\%$, $79.6\%$, $84.6\%$, and $97.4\%$ by merely increasing the number of altered pixels to three. Furthermore, when launching a three-pixel attack, nearly $100\%$ of the test data from the normal state can be attacked into other attack strategies for each model, which provides the conditions for a denial of a service attack. All these consequences directly reveal the vulnerability of CV-QKD attack detection networks. Although the potential security threat brought about by using DNNs detecting CV-QKD attacks was solved, some security problems still remain.