Weak Randomness Analysis of Measurement-Device-Independent Quantum Key Distribution with Finite Resources
Abstract
:1. Introduction
2. Protocol Description
- Preparation: Alice and Bob randomly modulate the intensities and with probability of and , respectively. Where is the signal state intensity, is the decoy state intensity, 0 is the vacuum state. For signal states, Alice and Bob only choose the Z basis. For decoy states, Alice and Bob randomly choose a bit value from , and select Z basis and X basis in probability of and , respectively. Finally, they prepared a phase randomized, weak coherent pulse based on the selected value and send it to Charlie via a quantum channel.
- Measurement and alignment: Charlie performs Bell state measurements (BSM) of pulses from Alice and Bob, and then publishes the measurements to Alcie and Bob. Both parties conduct basis alignment in open channel and compare their intensity: . They retain correct measurement results and discard mismatched measurement results. At this time, the number of pulses successfully detected in the Z basis and X basis are and , and the subscript indicates the intensity combinations chosen by Alice and Bob: .
- Parameter estimation: Firstly, Alice and Bob calculate the number of bit error in X basis . Second, they calculate the number of successful measurement results corresponding to the single photon pulse in Z basis and the number of phase error . Finally, they calculate the phase error rate in Z basis , where refers to the phase bit error rate which needs to be met. Execution continues if complied, otherwise the agreement will be terminated.
- Post-processing: Alice and Bob perform error correction, and the process consumes information at most as bits. They also use hash functions to perform error verification to ensure that both parties get the same key, and it requires consumption information of bits, where is the probability of passing the error verification process for the key pairs . In the end, after the two parties perform the secret amplification operation, the key pairs are obtained by Alice is , and the key pairs obtained by Bob is .
3. Security Analysis
3.1. Security Bound
- . If the probability of keys , being not identical is maximal , the keys are said to be -correct:
- . The keys , are said to be -secure with respect to the Eve holding a quantum system E if:where denotes the probability of protocol failure aborted, denotes the classical-quantum states of the system for Alice (Bob) and system E, and denotes the fully mixed state on or .
3.2. Parameter Estimation
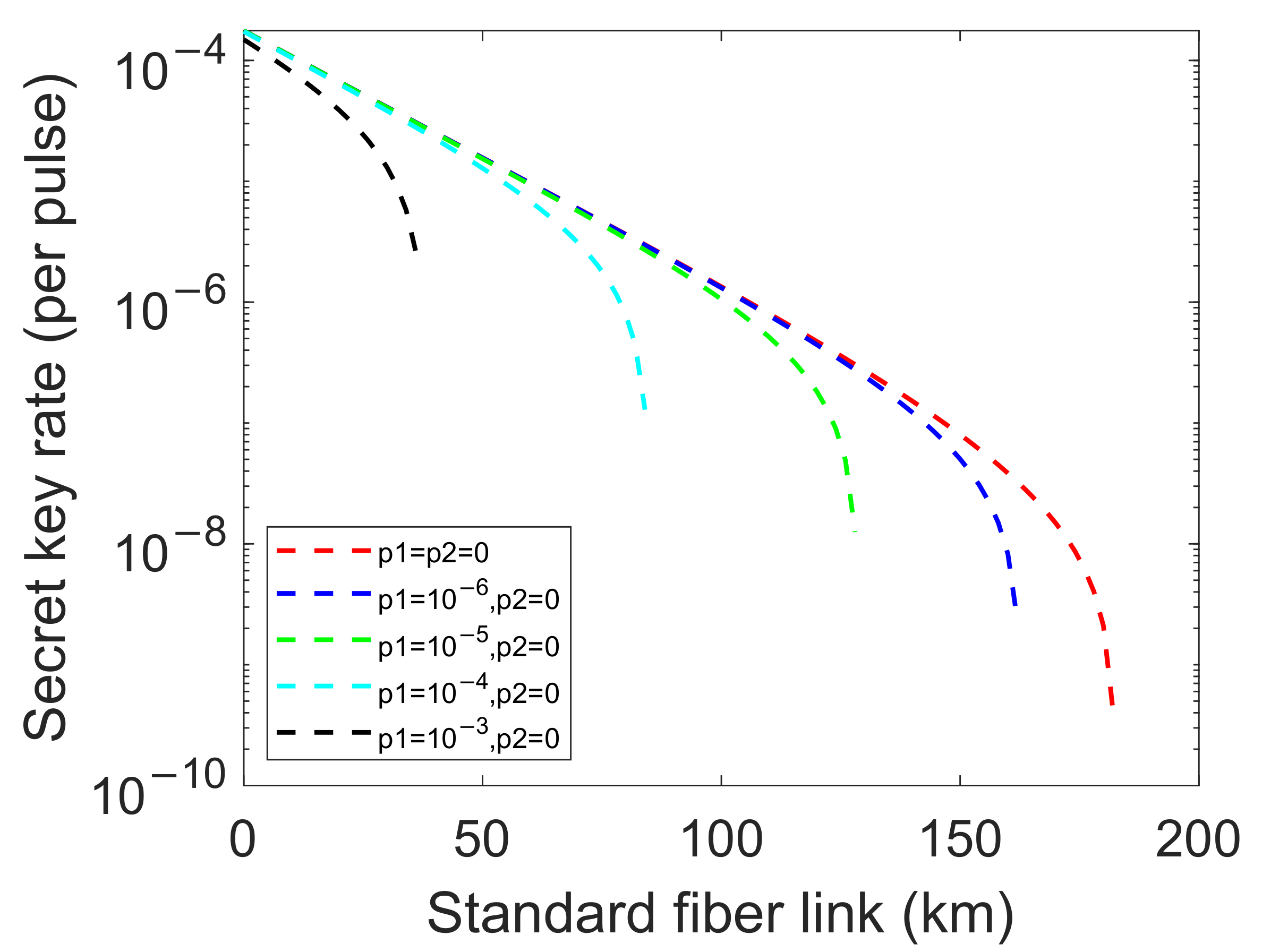
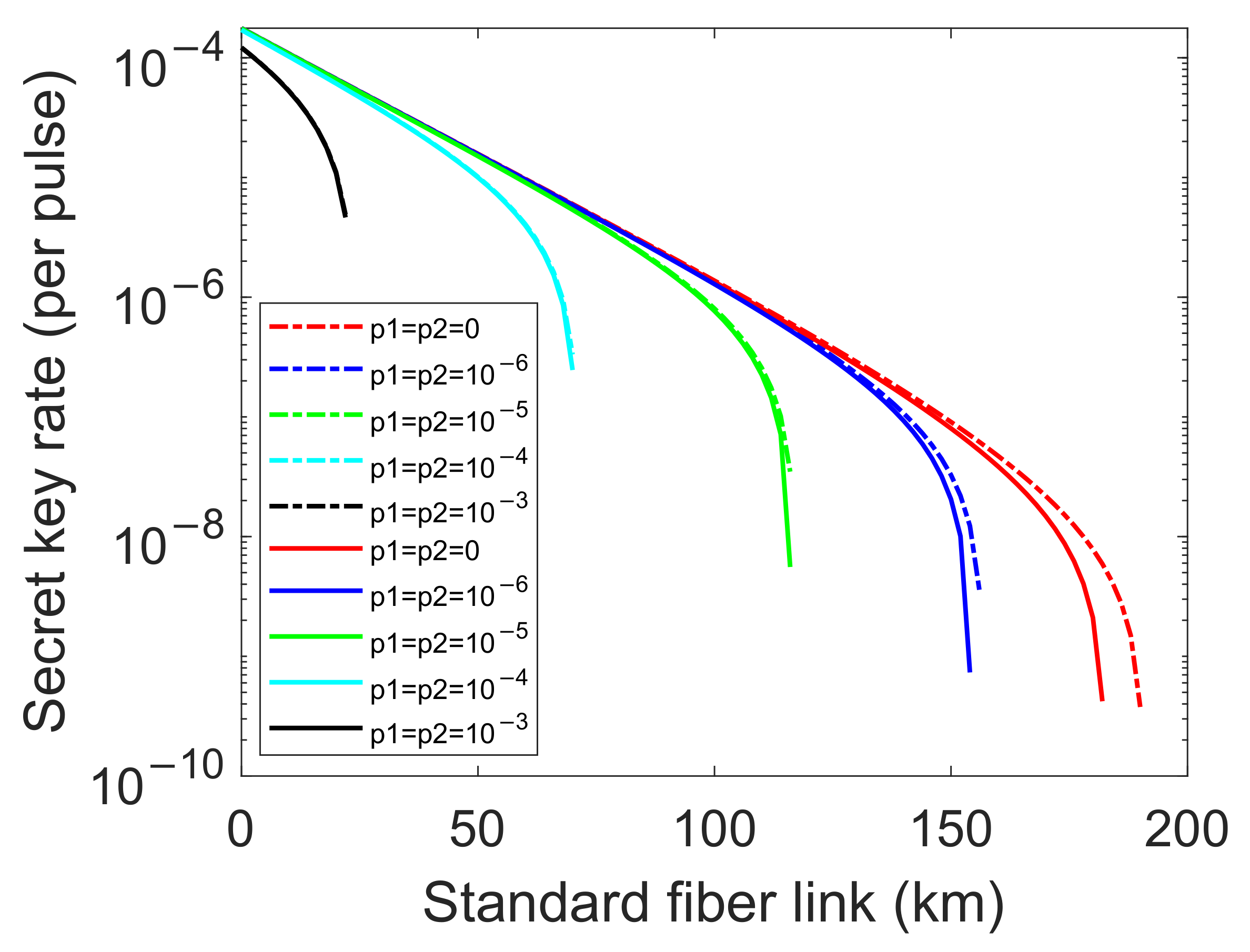
4. Numerical Simulations and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photonics 2020, 12, 1012–1236. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Huang, A. A Review of Security Evaluation of Practical Quantum Key Distribution System. Entropy 2022, 24, 260. [Google Scholar] [CrossRef] [PubMed]
- Li, H.W.; Wang, S.; Huang, J.Z.; Chen, W.; Yin, Z.Q.; Li, F.Y.; Zhou, Z.; Liu, D.; Zhang, Y.; Guo, G.C.; et al. Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources. Phys. Rev. A 2011, 84, 062308. [Google Scholar] [CrossRef] [Green Version]
- Lydersen, L.; Wiechers, C.; Wittmann, C.; Elser, D.; Skaar, J.; Makarov, V. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photonics 2010, 4, 686–689. [Google Scholar] [CrossRef] [Green Version]
- Qian, Y.J.; He, D.Y.; Wang, S.; Chen, W.; Yin, Z.Q.; Guo, G.C.; Han, Z.F. Robust countermeasure against detector control attack in a practical quantum key distribution system. Optica 2019, 6, 1178–1184. [Google Scholar] [CrossRef] [Green Version]
- Jain, N.; Anisimova, E.; Khan, I.; Makarov, V.; Marquardt, C.; Leuchs, G. Trojan-horse attacks threaten the security of practical quantum cryptography. New J. Phys. 2014, 16, 123030. [Google Scholar] [CrossRef] [Green Version]
- Lucamarini, M.; Choi, I.; Ward, M.B.; Dynes, J.F.; Yuan, Z.; Shields, A.J. Practical security bounds against the trojan-horse attack in quantum key distribution. Phys. Rev. X 2015, 5, 031030. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [Green Version]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Pirandola, S.; Laurenza, R.; Ottaviani, C. Fundamental limits of repeaterless quantum communications. Nat. Commun. 2017, 8, 15043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, H.L.; Chen, T.Y.; Yu, Z.W.; Liu, H.; You, L.X.; Zhou, Y.H.; Chen, S.J.; Mao, Y.; Huang, M.Q.; Zhang, W.J.; et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 2016, 117, 190501. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yin, Z.Q.; Wang, S.; Chen, W.; Guo, G.C.; Han, Z.F. Measurement-device-independent quantum key distribution robust against environmental disturbances. Optica 2017, 4, 1016–1023. [Google Scholar] [CrossRef]
- Ma, X.; Zeng, P.; Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 2018, 8, 031043. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, J.; Ma, H.; Sun, S. Polarization-multiplexing-based measurement-device-independent quantum key distribution without phase reference calibration. Optica 2018, 5, 902–909. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, W.; Wei, K.; Fang, X.T.; Li, L.; Liu, N.L.; Liang, H.; Zhang, S.J.; Zhang, W.; Li, H.; et al. Experimental demonstration of high-rate measurement-device-independent quantum key distribution over asymmetric channels. Phys. Rev. Lett. 2019, 122, 160501. [Google Scholar] [CrossRef] [Green Version]
- Wei, K.; Li, W.; Tan, H.; Li, Y.; Min, H.; Zhang, W.J.; Li, H.; You, L.; Wang, Z.; Jiang, X.; et al. High-speed measurement-device-independent quantum key distribution with integrated silicon photonics. Phys. Rev. X 2020, 10, 031030. [Google Scholar] [CrossRef]
- Woodward, R.I.; Lo, Y.; Pittaluga, M.; Minder, M.; Paraïso, T.; Lucamarini, M.; Yuan, Z.; Shields, A. Gigahertz measurement-device-independent quantum key distribution using directly modulated lasers. Npj Quantum Inf. 2021, 7, 58. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Jiang, M.; Lu, Y.; Li, H.; Zhou, C.; Bao, W. Phase-Matching Quantum Key Distribution with Discrete Phase Randomization. Entropy 2021, 23, 508. [Google Scholar] [CrossRef]
- Hu, X.L.; Jiang, C.; Yu, Z.W.; Wang, X.B. Practical Long-Distance Measurement-Device-Independent Quantum Key Distribution By Four-Intensity Protocol. Adv. Quantum Technol. 2021, 4, 2100069. [Google Scholar] [CrossRef]
- Wang, X.B.; Yu, Z.W.; Hu, X.L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 2018, 98, 062323. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Yin, Z.Q.; Wang, R.; Chen, W.; Wang, S.; Guo, G.C.; Han, Z.F. Twin-field quantum key distribution without phase postselection. Phys. Rev. Appl. 2019, 11, 034053. [Google Scholar] [CrossRef] [Green Version]
- Zhong, X.; Wang, W.; Qian, L.; Lo, H.K. Proof-of-principle experimental demonstration of twin-field quantum key distribution over optical channels with asymmetric losses. Npj Quantum Inf. 2021, 7, 8. [Google Scholar] [CrossRef]
- Fang, X.T.; Zeng, P.; Liu, H. Implementation of quantum key distribution surpassing the linear rate-transmittance bound. Nat. Photonics 2020, 14, 422–425. [Google Scholar] [CrossRef]
- Curty, M.; Azuma, K.; Lo, H.K. Simple security proof of twin-field type quantum key distribution protocol. Npj Quantum Inf. 2019, 5, 64. [Google Scholar] [CrossRef]
- Lu, Y.F.; Wang, Y.; Jiang, M.S.; Zhang, X.X.; Liu, F.; Li, H.W.; Zhou, C.; Tang, S.B.; Wang, J.Y.; Bao, W.S. Sending or Not-Sending Twin-Field Quantum Key Distribution with Flawed and Leaky Sources. Entropy 2021, 23, 1103. [Google Scholar] [CrossRef]
- Pittaluga, M.; Minder, M.; Lucamarini, M.; Sanzaro, M.; Woodward, R.I.; Li, M.J.; Yuan, Z.; Shields, A.J. 600-km repeater-like quantum communications with dual-band stabilization. Nat. Photonics 2021, 15, 530–535. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, C.; Zhu, H.T.; Zou, M.; Yu, Z.W.; Hu, X.L.; Xu, H.; Ma, S.; Han, Z.; Chen, J.P.; et al. Field test of twin-field quantum key distribution through sending-or-not-sending over 428 km. Phys. Rev. Lett. 2021, 126, 250502. [Google Scholar] [CrossRef]
- Chen, J.P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.J.; Han, Z.Y.; Ma, S.Z.; Hu, X.L.; Li, Y.H.; Liu, H.; et al. Twin-field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas. Nat. Photonics 2021, 15, 570–575. [Google Scholar] [CrossRef]
- Wang, S.; Yin, Z.Q.; He, D.Y.; Chen, W.; Wang, R.Q.; Ye, P.; Zhou, Y.; Fan-Yuan, G.J.; Wang, F.X.; Zhu, Y.G.; et al. Twin-field quantum key distribution over 830-km fibre. Nat. Photonics 2022, 16, 154–161. [Google Scholar] [CrossRef]
- Lu, F.Y.; Yin, Z.Q.; Wang, R.; Fan-Yuan, G.J.; Wang, S.; He, D.Y.; Chen, W.; Huang, W.; Xu, B.J.; Guo, G.C.; et al. Practical issues of twin-field quantum key distribution. New J. Phys. 2019, 21, 123030. [Google Scholar] [CrossRef] [Green Version]
- Yin, Z.Q.; Fung, C.H.F.; Ma, X.; Zhang, C.M.; Li, H.W.; Chen, W.; Wang, S.; Guo, G.C.; Han, Z.F. Measurement-device-independent quantum key distribution with uncharacterized qubit sources. Phys. Rev. A 2013, 88, 062322. [Google Scholar] [CrossRef] [Green Version]
- Pereira, M.; Kato, G.; Mizutani, A.; Curty, M.; Tamaki, K. Quantum key distribution with correlated sources. Sci. Adv. 2020, 6, eaaz4487. [Google Scholar] [CrossRef]
- Lu, Y.F.; Wang, Y.; Jiang, M.S.; Liu, F.; Zhang, X.X.; Bao, W.S. Finite-key analysis of sending-or-not-sending twin-field quantum key distribution with intensity fluctuations. Quantum Inf. Process. 2021, 20, 135. [Google Scholar] [CrossRef]
- Mizutani, A.; Kato, G.; Azuma, K.; Curty, M.; Ikuta, R.; Yamamoto, T.; Imoto, N.; Lo, H.K.; Tamaki, K. Quantum key distribution with setting-choice-independently correlated light sources. Npj Quantum Inf. 2019, 5, 8. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.X.; Wang, Y.; Jiang, M.S.; Zhou, C.; Lu, Y.F.; Bao, W.S. Finite-key analysis of asymmetric phase-matching quantum key distribution with unstable sources. J. Opt. Soc. Am. B 2021, 38, 724–731. [Google Scholar] [CrossRef]
- Li, H.W.; Yin, Z.Q.; Wang, S.; Qian, Y.J.; Chen, W.; Guo, G.C.; Han, Z.F. Randomness determines practical security of BB84 quantum key distribution. Sci. Rep. 2015, 5, 16200. [Google Scholar] [CrossRef]
- Li, H.W.; Xu, Z.M.; Cai, Q.Y. Small imperfect randomness restricts security of quantum key distribution. Phys. Rev. A 2018, 98, 062325. [Google Scholar] [CrossRef]
- Zhang, C.M.; Wang, W.B.; Li, H.W.; Wang, Q. Weak randomness impacts the security of reference-frame-independent quantum key distribution. Opt. Lett. 2019, 44, 1226–1229. [Google Scholar] [CrossRef]
- Müller-Quade, J.; Renner, R. Composability in quantum cryptography. New J. Phys. 2009, 11, 085006. [Google Scholar] [CrossRef] [Green Version]
- Tomamichel, M.; Lim, C.C.W.; Gisin, N.; Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 2012, 3, 634. [Google Scholar] [CrossRef] [PubMed]
- Curty, M.; Xu, F.; Cui, W.; Lim, C.C.W.; Tamaki, K.; Lo, H.K. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 2014, 5, 3732. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lim, C.C.W.; Curty, M.; Walenta, N.; Xu, F.; Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 2014, 89, 022307. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Bao, W.S.; Zhou, C.; Jiang, M.S.; Li, H.W. Tight finite-key analysis of a practical decoy-state quantum key distribution with unstable sources. Phys. Rev. A 2016, 94, 032335. [Google Scholar] [CrossRef]
- Li, H.W.; Xu, Z.M.; Yin, Z.Q.; Cai, Q.Y. Security of practical quantum key distribution with weak-randomness basis selection. Phys. Rev. A 2020, 102, 022605. [Google Scholar] [CrossRef]
- Zhou, C.; Bao, W.S.; Zhang, H.L.; Li, H.W.; Wang, Y.; Li, Y.; Wang, X. Biased decoy-state measurement-device-independent quantum key distribution with finite resources. Phys. Rev. A 2015, 91, 022313. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.L.; Yin, H.L.; Chen, S.J.; Liu, Y.; Zhang, W.J.; Jiang, X.; Zhang, L.; Wang, J.; You, L.X.; Guan, J.Y.; et al. Measurement-device-independent quantum key distribution over 200 km. Phys. Rev. Lett. 2014, 113, 190501. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Bao, W.S.; Zhou, C.; Jiang, M.S.; Li, H.W. Finite-key analysis of practical decoy-state measurement-device-independent quantum key distribution with unstable sources. J. Opt. Soc. Am. B 2019, 36, B83–B91. [Google Scholar] [CrossRef]
- Fung, C.H.F.; Ma, X.; Chau, H. Practical issues in quantum-key-distribution postprocessing. Phys. Rev. A 2010, 81, 012318. [Google Scholar] [CrossRef] [Green Version]

| f | |||||
|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.-L.; Deng, X.-Q.; Wang, Y.; Lu, Y.-F.; Li, J.-J.; Zhou, C.; Bao, W.-S. Weak Randomness Analysis of Measurement-Device-Independent Quantum Key Distribution with Finite Resources. Photonics 2022, 9, 356. https://doi.org/10.3390/photonics9050356
Jiang X-L, Deng X-Q, Wang Y, Lu Y-F, Li J-J, Zhou C, Bao W-S. Weak Randomness Analysis of Measurement-Device-Independent Quantum Key Distribution with Finite Resources. Photonics. 2022; 9(5):356. https://doi.org/10.3390/photonics9050356
Chicago/Turabian StyleJiang, Xiao-Lei, Xiao-Qin Deng, Yang Wang, Yi-Fei Lu, Jia-Ji Li, Chun Zhou, and Wan-Su Bao. 2022. "Weak Randomness Analysis of Measurement-Device-Independent Quantum Key Distribution with Finite Resources" Photonics 9, no. 5: 356. https://doi.org/10.3390/photonics9050356
APA StyleJiang, X.-L., Deng, X.-Q., Wang, Y., Lu, Y.-F., Li, J.-J., Zhou, C., & Bao, W.-S. (2022). Weak Randomness Analysis of Measurement-Device-Independent Quantum Key Distribution with Finite Resources. Photonics, 9(5), 356. https://doi.org/10.3390/photonics9050356





