Silicon-on-Insulator Optical Buffer Based on Magneto-Optical 1 × 3 Micro-Rings Array Coupled Sagnac Ring
Abstract
1. Introduction
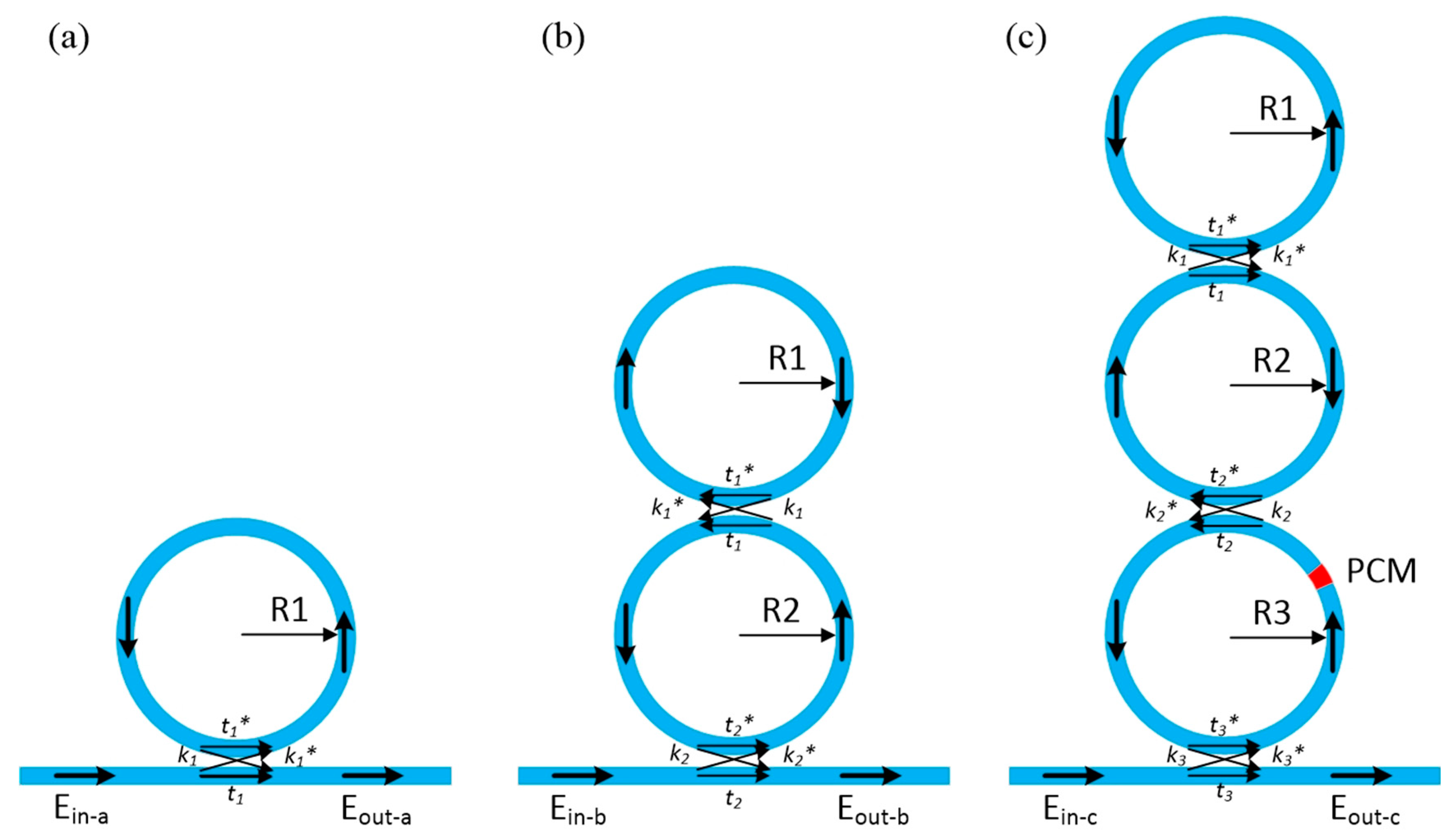
2. SOI Optical Buffer Based on Sagnac Ring Coupled with MOMR Array
2.1. Sagnac Ring with 1 × 3 MOMRs
2.2. Nonreciprocal Phase Shift (NRPS) of the SOI Nonreciprocal MO Waveguide
2.3. Mathematical Model
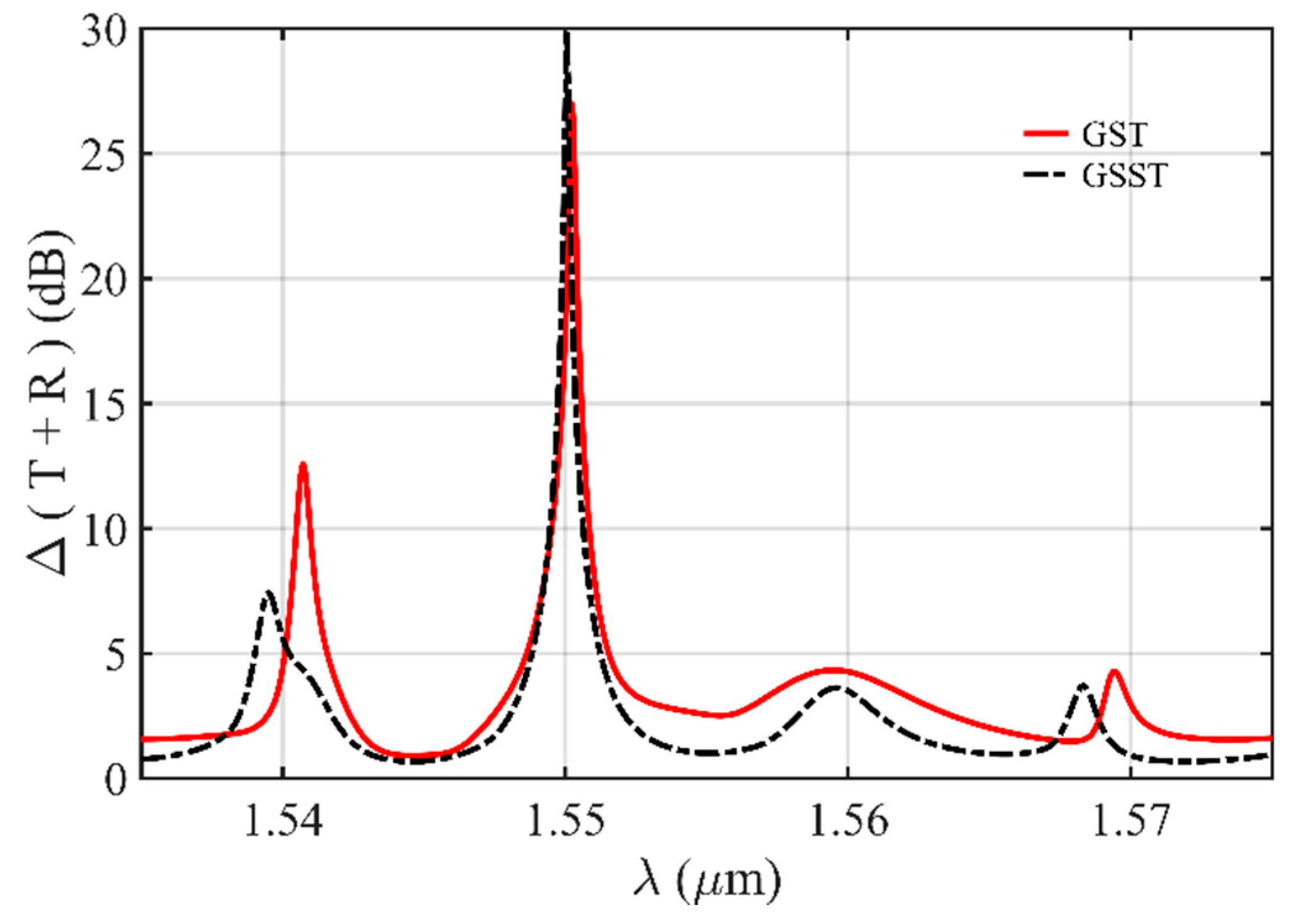
3. Results and Discussion
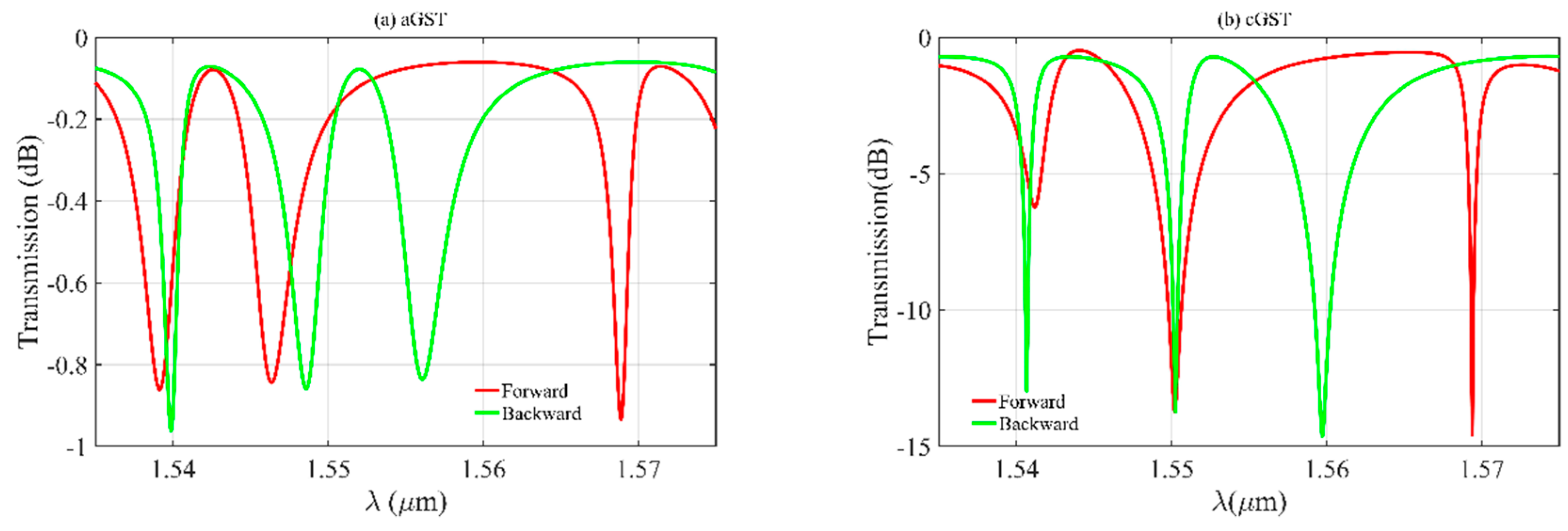
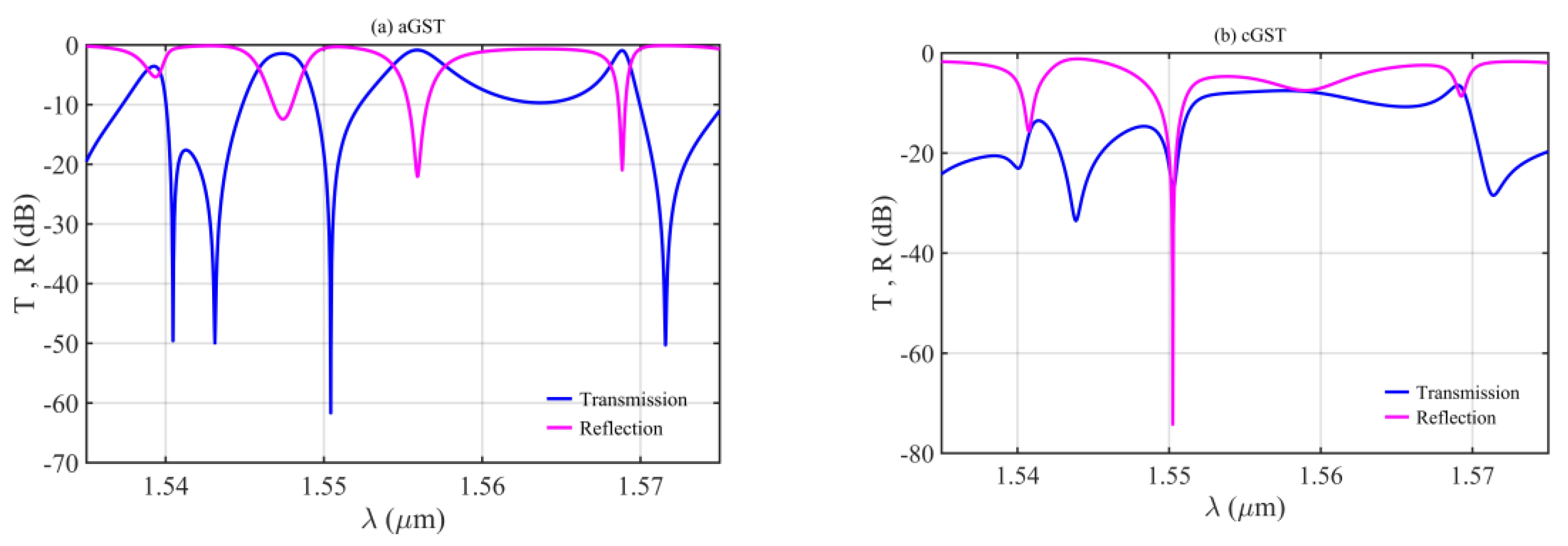
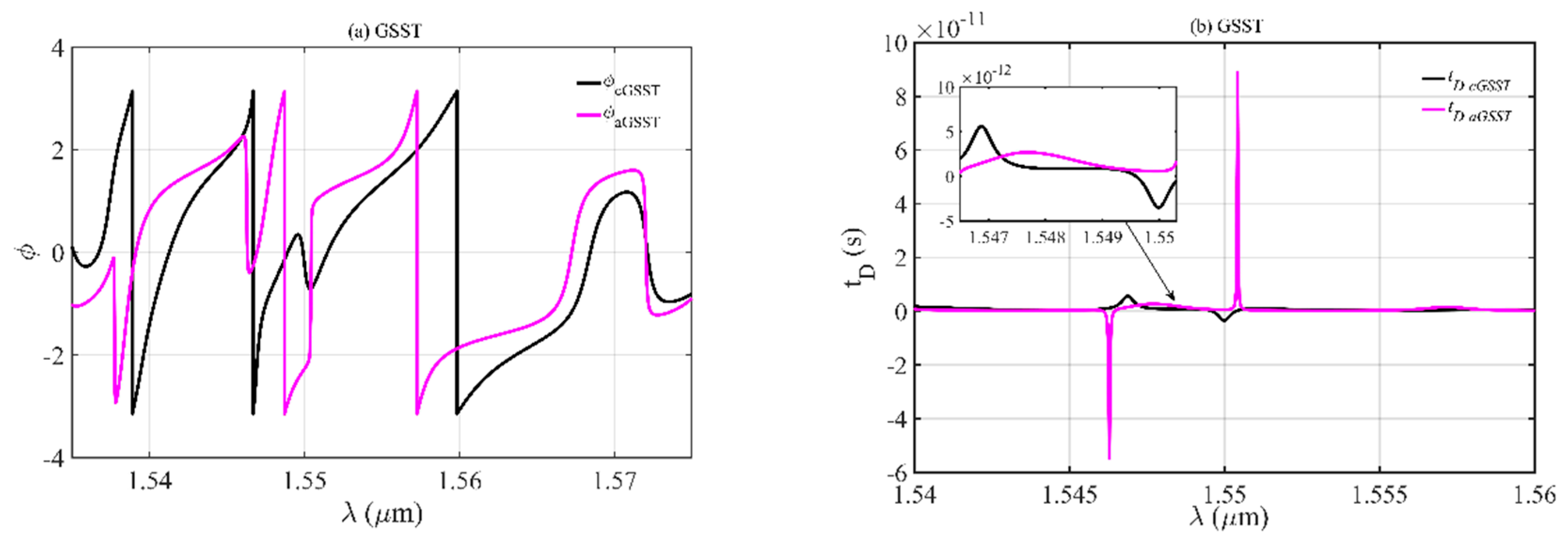
3.1. Transmission Characteristic Analysis
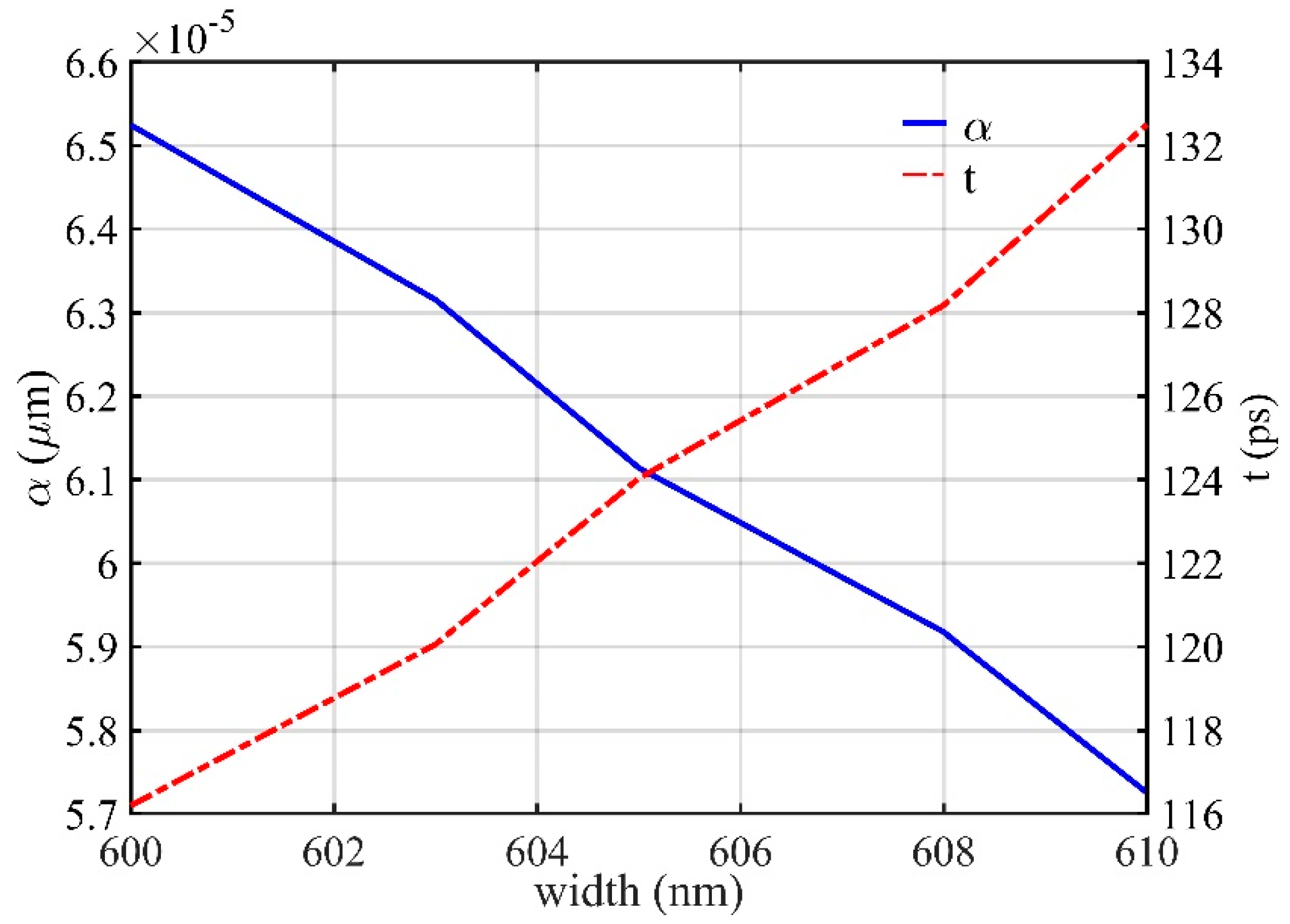
3.2. Write-in Operation and Effective Buffering Time
3.3. Read-Out Operation and Performance Comparison
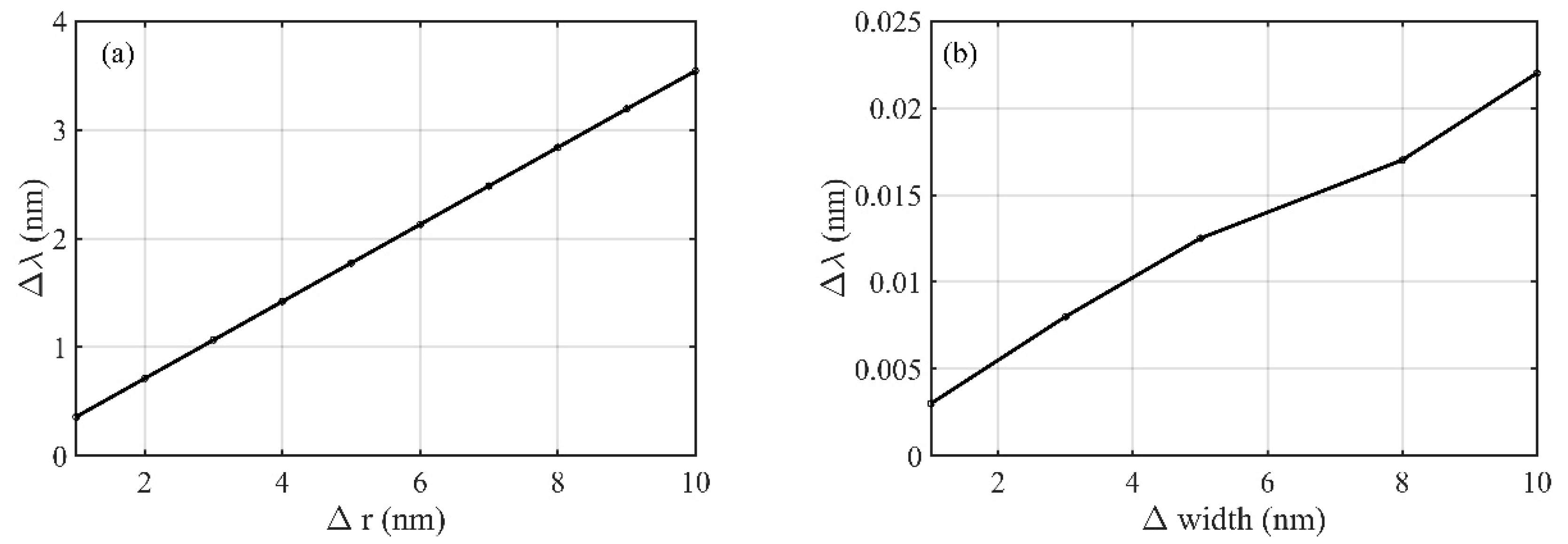
3.4. Tolerance Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Q.; Yu, L.; Gao, H.; Chu, S.; Peng, W. Electromagnetically induced transparency in an all-dielectric nano-metamaterial for slow light application. Opt. Express 2019, 27, 35012–35026. [Google Scholar] [CrossRef] [PubMed]
- Keleshtery, M.H. Analysis and investigation of slow light based on plasmonic induced transparency in metal-dielectric-metal ring resonator in a waveguide system with different geometrical designs. Opt. Photonics J. 2016, 6, 177. [Google Scholar] [CrossRef][Green Version]
- Zadok, A.; Eyal, A.; Tur, M. Stimulated Brillouin scattering slow light in optical fibers. Appl. Opt. 2011, 50, E38–E49. [Google Scholar] [CrossRef]
- McMillan, J.F.; Yang, X.; Panoiu, N.-C.; Osgood, R.M.; Wong, C.W. Enhanced stimulated Raman scattering in slow-light photonic crystal waveguides. Opt. Lett. 2006, 31, 1235–1237. [Google Scholar] [CrossRef] [PubMed]
- Baba, T. Slow light in photonic crystals. Nat. Photonics 2008, 2, 465. [Google Scholar] [CrossRef]
- Kassa-Baghdouche, L.; Boumaza, T.; Bouchemat, M. Optimization of Q-factor in nonlinear planar photonic crystal nanocavity incorporating hybrid silicon/polymer material. Phys. Scr. 2015, 90, 065504. [Google Scholar] [CrossRef]
- Kassa-Baghdouche, L.; Cassan, E. Mid-infrared refractive index sensing using optimized slotted photonic crystal waveguides. Photonics Nanostruct.-Fundam. Appl. 2018, 28, 32–36. [Google Scholar] [CrossRef]
- Elshahat, S.; Abood, I.; Liang, Z.; Pei, J.; Ouyang, Z. Sporadic-Slot Photonic-Crystal Waveguide for All-Optical Buffers with Low-Dispersion, Distortion, and Insertion Loss. IEEE Access 2020, 8, 77689–77700. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.; Li, R.; Xie, J.; Lu, L.; Wu, K.; Chen, J. Continuously tunable ultra-thin silicon waveguide optical delay line. Optica 2017, 4, 507–515. [Google Scholar] [CrossRef]
- Moralis-Pegios, M.; Mourgias-Alexandris, G.; Terzenidis, N.; Cherchi, M.; Harjanne, M.; Aalto, T.; Miliou, A.; Pleros, N.; Vyrsokinos, K. On-chip SOI delay line bank for optical buffers and time slot interchangers. IEEE Photonics Technol. Lett. 2017, 30, 31–34. [Google Scholar] [CrossRef]
- Liu, D.; Sun, S.; Yin, X.; Sun, B.; Sun, J.; Liu, Y.; Li, W.; Zhu, N.; Li, M. Large-capacity and low-loss integrated optical buffer. Opt. Express 2019, 27, 11585–11593. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Liu, X.; Zhang, M.; Zhou, P. Low dispersion broadband integrated double-slot microring resonators optical buffer. Front. Optoelectron. 2016, 9, 571–577. [Google Scholar] [CrossRef]
- Liu, W.; Romeira, B.; Li, M.; Guzzon, R.S.; Norberg, E.J.; Parker, J.S.; Coldren, L.A.; Yao, J. A wavelength tunable optical buffer based on self-pulsation in an active microring resonator. J. Lightwave Technol. 2016, 34, 3466–3472. [Google Scholar] [CrossRef]
- Kalantarov, D. Tunable low dispersion optical delay line using three coupled micro-resonators. J. Opt. 2017, 19, 115802. [Google Scholar] [CrossRef]
- Guo, Z. Photon Storage in a Dynamic Two-Ring-Two-Bus System. Opt. Photonics J. 2019, 9, 20. [Google Scholar] [CrossRef]
- Ni, S.; Wu, B.; Liu, Y. Characteristics of silicon-based Sagnac optical switches using magneto-optical micro-ring array. Fiber Integr. Opt. 2018, 37, 12–20. [Google Scholar] [CrossRef]
- Fan, L.; Li, Y.; Zhao, W.; Li, J.; Zhang, X.; Peng, C.; Wu, Y.; Zou, M.; Fang, B.; Wang, X. Optical Buffer Device Employing VO2 Embedded on SOI Waveguides With Microring Resonator. IEEE Photonics J. 2021, 13, 1–11. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, M.; Jindal, S.K.; Raghuwanshi, S.K.; Choudhary, R. Implementation of all-optical 1 × 4 memory register unit using the micro-ring resonator structures. Opt. Quantum Electron. 2021, 53, 492. [Google Scholar] [CrossRef]
- Tsakmakidis, K.L.; Shen, L.; Schulz, S.A.; Zheng, X.; Upham, J.; Deng, X.; Altug, H.; Vakakis, A.F.; Boyd, R.W. Breaking Lorentz reciprocity to overcome the time-bandwidth limit in physics and engineering. Science 2017, 356, 1260–1264. [Google Scholar] [CrossRef]
- Hui-Ying, W.; Zhi, W.; Can, C.; Hang-Tian, L.; Qiang, L.; Xiang-Kong, Z.; Jian, W.; Chong-Qing, W. Dispersion characteristics of nonreciprocal gyroelectric silicon-on-insulator rectangular waveguide. Acta Phys. Sin. 2019, 68. [Google Scholar]
- Wang, H.; Wang, Z.; Li, H.; Zhan, X.; Cui, C.; Fu, Z.; Li, Z.; Liu, L.; Wu, C. Signal evolution of an optical buffer based on the nonreciprocal silicon-on-insulator waveguide. Opt. Commun. 2020, 474, 126158. [Google Scholar] [CrossRef]
- Cheng, Z.; Ríos, C.; Youngblood, N.; Wright, C.D.; Pernice, W.H.P.; Bhaskaran, H. Device-level photonic memories and logic applications using phase-change materials. Adv. Mater. 2018, 30, 1802435. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Ghosh, S.; Dhingra, N.; Zhang, H.; Zhou, L.; Rahman, B.M.A. Feasibility study of a Ge2Sb2Te5-clad silicon waveguide as a non-volatile optical on-off switch. OSA Contin. 2019, 2, 49–63. [Google Scholar] [CrossRef]
- Xu, P.; Zheng, J.; Doylend, J.K.; Majumdar, A. Low-loss and broadband nonvolatile phase-change directional coupler switches. ACS Photonics 2019, 6, 553–557. [Google Scholar] [CrossRef]
- Bahlmann, N.; Chandrasekhara, V.; Erdmann, A.; Gerhardt, R.; Hertel, P.; Lehmann, R.; Salz, D.; Schroteler, F.-J.; Wallenhorst, M.; Dotsch, H. Improved design of magnetooptic rib waveguides for optical isolators. J. Lightwave Technol. 1998, 16, 818–823. [Google Scholar] [CrossRef]
- Zhou, H.; Chee, J.; Song, J.; Lo, G. Analytical calculation of nonreciprocal phase shifts and comparison analysis of enhanced magneto-optical waveguides on SOI platform. Opt. Express 2012, 20, 8256–8269. [Google Scholar] [CrossRef] [PubMed]
- Dötsch, H.; Bahlmann, N.; Zhuromskyy, O.; Hammer, M.; Wilkens, L.; Gerhardt, R.; Hertel, P.; Popkov, A.F. Applications of magneto-optical waveguides in integrated optics: Review. JOSA B 2005, 22, 240–253. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, L.; Xu, J.; Lu, L.; Chen, J.; Rahman, B.M.A. All-optical non-volatile tuning of an AMZI-coupled ring resonator with GST phase-change material. Opt. Lett. 2018, 43, 5539–5542. [Google Scholar] [CrossRef]
- Zhang, Y.; Fowler, C.; Liang, J.; Azhar, B.; Shalaginov, M.Y.; Deckoff-Jones, S.; An, S.; Chou, J.B.; Roberts, C.M.; Liberman, V.; et al. Electrically reconfigurable non-volatile metasurface using low-loss optical phase-change material. Nat. Nanotechnol. 2021, 16, 661–666. [Google Scholar] [CrossRef]
- Heebner, J.; Grover, R.; Ibrahim, T. Optical Microresonator Theory; Springer: New York, NY, USA, 2008. [Google Scholar]
- Kato, K.; Kuwahara, M.; Kawashima, H.; Tsuruoka, T.; Tsuda, H. Current-driven phase-change optical gate switch using indium–tin-oxide heater. Appl. Phys. Express 2017, 10, 072201. [Google Scholar] [CrossRef]
- Ríos, C.; Stegmaier, M.; Hosseini, P.; Wang, D.; Scherer, T.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. Integrated all-photonic non-volatile multi-level memory. Nat. Photonics 2015, 9, 725–732. [Google Scholar] [CrossRef]
- Ríos, C.; Youngblood, N.; Cheng, Z.; Le Gallo, M.; Pernice, W.H.P.; Wright, C.D.; Sebastian, A.; Bhaskaran, H. In-memory computing on a photonic platform. Sci. Adv. 2019, 5, eaau5759. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Ríos, C.; Pernice, W.H.P.; Wright, C.D.; Bhaskaran, H. On-chip photonic synapse. Sci. Adv. 2017, 3, e1700160. [Google Scholar] [CrossRef]
- Li, X.; Youngblood, N.; Ríos, C.; Cheng, Z.; Wright, C.D.; Pernice, W.H.; Bhaskaran, H. Fast and reliable storage using a 5 bit, nonvolatile photonic memory cell. Optica 2019, 6, 1–6. [Google Scholar] [CrossRef]
- Stegmaier, M.; Ríos, C.; Bhaskaran, H.; Pernice, W.H.P. Thermo-optical effect in phase-change nanophotonics. Acs Photonics 2016, 3, 828–835. [Google Scholar] [CrossRef]
- Fu, Z.; Wang, Z.; Wang, H.; Jiang, R.; Liu, L.; Wu, C.; Wang, J. Thermal dynamics of phase switching process of an SOI rib waveguide covered with a Ge2Sb2Te5 phase change material film. Opt. Mater. 2022, 124, 112046. [Google Scholar] [CrossRef]






| Ref. | Year | Device Type | Wavelength (nm) | Buffer Time (ps) | Size | Experiment/Simulation |
|---|---|---|---|---|---|---|
| [12] | 2016 | SOI | 1550 | 150 | 5.1 × 10−5 mm | Simulation |
| [13] | 2016 | InP MZI | 1558.825 | 1.72 × 105 | mm dimension | Experiment |
| [15] | 2019 | SOI | 1532.56 | 20 | μm dimension | Simulation |
| [17] | 2021 | SOI | 1553.7 | 78.28 | μm dimension | Simulation |
| this work | 2022 | Si + MO | 1550 | 116.19 | μm dimension | Simulation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, Z.; Fu, Z.; Jiang, R.; Liu, L.; Wang, J.; Wu, C. Silicon-on-Insulator Optical Buffer Based on Magneto-Optical 1 × 3 Micro-Rings Array Coupled Sagnac Ring. Photonics 2022, 9, 366. https://doi.org/10.3390/photonics9060366
Wang H, Wang Z, Fu Z, Jiang R, Liu L, Wang J, Wu C. Silicon-on-Insulator Optical Buffer Based on Magneto-Optical 1 × 3 Micro-Rings Array Coupled Sagnac Ring. Photonics. 2022; 9(6):366. https://doi.org/10.3390/photonics9060366
Chicago/Turabian StyleWang, Huiying, Zhi Wang, Ziling Fu, Rui Jiang, Lanlan Liu, Jian Wang, and Chongqing Wu. 2022. "Silicon-on-Insulator Optical Buffer Based on Magneto-Optical 1 × 3 Micro-Rings Array Coupled Sagnac Ring" Photonics 9, no. 6: 366. https://doi.org/10.3390/photonics9060366
APA StyleWang, H., Wang, Z., Fu, Z., Jiang, R., Liu, L., Wang, J., & Wu, C. (2022). Silicon-on-Insulator Optical Buffer Based on Magneto-Optical 1 × 3 Micro-Rings Array Coupled Sagnac Ring. Photonics, 9(6), 366. https://doi.org/10.3390/photonics9060366





