Review of a Specialty Fiber for Distributed Acoustic Sensing Technology
Abstract
:1. Introduction
2. Fundamental Principle
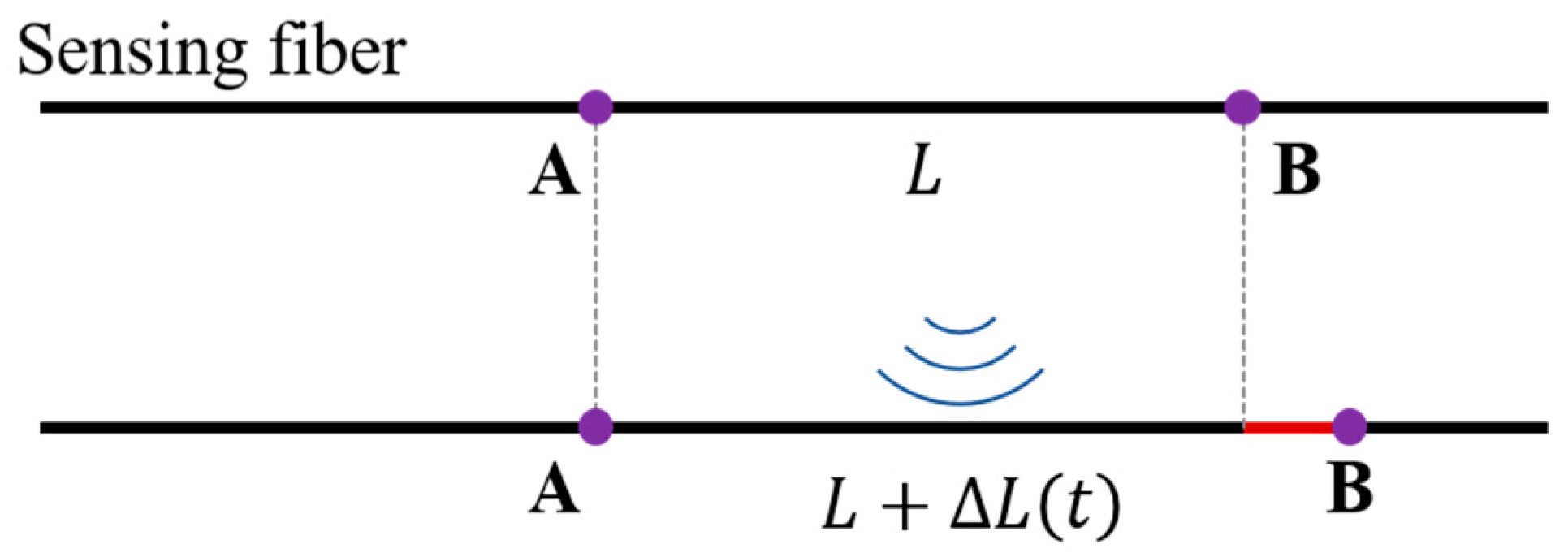
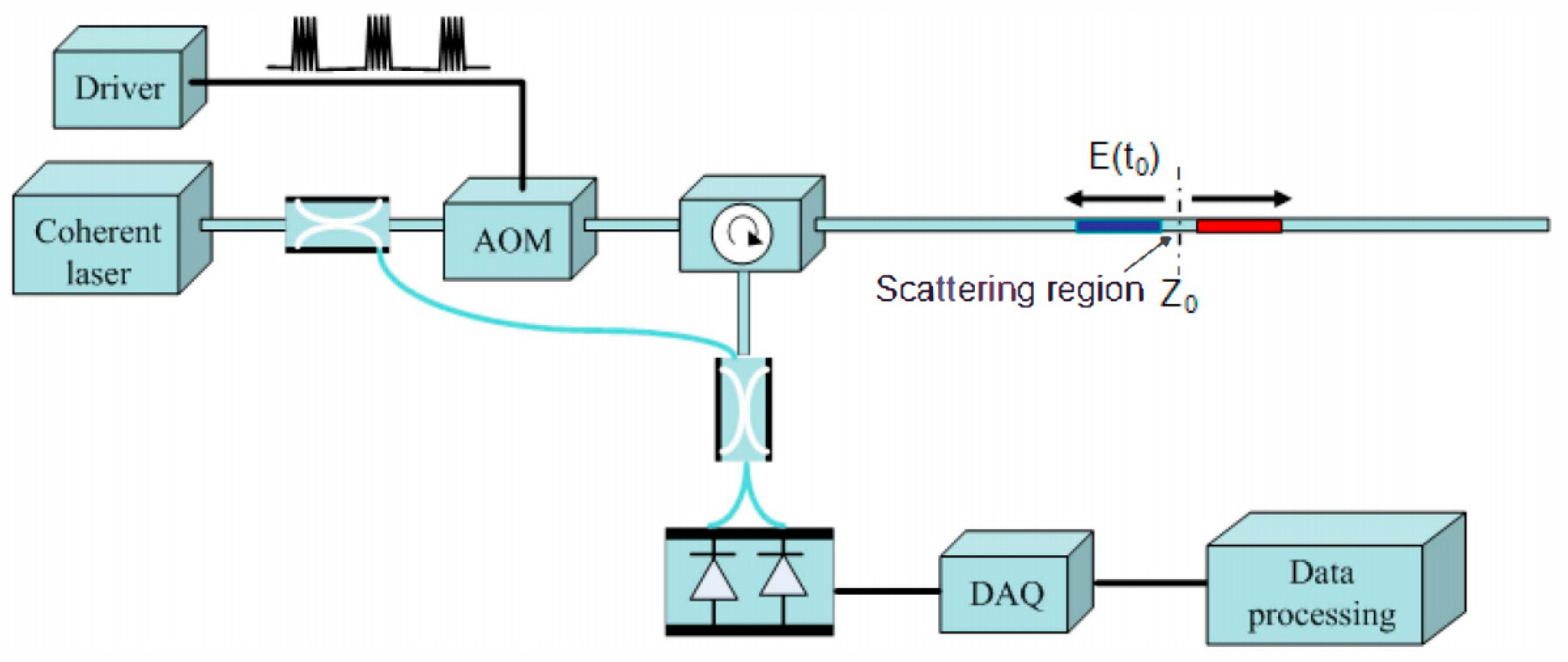
2.1. Principle of DAS Technology
2.2. Limitations of Single-Mode Fiber (SMF) DAS
3. Reviews of Specialty-Fiber-Based DAS Technology
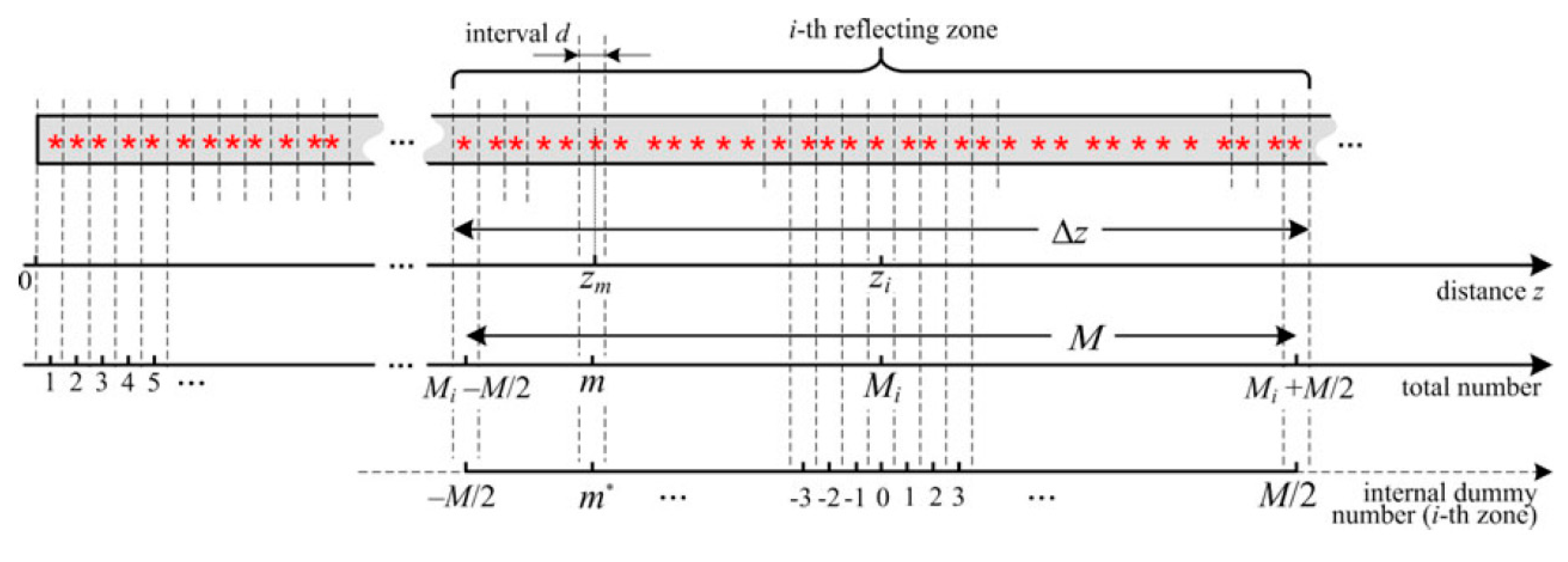
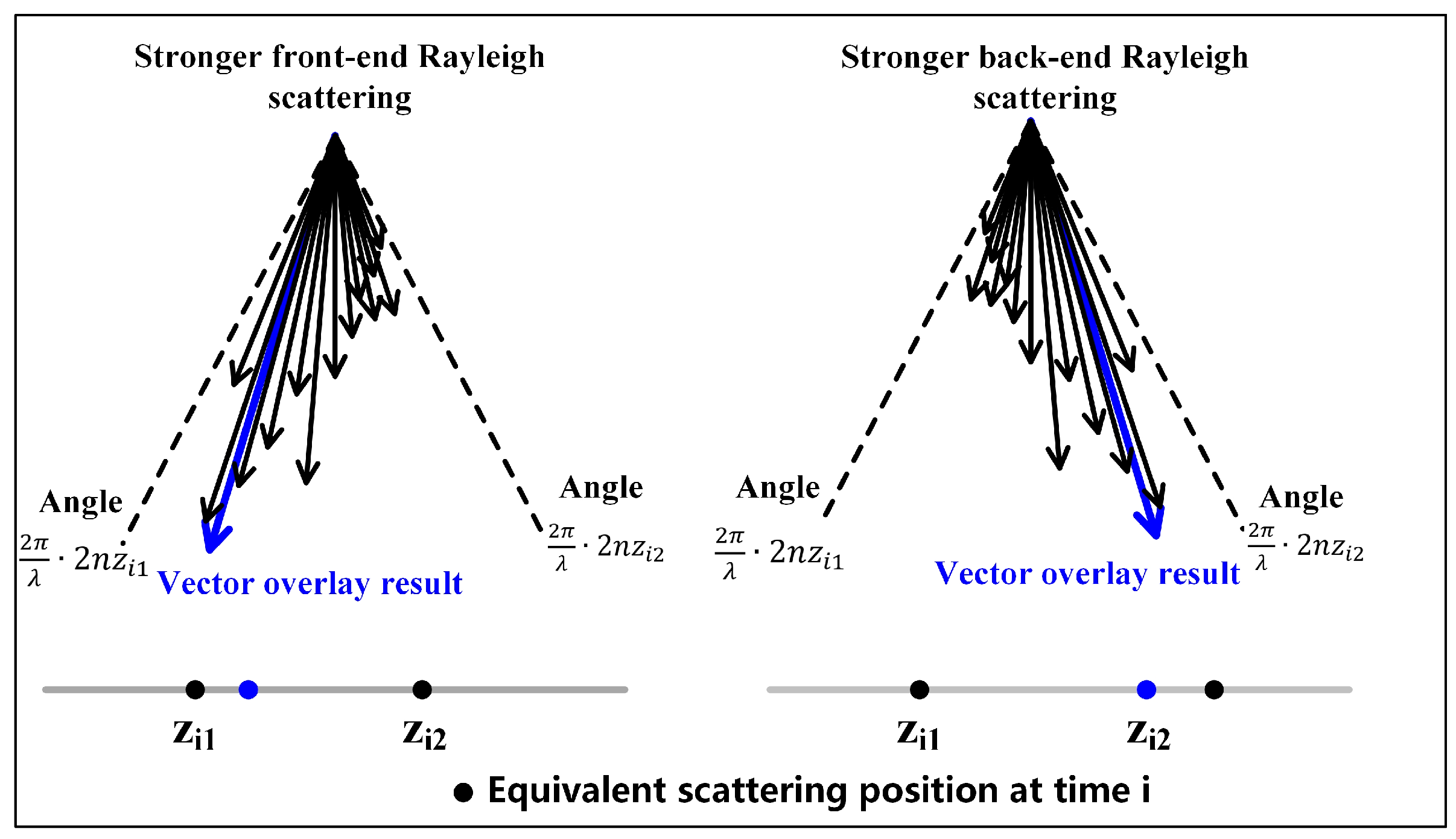
3.1. Continuous Scattering-Enhanced Fiber-Based DAS
3.2. Discrete Scattering-Enhanced Fiber Based DAS
3.3. Preparation and Implementation of DSE Fiber
3.4. Methods to Improve the Performance of Specialty Fiber DAS
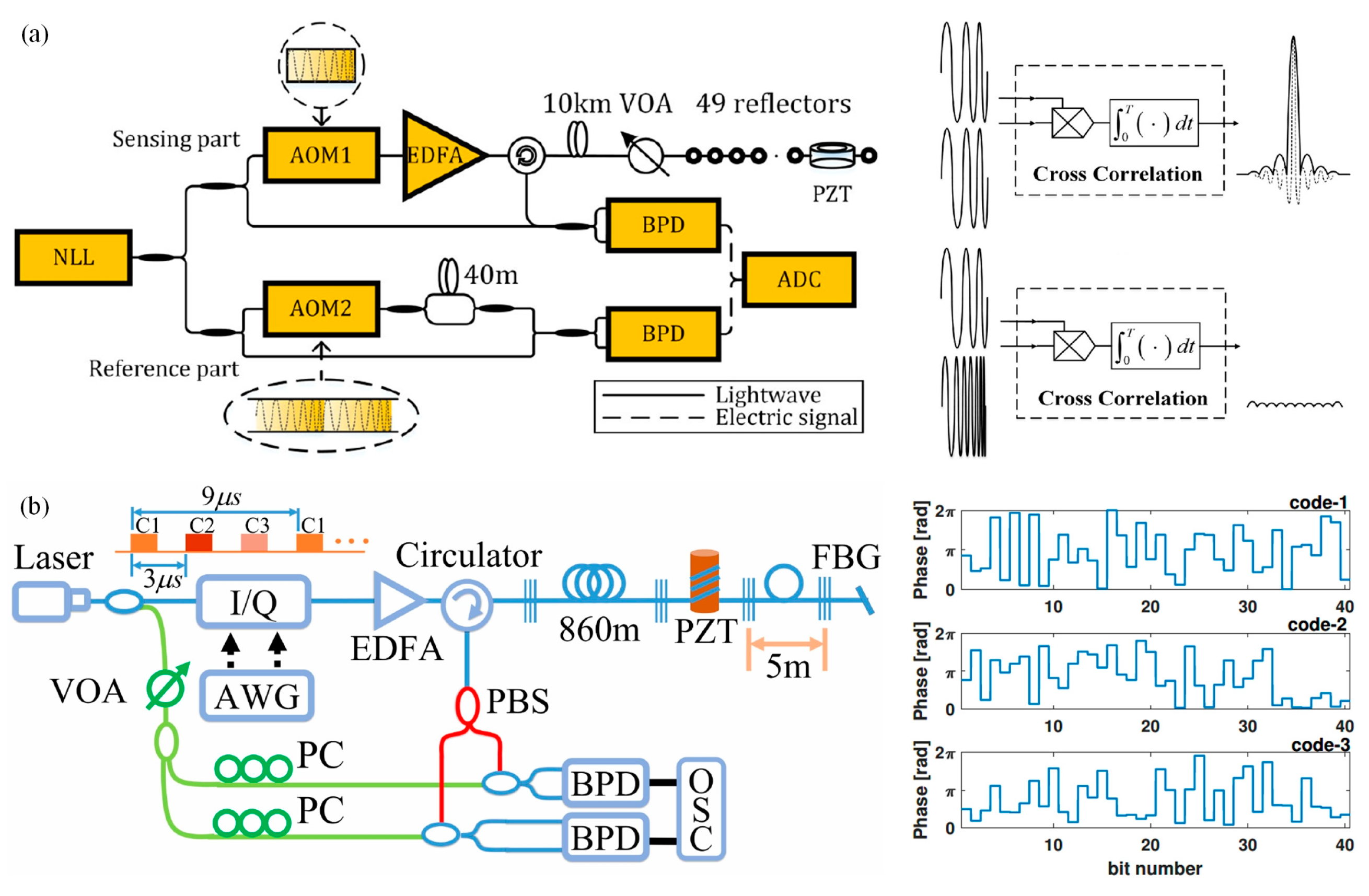
3.4.1. Low-Frequency Phase Drift Compensation Technology
3.4.2. Polarization Fading Suppression Technology
3.4.3. Pulse Width Compression Technology
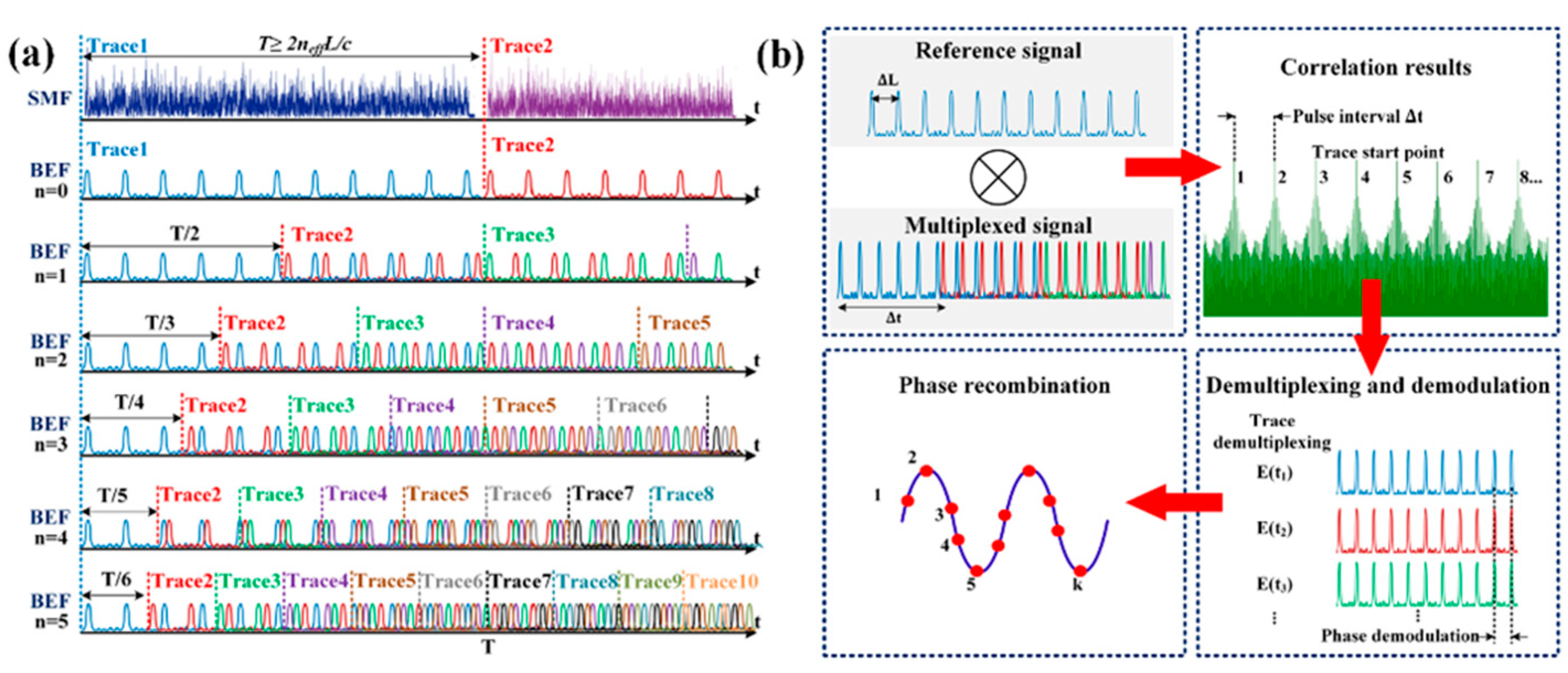
3.4.4. Sampling Frequency Expansion Technology
4. Significant Application Progress
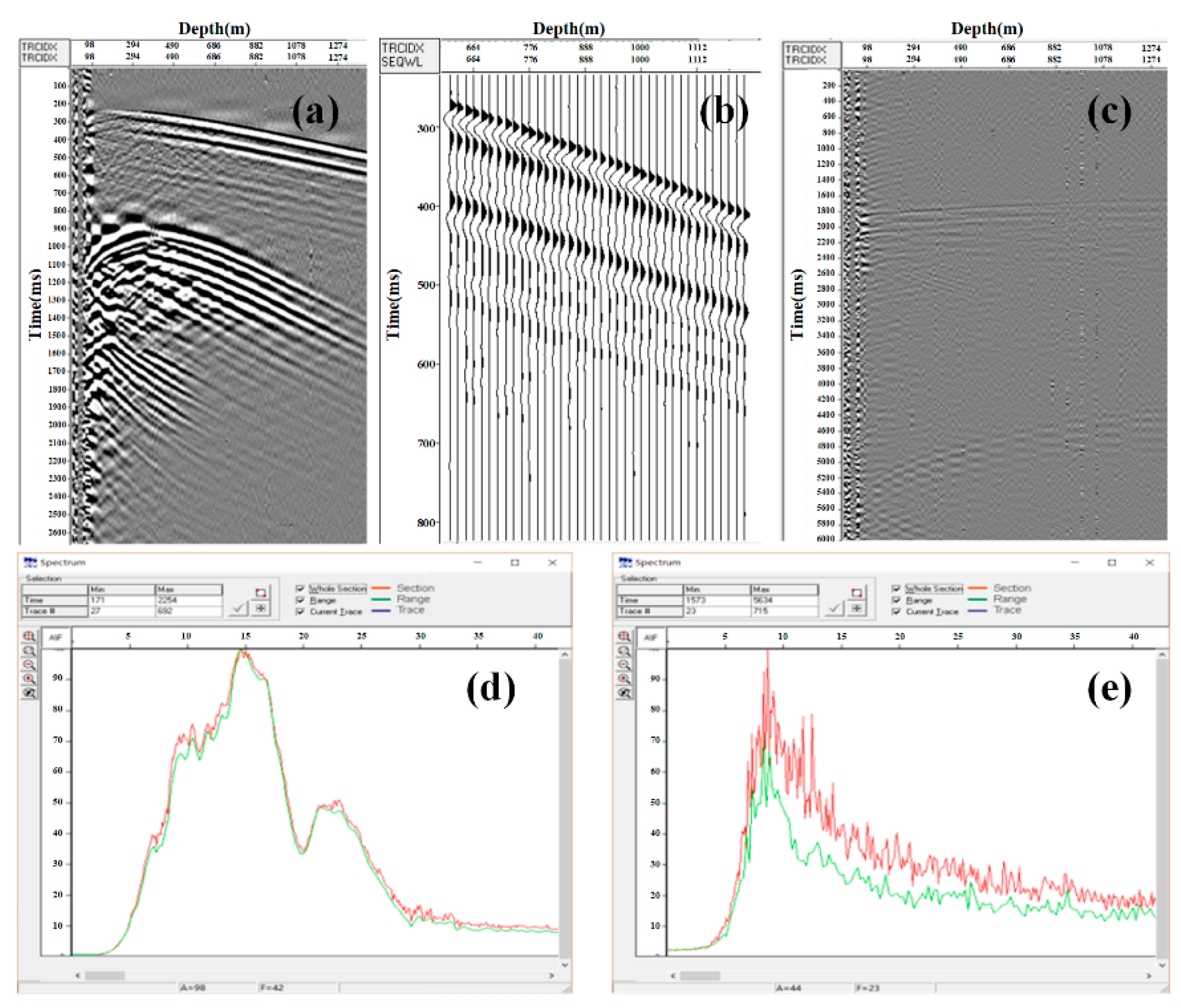
4.1. Geological and Resource Exploration
4.2. Structural Health Monitoring
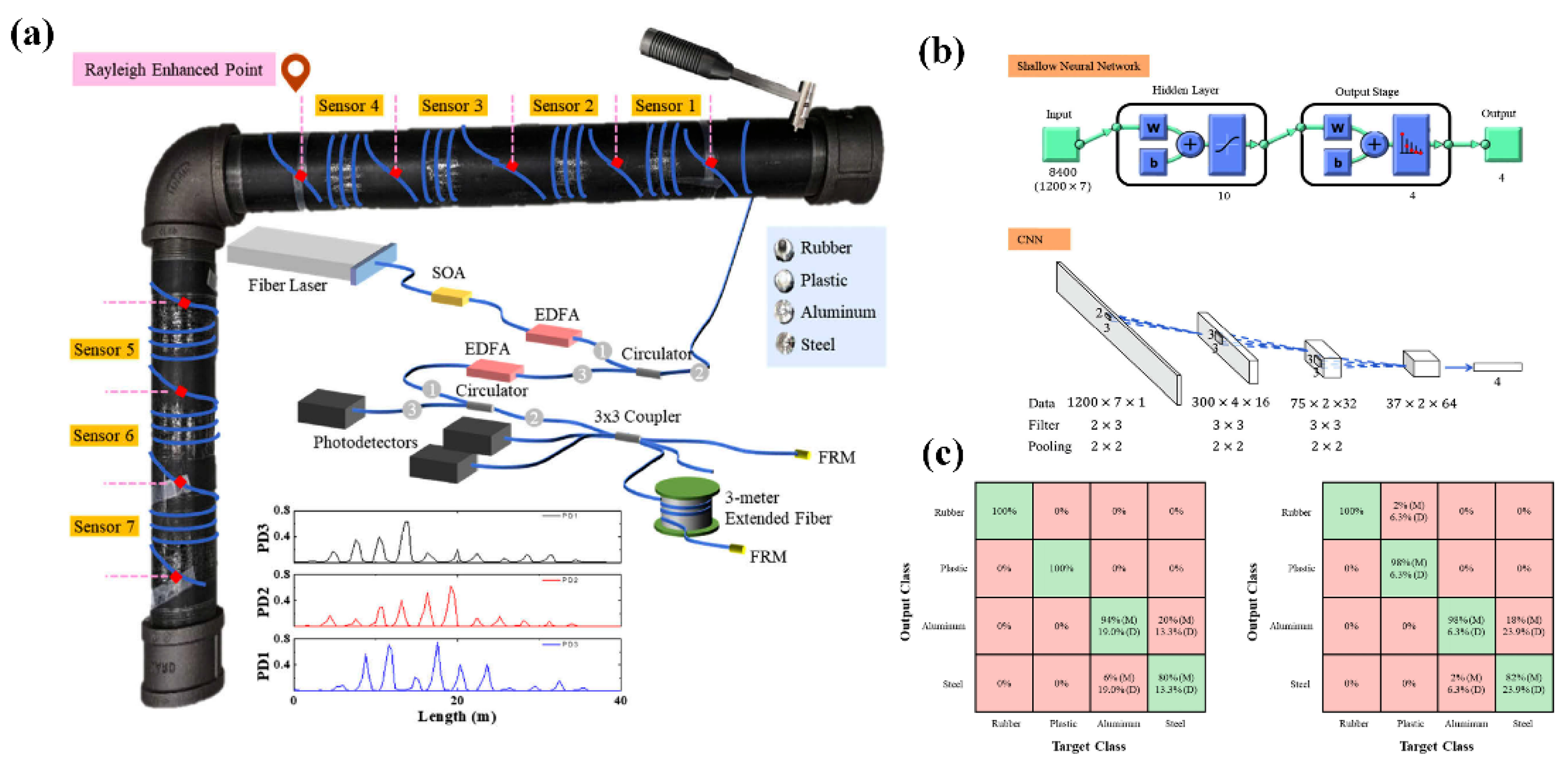
4.2.1. Pipeline Monitoring
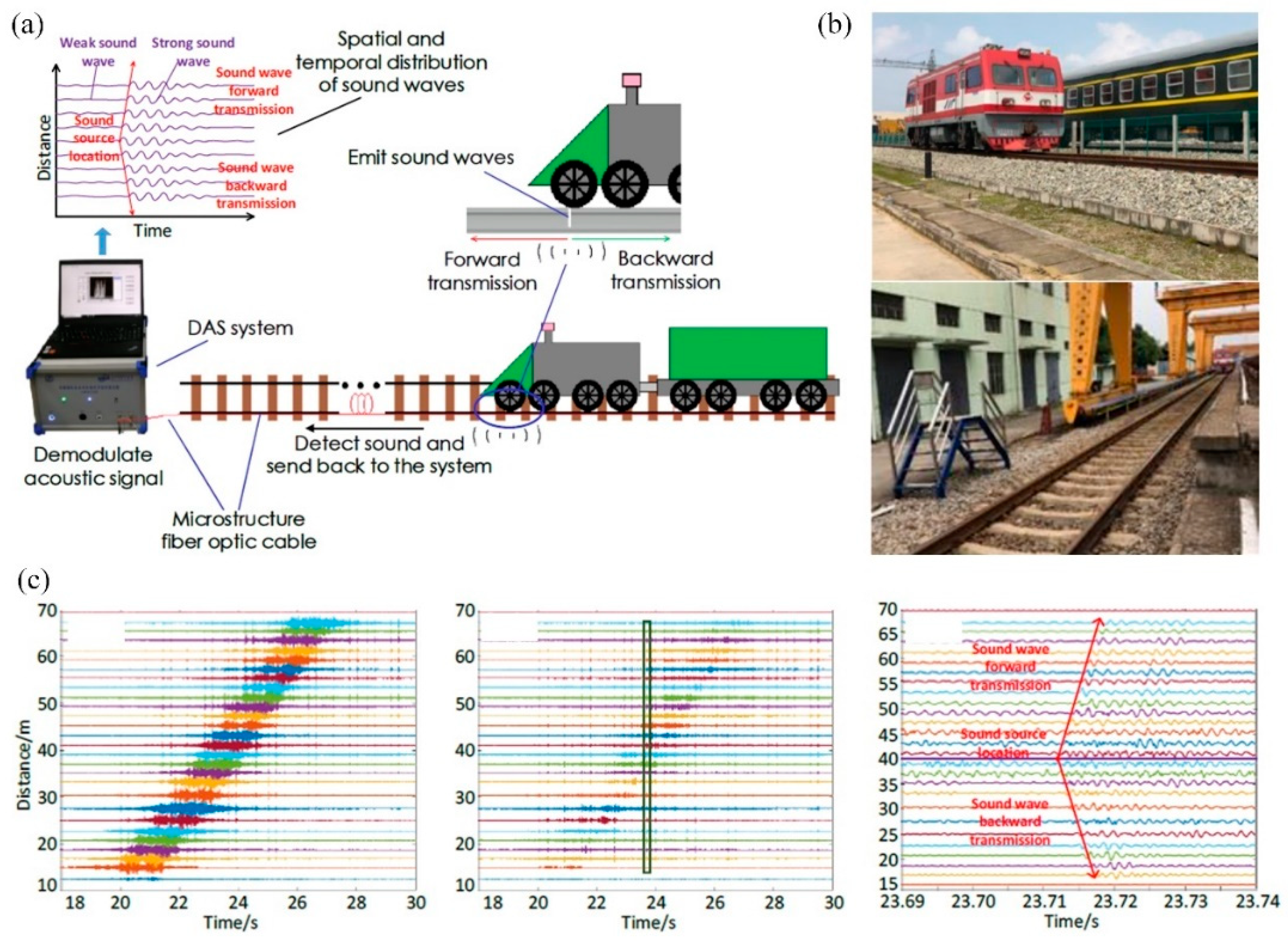
4.2.2. Track Defect Monitoring
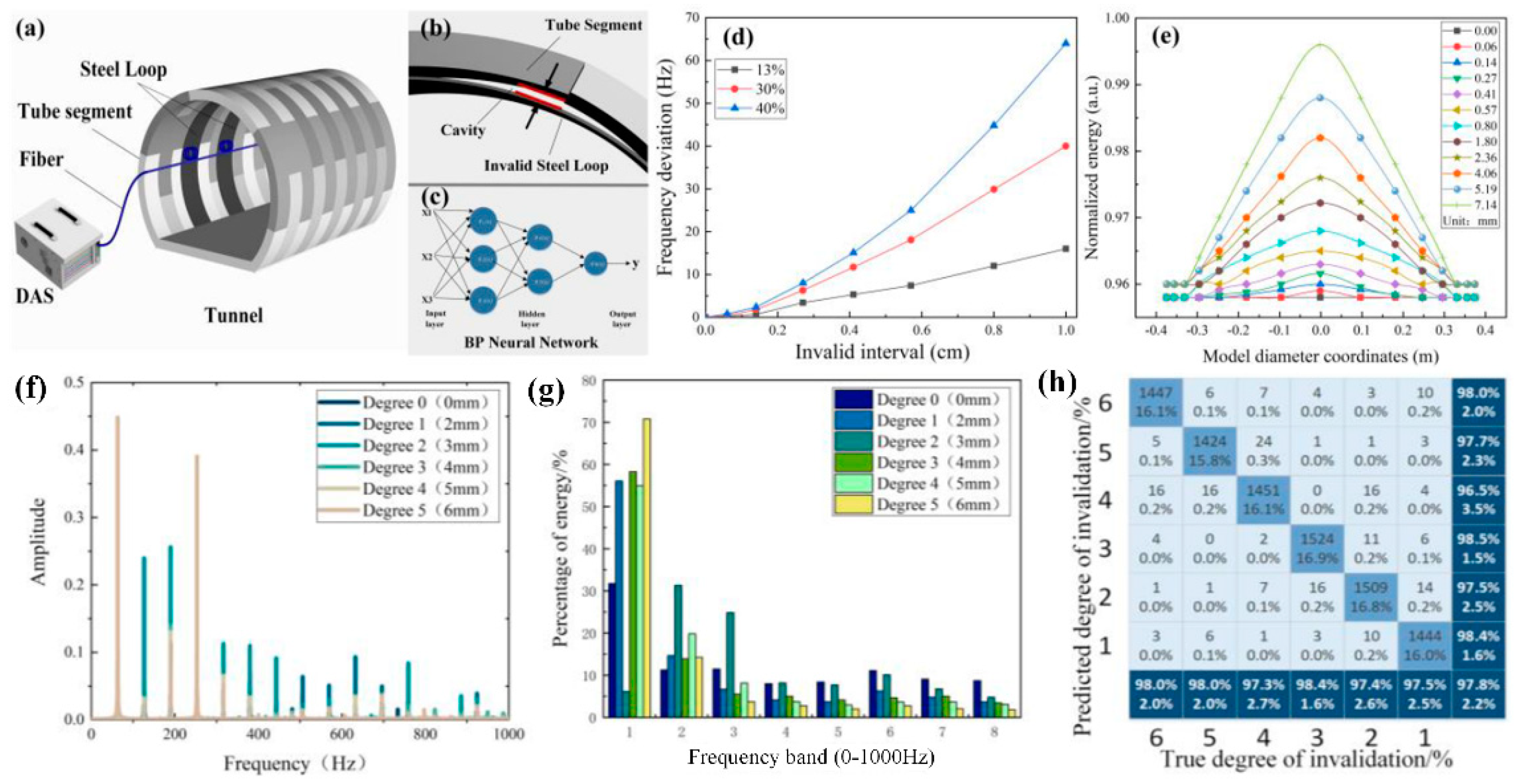
4.2.3. Tunnel Safety Monitoring
4.2.4. Geological Structural Monitoring
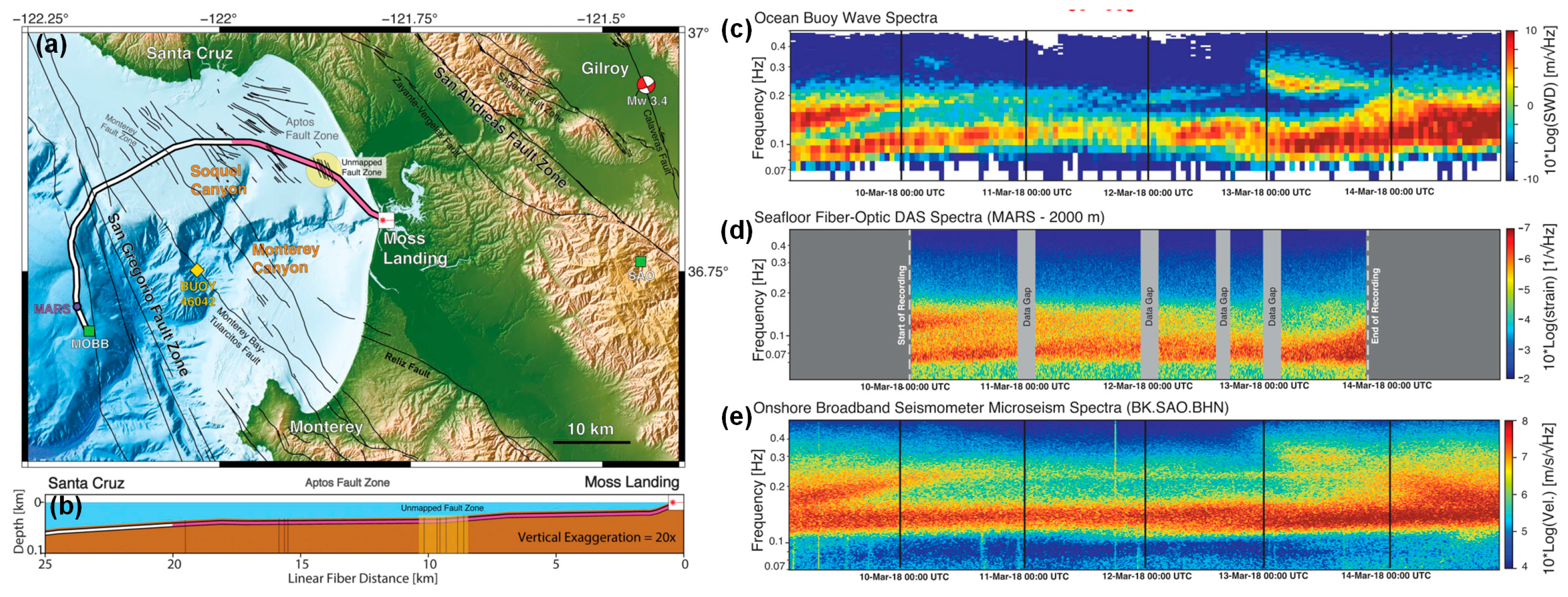
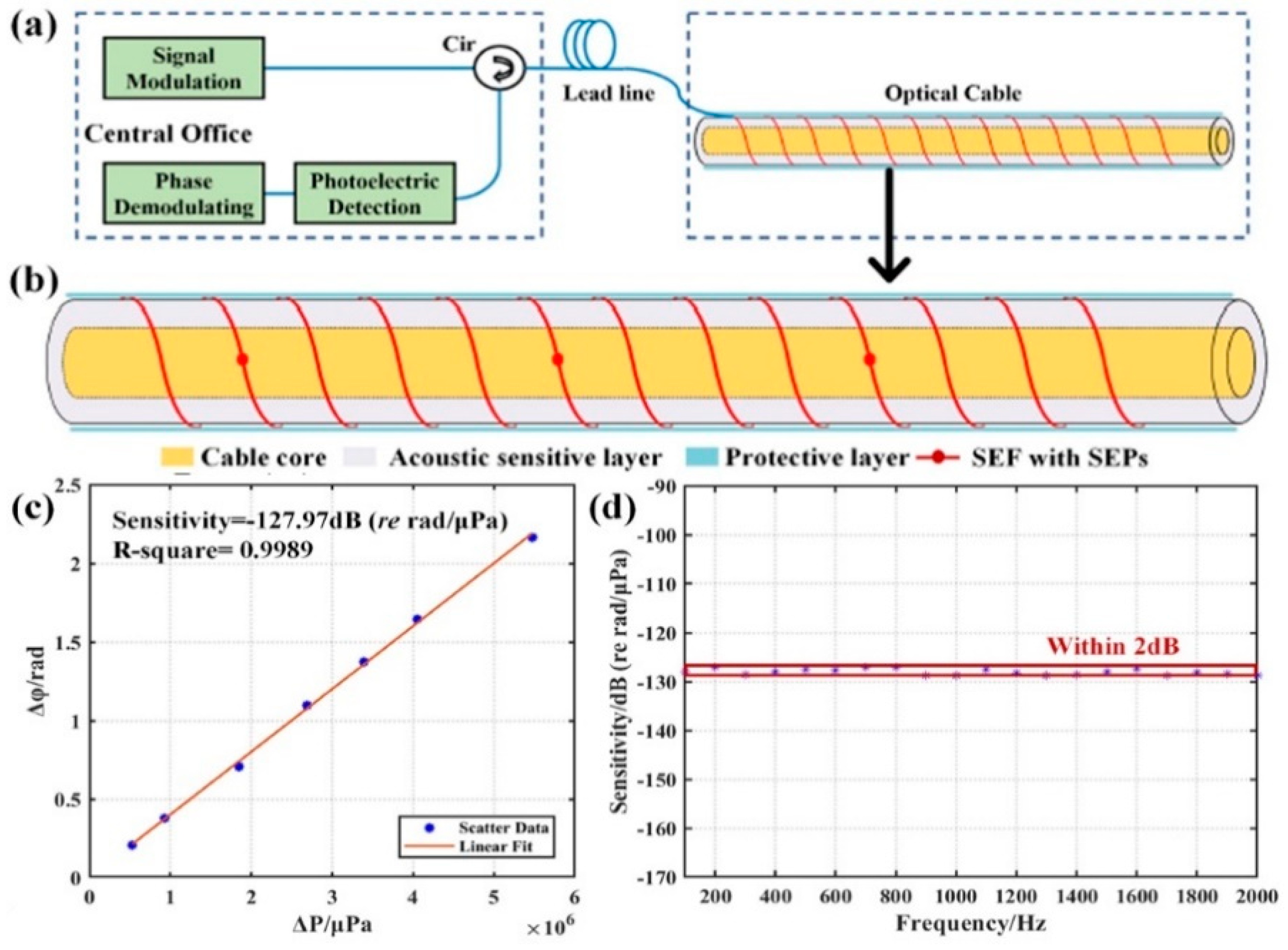
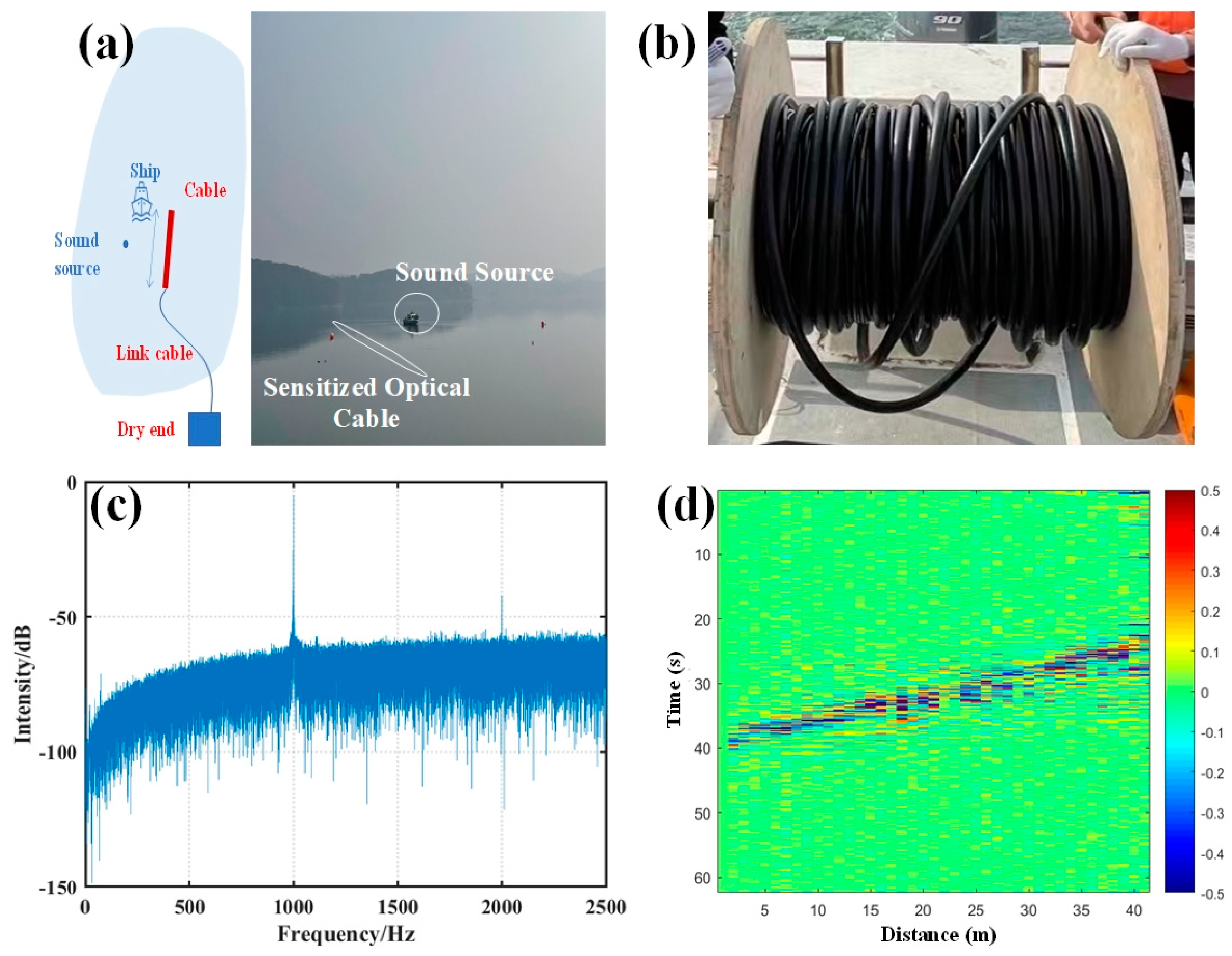
4.3. Hydroacoustic Exploration
5. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yatman, G.; Üzumcü, S.; Pahsa, A.; Mert, A.A. Intrusion detection sensors used by electronic security systems for critical facilities and infrastructures: A review. Safe 2015, 151, 131–141. [Google Scholar] [CrossRef] [Green Version]
- Shelef, E.; Oskin, M. Deformation processes adjacent to active faults: Examples from eastern California. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Mu, D.; Lee, E.J.; Chen, P. Seismic Imaging, Fault Damage and Heal; De Gruyter: Berlin, Germany, 2014; ISBN 9787040390988. [Google Scholar]
- Thun, J.; Lokmer, I.; Bean, C.; Eibl, E.; Bergsson, B.H.; Braiden, A. Micrometre-scale deformation observations reveal fundamental controls on geological rifting. Sci. Rep. 2016, 6, 36676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartog, A.; Frignet, B.; Mackie, D.; Clark, M. Vertical seismic optical profiling on wireline logging cable. Geophys. Prospect. 2014, 62, 693–701. [Google Scholar] [CrossRef]
- Tejedor, J.; Ahlen, C.H.; Gonzalez-Herraez, M.; Macias-Guarasa, J.; Martins, H.F.; Pastor-Graells, J.; Martin-Lopez, S.; Guillen, P.C.; De Pauw, G.; De Smet, F.; et al. Real Field Deployment of a Smart Fiber-Optic Surveillance System for Pipeline Integrity Threat Detection: Architectural Issues and Blind Field Test Results. J. Light. Technol. 2017, 36, 1052–1062. [Google Scholar] [CrossRef]
- Lyu, C.; Huo, Z.; Cheng, X.; Jiang, J.; Alimasi, A.; Liu, H. Distributed Optical Fiber Sensing Intrusion Pattern Recognition Based on GAF and CNN. J. Light. Technol. 2020, 38, 4174–4182. [Google Scholar] [CrossRef]
- Masoudi, A.; Belal, M.; Newson, T.P. A distributed optical fibre dynamic strain sensor based on phase-OTDR. Meas. Sci. Technol. 2013, 24, 085204. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, F.; Wang, X.; Pan, Y.; Sun, Z.; Hua, J.; Zhang, X. Distributed Strain and Vibration Sensing System Based on Phase-Sensitive OTDR. IEEE Photon. Technol. Lett. 2015, 27, 1884–1887. [Google Scholar] [CrossRef]
- Gabai, H.; Eyal, A. On the sensitivity of distributed acoustic sensing. Opt. Lett. 2016, 41, 5648–5651. [Google Scholar] [CrossRef]
- Healey, P. Fading in heterodyne OTDR. Electron. Lett. 1984, 20, 30–32. [Google Scholar] [CrossRef]
- Zabihi, M.; Chen, Y.; Zhou, T.; Liu, J.; Shan, Y.; Meng, Z.; Wang, F.; Zhang, Y.; Zhang, X.; Chen, M. Continuous Fading Suppression Method for Φ-OTDR Systems Using Optimum Tracking Over Multiple Probe Frequencies. J. Light. Technol. 2019, 37, 3602–3610. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, Z.; Ye, Q.; Cai, H.; Qu, R.; Fang, Z. Characteristics and Explanations of Interference Fading of a Φ-OTDR With a Multi-Frequency Source. J. Light. Technol. 2013, 31, 2947–2954. [Google Scholar] [CrossRef]
- Ren, M.; Lu, P.; Chen, L.; Bao, X. Theoretical and Experimental Analysis of O-OTDR Based on Polarization Diversity Detection. IEEE Photon. Technol. Lett. 2015, 28, 697–700. [Google Scholar] [CrossRef]
- Mompo, J.J.; Shiloh, L.; Arbel, N.; Levanon, N.; Loayssa, A.; Eyal, A. Distributed Dynamic Strain Sensing via Perfect Periodic Coherent Codes and a Polarization Diversity Receiver. J. Light. Technol. 2019, 37, 4597–4602. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Y.; Wei, T.; Zhang, Y.; Ji, W.; Zong, M.; Zhang, X. Polarization fading elimination for ultra-weak FBG array-based Φ-OTDR using a composite double probe pulse approach. Opt. Express 2019, 27, 20468–20478. [Google Scholar] [CrossRef]
- Qin, Z.; Zhu, T.; Chen, L.; Bao, X. High Sensitivity Distributed Vibration Sensor Based on Polarization-Maintaining Configurations of Phase-OTDR. IEEE Photon. Technol. Lett. 2011, 23, 1091–1093. [Google Scholar] [CrossRef]
- He, X.; Zhang, M.; Gu, L.; Xie, S.; Liu, F.; Lu, H. Performance Improvement of Dual-Pulse Heterodyne Distributed Acoustic Sensor for Sound Detection. Sensors 2020, 20, 999. [Google Scholar] [CrossRef] [Green Version]
- Juarez, J.C.; Maier, E.W.; Choi, K.N.; Taylor, H.F. Distributed fiber-optic intrusion sensor system. J. Lightwave Technol. 2005, 23, 2081–2087. [Google Scholar] [CrossRef]
- Rao, Y.-J.; Luo, J.; Ran, Z.-L.; Yue, J.-F.; Luo, X.-D.; Zhou, Z. Long-distance fiber-optic Φ-OTDR intrusion sensing system. In Proceedings of the Spie the International Society for Optical Engineering, San Diego, CA, USA, 3–4 August 2009; Volume 7503, p. 75031O. [Google Scholar] [CrossRef]
- Juarez, J.C.; Taylor, H.F. Polarization discrimination in a phase-sensitive optical time-domain reflectometer intrusion-sensor system. Opt. Lett. 2005, 30, 3284–3286. [Google Scholar] [CrossRef]
- Pan, Z.; Liang, K.; Ye, Q.; Cai, H.; Qu, R.; Fa Ng, Z. Phase-sensitive OTDR system based on digital coherent detection. In Proceedings of the SPIE Proceedings (SPIE SPIE/OSA/IEEE Asia Communications and Photonics-Shanghai, China), Shanghai China, 13–16 November 2011; Volume 8311, p. 83110S-2. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Z.; Shan, Y.; Li, Y.; Wang, F.; Zeng, J.; Zhang, Y. A high performance distributed optical fiber sensor based on Φ-OTDR for dynamic strain measurement. IEEE Photon. J. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Fang, G.; Xu, T.; Feng, S.; Li, F. Phase-Sensitive Optical Time Domain Reflectometer Based on Phase-Generated Carrier Algorithm. J. Light. Technol. 2015, 33, 2811–2816. [Google Scholar] [CrossRef]
- Chen, D.; Liu, Q.; Fan, X.; He, Z. Distributed Fiber-Optic Acoustic Sensor with Enhanced Response Bandwidth and High Signal-to-Noise Ratio. J. Light. Technol. 2017, 35, 2037–2043. [Google Scholar] [CrossRef]
- Liokumovich, L.; Ushakov, N.; Kotov, O.; Bisyarin, M.; Hartog, A.H. Fundamentals of Optical Fiber Sensing Schemes Based on Coherent Optical Time Domain Reflectometry: Signal Model Under Static Fiber Conditions. J. Light. Technol. 2015, 33, 3660–3671. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, H.; Zheng, H.; Huang, J.; Yin, G.; Zhu, T.; Qiu, F.; Huang, X.; Qu, D.; Bai, Y.; et al. 80 km Fading Free Phase-Sensitive Reflectometry Based on Multi-Carrier NLFM Pulse Without Distributed Amplification. J. Light. Technol. 2019, 37, 4748–4754. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; He, T.; Fan, C.; Liu, T.; Yan, Z.; Liu, D.; Sun, Q. Dual-pulse Complex Superposition Based Noise Suppression for Distributed Acoustic Sensing. In Proceedings of the CLEO: Applications and Technology, Washington, DC, USA, 10–15 May 2020; p. JW2E.28. [Google Scholar] [CrossRef]
- Ai, F.; Sun, Q.; Zhang, W.; Liu, T.; Yan, Z.; Liu, D. Wideband Fully-Distributed Vibration Sensing by Using UWFBG Based Coherent OTDR. In Proceedings of the Optical Fiber Communications Conference & Exhibition, Los Angeles, CA, USA, 19–23 March 2017; p. W2A.19. [Google Scholar] [CrossRef]
- Lin, S.T.; Wang, Z.N.; Xiong, J.; Wu, Y.; Rao, Y.J. Progresses of Anti-Interference-Fading Technologies for Ray-leigh-Scattering-Based Optical Fiber Sensing. Laser Optoelectron. Prog. 2021, 58, 1306008. [Google Scholar] [CrossRef]
- Westbrook, P.S.; Feder, K.S.; Ortiz, R.M.; Kremp, T.; Monberg, E.M.; Wu, H.; Simoff, D.A.; Shenk, S. Kilometer length low loss enhanced back scattering fiber for distributed sensing. In Proceedings of the 25th International Conference on Optical Fiber Sensors, Jeju, Korea, 24–28 April 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Handerek, V.A.; Karimi, M.; Nkansah, A.; Yau, A.; Westbrook, P.S.; Feder, K.S.; Ortiz, R.M.; Kremp, T.; Monberg, E.M.; Wu, H.; et al. Improved Optical Power Budget in Distributed Acoustic Sensing Using Enhanced Scattering Optical Fibre. In Proceedings of the 26th International Conference on Optical Fiber Sensors, Vaud, Switzerland, 24–28 September 2018; p. TuC5. [Google Scholar] [CrossRef]
- Westbrook, P.S.; Kremp, T.; Feder, K.S.; Ko, W.; Monberg, E.M.; Wu, H.; Simoff, D.A.; Ortiz, R.M. Improving distributed sensing with continuous gratings in single and multi-core fibers. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018; p. W1K.1. [Google Scholar] [CrossRef]
- Lalam, N.; Westbrook, P.S.; Li, J.; Lu, P.; Buric, M.P. Phase-Sensitive Optical Time Domain Reflectometry with Rayleigh Enhanced Optical Fiber. IEEE Access 2021, 9, 114428–114434. [Google Scholar] [CrossRef]
- Butov, O.V.; Chamorovskii, Y.K.; Golant, K.M.; Fotiadi, A.A.; Jason, J.; Popov, S.M.; Wuilpart, M. Sensitivity of high Rayleigh scattering fiber in acoustic/vibration sensing using phase-OTDR. In Proceedings of the Optical Sensing and Detection V, Strasbourg, France, 9 May 2018. [Google Scholar] [CrossRef]
- Feng, S.; Xu, T.; Huang, J.; Yang, Y.; Li, F.; Zhou, J.; Yu, H. Enhanced SNR phase-sensitive OTDR system with active fiber. In Proceedings of the Fiber Optic Sensing and Optical Communication, Beijing, China, 12 December 2018. [Google Scholar] [CrossRef]
- Huang, J.B.; Ding, P.; Tang, J.S. Progress in Fabrication, Demodulation and Application of Weak-Reflection Fiber Bragg Grating Array. Laser Optoelectron. Prog. 2021, 58, 1700005. [Google Scholar] [CrossRef]
- Wu, M.; Fan, X.; Zhang, X.; Yan, L.; He, Z. Frequency Response Enhancement of Phase-Sensitive OTDR for Interrogating Weak Reflector Array by Using OFDM and Vernier Effect. J. Light. Technol. 2020, 38, 4874–4882. [Google Scholar] [CrossRef]
- Hicke, K.; Eisermann, R.; Chruscicki, S. Enhanced Distributed Fiber Optic Vibration Sensing and Simultaneous Temperature Gradient Sensing Using Traditional C-OTDR and Structured Fiber with Scattering Dots. Sensors 2019, 19, 4114. [Google Scholar] [CrossRef] [Green Version]
- Redding, B.; Murray, M.J.; Donko, A.; Beresna, M.; Masoudi, A.; Brambilla, G. Low-noise distributed acoustic sensing using enhanced backscattering fiber with ultra-low-loss point reflectors. Opt. Express 2020, 28, 14638–14647. [Google Scholar] [CrossRef]
- Hill, K.O.; Fujii, Y.; Johnson, D.C.; Kawasaki, B.S. Photosensitivity in optical fiber waveguides: Application to reflection filter fabrication. Appl. Phys. Lett. 1978, 32, 647–649. [Google Scholar] [CrossRef]
- Meltz, G.; Morey, W.W.; Glenn, W.H. Formation of Bragg gratings in optical fibers by a transverse holographic method. Opt. Lett. 1989, 14, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Yu, H.; Guo, H.; Li, X.; Jiang, D. Analysis of the Spectrum Distortions of Weak Fiber Bragg Gratings Fabricated In-Line on a Draw Tower by the Phase Mask Technique. J. Light. Technol. 2014, 33, 2670–2673. [Google Scholar] [CrossRef]
- Martinez, A.; Dubov, M.; Khrushchev, I.; Bennion, I. Direct writing of fibre Bragg gratings by femtosecond laser. Electron. Lett. 2004, 40, 1170–1172. [Google Scholar] [CrossRef]
- Chen, Z.; He, J.; Xu, X.; He, J.; Xu, B.; Du, B.; Liao, C.; Wang, Y. High-Temperature Sensor Array Based on Fiber Bragg Gratings Fabricated by Femtosecond Laser Point-by-Point Method. Acta Opt. Sin. 2021, 41, 1306002. [Google Scholar] [CrossRef]
- Yang, M.; Bai, W.; Guo, H.; Wen, H.; Yu, H.; Jiang, D. Huge capacity fiber-optic sensing network based on ultra-weak draw tower gratings. Photon. Sens. 2016, 6, 26–41. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Cai, L.; Li, C.; Yang, M.; Guo, H.; Gan, W. Distributed acoustic sensors with wide frequency response based on UWFBG array utilizing dual-pulse detection. Opt. Fiber Technol. 2021, 61, 102452. [Google Scholar] [CrossRef]
- Ai, F.; Li, H.; He, T.; Yan, Z.; Liu, D.; Sun, Q. Simultaneous Distributed Temperature and Vibration Measurement with UWFBG based Coherent OTDR. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018; p. W2A.12. [Google Scholar] [CrossRef]
- Yang, M.; Li, C.; Mei, Z.; Tang, J.; Guo, H.; Jiang, D. Thousand of fiber grating sensor array based on draw tower: A new platform for fiber-optic sensing. In Proceedings of the Optical Fiber Sensors, OFS 2018, Lausanne, Switzerland, 24–28 September 2018; p. FB6. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Jian, J.; Wen, H.; Wang, M.; Liu, H.; Jiang, D.; Mao, Z.; Chen, K.P. Fiber-optical distributed acoustic sensing signal enhancements using ultrafast laser and artificial intelligence for human movement detection and pipeline monitoring. Opt. Data Sci. II 2019, 10937, 109370J. [Google Scholar] [CrossRef]
- Liu, D.M.; He, T.; Xu, Z.J.; Sun, Q. New type of microstructure-fiber distributed acoustic sensing technology and its applications. J. Appl. Sci. 2020, 38, 296–309. [Google Scholar] [CrossRef]
- Ai, F. Investigation on Discrete Enhanced Fiber Based Distributed Sensing Technologies and Their Applications. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Li, H.; Sun, Q.; Liu, T.; Fan, C.; He, T.; Yan, Z.; Liu, D.; Shum, P.P. Ultra-High Sensitive Quasi-Distributed Acoustic Sensor Based on Coherent OTDR and Cylindrical Transducer. J. Light. Technol. 2019, 38, 929–938. [Google Scholar] [CrossRef]
- Wu, M.; Li, C.; Fan, X.; Liao, C.; He, Z. Large-scale multiplexed weak reflector array fabricated with a femtosecond laser for a fiber-optic quasi-distributed acoustic sensing system. Opt. Lett. 2020, 45, 3685. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Shang, Y.; Liu, X.-H.; Wang, C.; Yu, H.-H.; Jiang, D.-S.; Peng, G.-D. Distributed OTDR-interferometric sensing network with identical ultra-weak fiber Bragg gratings. Opt. Express 2015, 23, 29038–29046. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Ma, L.; Wang, W.; Hu, Z.; Hu, Y. Crosstalk Reduction and Demodulation Stability Promotion in Inline Fiber Fabry–Pérot Sensor Array Using Phase Generated Carrier Scheme. J. Light. Technol. 2015, 34, 1006–1014. [Google Scholar] [CrossRef]
- Peng, Z.; Wen, H.; Jian, J.; Gribok, A.; Wang, M.; Huang, S.; Liu, H.; Mao, Z.-H.; Chen, K.P. Identifications and classifications of human locomotion using Rayleigh-enhanced distributed fiber acoustic sensors with deep neural networks. Sci. Rep. 2020, 10, 21014. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Liu, Y.; Li, C.; Guo, H.; Yang, M. Distributed Vibration Sensing System with High Signal-to-Noise Ratio Based on Ultra-Weak Fiber Bragg Grating. Acta Opt. Sin. 2021, 41, 1306014. [Google Scholar] [CrossRef]
- Fan, X.; Yang, G.; Wang, S.; Liu, Q.; He, Z. Distributed Fiber-Optic Vibration Sensing Based on Phase Extraction from Optical Reflectometry. J. Light. Technol. 2016, 35, 3281–3288. [Google Scholar] [CrossRef]
- Wu, M.; Fan, X.; Liu, Q.; He, Z. Highly sensitive quasi-distributed fiber-optic acoustic sensing system by interrogating a weak reflector array. Opt. Lett. 2018, 43, 3594–3597. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Fan, X.; Liu, Q.; He, Z. Quasi-distributed Fiber-optic Acoustic Sensor using Ultra-weak Reflecting Point Array. In Proceedings of the 26th International Conference on Optical Fiber Sensors, Vaud, Switzerland, 24–28 September 2018; p. WF19. [Google Scholar] [CrossRef]
- Liu, T.; Li, H.; Ai, F.; Wang, J.; Fan, C.; Luo, Y.; Yan, Z.; Liu, D.; Sun, Q. Ultra-high Resolution Distributed Strain Sensing based on Phase-OTDR. In Proceedings of the Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 3–7 March 2019; p. Th2A.16. [Google Scholar] [CrossRef]
- He, T.; Liu, Y.; Zhang, S.; Yan, Z.; Liu, D.; Sun, Q. High Accuracy Intrusion Pattern Recognition using a Dual-Stage-Recognition Network for Fiber Optic Distributed Sensing System. In Proceedings of the Conference on Lasers and Electro-Optics, Munich, Germany, 21–25 June 2021; p. JW1A.119. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Zhang, X.; Zhang, Y.; Xu, W.; Zhang, L. High performance interrogation by a composite-double-probe-pulse for ultra-weak FBG array. In Proceedings of the 17th International Conference on Optical Communications and Networks (ICOCN2018), International Society for Optics and Photonics. Bellingham, WA, USA, 14 February 2019. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, H.; Liu, T.; Fan, C.; Yan, Z.; Liu, D.; Sun, Q. Polarization dependent noise suppression for fiber distributed acoustic sensor with birefringence estimation. In Proceedings of the Conference on Lasers and Electro-Optics: Applications and Technology, Washington, DC, USA, 10–15 May 2020; p. JW2E.18. [Google Scholar] [CrossRef]
- Liu, T.; Li, H.; He, T.; Fan, C.; Yan, Z.; Liu, D.; Sun, Q. Fading Noise Free Distributed Acoustic Sensor Assisted with Double Wavelength lasers. In Proceedings of the Conference on Lasers and Electro-Optics: Applications and Technology, Anaheim, CA, USA, 23–25 October 2020; p. JW2E.10. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, D.W.; Xia, X.X.; Wang, G.Y.; Wang, X.S. A countering technique for LFM PC radar against shift-frequency jamming. Mod. Radar 2006, 28, 84–86. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, C.; Wei, T.; Shangguan, M.; Xia, H. Simulation Research of Coherent Lidar Based on Golay Coding Technology. Chin. J. Lasers 2018, 45, 0810004. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Xiong, J.; Wang, Z.; Qiu, Z.; Liu, C.; Deng, Z.; Rao, Y.-J. Quasi-Distributed Fiber-Optic Acoustic Sensing with MIMO Technology. IEEE Internet Things J. 2021, 8, 15284–15291. [Google Scholar] [CrossRef]
- Wu, M.; Fan, X.; He, Z. Phase Noise Compensation for Ultra-highly Sensitive Fiber-optic Quasi-distributed Acoustic Sensing System. In Proceedings of the Conference on Lasers and Electro-Optics: Science and Innovations, San Jose, CA, USA, 5–10 May 2019. [Google Scholar] [CrossRef]
- Wu, M.; Fan, X.; Liu, Q.; He, Z. Quasi-distributed fiber-optic acoustic sensing system based on pulse compression technique and phase-noise compensation. Opt. Lett. 2019, 44, 5969–5972. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.T.; Jiang, J.L.; Xiong, J.; Wang, Z.N. Fiber-optic Quasi-distributed Acoustic Sensing System at Doubled Repetition Rate. In Proceedings of the Asia Communications and Photonics Conference (ACP), Chengdu, China, 2–5 November 2019; OSA Technical Digest (Optica Publishing Group). 2019; p. M4A.183. [Google Scholar]
- Zhang, Y.X.; Fu, S.Y.; Chen, Y.S.; Ding, Z.W.; Shan, Y.Y.; Wang, F.; Chen, M.M.; Zhang, X.P.; Meng, Z. A visibility enhanced broadband phase-sensitive OTDR based on the UWFBG array and frequency-division-multiplexing. Opt. Fiber Technol. 2019, 53, 101995. [Google Scholar] [CrossRef]
- Li, H.; Fan, C.; Liu, T.; Liu, Y.; Yan, Z.; Shum, P.; Sun, Q. Time-slot multiplexing based bandwidth enhancement for fiber distributed acoustic sensing. Sci. China Inf. Sci. 2021, 65, 119303. [Google Scholar] [CrossRef]
- Li, Y.P.; Karrenbach, M.; Ajo, J. Distributed Acoustic Sensing in Geophysics: Methods and Applications; American Geophysical Union: Washington, DC, USA, 2022. [Google Scholar]
- Li, C.; Mei, Z.; Cheng, C.; Tang, J.; Jiang, Y.; Yang, M. Draw Tower Grating-based Distributed Acoustic Sensing System and its Applications. In Proceedings of the Asia Communications and Photonics Conference, Chengdu, China, 2–5 November 2019; p. T2A.5. [Google Scholar] [CrossRef]
- Li, T.; Fan, C.; Li, H.; He, T.; Qiao, W.; Shi, Z.; Yan, Z.; Liu, C.; Liu, D.; Sun, Q. Nonintrusive Distributed Flow Rate Sensing System Based on Flow-Induced Vibrations Detection. IEEE Trans. Instrum. Meas. 2021, 70, 7001808. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, F.; Wang, H.; Li, S.; Gan, W.; Jiang, R. Lateral positioning of vibration source for underground pipeline monitoring based on ultra-weak fiber Bragg grating sensing array. Measurement 2020, 172, 108892. [Google Scholar] [CrossRef]
- Peng, Z.; Jian, J.; Wen, H.; Gribok, A.; Wang, M.; Liu, H.; Huang, S.; Mao, Z.-H.; Chen, K. Distributed Fiber Sensor and Machine Learning Data Analytics for Pipeline Protection against Extrinsic Intrusions and Intrinsic Corrosions. Opt. Express 2020, 28, 27277–27292. [Google Scholar] [CrossRef]
- Fan, C.; Ai, F.; Liu, Y.; Xu, Z.; Wu, G.; Zhang, W.; Liu, C.; Yan, Z.; Liu, D.; Sun, Q. Rail Crack Detection by Analyzing the Acoustic Transmission Process Based on Fiber Distributed Acoustic Sensor. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 3–7 March 2019; p. Th2A.17. [Google Scholar] [CrossRef]
- Hu, D.; Tian, B.; Li, H.; Fan, C.; Liu, T.; He, T.; Liu, Y.; Yan, Z.; Sun, Q. Intelligent Structure Monitoring for Tunnel Steel Loop Based on Distributed Acoustic Sensing. In Proceedings of the Conference on Lasers and Electro-Optics, Munich, Germany, 21–25 June 2021; p. ATh1S.4. [Google Scholar] [CrossRef]
- Min, R.; Liu, Z.; Pereira, L.; Yang, C.; Sui, Q.; Marques, C. Optical fiber sensing for marine environment and marine structural health monitoring: A review. Opt. Laser Technol. 2021, 140, 107082. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Martin, E.R.; Dreger, D.S.; Freifeld, B.; Cole, S.; James, S.R.; Biondi, B.L.; Ajo-Franklin, J.B. Fiber-Optic Network Observations of Earthquake Wavefields. Geophys. Res. Lett. 2017, 44, 11792–11799. [Google Scholar] [CrossRef] [Green Version]
- Jousset, P.; Reinsch, T.; Ryberg, T.; Blanck, H.; Clarke, A.; Aghayev, R.; Hersir, G.P.; Henninges, J.; Weber, M.; Krawczyk, C.M. Dynamic strain determination using fibre-optic cables allows imaging of seismological and structural features. Nat. Commun. 2018, 9, 2509. [Google Scholar] [CrossRef]
- Sladen, A.; Rivet, D.; Ampuero, J.P.; De Barros, L.; Hello, Y.; Calbris, G.; Lamare, P. Distributed sensing of earthquakes and ocean-solid Earth interactions on seafloor telecom cables. Nat. Commun. 2019, 10, 5777. [Google Scholar] [CrossRef] [Green Version]
- Lindsey, N.J.; Dawe, T.C.; Ajo-Franklin, J.B. Illuminating seafloor faults and ocean dynamics with dark fiber distributed acoustic sensing. Science 2019, 366, 1103–1107. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Pang, Y.; Qian, L.; Chen, X.; Xu, Q.; Zhao, C.; Zhang, H.; Tu, Z.; Huang, J.; Gu, H.; et al. Demodulation of a Hydroacoustic Sensor Array of Fiber Interferometers Based on Ultra-Weak Fiber Bragg Grating Reflectors Using a Self-Referencing Signal. J. Light. Technol. 2018, 37, 2568–2576. [Google Scholar] [CrossRef]
- Chen, J.F.; Li, H.; Liu, T.; Fan, C.Z.; Yan, Z.J.; Sun, Q.Z. Fully distributed hydroacoustic sensing based on lightweight optical cable assisted with scattering enhanced fiber. In Proceedings of the Optical Fiber Communication Conference (OFC), Washington, DC, USA, 6–11 June 2021; p. W7C.3. [Google Scholar] [CrossRef]
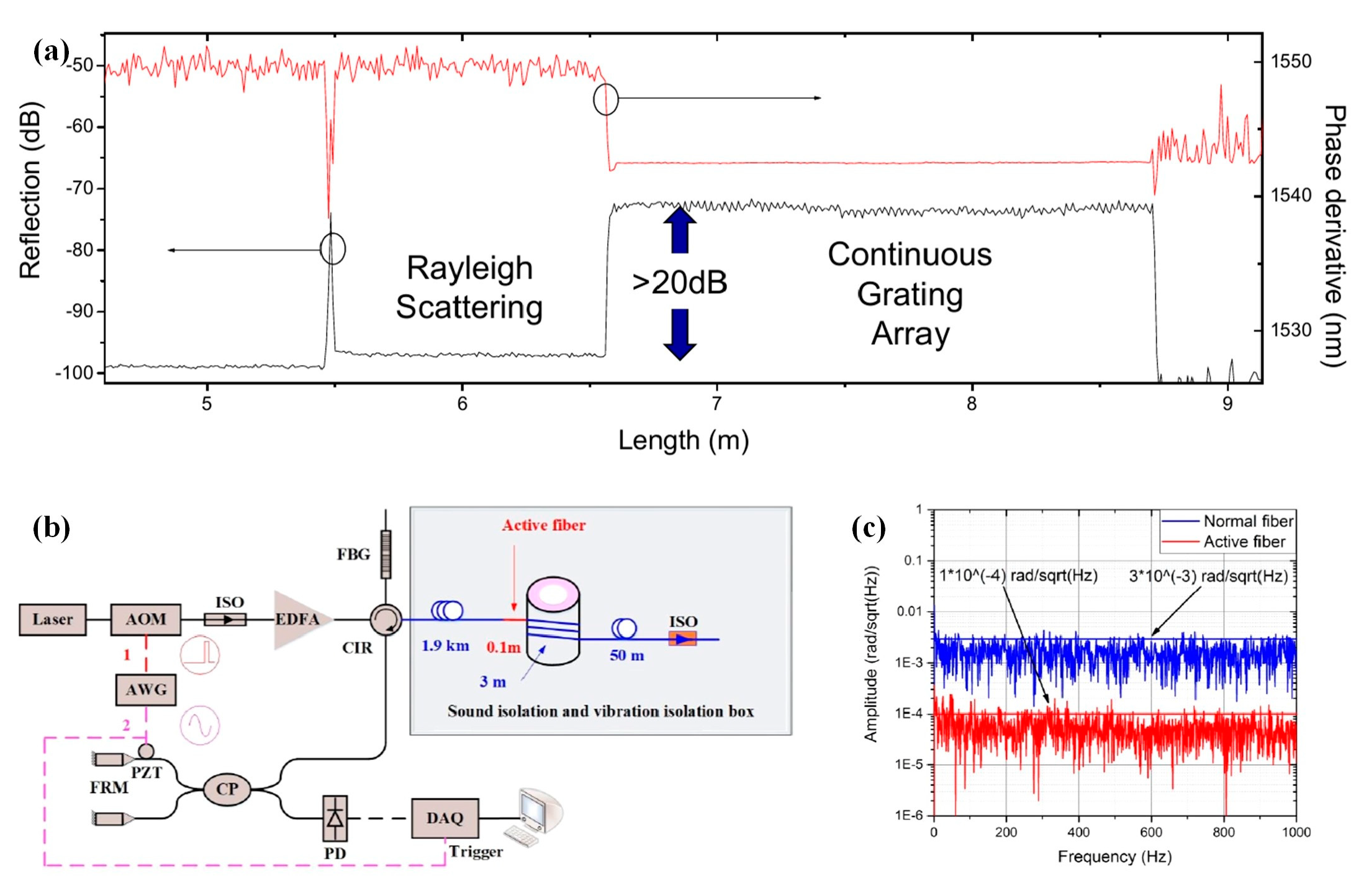
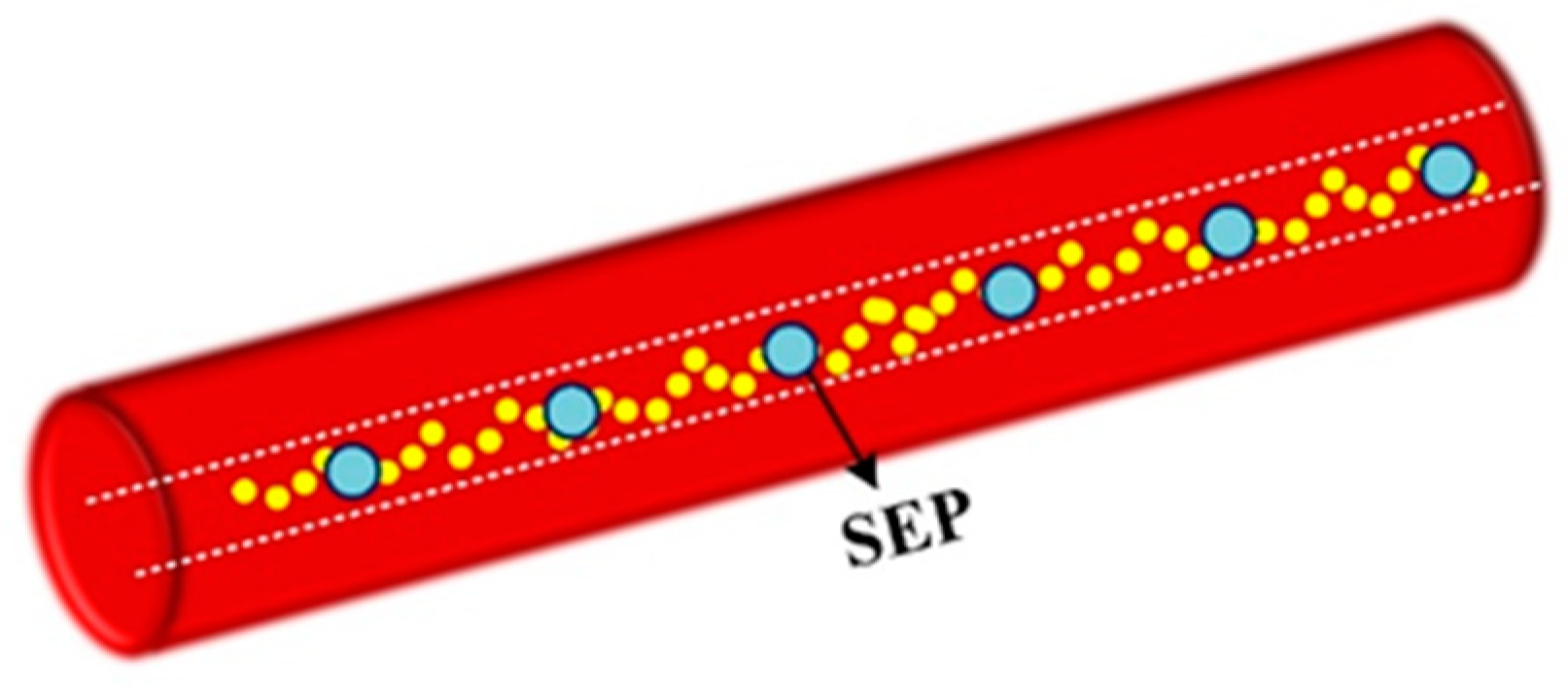
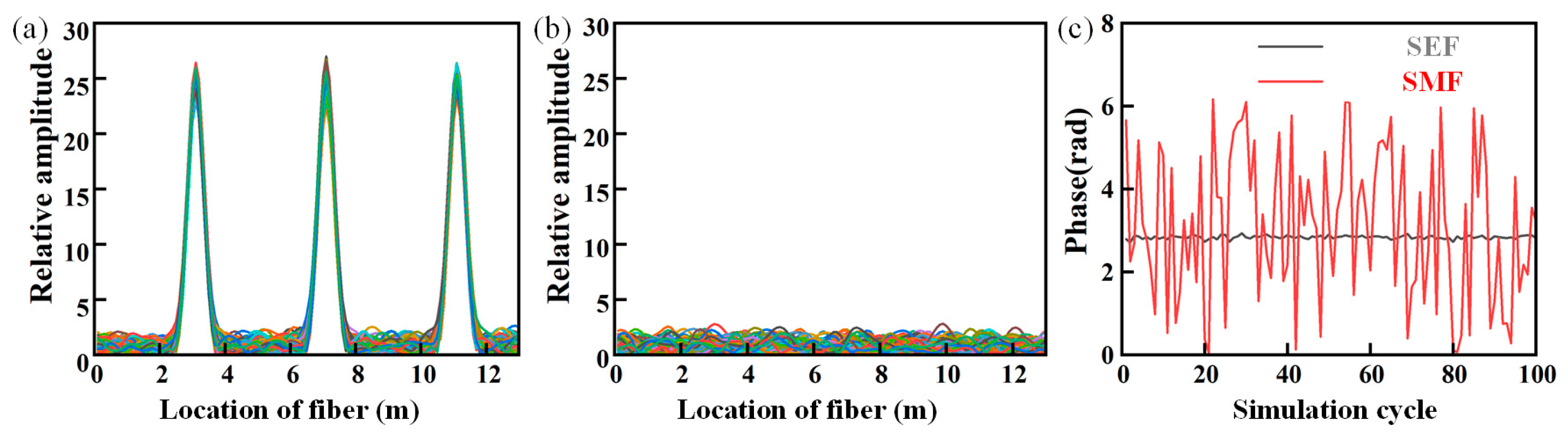
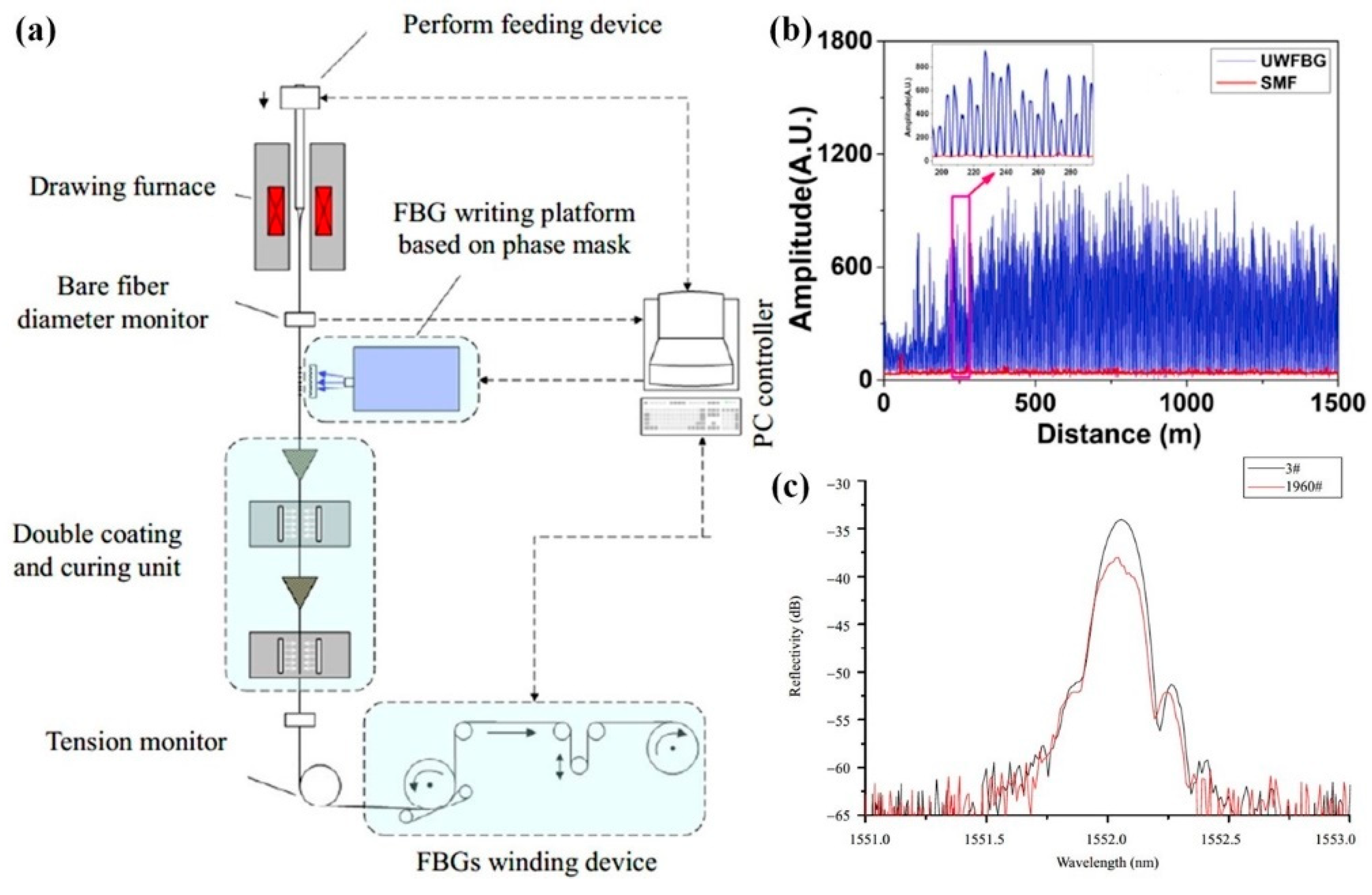
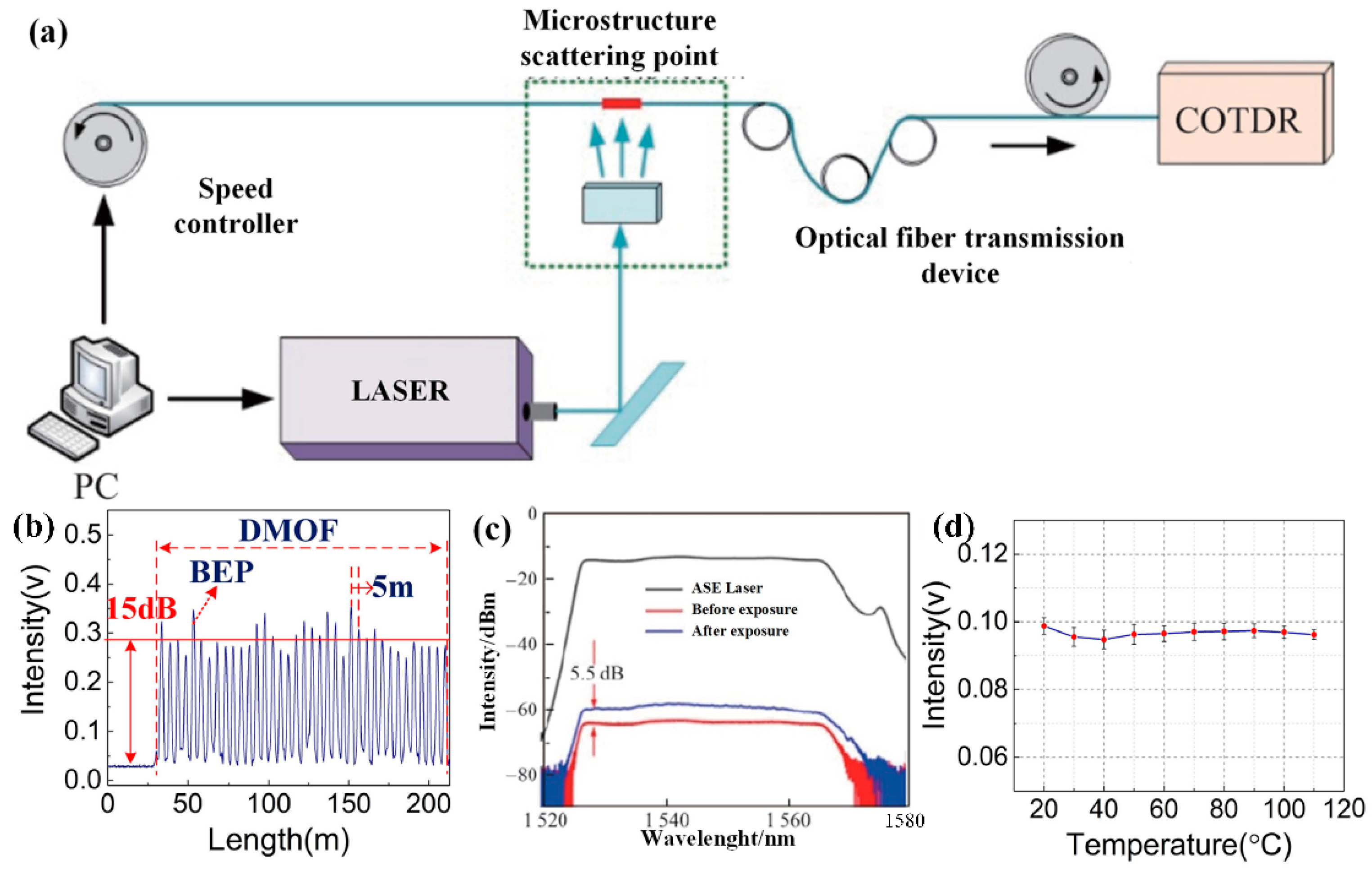

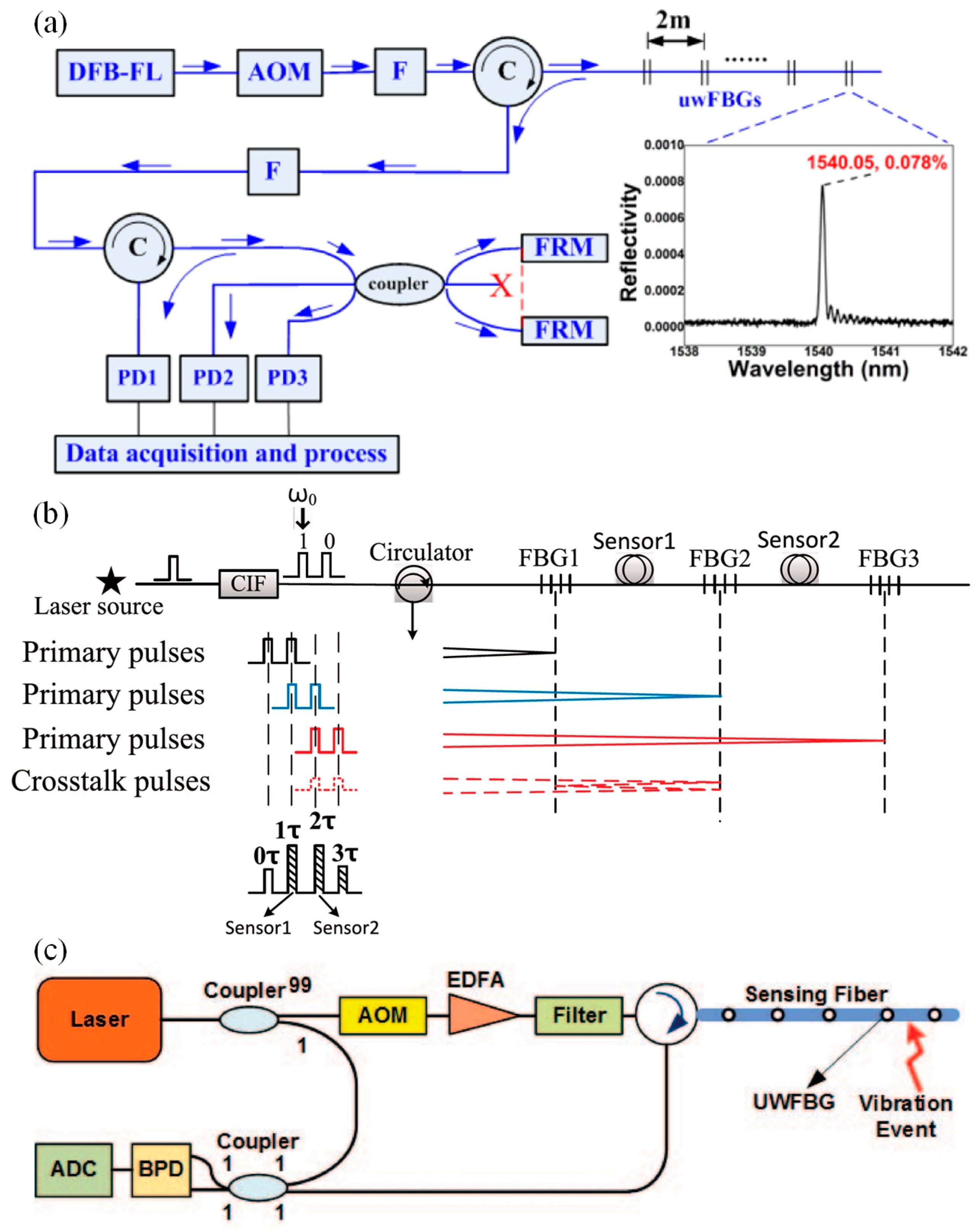
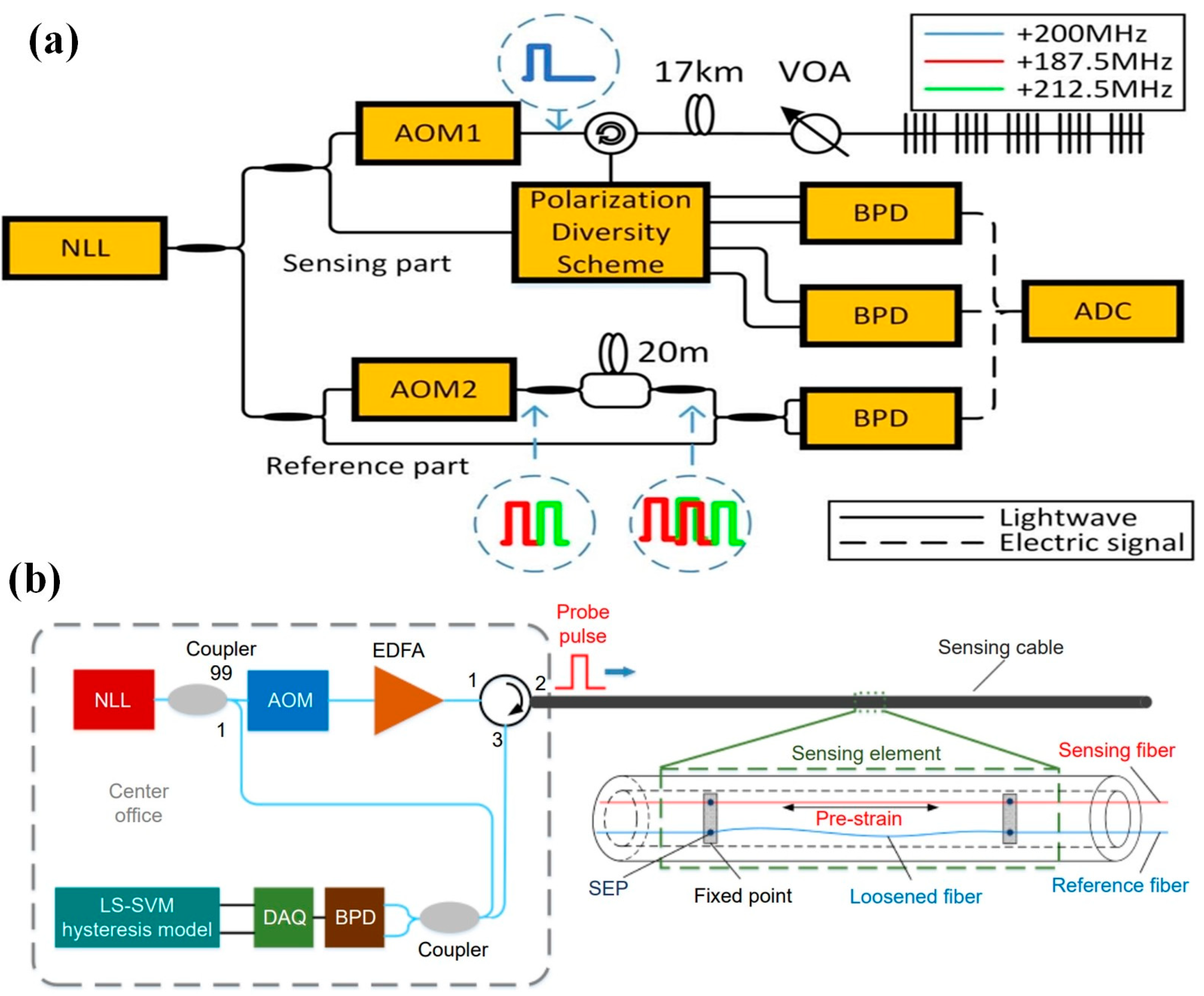
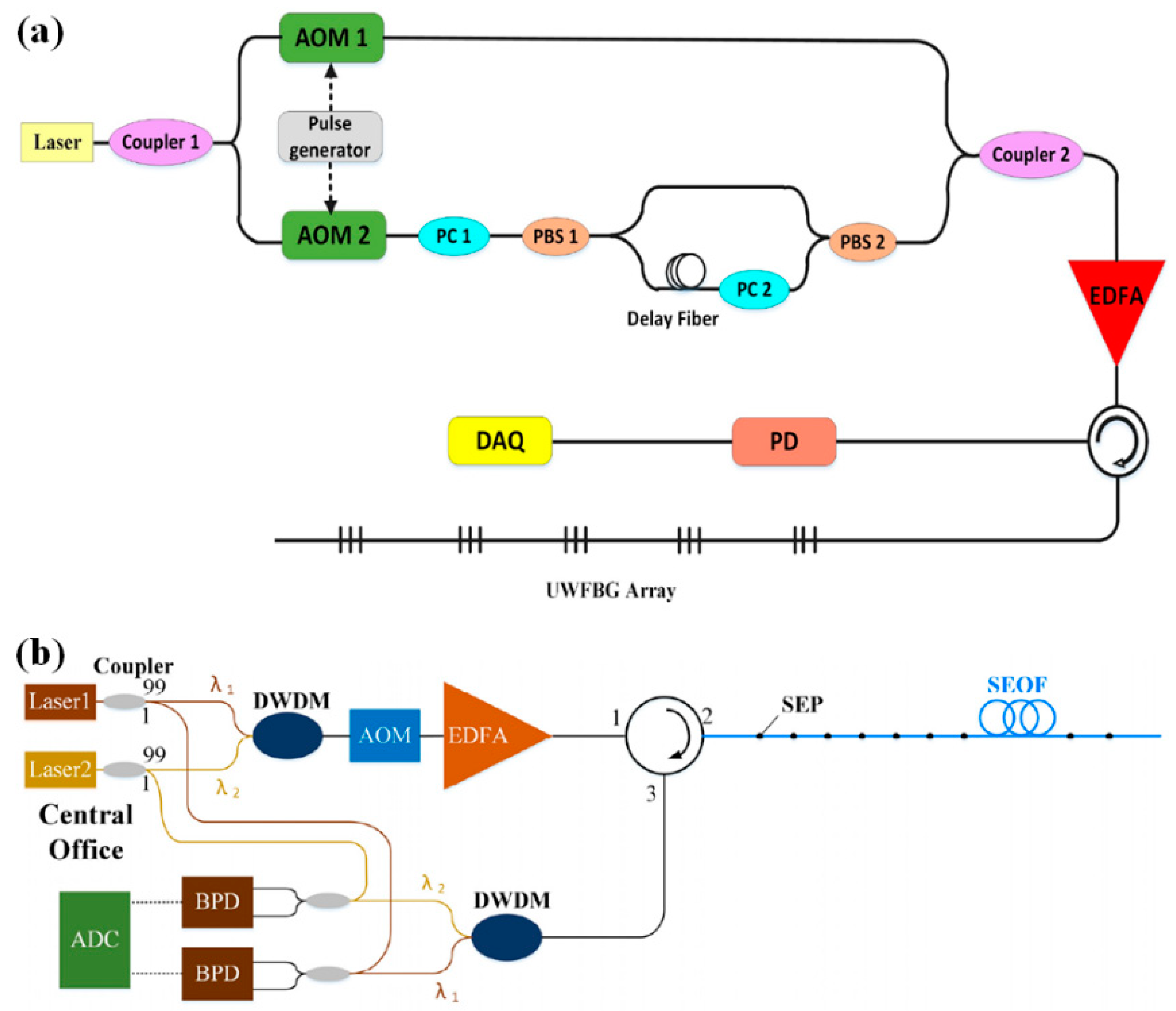

| Fiber Length | Spacing of SEP | Pulse Width | Spacing of ERSP d | Repeat Times |
|---|---|---|---|---|
| 13 m | 4 m | 20 ns | 1 um | 100 |
| Fabrication Method | SNR Enhancements | Sensing Distance | |
|---|---|---|---|
| CSE fiber | Continuously inscribe Bragg gratings [31,32,33,34] | 15 dB [31] | 1 km [31] |
| Highly doped fiber [35,36] | 14 dB [36] | 1.9 km [36] | |
| DSE fiber | UV exposure [41,42,43,47,51,52,53] | 5.5–21.1 dB [41,42,43,47,51] | 50 km [51] |
| Femtosecond laser inscription [40,44,45,54] | 13–15.8 dB [40,54] | 9.8 km [54] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Li, H.; Fan, C.; Yan, B.; Chen, J.; Yan, Z.; Sun, Q. Review of a Specialty Fiber for Distributed Acoustic Sensing Technology. Photonics 2022, 9, 277. https://doi.org/10.3390/photonics9050277
Sun Y, Li H, Fan C, Yan B, Chen J, Yan Z, Sun Q. Review of a Specialty Fiber for Distributed Acoustic Sensing Technology. Photonics. 2022; 9(5):277. https://doi.org/10.3390/photonics9050277
Chicago/Turabian StyleSun, Yixiang, Hao Li, Cunzheng Fan, Baoqiang Yan, Junfeng Chen, Zhijun Yan, and Qizhen Sun. 2022. "Review of a Specialty Fiber for Distributed Acoustic Sensing Technology" Photonics 9, no. 5: 277. https://doi.org/10.3390/photonics9050277
APA StyleSun, Y., Li, H., Fan, C., Yan, B., Chen, J., Yan, Z., & Sun, Q. (2022). Review of a Specialty Fiber for Distributed Acoustic Sensing Technology. Photonics, 9(5), 277. https://doi.org/10.3390/photonics9050277





