High-Efficiency Grating Couplers for Pixel-Level Flat-Top Beam Generation
Abstract
:1. Introduction
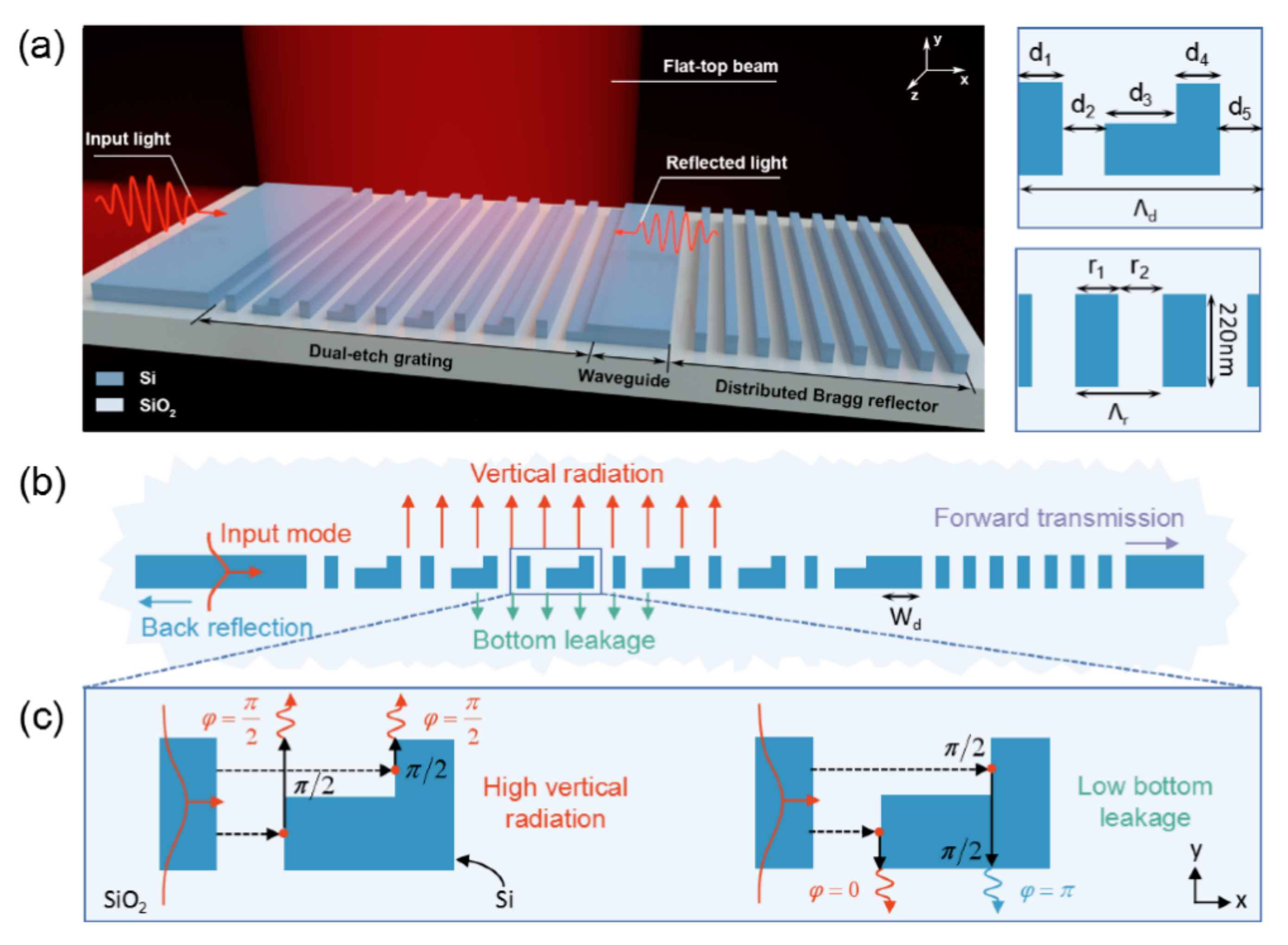
2. Design Concept and Methodology
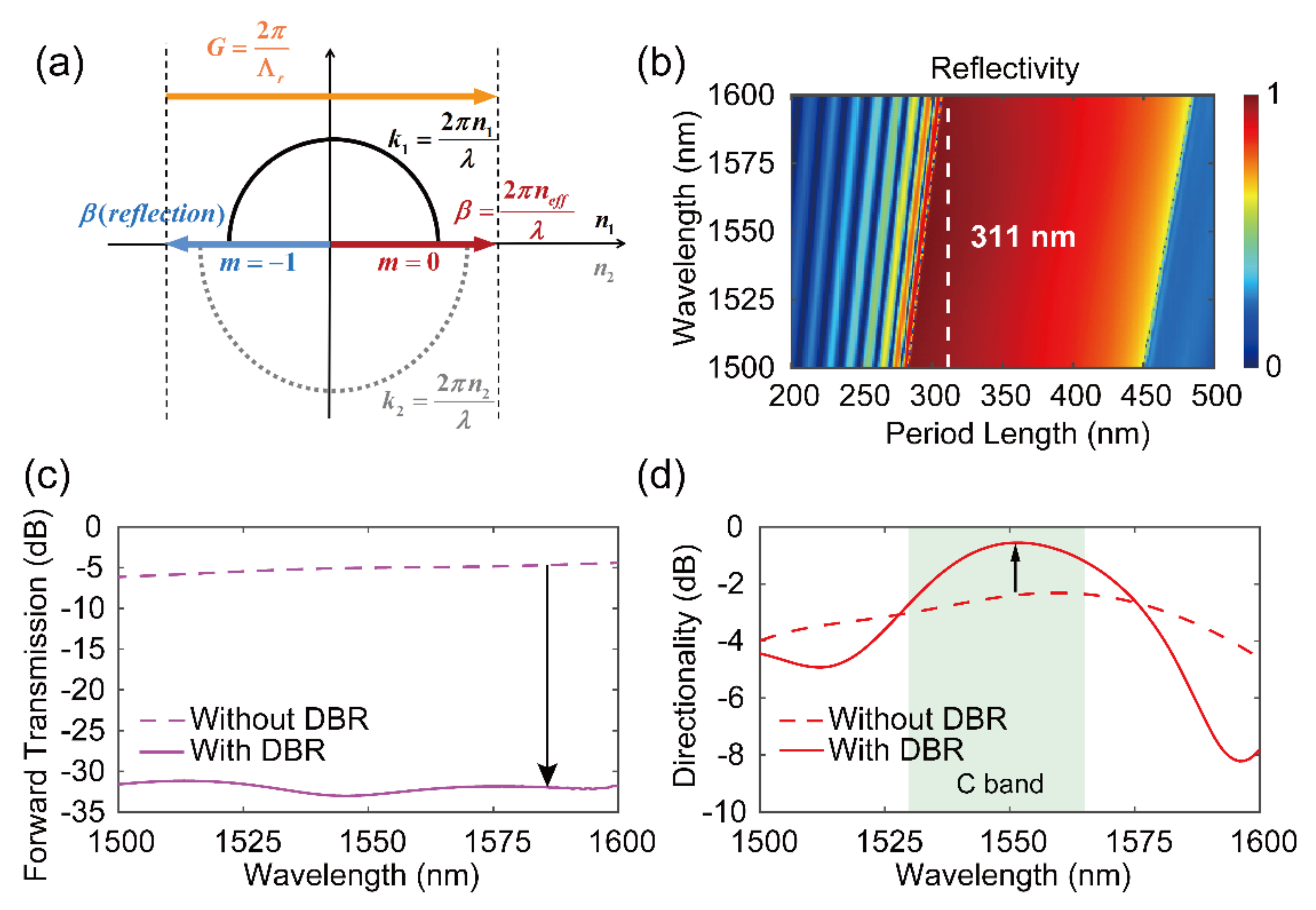
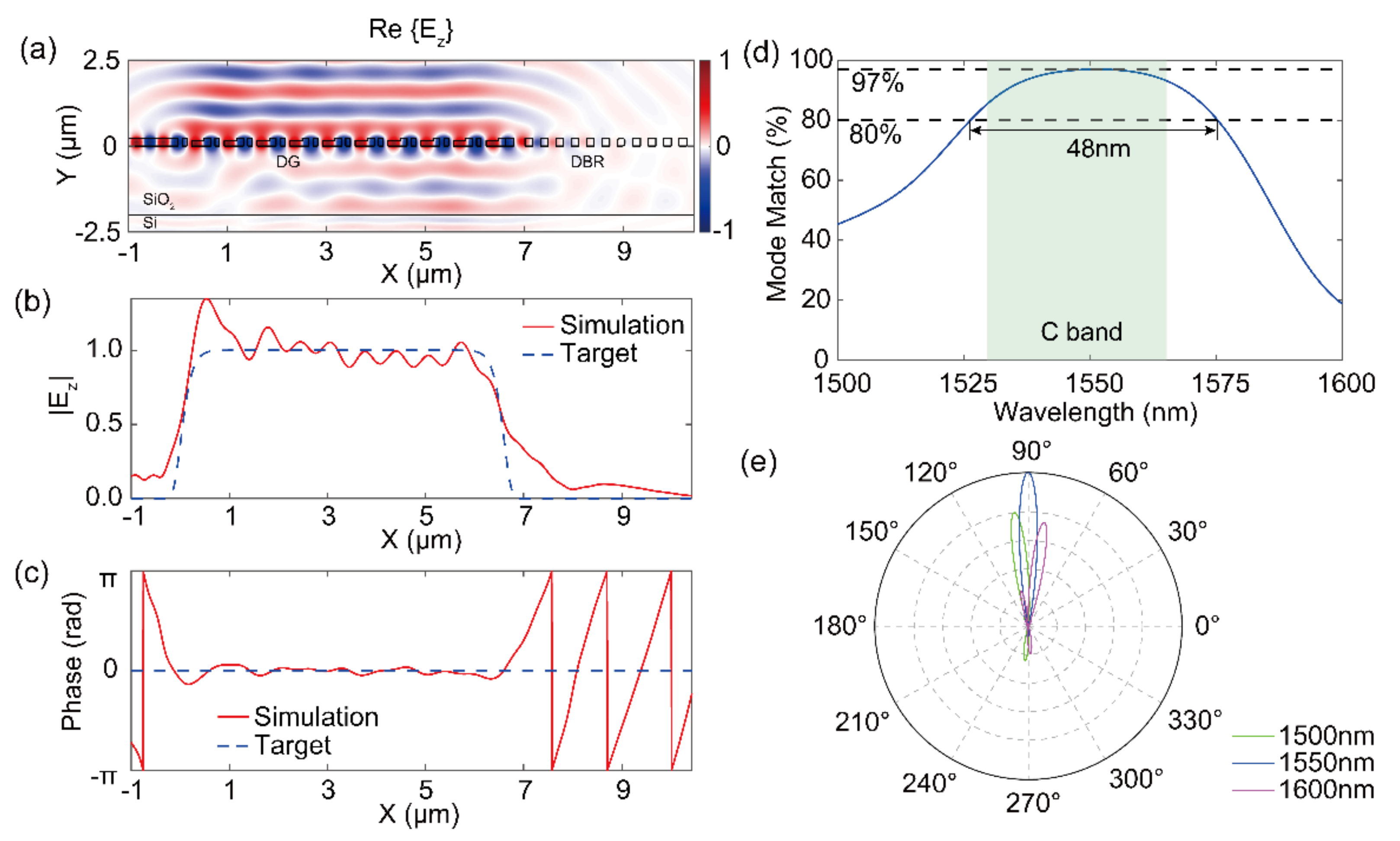
3. Results and Discussion
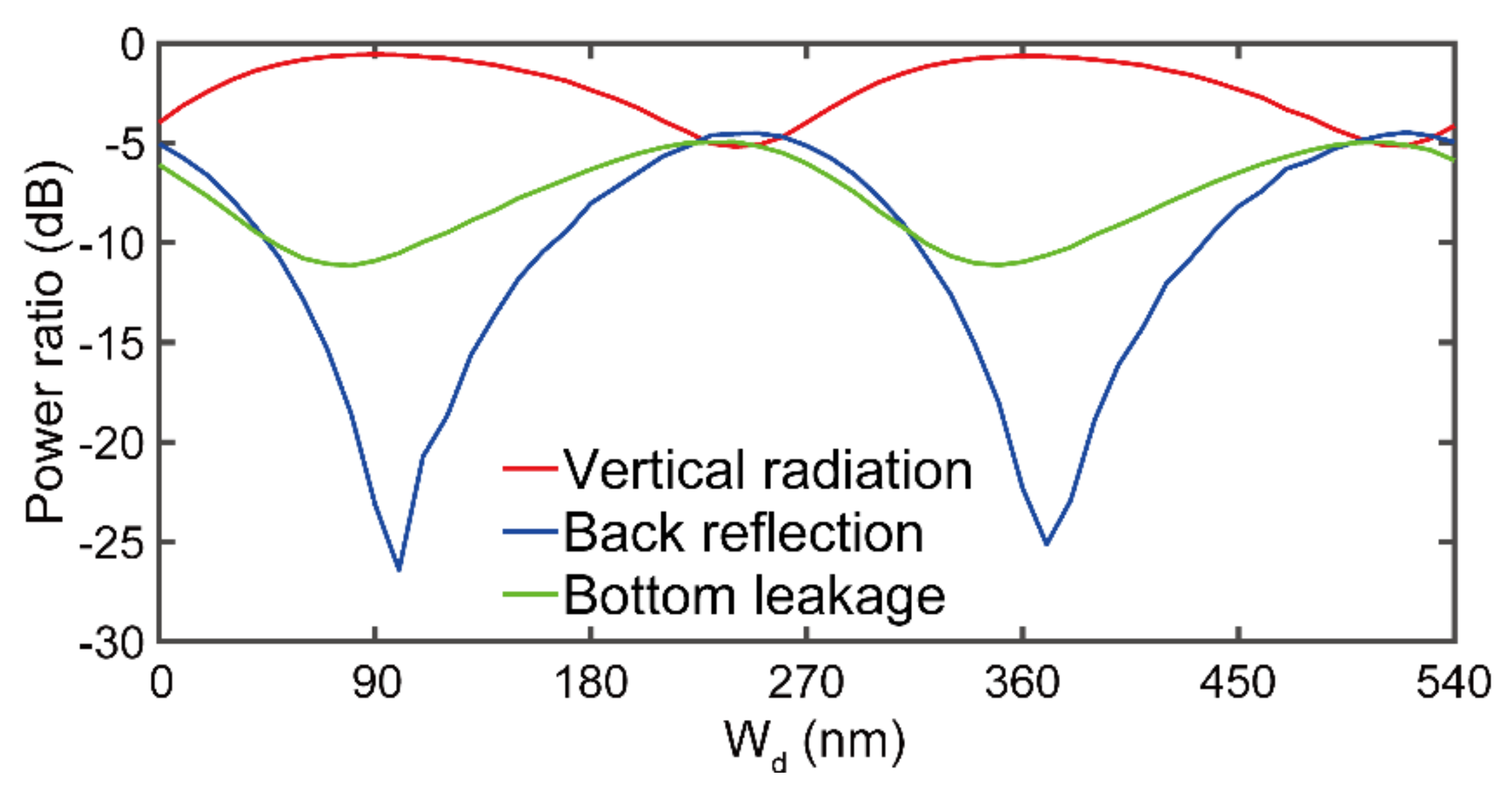
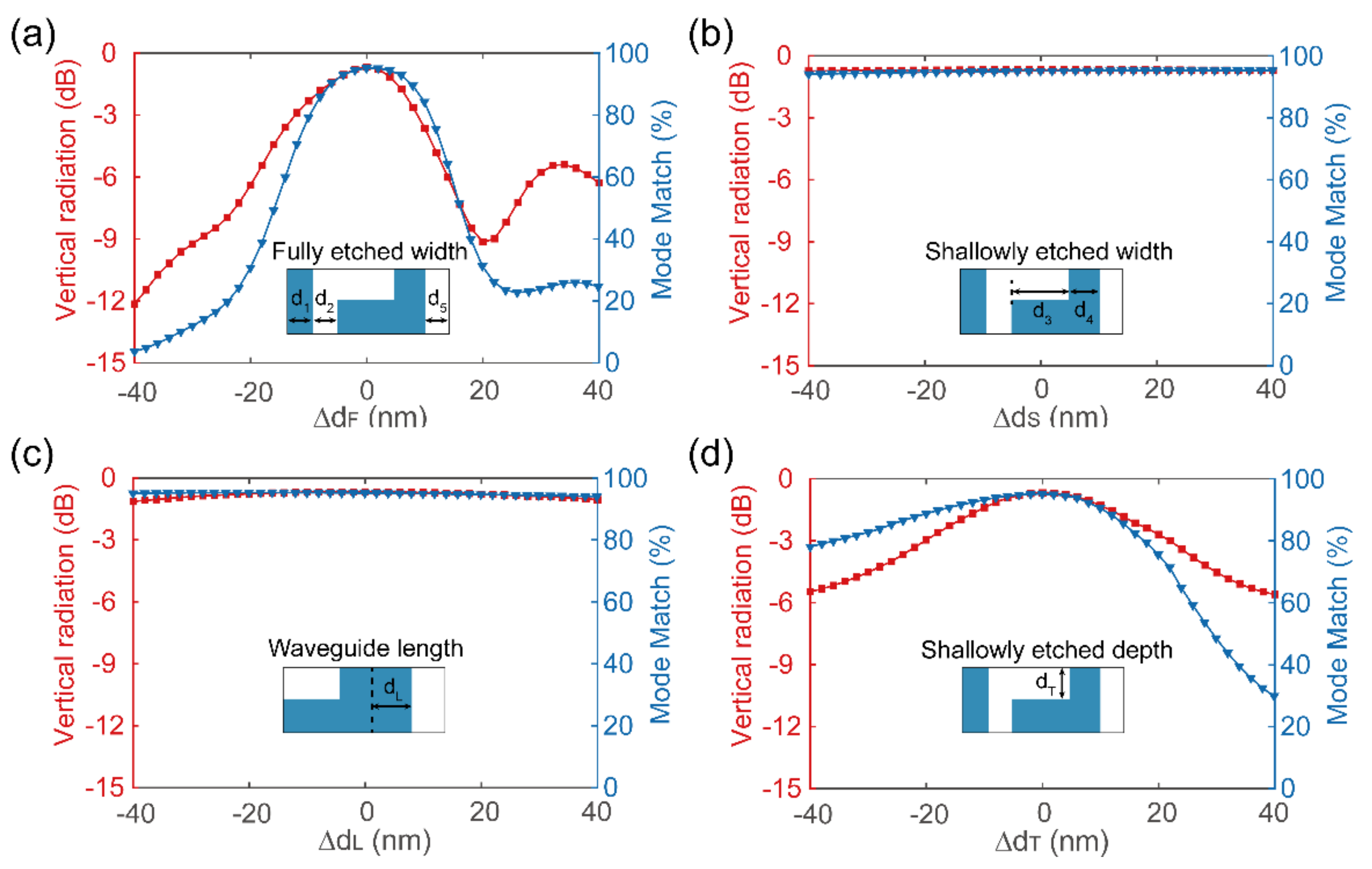
4. Fabrication Tolerance Analysis
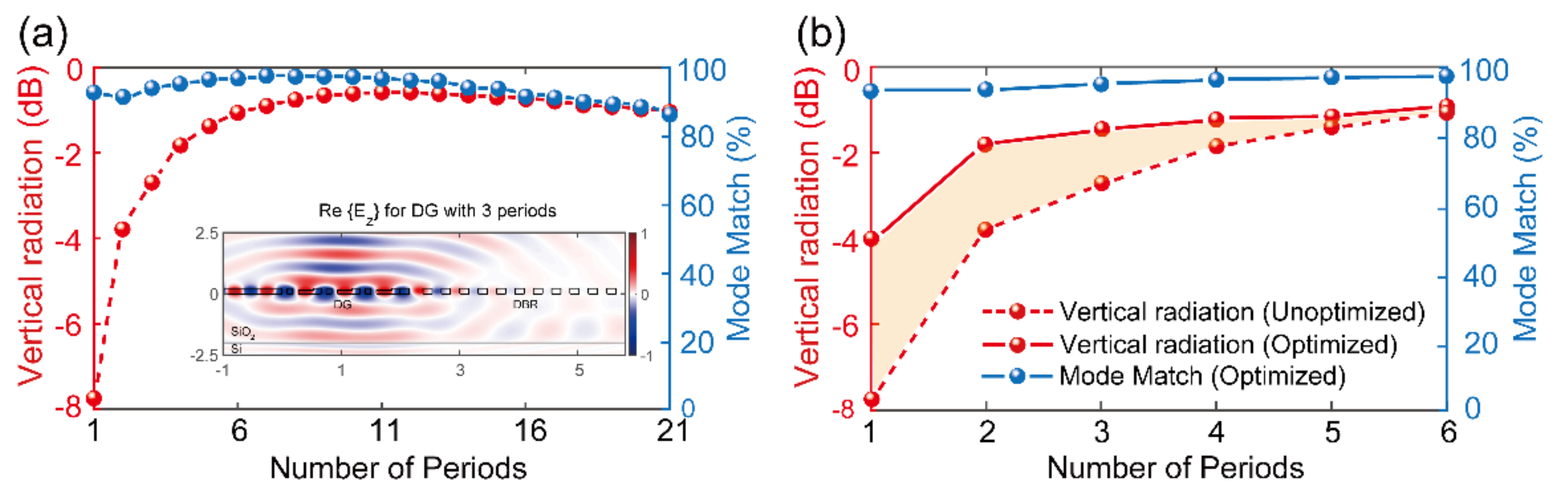
5. Grating Couplers with Different Lengths
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taillaert, D.; Bienstman, P.; Baets, R. Compact efficient broadband grating coupler for silicon-on-insulator waveguides. Opt. Lett. 2004, 29, 2749–2751. [Google Scholar] [CrossRef] [PubMed]
- Zaoui, W.S.; Kunze, A.; Vogel, W.; Berroth, M.; Butschke, J.; Letzkus, F.; Burghartz, J. Bridging the gap between optical fibers and silicon photonic integrated circuits. Opt. Express 2014, 22, 1277–1286. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Subbaraman, H.; Covey, J.; Kwong, D.; Hosseini, A.; Chen, R.T. Complementary metal–oxide–semiconductor compatible high efficiency subwavelength grating couplers for silicon integrated photonics. Appl. Phys. Lett. 2012, 101, 031109. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Liu, Y.; Galland, C.; Lim, A.E.-J.; Lo, G.-Q.; Baehr-Jones, T.; Hochberg, M. A High-Efficiency Nonuniform Grating Coupler Realized With 248-nm Optical Lithography. IEEE Photonics Technol. Lett. 2013, 25, 1358–1361. [Google Scholar] [CrossRef]
- Song, J.H.; Doany, F.E.; Medhin, A.K.; Dupuis, N.; Lee, B.G.; Libsch, F.R. Polarization-independent nonuniform grating couplers on silicon-on-insulator. Opt. Lett. 2015, 40, 3941–3944. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips. Photonics Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Melati, D.; Grinberg, Y.; Dezfouli, M.K.; Janz, S.; Cheben, P.; Schmid, J.H.; Sánchez-Postigo, A.; Xu, D.-X. Mapping the global design space of nanophotonic components using machine learning pattern recognition. Nat. Commun. 2019, 10, 4775. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Mao, S.; Li, Z.; Han, Y.; Fu, H.Y. Grating Couplers on Silicon Photonics: Design Principles, Emerging Trends and Practical Issues. Micromachines 2020, 11, 666. [Google Scholar] [CrossRef]
- Son, G.; Han, S.; Park, J.; Kwon, K.; Yu, K. High-efficiency broadband light coupling between optical fibers and photonic integrated circuits. Nanophotonics 2018, 7, 1845–1864. [Google Scholar] [CrossRef]
- Kim, S.; Westly, D.A.; Roxworthy, B.; Li, Q.; Yulaev, A.; Srinivasan, K.; Aksyuk, V.A. Photonic waveguide to free-space Gaussian beam extreme mode converter. Light. Sci. Appl. 2018, 7, 72. [Google Scholar] [CrossRef]
- Ropp, C.; Yulaev, A.; Westly, D.; Simelgor, G.; Aksyuk, V. Meta-grating outcouplers for optimized beam shaping in the visible. Opt. Express 2021, 29, 14789–14798. [Google Scholar] [CrossRef]
- Romero, J.; Giovannini, D.; Franke-Arnold, S.; Barnett, S.; Padgett, M. Increasing the dimension in high-dimensional two-photon orbital angular momentum entanglement. Phys. Rev. A 2012, 86, 012334. [Google Scholar] [CrossRef] [Green Version]
- Ropp, C.; Yulaev, A.; Zhu, W.; Westly, D.A.; Simelgor, G.; Agrawal, A.; Papp, S.; Aksyuk, V. Multi-Beam Integration for On-chip Quantum Devices. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 9 May 2021; p. STh4A.7. [Google Scholar]
- Roelkens, G.; van Thourhout, D.; Baets, R. High efficiency Silicon-on-Insulator grating coupler based on a poly-Silicon overlay. Opt. Express 2006, 14, 11622–11630. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vermeulen, D.; Selvaraja, S.K.; Verheyen, P.; Lepage, G.; Bogaerts, W.; Absil, P.; van Thourhout, D.; Roelkens, G. High-efficiency fiber-to-chip grating couplers realized using an advanced CMOS-compatible Silicon-On-Insulator platform. Opt. Express 2010, 18, 18278–18283. [Google Scholar] [CrossRef] [PubMed]
- Romero-García, S.; Merget, F.; Zhong, F.; Finkelstein, H.; Witzens, J. Visible wavelength silicon nitride focusing grating coupler with AlCu/TiN reflector. Opt. Lett. 2013, 38, 2521–2523. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Nong, Z.; Gao, S.; Huang, H.; Zhu, Y.; Liu, L.; Zhou, L.; Xu, J.; Liu, L.; Yu, S.; et al. Low-loss two-dimensional silicon photonic grating coupler with a backside metal mirror. Opt. Lett. 2018, 43, 474–477. [Google Scholar] [CrossRef]
- Zaoui, W.S.; Kunze, A.; Vogel, W.; Berroth, M. CMOS-Compatible Polarization Splitting Grating Couplers with a Backside Metal Mirror. IEEE Photonics Technol. Lett. 2013, 25, 1395–1397. [Google Scholar] [CrossRef]
- Schrauwen, J.; van Laere, F.; van Thourhout, D.; Baets, R. Focused-Ion-Beam Fabrication of Slanted Grating Couplers in Silicon-on-Insulator Waveguides. IEEE Photonics Technol. Lett. 2007, 19, 816–818. [Google Scholar] [CrossRef] [Green Version]
- Bin, W.; Jianhua, J.; Nordin, G.P. Embedded slanted grating for vertical coupling between fibers and silicon-on-insulator planar waveguides. IEEE Photonics Technol. Lett. 2005, 17, 1884–1886. [Google Scholar] [CrossRef]
- Michaels, A.; Yablonovitch, E. Inverse design of near unity efficiency perfectly vertical grating couplers. Opt. Express 2018, 26, 4766–4779. [Google Scholar] [CrossRef]
- Dai, M.; Ma, L.; Xu, Y.; Lu, M.; Liu, X.; Chen, Y. Highly efficient and perfectly vertical chip-to-fiber dual-layer grating coupler. Opt. Express 2015, 23, 1691–1698. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Trivedi, R.; Sapra, N.V.; Piggott, A.Y.; Vercruysse, D.; Vuckovic, J. Fully-automated optimization of grating couplers. Opt. Express 2018, 26, 4023–4034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mossberg, T.W.; Greiner, C.; Iazikov, D. Interferometric amplitude apodization of integrated gratings. Opt. Express 2005, 13, 2419–2426. [Google Scholar] [CrossRef] [Green Version]
- Marchetti, R.; Lacava, C.; Khokhar, A.; Chen, X.; Cristiani, I.; Richardson, D.; Reed, G.T.; Petropoulos, P.; Minzioni, P. High-efficiency grating-couplers: Demonstration of a new design strategy. Sci. Rep. 2017, 7, 16670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taillaert, D.; Bogaerts, W.; Bienstman, P.; Krauss, T.; van Daele, P.; Moerman, I.; Verstuyft, S.; de Mesel, K.; Baets, R. An out-of-plane grating coupler for efficient butt-coupling between compact planar waveguides and single-mode fibers. IEEE J. Quantum Electron. 2002, 38, 949–955. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Ramos, C.; Cheben, P.; Ortega-Moñux, A.; Schmid, J.H.; Xu, D.-X.; Molina-Fernández, I. Fiber-chip grating coupler based on interleaved trenches with directionality exceeding 95. Opt. Lett. 2014, 39, 5351–5354. [Google Scholar] [CrossRef] [PubMed]
- Benedikovic, D.; Alonso-Ramos, C.; Guerber, S.; le Roux, X.; Cheben, P.; Dupré, C.; Szelag, B.; Fowler, D.; Cassan, E.; Marris-Morini, D.; et al. Sub-decibel silicon grating couplers based on L-shaped waveguides and engineered subwavelength metamaterials. Opt. Express 2019, 27, 26239–26250. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Thomson, D.J.; Crudginton, L.; Khokhar, A.Z.; Reed, G.T. Dual-etch apodised grating couplers for efficient fibre-chip coupling near 1310 nm wavelength. Opt. Express 2017, 25, 17864–17871. [Google Scholar] [CrossRef]
- Watanabe, T.; Fedoryshyn, Y.; Leuthold, J. 2-D Grating Couplers for Vertical Fiber Coupling in Two Polarizations. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Watanabe, T.; Ayata, M.; Koch, U.; Fedoryshyn, Y.; Leuthold, J. Perpendicular Grating Coupler Based on a Blazed Antiback-Reflection Structure. J. Light. Technol. 2017, 35, 4663–4669. [Google Scholar] [CrossRef]
- Zhou, W.; Cheng, Z.; Chen, X.; Xu, K.; Sun, X.; Tsang, H.K. Subwavelength Engineering in Silicon Photonic Devices. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–13. [Google Scholar] [CrossRef]
- Benedikovic, D.; Alonso-Ramos, C.; Galacho, D.P.; Guerber, S.; Vakarin, V.; Marcaud, G.; le Roux, X.; Cassan, E.; Marris-Morini, D.; Cheben, P.; et al. L-shaped fiber-chip grating couplers with high directionality and low reflectivity fabricated with deep-UV lithography. Opt. Lett. 2017, 42, 3439–3442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dezfouli, M.K.; Grinberg, Y.; Melati, D.; Cheben, P.; Schmid, J.H.; Sánchez-Postigo, A.; Ortega-Moñux, A.; Wangüemert-Pérez, J.G.; Cheriton, R.; Janz, S.; et al. Perfectly vertical surface grating couplers using subwavelength engineering for increased feature sizes. Opt. Lett. 2020, 45, 3701–3704. [Google Scholar] [CrossRef] [PubMed]
- Halir, R.; Cheben, P.; Schmid, J.H.; Ma, R.; Bedard, D.; Janz, S.; Xu, D.-X.; Densmore, A.; Lapointe, J.; Molina-Fernández, Í. Continuously apodized fiber-to-chip surface grating coupler with refractive index engineered subwavelength structure. Opt. Lett. 2010, 35, 3243–3245. [Google Scholar] [CrossRef] [PubMed]
- Cheben, P.; Halir, R.; Schmid, J.H.; Atwater, H.A.; Smith, D.R. Subwavelength integrated photonics. Nature 2018, 560, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Khajavi, S.; Melati, D.; Cheben, P.; Schmid, J.H.; Liu, Q.; Xu, D.X.; Ye, W.N. Compact and highly-efficient broadband surface grating antenna on a silicon platform. Opt. Express 2021, 29, 7003–7014. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, C.; Fung, C.K.Y.; Lo, S.M.G.; Tsang, H.K. Apodized Waveguide Grating Couplers for Efficient Coupling to Optical Fibers. IEEE Photonics Technol. Lett. 2010, 22, 1156–1158. [Google Scholar] [CrossRef]
- Khaw, I.; Croop, B.; Tang, J.; Möhl, A.; Fuchs, U.; Han, K.Y. Flat-field illumination for quantitative fluorescence imaging. Opt. Express 2018, 26, 15276–15288. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef]
- Pita, J.L.; Aldaya, I.; Dainese, P.; Hernandez-Figueroa, H.E.; Gabrielli, L.H. Design of a compact CMOS-compatible photonic antenna by topological optimization. Opt. Express 2018, 26, 2435–2442. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Wang, J.; Xie, W.; Tian, B.; Li, Y.; Brainis, E.; Jiao, Y.; van Thourhout, D. Ultra-compact silicon nitride grating coupler for microscopy systems. Opt. Express 2017, 25, 33297–33304. [Google Scholar] [CrossRef] [Green Version]
- Luxmoore, I.J.; Wasley, N.A.; Ramsay, A.J.; Thijssen, A.C.T.; Oulton, R.; Hugues, M.; Kasture, S.; Achanta, V.G.; Fox, A.M.; Skolnick, M.S. Interfacing spins in an InGaAs quantum dot to a semiconductor waveguide circuit using emitted photons. Phys. Rev. Lett. 2013, 110, 037402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shimizu, W.; Nagai, N.; Kohno, K.; Hirakawa, K.; Nomura, M. Waveguide coupled air-slot photonic crystal nanocavity for optomechanics. Opt. Express 2013, 21, 21961–21969. [Google Scholar] [CrossRef] [PubMed]
- Faraon, A.; Fushman, I.; Englund, D.; Stoltz, N.G.; Petroff, P.; Vuckovic, J. Dipole induced transparency in waveguide coupled photonic crystal cavities. Opt. Express 2008, 16, 12154–12162. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Postigo, A.; Ortega-Moñux, A.; Pereira-Martín, D.; Molina-Fernández, Í.; Halir, R.; Cheben, P.; Penadés, J.S.; Nedeljkovic, M.; Mashanovich, G.Z.; Wangüemert-Pérez, J.G. Design of a suspended germanium micro-antenna for efficient fiber-chip coupling in the long-wavelength mid-infrared range. Opt. Express 2019, 27, 22302–22315. [Google Scholar] [CrossRef]
- Douglass, K.M.; Sieben, C.; Archetti, A.; Lambert, A.; Manley, S. Super-resolution imaging of multiple cells by optimized flat-field epi-illumination. Nat. Photonics 2016, 10, 705–708. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Miao, C.; Zhang, M.; Zhou, W.; Tang, C.; Li, E. High-performance binary blazed grating coupler used in silicon-based hybrid photodetector integration. Opt. Eng. 2014, 53, 097106. [Google Scholar] [CrossRef] [Green Version]
- Roelkens, G.; Brouckaert, J.; Taillaert, D.; Dumon, P.; Bogaerts, W.; van Thourhout, D.; Baets, R.; Nötzel, R.; Smit, M. Integration of InP/InGaAsP photodetectors onto silicon-on-insulator waveguide circuits. Opt. Express 2005, 13, 10102–10108. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Y.; Yu, Y.; Zhang, Y.; Zhou, D.; Zhang, X. Integrated high-power germanium photodetectors assisted by light field manipulation. Opt. Lett. 2019, 44, 3338–3341. [Google Scholar] [CrossRef]
- Benedikovic, D.; Alonso-Ramos, C.; Cheben, P.; Schmid, J.H.; Wang, S.; Xu, D.-X.; Lapointe, J.; Janz, S.; Halir, R.; Ortega-Moñux, A.; et al. High-directionality fiber-chip grating coupler with interleaved trenches and subwavelength index-matching structure. Opt. Lett. 2015, 40, 4190–4193. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Flueckiger, J.; Yun, H.; Shi, W.; Bojko, R.; Jaeger, N.A.F.; Chrostowski, L. Focusing sub-wavelength grating couplers with low back reflections for rapid prototyping of silicon photonic circuits. Opt. Express 2014, 22, 20652–20662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flory, C. Analysis of directional grating-coupled radiation in waveguide structures. IEEE J. Quantum Electron. 2004, 40, 949–957. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Chen, B.; Li, Y.; Zhang, L.; Li, Y.; Liu, X.; Tao, M.; Hou, Y.; Tang, H.; Zhi, Z.; et al. Unidirectional large-scale waveguide grating with uniform radiation for optical phased array. Opt. Express 2021, 29, 20995–21010. [Google Scholar] [CrossRef]
- Duan, F.; Zhu, W.-L.; Han, Y.; Ju, B.-F.; Beaucamp, A.; Yanjun, H. Chromatically multi-focal optics based on micro-lens array design. Opt. Express 2020, 28, 24123. [Google Scholar] [CrossRef]
- Digani, J.; Hon, P.W.; Davoyan, A.R. Framework for Expediting Discovery of Optimal Solutions with Blackbox Algorithms in Non-Topology Photonic Inverse Design. ACS Photonics 2022, 9, 432–442. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.-T.; Zhuang, Z.-P.; Fan, Z.-B.; Chen, X.-D.; Dong, J.-W. High-Efficiency Grating Couplers for Pixel-Level Flat-Top Beam Generation. Photonics 2022, 9, 207. https://doi.org/10.3390/photonics9040207
Tian Z-T, Zhuang Z-P, Fan Z-B, Chen X-D, Dong J-W. High-Efficiency Grating Couplers for Pixel-Level Flat-Top Beam Generation. Photonics. 2022; 9(4):207. https://doi.org/10.3390/photonics9040207
Chicago/Turabian StyleTian, Zhong-Tao, Ze-Peng Zhuang, Zhi-Bin Fan, Xiao-Dong Chen, and Jian-Wen Dong. 2022. "High-Efficiency Grating Couplers for Pixel-Level Flat-Top Beam Generation" Photonics 9, no. 4: 207. https://doi.org/10.3390/photonics9040207
APA StyleTian, Z.-T., Zhuang, Z.-P., Fan, Z.-B., Chen, X.-D., & Dong, J.-W. (2022). High-Efficiency Grating Couplers for Pixel-Level Flat-Top Beam Generation. Photonics, 9(4), 207. https://doi.org/10.3390/photonics9040207




