Demonstration of Performance Improvement in Multi-User NOMA VLC System Using Joint Transceiver Optimization
Abstract
:1. Introduction
2. System Model
3. Performance Analysis and Optimization under SC-SIC-A Scheme
3.1. Derivation of BER
3.1.1. BER Expression of User 1
3.1.2. BER Expression of User 2
3.1.3. BER Expression of User k
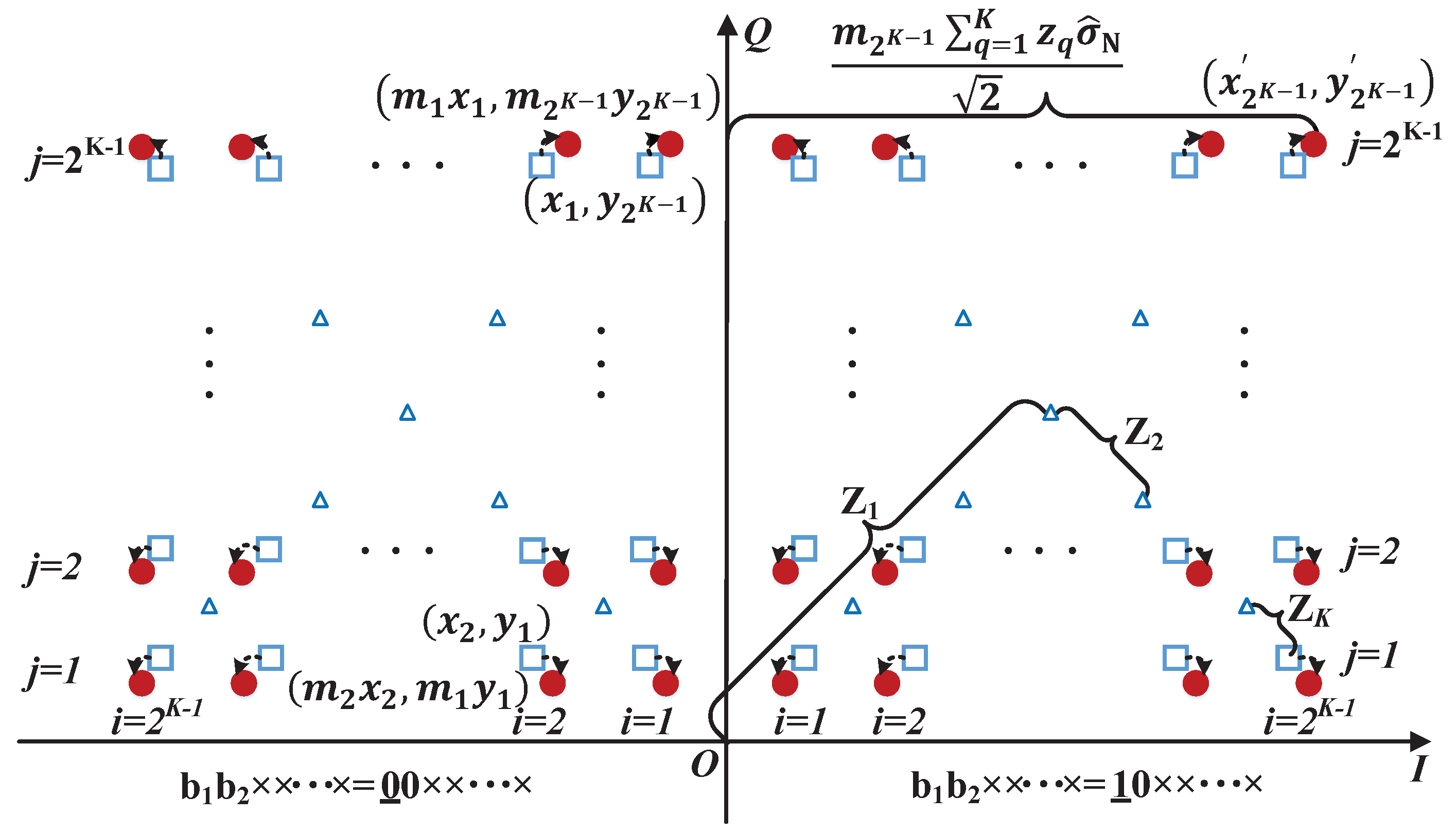
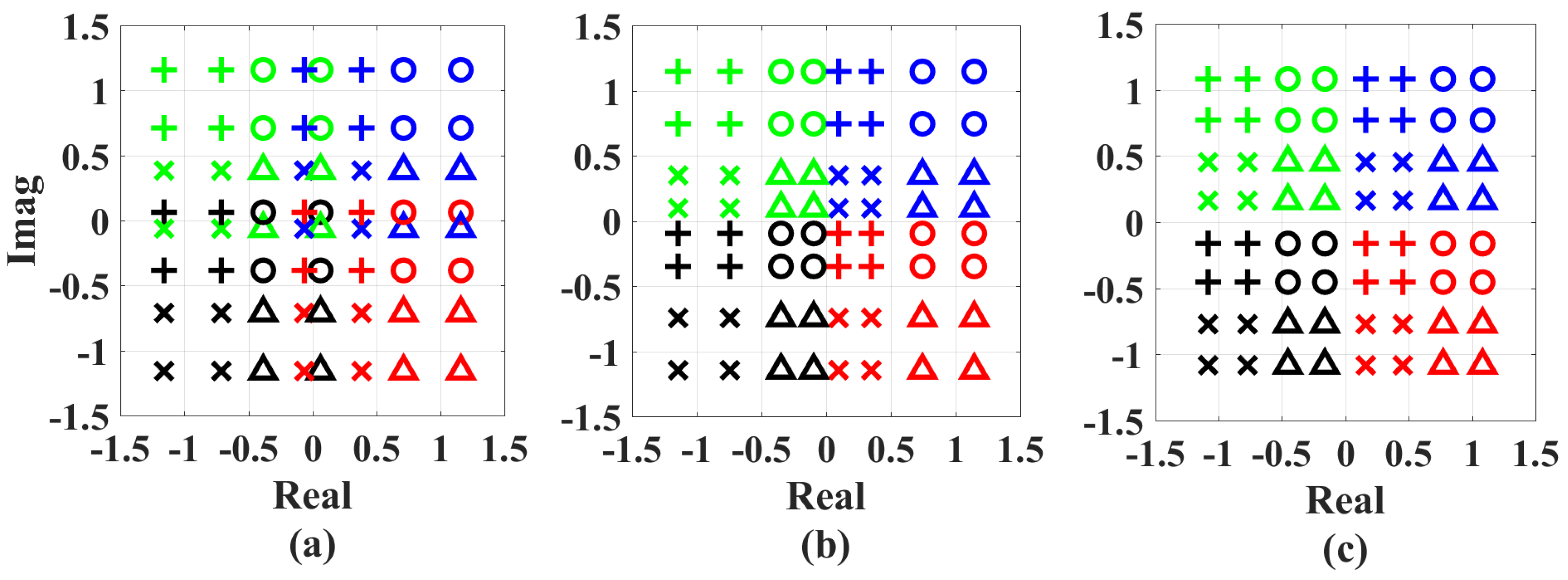
3.2. NOMA Triangle Regarding the Terms of Q-Function
3.3. Optimization of BER Performance
3.4. Derivation of Capacity
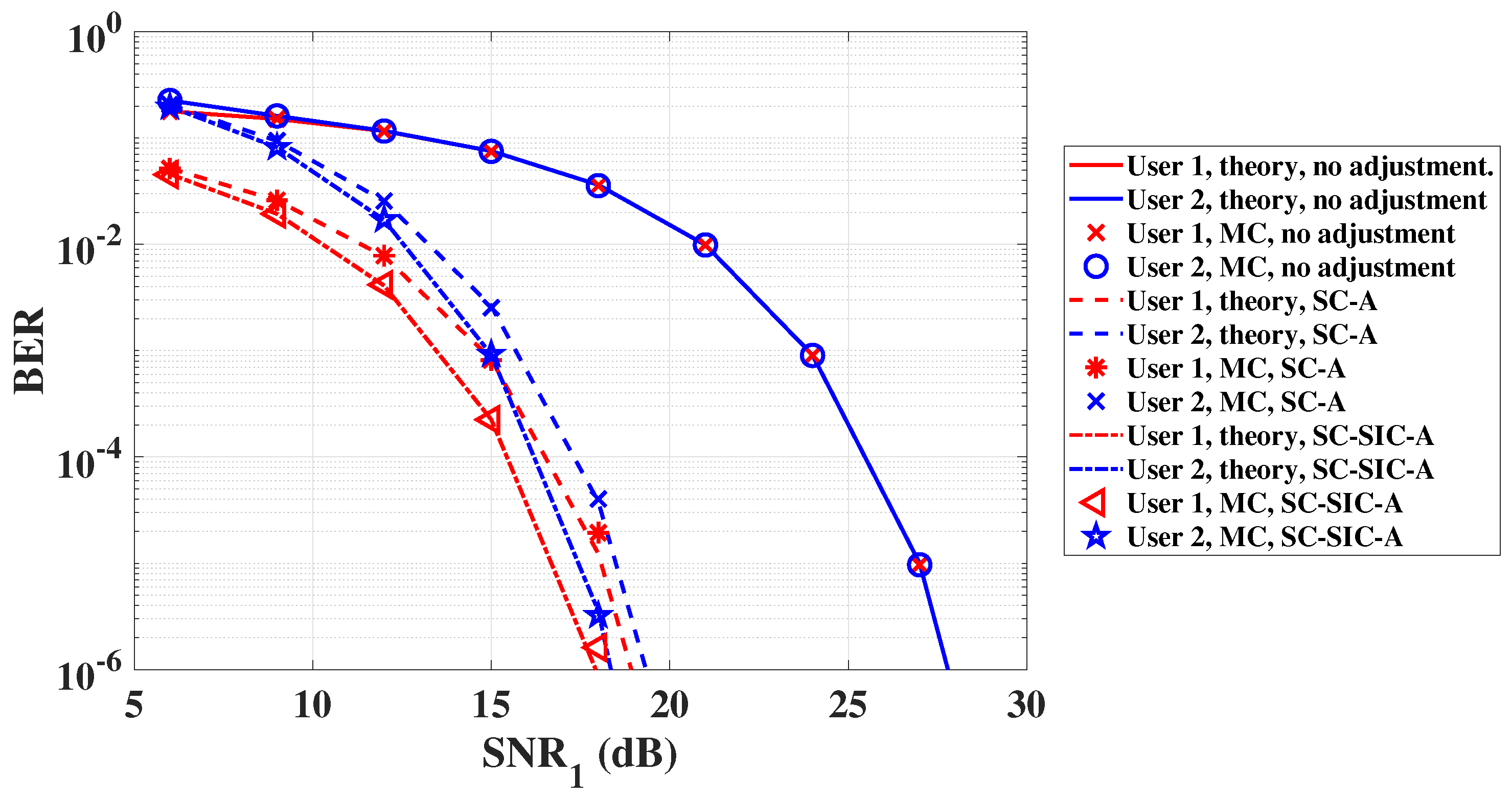
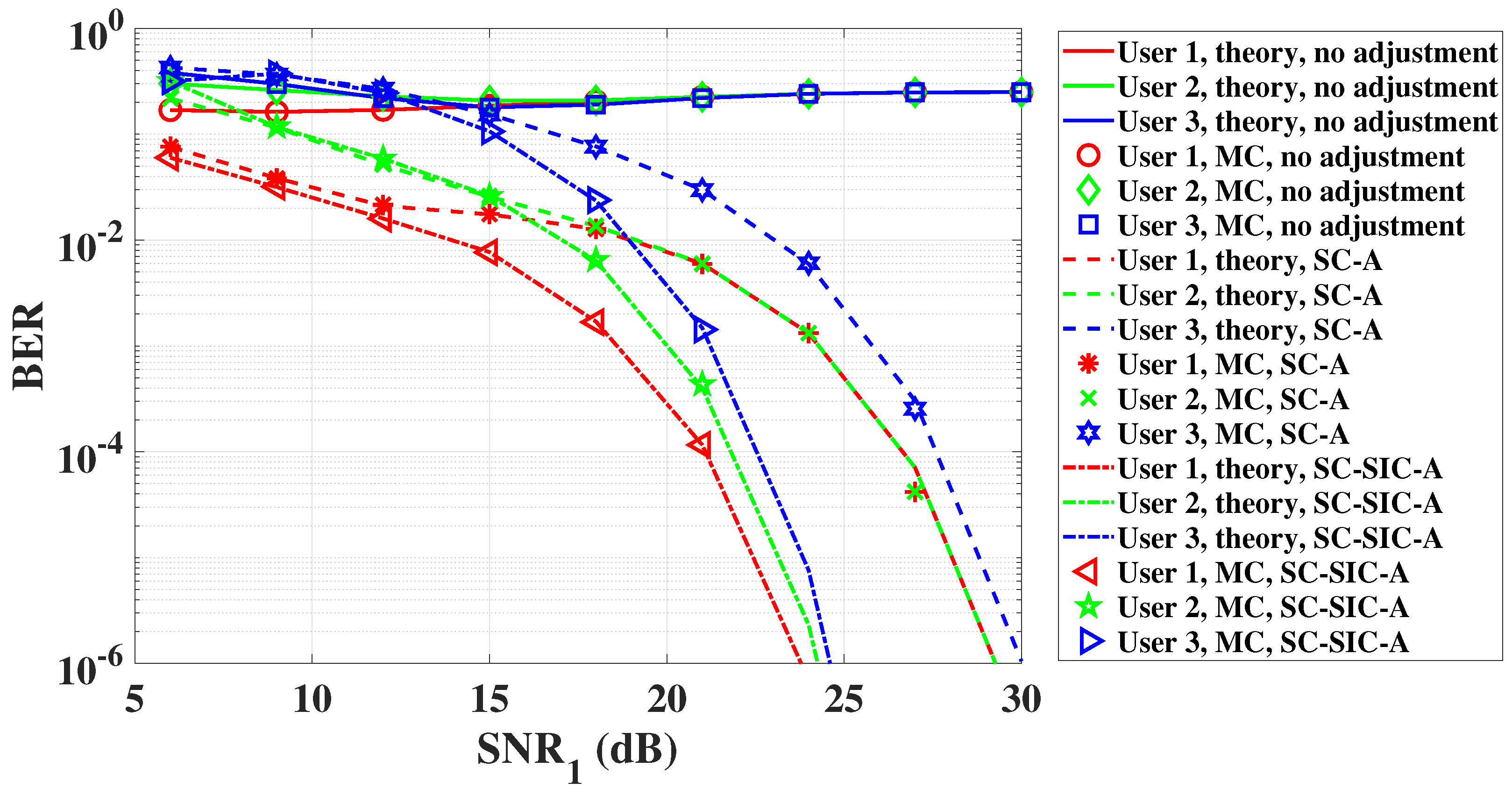
4. Results and Discussion
4.1. Benchmark Schemes
4.2. Theoretical Analysis and MC Simulation
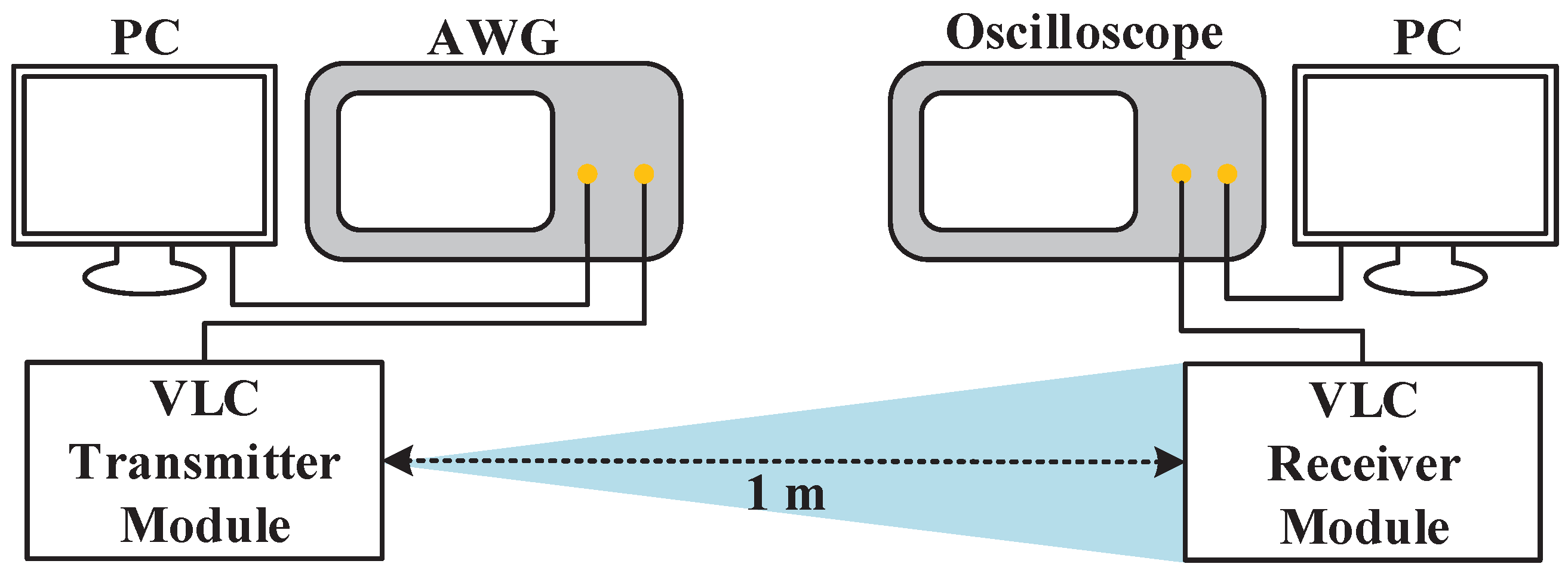
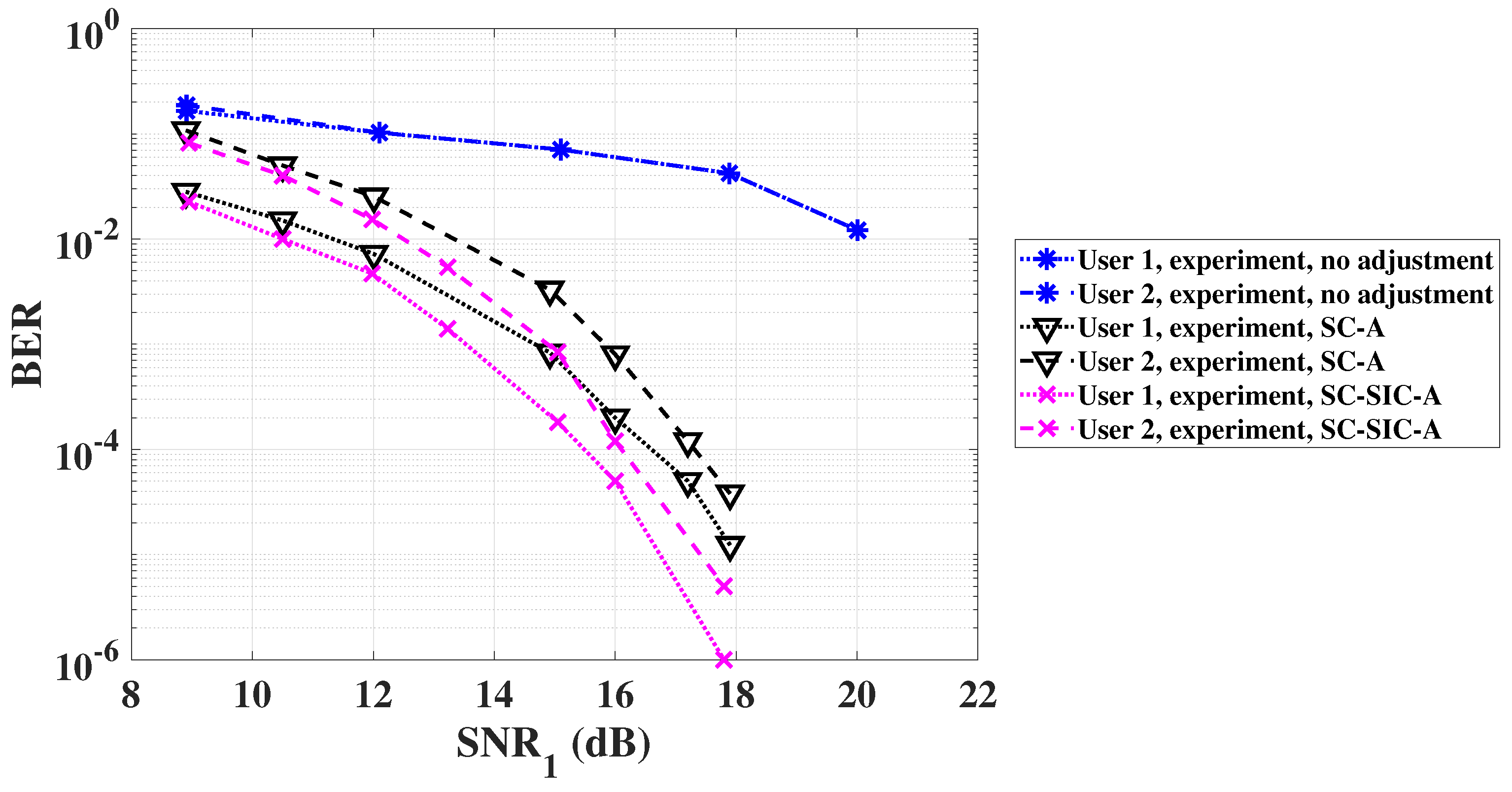
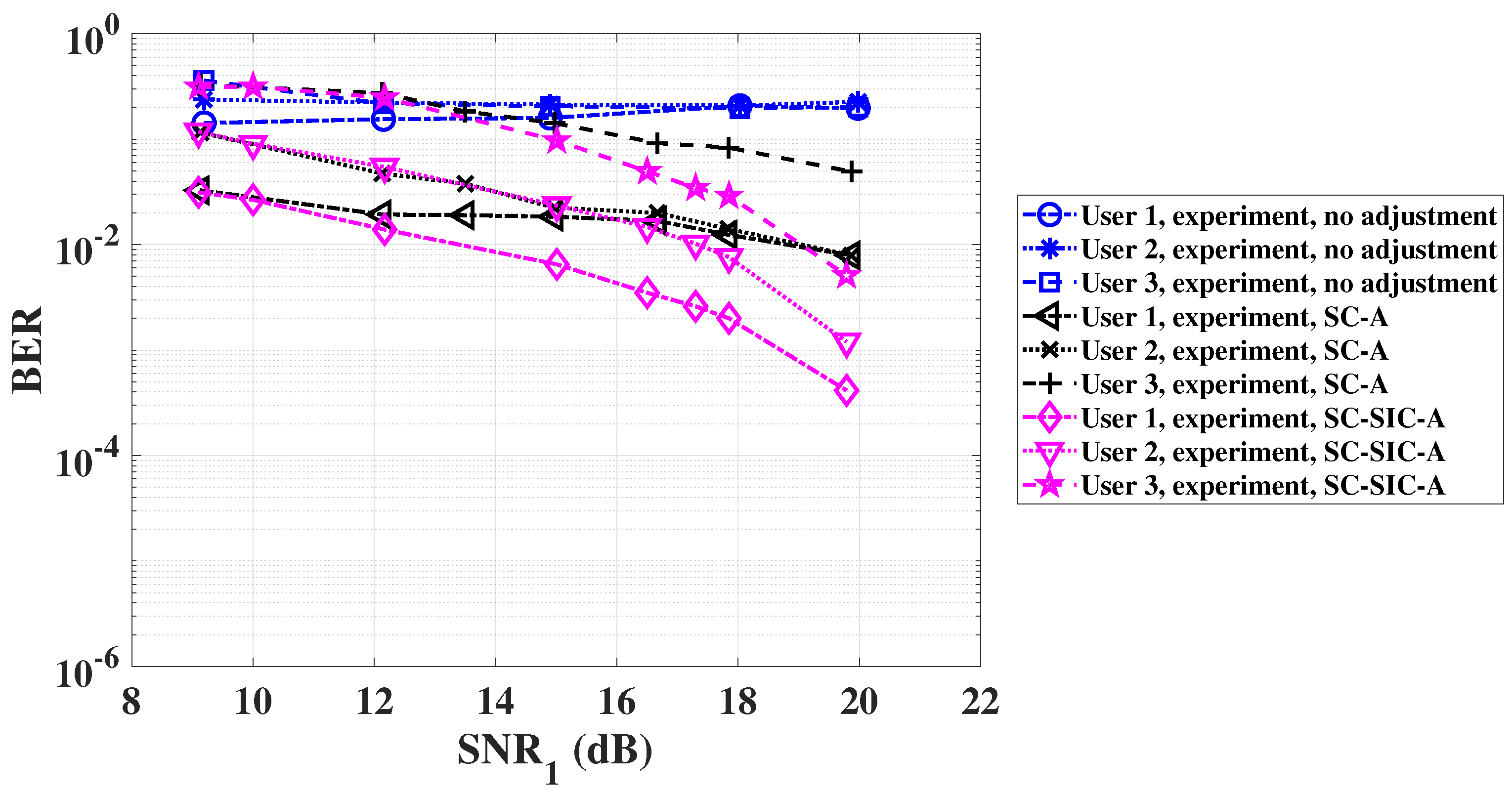
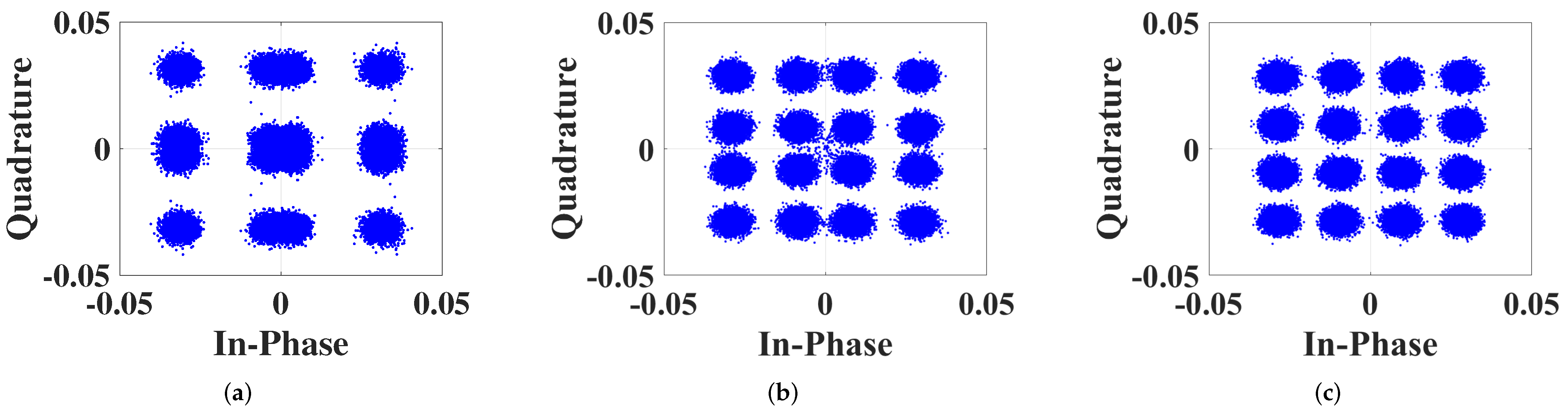
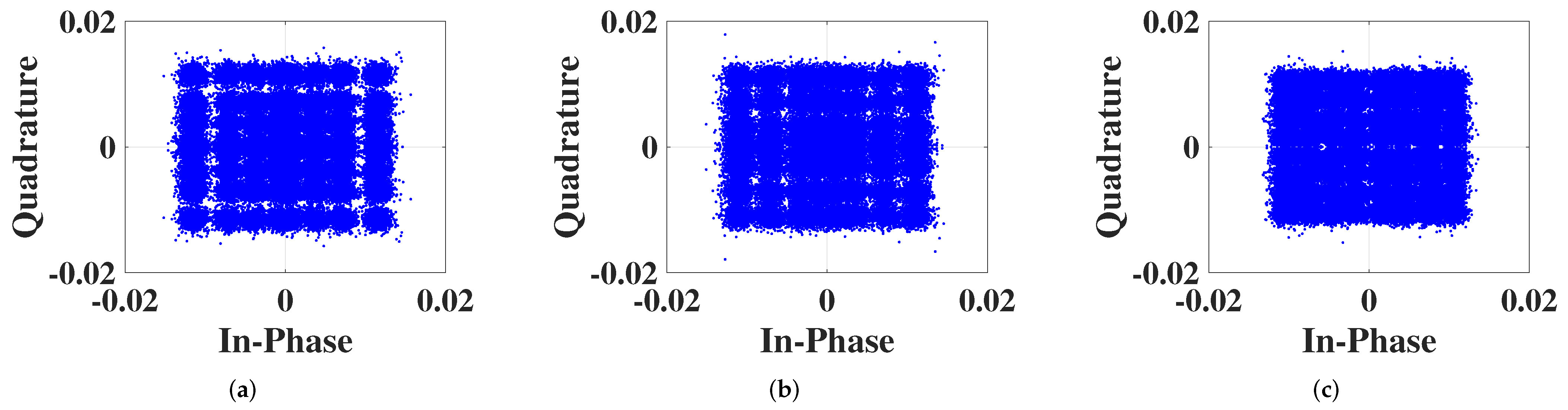
4.3. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
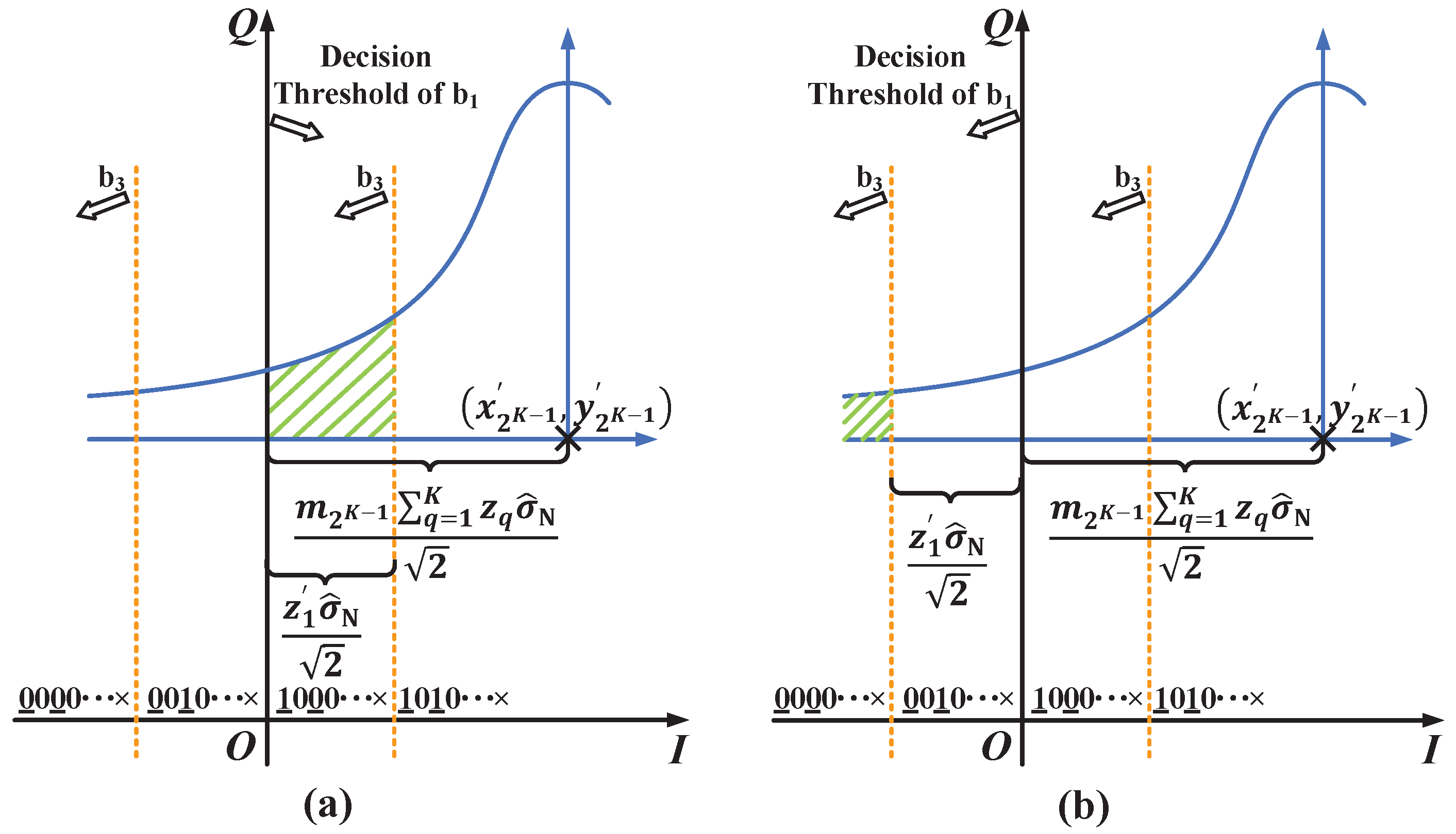
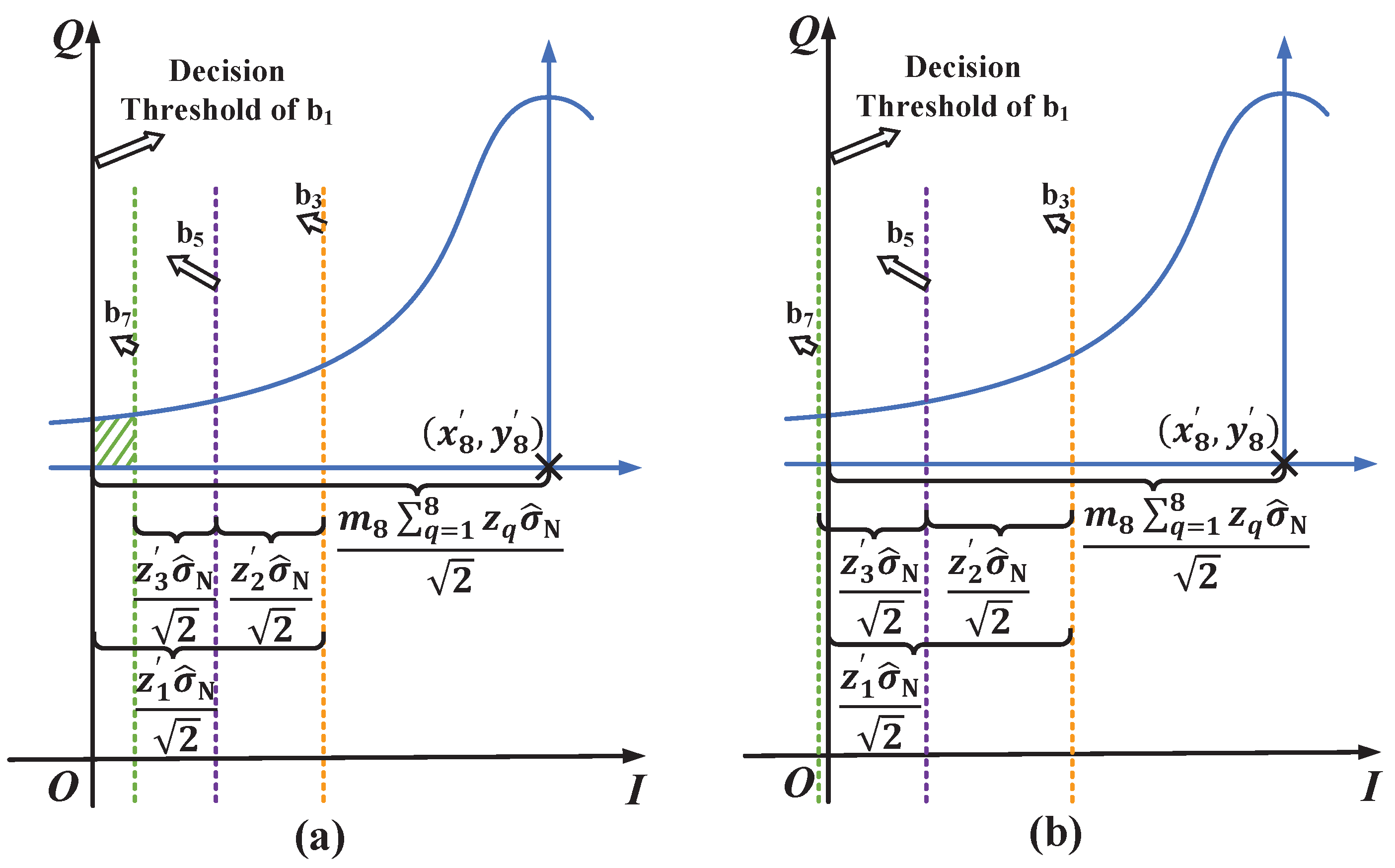
Appendix A.3
References
- Yang, H.; Alphones, A.; Zhong, W.; Chen, C.; Xie, X. Learning-Based Energy-Efficient Resource Management by Heterogeneous RF/VLC for Ultra-Reliable Low-Latency Industrial IoT Networks. IEEE Trans. Ind. Inform. 2020, 16, 5565–5576. [Google Scholar] [CrossRef]
- Al Hammadi, A.; Sofotasios, P.C.; Muhaidat, S.; Al-Qutayri, M.; Elgala, H. Non-Orthogonal Multiple Access for Hybrid VLC-RF Networks with Imperfect Channel State Information. IEEE Trans. Veh. Technol. 2021, 70, 398–411. [Google Scholar] [CrossRef]
- Karunatilaka, D.; Zafar, F.; Kalavally, V.; Parthiban, R. LED Based Indoor Visible Light Communications: State of the Art. IEEE Commun. Surv. Tutor. 2015, 17, 1649–1678. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Zhou, F.; Ma, S.; Hu, R.Q.; Ng, D.W.K. Beamforming Design for Secure MISO Visible Light Communication Networks with SLIPT. IEEE Trans. Commun. 2020, 68, 7795–7809. [Google Scholar] [CrossRef]
- Obeed, M.; Dahrouj, H.; Salhab, A.M.; Zummo, S.A.; Alouini, M.S. User Pairing, Link Selection, and Power Allocation for Cooperative NOMA Hybrid VLC/RF Systems. IEEE Trans. Wirel. Commun. 2021, 20, 1785–1800. [Google Scholar] [CrossRef]
- Pathak, P.H.; Feng, X.; Hu, P.; Mohapatra, P. Visible Light Communication, Networking, and Sensing: A Survey, Potential and Challenges. IEEE Commun. Surv. Tutor. 2015, 17, 2047–2077. [Google Scholar] [CrossRef]
- Chen, C.; Zhong, W.D.; Yang, H.; Du, P. On the Performance of MIMO-NOMA-Based Visible Light Communication Systems. IEEE Photon. Technol. Lett. 2018, 30, 307–310. [Google Scholar] [CrossRef]
- Shi, J.; He, J.; Wu, K.; Ma, J. Enhanced Performance of Asynchronous Multi-Cell VLC System Using OQAM/OFDM-NOMA. J. Lightw. Technol. 2019, 37, 5212–5220. [Google Scholar] [CrossRef]
- Janjua, M.B.; da Costa, D.B.; Arslan, H. User Pairing and Power Allocation Strategies for 3D VLC-NOMA Systems. IEEE Wirel. Commun. Lett. 2020, 9, 866–870. [Google Scholar] [CrossRef]
- Wang, G.; Shao, Y.; Chen, L.K.; Zhao, J. Subcarrier and Power Allocation in OFDM-NOMA VLC Systems. IEEE Photon. Technol. Lett. 2021, 33, 189–192. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A Survey of Non-Orthogonal Multiple Access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Hong, Y.; Deng, R.; He, J.; Chen, L.K.; Chang, G.K. Demonstration of Real-Time Software Reconfigurable Dynamic Power-and-Subcarrier Allocation Scheme for OFDM-NOMA-Based Multi-User Visible Light Communications. J. Lightw. Technol. 2019, 37, 4401–4409. [Google Scholar] [CrossRef]
- Qiu, H.; Gao, S.; Tu, G. An Opportunistic NOMA Scheme for Multiuser Spatial Multiplexing VLC Systems. IEEE Commun. Lett. 2021, 25, 3017–3021. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.; Schober, R.; Yuan, J.; Bhargava, V. A Survey on Non-Orthogonal Multiple Access for 5G Networks: Research Challenges and Future Trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal Multiple Access for 5G and Beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar] [CrossRef] [Green Version]
- Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K.S. Power-Domain Non-Orthogonal Multiple Access (NOMA) in 5G Systems: Potentials and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar] [CrossRef] [Green Version]
- Almohimmah, E.M.; Alresheedi, M.T. Error Analysis of NOMA-Based VLC Systems with Higher Order Modulation Schemes. IEEE Access 2020, 8, 2792–2803. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Z.; Wang, Y.; Zhou, F.; Luo, Y.; Hu, R.Q. BER Analysis of NOMA-Enabled Visible Light Communication Systems with Different Modulations. IEEE Trans. Veh. Technol. 2019, 68, 10807–10821. [Google Scholar] [CrossRef]
- Guan, X.; Yang, Q.; Hong, Y.; Chan, C.C.K. Non-orthogonal multiple access with phase pre-distortion in visible light communication. Opt. Express 2016, 24, 25816–25823. [Google Scholar] [CrossRef]
- Ren, H.; Wang, Z.; Du, S.; He, Y.; Chen, J.; Han, S.; Yu, C.; Xu, C.; Yu, J. Performance improvement of NOMA visible light communication system by adjusting superposition constellation: A convex optimization approach. Opt. Express 2018, 26, 29796–29806. [Google Scholar] [CrossRef] [Green Version]
- Marshoud, H.; Sofotasios, P.; Muhaidat, S.; Karagiannidis, G.; Sharif, B. On the Performance of Visible Light Communication Systems with Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2017, 16, 6350–6364. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Ma, S.; He, Y.; Lu, S.; Li, H.; Zhang, H.; Li, S. Nonorthogonal Multiple Access for Visible Light Communication IoT Networks. Wirel. Commun. Mob. Com. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Wu, T.; Wang, Z.; Yu, J.; Han, S.; Jiang, Y. Joint Transceiver Optimization for Performance Improvement of Multi-User NOMA VLC System. In Proceedings of the 2021 IEEE 21th International Conference on Communication Technology (ICCT), Tianjin, China, 13–16 October 2021; pp. 1477–1481. [Google Scholar]
- Yin, L.; Popoola, W.; Wu, X.; Haas, H. Performance Evaluation of Non-Orthogonal Multiple Access in Visible Light Communication. IEEE Trans. Commun. 2016, 64, 5162–5175. [Google Scholar] [CrossRef] [Green Version]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Baig, S.; Ali, U.; Asif, H.M.; Khan, A.A.; Mumtaz, S. Closed-Form BER Expression for Fourier and Wavelet Transform-Based Pulse-Shaped Data in Downlink NOMA. IEEE Commun. Lett. 2019, 23, 592–595. [Google Scholar] [CrossRef]
- Assaf, T.; Al-Dweik, A.; Moursi, M.E.; Zeineldin, H. Exact BER Performance Analysis for Downlink NOMA Systems Over Nakagami-m Fading Channels. IEEE Access 2019, 7, 134539–134555. [Google Scholar] [CrossRef]
- Wang, X.; Labeau, F.; Mei, L. Closed-Form BER Expressions of QPSK Constellation for Uplink Non-Orthogonal Multiple Access. IEEE Commun. Lett. 2017, 21, 2242–2245. [Google Scholar] [CrossRef]

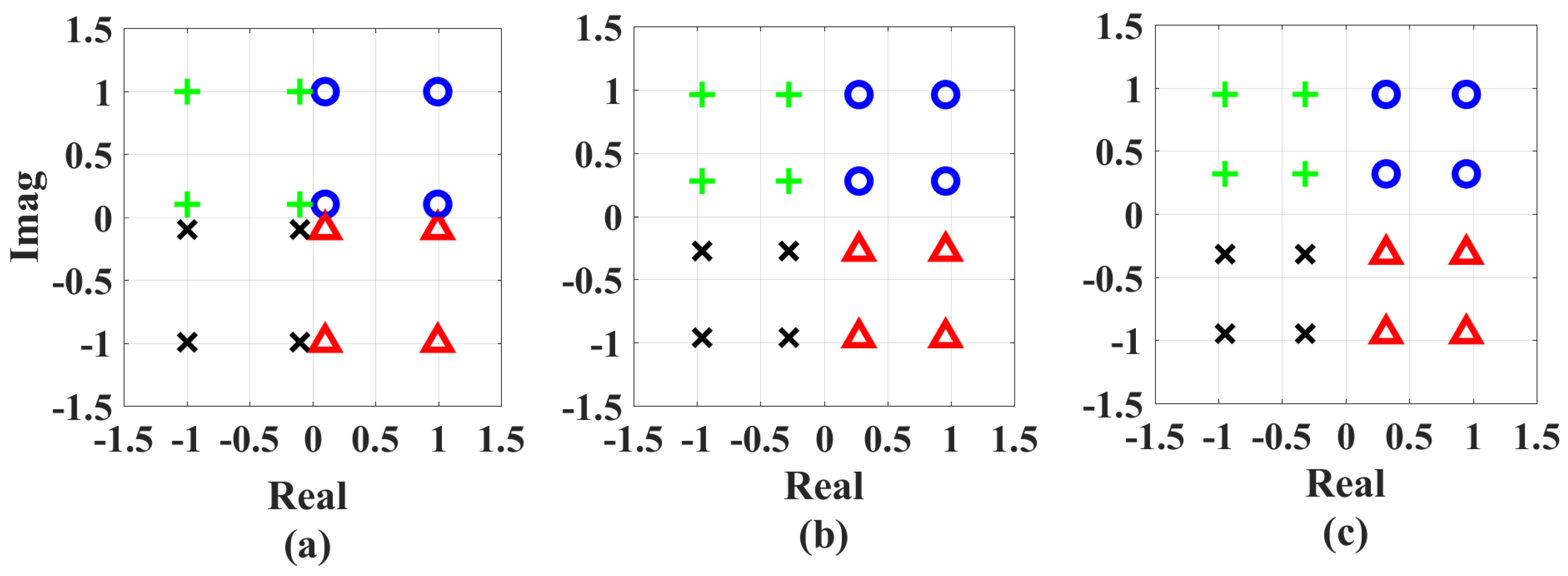

| 1 | 2 | 3 | 4 | 5 | ⋯ | k | ⋯ | K | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 2 | |||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
| 5 | |||||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ | |||||
| k | ⋯ | ||||||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ | |||
| K | ⋯ | ⋯ | |||||||||
| Parameter | Value |
|---|---|
| Population size | 500 |
| Generation number | 1000 |
| Mutation factor | 0.5 |
| Crossover probability | 0.2 |
| Parameter | Value |
|---|---|
| FOV at a receiver, | |
| PD detection area, A | 1 |
| Optical filter, | 1 |
| Semiangle at half power, | |
| Refractive index, | 1.5 |
| Responsivity of PD, R | 1 A/W |
| Current-to-light conversion efficiency, | 1 W/A |
| Power allocation coefficient vector when , | |
| Power allocation coefficient vector when , |
| Parameter | Value |
|---|---|
| Power allocation coefficient vector when , | |
| Power allocation coefficient vector when , | |
| Data rate | 10 M symbol/s |
| Semiangle at half power of VLC transmitter module | |
| Optical wavelength of VLC transmitter module | 459.3 nm |
| Active area of VLC receiver module | 1 |
| Power Allocation Coefficient Vector | Reduction for User 1 | Reduction for User 2 | Reduction for User 3 |
|---|---|---|---|
| 1.3 dB | 0.8 dB | - | |
| 0.6 dB | 0.3 dB | - | |
| 0 dB | 0 dB | - | |
| 8.6 dB | 0.8 dB | 6.4 dB | |
| 5.7 dB | 4.3 dB | 4.6 dB | |
| 0.4 dB | 0 dB | 0.3 dB | |
| 0.7 dB | 0.8 dB | 0.1 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Wang, Z.; Han, S.; Yu, J.; Jiang, Y. Demonstration of Performance Improvement in Multi-User NOMA VLC System Using Joint Transceiver Optimization. Photonics 2022, 9, 168. https://doi.org/10.3390/photonics9030168
Wu T, Wang Z, Han S, Yu J, Jiang Y. Demonstration of Performance Improvement in Multi-User NOMA VLC System Using Joint Transceiver Optimization. Photonics. 2022; 9(3):168. https://doi.org/10.3390/photonics9030168
Chicago/Turabian StyleWu, Tong, Zixiong Wang, Shiying Han, Jinlong Yu, and Yang Jiang. 2022. "Demonstration of Performance Improvement in Multi-User NOMA VLC System Using Joint Transceiver Optimization" Photonics 9, no. 3: 168. https://doi.org/10.3390/photonics9030168
APA StyleWu, T., Wang, Z., Han, S., Yu, J., & Jiang, Y. (2022). Demonstration of Performance Improvement in Multi-User NOMA VLC System Using Joint Transceiver Optimization. Photonics, 9(3), 168. https://doi.org/10.3390/photonics9030168






