Improved Search Algorithm of Digital Speckle Pattern Based on PSO and IC-GN
Abstract
:1. Introduction
2. Related Work
2.1. Related Principles of Integer-Pixel Search
2.2. Coarse and Fine Search Algorithm
2.3. PSO-W Algorithm
- Customize the integer-pixel position and velocity of the initial particles, where the fitness value of each particle is the correlation coefficient calculated by Equation (1), and set the iteration termination parameters as: trustworthy threshold , maximum iteration number .
- Update the velocities and positions of all particles with the linear inertia weight (see Equation (5)), and keep the velocities and positions of the particles within the search range. If exceeds the specified search range, set the positions and velocities to their proximity boundaries. The particle updated velocity and position formulas are shown in Equations (6) and (7).where, t represents the current generation, and represents the next generation, is the velocity of the i-th particle in the d direction, and is the position of the i-th particle in the d direction. When , it flies in the X direction, and when , it flies in the Y direction. and are positive acceleration coefficients, respectively. and are two uniform random variables between 0 and 1. is the position where the particle finds the maximum fitness value , and is the position of the maximum fitness value in the particle swarm, which is a global optimal position.
- For each particle, if the current fitness value is greater than the previous , update it. For the entire population, if the current fitness value is greater than the previous , then update.
- The algorithm terminates until either is greater than or is reached. Then output and its corresponding displacement vector , otherwise go back to step 2.
- If , the block-based gradient descent search (BBGDS) algorithm will not be executed. Otherwise, take as the starting point of the BBGDS algorithm, and finally output the integer-pixel with the largest correlation coefficient in the center.
2.4. Sub-Pixel Reconstruction
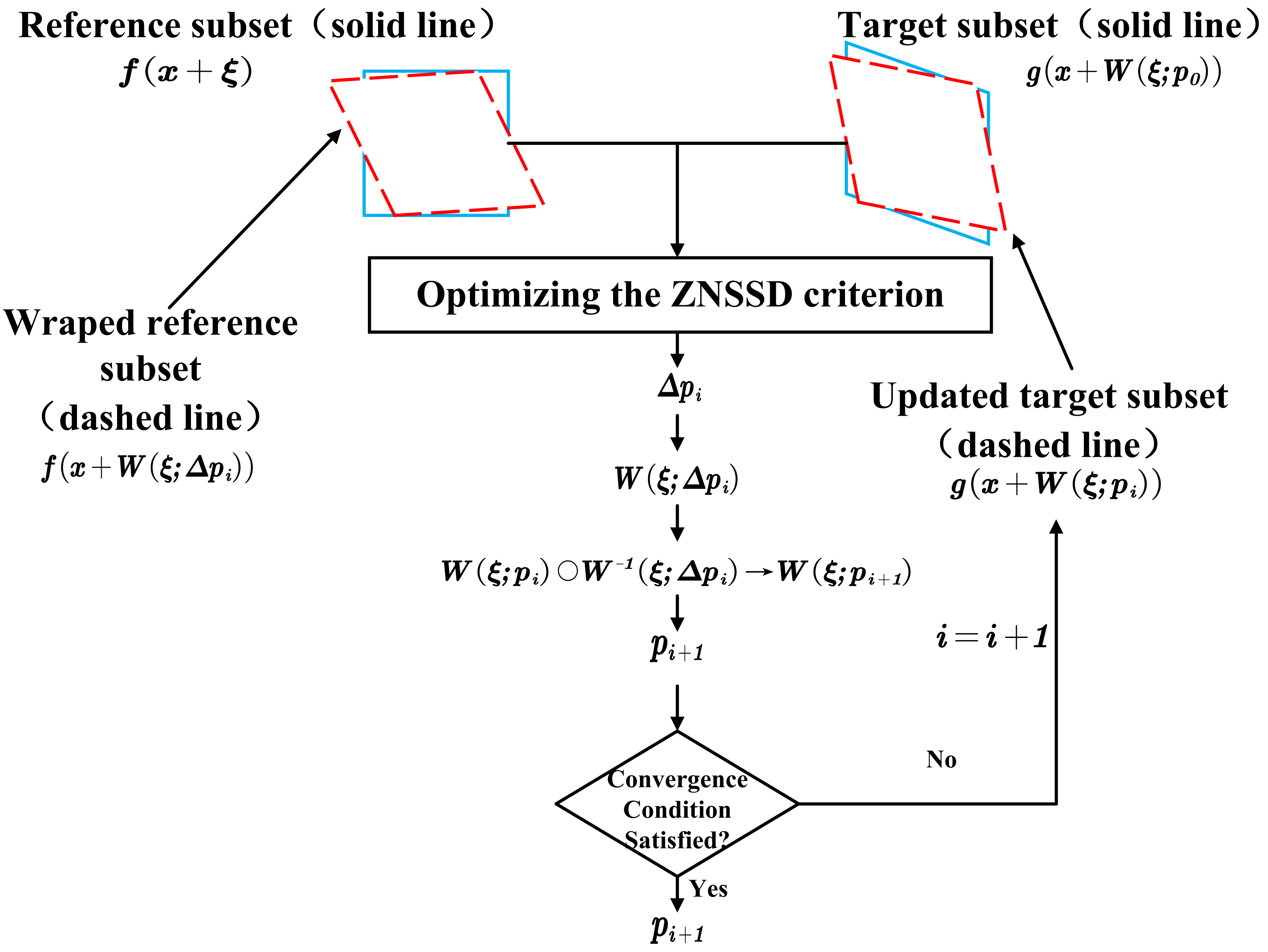
2.5. IC-GN Algorithm
2.6. Generate Simulated Speckle Images
2.7. Algorithm Performance Evaluation Index
3. Improved PSO-Based Efficient Integer-Pixel Displacement Search Algorithm
- 1.
- The maximum value is not unique
- 2.
- Using linear inertia weighting factors
| Algorithm 1: PSO-1. |
 |
4. Sub-Pixel Displacement Search Algorithm
4.1. Improved Sub-Pixel Displacement Search Algorithm IV-ICGN
| Algorithm 2: Algorithm IV-ICGN. |
 |
4.2. Sub-Pixel Displacement Simulation Experiment
4.3. Real Rigid Body Translation Experiment
- Making speckles. Clean the glass surface with alcohol first and then spray the matte black paint evenly on the glass surface to form randomly distributed and uniformly sized speckles. During the painting process, keep the distance between the spray gun and the glass constant and vertical.
- Fixing the experimental device. The first step is to fix the glass with speckles on the holder. The second step is to fix the electronically controlled translation stage and the light source equipment on the optical platform. The third step is to fix the CCD camera on the electronically controlled translation stage.
- Determine the pixel equivalent of the camera system, which is 0.400 mm/pixel in this experiment.
- Collecting speckle images. Firstly, the real speckle image before displacement is acquired as the reference image, as shown in Figure 13, the size of the image is 512 pixel × 512 pixel. Then, several speckle images after the displacements in the X and Y directions, respectively, applied on the electronically controlled translation stage are collected as target images. All images are the region of interest after the surrounding environment and glass edges have been removed, which contains the full-field displacement.
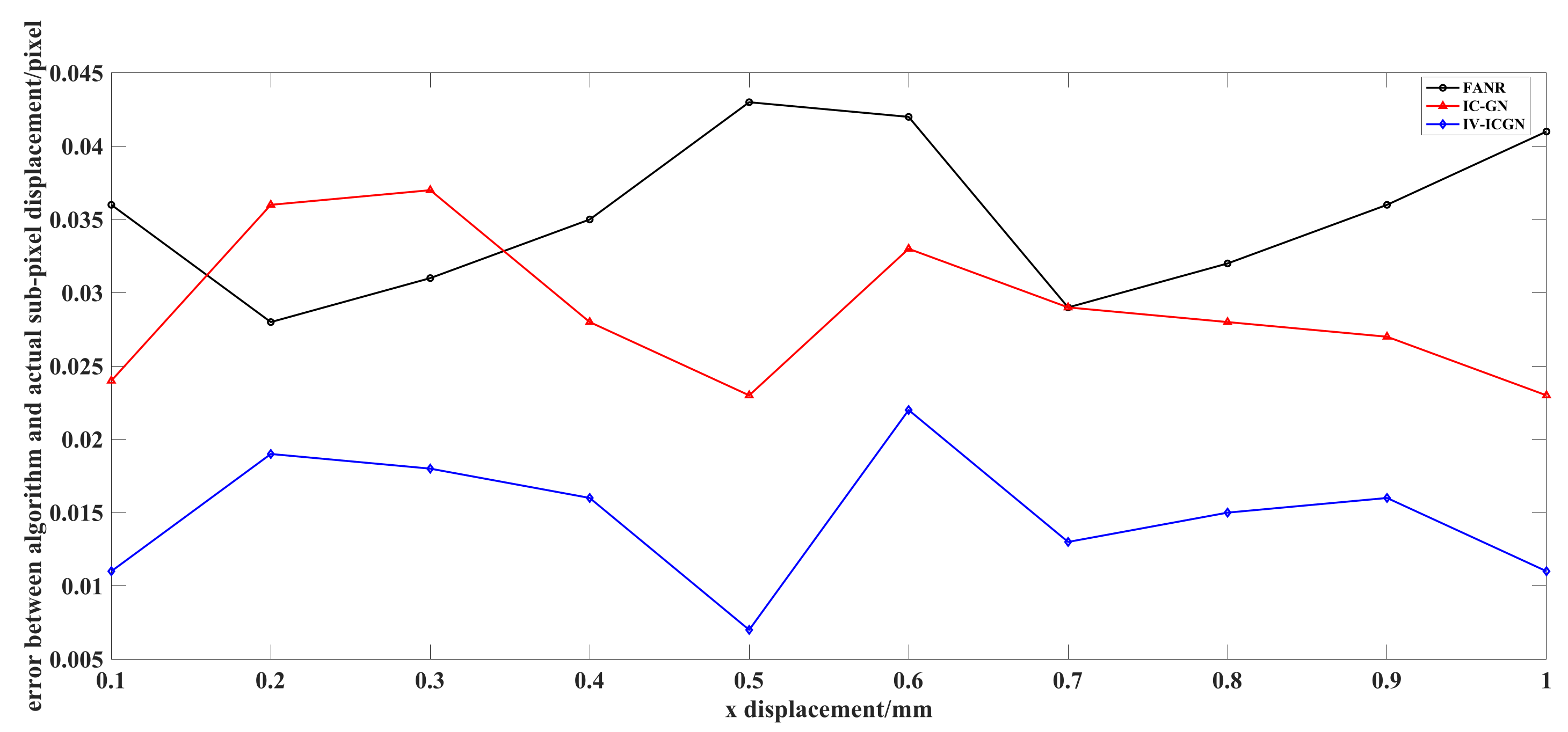
- Calculating the pixel displacement value. The proposed algorithm is used to calculate the pixel displacement values, and then compare and analyze the calculated displacement value with the real value.
5. Discussion
- In the integer pixel search, in view of the two problems of non-unique maximum value and parameter setting in PSO-W [36] algorithm, PSO-1 algorithm with higher search efficiency is proposed. The simulation results show that PSO-1 has higher search efficiency. In terms of sub-pixels, based on IC-GN [42] algorithm with the highest accuracy at present, IV-ICGN algorithm is proposed. Sub-pixel level iterative initial values will make the algorithm converge more easily and with fewer iterations, while improving accuracy and efficiency. The simulation results show that the proposed algorithm has higher precision and higher efficiency than the comparison algorithms.
- However, this study can consider parallel computing to improve computational efficiency. CUDA-based programming can take advantage of the GPU’s parallel computing engine to improve floating-point computing capabilities, thereby improving computing efficiency. At the same time, many floating-point operations are involved in the iterative calculation, and the iterative initial value of multiple points is calculated in parallel to quickly achieve the full-field matching effect.
- At the same time, the research should consider the effect of noise on the algorithm. Although, real experiments show that IV-ICGN algorithm has the best performance; however, we can further improve the accuracy of the algorithm through noise compensation methods. At the same time, we suggest that the results can be compared with some other free 2D DIC software in future work [56].
6. Conclusions
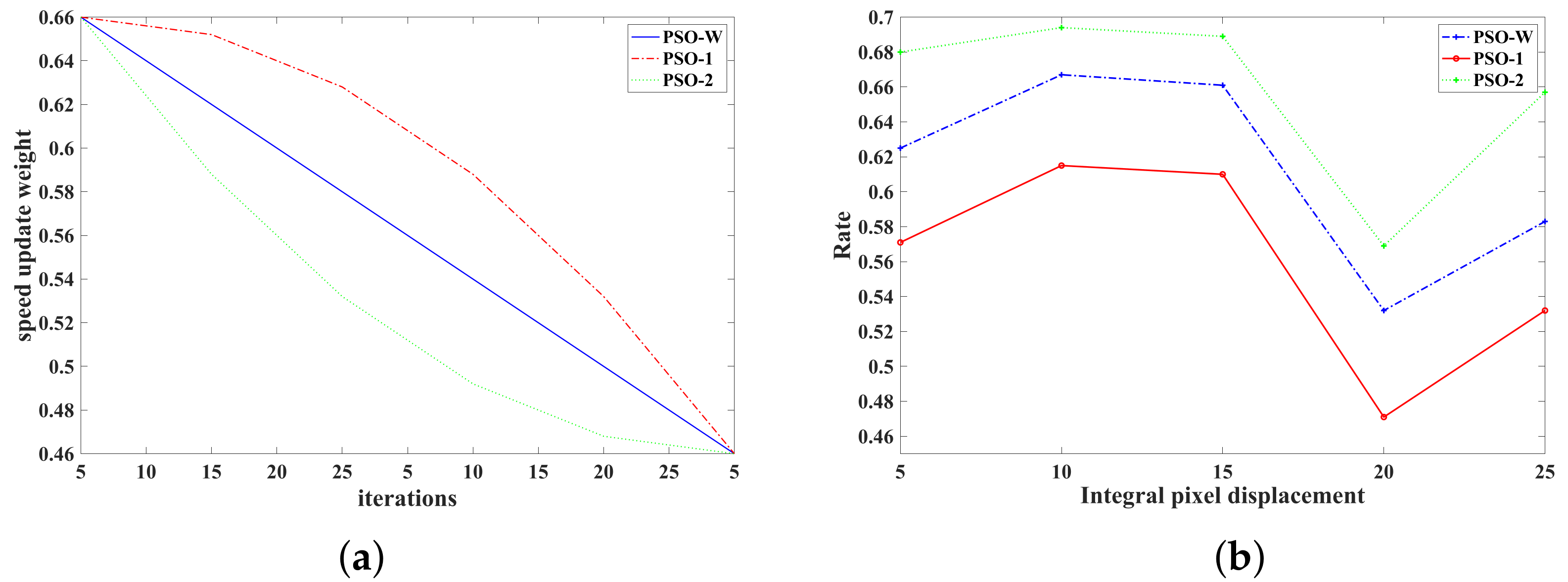
- The search efficiency of PSO-1 algorithm is higher than that of PSO-W algorithm. In the best case, the efficiency of the PSO-1 algorithm is 52.9% higher than that of the coarse and fine search algorithm, and 11.5% higher than that of the PSO-W algorithm. In the worst case, the efficiency of the PSO-1 algorithm is 38.5% higher than that of the coarse and fine search algorithm and 7.7% higher than that of the PSO-W algorithm. In general, the search efficiency of PSO-1 algorithm is 8.8% higher than that of PSO-W on average.
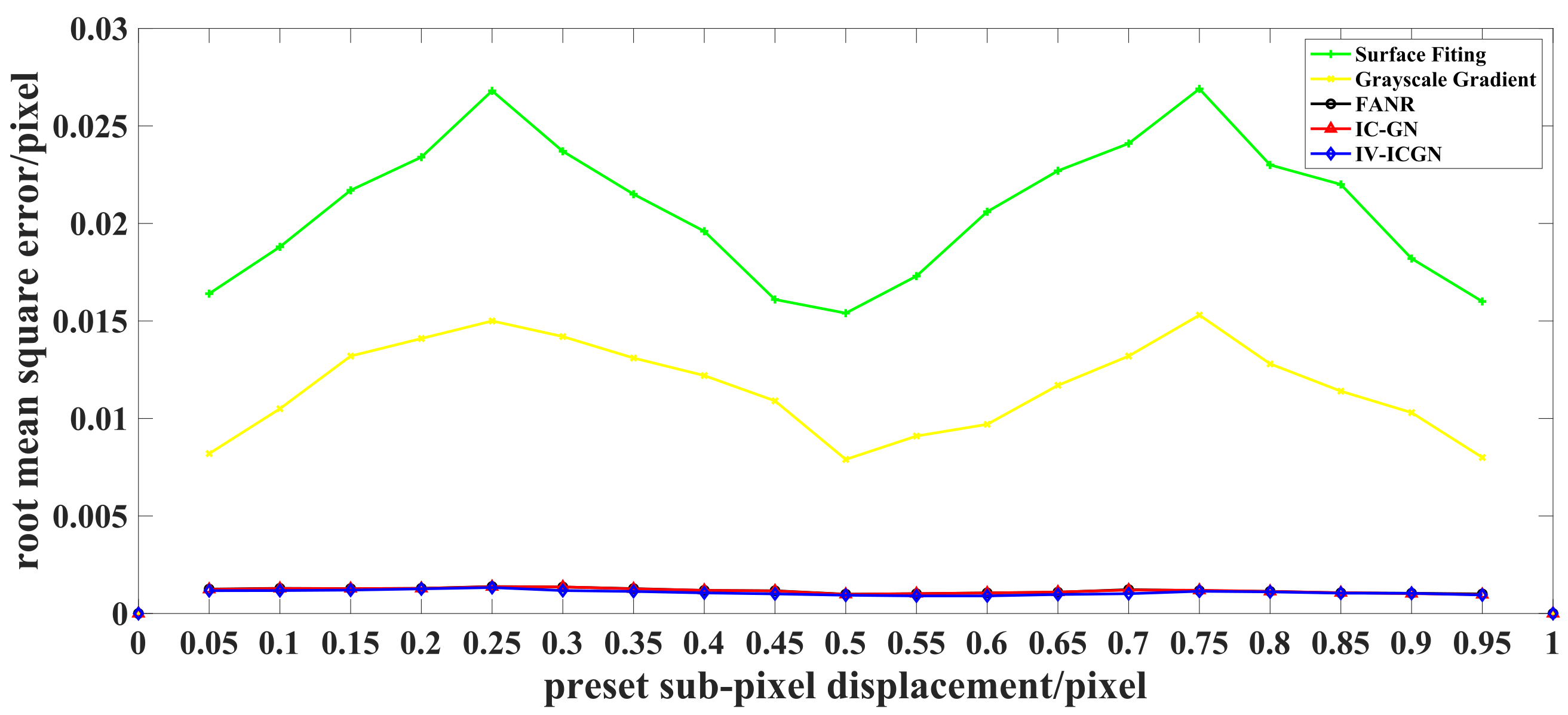
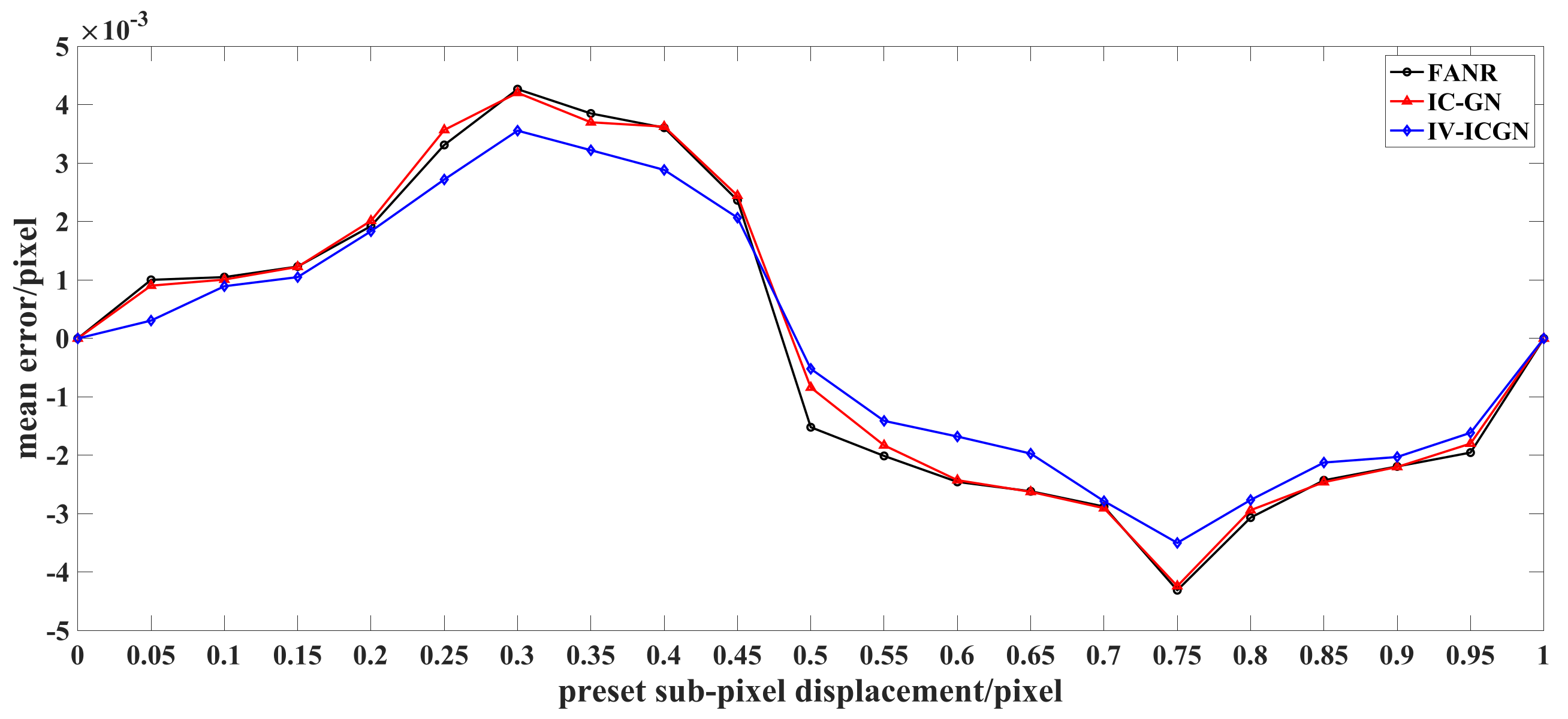
- IV-ICGN algorithm is better than surface fitting, grayscale gradient, FANR and IC-GN algorithms in calculation accuracy and efficiency. The results of simulation experiments show that the mean error value of the IV-ICGN algorithm is smaller than both of the IC-GN and FANR algorithms. In the best case, the mean error of the IV-ICGN algorithm is 66.2% lower than that of the IC-GN algorithm and 69.5% lower than that of the FANR algorithm, the root mean square error of the IV-ICGN algorithm is 15.6% lower than that of the IC-GN algorithm and 17.1% lower than that of the FANR algorithm. In the worst case, the mean error of the IV-ICGN algorithm is 6.0% lower than that of the IC-GN algorithm and 4.6% lower than that of the FANR algorithm, the root mean square error of the IV-ICGN algorithm is 1.4% lower than that of the IC-GN algorithm and 0.3% lower than that of the FANR algorithm. Among the IV-ICGN algorithm, IC-GN algorithm and FANR algorithm, the IV-ICGN algorithm has the least number of iterations.
- Compared with the IC-GN algorithm and FANR algorithm, the accuracy of the IV-ICGN algorithm in real rigid body translation experiments also performs best. The experimental results show that the absolute value of the mean error of the IV-ICGN algorithm is the smallest among the three algorithms, basically between pixel and pixel, even up to pixel. While the other two algorithms are basically between pixel and pixel.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Suchorzewski, J.; Prieto, M.; Mueller, U. An experimental study of self-sensing concrete enhanced with multi-wall carbon nanotubes in wedge splitting test and DIC. Constr. Build. Mater. 2020, 262, 120871. [Google Scholar] [CrossRef]
- Wang, X.; Jin, Z.; Liu, J.; Chen, F.; Feng, P.; Tang, J. Research on internal monitoring of reinforced concrete under accelerated corrosion, using XCT and DIC technology. Constr. Build. Mater. 2021, 266, 121018. [Google Scholar] [CrossRef]
- Dénes, F.; Gábor, S.; Tamás, T.; Rita, K.M.; Károly, P. Evaluation of the Effect of Freezing and Gamma Irradiation on Different Types of Tendon Allografts by DIC Assisted Tensile Testing. Appl. Sci. 2020, 10, 5369. [Google Scholar]
- Qiao, X.; Chen, D.; Huo, H.; Tang, M.; Tang, Z.; Dong, Y.; Liu, X.; Fan, Y. Full-field strain mapping for characterization of structure-related variation in corneal biomechanical properties using digital image correlation (DIC) technology. Med. Nov. Technol. Devices 2021, 11, 100086. [Google Scholar] [CrossRef]
- Ha, N.S.; Jin, T.L.; Goo, N.S. Anisotropy and non-homogeneity of an Allomyrina Dichotoma beetle hind wing membrane. Bioinspiration Biomimetics 2011, 6, 046003. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, S.; Li, W.; Wang, Y.; Yang, L. Precise Detection of Wrist Pulse Using Digital Speckle Pattern Interferometry. Evid.-Based Complement. Altern. Med. 2018, 2018, 4187349. [Google Scholar] [CrossRef] [Green Version]
- Polanczyk, A.; Podgorski, M.; Polanczyk, M.; Piechota-Polanczyk, A.; Strzelecki, M. A novel vision-based system for quantitative analysis of abdominal aortic aneurysm deformation. Med. Nov. Technol. Devices 2019, 18, 56. [Google Scholar] [CrossRef] [Green Version]
- Barile, C.; Casavola, C.; Pappalettera, G. Digital Image Correlation Comparison of Damaged and Undamaged Aeronautical CFRPs During Compression Tests. Materials 2019, 12, 249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siebert, T.; Hack, E.; Lampeas, G.; Patterson, E.A.; Splitthof, K. Uncertainty Quantification for DIC Displacement Measurements in Industrial Environments. Exp. Tech. 2021, 45, 685–694. [Google Scholar] [CrossRef]
- Ha, N.S.; Vang, H.M.; Goo, N.S. Modal Analysis Using Digital Image Correlation Technique: An Application to Artificial Wing Mimicking Beetle’s Hind Wing. Exp. Mech. 2015, 55, 989–998. [Google Scholar] [CrossRef]
- Xie, R.; Chen, G.; Zhao, Y.; Zhang, S.; Yan, W.; Lin, X.; Shi, Q.R.X. In-situ observation and numerical simulation on the transient strain and distortion prediction during additive manufacturing. J. Manuf. Process. 2019, 38, 494–501. [Google Scholar] [CrossRef]
- Isaac, J.P.; Dondeti, S.; Tippur, H.V. Crack initiation and growth in additively printed ABS: Effect of print architecture studied using DIC. Med. Nov. Technol. Devices 2020, 36, 101536. [Google Scholar] [CrossRef]
- Stinville, J.C.; Callahan, P.G.; Charpagne, M.A.; Echlin, M.P.; Valle, V.; Pollock, T.M. Direct measurements of slip irreversibility in a nickel-based superalloy using high resolution digital image correlation. Acta Mater. 2020, 186, 172–189. [Google Scholar] [CrossRef]
- Pan, K.; Yu, R.C.; Ruiz, G.; Zhang, X.; Wu, Z.; De La Rosa, Á. The propagation speed of multiple dynamic cracks in fiber-reinforced cement-based composites measured using DIC. Cem. Concr. Compos. 2021, 122, 104140. [Google Scholar] [CrossRef]
- Ha, N.S.; Le, V.T.; Goo, N.S. Investigation of fracture properties of a piezoelectric stack actuator using the digital image correlation technique. Int. J. Fatigue 2017, 101, 106–111. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, Z.; Zhu, R.; Wang, J.; Ma, M. Edge sensing data-imaging conversion scheme of load forecasting in smart grid. Sustain. Cities Soc. 2020, 62, 102363. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.S.; Jeong, S.; Park, J.H.; Kim, H.K. Cybersecurity for autonomous vehicles: Review of attacks and defense. Comput. Secur. 2021, 103, 102150. [Google Scholar] [CrossRef]
- Boukhtache, S.; Abdelouahab, K.; Berry, F.; Blaysat, B.; Grédiac, M.; Sur, F. When Deep Learning Meets Digital Image Correlation. Opt. Lasers Eng. 2021, 136, 106308. [Google Scholar] [CrossRef]
- Sperry, R.; Han, S.; Chen, Z.; Daly, S.H.; Crimp, M.A.; Fullwood, D.T. Comparison of EBSD, DIC, AFM, and ECCI for active slip system identification in deformed Ti-7Al. Mater. Charact. 2021, 173, 110941. [Google Scholar] [CrossRef]
- Yang, S.; Chen, M.; Huang, Y.; Jing, H.; Ranjith, P.G. An experimental study on fracture evolution mechanism of a non-persistent jointed rock mass with various anchorage effects by DSCM, AE and X-ray CT observations. Int. J. Rock Mech. Min. Sci. 2020, 134, 104469. [Google Scholar] [CrossRef]
- Chen, M.; Yang, S.; Ranjith, P.G.; Zhang, Y. Cracking behavior of rock containing non-persistent joints with various joints inclinations. Theor. Appl. Fract. Mech. 2020, 109, 102701. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital Imaging Techniques In Experimental Stress Analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F.; Sutton, M.A.; Chu, T.; Anderson, J. Application Of Digital Correlation Methods To Rigid Body Mechanics. Opt. Eng. 1983, 22, 738–742. [Google Scholar] [CrossRef]
- Chen, D.; Chiang, F.; Tan, Y.; Don, H. Digital speckle-displacement measurement using a complex spectrum method. Appl. Opt. 1993, 32, 1839. [Google Scholar] [CrossRef] [PubMed]
- Schreier, H.W.; Sutton, M.A. Systematic errors in digital image correlation due to undermatched subset shape functions. Exp. Mech. 2002, 42, 303–310. [Google Scholar] [CrossRef]
- Wang, H.; Kang, Y. Improved digital speckle correlation method and its application in fracture analysis of metallic foil. Opt. Eng. 2002, 41, 2793–2798. [Google Scholar] [CrossRef]
- Rui, J.; Jin, G.; Xu, B. A new digital speckle correlation method and its application. Appl. Mech. 1994, 26, 599–607. [Google Scholar]
- Liu, G.; Li, M.; Zhang, W. Adaptive Search Algorithm Method of Whole-pixel Deformation for Ancient Building Painted Beams. Hunan Daxue Xuebao/J. Hunan Univ. Nat. Sci. 2020, 47, 106–113. [Google Scholar]
- Ge, P.; Ye, P.; Li, G. Application of Digital Image Correlation Method Based on Genetic Algorithm in Micro-Displacement Measurement. Guangxue Xuebao/Acta Opt. Sin. 2018, 38, 206–211. [Google Scholar]
- Zhao, J.; Pan, Z.; Yuan, M.J.Q.Z. Initial guess by improved population-based intelligent algorithms for large inter-frame deformation measurement using digital image correlation. Opt. Lasers Eng. 2012, 50, 473–490. [Google Scholar] [CrossRef]
- Jiang, Z.; Qian, K.; Hong, M.; Yang, J.; Tang, L. Path-independent digital image correlation with high accuracy, speed and robustness. Opt. Lasers Eng. 2015, 65, 93–102. [Google Scholar] [CrossRef]
- Zhong, F.; Quan, C. Efficient digital image correlation using gradient orientation. Opt. Laser Technol. 2018, 106, 417–426. [Google Scholar] [CrossRef]
- Wang, L.; Bi, S.; Lu, X.; Gu, Y.; Zhai, C. Deformation measurement of high-speed rotating drone blades based on digital image correlation combined with ring projection transform and orientation codes. Measurement 2019, 148, 106899. [Google Scholar] [CrossRef]
- Wu, X.; Yang, Y.; Han, S.; Zhao, Z.; Fang, P.; Gao, Q. Multi-objective optimization method for nuclear reactor radiation shielding design based on PSO algorithm. Ann. Nucl. Energy 2021, 160, 108404. [Google Scholar] [CrossRef]
- Zhu, W.; Rad, H.N.; Hasanipanah, M. A chaos recurrent ANFIS optimized by PSO to predict ground vibration generated in rock blasting. Appl. Soft Comput. 2021, 108, 107434. [Google Scholar] [CrossRef]
- Wu, R.; Kong, C.; Zhang, D. Real-Time Digital Image Correlation for Dynamic Strain Measurement. Exp. Mech. 2016, 56, 833–843. [Google Scholar] [CrossRef]
- Liu, H.; Chen, W.; Xu, Z. An image sub-pixel registration algorithm based on combination of curved surface fitting method and gradient method. Guofang Keji Daxue Xuebao/J. Natl. Univ. Def. Technol. 2015, 37, 180–185. [Google Scholar]
- ZHou, P.; Goodson, K.E.P.Z. Subpixel displacement and deformation gradient measurement using digital image/speckle correlation (DISC). Opt. Eng. 2001, 40, 1613–1620. [Google Scholar] [CrossRef]
- Bruck, H.A.; Mcneill, S.R.; Sutton, M.A.; Peters, W.H. Digital image correlation using Newton-Raphson method of partial differential correction. Exp. Mech. 1989, 29, 261–267. [Google Scholar] [CrossRef]
- Baker, S.; Matthews, I. Equivalence and efficiency of image alignment algorithms. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition CVPR 2001, Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Baker, S.; Matthews, I. Lucas-Kanade 20 years on: A unifying framework. Int. J. Comput. Vis. 2004, 56, 221–255. [Google Scholar] [CrossRef]
- Pan, B.; Li, K.; Tong, W. Fast, robust and accurate digital image correlation calculation without redundant computations. Exp. Mech. 2013, 53, 1277–1289. [Google Scholar] [CrossRef]
- Li, K.; Cai, P. Study on the performance of sub-pixel algorithm for digital image correlation. Yi Qi Yi Biao Xue Bao/Chin. J. Sci. Instrum. 2020, 41, 180–187. [Google Scholar]
- Pan, B.; Xie, H.; Dai, F. An investigation of sub-pixel displacements registration algorithms in digital image correlation. Chin. J. Theor. Appl. Mech. 2007, 23, 245–252. [Google Scholar]
- Schreier, H.; Orteu, J.J.; Sutton, M.A. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer Science & Business Media: Boston, MA, USA, 2009. [Google Scholar]
- Shao, X.; Dai, X.; He, X. Noise robustness and parallel computation of the inverse compositional Gauss–Newton algorithm in digital image correlation. Opt. Lasers Eng. 2015, 71, 9–19. [Google Scholar] [CrossRef]
- Pan, B.; Wang, B. Digital Image Correlation with Enhanced Accuracy and Efficiency: A Comparison of Two Subpixel Registration Algorithms. Exp. Mech. 2016, 56, 1395–1409. [Google Scholar] [CrossRef]
- Jiang, L.; Xie, H.; Pan, B. Speeding up digital image correlation computation using the integral image technique. Opt. Lasers Eng. 2015, 65, 117–122. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Jiang, Z.; Qian, K.; Liu, Y.; Liu, Z.; Tang, L.; Dong, S. High accuracy digital image correlation powered by GPU-based parallel computing. Opt. Lasers Eng 2015, 69, 7–12. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, L.; Jiang, Z.; Dong, S.; Chen, W.; Liu, Y.; Liu, Z.; Zhou, L.; Tang, L.Z. Heterogeneous parallel computing accelerated iterative subpixel digital image correlation. Sci. China Technol. Sci. 2017, 61, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Huang, J.; Jiang, Z.; Dong, S.; Tang, L.; Liu, Y.; Liu, Z.; Zhou, L. SIFT-aided path-independent digital image correlation accelerated by parallel computing. Opt. Lasers Eng. 2020, 127, 105964. [Google Scholar] [CrossRef]
- Tong, W. An Evaluation of Digital Image Correlation Criteria for Strain Mapping Applications. Strain 2005, 41, 167–175. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Wang, Z. Equivalence of digital image correlation criteria for pattern matching. Appl. Opt. 2010, 49, 5501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, J.; Yan, W.; Lei, G. Hierarchical coherency sensitive hashing and interpolation with RANSAC for large displacement optical flow. Comput. Vis. Image Underst. 2018, 175, 1–10. [Google Scholar] [CrossRef]
- Pan, B.; Lu, Z.; Xie, H. Mean intensity gradient: An effective global parameter for quality assessment of the speckle patterns used in digital image correlation. Opt. Lasers Eng. 2010, 48, 469–477. [Google Scholar] [CrossRef]
- Jin, T.; Ha, N.S.; Le, V.T.; Goo, N.S.; Jeon, H.C. Thermal buckling measurement of a laminated composite plate under a uniform temperature distribution using the digital image correlation method. Compos. Struct. 2015, 123, 420–429. [Google Scholar] [CrossRef]





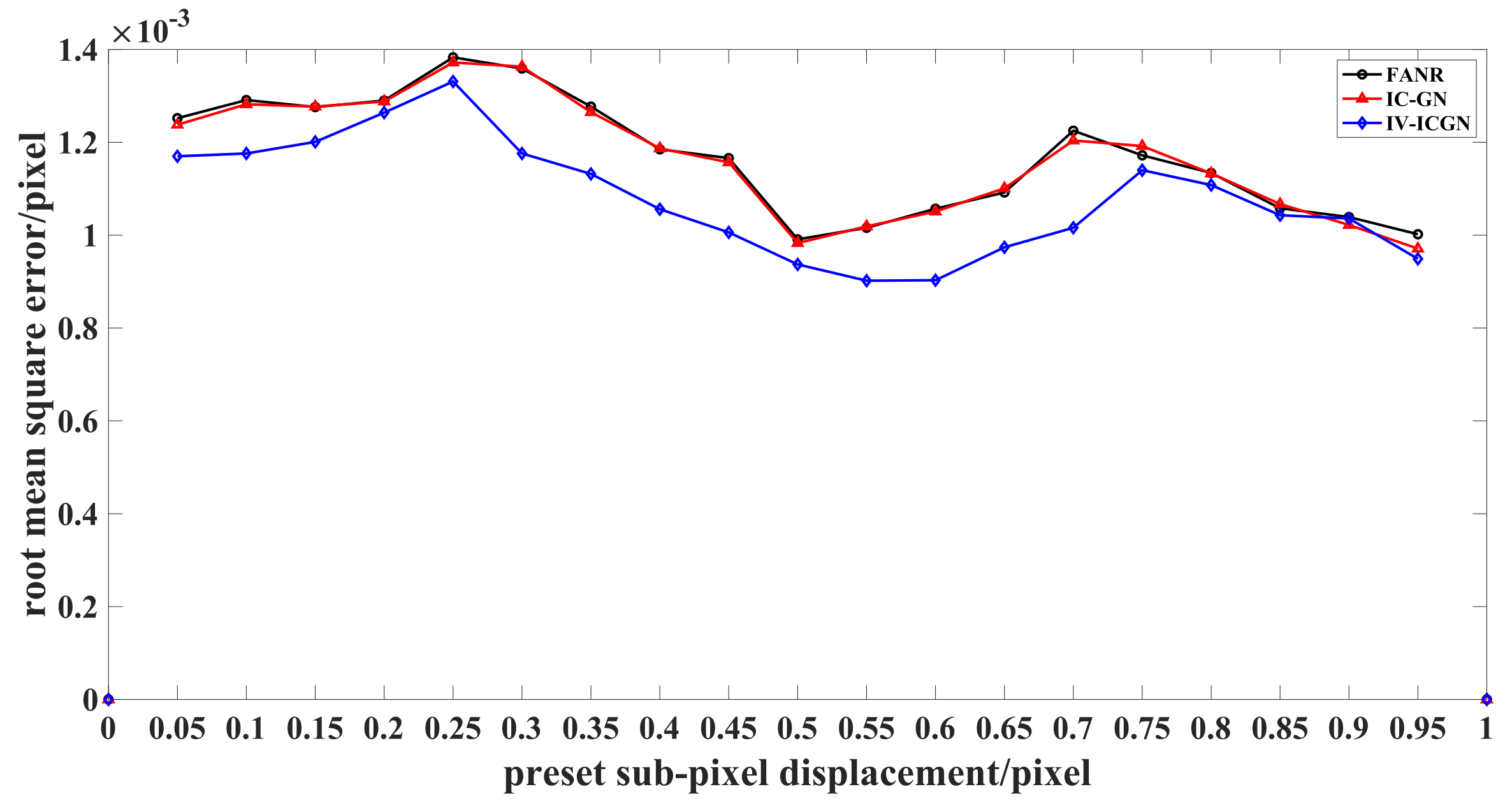
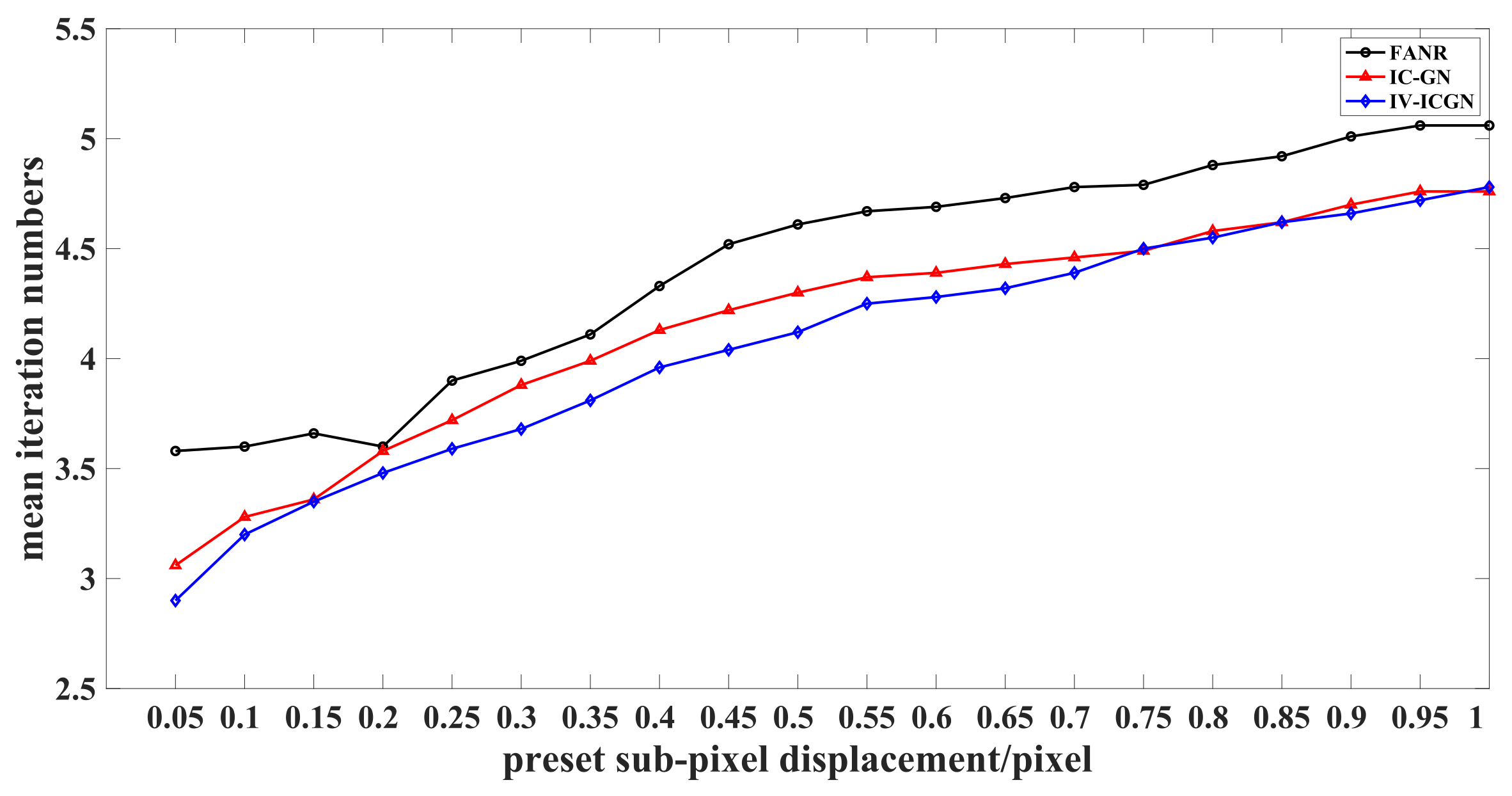


| Algorithm | AVME ( Pixel) | RMSE ( Pixel) | ||
|---|---|---|---|---|
| Minimum | Maximum | Minimum | Maximum | |
| SF | 13.8 | 24.9 | 16.0 | 26.9 |
| GG | 6.0 0 | 13.5 | 8.0 0 | 15.3 |
| FANR | 1.00 | 4.31 | 1.0 0 | 1.38 |
| IC-GN | 0.90 | 4.24 | 0.97 | 1.37 |
| IV-ICGN | 0.31 | 3.56 | 0.90 | 1.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Tie, Z.; Hong, L.; Qu, Y.; Wang, D. Improved Search Algorithm of Digital Speckle Pattern Based on PSO and IC-GN. Photonics 2022, 9, 167. https://doi.org/10.3390/photonics9030167
Chen Q, Tie Z, Hong L, Qu Y, Wang D. Improved Search Algorithm of Digital Speckle Pattern Based on PSO and IC-GN. Photonics. 2022; 9(3):167. https://doi.org/10.3390/photonics9030167
Chicago/Turabian StyleChen, Qiang, Zhixin Tie, Liang Hong, Youtian Qu, and Dengwen Wang. 2022. "Improved Search Algorithm of Digital Speckle Pattern Based on PSO and IC-GN" Photonics 9, no. 3: 167. https://doi.org/10.3390/photonics9030167
APA StyleChen, Q., Tie, Z., Hong, L., Qu, Y., & Wang, D. (2022). Improved Search Algorithm of Digital Speckle Pattern Based on PSO and IC-GN. Photonics, 9(3), 167. https://doi.org/10.3390/photonics9030167





