An Indoor Visible Light Positioning System for Multi-Cell Networks
Abstract
:1. Introduction
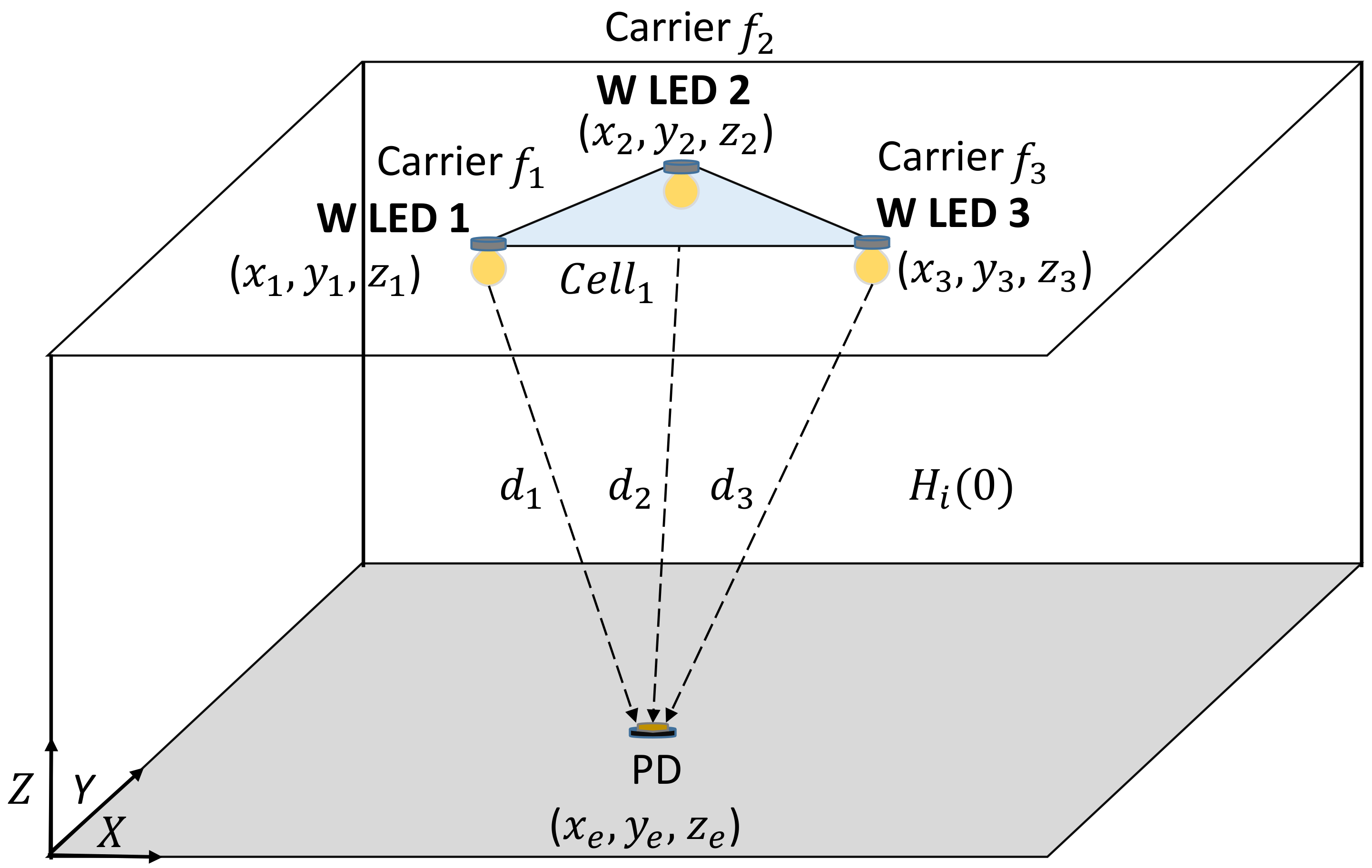
2. VLP System Model Based on WLEDs
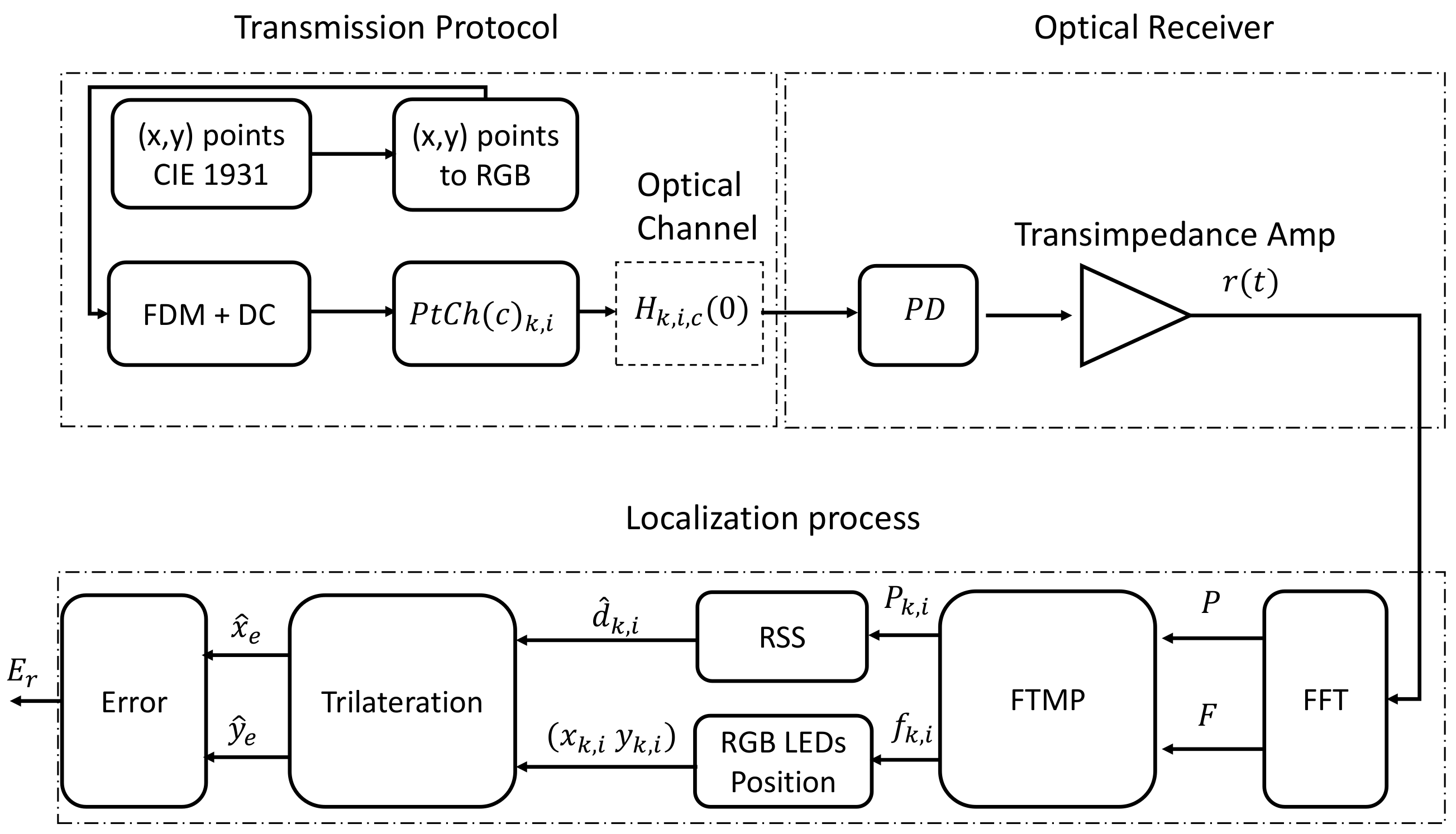
3. Proposed VLP System Model Based on RGB LEDs
3.1. System Model
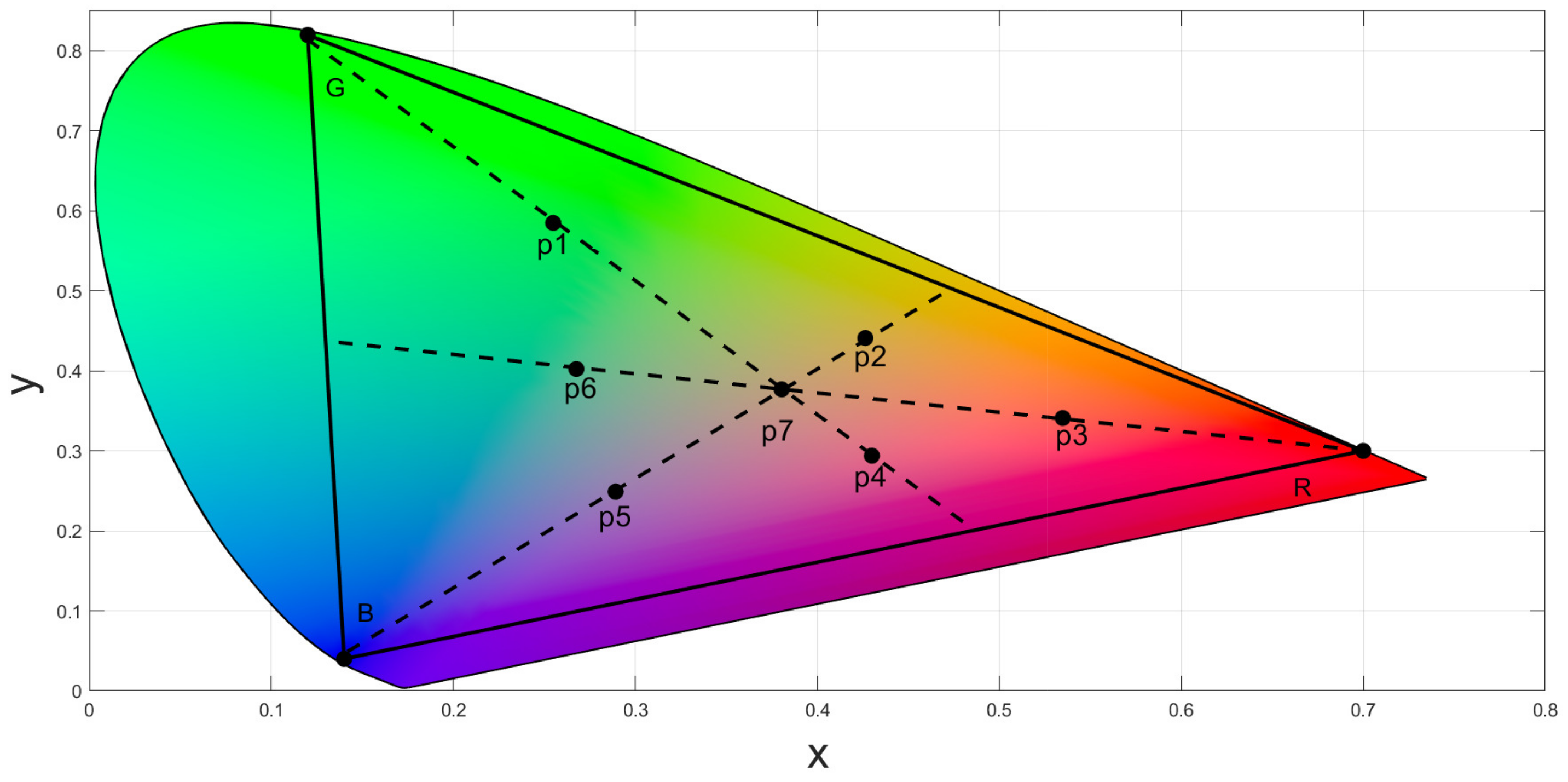
3.2. Transmission Protocol
3.3. Optical Receiver
3.4. Localization
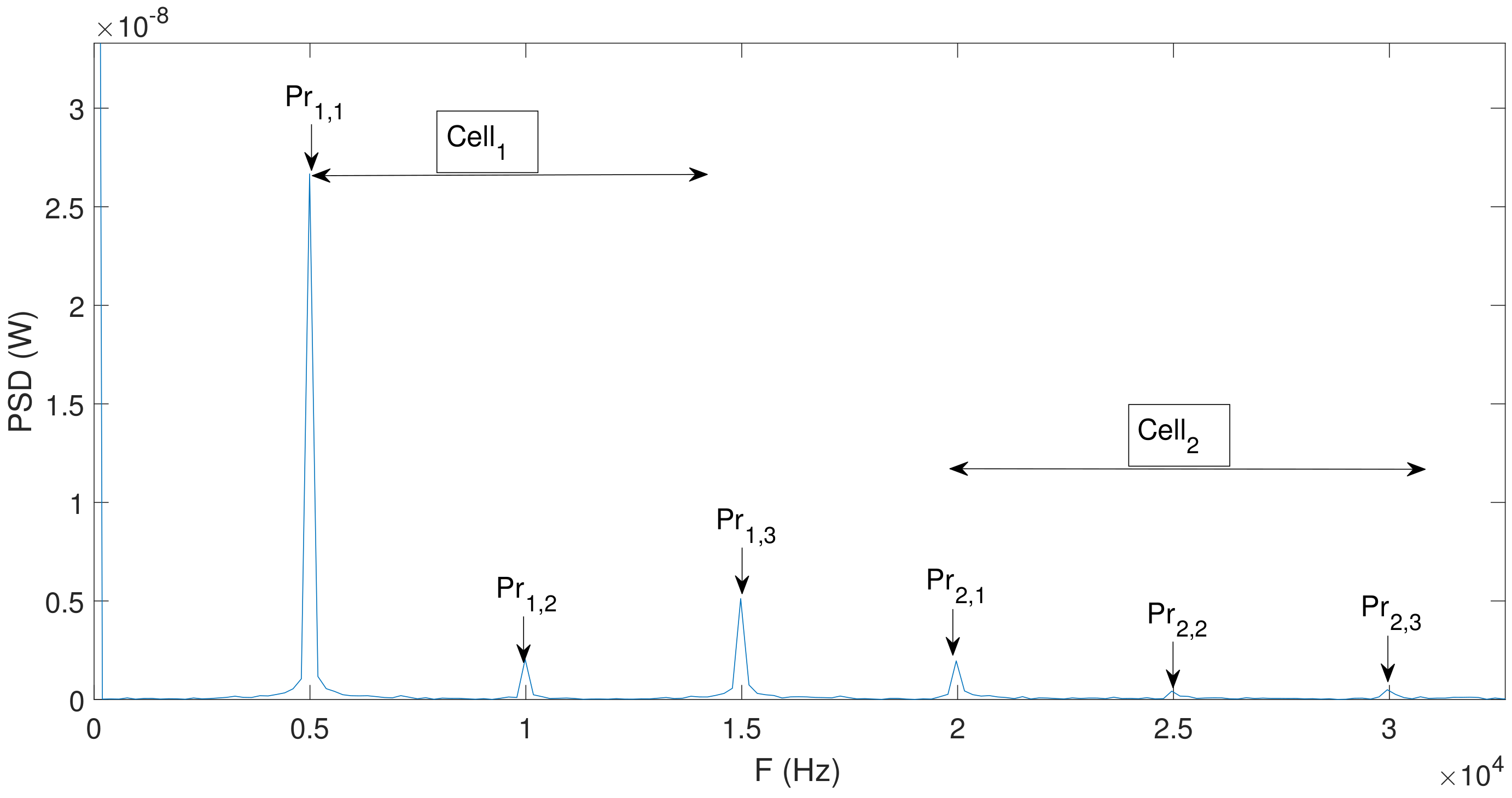
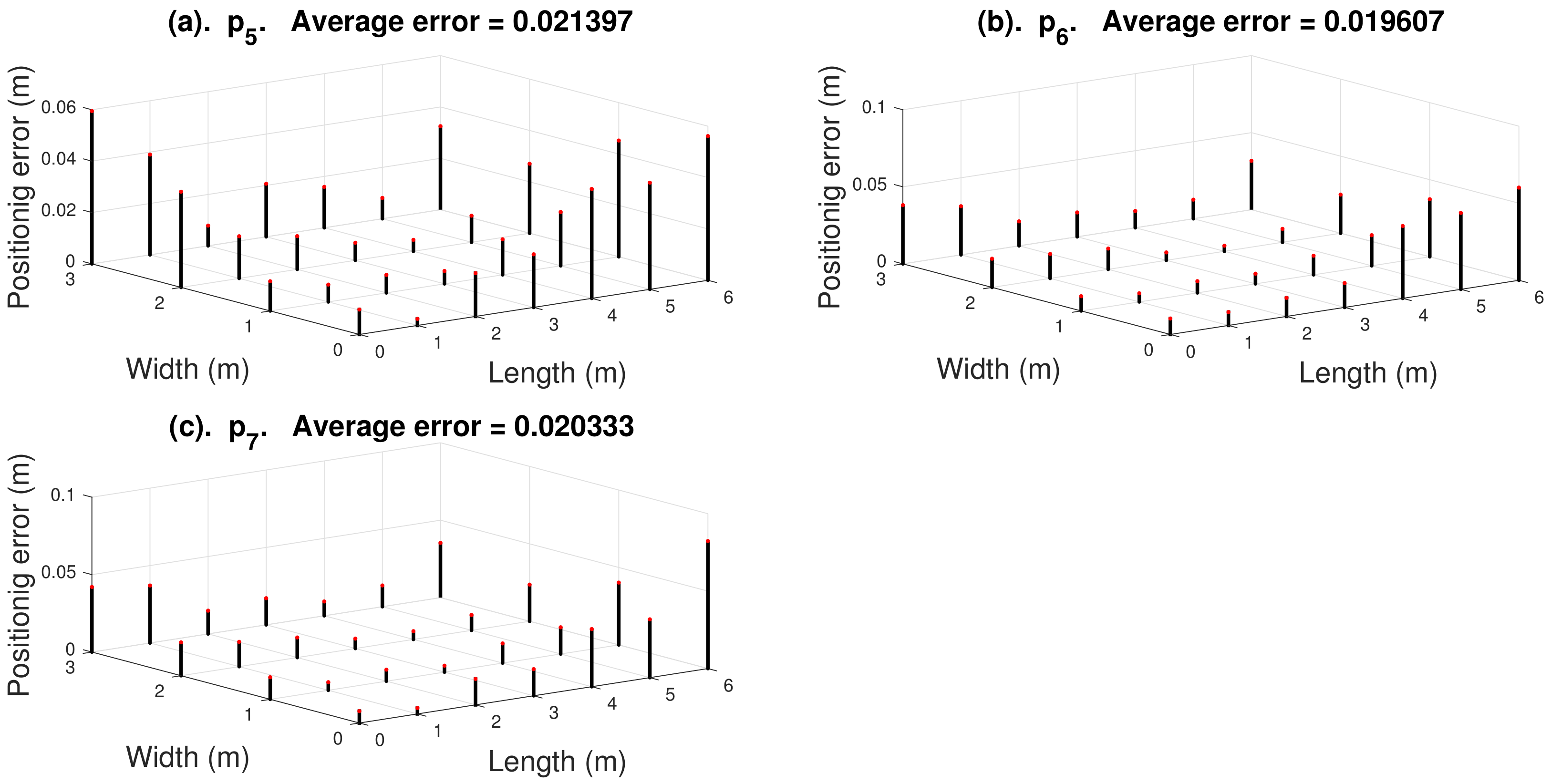
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Y.; Cao, Y.; Wu, Y.; Member, S.; Thompson, J.; Haas, H. A Survey of Positioning Systems Using Visible LED Lights. IEEE Commun. Surv. Tutor. 2018, 20, 1963–1988. [Google Scholar] [CrossRef] [Green Version]
- Yasir, M.; Ho, S.; Vellambi, B. Indoor Position Tracking Using Multiple Optical Receivers. J. Lightwave Technol. 2016, 34, 1166–1176. [Google Scholar] [CrossRef]
- Rahman, A.B.M.M.; Li, T.; Wang, Y. Recent Advances in Indoor Localization via Visible Lights: A Survey. Sensors 2020, 20, 1382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, P.; Pang, M.; Che, D.; Yin, Y.; Hu, D.; Gao, S. A Survey on Visible Light Positioning from Software Algorithms to Hardware. Wirel. Commun. Mob. Comput. 2021, 2021, 9739577. [Google Scholar] [CrossRef]
- Almadani, Y.; Ijaz, M.; Rajbhandari, S.; Raza, U.; Adebisi, B. Applications of Visible Light Communication for Distance Estimation: A Short Survey. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 261–265. [Google Scholar] [CrossRef]
- Chaudhary, N.; Alves, L.N.; Ghassemblooy, Z. Current Trends on Visible Light Positioning Techniques. In Proceedings of the 2019 2nd West Asian Colloquium on Optical Wireless Communications (WACOWC), Tehran, Iran, 27–28 April 2019; pp. 100–105. [Google Scholar] [CrossRef]
- Stevens, N.; Steendam, H. Magnitude of the Distance Estimation Bias in Received Signal Strength Visible Light Positioning. IEEE Commun. Lett. 2018, 22, 2250–2253. [Google Scholar] [CrossRef]
- Guo, X.; Ansari, N.; Hu, F.; Shao, Y.; Elikplim, N.R.; Li, L. A survey on fusion-based indoor positioning. IEEE Commun. Surv. Tutor. 2020, 22, 566–594. [Google Scholar] [CrossRef]
- Luo, J.; Fan, L.; Li, H. Indoor Positioning Systems Based on Visible Light Communication: State of the Art. IEEE Commun. Surv. Tutor. 2017, 19, 2871–2893. [Google Scholar] [CrossRef]
- Karunatilaka, D.; Zafar, F.; Kalavally, V.; Parthiban, R. LED Based Indoor Visible Light Communications: State of the Art. IEEE Commun. Surv. Tutor. 2015, 17, 1649–1678. [Google Scholar] [CrossRef]
- Do, T.H.; Yoo, M. An in-depth survey of visible light communication based positioning systems. Sensors 2016, 16, 678. [Google Scholar] [CrossRef] [Green Version]
- Popoola, O.; Sinanović, S.; Popoola, W.; Ramirez, R. Optical Boundaries for LED-Based Indoor Positioning System. Computation 2019, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.S.; Kim, D.R.; Yang, S.H.; Son, Y.H.; Han, S.K.; Liao, X.; Lin, K.; Chen, Y. An Indoor Visible Light Communication Positioning System Using a RF Carrier Allocation Technique. J. Lightwave Technol. 2013, 31, 131–144. [Google Scholar] [CrossRef]
- Hsu, C.W.; Wu, J.T.; Wang, H.Y.; Chow, C.W.; Lee, C.H.; Chu, M.T.; Yeh, C.H. Visible Light Positioning and Lighting Based on Identity Positioning and RF Carrier Allocation Technique Using a Solar Cell Receiver. IEEE Photonics J. 2016, 12, 1–7. [Google Scholar] [CrossRef]
- Wu, Y.C.; Hsu, K.L.; Liu, Y.; Hong, C.Y.; Chow, C.W.; Yeh, C.H.; Liao, X.L.; Lin, K.H.; Chen, Y.Y. Using Linear Interpolation to Reduce the Training Samples for Regression Based Visible Light Positioning System. IEEE Photonics J. 2020, 12, 1–5. [Google Scholar] [CrossRef]
- Xu, W.; Wang, J.; Shen, H.; Zhang, H.; You, X. Indoor Positioning for Multiphotodiode Device Using Visible-Light Communications. IEEE Photonics J. 2016, 8, 1–11. [Google Scholar]
- Cai, Y.; Guan, W.; Wu, Y.; Xie, C.; Chen, Y.; Fang, L. Indoor High Precision Three-Dimensional Positioning System Based on Visible Light Communication Using Particle Swarm Optimization. IEEE Photonics J. 2017, 9, 1–20. [Google Scholar] [CrossRef]
- Huang, N.; Gong, C.; Luo, J.; Xu, Z. Design and Demonstration of Robust Visible Light Positioning Based on Received Signal Strength. J. Lightwave Technol. 2020, 38, 5695–5707. [Google Scholar] [CrossRef]
- Costanzo, A.; Loscri, V. Error compensation in indoor positioning systems based on software defined visible light communication. Phys. Commun. 2019, 34, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zheng, H.; Liu, H.; Han, Z.; Ren, Z. Indoor High Precision Three-Dimensional Positioning System Based on Visible Light Communication Using Improved Hybrid Bat Algorithm. IEEE Photonics J. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Alam, F.; Parr, B.; Mander, S. Visible Light Positioning Based on Calibrated Propagation Model. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Anastou, A.C.; Delibasis, K.K.; Boulogeorgos, A.A.; Sandalidis, H.G.; Vavoulas, A.; Tasoulis, S.K. A Low Complexity Indoor Visible Light Positioning Method. IEEE Access 2021, 9, 57658–57673. [Google Scholar] [CrossRef]
- Little, T.; Rahaim, M.; Abdalla, I.; Lam, E.; Mcallister, R.; Vegni, A. A multi-cell lighting testbed for VLC and VLP. In Proceedings of the 2018 Global LiFi Congress, Paris, France, 8–9 February 2018; Volume 1, pp. 1–6. [Google Scholar]
- Yang, H.; Zhong, W.; Chen, C.; Alphones, A.; Du, P.; Zhang, S.; Xie, X. Coordinated Resource Allocation-Based Integrated Visible Light Communication and Positioning Systems for Indoor IoT. IEEE Trans. Wirel. Commun. 2020, 19, 4671–4684. [Google Scholar] [CrossRef]
- Vieira, M.A.; Vieira, M.; Louro, P.; Mateus, L.; Vieira, P. Indoor positioning system using a WDM device based on a-SiC:H technology. J. Lumin. 2017, 191, 135–138. [Google Scholar] [CrossRef]
- Martínez Ciro, R.A.; López Giraldo, F.E.; Betancur Perez, A.F.; Luna Rivera, J.M. Design and Implementation of a Multi-Colour Visible Light Communication System Based on a Light-to-Frequency Receiver. Photonics 2019, 6, 42. [Google Scholar] [CrossRef] [Green Version]
- IEEE Computer Society Sponsored by the IEEE Standards Association: IEEE Standard for Local and Metropolitan Area Networks—Part 15.7: Short-Range Wireless Optical Communication Using Visible Light. September 2011. Available online: https://standards.ieee.org/findstds/standard/802.15.7-2011.html (accessed on 27 November 2018).
- Mendes Matheus, L.E.; Borges Vieira, A.; Vieira, L.F.; Vieira, M.A.; Gnawali, O. Visible Light Communication: Concepts, Applications and Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 3204–3237. [Google Scholar] [CrossRef]
- Martínez Ciro, R.A.; López Giraldo, F.E.; Betancur Perez, A.F.; Luna Rivera, M. Characterization of Light-To-Frequency Converter for Visible Light Communication Systems. Electronics 2018, 7, 165. [Google Scholar] [CrossRef] [Green Version]
- Luna-Rivera, J.M.; Suarez-Rodriguez, C.; Guerra, V.; Perez-Jimenez, R.; Rabadan-Borges, J.; Rufo-Torres, J. Low-complexity colour-shift keying-based visible light communications system. IET Optoelectron. 2015, 9, 191–198. [Google Scholar] [CrossRef]
- CIE-1931, International Commission on Illumination, Colorimetry—Part 3: CIE Tristimulus Values, ISO 11664-3:2012(E)/CIE S014-3/E:2011. Available online: http://www.cie.co.at/publications/colorimetry-part-3-cie-tristimulus-values (accessed on 20 October 2020).
- Zhang, X.; Duan, J.; Fu, Y.; Shi, A. Theoretical accuracy analysis of indoor visible light communication positioning system based on Received Signal Strength Indicator. J. Lightwave Technol. 2014, 32, 4180–4186. [Google Scholar] [CrossRef]
- Lee, K.; Park, H.; Barry, J. Indoor channel characteristics for visible light communications. IEEE Commun. Lett. 2011, 15, 217–219. [Google Scholar] [CrossRef]
- Plets, D.; Bastiaens, S.; Martens, L.; Joseph, W. An Analysis of the Impact of LED Tilt on Visible Light Positioning Accuracy. Electronics 2019, 8, 389. [Google Scholar] [CrossRef] [Green Version]
- THORLABS, PDA36A(-EC) Si Switchable Gain Detector. Available online: https://www.thorlabs.com/thorproduct.cfm?partnumber=PDA36A-EC (accessed on 11 January 2021).


| Chromatic Point | ||
|---|---|---|
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Dimension space | m | RGB LED optical power for channel | 3.333 W |
| RGB 1 coordinates | (0.75, 0.75, 3) m | 5 kHz | |
| RGB 2 coordinates | (1.50, 2.25, 3) m | 10 kHz | |
| RGB 3 coordinates | (2.25, 0.75, 3) m | 15 kHz | |
| RGB 4 coordinates | (3.75, 2.25, 3) m | 20 kHz | |
| RGB 5 coordinates | (4.50, 0.75, 3) m | 25 kHz | |
| RGB 6 coordinates | (5.25, 2.25, 3) m | 30 kHz | |
| RGB LED half-power angle | 0.41 A/W | ||
| Detector area | m | 0.2 A/W | |
| V/A | 0.12 A/W | ||
| Scale factor | Noise (RMS) | V | |
| 1 | 1 | ||
| Sampling rate | 96,000 kHz | FFT points | 1500 |
| 300 Hz | 0.0733 | ||
| 0.0558 | |||
| 90 m | m | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Ciro, R.A.; López-Giraldo, F.E.; Luna-Rivera, J.M.; Ramírez-Aguilera, A.M. An Indoor Visible Light Positioning System for Multi-Cell Networks. Photonics 2022, 9, 146. https://doi.org/10.3390/photonics9030146
Martínez-Ciro RA, López-Giraldo FE, Luna-Rivera JM, Ramírez-Aguilera AM. An Indoor Visible Light Positioning System for Multi-Cell Networks. Photonics. 2022; 9(3):146. https://doi.org/10.3390/photonics9030146
Chicago/Turabian StyleMartínez-Ciro, Roger Alexander, Francisco Eugenio López-Giraldo, José Martín Luna-Rivera, and Atziry Magaly Ramírez-Aguilera. 2022. "An Indoor Visible Light Positioning System for Multi-Cell Networks" Photonics 9, no. 3: 146. https://doi.org/10.3390/photonics9030146
APA StyleMartínez-Ciro, R. A., López-Giraldo, F. E., Luna-Rivera, J. M., & Ramírez-Aguilera, A. M. (2022). An Indoor Visible Light Positioning System for Multi-Cell Networks. Photonics, 9(3), 146. https://doi.org/10.3390/photonics9030146






