Depolarization of Vector Light Beams on Propagation in Free Space
Abstract
:1. Introduction
2. Problem Formulation
Degree of Polarization
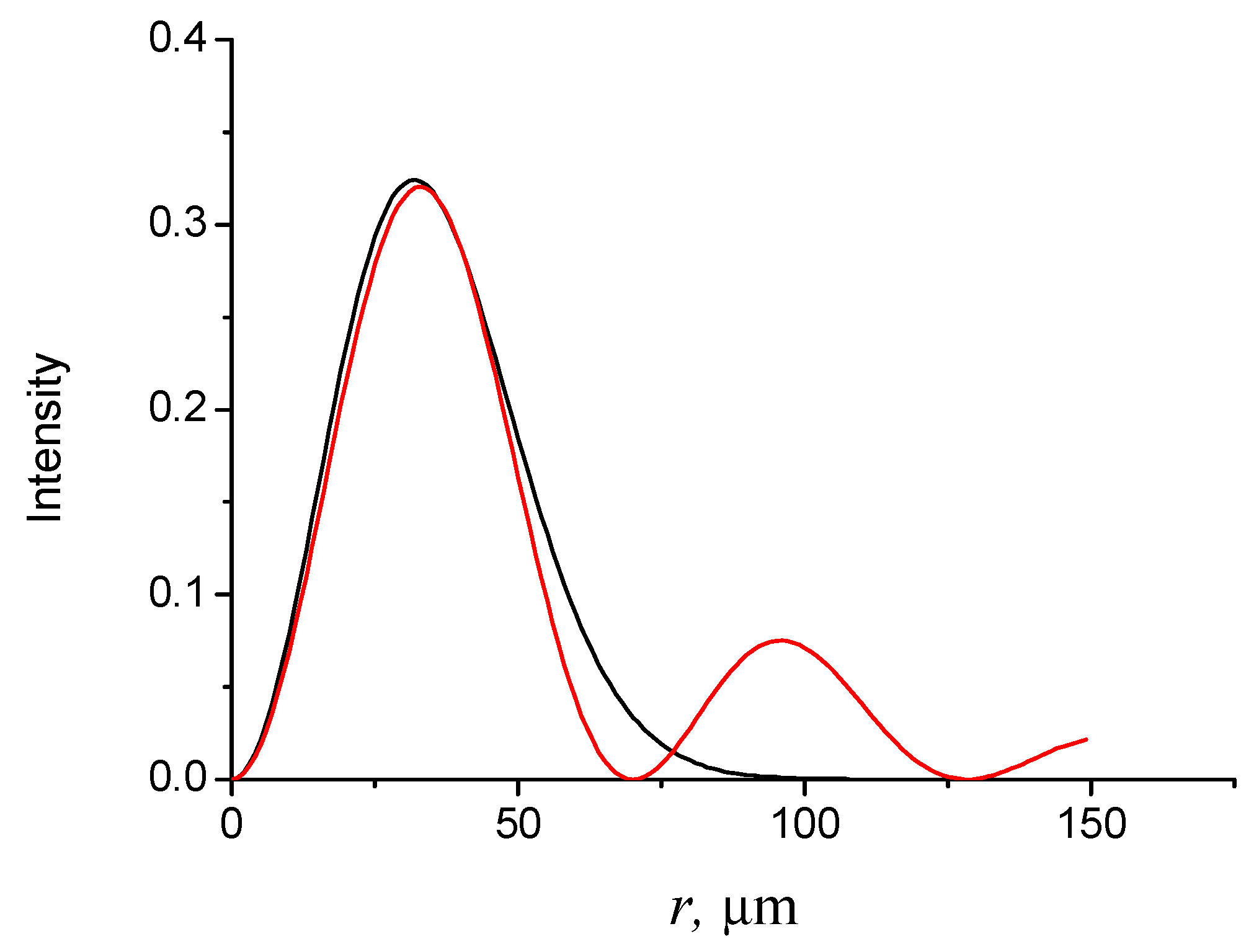
3. Simulation Results
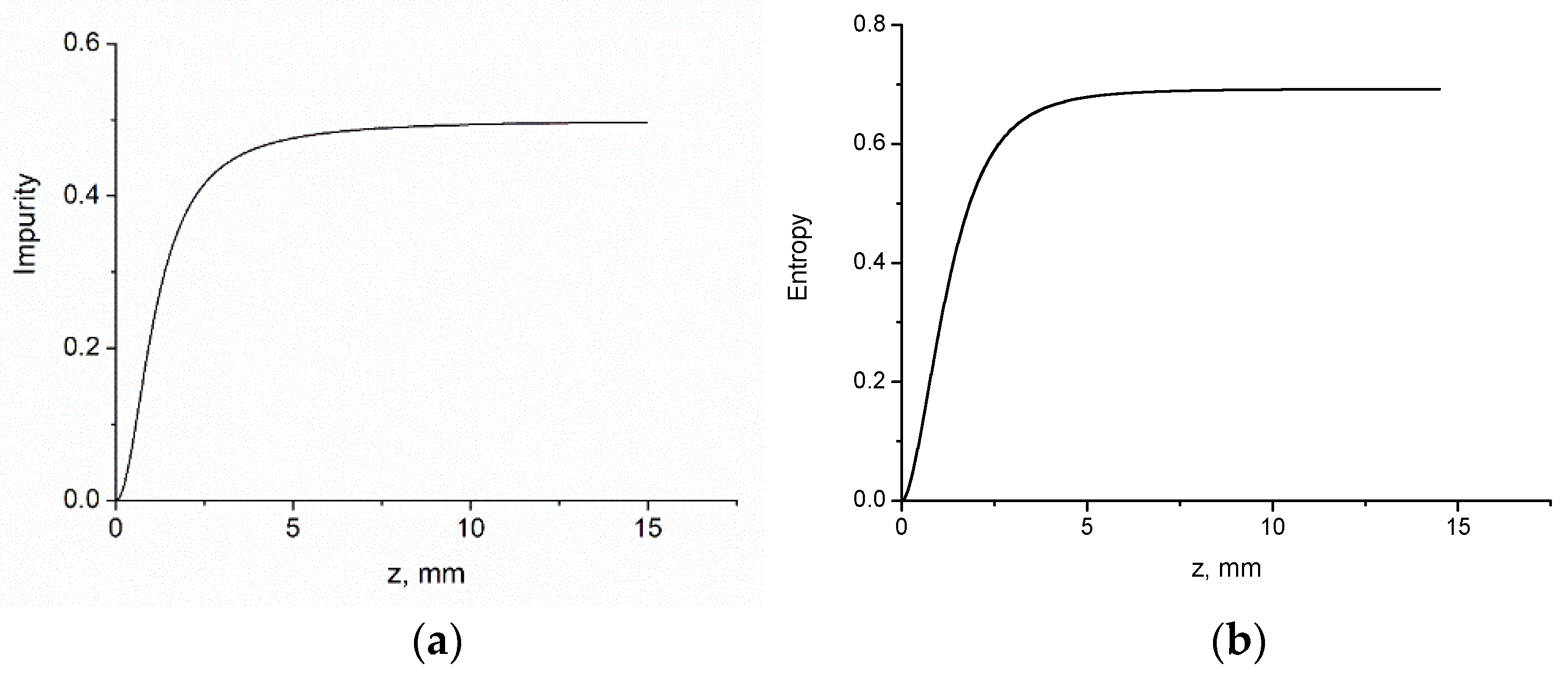
3.1. Purity
Purity Parameter
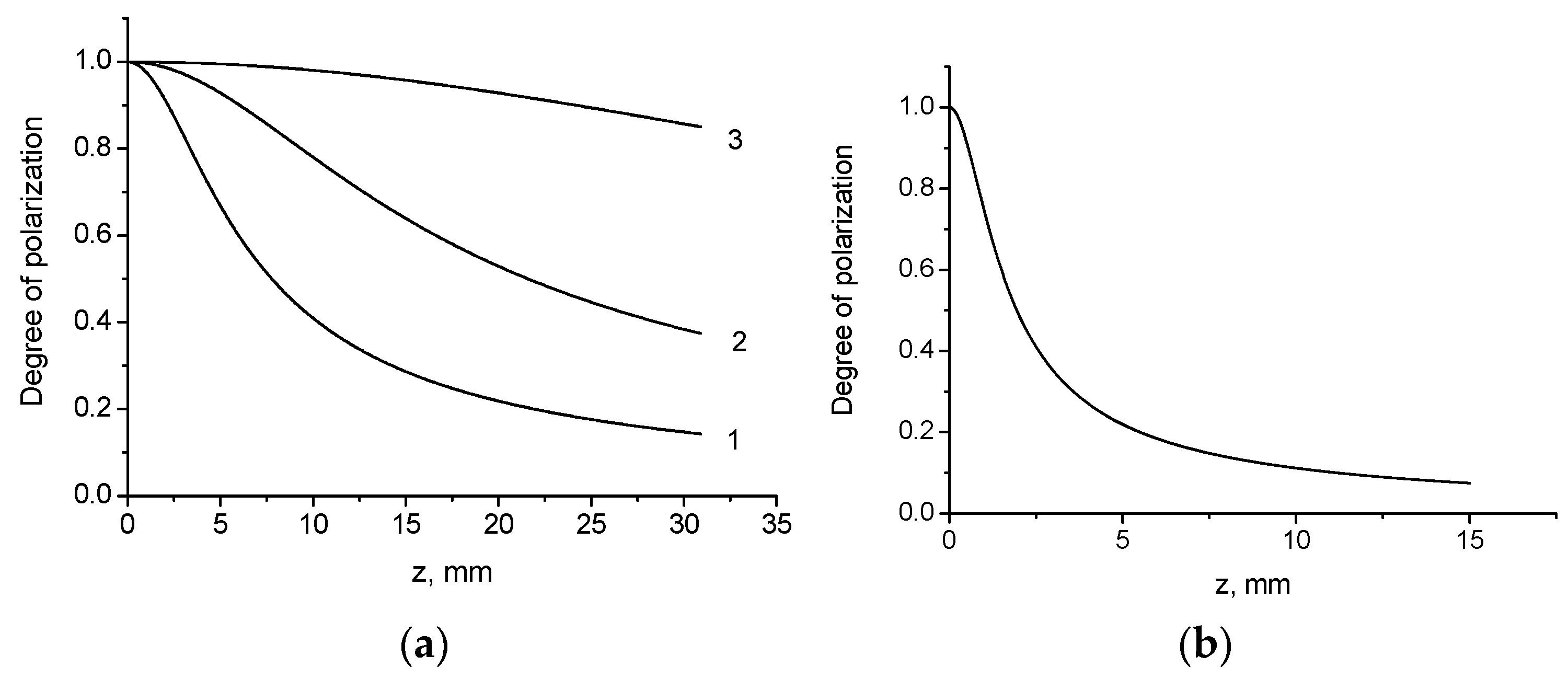
3.2. Degree of Polarization
3.2.1. Linear Polarization
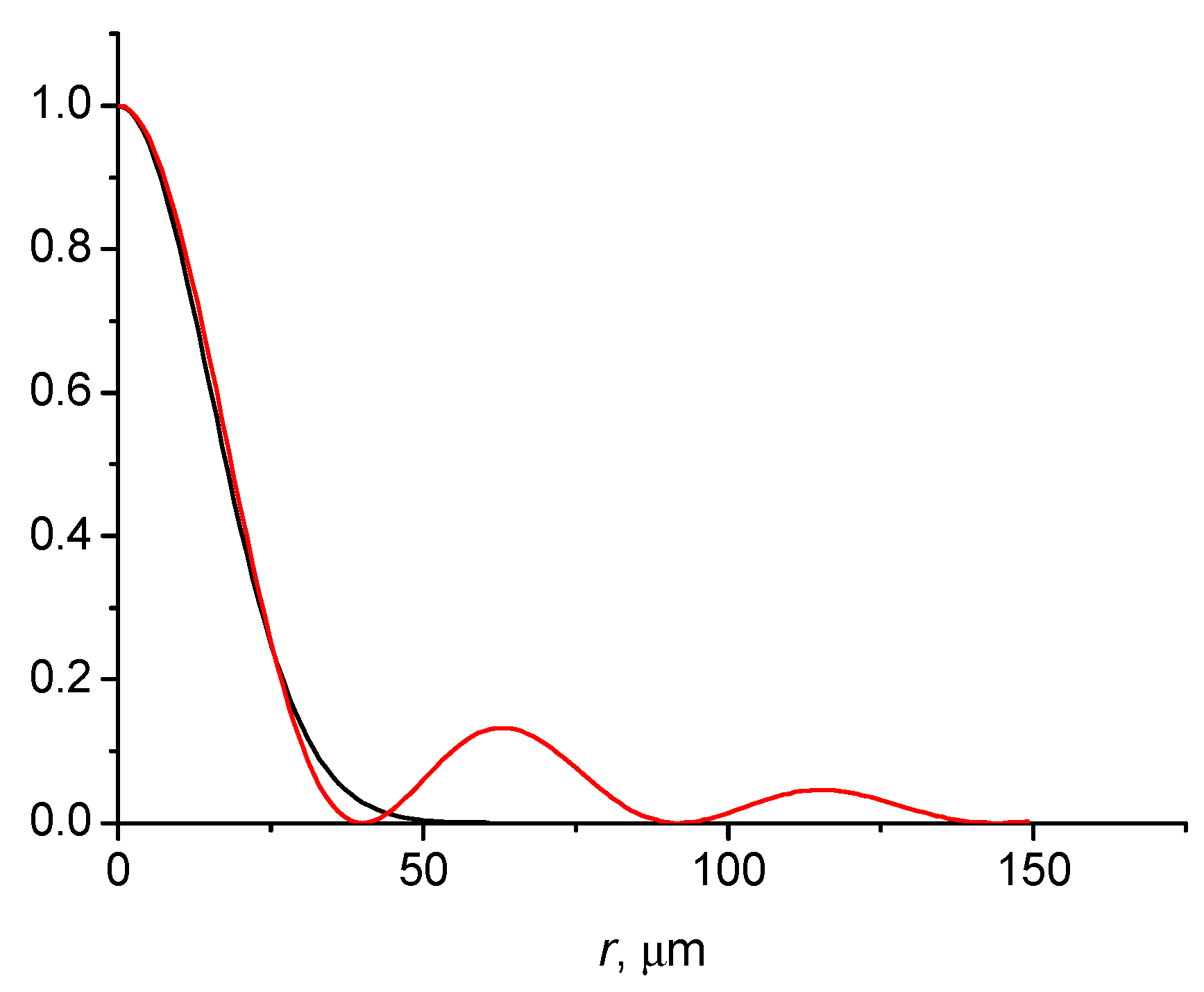
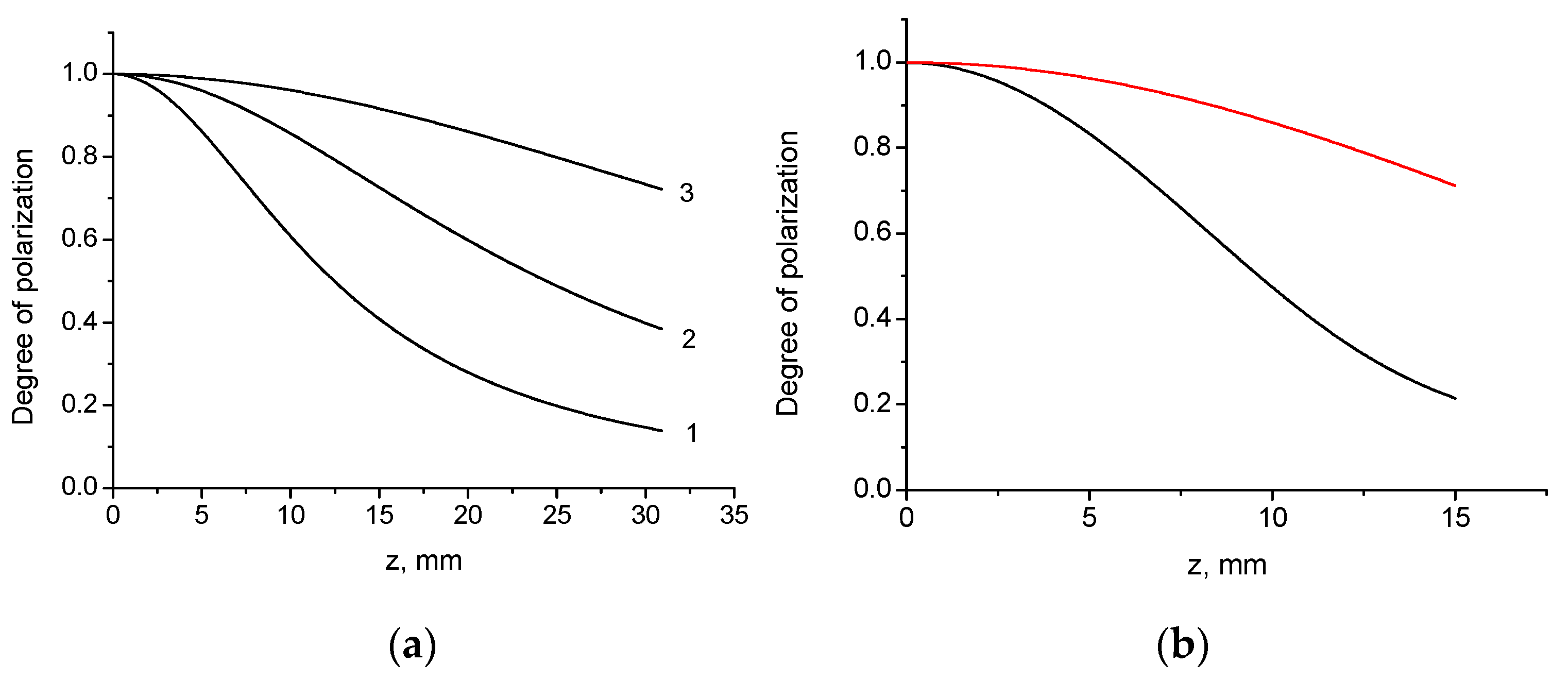
3.2.2. Radial Polarization
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Azzam, R.; Bashara, N. Ellipsometry and Polarized Light; North-Holland Publishing Company: New York, NY, USA, 1977. [Google Scholar]
- Chipman, R.; Lam, W.; Young, G. Polarized Light and Optical Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Tatarskii, V.I. Estimation of light depolarization by turbulent inhomogeneities of the atmosphere. Izv. VUZov Radiofizika 1967, 10, 1762–1765. [Google Scholar]
- Kravtzov, I.; Yu, A. Geometrical depolarization of light in a turbulent atmosphere. Izv. VUZov Radiofizika 1970, 13, 281–284. [Google Scholar]
- Rytov, S.M. On transition from wave to geometrical optics. Dokl. Akad. Nauk USSR 1938, 18, 263–266. [Google Scholar]
- Vladimirsky, V.V. On rotation of polarization plane in twisted ray of light. Dokl. Akad. Nauk USSR 1941, 31, 222–225. [Google Scholar]
- Cohen, L.G. Measured attenuation and depolarization of light transmitted along glass fibers. Bell Syst. Tech. J. 1971, 50, 23–42. [Google Scholar] [CrossRef]
- Smith, A.M. Polarization and magnetooptic properties of single-mode optical fiber. Appl. Opt. 1978, 17, 52–56. [Google Scholar] [CrossRef]
- Kaminov, I.P. Polarization in optical fibers. IEEE J. Quantum Electron. 1981, 17, 15–22. [Google Scholar] [CrossRef]
- Shatrov, A.D. Polarization effects in multimode graded-index fibers. Radiotekh. Elektr. 1988, 26, 505–512. [Google Scholar]
- Esayan, A.A.; Zel’dovich, B.Y. Depolarization of radiation in an ideal multimode graded-index optical fiber. Sov. J. Quantum Electron. 1988, 18, 149–150. [Google Scholar] [CrossRef]
- Kotov, O.I.; Marusov, O.L.; Nikolaev, O.L.; Filippov, V.N. Polarization properties of optical fibers. Modal approach. Opt. Spectr. 1991, 70, 924–927. [Google Scholar]
- Petrov, N.I. Depolarization of light in a graded-index isotropic medium. J. Mod. Opt. 1996, 43, 2239–2249. [Google Scholar] [CrossRef]
- Petrov, N.I. Evolution of polarization in an inhomogeneous isotropic medium. JETP 1997, 85, 1085–1093. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of Light in Optical Fibers: Effects of Diffraction and Spin-Orbit Interaction. Fibers 2021, 9, 34. [Google Scholar] [CrossRef]
- Zel’dovich, B.Y.; Kundikova, N.D. Intrafibre rotation of the plane of polarization. Quantum Electr. 1995, 25, 172–174. [Google Scholar] [CrossRef]
- James, D.F.V. Change of polarization of light beams on propagation in free space. J. Opt. Soc. Am. A 1994, 11, 1641–1643. [Google Scholar] [CrossRef]
- Agrawal, G.P.; Wolf, E. Propagation-induced polarization changes in partially coherent optical beams. J. Opt. Soc. Am. A 2000, 17, 2019–2023. [Google Scholar] [CrossRef] [Green Version]
- Korotkova, O.; Wolf, E. Changes in the state of polarization of a random electromagnetic beam on propagation. Opt. Commun. 2005, 246, 35–43. [Google Scholar] [CrossRef]
- Korotkova, O.; Hoover, B.G.; Gamiz, V.L.; Wolf, E. Coherence and polarization properties of far fields generated by quasi-homogeneous planar electromagnetic sources. J. Opt. Soc. Am. A 2005, 22, 2547–2556. [Google Scholar] [CrossRef]
- Korotkova, O.; Visser, T.D.; Wolf, E. Polarization properties of stochastic electromagnetic beams. Opt. Commun. 2008, 281, 515–520. [Google Scholar] [CrossRef]
- Ellis, J.; Dogariu, A.; Ponomarenko, S.; Wolf, E. Degree of polarization of statistically stationary electromagnetic fields. Opt. Commun. 2005, 248, 333–337. [Google Scholar] [CrossRef]
- Salem, M.; Wolf, E. Coherence-induced polarization changes in light beams. Opt. Lett. 2008, 33, 1180–1182. [Google Scholar] [CrossRef] [PubMed]
- Vidal, I.; Fonseca, E.J.S.; Hickmann, J.M. Light polarization control during free-space propagation using coherence. Phys. Rev. A 2011, 84, 033836. [Google Scholar] [CrossRef]
- Wu, G.; Wang, F.; Cai, Y. Coherence and polarization properties of a radially polarized beam with variable spatial coherence. Opt. Express 2012, 20, 28301–28318. [Google Scholar] [CrossRef] [PubMed]
- Wolf, E. Polarization invariance in beam propagation. Opt. Lett. 2007, 32, 3400–3401. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Wolf, E. Light beams whose degree of polarization does not change on propagation. Opt. Commun. 2008, 281, 3067–3070. [Google Scholar] [CrossRef]
- Gori, F. Polarization basis for vortex beams. J. Opt. Soc. Am. A 2001, 18, 1612–1617. [Google Scholar] [CrossRef] [Green Version]
- Martınez-Herrero, R.; Mejıas, P.M. Propagation of light fields with radial or azimuthal polarization distribution at a transverse plane. Opt. Express 2008, 16, 9021–9033. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Santarsiero, M.; de Sande, J.C.G.; Piquero, G.; Gori, F. Coherence-polarization properties of fields radiated from transversely periodic electromagnetic sources. J. Opt. 2013, 15, 055701. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G. Sharp Focusing of a Hybrid Vector Beam with a Polarization Singularity. Photonics 2021, 8, 227. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Volotovskiy, S.G.; Ustinov, A.V.; Fomchenkov, S.A.; Pavelyev, V.S.; Schröter, S.; Duparré, M. Generation of Multiple Vector Optical Bottle Beams. Photonics 2021, 8, 218. [Google Scholar] [CrossRef]
- Pääkkönen, P.; Tervo, J.; Vahimaa, P.; Turunen, J.; Gori, F. General vectorial decomposition of electromagnetic fields with application to propagation-invariant and rotating fields. Opt. Express 2002, 10, 949–959. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O. Sufficient condition for polarization invariance of beams generated by quasi-homogeneous sources. Opt. Lett. 2011, 36, 3768–3770. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Herrero, R.; Mejías, P.M. Electromagnetic fields that remain totally polarized under propagation. Opt. Commun. 2007, 279, 20–22. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Piquero, G.; Suárez-Bermejo, J.C.; Santarsiero, M. Mueller Matrix Polarimetry with Invariant Polarization Pattern Beams. Photonics 2021, 8, 491. [Google Scholar] [CrossRef]
- Philip, G.M.; Viswanathan, N.K. Generation of spirally polarized propagation-invariant beam using fiber microaxicon. Opt. Lett. 2011, 36, 3906–3908. [Google Scholar] [CrossRef]
- Alieva, T.; Rodrigo, J.A.; Camara, A.; Abramochkin, E. Partially coherent stable and spiral beams. J. Opt. Soc. Am. A 2013, 30, 2237–2243. [Google Scholar] [CrossRef] [Green Version]
- Freund, I. Polarization singularities in optical lattices. Opt. Lett. 2004, 29, 875–877. [Google Scholar] [CrossRef]
- Freund, I. Ordinary polarization singularities in three-dimensional optical fields. Opt. Lett. 2012, 37, 2223–2225. [Google Scholar] [CrossRef]
- Khonina, S.N. Vortex beams with high-order cylindrical polarization: Features of focal distributions. Appl. Phys. B 2019, 125, 100. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, K.; Hu, G.; Hu, M.; Tong, T.; Mu, Q.; Gao, H.; Li, F.; Qiu, C.-W.; Zhang, P. Arbitrary cylindrical vector beam generation enabled by polarization-selective Gouy phase shifter. Photonics Res. 2021, 9, 1048–1054. [Google Scholar] [CrossRef]
- Ruchi; Senthilkumaran, P.; Pal, S.K. Phase Singularities to Polarization Singularities. Int. J. Opt. 2020, 2020, 2812803. [Google Scholar] [CrossRef]
- Wang, Q.; Tu, C.H.; Li, Y.N.; Wang, H.T. Polarization singularities: Progress, fundamental physics, and prospects. APL Photonics 2021, 6, 040901. [Google Scholar] [CrossRef]
- Tovar, A.A. Production and propagation of cylindrically polarized Laguerre–Gaussian laser beams. J. Opt. Soc. Am. A 1998, 15, 2705–2711. [Google Scholar] [CrossRef]
- Deng, D. Nonparaxial propagation of radially polarized light beams. J. Opt. Soc. Am. B 2006, 23, 1228–1234. [Google Scholar] [CrossRef]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-order Poincaré sphere, Stokes parameters, and the angular momentum of light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, X.; Liu, Y.; Ling, X.; Luo, H.; Wen, S. Generation of arbitrary cylindrical vector beams on the higher order Poincaré sphere. Opt. Lett. 2014, 39, 5274–5276. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Liu, Y.; Ke, Y.; Liu, Y.; Shu, W.; Luo, H.; Wen, S. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere. Photonics Res. 2017, 5, 15–21. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Liu, W.; Shi, L.; Kivshar, Y. Topological polarization singularities in metaphotonics. Nanophotonics 2021, 10, 1469–1486. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarization optics for biomedical and clinical applications: A review. Light Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef]
- Lim, S.W.D.; Park, J.S.; Meretska, M.L.; Dorrah, A.H.; Capasso, F. Engineering phase and polarization singularity sheets. Nat. Commun. 2021, 12, 4190. [Google Scholar]
- Zhang, Y.B.; Liu, H.; Cheng, H.; Tian, J.G.; Chen, S.Q. Multidimensional manipulation of wave fields based on artificial microstructures. Opto-Electron. Adv. 2020, 3, 200002. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, S.; Pu, M.; He, Q.; Jin, J.; Xu, M.; Zhang, Y.; Gao, P.; Luo, X. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light Sci. Appl. 2021, 10, 63. [Google Scholar] [CrossRef] [PubMed]
- Gori, F. Matrix treatment for partially polarized, partially coherent beams. Opt. Lett. 1998, 23, 241–243. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. J. Opt. Soc. Am. 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Turunen, J.; Friberg, A.T. Self-imaging and propagation-invariance in electromagnetic fields. Pure Appl. Opt. 1993, 2, 51–60. [Google Scholar] [CrossRef]
- Bouchal, Z.; Olivik, M. Non-diffractive vector Bessel beams. J. Mod. Opt. 1995, 42, 1555–1566. [Google Scholar] [CrossRef]
- Petrov, N.I. Speed of structured light pulses in free space. Sci. Rep. 2019, 9, 18332. [Google Scholar] [CrossRef]
- Krivoshlykov, S.G.; Petrov, N.I.; Sisakyan, I.N. Density-matrix formalism for partially coherent optical fields propagating in slightly inhomogeneous media. Opt. Quantum Electr. 1986, 18, 253–264. [Google Scholar] [CrossRef]
- Moya-Cessa, H.; Moya-Cessa, J.R.; Landgrave, J.E.A.; Martinez-Niconoff, G.; Perez-Leija, A.; Friberg, A.T. Degree of polarization and quantum-mechanical purity. J. Eur. Opt. Soc. Rapid Publ. 2008, 3, 08014. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector and Tensor Polarizations of Light Beams. Laser Phys. 2008, 18, 522–525. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-orbit and tensor interactions of light in inhomogeneous isotropic media. Phys. Rev. A 2013, 88, 023815. [Google Scholar] [CrossRef]
- Qian, X.F.; Eberly, J.H. Entanglement and classical polarization states. Opt. Lett. 2011, 36, 4110–4112. [Google Scholar] [CrossRef] [PubMed]
- Otte, E.; Rosales-Guzmán, C.; Ndagano, B.; Denz, C.; Forbes, A. Entanglement beating in free space through spin–orbit coupling. Light Sci. Appl. 2018, 7, 18009. [Google Scholar] [CrossRef]
- Otte, E.; Nape, I.; Rosales-Guzmán, C.; Valles, A.; Denz, C.; Forbes, A. Recovery of nonseparability in self-healing vector Bessel beams. Phys. Rev. A 2018, 98, 053818. [Google Scholar] [CrossRef] [Green Version]
- Aiello, A.; Toppel, F.; Marquardt, C.; Giacobino, E.; Leuchs, G. Quantum−like nonseparable structures in optical beams. New J. Phys. 2015, 17, 043024. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector Laguerre–Gauss beams with polarization-orbital angular momentum entanglement in a graded-index medium. J. Opt. Soc. Am. A 2016, 33, 1363–1369. [Google Scholar] [CrossRef] [Green Version]
- Petrov, N.I. Splitting of levels in a cylindrical dielectric waveguide. Opt. Lett. 2013, 38, 2020–2022. [Google Scholar] [CrossRef] [Green Version]
- Carozzi, T.; Karlsson, R.; Bergman, J. Parameters characterizing electromagnetic wave polarization. Phys. Rev. E 2000, 61, 2024–2028. [Google Scholar] [CrossRef] [Green Version]
- Setälä, T.; Shevchenko, A.; Kaivola, M.; Friberg, A.T. Degree of polarization for optical near fields. Phys. Rev. E 2002, 66, 016615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindfors, K.; Setälä, T.; Kaivola, M.; Friberg, A.T. Degree of polarization in tightly focused optical fields. J. Opt. Soc. Am. A 2005, 22, 561–568. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sheppard, C.J.R. Jones and Stokes parameters for polarization in three dimensions. Phys. Rev. A 2014, 90, 023809. [Google Scholar] [CrossRef]
- Sheppard, C.J.R. Partial polarization in three dimensions. J. Opt. Soc. Am. A 2011, 28, 1938–1947. [Google Scholar] [CrossRef]
- Gil, J.J. Geometric Interpretation and General Classification of Three-Dimensional Polarization States through the Intrinsic Stokes Parameters. Photonics 2021, 8, 315. [Google Scholar] [CrossRef]
- Wu, G. Propagation properties of a radially polarized partially coherent twisted beam in free space. J. Opt. Soc. Am. A 2016, 33, 345–350. [Google Scholar] [CrossRef]
- Zhao, X.; Visser, T.D.; Agrawal, G.P. Controlling the degree of polarization of partially coherent electromagnetic beams with lenses. Opt. Lett. 2018, 43, 2344–2347. [Google Scholar] [CrossRef]
- Ostrovsky, A.S.; García-García, J.; Rickenstorff-Parrao, C.; Olvera-Santamaria, M.A. Partially coherent diffraction-free vortex beams with a Bessel-mode structure. Opt Lett. 2017, 42, 5182–5185. [Google Scholar] [CrossRef]
- Krivoshlykov, S.G.; Petrov, N.I.; Sisakyan, I.N. Spatial coherence of optical fields in longitudinally inhomogeneous media with the square-law index profile. Sov. J. Quantum Electron. 1985, 15, 330–338. [Google Scholar] [CrossRef]
- Joshi, S.; Khan, S.N.; Manisha; Senthilkumaran, P.; Kanseri, B. Coherence-induced polarization effects in vector vortex beams. Opt. Lett. 2020, 45, 4815–4818. [Google Scholar] [CrossRef]
- Dong, Y.; Feng, F.; Chen, Y.; Zhao, C.; Cai, Y. Statistical properties of a nonparaxial cylindrical vector partially coherent field in free space. Opt. Express 2012, 20, 15908–15927. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Du, S.; Dong, Y.; Wang, F.; Zhao, C.; Cai, Y. Nonparaxial propagation properties of a vector partially coherent dark hollow beam. J. Opt. Soc. Am. A 2013, 30, 1358–1372. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Cui, Y. Nonparaxial and paraxial focusing of azimuthal-variant vector beams. Opt. Express 2012, 20, 17684–17694. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Xu, D.; Pan, Y.; Cui, Y. Nonparaxial propagation and focusing properties of azimuthal-variant vector fields diffracted by an annular aperture. J. Opt. Soc. Am. A 2014, 31, 1657–1665. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Guo, Q.; Wu, L.; Yang, X. Propagation of radially polarized elegant light beams. J. Opt. Soc. Am. B 2007, 24, 636–643. [Google Scholar] [CrossRef]
- Deng, D.; Guo, Q. Analytical vectorial structure of radially polarized light beams. Opt. Lett. 2007, 32, 2711–2713. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, P.P.; Cook, G.; Evans, D.R. A q-parameter approach to analysis of propagation, focusing, and waveguiding of radially polarized Gaussian beams. J. Opt. Soc. Am. A 2009, 26, 1366–1374. [Google Scholar] [CrossRef]
- Borghi, R.; Santarsiero, M. Nonparaxial propagation of spirally polarized optical beams. J. Opt. Soc. Am. A 2004, 21, 2029–2037. [Google Scholar] [CrossRef]
- Cui, X.; Wang, C.; Jia, X. Nonparaxial propagation of vector vortex beams diffracted by a circular aperture. J. Opt. Soc. Am. A 2019, 36, 115–123. [Google Scholar] [CrossRef]
- Guo, L.; Chen, L.; Lin, R.; Zhang, M.; Dong, Y.; Chen, Y.; Cai, Y. Nonparaxial Propagation Properties of Specially Correlated Radially Polarized Beams in Free Space. Appl. Sci. 2019, 9, 997. [Google Scholar] [CrossRef] [Green Version]
- Petrov, N.I. Nonparaxial focusing of wave beams in a graded-index medium. Rus. J. Quantum Electr. 1999, 29, 249–255. [Google Scholar] [CrossRef]
- Petrov, N.I. Focusing of beams into subwavelength area in an inhomogeneous medium. Opt. Express 2001, 9, 658–673. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I. Macroscopic quantum effects for classical light. Phys. Rev. A 2014, 90, 043814. [Google Scholar] [CrossRef] [Green Version]
- Petrov, N.I. Reflection and transmission of strongly focused light beams at a dielectric interface. J. Mod. Opt. 2005, 52, 1545–1556. [Google Scholar] [CrossRef]
- Norrman, A.; Gil, J.J.; Friberg, A.T.; Setälä, T. Polarimetric nonregularity of evanescent waves. Opt. Lett. 2019, 44, 215–218. [Google Scholar] [CrossRef]
- Petrov, N.I. Evanescent and propagating fields of a strongly focused beam. J. Opt. Soc. Am. A 2003, 20, 2385–2389. [Google Scholar] [CrossRef]
- Voipio, T.; Setala, T.; Friberg, A.T. Partial polarization theory of pulsed optical beams. J. Opt. Soc. Am. A 2013, 30, 71–81. [Google Scholar] [CrossRef]
- Petrov, N.I.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Large positive and negative Goos-Hänchen shifts near the surface plasmon resonance in subwavelength grating. Opt. Express 2020, 28, 7552–7564. [Google Scholar] [CrossRef]
- Petrov, N.I. Splitting the bandwidth of a frustrated total internal reflection filter with nanoparticle inclusions. OSA Contin. 2020, 3, 2591–2601. [Google Scholar] [CrossRef]
- Petrov, N.I. Frustrated-total-internal-reflection-based thin-film color separator. Opt. Lett. 2007, 32, 2744–2746. [Google Scholar] [CrossRef]
- Petrov, N.I. Achromatic Polarization rotator. Appl. Opt. 2007, 46, 6340–6343. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I.; Nikitin, V.G.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Subwavelength diffractive color beam combiner. Appl. Opt. 2014, 53, 5740–5744. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.; Khromov, M.; Sokolov, Y. Multi-View 3D Integral Imaging Systems Using Projectors and Mobile Devices. Photonics 2021, 8, 331. [Google Scholar] [CrossRef]
- Petrov, N.I.; Petrova, G.N. Diffraction of partially-coherent light beams by microlens arrays. Opt. Express 2017, 25, 22545–22564. [Google Scholar] [CrossRef]
- Soifer, V.A.; Kharitonov, S.I.; Khonina, S.N.; Strelkov, Y.S.; Porfirev, A.P. Spiral Caustics of Vortex Beams. Photonics 2021, 8, 24. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Karpeev, S.V.; Porfirev, A.P. Diffractive optical elements for multiplexing structured laser beams. Quantum Electron. 2020, 50, 629–635. [Google Scholar] [CrossRef]
- Bezus, E.A.; Bykov, D.A.; Doskolovich, L.L. Integrated diffraction gratings on the Bloch surface wave platform supporting bound states in the continuum. Nanophotonics 2021, 10, 4331–4340. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Tamagnone, M.; Rubin, N.A.; Zaidi, A.; Capasso, F. Introducing Berry phase gradients along the optical path via propagation-dependent polarization transformations. Nanophotonics 2021, 11, 19. [Google Scholar] [CrossRef]
- Petrov, N.I. Evolution of Berry’s phase in a graded-index medium. Phys. Lett. A 1997, 234, 239–250. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse and longitudinal angular momenta of light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Eismann, J.S.; Nicholls, L.H.; Roth, D.J.; Alonso, M.A.; Banzer, P.; Rodríguez-Fortuño, F.J.; Zayats, A.V.; Nori, F.; Bliokh, K.Y. Transverse spinning of unpolarized light. Nat. Photonics 2021, 15, 156–161. [Google Scholar] [CrossRef]
- Ketara, M.L.; Kobayashi, H.; Brasselet, E. Sensitive vectorial optomechanical footprint of light in soft condensed matter. Nat. Photonics 2021, 15, 121–124. [Google Scholar] [CrossRef]
- Cardano, F.; Marrucci, L. Longitudinal fields and transverse rotations. Nat. Photonics 2021, 15, 72–74. [Google Scholar] [CrossRef]
- Lindfors, K.; Priimagi, A.; Setälä, T.; Shevchenko, A.; Friberg, A.T.; Kaivola, M. Local polarization of tightly focused unpolarized light. Nat. Photonics 2007, 1, 228–231. [Google Scholar] [CrossRef]
- Marrucci, L. Spin gives direction. Nat. Photonics 2014, 11, 9–10. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Sciarrino, F.; Laing, A.; Thomson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, N. Depolarization of Vector Light Beams on Propagation in Free Space. Photonics 2022, 9, 162. https://doi.org/10.3390/photonics9030162
Petrov N. Depolarization of Vector Light Beams on Propagation in Free Space. Photonics. 2022; 9(3):162. https://doi.org/10.3390/photonics9030162
Chicago/Turabian StylePetrov, Nikolai. 2022. "Depolarization of Vector Light Beams on Propagation in Free Space" Photonics 9, no. 3: 162. https://doi.org/10.3390/photonics9030162
APA StylePetrov, N. (2022). Depolarization of Vector Light Beams on Propagation in Free Space. Photonics, 9(3), 162. https://doi.org/10.3390/photonics9030162




