A Chaotic Second Order Oscillation JAYA Algorithm for Parameter Extraction of Photovoltaic Models

Abstract

In order to identify the parameters of photovoltaic (PV) cells and modules more accurately, reliably and efficiently, a chaotic second order oscillation JAYA algorithm (CSOOJAYA) is proposed. Firstly, both logical chaotic map and the mutation strategy are brought in enhancing the population diversity and improving exploitation. Secondly, in order to better balance exploration and exploitation, the second order oscillation factor is added, which not only improves the diversity of the population, but also has strong exploration at the beginning of the iteration and strong exploitation at the end of the iteration. In order to balance the two abilities, the self-adaptive weight is introduced into the CSOOJAYA algorithm to regulate individuals the tendency of moving toward the optimal solution and escaping from the worst solution, so as to enhance the search efficiency and exploitation. In order to validate the behavior of CSOOJAYA, it is employed to the parameter identification problem of PV models. Finally, the experimental results show that CSOOJAYA delivers excellent behavior in the aspects of convergence, reliability and accuracy.

1. Introduction

In order to alleviate the greenhouse effect and solve problems such as global warming, the application of renewable energy has attracted much attention [1]. Among the renewable energy sources, solar energy is considered as one of the most promising renewable energy source because of its green, clean, widely distributed and free energy [2]. Solar PV systems can directly convert solar energy into electrical energy, so it has become one of the most widely used power generation technologies [3]. However, PV systems are susceptible to external factors, especially irradiance and temperature [4]. PV arrays tend to degrade over time under harsh environmental conditions, significantly affecting the behavior and utilization efficiency of PV systems [5]. 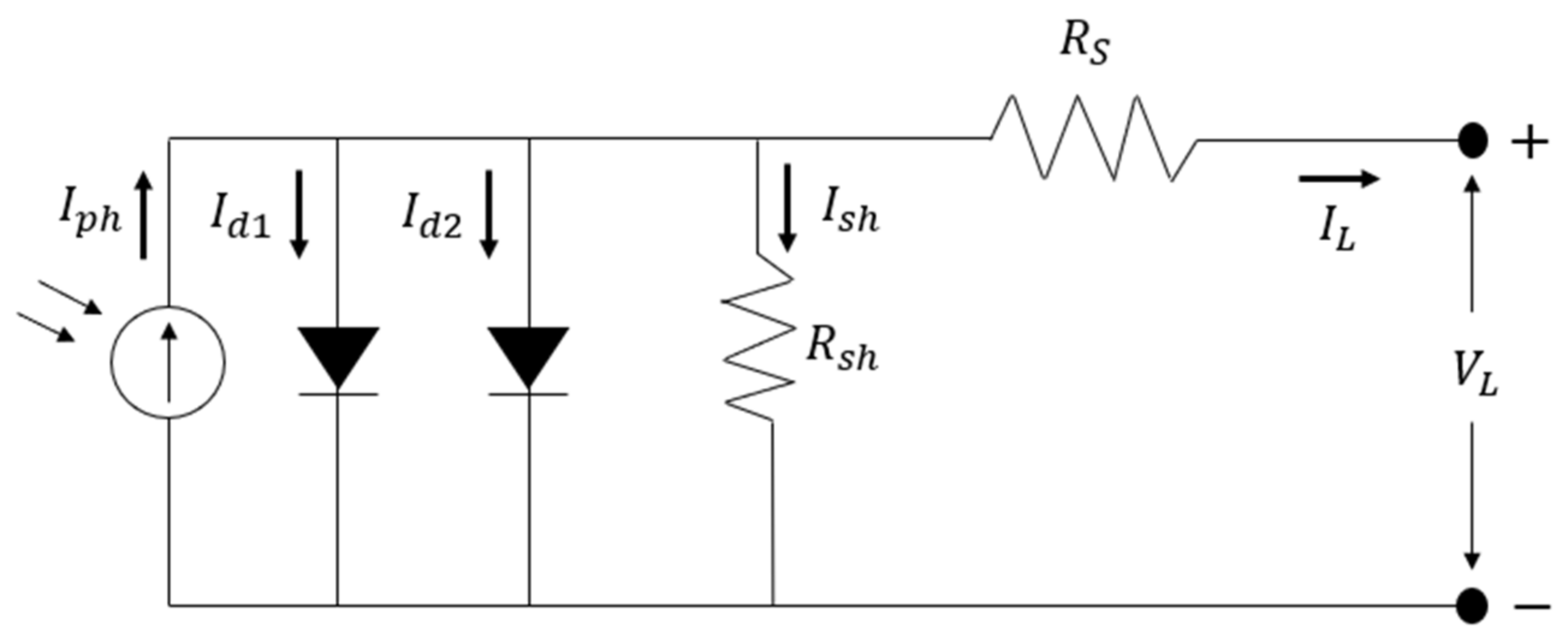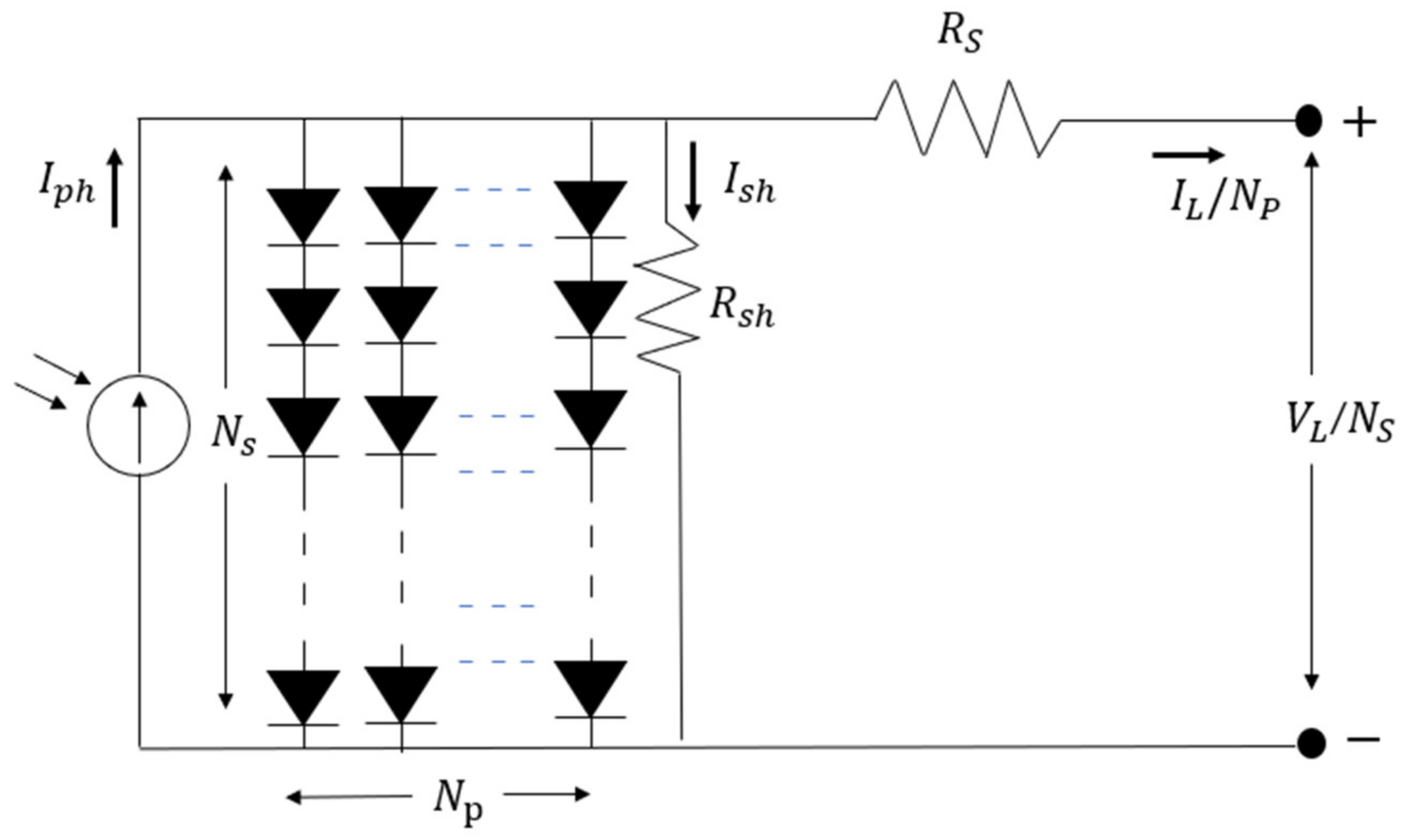Therefore, in order to accurately control PV systems, it is significant to adopt the experimentally measured current-voltage (I-V) data to estimate the actual behavior of PV systems at work [6]. The single diode model (SDM) and the double diode model (DDM) are widely employed and can accurately reflect the nonlinear behavior of PV panels [7]. The parameter accuracy of these models is essential for modeling, control and optimization of PV panels [8]. However, these parameters are susceptible to various environmental factors and become unavailable [9]. PV models are implicitly nonlinear transcendental equations [10]. It is very significant and challenging to employ an efficient and reliable methods to identify the PV parameters.

Many methods have been proposed to solve PV parameter identification. In principle, these methods can be divided into analytical methods and optimization methods [11]. The analytical methods mainly employ several key data (short-circuit current, open-circuit voltage, and maximum power) provided by the manufacturer, and use mathematical equations to deduce the parameters [12]. The analytical methods have the advantages of simple, fast and direct calculation. However, these data are obtained under standard test conditions [13]. Therefore, the extracted parameters above cannot precisely predict the I-V curves at different temperatures and solar irradiance [14]. Furthermore, this approach depends heavily on the key points of the selected I-V characteristics. If the crucial points are wrongly selected, the computational accuracy will be significantly reduced [11].

Instead of choosing a few key points, the optimization method takes into account all the actual measured current and voltage data. From the algorithm point of view, optimization methods can be divided into meta-heuristic methods and deterministic methods [15]. The optimization methods transform the PV parameter identification problem into an optimization problem, and then the parameters are identified according to all the reference points on the I-V characteristic curve. Deterministic methods, such as Newton–Raphson method [16,17], iterative curve fitting [18,19] and Lambert W-function [20,21], require the objective function to be continuous, convex, and differentiable [22]. The I-V curve of the PV cell model is non-linear, multi-peak and multi-mode. And the deterministic method is easily affected by the initial conditions and gradient information, so it is free to become trapped in a local optimum when resolving such complicated problems [23].

The heuristic methods have no strict requirements on the form of the optimization problem and are not affected by initial conditions and gradient information [24]. Therefore, many heuristic methods have been used to identify the parameters of PV models in the past ten years. These include the classified perturbation mutation based particle swarm optimization algorithm (CPMPSO) [1], efficient teaching-learning-based optimization algorithm (MTLBO) [16], multiswarm spiral leader particle swarm optimization algorithm (MSLPSO) [18], enhanced adaptive differential evolution algorithm (EJADE) [22], memetic adaptive differential evolution (MADE) [23], modified Rao-1 optimization algorithm (MRAO-1) [25], improved gaining-sharing knowledge algorithm (IGSK) [26] and chaos induced coyote algorithm (CICA) [27]. The characteristics of the three existing methods are summarized in

Table 1. The characteristics of the three methods.

Method	Characteristic	Instance
Analytical method	- Advantages such as simple, fast and direct calculation. - If the initial value is not selected well, it is necessary to repeatedly assign a new initial value for a new round of solution, and the error in the solution process will also increase with the increase of the number of identification parameters, which requires a large amount of calculation and a long time.
Deterministic method	- Convert the PV parameter identification problem into an optimization problem - The objective function has characteristics such as continuity, convexity and differentiability. Easily affected by initial conditions and gradient information. - It is easy to get stuck in local optima when dealing with complex multimodal problems.	Newton–Raphson method [16,17], iterative curve fitting [18,19] and Lambert W-function [20,21]
Heuristic method	- Overcome the shortcomings of the above two methods, the solution speed is significantly improved, and the accuracy is improved - contains some control parameters	CPMPSO [1], MTLBO [16], MSLPSO [18], EJADE [22], MADE [23], MRAO-1 [25]

.

Compared with deterministic methods, heuristic methods can acquire more precise and robust PV parameter identification results. However, PV models are nonlinear and multi-mode, so some heuristic methods may become trapped in local optima during the optimization process [8]. In addition to the basic parameters of population size and termination condition, most heuristic algorithms have specific parameters related to their own mechanisms. The behavior of the heuristic algorithm depends to some extent on these specific parameters. Choosing inappropriate parameters will not only increase the computational burden of the algorithm, but it may also converge prematurely or fall into a local optimum [28].

Rao proposed a new and efficient heuristic algorithm in 2016, namely the JAYA algorithm [29]. The structure of the JAYA algorithm is relatively simple, with only two parameters: population size and termination conditions [28]. Therefore, the advantage of the JAYA algorithm is that it can reduce the time of the optimization process and avoid the difficulties caused by parameter adjustment. However, the individual position is only affected by the current optimal individual and the worst individual in the JAYA algorithm, which cannot effectively maintain the diversity of the population [8]. Therefore, JAYA algorithm is free to trap in local optimum when solving complicated problems such as multi-peak and multi-mode.

Although the performance of some improved JAYA algorithms such as the performance-guided JAYA algorithm or PGJAYA [8], comprehensive learning JAYA algorithm (CLJAYA) [10], improved JAYA algorithm (IJAYA) [28], logistic chaotic JAYA algorithm (LCJAYA) [29], and elite opposition-based JAYA algorithm (EO-JAYA) [30] have been improved to some extent, the imbalance between exploration and exploitation is not fully considered. The corresponding summary of the extraction parameters of existing heuristic methods is shown in

Table 2. Summary of some existing heuristic methods.

Algorithm	Summary
CPMPSO [1]	- Introducing the classification perturbation mutation strategy to improve the local search ability and population diversity of the algorithm.
PGJAYA [8]	- The performance of each individual is quantified by probability. An adaptive chaotic perturbation mechanism is introduced to improve the quality of the population.
CLJAYA [10]	- Introducing a comprehensive learning mechanism to improve the global search ability of the algorithm.
MTLBO [16]	According to the score level of each learner, each teaching stage is divided into three levels to update the population.
MSLPSO [18]	- Combine multiple populations with different search mechanisms to maintain a balance between exploration and exploitation. - Guided by several different spiral trajectories, the algorithm maintains the diversity of the population while exploring different regions of the multidimensional space.
EJADE [22]	- Introduce crossover rate sorting mechanism to retain excellent individuals. - Introduce a dynamic population reduction strategy to improve convergence speed and balance exploration and exploitation.
MADE [23]	- Adaptive differential evolution strategy based on success-history improves global search ability. - A ranking-based elimination strategy is proposed to retain promising individuals in the population.
MRAO-1 [25]	- A bidirectional update strategy is proposed to improve population diversity.
IGSK [26]	- Introduce an adaptive mechanism to automatically adjust the knowledge rate parameter. - A constraint handling method is proposed to improve the convergence speed and maintain the balance between exploration and exploitation. - Automatically select a binding processing strategy from three algorithm pools to improve the performance of the algorithm.
CICA [27]	- Chaos map can solve problems such as easy to fall into local optimum and slow algorithm convergence speed.
IJAYA [28]	- Experience-based learning strategies maintain the diversity of the population and improve the exploration ability of the population. - A chaotic elite learning method is proposed to improve the quality of the best solution in each generation.
LCJAYA [29]	- Introduces a chaotic mutation strategy to improve and balance exploration and exploitation.
EO-JAYA [30]	- Introducing an elite opposition learning strategy to increase population diversity.

.

In order to improve the performance of JAYA algorithm, this paper proposes a chaotic second order oscillation JAYA algorithm (CSOOJAYA), which can identify parameters more accurately and stably. Firstly, the introduction of logical chaotic mapping mechanism improves the population diversity and exploration. Secondly, the introduction of the second order oscillation mechanism not only improves the diversity of the population, but also has strong exploration ability due to the oscillation convergence of the solution vector in the early iteration. The solution vector converges asymptotically in the later iteration and has strong exploitation ability. The self-adaptive weight mechanism is introduced to adjust the tendency of individuals to approach the optimal solution and escape the worst solution, improve the search efficiency of the population and the exploitation. The algorithm improves and balances the global search ability and local optimization ability as a whole. The introduction of mutation mechanisms ensures that individuals avoid getting stuck in local optima. The structure of CSOOJAYA is similar to the JAYA algorithm, and it only has two parameters: population size and termination condition. In order to verify the effectiveness of the proposed CSOOJAYA algorithm, CSOOJAYA and other novel algorithms are used to extract the parameters of three PV models. The experimental results show that CSOOJAYA has the best performance in terms of identification accuracy, stability and convergence speed.

2. PV Models and Objective Function

2.1. Formula of SDM

Figure 1 presents the circuit diagram of the SDM. Obviously, the framework of the SDM is relatively simple. There are photogenerated current $I_{ph}$, output current $I_L$, diode current $I_d$, and shunt current $I_{sh}$ in the circuit. According to Kirchhoff current law, $I_L$ can be get by Equation (1). According to the diode Shockley equation and Ohm law, $I_d$ can be get by Equation (2), and $I_{sh}$ can be obtained by Equation (3):

$$I_L = I_{ph}-I_d-I_{sh}$$

(1)

$$I_d=I_{sd}·\left[\exp \left(\frac{q·\left(V_L+R_S·I_L\right)}{n·k·T}\right)-1\right]$$

(2)

$$I_{sh}=\frac{V_L+R_S·I_L}{R_{sh}}$$

(3)

$$I_L=I_{ph}-I_d·\left[\exp \left(\frac{q·\left(V_L+R_S·I_L\right)}{n·k·T}\right)-1\right]-\frac{V_L+R_S·I_L}{R_{sh}}$$

(4)

$R_S$ refers to the series resistance, $R_{sh}$ stands for the parallel resistance, $V_L$ stands for the output voltage, n is the ideality factor of the diode. k refers to the Boltzmann constant (1.3806503 × ${10}^{-23}$ J/K), q stands for the elementary charge (1.60217646 × ${10}^{-19}$ C), and T refers to the absolute temperature. Therefore, we can substitute Equations (2) and (3) into Equation (1) to get Equation (4).

Obviously, SDM needs to identify five unknown different parameters ($I_{ph}$, $I_d$, $R_S$, $R_{sh}$, n).

2.2. Formula of DDM

Taking into account the inherent drawbacks of SDM, DDM can more accurately illustrate the relationship between voltage and current. Figure 2 presents the circuit diagram of the DDM. It can be seen from the Figure 2, DDM differs from SDM in that it has one more diode in parallel with the current source than SDM. $I_L$ can be obtained by Equation (5):

$$I_L=I_{ph}-I_{d1}·\left[\exp \left(\frac{q·\left(V_L+R_S·I_L\right)}{n_1·k·T}\right)-1\right]-I_{d2}·\left[\exp \left(\frac{q·\left(V_L+R_S·I_L\right)}{n_2·k·T}\right)-1\right]-\frac{V_L+R_S·I_L}{R_{sh}}$$

(5)

$I_{d1}$ refers to the diode diffusion current, and $I_{d2}$ stands for the saturation current. $n_1$ and $n_2$ represent the ideal saturation factor of two diodes, respectively. Obviously, the DDM needs to extract seven unknown different parameters ($I_{ph}$, $I_{d1}$, $I_{d2}$, $R_S$, $R_{sh}$, $n_1$, $n_2$).

2.3. Formula of PV Module

Figure 3 presents the circuit diagram of a PV module, which consists of several PV cells in parallel or in series. $I_L$ can be obtained by Equation (6):

$$I_L=N_P·I_{ph}-N_P·I_d·\left[\exp \left(\frac{q·\left(V_L/N_S+R_S·I_L/N_P\right)}{n·k·T}\right)-1\right]-\frac{N_P·V_L/N_S+R_S·I_L}{R_{sh}}$$

(6)

$N_S$ and $N_P$ refer to the number of serial and parallel connections of PV cells, respectively. This paper adopts the SDM of PV modules. Therefore, the PV module needs to identify five unknown different parameters ($I_{ph}$, $I_d$, $R_S$, $R_{sh}$, n).

2.4. Objective Function

An objective function is determined to quantitatively evaluate the difference between the actual measured value and the calculated value. Equations (7)–(9) represent the error functions for the experimental and calculated data points of the SDM, DDM, and PV module, respectively:

$$\left\{\begin{array}{c}{f}_{SD}\left(V_L,I_L,\mathit{X}\right)=I_L-I_{ph}+I_d·\left[\exp \left(\frac{q·\left(V_L+R_S·I_L\right)}{n·k·T}\right)-1\right]+\frac{V_L+R_S·I_L}{R_{sh}}\\ \mathit{X}=\left\{I_{ph},I_d,R_S,R_{sh},n\right\}\end{array}\right.$$

(7)

$$\left\{\begin{array}{c}{f}_{DD}\left(V_L,I_L,\mathit{X}\right)=I_L-I_{ph}+I_{d1}·\left[\exp \left(\frac{q·\left(V_L+R_S·I_L\right)}{n_1·k·T}\right)-1\right]\\ +I_{d2}·\left[\exp \left(\frac{q·\left(V_L+R_S·I_L\right)}{n_2·k·T}\right)-1\right]+\frac{V_L+R_S·I_L}{R_{sh}}\\ \mathit{X}=\left\{I_{ph},I_{d1},I_{d2},R_S,R_{sh},n_1,n_2\right\}\end{array}\right.$$

(8)

$$\left\{\begin{array}{c}{f}_{MD}\left(V_L,I_L,\mathit{X}\right)=I_L-N_P·I_{ph}+N_P·I_d·\left[\exp \left(\frac{q·\left(V_L/N_S+R_S·I_L/N_P\right)}{n·k·T}\right)-1\right]\\ +\frac{N_P·V_L/N_S+R_S·I_L}{R_{sh}}\\ \mathit{X}=\left\{I_{ph},I_d,R_S,R_{sh},n\right\}\end{array}\right.$$

(9)

$$\mathrm{RMSE}\left(\mathit{X}\right)=\sqrt{\frac{1}{N}{\displaystyle \sum }_{k=1}^N{f}_k{(V_L,I_L,\mathit{X})}^2}$$

(10)

However, the error function cannot reflect all the differences between the calculated and experimental data. The root mean square error (RMSE) defined by Equation (10) is used as the objective function to quantitatively evaluate the overall difference between the experimental and calculated data. References like [10,11,14] generally use the objective function. X represents the solution composed of different unknown parameters, and N represents the number of actual measured data.

3. JAYA Algorithm

JAYA is a new population-based intelligent optimization algorithm [29]. In each generation of the JAYA algorithm, the solution vector is optimized by approaching the optimal solution while staying away from the worst solution. JAYA does not need to tune algorithm-specific parameters. The only two parameters are population size and maximum number of evaluation functions ($ma{x}_{FES}$).

For the objective function with d unknown variables (j = 1,2,3...d), $x_{i,j}$ represent the value of the j-th variable of the i-th unknown solution, then ${\mathit{X}}_i$ = ($x_{i,1}$, $x_{i,2}$...... $x_{i,d}$) represents the i-th unknown solution. If an individual can get the worst/best value of f(X) among all individuals, then this is the worst/best individual, expressed as $x_{best}$= ($x_{best,1}$, $x_{best,2}$,… $x_{best,d}$)/$x_{worst}$= ($x_{worst,1}$, $x_{worst,2}$,... $x_{worst,d}$). Each solution $x_{i,j}$ of the JAYA algorithm can be updated by Equation (11):

$$x_{newi,j}=x_{i,j}+ran{d}_1·\left(x_{best,j}-\left|x_{i,j}\right|\right)-ran{d}_2·\left(x_{worst,j}-\left|x_{i,j}\right|\right)$$

(11)

$\left|x_{i,j}\right|$ represents the absolute value of $x_{i,j}$, and $x_{newi,j}$ represents the updated value of $x_{i,j}$. $ran{d}_1$ and $ran{d}_2$ represent random numbers in [0,1]. The second and third terms in the above Equation (11) represent the tendency of the solution vector x to move towards the optimal solution and escape from the worst solution, respectively. In order to retain a better solution vector, the updated solution $x_{newi}$= ($x_{newi,1}$, $x_{newi,2}$,…, $x_{newi,d}$) is received if it can provide a better function value.

4. Chaotic Second Order Oscillation JAYA Algorithm

4.1. Motivation

At present, the identification of PV parameters is considered to be a multi-peak and multi-modal problem, that is, there are multiple local optimal solutions. When the JAYA algorithm deals with such problems, it easily falls into a local optimum because it cannot effectively explore different regions of the space. How to effectively enhance the behavior of the algorithm while balancing the exploitation and exploration? Therefore, a chaotic second order oscillation JAYA (CSOOJAYA) algorithm is proposed in this research.

4.2. Logistic Chaotic Map Strategy

In the optimization process of the JAYA algorithm, it is hard to use two uniformly distributed random numbers to maintain the population diversity. However, the number of chaotic sequences generated by the logical chaotic mapping strategy is aperiodic and does not converge to a specific value. It enhances the population diversity of the heuristic algorithm, improves the global search ability, and avoids falling into the local optimum. Therefore, two random numbers are replaced by chaotic sequence numbers, and Equation (12) represents the new update solution:

$$x_{newi,j}=x_{i,j}+C_{1i,j}·\left(x_{best,j}-\left|x_{i,j}\right|\right)-C_{2i,j}·\left(x_{worst,j}-\left|x_{i,j}\right|\right)$$

(12)

where $C_{1i,j}$ and $C_{2i,j}$ represent two chaotic sequence numbers, which are generated by Equation (13):

$$C_{n+1}=4\ast C_n·\left(1-C_n\right)$$

(13)

$C_n$ represents the chaotic value of the n-th iteration. Its value range is [0,1], and $C_1$ is usually set to 0.8.

4.3. Second Order Oscillation Strategy

According to the update equation of the JAYA algorithm, When the i-th solution is the best/worst solution, one term on the right side of Equation (11) is 0, which cannot maintain the diversity of the population. There are only two factors that affect the population position of the JAYA algorithm, namely the current optimal individual and the worst individual. Although the algorithm can speed up the convergence speed and improve the exploitation, it cannot effectively enhance the diversity of the population and weaken the exploration ability in the optimization process.

Considering the above two situations, the population individuals may fall into a local optimum in the JAYA algorithm. It can be seen from Equations (11) and (12) that $x_{\mathit{best}}$ and $x_{\mathit{worst}}$ have a significant impact on the performance of JAYA. Therefore, taking advantages of population information and enhancing exploration capabilities are the available methods to improve the behavior of the JAYA. How to balance exploitation and exploration while improving population diversity. Therefore, the second order oscillation factor is introduced into Equation (12), that is, two unequal second order oscillation factors are added respectively to the two rightmost terms of Equation (12), as shown in Equation (14). The difference between the current optimal individual and the optimal individual of the previous generation and the difference between the current worst individual and the worst individual of the previous generation can guide the individual to update a better range, maintain population diversity and improve exploration ability. After adopting the second order oscillation strategy, because the solution vector has oscillation convergence in the early iteration, the algorithm has strong global search ability; The solution vector converges asymptotically in the later stage of iteration, and the algorithm has strong local optimization ability. This strategy improves the convergence accuracy of the algorithm as a whole:

$$\begin{gathered} x_{newi,j}=x_{i,j}+C_{1i,j}·\left(\left(1+k1\right)·x_{best,j}-k1·x_{bestp,j}-\left|x_{i,j}\right|\right)-C_{2i,j}·\left(\left(1 \\ +k2\right)· x_{worst,j}-k2·x_{worstp,j}-\left|x_{i,j}\right|\right) \end{gathered}$$

(14)

where $x_{bestp,j}$ and $x_{worstp,j}$ represent the optimal solution and the worst solution of the jth variable of the previous generation of population individuals, respectively. $k1$ and $k2$ are two randomly generated numbers in [0,1], and $k1$ is not equal to $k2$.

4.4. Self-Adaptive Weight

Equation (12) enhances the population diversity and exploration, and Equation (14) not only improves exploitation and exploration, but also effectively balances the two abilities of the algorithm. However, how to balance the two abilities as a whole is the core problem of the algorithm. Considering that the strategy is dedicated to improving exploitation ability, the self-adaptive weight strategy is introduced into Equation (14) to obtain Equation (15). w is obtained from Equation (16). It can be seen from Equation (16) that the value of w increases gradually with the increase of the number of function evaluations. Because the difference between the optimal solution and the worst solution becomes smaller and smaller as the search process progresses. Therefore, in the optimization process of the JAYA algorithm, the population can approach the promising solution at the beginning of the iteration and conduct local optimization in the area of the promising solution at the end of the iteration. Thus, it enhances the search efficiency of the population and the exploitation of the algorithm:

$$\begin{gathered} x_{newi,j}=x_{i,j}+C_{1i,j}·\left(\left(1+k1\right)·x_{best,j}-k1·x_{bestp,j}-\left|x_{i,j}\right|\right)-w·C_{2i,j}·\left(\left(1 \\ +k2\right)· x_{worst,j}-k2·x_{worstp,j}-\left|x_{i,j}\right|\right) \end{gathered}$$

(15)

$$\mathrm{w}=\left\{\begin{array}{c}{(\frac{f\left(x_{best}\right)}{f\left(x_{worst}\right)})}^2, \mathrm{i}\mathrm{f} \mathrm{f}\left(x_{worst}\right)\ne 0\\ 1 , \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.$$

(16)

$f\left(x_{best}\right)$ and $f\left(x_{worst}\right)$ represent the values of the optimal and worst individual of the objective function, respectively. Furthermore, the self-adaptive weight is automatically determined, so there is no need to adjust parameters.

4.5. Mutation Mechanism

The three position update equations based on the JAYA algorithm not only improve the overall exploration and exploitation, but also effectively balance the two abilities. However, the optimal individual may still have a very small probability of being in a local optimal state to solve the identification of PV parameters. In order to make the individual jump out of the local optimum, the mutation mechanism is proposed. If from the first function evaluation to a quarter of the maximum function evaluation time, and so on, if the RMSE values of the two are equal, the population individual is reinitialized. And if the best RMSE of the previous generation is better than the current optimal RMSE, the RMSE of the previous generation is accepted.

4.6. Framework of CSOOJAYA

The overall update equation of the improved algorithm based on the above strategy is shown in Equation (17). p is the probability, which represents random numbers in [0,1]:

$$x_{newi,j}=\{\begin{array}{c}{x}_{i,j}+C_{1i,j}·\left(\left(1+k1\right)·x_{best,j}-k1·x_{bestp,j}-\left|x_{i,j}\right|\right)-\\ C_{2i,j}·\left(\left(1+k1\right)·x_{worst,j}-k2·x_{worstp,j}-\left|x_{i,j}\right|\right),\\ if 0\le p<1/2\\ x_{i,j}+C_{1i,j}·\left(\left(1+k1\right)·x_{best,j}-k1·x_{bestp,j}-\left|x_{i,j}\right|\right)-\\ C_{2i,j}·w·\left(\left(1+k2\right)·x_{worst,j}-k2·x_{worstp,j}-\left|x_{i,j}\right|\right),\\ if\frac{1}{2}\le p<3/4\\ x_{i,j}+C_{1i,j}·\left(x_{best,j}-\left|x_{i,j}\right|\right)-C_{2i,j}·\left(x_{worst,j}-\left|x_{i,j}\right|\right),\\ if \frac{3}{4}\le p\le 1\end{array}$$

(17)

The pseudocode of the CSOOJAYA algorithm can be summarized by the Algorithm 1. In addition, Figure 4 shows the flow chart of the specific implementation of CSOOJAYA. Similar to the JAYA algorithm, the CSOOJAYA does not need to adjust the specific algorithm parameters.

Algorithm 1: CSOOJAYA algorithm.

Set the population size (NP) and $ma{x}_{FES}$; Randomly initialize the population and RMSE values of all individuals are calculated; FES = NP; While FES < $ma{x}_{FES}$ do   Identify the best xi and worst xi of all individuals;     For i = 1 to NP do       if (0 ≤ p < 1/2) then         Update the xi using Equation (14);       else if (1/2 ≤ p < 3/4) then         Calculate the w using Equation (15);         Update the xi using Equation (16)       else         Update the xi using Equation (12)       End if        Obtain the new population and Calculate the RMSE for the updated individual $x_{newi}$;       Receive the updated solution if it is more excellent than the pre-update one     End For     If the conditions of the mutation strategy are met      Randomly initialize the population and Save the current optimal solution and RMSE      End if End While

5. Experimental Results and Discussion

In order to estimate the effective behavior of CSOOJAYA, it was applied to the identification of PV parameters. The benchmark data are extracted from reference [11]. where the data for SDM and DDM were obtained from a commercial RTC silicon PV cell (1000 w/m² at 33 °C, Photowatt, Bourgoin-Jallieu, France) with a diameter of 57 mm, and the data for the PV module was obtained from a Photowatt-PWP201 (1000 w/m² at 45 °C) solar module consisting of 36 polycrystalline silicon cells connected in series (Photowatt, Bourgoin-Jallieu, France). In order to ensure fairness, the search space of the solution vector is the same, and the value range of the identification parameter is the same as that adopted in the previous literature.

Table 3. Parameters ranges of PV models.

Parameter	SDM/DDM		PV Module
	Lower	Upper	Lower	Upper
	0	1	0	2
	0	1	0	50
	0	0.5	0	2
	0	100	0	2000
	1	2	1	50

shows the value ranges of the parameters corresponding to different PV models.

CSOOJAYA is compared with other novel algorithms to verify its superior performance. These algorithms are DE/WOA, MLBSA, EJADE, MTLBO, MPPCEDE, MADE, ITLBO, CPMPSO, DERAO, JAYA, IJAYA, LCJAYA and PGJAYA. Because these optimization algorithms have better performance in PV model parameter identification, they are used for comparison with CSOOJAYA.

Table 4. Parameter settings of the compared algorithms.

Algorithm	Parameters
DE/WOA	Np = 40, F = rand (0.1,1), Cr = rand (0,1)
MLBSA	Np = 50
EJADE	${\mathrm{Np}}_{\max }$ = 50, ${\mathrm{Np}}_{\min }$ = 4
MTLBO	Np = 50
MPPCEDE	Np = 40; F = rand (0.1,1); Cr = rand (0,1)
MADE	NP = 20; 0.05 for the SDM and PV module; 0.01 for the DDM
IJAYA	NP = 20
ITLBO	Np = 50
CPMPSO	NP = 50, w = 0.729, c1 = 1.49455, c2 = 1.49455
DERAO	NP = 20
JAYA	NP = 20
PGJAYA	NP = 20
LCJAYA	NP = 20
CSOOJAYA	NP = 20

presents the corresponding parameter settings for the selected algorithms, which are extracted from their respective references. For fair comparison, set $ma{x}_{FES}$ to 50,000 for all algorithms and run 30 times independently. The results of DE/WOA [11], MLBSA [5], EJADE [22], MTLBO [16], MPPCEDE [15], MADE [23], ITLBO [2], CPMPSO [1], DERAO [25], JAYA [31], IJAYA [28], LCJAYA [29] and PGJAYA [8] were obtained directly from the corresponding references. The selected algorithms are all executed in MATLAB R2016b on a PC configured with an Intel(I) Core (TM) i5-7200u CPU operating at 3.1 GHz and equipped with 4 Gb of RAM.

5.1. Results on the SDM

For SDM,

Table 5. Comparison of the extracted optimal parameters of the SDM.

Algorithm	${\mathit{I}}_{\mathit{p}\mathit{h}}$ (A)	${\mathit{I}}_{\mathit{d}}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{S}}$ ($\mathbf{\Omega }$)	${\mathit{R}}_{\mathit{s}\mathit{h}}$ ($\mathbf{\Omega }$)	n	RMSE
DE/WOA	0.760776	0.323021	0.036377	53.718524	1.481184	9.860219 × 10−4
MLBSA	0.7608	0.32302	0.0364	53.7185	1.4812	9.8602 × 10−4
EJADE	0.7608	0.3230	0.0364	53.7185	1.4812	9 8602 × 10−4
MTLBO	0.76077553	0.32300	0.03637709	53.7185251	1.48118359	9 860219 × 10−4
MPPCEDE	0.7608	0.32302	0.0364	53.7185	1.4812	9.8602 × 10−4
MADE	0.7608	0.3230	0.0364	53.7185	1.4812	9.8602 × 10−4
IJAYA	0.7608	0.3228	0.0364	53.7595	1.4811	9.8603 × 10−4
ITLBO	0.7608	0.3230	0.0364	53.7185	1.4812	9.8602 × 10−4
CPMPSO	0.760776	0.323021	0.036377	53.718522	1.481184	9.860219 × 10−4
DERAO	0.760776	0.323021	0.036377	53.718522	1.481135	9.860219 × 10−4
JAYA	0.7608	0.3281	0.0364	54.9298	1.4828	9.8946 × 10−4
PGJAYA	0.7608	0.3230	0.0364	53.7185	1.4812	9.8602 × 10−4
LCJAYA	0.7608	0.3230	0.0364	53.7185	1.4819	9.8602 × 10−4
CSOOJAYA	0.760776	0.323021	0.036377	53.718525	1.481184	9.860219 × 10−4

illustrates the best parameters and RMSE obtained for all selected algorithms. The overall best RMSE values of all compared algorithms are indicated in bold. It is obvious from Table 5 that CSOOJAYA, DE/WOA, MLBSA, EJADE, MTLBO, MPPCEDE, MADE, ITLBO, CPMPSO, DERAO, LCJAYA and PGJAYA obtained the smallest RMSE (9.8602 × 10⁻⁴), followed by IJAYA. Although accurate parameter value information cannot be obtained, it can be seen from the literature [1,2] that the RMSE can be employed to represent the accuracy. Furthermore, the smaller the RMSE, the more precise the identified parameters.

To further confirm the performance of CSOOJAYA, the IAE of power and current between the measured data and the calculated data was used. The $IA{E}_{current}$ can be calculated by Equation (18), and the $IA{E}_{power}$ can be obtained by Equation (19):

$$IA{E}_{current}=\left|I_{measured}-I_{estimated}\right|$$

(18)

$$IA{E}_{power}=\left|V\ast I_{measured}-V\ast I_{estimated}\right|$$

(19)

where $I_{estimated}$ represents the output current estimated by different models through Equations (4), (5) or (6), and $I_{measured}$ represents the actual measured current. V represents the actual measured voltage. $IA{E}_{current}$ represents the individual absolute error of current, and $IA{E}_{power}$ represents the individual error of power.

The IAE of power and current are shown in

Table 6. IAE of CSOOJAYA for the SDM.

Item	${\mathit{V}}_{\mathit{m}\mathit{e}\mathit{a}\mathit{s}\mathit{u}\mathit{r}\mathit{e}\mathit{d}}\mathbf{/}\mathit{V}$	${\mathit{I}}_{\mathit{m}\mathit{e}\mathit{a}\mathit{s}\mathit{u}\mathit{r}\mathit{e}\mathit{d}}\mathbf{/}\mathit{A}$	${\mathit{I}}_{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\mathbf{/}\mathit{A}$	$\mathit{I}\mathit{A}{\mathit{E}}_{\mathit{c}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}}$	${\mathit{P}}_{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\mathbf{/}\mathit{W}$	$\mathit{I}\mathit{A}{\mathit{E}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}$
1	−0.2057	0.7640	0.7640881747	0.0000881747	−0.1571729375	0.0000181375
2	−0.1291	0.7620	0.7626635570	0.0006635570	−0.0984598652	0.0000856652
3	−0.0588	0.7605	0.7613557780	0.0008557780	−0.0447677197	0.0000503197
4	0.0057	0.7605	0.7601544618	0.0003455381	0.0043328804	0.0000019695
5	0.0646	0.7600	0.7590556797	0.0009443202	0.0490349969	0.0000610030
6	0.1185	0.7590	0.7580428161	0.0009571838	0.0898280737	0.0001134262
7	0.1678	0.7570	0.7570921248	0.0000921248	0.1270400585	0.0000154585
8	0.2132	0.7570	0.7561418358	0.0008581641	0.1612094393	0.0001829606
9	0.2545	0.7555	0.7550873439	0.0004126560	0.1921697290	0.0001050209
10	0.2924	0.7540	0.7536643499	0.0003356500	0.2203714559	0.0000981440
11	0.3269	0.7505	0.7513914392	0.0008914392	0.2456298615	0.0002914115
12	0.3585	0.7465	0.7473543260	0.0008543260	0.2679265258	0.0003062758
13	0.3873	0.7385	0.7401176997	0.0016176997	0.2866475851	0.0006265351
14	0.4137	0.7280	0.7273827075	0.0006172924	0.3009182261	0.0002553738
15	0.4373	0.7065	0.7069731390	0.0004731390	0.3091593537	0.0002069037
16	0.4590	0.6755	0.6752806425	0.0002193574	0.3099538149	0.0001006850
17	0.4784	0.6320	0.6307587591	0.0012412408	0.3017549903	0.0005938096
18	0.4960	0.5730	0.5719288231	0.0010711768	0.2836766963	0.0005313036
19	0.5119	0.4990	0.4996074317	0.0006074317	0.2557490442	0.0003109442
20	0.5265	0.4130	0.4136491106	0.0006491106	0.2177862567	0.0003417567
21	0.5398	0.3165	0.3175102788	0.0010102788	0.1713920485	0.0005453485
22	0.5521	0.2120	0.2121548945	0.0001548945	0.1171307172	0.0000855172
23	0.5633	0.1035	0.1022509879	0.0012490120	0.0575979815	0.0007035684
24	0.5736	−0.0100	−0.0087182129	0.0012817870	−0.0050007669	0.0007352330
25	0.5833	−0.1230	−0.1255085017	0.0025085017	−0.0732091090	0.0014632090
26	0.5900	−0.2100	−0.2084737660	0.0015262339	−0.1229995219	0.0009004780

. All values of $IA{E}_{current}$ are less than 2.50 × 10⁻³ and all values of $IA{E}_{power}$ are less than 1.46 × 10⁻³, proving the accuracy of extracted parameters. To further verify the accuracy of the results, Figure 5 illustrates the best results obtained using CSOOJAYA to plot the I-V and P-V curves. Obviously, the data calculated by CSOOJAYA are in good agreement with the measured data across the entire voltage range.

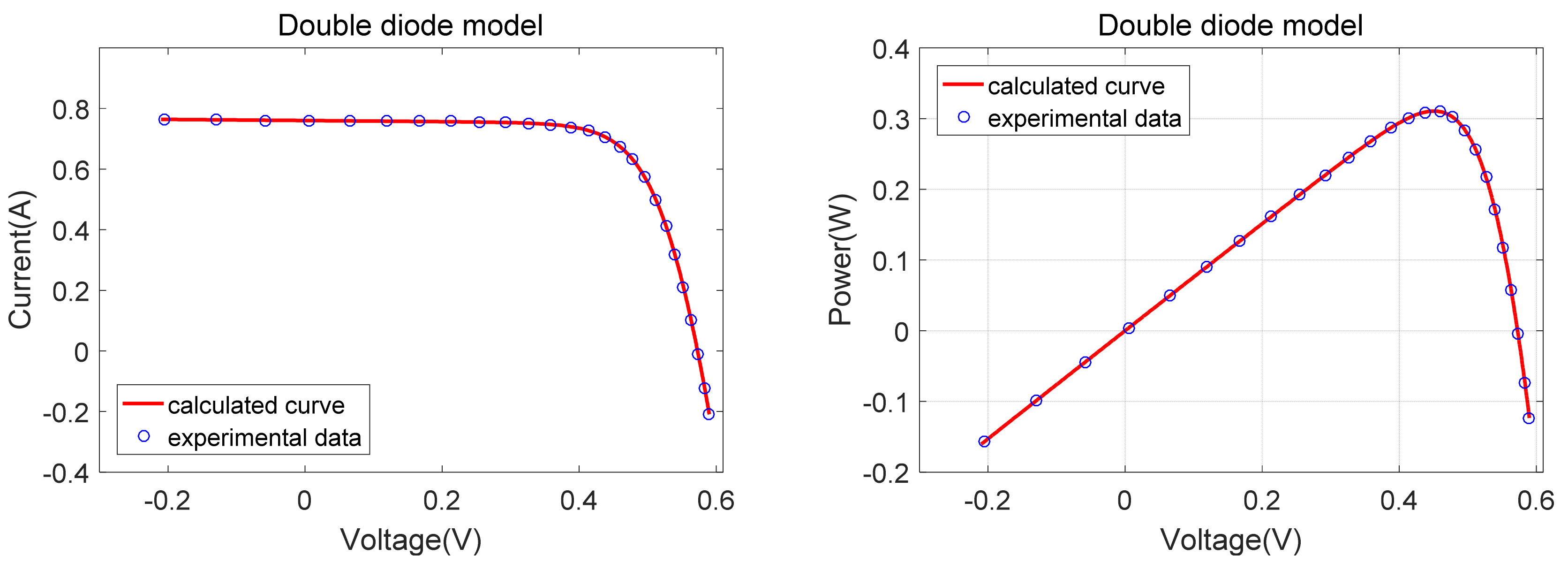
5.2. Results on the DDM

For DDM, the extraction of seven parameters increases the difficulty of parameter identification.

Table 7. Comparison of the extracted optimal parameters of the DDM.

Algorithm	${\mathit{I}}_{\mathit{p}\mathit{h}}$ (A)	${\mathit{I}}_{\mathit{d}\mathbf{1}}$ ($\mathsf{\mu }$A)	${\mathit{I}}_{\mathit{d}\mathbf{2}}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{S}}$ ($\Omega$)	${\mathit{R}}_{\mathit{s}\mathit{h}}$ ($\Omega$)	n1	n2	RMSE
DE/WOA	0.760781	0.225974	0.749346	0.036740	55.485437	1.451017	2	9.824849 × 10−4
MLBSA	0.7608	0.22728	0.73835	0.0367	55.4612	1.4515	2	9.8249 × 10−4
EJADE	0.7608	0.2260	0.7493	0.0367	55.4854	1.4510	2	9.8248 × 10−4
MTLBO	0.7607810	0.22597	0.7493	0.03674043	55.485447	1.451016	2	9.824849 × 10−4
MPPCEDE	0.7608	0.22728	0.73835	0.0367	55.4612	1.4515	2	9.82485 × 10−4
MADE	0.7608	0.2246	0.7394	0.0368	55.4329	1.4505	1.9963	9.8261 × 10−4
IJAYA	0.7601	0.0050445	0.75094	0.0376	77.8519	1.2186	1.6247	9.8293 × 10−4
ITLBO	0.7608	0.2260	0.7493	0.0367	55.4854	1.4510	2	9.8248 × 10−4
CPMPSO	0.76078	0.22597	0.74935	0.03674	55.48544	1.45102	2	9.824849 × 10−4
DERAO	0.760781	0.225959	0.749667	0.036740	55.486045	1.450963	2	9.824849 × 10−4
JAYA	0.7607	0.0060763	0.31507	0.0364	52.6575	1.4788	1.8436	9.8934 × 10−4
PGJAYA	0.7608	0.21031	0.88534	0.0368	55.8135	1.4450	2	9.8263 × 10−4
LCJAYA	0.7608	0.22596	0.74640	0.0367	55.4815	1.4518	2.0000	9.8250 × 10−4
CSOOJAYA	0.760781	0.225974	0.749345	0.036740	55.485437	1.451017	2.000000	9.824849 × 10−4

illustrates the best parameters and RMSE obtained for all selected algorithms. The overall best RMSE value of all compared algorithms are indicated in bold. It is obvious from Table 7 that CSOOJAYA, DE/WOA, EJADE, MTLBO, ITLBO, CPMPSO, DERAO have the smallest RMSE (9.8248 × 10⁻⁴), followed by MLBSA and MPPCEDE. To further verify the accuracy of the results, Figure 6 illustrates the best results obtained using CSOOJAYA to plot the I-V and P-V curves. Obviously, the data calculated by CSOOJAYA are in good agreement with the measured data across the entire voltage range.

The IAE of power and current are shown in

Table 8. IAE of CSOOJAYA for the DDM.

Item	${\mathit{V}}_{\mathit{m}\mathit{e}\mathit{a}\mathit{s}\mathit{u}\mathit{r}\mathit{e}\mathit{d}}\mathbf{/}\mathit{V}$	${\mathit{I}}_{\mathit{m}\mathit{e}\mathit{a}\mathit{s}\mathit{u}\mathit{r}\mathit{e}\mathit{d}}\mathbf{/}\mathit{A}$	${\mathit{I}}_{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\mathbf{/}\mathit{A}$	$\mathit{I}\mathit{A}{\mathit{E}}_{\mathit{c}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}}$	${\mathit{P}}_{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\mathbf{/}\mathit{W}$	$\mathit{I}\mathit{A}{\mathit{E}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}$
1	−0.2057	0.7640	0.7639834118	0.0000165881	−0.1571513878	0.0000034121
2	−0.1291	0.7620	0.7626040957	0.0006040957	−0.0984521887	0.0000779887
3	−0.0588	0.7605	0.7613376980	0.0008376980	−0.0447666566	0.0000492566
4	0.0057	0.7605	0.7601737877	0.0003262122	0.0043329905	0.0000018594
5	0.0646	0.7600	0.7591076801	0.0008923198	0.0490383561	0.0000576438
6	0.1185	0.7590	0.7581214198	0.0008785801	0.0898373882	0.0001041117
7	0.1678	0.7570	0.7571886136	0.0001886136	0.1270562493	0.0000316493
8	0.2132	0.7570	0.7562436068	0.0007563931	0.1612311369	0.0001612630
9	0.2545	0.7555	0.7551773015	0.0003226984	0.1921926232	0.0000821267
10	0.2924	0.7540	0.7537223535	0.0002776464	0.2203884161	0.0000811838
11	0.3269	0.7505	0.7513991342	0.0008991342	0.2456323769	0.0002939269
12	0.3585	0.7465	0.7473014432	0.0008014432	0.2679075674	0.0002873174
13	0.3873	0.7385	0.7400106607	0.0015106607	0.2866061288	0.0005850788
14	0.4137	0.7280	0.7272469525	0.0007530474	0.3008620642	0.0003115357
15	0.4373	0.7065	0.7068502977	0.0003502977	0.3091056352	0.0001531852
16	0.4590	0.6755	0.6752105425	0.0002894574	0.3099216390	0.0001328609
17	0.4784	0.6320	0.6307607576	0.0012392423	0.3017559464	0.0005928535
18	0.4960	0.5730	0.5719947329	0.0010052670	0.2837093875	0.0004986124
19	0.5119	0.4990	0.4997061352	0.0007061352	0.2557995706	0.0003614706
20	0.5265	0.4130	0.4137336728	0.0007336728	0.2178307787	0.0003862787
21	0.5398	0.3165	0.3175462057	0.0010462057	0.1714114418	0.0005647418
22	0.5521	0.2120	0.2121229960	0.0001229960	0.1171131061	0.0000679061
23	0.5633	0.1035	0.1021632765	0.0013367234	0.0575485736	0.0007529763
24	0.5736	−0.0100	−0.0087917509	0.0012082490	−0.0050429483	0.0006930516
25	0.5833	−0.1230	−0.1255434350	0.0025434350	−0.0732294856	0.0014835856
26	0.5900	−0.2100	−0.2083715891	0.0016284108	−0.1229392376	0.0009607623

. All values of $IA{E}_{current}$ are less than 2.54 × 10⁻³ and all values of $IA{E}_{power}$ are less than 1.48 × 10⁻³, which demonstrates the accuracy of CSOOJAYA parameter identification.

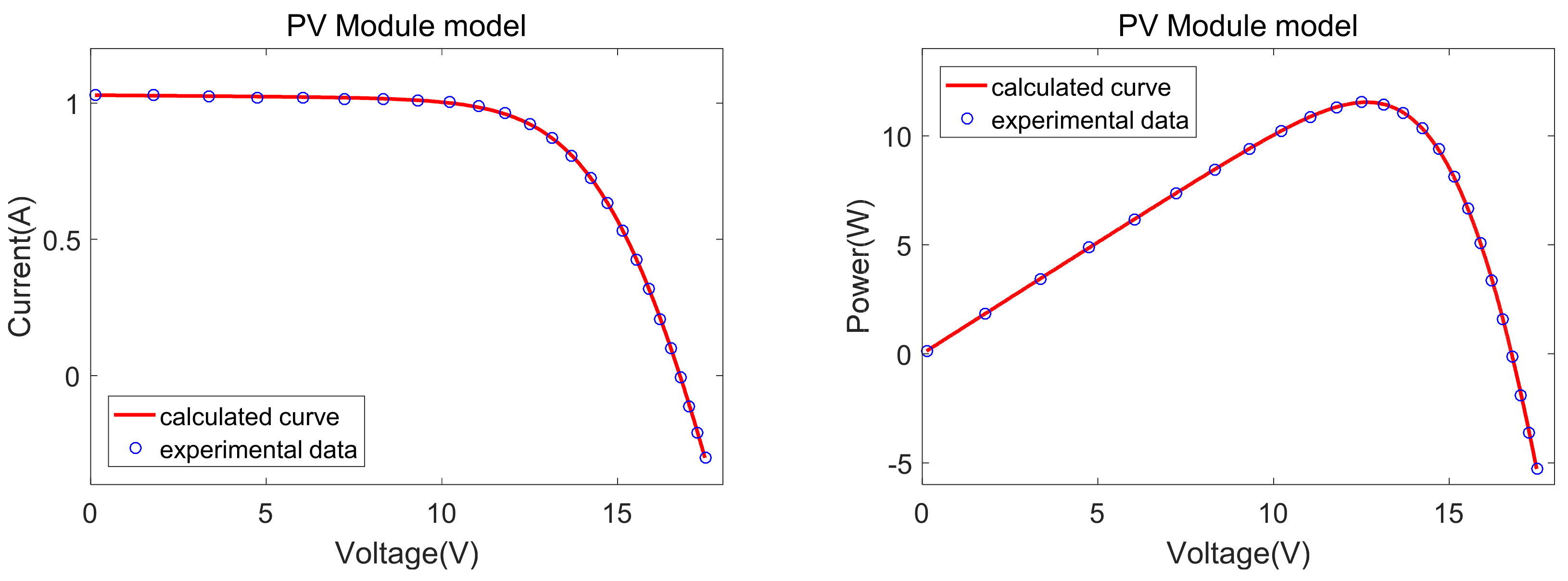
5.3. Results on the PV Module

The effectiveness of CSOOJAYA is further verified using the PhotoWatt-PWP201 PV module.

Table 9. Comparison of the extracted optimal parameters of the PV module.

Algorithm	${\mathit{I}}_{\mathit{p}\mathit{h}}$ (A)	${\mathit{I}}_{\mathit{d}}$ ($\mathsf{\mu }$A)	${\mathit{R}}_{\mathit{S}}$ ($\Omega$)	${\mathit{R}}_{\mathit{s}\mathit{h}}$ ($\Omega$)	n	RMSE
DE/WOA	1.030514	3.482263	1.201271	981.982143	48.642835	2.425075 × 10−3
MLBSA	1.0305	3.4823	1.2013	981.9823	48.6428	2.4251 × 10−3
EJADE	1.0305	3.4823	1.2013	981.9824	48.6428	2.4251 × 10−3
MTLBO	1.0305143	3.4823	1.2012710	981.9823732	48.6428349	2425075 × 10−3
MPPCEDE	1.030514	3.482263	1.201271	981.982143	48.642835	2.42507 × 10−3
MADE	1.0305	3.4823	1.2013	981.9823	48.6428	2.4250 × 10−3
IJAYA	1.0305	3.4703	1.2016	977.3752	48.6298	2.4251 × 10−3
ITLBO	1.0305	3.4823	1.2013	981.9823	48.6428	2.4251 × 10−3
CPMPSO	1.030514	3.4823	1.201271	981.9823	48.64284	2.425075 × 10−3
DERAO	1.030514	3.4823	1.201271	981.9821	48.64131	2.425075 × 10−3
JAYA	1.0302	3.4931	1.2014	1022.5	48.6531	2.427785 × 10−3
PGJAYA	1.0305	3.4818	1.2013	981.8545	48.6424	2.425075 × 10−3
LCJAYA	1.0305	3.4823	1.2024	981.9828	48.6684	2.425075 × 10−3
CSOOJAYA	1.030514	3.482263	1.201271	981.982243	48.642834	2.425075 × 10−3

illustrates the best parameters and RMSE obtained for all selected algorithms. The overall best RMSE value of all the compared algorithms are marked in bold. Among all the comparison algorithms, CSOOJAYA, DE/WOA, MLBSA, EJADE, MTLBO, MPPCEDE, MADE, ITLBO, CPMPSO, PGJAYA, IJAYA, LCJAYA and DERAO obtained the best RMSE value, followed by JAYA. To further verify the accuracy of the results, Figure 7 illustrates the best results obtained using CSOOJAYA to plot the I-V and P-V curves. Obviously, the data calculated by CSOOJAYA are in good agreement with the measured data across the entire voltage range. The IAE of power and current are shown in

Table 10. IAE of CSOOJAYA for PV module.

Item	${\mathit{V}}_{\mathit{m}\mathit{e}\mathit{a}\mathit{s}\mathit{u}\mathit{r}\mathit{e}\mathit{d}}\mathbf{/}\mathit{V}$	${\mathit{I}}_{\mathit{m}\mathit{e}\mathit{a}\mathit{s}\mathit{u}\mathit{r}\mathit{e}\mathit{d}}\mathbf{/}\mathit{A}$	${\mathit{I}}_{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\mathbf{/}\mathit{A}$	$\mathit{I}\mathit{A}{\mathit{E}}_{\mathit{c}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}}$	${\mathit{P}}_{\mathit{e}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{e}\mathit{d}}\mathbf{/}\mathit{W}$	$\mathit{I}\mathit{A}{\mathit{E}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}$
1	0.1248	1.0315	1.0291188622	0.0023811377	0.1284340340	0.0002971659
2	1.8093	1.0300	1.0273807740	0.0026192259	1.8588400345	0.0047389654
3	3.3511	1.0260	1.0257414978	0.0002585021	3.4373623333	0.0008662666
4	4.7622	1.0220	1.0241068556	0.0021068556	4.8770016680	0.0100332680
5	6.0538	1.0180	1.0222915054	0.0042915054	6.1887483154	0.0259799154
6	7.2364	1.0155	1.0199303816	0.0044303816	7.3806242138	0.0320600138
7	8.3189	1.0140	1.0163628063	0.0023628063	8.4550205496	0.0196559496
8	9.3097	1.0100	1.0104958517	0.0004958517	9.4074132312	0.0046162312
9	10.2163	1.0035	1.0006286698	0.0028713301	10.2227226794	0.0293343705
10	11.0449	0.9880	0.9845480779	0.0034519220	10.8742350664	0.0381261335
11	11.8018	0.9630	0.9595213746	0.0034786253	11.3240793592	0.0410540407
12	12.4929	0.9255	0.9228385152	0.0026614847	11.5289292866	0.0332496633
13	13.1231	0.8725	0.8725993581	0.0000993581	11.4512086365	0.0013038865
14	13.6983	0.8075	0.8072739566	0.0002260433	11.0582808396	0.0030964103
15	14.2221	0.7265	0.7283361680	0.0018361680	10.3584698161	0.0261141661
16	14.6995	0.6345	0.6371376868	0.0026376868	9.3656054279	0.0387726779
17	15.1346	0.5345	0.5362127464	0.0017127464	8.1153654320	0.0259217320
18	15.5311	0.4275	0.4295110044	0.0020110044	6.6707783610	0.0312331110
19	15.8929	0.3185	0.3187741584	0.0002741584	5.0662458227	0.0043571727
20	16.2229	0.2085	0.2073891784	0.0011108215	3.3644539035	0.0180207464
21	16.5241	0.1010	0.0961668397	0.0048331602	1.5890704768	0.0798636231
22	16.7987	−0.0080	−0.0083257217	0.0003257217	−0.1398613011	0.0054717011
23	17.0499	−0.1110	−0.1109368217	0.0000631782	−1.8914617173	0.0010771826
24	17.2793	−0.2090	−0.2092476082	0.0002476082	−3.6156521970	0.0042784970
25	17.4885	−0.3030	−0.3008639322	0.0021360677	−5.2616588799	0.0373566200

. All values of $IA{E}_{current}$ are less than 4.83 × 10⁻³ and all values of $IA{E}_{power}$ are less than 7.99 × 10⁻², which verifies the accuracy of CSOOJAYA parameter identification again.

5.4. Statistical Results and Convergence Curve

The above three sections demonstrate the superior accuracy of CSOOJAYA in solving parameter identification on different PV models. However, convergence and robustness should also be considered. Therefore, this section compares the convergence curves and statistical results of the three PV models.

The maximum RMSE (Max), minimum RMSE(Min), average RMSE (Mean) and standard deviation (SD) of RMSE obtained by running all the comparison algorithms 30 times independently on three different PV models are shown in

Table 11. Comparison of statistical results for PV models.

Model	Algorithm	RMSE
		Min	Max	Mean	SD
SDM	DE/WOA	9.860219 × 10−4	9.860219 × 10−4	9.860219 × 10−4	3.545178 × 10−17
	MLBSA	9.8602 × 10−4	9.8602 × 10−4	9.8602 × 10−4	9.1461 × 10−12
	EJADE	9.8602 × 10−4	9.8602 × 10−4	9.8602 × 10−4	5.13 × 10−17
	MTLBO	9.860219 × 10−4	9.860219 × 10−4	9.860219 × 10−4	1.9092749 × 10−17
	MPPCEDE	9.86022 × 10−4	9.86022 × 10−4	9.86022 × 10−4	2.44932 × 10−17
	MADE	9.8602 × 10−4	9.8602 × 10−4	9.8602 × 10−4	2.74 × 10−15
	IJAYA	9.8603 × 10−4	1.0622 × 10−3	9.9204 × 10−4	1.4033 × 10−5
	ITLBO	9.8602 × 10−4	9.8602 × 10−4	9.8602 × 10−4	2.19 × 10−17
	CPMPSO	9.86022 × 10−4	9.86022 × 10−4	9.86022 × 10−4	2.17556 × 10−17
	DERAO	9.860219 × 10−4	9.860219 × 10−4	9.860219 × 10−4	3.642031 × 10−17
	JAYA	9.8946 × 10−4	1.4783 × 10−3	1.1617 × 10−3	1.8796 × 10−4
	PGJAYA	9.8602 × 10−4	9.8603 × 10−4	9.8602 × 10−4	1.4485 × 10−9
	LCJAYA	9.8602 × 10−4	9.8602 × 10−4	9.8602 × 10−4	5.6997 × 10−16
	CSOOJAYA	9.860219 × 10−4	9.860219 × 10−4	9.860219 × 10−4	4.717305 × 10−17
DDM	DE/WOA	9.824849 × 10−4	9.860377 × 10−4	9.829703 × 10−4	9.152178 × 10−7
	MLBSA	9.8249 × 10−4	9.8518 × 10−4	9.8798 × 10−4	1.3482 × 10−6
	EJADE	9.8248 × 10−4	9.8602 × 10−4	9.8363 × 10−4	1.36 × 10−6
	MTLBO	9.824849 × 10−4	9.825026 × 10−4	9.824855 × 10−4	3.30000 × 10−9
	MPPCEDE	9.82485 × 10−4	9.82908 × 10−4	9.82504 × 10−4	8.02951 × 10−8
	MADE	9.8261 × 10−4	9.8786 × 10−4	9.8608 × 10−4	8.02 × 10−5
	IJAYA	9.8293 × 10−4	1.4055 × 10−3	1.0269 × 10−3	9.8325 × 10−5
	ITLBO	9.8248 × 10−4	9.8812 × 10−4	9.8497 × 10−4	1.54 × 10−6
	CPMPSO	9.82485 × 10−4	9.83137 × 10−4	9.86022 × 10−4	1.3398 × 10−6
	DERAO	9.824841 × 10−4	9.824897 × 10−4	9.824845 × 10−4	1.01560 × 10−9
	JAYA	9.8934 × 10−4	1.4793 × 10−3	1.1767 × 10−3	1.9356 × 10−4
	PGJAYA	9.8263 × 10−4	9.9499 × 10−4	9.8582 × 10−4	2.5375 × 10−6
	LCJAYA	9.8250 × 10−4	9.8602 × 10−4	9.8308 × 10−4	1.3118 × 10−6
	CSOOJAYA	9.824849 × 10−4	9.824849 × 10−4	9.824849 × 10−4	5.576332 × 10−17
PV module	DE/WOA	2.425075 × 10−3	2.425442 × 10−3	2.425092 × 10−3	6.270718 × 10−8
	MLBSA	2.425075 × 10−3	2.425084 × 10−3	2.425312 × 10−3	4.336794 × 10−8
	EJADE	2.4251 × 10−3	2.4251 × 10−3	2.4251 × 10−3	3.27 × 10−17
	MTLBO	2.425075 × 10−3	2.425075 × 10−3	2.425075 × 10−3	1.3070107 × 10−17
	MPPCEDE	2.42507 × 10−3	2.42507 × 10−3	2.42507 × 10−3	2.23156 × 10−17
	MADE	2.4250 × 10−3	2.4251 × 10−3	2.4251 × 10−3	3.07 × 10−17
	IJAYA	2.4251 × 10−3	2.4393 × 10−3	2.4289 × 10−3	3.7755 × 10−6
	ITLBO	2.4251 × 10−3	2.4251 × 10−3	2.4251 × 10−3	1.27 × 10−17
	CPMPSO	2.425075 × 10−3	2.425075 × 10−3	2.425075 × 10−3	1.515959 × 10−17
	DERAO	2.425075 × 10−3	2.425075 × 10−3	2.425075 × 10−3	1.716113 × 10−17
	JAYA	2.427785 × 10−3	2.595873 × 10−3	2.453710 × 10−3	3.456290 × 10−5
	PGJAYA	2.425075 × 10−3	2.426764 × 10−3	2.425144 × 10−3	3.071420 × 10−7
	LCJAYA	2.425075 × 10−3	2.425075 × 10−3	2.425075 × 10−3	2.415229 × 10−16
	CSOOJAYA	2.425075 × 10−3	2.425075 × 10−3	2.425075 × 10−3	2.699858 × 10−17

. The overall best RMSE values for all compared algorithms are marked in bold. where Max represents the worst accuracy, Min is the best accuracy, and Mean is the average accuracy, and SD represents the stability of algorithm. It can be seen from the Table 11:

(1)

For the best RMES value, only CSOOJAYA, DE/WOA, EJADE, MTLBO, ITLBO, CPMPSO and DERAO get the best RMSE values for all PV models.

(2)

For the worst RMSE value, only CSOOJAYA and DE/WOA can obtain the optimal worst value of all PV models

(3)

For the average RMSE value, only CSOOJAYA can obtain the optimal average value for all PV models.

(4)

Taking into account the SD, it can reflect the reliability of the algorithm. Although the SD of MTLBO, MPPCEDE, ITLBO, CPMPSO and DERAO are slightly better than those of the CSOOJAYA algorithm in the SDM and the PV module, the SD of CSOOJAYA is far superior to other algorithms in the DDM. On the whole, the CSOOJAYA algorithm has stronger reliability than other algorithms. Based on the superior stability and accuracy of three PV models, CSOOJAYA can obtain the best parameter identification results.

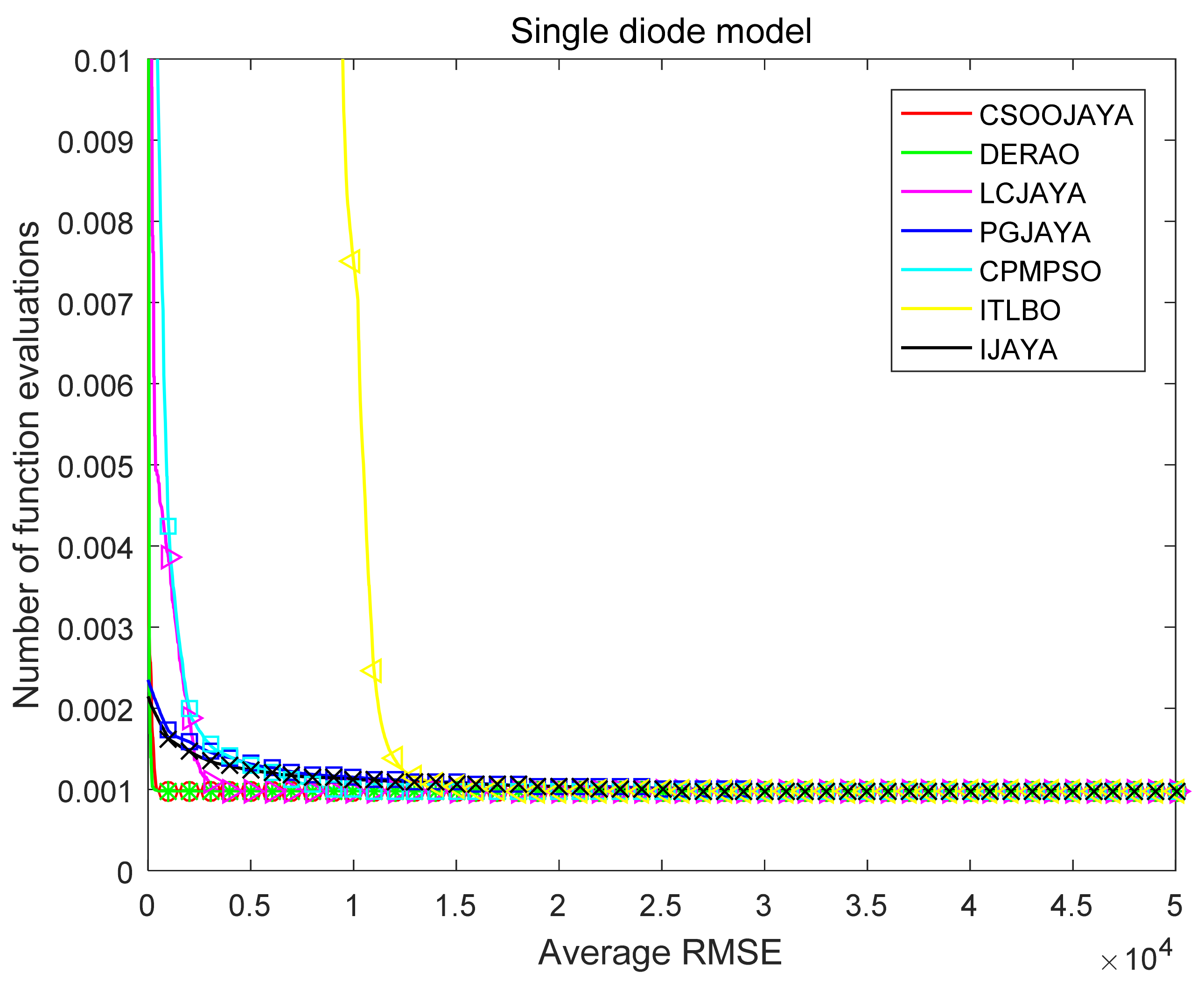
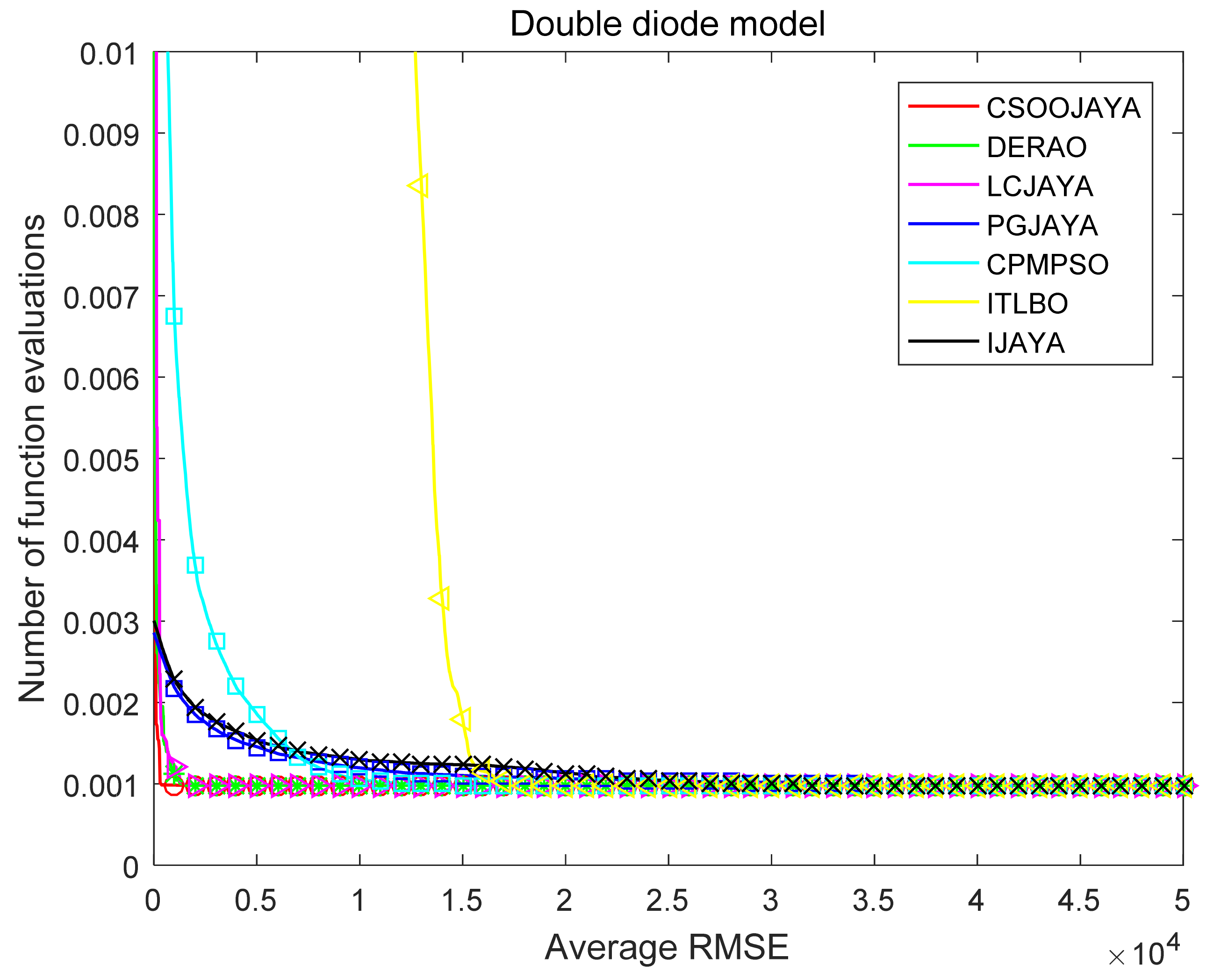
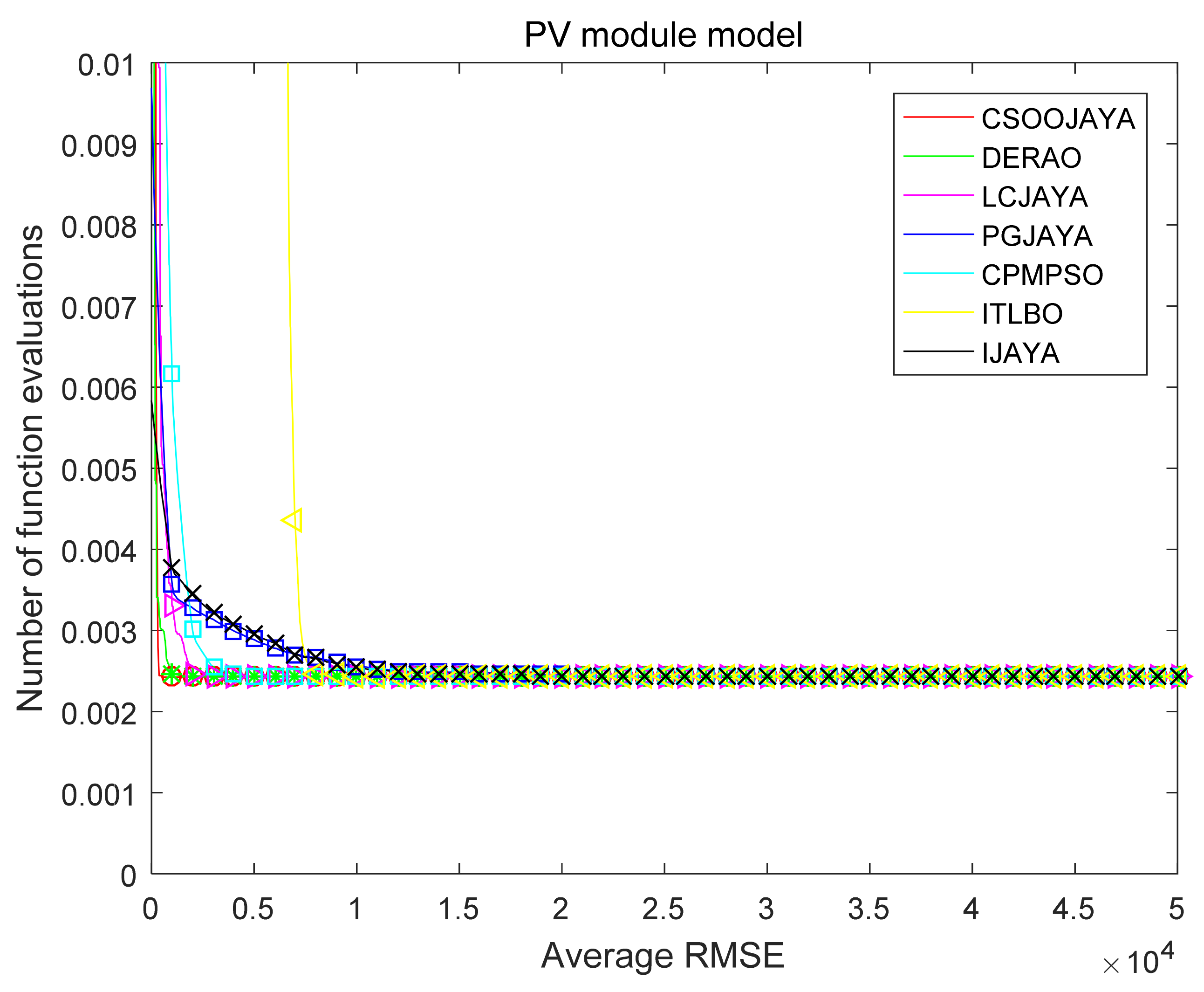
In order to validate the convergence speed of CSOOJAYA, Figure 8, Figure 9 and Figure 10 plot the iterative curves of several algorithms on the PV models. Obviously, CSOOJAYA not only get the best results among these three models, but also converges faster than other algorithms.

In summary, the above comparison shows that CSOOJAYA has faster convergence, better accuracy and robustness in extracting the parameters of PV models. Furthermore, the behavior of CSOOJAYA is competitive when compared to other algorithms.

6. Conclusions

This paper proposes a chaotic second order oscillation JAYA algorithm to provide an accurate and stable way to identify the PV parameters. The algorithm introduces the logical chaotic map strategy, and the generated random sequence numbers are non-periodic and non-convergent, which can enhance the diversity of the population and improve the exploration. In order to improve and balance the above two abilities, the second order oscillation strategy is introduced into the algorithm. The strategy can not only maintain the diversity of the population, but also has strong exploration ability due to the oscillation convergence of the solution vector in the early iteration; The solution vector converges asymptotically in the later iteration and has strong exploitation ability. In order to balance the exploitation and exploration as a whole, the self-adaptive weight mechanism is introduced to adjust the tendency of individuals to approach the optimal solution and escape the worst solution and improve the search efficiency of the population and the exploitation. The introduction of mutation mechanisms ensures that individuals avoid getting stuck in local optima. In order to validate the behavior of CSOOJAYA, which is employed to the parameter identification problem of PV models. Finally, the experimental results present that CSOOJAYA delivers excellent behavior in the aspects of convergence, reliability and accuracy.

The data of the PV cells used in this article are measured under certain temperature and light irradiance conditions. In order to further verify the applicability of CSOOJAYA algorithm to parameter identification under different PV cell or module operating scenarios. The next step of the research group will be to study the parameter identification of PV cells or components in multiple scenarios.