Leveraging AI in Photonics and Beyond
Abstract
:1. Introduction
2. AI for Photonics: Modeling and Simulation
2.1. Neural Networks
2.2. Optical Mode Solving
2.2.1. Modal Classifications
2.2.2. Effective Refractive Indices
2.2.3. Optical Mode Profile
2.3. Inverse Design of Photonic Structures: Deep Generative Models
3. Photonics for AI: Using Photonics Computing to Implement AI Algorithms
3.1. Current Developments in Photonics Computing
3.2. Photonic Accelerator
3.3. Coherent Feed-Forward Neural Network
3.4. Continuous-Time Recurrent Neural Network
3.5. Spiking Neural Network with Phase-Change Materials
3.6. Reservoir Computing
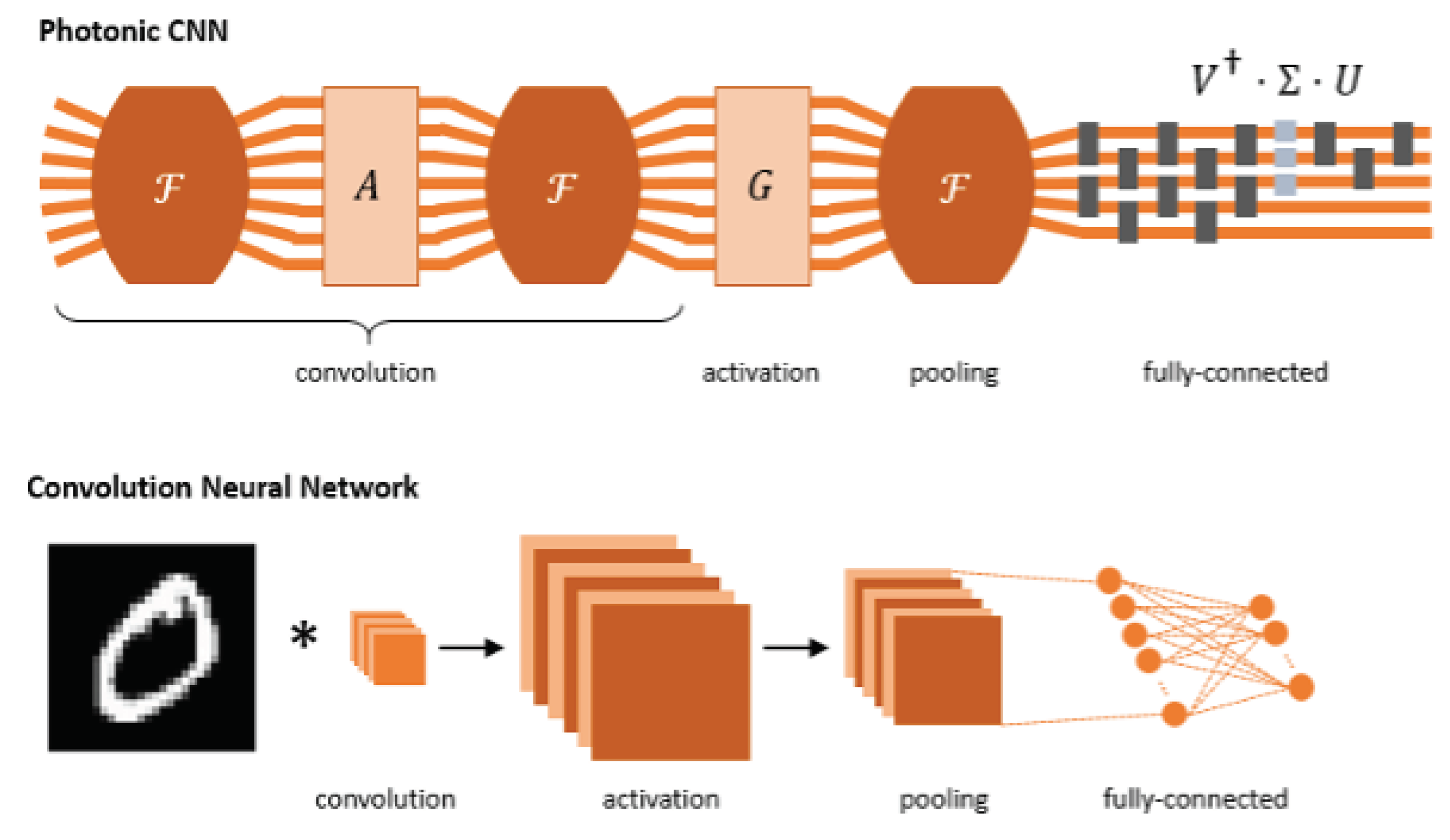
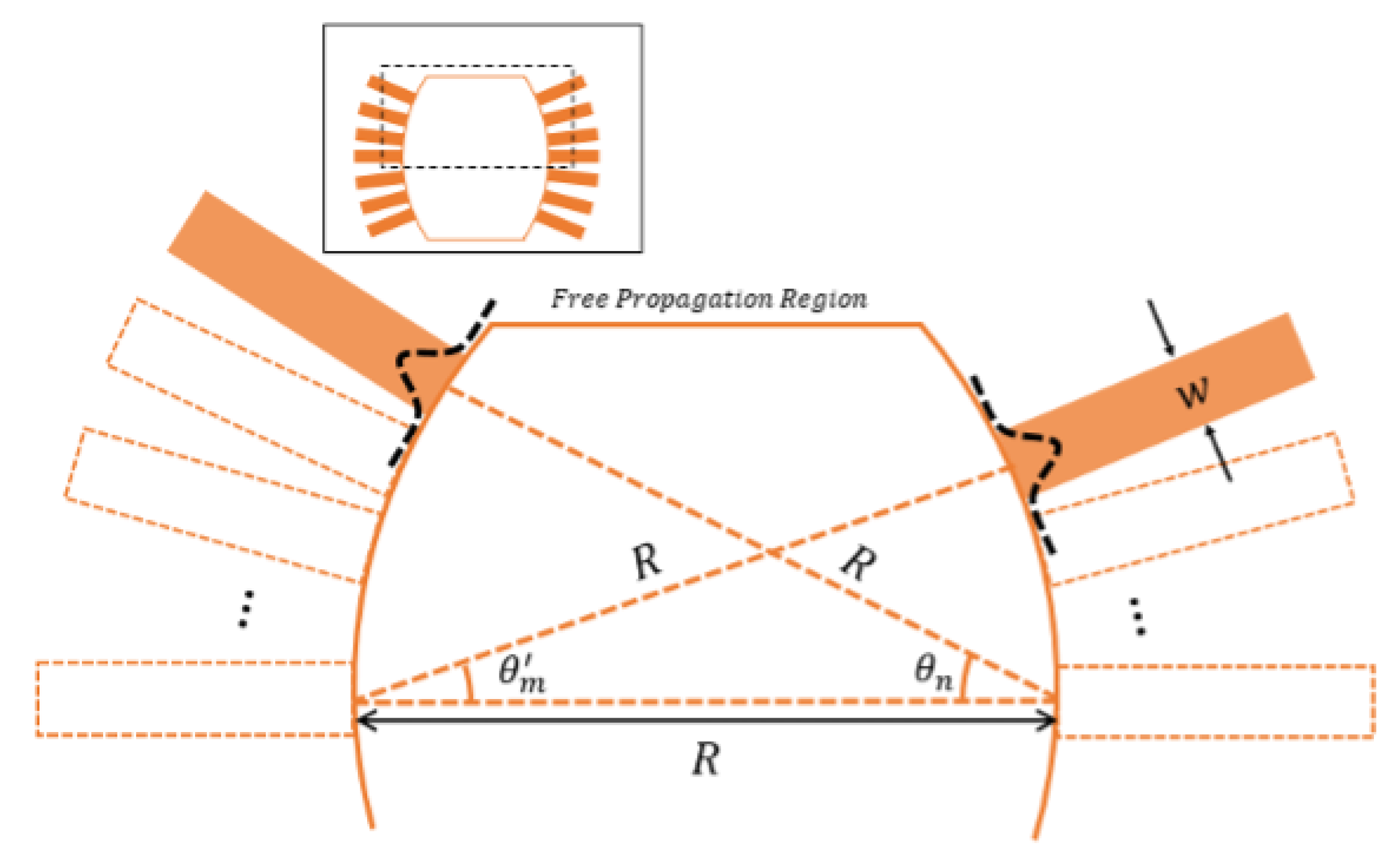
3.7. On-Chip Fourier Transform and Convolutions Using Star Couplers
4. AI Beyond Photonics
4.1. AI for Computational Electromagnetic Solvers: Forward and Inverse
4.2. AI for Microwave Devices: Design, Optimization, and Applications
4.3. AI for Electromagnetic Compatibility (EMC) and Electromagnetic Interference (EMI) Applications
4.4. AI for Quantum Related Topics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Networks |
| CEM | Computational Electromagnetics |
| CNN | Convolutional Neural Network |
| cGAN | Conditional Generative Adversarial Network |
| DL | Deep Learning |
| DNN | Deep Neural Networks |
| DGM | Deep Generative Model |
| DCGAN | Deep Convolutional Generative Adversarial Network |
| DRL | Deep Reinforcement Learning |
| DQN | Deep Q-learning Network |
| DDQN | Double Deep Q-learning Network |
| DE | Differential Evolution |
| EM | Electromagnetics |
| EMC | Electromagnetic Compatibility |
| EMI | Electromagnetic Interference |
| FDTD | Finite-Difference Time-Domain |
| FDFD | Finite-Difference Frequency-Domain |
| FEM | Finite Element Method |
| GAN | Generative Adversarial Network |
| GP | Gaussian Process |
| ISP | Inverse Scattering Problems |
| MOM | Method of Moment |
| ML | Machine Learning |
| NN | Neural Network |
| NLP | Natural Language Processing |
| NISQ | Noisy Intermediate-Scale Quantum |
| PEEC | Partial Element Equivalent Circuit |
| RF | Radiofrequency |
| RNN | Recurrent Neural Network |
| ReLU | Rectified Linear Unit |
| RL | Reinforcement Learning |
| SVM | Support Vector Machine |
| TLM | Transmission-Line Matrix |
| VAE | Variational Autoencoder |
| VQA | Variational Quantum-Based Algorithm |
| VQE | Variational Quantum Eigensolver |
References
- Kong, J.A. Theory of Electromagnetic Waves; Wiley-Interscience: New York, NY, USA, 1975. [Google Scholar]
- Ulaby, F.T.; Michielssen, E.; Ravaioli, U. Fundamentals of Applied Electromagnetics; Pearson Boston: Boston, MA, USA, 2015. [Google Scholar]
- Hayt, W.H., Jr.; Buck, J.A.; Akhtar, M.J. Engineering Electromagnetics|(SIE); McGraw-Hill Education: New York, NY, USA, 2020. [Google Scholar]
- Tsang, L.; Kong, J.A.; Ding, K.H. Scattering of Electromagnetic Waves: Theories And applications; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 27. [Google Scholar]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hecht, E. Optics, 5th ed.; Pearson: London, UK, 2017. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Shi, D.; Wang, N.; Zhang, F.; Fang, W. Intelligent electromagnetic compatibility diagnosis and management with collective knowledge graphs and machine learning. IEEE Trans. Electromagn. Compat. 2020, 63, 443–453. [Google Scholar] [CrossRef]
- Huang, Q.; Fan, J. Machine learning based source reconstruction for RF desense. IEEE Trans. Electromagn. Compat. 2018, 60, 1640–1647. [Google Scholar] [CrossRef]
- Ohira, M.; Takano, K.; Ma, Z. A Novel Deep-Q-Network-Based Fine-Tuning Approach for Planar Bandpass Filter Design. IEEE Microw. Wirel. Components Lett. 2021, 31, 638–641. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.X.; Dong, W.H.; Wang, X.; Shi, J.; Teng, H.L.; Dai, X.W.; Yau, S.S.T.; Liang, C.H.; Feng, P.F. Microwave integrated circuits design with relational induction neural network. arXiv 2019, arXiv:1901.02069. [Google Scholar]
- Bulgarevich, D.S.; Talara, M.; Tani, M.; Watanabe, M. Machine learning for pattern and waveform recognitions in terahertz image data. Sci. Rep. 2021, 11, 1–8. [Google Scholar]
- Cao, Z.; Yang, H.; Zhao, J.; Pan, X.; Zhang, L.; Liu, Z. A new region proposal network for far-infrared pedestrian detection. IEEE Access 2019, 7, 135023–135030. [Google Scholar] [CrossRef]
- Denholm, S.; Brand, W.; Mitchell, A.; Wells, A.; Krzyzelewski, T.; Smith, S.; Wall, E.; Coffey, M. Predicting bovine tuberculosis status of dairy cows from mid-infrared spectral data of milk using deep learning. J. Dairy Sci. 2020, 103, 9355–9367. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Z. Learning From Paired and Unpaired Data: Alternately Trained CycleGAN for Near Infrared Image Colorization. In Proceedings of the 2020 IEEE International Conference on Visual Communications and Image Processing (VCIP), Macau, China, 1–4 December 2020; pp. 467–470. [Google Scholar]
- Chen, J.; Hou, J.; Ni, Y.; Chau, L.P. Accurate light field depth estimation with superpixel regularization over partially occluded regions. IEEE Trans. Image Process. 2018, 27, 4889–4900. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Hou, J.; Chau, L.P. Light field compression with disparity-guided sparse coding based on structural key views. IEEE Trans. Image Process. 2017, 27, 314–324. [Google Scholar] [CrossRef] [Green Version]
- Lai, P.Y.; Liu, H.; Ng, R.J.H.; Wint Hnin Thet, B.; Chu, H.S.; Teo, J.W.R.; Ong, Q.; Liu, Y.; Png, C.E. Investigation of SARS-CoV-2 inactivation using UV-C LEDs in public environments via ray-tracing simulation. Sci. Rep. 2021, 11, 1–10. [Google Scholar]
- Massa, A.; Marcantonio, D.; Chen, X.; Li, M.; Salucci, M. DNNs as applied to electromagnetics, antennas, and propagation—A review. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2225–2229. [Google Scholar] [CrossRef]
- Erricolo, D.; Chen, P.Y.; Rozhkova, A.; Torabi, E.; Bagci, H.; Shamim, A.; Zhang, X. Machine learning in electromagnetics: A review and some perspectives for future research. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019; pp. 1377–1380. [Google Scholar]
- Chen, X.; Wei, Z.; Li, M.; Rocca, P. A review of deep learning approaches for inverse scattering problems (invited review). Prog. Electromagn. Res. 2020, 167, 67–81. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Jiao, L.; Zhao, J. A Survey on the New Generation of Deep Learning in Image Processing. IEEE Access 2019, 7, 172231–172263. [Google Scholar] [CrossRef]
- Chen, J.; Tan, C.H.; Hou, J.; Chau, L.P.; Li, H. Robust video content alignment and compensation for rain removal in a cnn framework. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6286–6295. [Google Scholar]
- Chowdhury, G.G. Natural language processing. Annu. Rev. Inf. Sci. Technol. 2003, 37, 51–89. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Xu, W.; Yu, K. Bidirectional LSTM-CRF models for sequence tagging. arXiv 2015, arXiv:1508.01991. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the 2017 IEEE international conference on robotics and automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3389–3396. [Google Scholar]
- Waltman, V.E. VOSviewer. Available online: www.vosviewer.com (accessed on 20 November 2021).
- Jiang, J.; Chen, M.; Fan, J.A. Deep neural networks for the evaluation and design of photonic devices. Nat. Rev. Mater. 2021, 6, 679–700. [Google Scholar] [CrossRef]
- Ma, W.; Liu, Z.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.; Liu, Y. Deep learning for the design of photonics structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Pfau, D.; Spencer, J.S.; Matthews, A.G.; Foulkes, W.M.C. Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Phys. Rev. Res. 2020, 2, 033429. [Google Scholar] [CrossRef]
- Malkiel, I.; Mrejen, M.; Nagler, A.; Arieli, U.; Wolf, L.; Suchowski, H. Plasmonic nanostructure design and characterization via deep learning. Light. Sci. Appl. 2018, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Alagappan, G.; Png, C.E. Universal deep learning representation of effective refractive index for photonics channel waveguides. JOSA B 2019, 36, 2636–2642. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Muskens, O.L. Deep learning meets nanophotonics: A generalized accurate predictor for near fields and far fields of arbitrary 3D nanostructures. Nano Lett. 2019, 20, 329–338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alagappan, G.; Png, C.E. Prediction of electromagnetic field patterns of optical waveguide using neural network. Neural Comput. Appl. 2021, 33, 2195–2206. [Google Scholar] [CrossRef]
- Lio, G.E.; Ferraro, A. LIDAR and Beam Steering Tailored by Neuromorphic Metasurfaces Dipped in a Tunable Surrounding Medium. In Photonics; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2021; Volume 8, p. 65. [Google Scholar]
- Colburn, S.; Majumdar, A. Inverse design and flexible parameterization of meta-optics using algorithmic differentiation. Commun. Phys. 2021, 4, 1–11. [Google Scholar] [CrossRef]
- Nadell, C.C.; Huang, B.; Malof, J.M.; Padilla, W.J. Deep learning for accelerated all-dielectric metasurface design. Opt. Express 2019, 27, 27523–27535. [Google Scholar] [CrossRef]
- Inampudi, S.; Mosallaei, H. Neural network based design of metagratings. Appl. Phys. Lett. 2018, 112, 241102. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, W.; Long, Y.; Guo, S.; Liang, H.; Qiu, Z.; Fu, X.; Li, J. A Metasurface Beam Combiner Based on the Control of Angular Respons. In Photonics; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2021; Volume 8, p. 489. [Google Scholar]
- Pilozzi, L.; Farrelly, F.A.; Marcucci, G.; Conti, C. Machine learning inverse problem for topological photonics. Commun. Phys. 2018, 1, 1–7. [Google Scholar] [CrossRef]
- Cao, Y.; Li, S.; Petzold, L.; Serban, R. Adjoint sensitivity analysis for differential-algebraic equations: The adjoint DAE system and its numerical solution. SIAM J. Sci. Comput. 2003, 24, 1076–1089. [Google Scholar] [CrossRef] [Green Version]
- Hughes, T.W.; Minkov, M.; Williamson, I.A.; Fan, S. Adjoint method and inverse design for nonlinear nanophotonics devices. ACS Photonics 2018, 5, 4781–4787. [Google Scholar] [CrossRef] [Green Version]
- Minkov, M.; Williamson, I.A.; Andreani, L.C.; Gerace, D.; Lou, B.; Song, A.Y.; Hughes, T.W.; Fan, S. Inverse design of photonics crystals through automatic differentiation. ACS Photonics 2020, 7, 1729–1741. [Google Scholar] [CrossRef]
- Lio, G.E.; Ferraro, A.; Ritacco, T.; Aceti, D.M.; De Luca, A.; Giocondo, M.; Caputo, R. Leveraging on ENZ Metamaterials to Achieve 2D and 3D Hyper-Resolution in Two-Photon Direct Laser Writing. Adv. Mater. 2021, 33, 2008644. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Fan, J.A. Global optimization of dielectric metasurfaces using a physics-driven neural network. Nano Lett. 2019, 19, 5366–5372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, J.; Sell, D.; Hoyer, S.; Hickey, J.; Yang, J.; Fan, J.A. Free-form diffractive metagrating design based on generative adversarial networks. ACS Nano 2019, 13, 8872–8878. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mellit, A.; Eleuch, H.; Benghanem, M.; Elaoun, C.; Pavan, A.M. An adaptive model for predicting of global, direct and diffuse hourly solar irradiance. Energy Convers. Manag. 2010, 51, 771–782. [Google Scholar] [CrossRef]
- Yang, Z.; Hou, Y.; Chen, Z.; Zhang, L.; Chen, J. A Multi-Stage Progressive Learning Strategy for Covid-19 Diagnosis Using Chest Computed Tomography with Imbalanced Data. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 8578–8582. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the IEEE Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Alagappan, G.; Png, C.E. Modal classification in optical waveguides using deep learning. J. Mod. Opt. 2019, 66, 557–561. [Google Scholar] [CrossRef]
- Alagappan, G.; Png, C.E. Deep learning models for effective refractive indices in silicon nitride waveguides. J. Opt. 2019, 21, 035801. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Larochelle, H.; Murray, I. The neural autoregressive distribution estimator. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 29–37. [Google Scholar]
- Liu, Z.; Zhu, D.; Rodrigues, S.P.; Lee, K.T.; Cai, W. Generative model for the inverse design of metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- An, S.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.M.; Rivero-Baleine, C.; Kang, M.; et al. Deep learning modeling approach for metasurfaces with high degrees of freedom. Opt. Express 2020, 28, 31932–31942. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, F.; Liu, Y. Deep-learning-enabled on-demand design of chiral metamaterials. ACS Nano 2018, 12, 6326–6334. [Google Scholar] [CrossRef]
- Es-saidi, S.; Blaize, S.; Macías, D. Hybrid modes and hybrid metastructures for color reproduction. In Hybrid Flatland Metastructures; Caputo, R., Lio, G.E., Eds.; AIP Publishing: Melville, NY, USA, 2021; pp. 5-1–5-18. [Google Scholar]
- Pilozzi, L.; Farrelly, F.A.; Marcucci, G.; Conti, C. Topological nanophotonics and artificial neural networks. Nanotechnology 2021, 32, 142001. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Industry 4.0: From Big Data, AI, Robotics, to 3D Printing—Partnerships Are Key. Available online: https://www.edb.gov.sg/en/news-and-events/insights/manufacturing/industry-4-from-big-data-ai-robotics-to-3d-printing-partnerships-are-key.html (accessed on 7 February 2020).
- PwC’s Global Artificial Intelligence Study: Sizing the Prize. Available online: https://www.pwc.com/gx/en/issues/data-and-analytics/publications/artificial-intelligence-study.html (accessed on 7 February 2020).
- Making AI Work for Everyone. 17 May 2017. Available online: https://blog.google/technology/ai/making-ai-work-for-everyone/ (accessed on 7 February 2020).
- Jouppi, N.; Young, C.; Patil, N.; Patterson, D. Motivation for and evaluation of the first tensor processing unit. IEEE Micro 2018, 38, 10–19. [Google Scholar] [CrossRef]
- AI and Compute, OpenAI. 16 May 2018. Available online: https://openai.com/blog/ai-and-compute/ (accessed on 7 February 2020).
- Cavin, R.K.; Lugli, P.; Zhirnov, V.V. Science and engineering beyond Moore’s law. Proc. IEEE 2012, 100, 1720–1749. [Google Scholar] [CrossRef]
- Driscoll, J.B.; Doussiere, P.; Islam, S.; Narayan, R.; Lin, W.; Mahalingam, H.; Park, J.S.; Lin, Y.; Nguyen, K.; Roelofs, K.; et al. First 400G 8-channel CWDM silicon photonics integrated transmitter. In Proceedings of the 2018 IEEE 15th International Conference on Group IV Photonics (GFP), Cancun, Mexico, 29–31 August 2018; pp. 1–2. [Google Scholar]
- Maniloff, E.; Gareau, S.; Moyer, M. 400G and beyond: Coherent evolution to high-capacity inter data center links. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Lim, A.E.J.; Song, J.; Fang, Q.; Li, C.; Tu, X.; Duan, N.; Chen, K.K.; Tern, R.P.C.; Liow, T.Y. Review of silicon photonics foundry efforts. IEEE J. Sel. Top. Quantum Electron. 2013, 20, 405–416. [Google Scholar] [CrossRef]
- Sacher, W.D.; Huang, Y.; Lo, G.Q.; Poon, J.K. Multilayer silicon nitride-on-silicon integrated photonics platforms and devices. J. Light. Technol. 2015, 33, 901–910. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-range LiDAR and free-space data communication with high-performance optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–8. [Google Scholar] [CrossRef]
- Qiang, X.; Zhou, X.; Wang, J.; Wilkes, C.M.; Loke, T.; O’Gara, S.; Kling, L.; Marshall, G.D.; Santagati, R.; Ralph, T.C.; et al. Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat. Photonics 2018, 12, 534–539. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.T.; Nahmias, M.A.; De Lima, T.F.; Tait, A.N.; Shastri, B.J. Neuromorphic photonics integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–15. [Google Scholar] [CrossRef]
- Kitayama, K.i.; Notomi, M.; Naruse, M.; Inoue, K.; Kawakami, S.; Uchida, A. Novel frontier of photonics for data processing—Photonic accelerator. APL Photonics 2019, 4, 090901. [Google Scholar] [CrossRef] [Green Version]
- Miller, D.A. Attojoule optoelectronics for low-energy information processing and communications. J. Light. Technol. 2017, 35, 346–396. [Google Scholar] [CrossRef] [Green Version]
- Xia, Q.; Yang, J.J. Memristive crossbar arrays for brain-inspired computing. Nat. Mater. 2019, 18, 309–323. [Google Scholar] [CrossRef]
- Ambrogio, S.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Boybat, I.; Di Nolfo, C.; Sidler, S.; Giordano, M.; Bodini, M.; Farinha, N.C.; et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 2018, 558, 60–67. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Hamerly, R.; Bernstein, L.; Sludds, A.; Soljačić, M.; Englund, D. Large-scale optical neural networks based on photoelectric multiplication. Phys. Rev. X 2019, 9, 021032. [Google Scholar] [CrossRef] [Green Version]
- Nahmias, M.A.; De Lima, T.F.; Tait, A.N.; Peng, H.T.; Shastri, B.J.; Prucnal, P.R. Photonic multiply-accumulate operations for neural networks. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–18. [Google Scholar] [CrossRef]
- Caulfield, H.J.; Kinser, J.; Rogers, S.K. Optical neural networks. Proc. IEEE 1989, 77, 1573–1583. [Google Scholar] [CrossRef]
- Ambs, P. Optical Computing: A 60-Year Adventure. Adv. Opt. Technol. 2010. [Google Scholar] [CrossRef] [Green Version]
- Light May Be Key To New Generation of Fast Computers—The New York Times. Available online: https://www.nytimes.com/1985/10/22/science/light-may-be-key-to-new-generation-of-fast-computers.html (accessed on 7 February 2020).
- Tucker, R.S. The role of optics in computing. Nat. Photonics 2010, 4, 405. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Su, Z.; Hosseini, E.S.; Cole, D.B.; Watts, M.R. Large-scale silicon photonics circuits for optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2013, 20, 264–278. [Google Scholar] [CrossRef]
- Harris, N.C.; Carolan, J.; Bunandar, D.; Prabhu, M.; Hochberg, M.; Baehr-Jones, T.; Fanto, M.L.; Smith, A.M.; Tison, C.C.; Alsing, P.M.; et al. Linear programmable nanophotonics processors. Optica 2018, 5, 1623–1631. [Google Scholar] [CrossRef]
- Nejadriahi, H.; HillerKuss, D.; George, J.K.; Sorger, V.J. Integrated all-optical fast Fourier transform: Design and sensitivity analysis. arXiv 2017, arXiv:1711.02500. [Google Scholar]
- Mehrabian, A.; Al-Kabani, Y.; Sorger, V.J.; El-Ghazawi, T. PCNNA: A photonics convolutional neural network accelerator. In Proceedings of the 2018 31st IEEE International System-on-Chip Conference (SOCC), Arlington, VA, USA, 4–7 September 2018; pp. 169–173. [Google Scholar]
- Liu, W.; Liu, W.; Ye, Y.; Lou, Q.; Xie, Y.; Jiang, L. Holylight: A nanophotonics accelerator for deep learning in data centers. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019; pp. 1483–1488. [Google Scholar]
- Mehrabian, A.; Miscuglio, M.; Alkabani, Y.; Sorger, V.J.; El-Ghazawi, T. A winograd-based integrated photonics accelerator for convolutional neural networks. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–12. [Google Scholar] [CrossRef]
- Bangari, V.; Marquez, B.A.; Miller, H.; Tait, A.N.; Nahmias, M.A.; De Lima, T.F.; Peng, H.T.; Prucnal, P.R.; Shastri, B.J. Digital electronics and analog photonics for convolutional neural networks (DEAP-CNNs). IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; Larochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonics circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Zhang, X.M.; Yung, M.H. Low-Depth Optical Neural Networks. arXiv 2019, arXiv:1904.02165. [Google Scholar]
- Fang, M.Y.S.; Manipatruni, S.; Wierzynski, C.; Khosrowshahi, A.; DeWeese, M.R. Design of optical neural networks with component imprecisions. Opt. Express 2019, 27, 14009–14029. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Williamson, I.A.; Hughes, T.W.; Minkov, M.; Bartlett, B.; Pai, S.; Fan, S. Reprogrammable electro-optic nonlinear activation functions for optical neural networks. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Tait, A.N.; De Lima, T.F.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonics networks using silicon photonics weight banks. Sci. Rep. 2017, 7, 1–10. [Google Scholar]
- Tait, A.N.; De Lima, T.F.; Nahmias, M.A.; Miller, H.B.; Peng, H.T.; Shastri, B.J.; Prucnal, P.R. Silicon photonics modulator neuron. Phys. Rev. Appl. 2019, 11, 064043. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, I.; Saha, G.; Roy, K. Photonic in-memory computing primitive for spiking neural networks using phase-change materials. Phys. Rev. Appl. 2019, 11, 014063. [Google Scholar] [CrossRef] [Green Version]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef] [Green Version]
- Vandoorne, K.; Mechet, P.; Van Vaerenbergh, T.; Fiers, M.; Morthier, G.; Verstraeten, D.; Schrauwen, B.; Dambre, J.; Bienstman, P. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Mesaritakis, C.; Papataxiarhis, V.; Syvridis, D. Micro ring resonators as building blocks for an all-optical high-speed reservoir-computing bit-pattern-recognition system. JOSA B 2013, 30, 3048–3055. [Google Scholar] [CrossRef]
- Denis-Le Coarer, F.; Sciamanna, M.; Katumba, A.; Freiberger, M.; Dambre, J.; Bienstman, P.; Rontani, D. All-optical reservoir computing on a photonics chip using silicon-based ring resonators. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Mesaritakis, C.; Syvridis, D. Reservoir computing based on transverse modes in a single optical waveguide. Opt. Lett. 2019, 44, 1218–1221. [Google Scholar] [CrossRef] [PubMed]
- Paudel, U.; Luengo-Kovac, M.; Pilawa, J.; Shaw, T.J.; Valley, G.C. Classification of time-domain waveforms using a speckle-based optical reservoir computer. Opt. Express 2020, 28, 1225–1237. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Ji, R.; Zhang, L.; Ding, J.; Xu, Q. On-chip CMOS-compatible optical signal processor. Opt. Express 2012, 20, 13560–13565. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics, Roberts & Co; Macmillan Learning: New York, NY, USA, 2005. [Google Scholar]
- Lightmatter—Accelerating AI with Light. Available online: https://lightmatter.co/ (accessed on 7 February 2020).
- Lightelligence—Empower AI with light, Lightelligence—Empower AI with light. Available online: https://www.lightelligence.ai (accessed on 7 February 2020).
- Home, Luminous Computing. Available online: https://www.luminouscomputing.com (accessed on 7 February 2020).
- Banner, R.; Hubara, I.; Hoffer, E.; Soudry, D. Scalable methods for 8-bit training of neural networks. arXiv 2018, arXiv:1805.11046. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized neural networks: Training neural networks with low precision weights and activations. J. Mach. Learn. Res. 2017, 18, 6869–6898. [Google Scholar]
- Bishop, C.M. Training with noise is equivalent to Tikhonov regularization. Neural Comput. 1995, 7, 108–116. [Google Scholar] [CrossRef]
- Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58. [Google Scholar] [CrossRef]
- Arjovsky, M.; Shah, A.; Bengio, Y. Unitary evolution recurrent neural networks. In International Conference on Machine Learning; PMLR: New York, NY, USA, 2016; pp. 1120–1128. [Google Scholar]
- Steinbrecher, G.R.; Olson, J.P.; Englund, D.; Carolan, J. Quantum optical neural networks. Npj Quantum Inf. 2019, 5, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Miscuglio, M.; Adam, G.C.; Kuzum, D.; Sorger, V.J. Roadmap on material-function mapping for photonic-electronic hybrid neural networks. APL Mater. 2019, 7, 100903. [Google Scholar] [CrossRef]
- Takiguchi, K.; Kitoh, T.; Mori, A.; Oguma, M.; Takahashi, H. Optical orthogonal frequency division multiplexing demultiplexer using slab star coupler-based optical discrete Fourier transform circuit. Opt. Lett. 2011, 36, 1140–1142. [Google Scholar] [CrossRef]
- Dragone, C. Efficient N*N star couplers using Fourier optics. J. Light. Technol. 1989, 7, 479–489. [Google Scholar] [CrossRef]
- Ong, J.R.; Ooi, C.C.; Ang, T.Y.; Lim, S.T.; Png, C.E. Photonic convolutional neural networks using integrated diffractive optics. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Taflove, A.; Hagness, S.C. Computational Electromagnetics: The Finite-Difference Time-Domain Method; Artech House Publishers: Norwood, MA, USA, 2005. [Google Scholar]
- Jin, J.M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Gibson, W.C. The Method of Moments in Electromagnetics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Yao, H.M.; Qin, Y.W.; Jiang, L.J. Machine learning based MoM (ML-MoM) for parasitic capacitance extractions. In Proceedings of the 2016 IEEE Electrical Design of Advanced Packaging and Systems (EDAPS), Honolulu, HI, USA, 14–16 December 2016; pp. 171–173. [Google Scholar]
- Yao, H.M.; Jiang, L.J.; Qin, Y.W. Machine learning based method of moments (ML-MoM). In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 973–974. [Google Scholar]
- Barmada, S.; Fontana, N.; Sani, L.; Thomopulos, D.; Tucci, M. Deep Learning and Reduced Models for Fast Optimization in Electromagnetics. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Tang, W.; Shan, T.; Dang, X.; Li, M.; Yang, F.; Xu, S.; Wu, J. Study on a Poisson’s equation solver based on deep learning technique. In Proceedings of the 2017 IEEE Electrical Design of Advanced Packaging and Systems Symposium (EDAPS), Haining, China, 14–16 December 2017; pp. 1–3. [Google Scholar]
- Bhardwaj, S.; Gohel, H.; Namuduri, S. A Multiple-Input Deep Neural Network Architecture for Solution of One-Dimensional Poisson Equation. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2244–2248. [Google Scholar] [CrossRef]
- Shan, T.; Dang, X.; Li, M.; Yang, F.; Xu, S.; Wu, J. Study on a 3D Possion’s Equation Slover Based on Deep Learning Technique. In Proceedings of the 2018 IEEE International Conference on Computational Electromagnetics (ICCEM), Chengdu, China, 26–28 March 2018; pp. 1–3. [Google Scholar]
- Özbay, A.G.; Hamzehloo, A.; Laizet, S.; Tzirakis, P.; Rizos, G.; Schuller, B. Poisson CNN: Convolutional neural networks for the solution of the Poisson equation on a Cartesian mesh. Data-Centric Eng. 2021, 2, e6. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Qi, S.; Wang, Y.; Li, Y.; Wu, X.; Ren, Q.; Ren, Y. Two-Dimensional Electromagnetic Solver Based on Deep Learning Technique. IEEE J. Multiscale Multiphys. Comput. Tech. 2020, 5, 83–88. [Google Scholar] [CrossRef]
- Guo, L.; Li, M.; Xu, S.; Yang, F. Study on a recurrent convolutional neural network based FDTD method. In Proceedings of the 2019 International Applied Computational Electromagnetics Society Symposium-China (ACES), Nanjing, China, 8–11 August 2019; Volume 1, pp. 1–2. [Google Scholar]
- Giannakis, I.; Giannopoulos, A.; Warren, C. A machine learning approach for simulating ground penetrating radar. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–4. [Google Scholar]
- Giannakis, I.; Giannopoulos, A.; Warren, C. A machine learning-based fast-forward solver for ground penetrating radar with application to full-waveform inversion. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4417–4426. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.M.; Jiang, L. Machine-learning-based PML for the FDTD method. IEEE Antennas Wirel. Propag. Lett. 2018, 18, 192–196. [Google Scholar] [CrossRef]
- Yao, H.M.; Jiang, L. Enhanced PML based on the long short term memory network for the FDTD method. IEEE Access 2020, 8, 21028–21035. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, N. Learning Unsplit-field-based PML for the FDTD Method by Deep Differentiable Forest. arXiv 2020, arXiv:2004.04815. [Google Scholar]
- Chen, X. Computational Methods for Electromagnetic Inverse Scattering; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Rayas-Sánchez, J.E. EM-based optimization of microwave circuits using artificial neural networks: The state-of-the-art. IEEE Trans. Microw. Theory Tech. 2004, 52, 420–435. [Google Scholar] [CrossRef]
- Chu, H.S.; Hoefer, W.J. Enhancement of time domain analysis and optimization through neural networks. Int. J. RF Microw. Comput.-Aided Eng. 2007, 17, 179–188. [Google Scholar] [CrossRef]
- Chu, H.S.; Hoefer, W.J. Time-Domain Analysis with Self-Optimizing Prony Predictor for Accelerated Field-Based Design. In Proceedings of the 2007 Workshop on Computational Electromagnetics in Time-Domain, Perugia, Italy, 15–17 October 2007; pp. 1–4. [Google Scholar]
- Zhao, P.; Wu, K. Homotopy Optimization of Microwave and Millimeter-Wave Filters Based on Neural Network Model. IEEE Trans. Microw. Theory Tech. 2020, 68, 1390–1400. [Google Scholar] [CrossRef]
- Roshani, S.; Heshmati, H.; Roshani, S. Design of a Microwave Lowpass–Bandpass Filter using Deep Learning and Artificial Intelligence. J. Inst. Electron. Comput. 2021, 3, 1–16. [Google Scholar] [CrossRef]
- Jin, J.; Zhang, C.; Feng, F.; Na, W.; Ma, J.; Zhang, Q.J. Deep neural network technique for high-dimensional microwave modeling and applications to parameter extraction of microwave filters. IEEE Trans. Microw. Theory Tech. 2019, 67, 4140–4155. [Google Scholar] [CrossRef]
- Jin, J.; Feng, F.; Zhang, J.; Yan, S.; Na, W.; Zhang, Q. A novel deep neural network topology for parametric modeling of passive microwave components. IEEE Access 2020, 8, 82273–82285. [Google Scholar] [CrossRef]
- Chen, X.; Tian, Y.; Zhang, T.; Gao, J. Differential evolution based manifold Gaussian process machine learning for microwave Filter’s parameter extraction. IEEE Access 2020, 8, 146450–146462. [Google Scholar] [CrossRef]
- Tak, J.; Kantemur, A.; Sharma, Y.; Xin, H. A 3-D-printed W-band slotted waveguide array antenna optimized using machine learning. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2008–2012. [Google Scholar] [CrossRef]
- Jain, S.K. Bandwidth enhancement of patch antennas using neural network dependent modified optimizer. Int. J. Microw. Wirel. Technol. 2016, 8, 1111–1119. [Google Scholar] [CrossRef]
- Gianfagna, C.; Yu, H.; Swaminathan, M.; Pulugurtha, R.; Tummala, R.; Antonini, G. Machine-learning approach for design of nanomagnetic-based antennas. J. Electron. Mater. 2017, 46, 4963–4975. [Google Scholar] [CrossRef]
- Gao, J.; Tian, Y.; Chen, X. Antenna optimization based on co-training algorithm of Gaussian process and support vector machine. IEEE Access 2020, 8, 211380–211390. [Google Scholar] [CrossRef]
- Feng, F.; Zhang, C.; Ma, J.; Zhang, Q.J. Parametric modeling of EM behavior of microwave components using combined neural networks and pole-residue-based transfer functions. IEEE Trans. Microw. Theory Tech. 2015, 64, 60–77. [Google Scholar] [CrossRef]
- Sekhri, E.; Kapoor, R.; Tamre, M. Double deep Q-learning approach for tuning microwave cavity filters using locally linear embedding technique. In Proceedings of the 2020 International Conference Mechatronic Systems and Materials (MSM), Bialystok, Poland, 1–3 July 2020; pp. 1–6. [Google Scholar]
- Wang, Z.; Ou, Y.; Wu, X.; Feng, W. Continuous reinforcement learning with knowledge-inspired reward shaping for autonomous cavity filter tuning. In Proceedings of the 2018 IEEE International Conference on Cyborg and Bionic Systems (CBS), Shenzhen, China, 25–27 October 2018; pp. 53–58. [Google Scholar]
- Wang, Z.; Yang, J.; Hu, J.; Feng, W.; Ou, Y. Reinforcement learning approach to learning human experience in tuning cavity filters. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 2145–2150. [Google Scholar]
- Isaksson, M.; Wisell, D.; Ronnow, D. Wide-band dynamic modeling of power amplifiers using radial-basis function neural networks. IEEE Trans. Microw. Theory Tech. 2005, 53, 3422–3428. [Google Scholar] [CrossRef]
- Mkadem, F.; Boumaiza, S. Physically inspired neural network model for RF power amplifier behavioral modeling and digital predistortion. IEEE Trans. Microw. Theory Tech. 2011, 59, 913–923. [Google Scholar] [CrossRef]
- Liu, W.; Na, W.; Zhu, L.; Ma, J.; Zhang, Q.J. A Wiener-type dynamic neural network approach to the modeling of nonlinear microwave devices. IEEE Trans. Microw. Theory Tech. 2017, 65, 2043–2062. [Google Scholar] [CrossRef]
- Liu, W.; Na, W.; Feng, F.; Zhu, L.; Lin, Q. A Wiener-Type Dynamic Neural Network Approach to the Modeling of Nonlinear Microwave Devices and Its Applications. In Proceedings of the 2020 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Hangzhou, China, 7–9 December 2020; pp. 1–3. [Google Scholar]
- Zhu, L.; Zhang, Q.; Liu, K.; Ma, Y.; Peng, B.; Yan, S. A novel dynamic neuro-space mapping approach for nonlinear microwave device modeling. IEEE Microw. Wirel. Components Lett. 2016, 26, 131–133. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, J.; Zhang, Q.J.; Root, D.E. Parallel matrix neural network training on cluster systems for dynamic FET modeling from large datasets. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–3. [Google Scholar]
- Huang, A.D.; Zhong, Z.; Wu, W.; Guo, Y.X. An artificial neural network-based electrothermal model for GaN HEMTs with dynamic trapping effects consideration. IEEE Trans. Microw. Theory Tech. 2016, 64, 2519–2528. [Google Scholar] [CrossRef]
- Monzó-Cabrera, J.; Pedreño-Molina, J.L.; Lozano-Guerrero, A.; Toledo-Moreo, A. A novel design of a robust ten-port microwave reflectometer with autonomous calibration by using neural networks. IEEE Trans. Microw. Theory Tech. 2008, 56, 2972–2978. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.; Zhu, Y. Beamforming design for large-scale antenna arrays using deep learning. IEEE Wirel. Commun. Lett. 2019, 9, 103–107. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Song, Y.; Yang, J.; Gui, G.; Adachi, F. Deep-learning-based millimeter-wave massive MIMO for hybrid precoding. IEEE Trans. Veh. Technol. 2019, 68, 3027–3032. [Google Scholar] [CrossRef] [Green Version]
- Alkhateeb, A.; Alex, S.; Varkey, P.; Li, Y.; Qu, Q.; Tujkovic, D. Deep learning coordinated beamforming for highly-mobile millimeter wave systems. IEEE Access 2018, 6, 37328–37348. [Google Scholar] [CrossRef]
- Huang, H.; Peng, Y.; Yang, J.; Xia, W.; Gui, G. Fast beamforming design via deep learning. IEEE Trans. Veh. Technol. 2019, 69, 1065–1069. [Google Scholar] [CrossRef]
- Elbir, A.M.; Mishra, K.V. Joint antenna selection and hybrid beamformer design using unquantized and quantized deep learning networks. IEEE Trans. Wirel. Commun. 2019, 19, 1677–1688. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Anees, A.; Zhong, Y.; Yang, Z.; Liu, Y.; Goh, R.S.M.; Liu, E.X. Crack Profile Reconstruction from Eddy Current Signals with an Encoder-Decoder Convolutional Neural Network. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), Singapore, 10–13 December 2019; pp. 96–98. [Google Scholar]
- Li, S.; Anees, A.; Zhong, Y.; Yang, Z.; Liu, Y.; Goh, R.S.M.; Liu, E.X. Learning to Reconstruct Crack Profiles for Eddy Current Nondestructive Testing. arXiv 2019, arXiv:1910.08721. [Google Scholar]
- Trinchero, R.; Manfredi, P.; Stievano, I.S.; Canavero, F.G. Machine learning for the performance assessment of high-speed links. IEEE Trans. Electromagn. Compat. 2018, 60, 1627–1634. [Google Scholar] [CrossRef]
- Li, Y.S.; Yu, H.; Jin, H.; Sarvey, T.E.; Oh, H.; Bakir, M.S.; Swaminathan, M.; Li, E.P. Dynamic thermal management for 3-d ics with time-dependent power map using microchannel cooling and machine learning. IEEE Trans. Components, Packag. Manuf. Technol. 2019, 9, 1244–1252. [Google Scholar] [CrossRef]
- Hung, S.Y.; Lee, C.Y.; Lin, Y.L. Data science for delamination prognosis and online batch learning in semiconductor assembly process. IEEE Trans. Components Packag. Manuf. Technol. 2019, 10, 314–324. [Google Scholar] [CrossRef]
- Jiang, Y.; Gao, R.X.K. A Deep Learning-Based Macro Circuit Modeling for Black-box EMC Problems. In Proceedings of the 2021 IEEE International Joint EMC/SI/PI and EMC Europe Symposium, Raleigh, NC, USA, 26 July–13 August 2021. [Google Scholar]
- Jiang, Y.; Wu, K.L. Quasi-static surface-PEEC modeling of electromagnetic problem with finite dielectrics. IEEE Trans. Microw. Theory Tech. 2018, 67, 565–576. [Google Scholar] [CrossRef]
- Schierholz, M.; Sánchez-Masís, A.; Carmona-Cruz, A.; Duan, X.; Roy, K.; Yang, C.; Rimolo-Donadio, R.; Schuster, C. SI/PI-Database of PCB-Based Interconnects for Machine Learning Applications. IEEE Access 2021, 9, 34423–34432. [Google Scholar] [CrossRef]
- Devabhaktuni, V.; Bunting, C.F.; Green, D.; Kvale, D.; Mareddy, L.; Rajamani, V. A new ANN-based modeling approach for rapid EMI/EMC analysis of PCB and shielding enclosures. IEEE Trans. Electromagn. Compat. 2012, 55, 385–394. [Google Scholar] [CrossRef]
- Kuo, M.J.; Lin, T.C. Dynamical optimal training for behavioral modeling of nonlinear circuit elements based on radial basis function neural network. In Proceedings of the 2008 Asia-Pacific Symposium on Electromagnetic Compatibility and 19th International Zurich Symposium on Electromagnetic Compatibility, Singapore, 19–23 May 2008; pp. 670–673. [Google Scholar]
- Magerl, M.; Stockreiter, C.; Eisenberger, O.; Minixhofer, R.; Baric, A. Building interchangeable black-box models of integrated circuits for EMC simulations. In Proceedings of the 2015 10th International Workshop on the Electromagnetic Compatibility of Integrated Circuits (EMC Compo), Edinburgh, UK, 10–13 November 2015; pp. 258–263. [Google Scholar]
- Ceperic, V.; Gielen, G.; Baric, A. Black-box modeling of conducted electromagnetic immunity by support vector machines. In Proceedings of the International Symposium on Electromagnetic Compatibility-EMC EUROPE, Rome, Italy, 17–21 September 2012; pp. 1–6. [Google Scholar]
- Shi, D.; Fang, W.; Zhang, F.; Xue, M.; Gao, Y. A novel method for intelligent EMC management using a “knowledge base”. IEEE Trans. Electromagn. Compat. 2018, 60, 1621–1626. [Google Scholar] [CrossRef]
- Watson, P.M.; Gupta, K.C. Design and optimization of CPW circuits using EM-ANN models for CPW components. IEEE Trans. Microw. Theory Tech. 1997, 45, 2515–2523. [Google Scholar] [CrossRef]
- Kim, H.; Sui, C.; Cai, K.; Sen, B.; Fan, J. Fast and precise high-speed channel modeling and optimization technique based on machine learning. IEEE Trans. Electromagn. Compat. 2017, 60, 2049–2052. [Google Scholar] [CrossRef]
- De Ridder, S.; Spina, D.; Toscani, N.; Grassi, F.; Ginste, D.V.; Dhaene, T. Machine-learning-based hybrid random-fuzzy uncertainty quantification for EMC and SI assessment. IEEE Trans. Electromagn. Compat. 2020, 62, 2538–2546. [Google Scholar] [CrossRef]
- Shu, Y.F.; Wei, X.C.; Fan, J.; Yang, R.; Yang, Y.B. An equivalent dipole model hybrid with artificial neural network for electromagnetic interference prediction. IEEE Trans. Microw. Theory Tech. 2019, 67, 1790–1797. [Google Scholar] [CrossRef]
- Regue, J.R.; Ribó, M.; Garrell, J.M.; Martín, A. A genetic algorithm based method for source identification and far-field radiated emissions prediction from near-field measurements for PCB characterization. IEEE Trans. Electromagn. Compat. 2001, 43, 520–530. [Google Scholar] [CrossRef]
- Wittek, P. Quantum Machine Learning: What Quantum Computing Means to Data Mining; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Sarma, S.D.; Deng, D.L.; Duan, L.M. Machine learning meets quantum physics. arXiv 2019, arXiv:1903.03516. [Google Scholar]
- Kudyshev, Z.A.; Shalaev, V.M.; Boltasseva, A. Machine learning for integrated quantum photonics. ACS Photonics 2020, 8, 34–46. [Google Scholar] [CrossRef]
- Haug, T.; Mok, W.K.; You, J.B.; Zhang, W.; Png, C.E.; Kwek, L.C. Classifying global state preparation via deep reinforcement learning. Mach. Learn. Sci. Technol. 2020, 2, 01LT02. [Google Scholar] [CrossRef]
- Wise, D.F.; Morton, J.J.; Dhomkar, S. Using Deep Learning to Understand and Mitigate the Qubit Noise Environment. PRX Quantum 2021, 2, 010316. [Google Scholar] [CrossRef]
- August, M.; Ni, X. Using recurrent neural networks to optimize dynamical decoupling for quantum memory. Phys. Rev. A 2017, 95, 012335. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Park, K.D.; Rhee, J.K. Quantum Error Mitigation With Artificial Neural Network. IEEE Access 2020, 8, 188853–188860. [Google Scholar] [CrossRef]
- IBM Quantum. Available online: https://quantum-computing.ibm.com (accessed on 20 November 2021).
- Rigetti. Available online: https://www.rigetti.com (accessed on 20 November 2021).
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Ewe, W.B.; Koh, D.E.; Goh, S.T.; Chu, H.S.; Png, C.E. Variational Quantum-Based Simulation of Waveguide Modes. arXiv 2021, arXiv:2109.12279. [Google Scholar]
- You, J.B.; Koh, D.E.; Kong, J.F.; Ding, W.J.; Png, C.E.; Wu, L. Exploring variational quantum eigensolver ansatzes for the long-range XY model. arXiv 2021, arXiv:2109.00288. [Google Scholar]
- Chen, S.Y.C.; Yang, C.H.H.; Qi, J.; Chen, P.Y.; Ma, X.; Goan, H.S. Variational Quantum Circuits for Deep Reinforcement Learning. IEEE Access 2020, 8, 141007–141024. [Google Scholar] [CrossRef]
- Lockwood, O.; Si, M. Reinforcement learning with quantum variational circuit. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, New York, NY, USA, 7–12 February 2020; Volume 16, pp. 245–251. [Google Scholar]

| Wave | Frequency | Wavelength Photon Energies | Applications Techniques | |
|---|---|---|---|---|
| RF | a few Hz–1 GHz | up to 300 mm | EMC/EMI [9,10] | |
| Microwave | 1 GHz–0.3 THz | 1–300 mm | Antenna/Filters [11,12] | |
| THz | 0.3–4 THz | 75 um–1 mm | Non-destructive testing [13] | |
| Optics | Far Infrared | 0.3–20 THz | 15 um–1 mm | Human body detection [14] |
| Mid Infrared | 20–100 THz | 3–15 um | Composition analysis [15] | |
| Near Infrared | 100–384 THz | 780–3000 nm | NIR imaging [16] | |
| Visible | 384–750 THz | 390–780 nm | Light field [17,18] | |
| Ultraviolet | 750 THz–10 PHz | 320–100 eV | UV-C LED [19] |
| Architecture | Description | Reference |
|---|---|---|
| Photonic Accelerator | Accelerated machine learning inference by speeding up expensive computations using photonics e.g., convolutions | [94,95,96,97,98] |
| Coherent Feed-forward Neural Network | Matrix multiplication by coherent interference in multi-port interferometers generally composed of mesh of beam-splitters and phase-shifters | [99,100,101,102] |
| Continuous-Time RNN | Summation of weighted WDM signals by photodetector which drives a nonlinear dynamical node producing output to next time step | [103,104] |
| Spiking Neural Network with Phase-change Materials | Summation of regular, WDM weighted, pulses using nonvolatile multi-state phase change material embedded in waveguide, emulating spike timing dependent plasticity | [105,106] |
| Reservoir Computing | Linear combination of outputs from a nonlinear dynamical system consisting of nodes with randomly weighted connections | [107,108,109,110,111] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alagappan, G.; Ong, J.R.; Yang, Z.; Ang, T.Y.L.; Zhao, W.; Jiang, Y.; Zhang, W.; Png, C.E. Leveraging AI in Photonics and Beyond. Photonics 2022, 9, 75. https://doi.org/10.3390/photonics9020075
Alagappan G, Ong JR, Yang Z, Ang TYL, Zhao W, Jiang Y, Zhang W, Png CE. Leveraging AI in Photonics and Beyond. Photonics. 2022; 9(2):75. https://doi.org/10.3390/photonics9020075
Chicago/Turabian StyleAlagappan, Gandhi, Jun Rong Ong, Zaifeng Yang, Thomas Yong Long Ang, Weijiang Zhao, Yang Jiang, Wenzu Zhang, and Ching Eng Png. 2022. "Leveraging AI in Photonics and Beyond" Photonics 9, no. 2: 75. https://doi.org/10.3390/photonics9020075
APA StyleAlagappan, G., Ong, J. R., Yang, Z., Ang, T. Y. L., Zhao, W., Jiang, Y., Zhang, W., & Png, C. E. (2022). Leveraging AI in Photonics and Beyond. Photonics, 9(2), 75. https://doi.org/10.3390/photonics9020075





