Line Field Optical Coherence Tomography
Abstract
1. Context, Introduction and Scope of Review
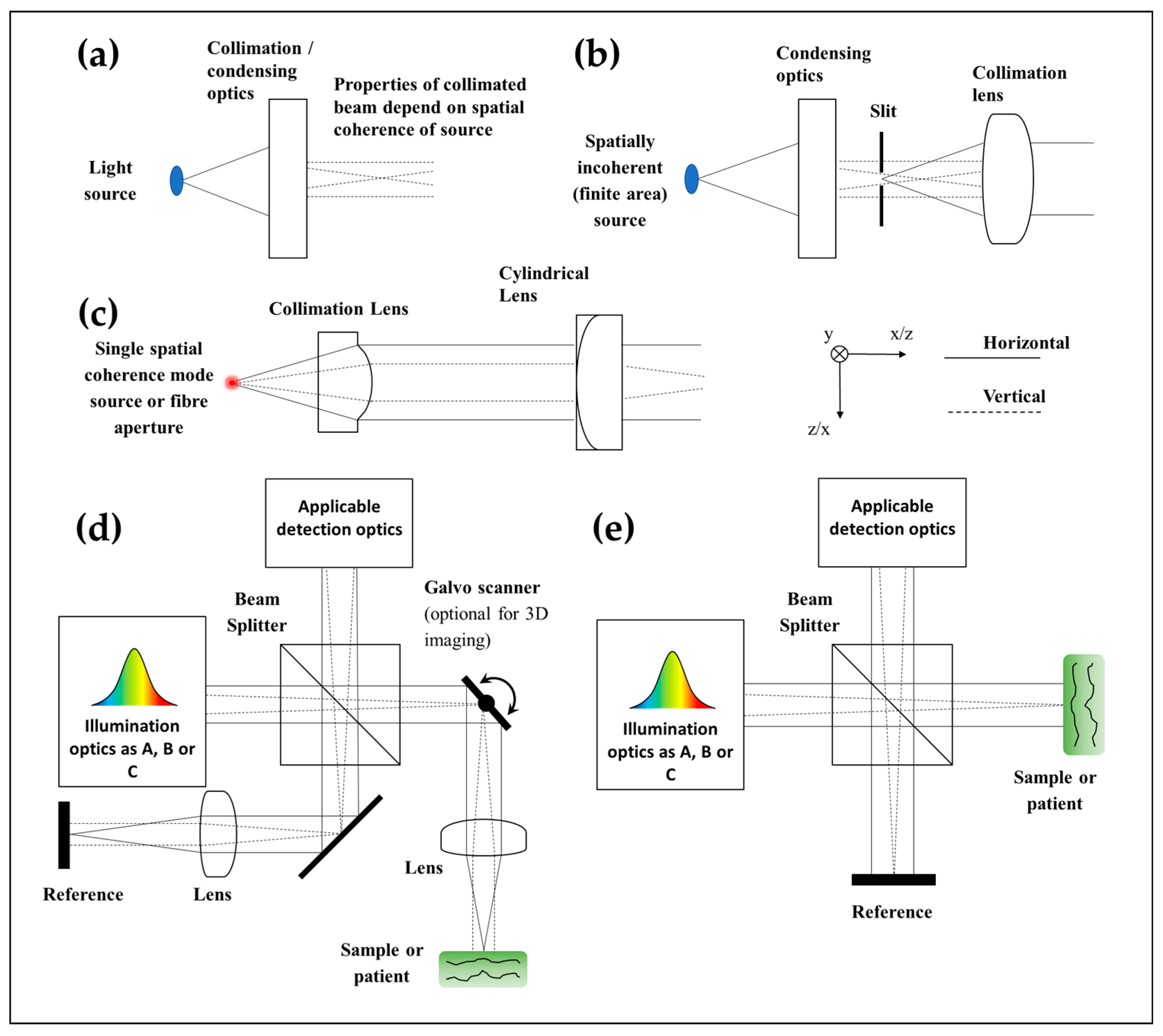
2. Design Choices Common to All LF-OCT Axial Formats
3. Spectral Domain (SD)
3.1. SD: Timeline of Published Developments and Applications
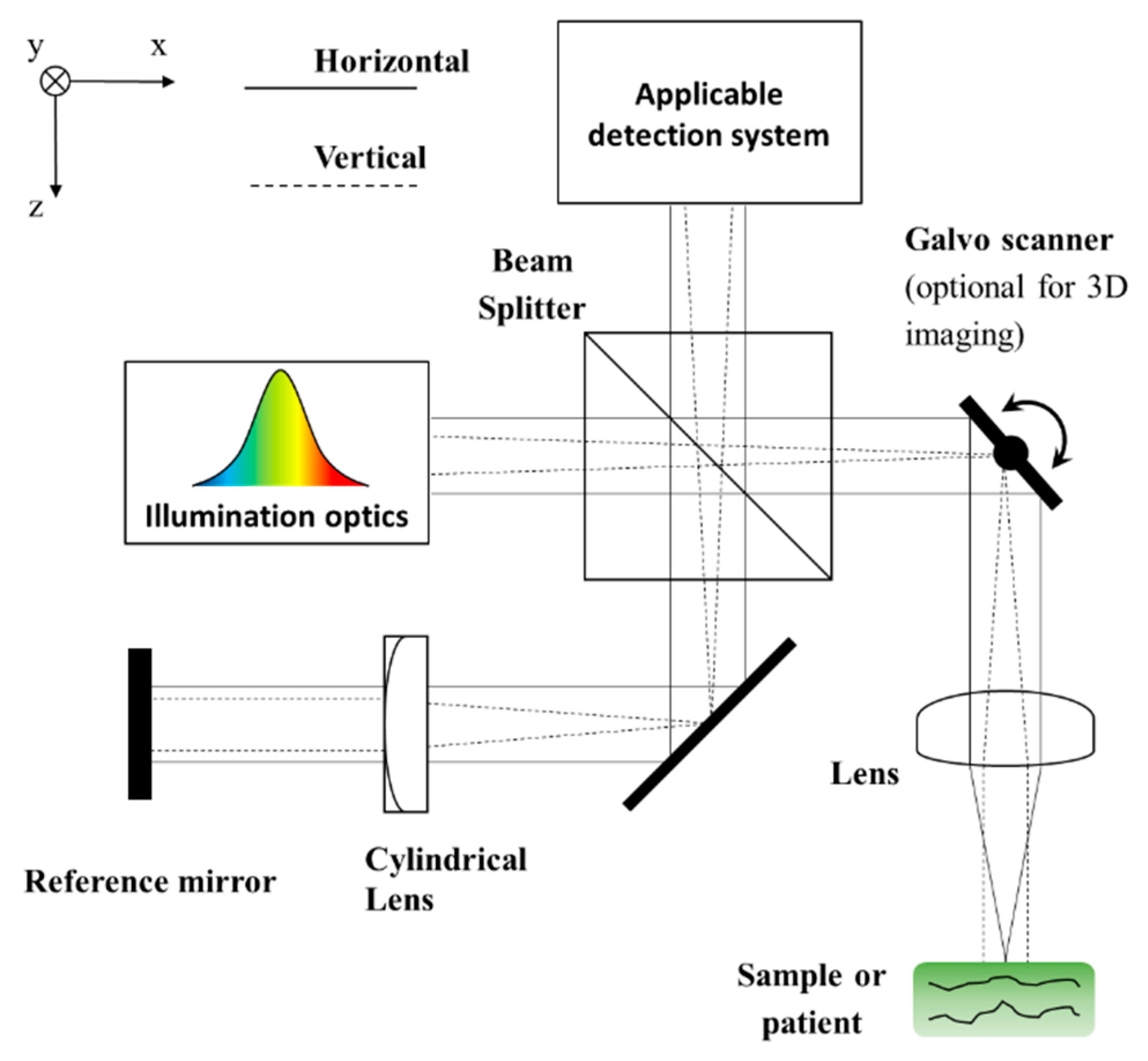
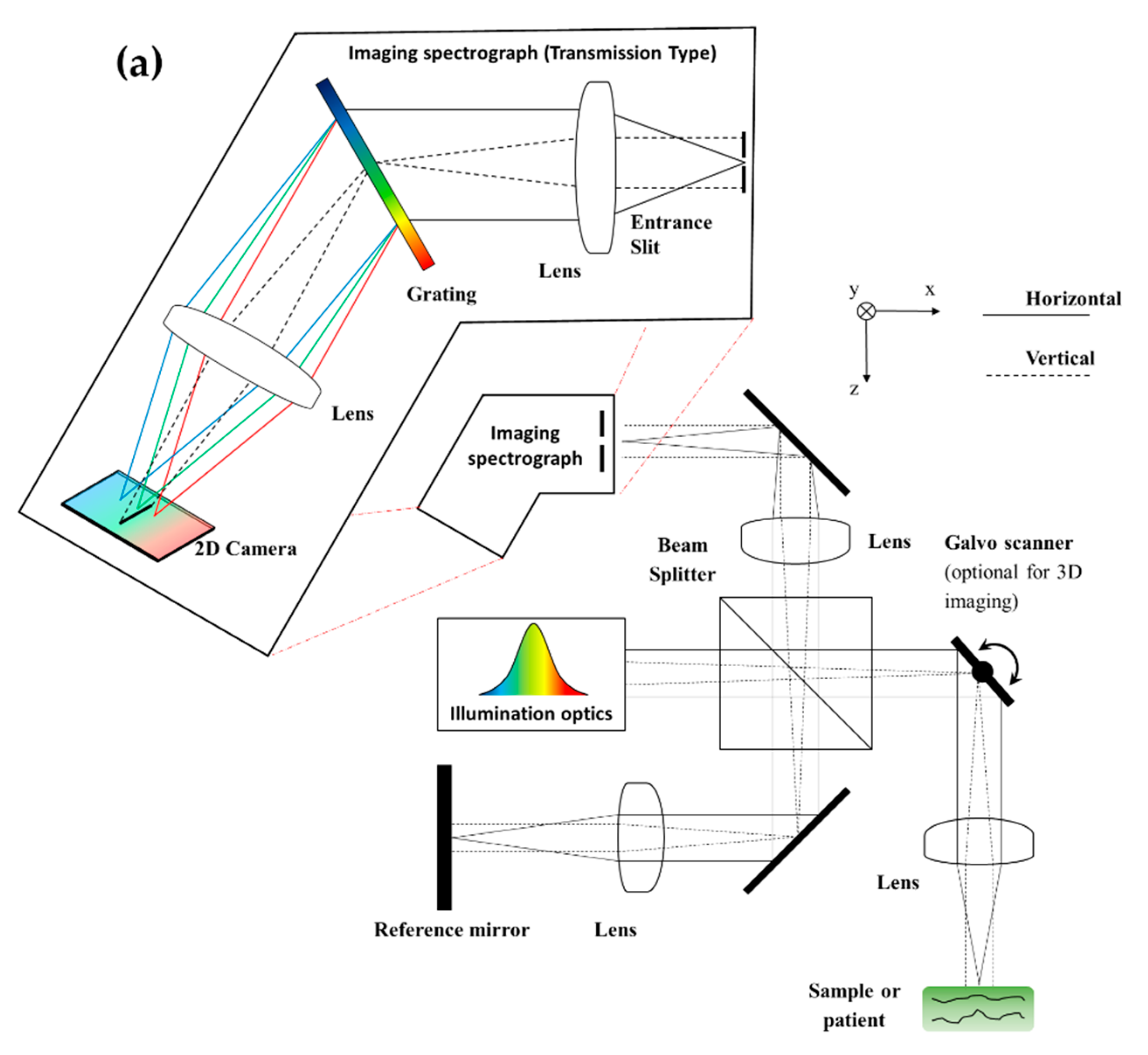
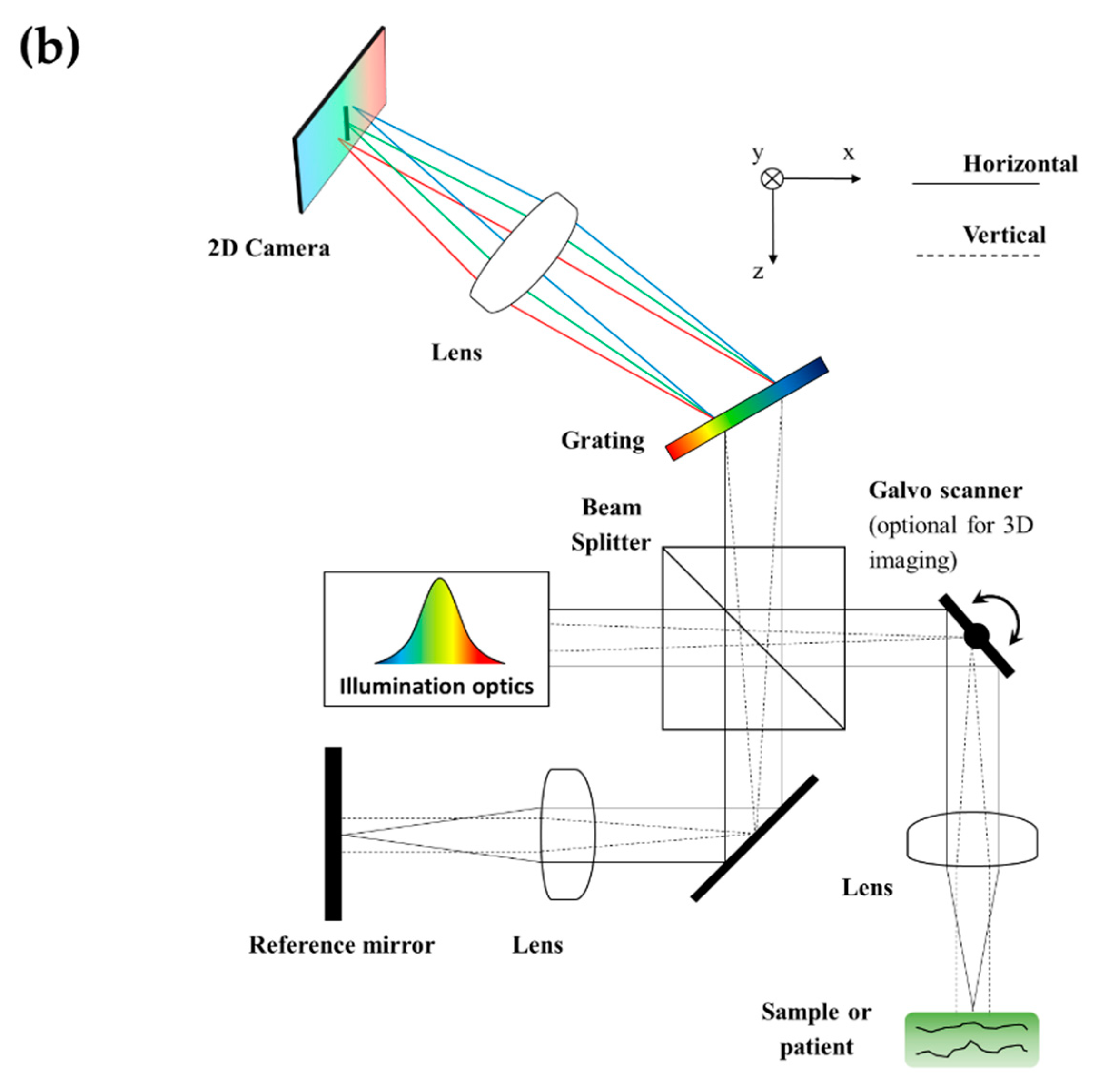
3.2. SD: System Construction Guide
4. Time Domain (TD) including Axial–Lateral (AL)
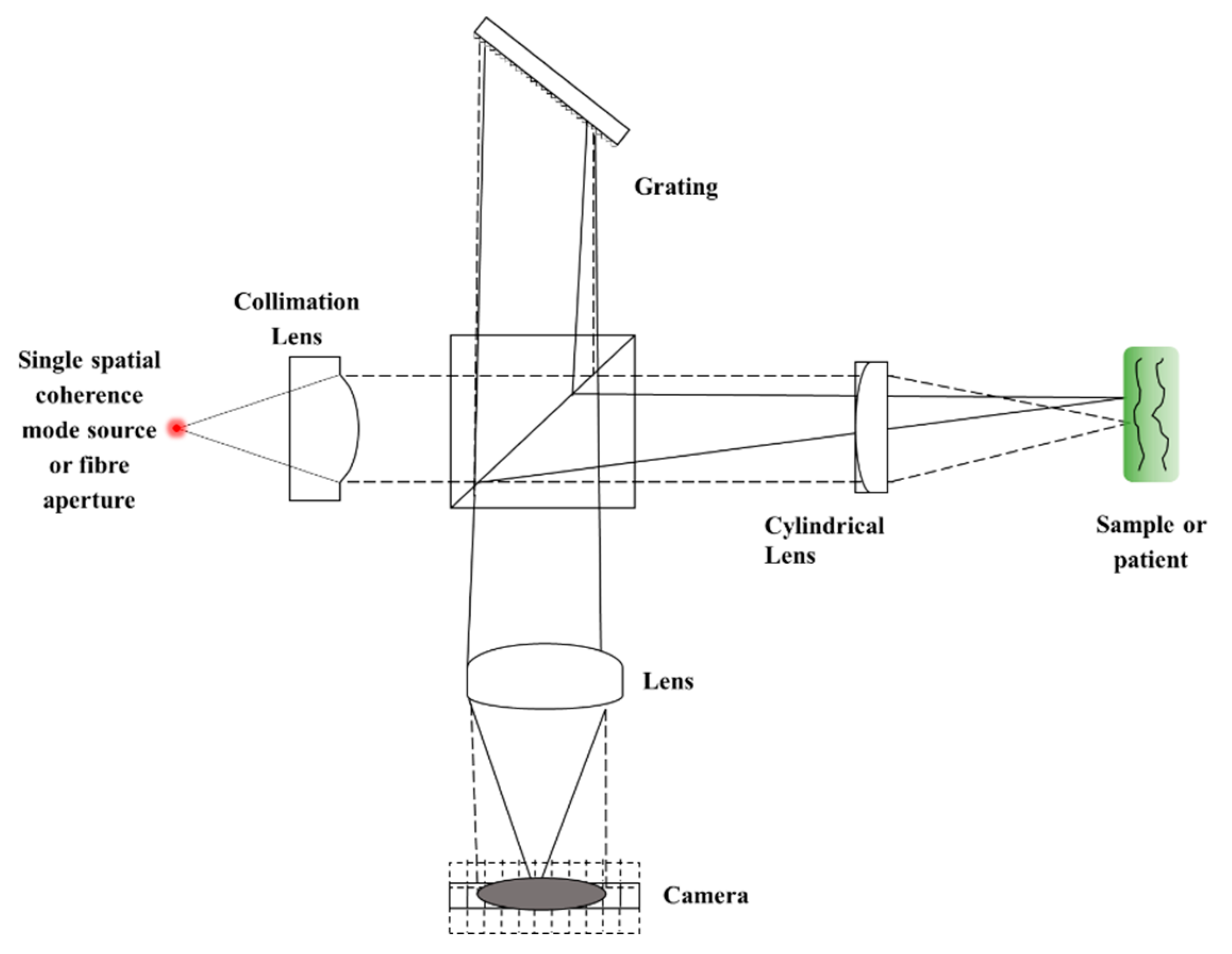
4.1. Axial–Lateral (AL) (Also Known as Grating Generated)
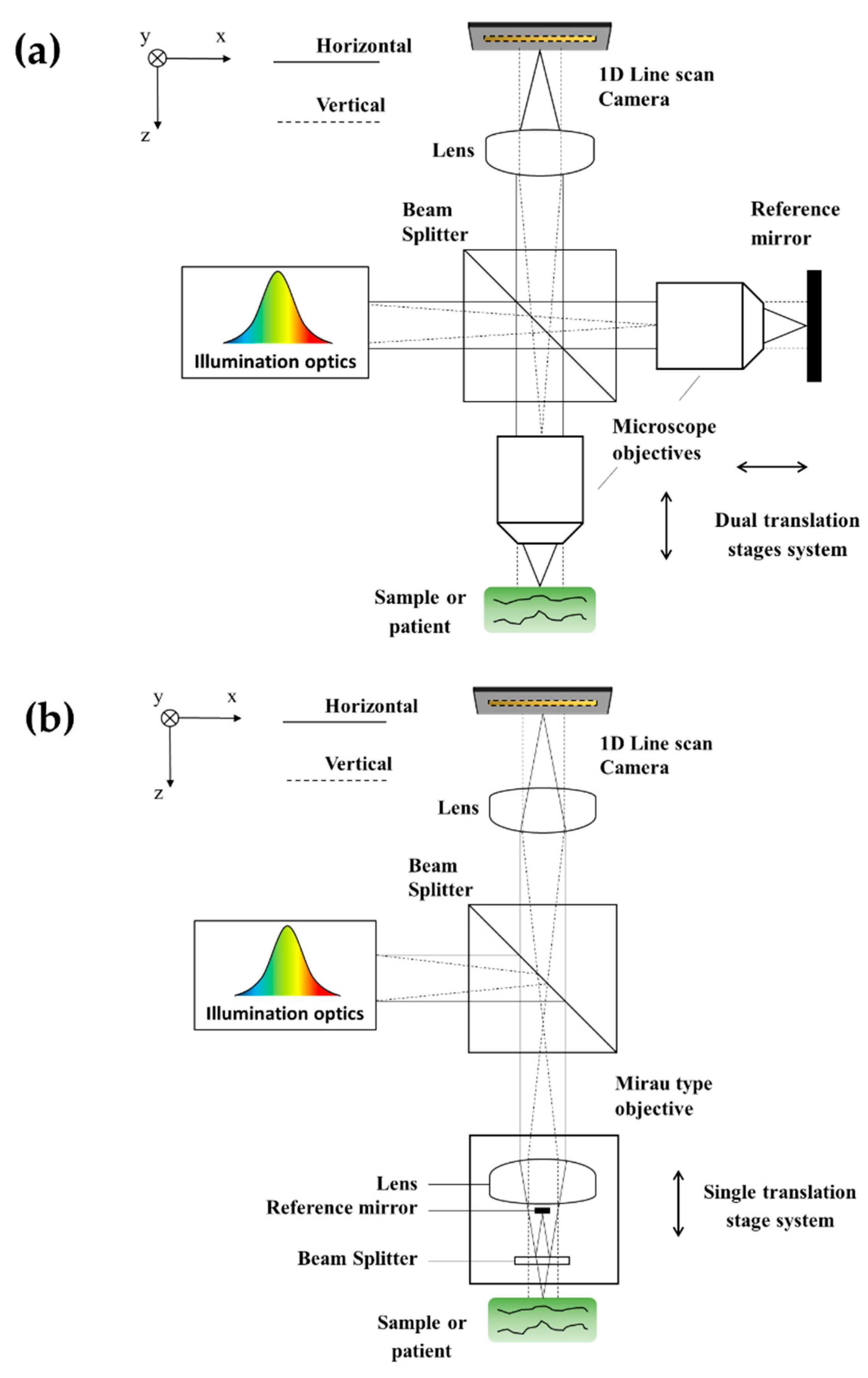
4.2. Sequential TD
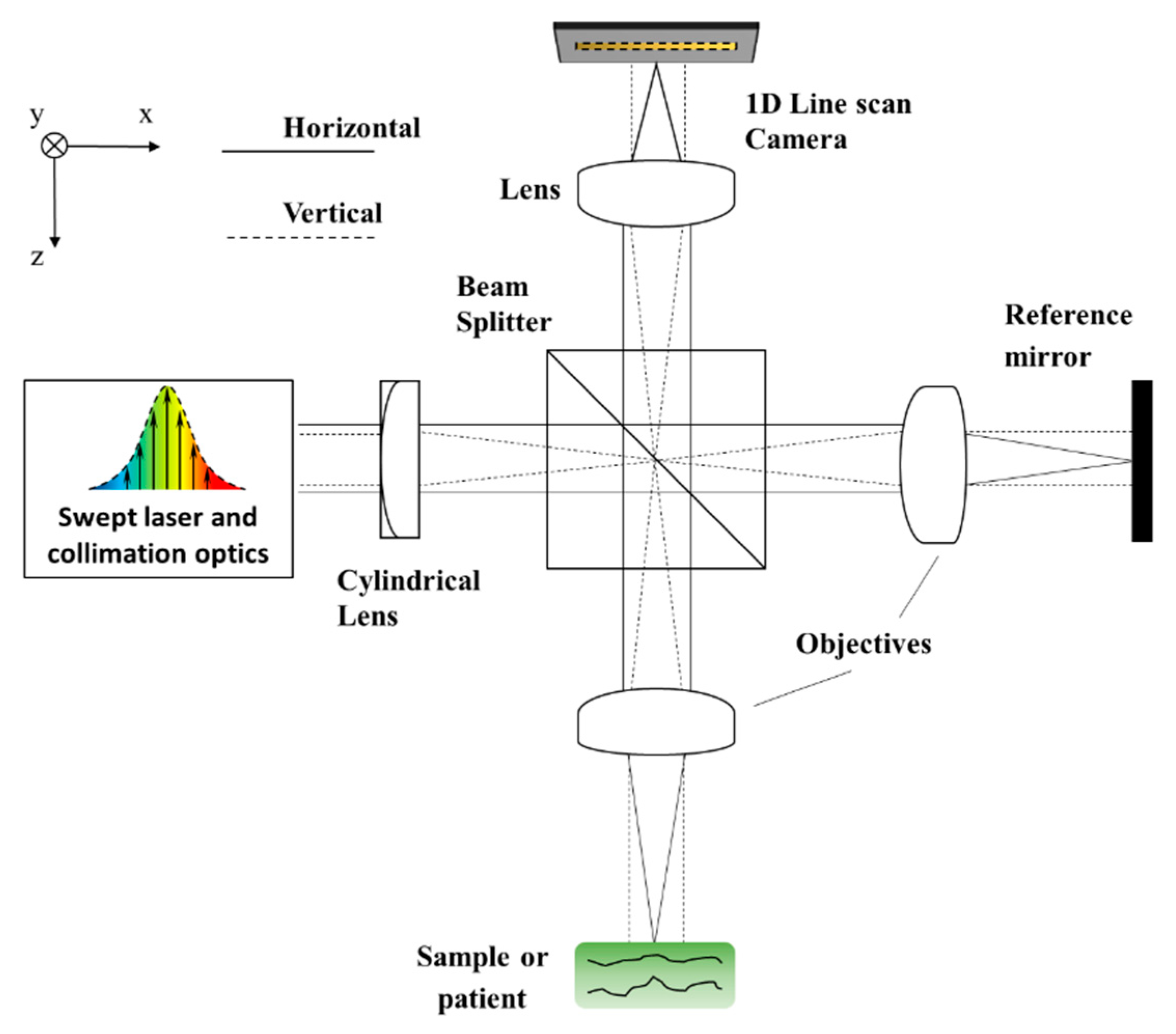
5. Swept Source (SS)
6. Discussion
6.1. Potential Benefits
6.1.1. Overcoming Hardware and Safety Limitations for Higher Speeds
6.1.2. Low-Cost and Industrial Setups
6.1.3. Benefits vs. FF
6.2. Potential Limitations vs. SP
6.2.1. Cross-Talk
6.2.2. Non-Fibre Optic
6.2.3. Washout (SD, AL, Linear and off-Axis TD) or A-Scan Motion Artefacts (SS, Sequential TD)
6.3. Likely Trends in Applications
6.4. Summary
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical Coherence Tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef]
- Clarivate. Web of Science. 2022. Available online: https://clarivate.com/webofsciencegroup/solutions/web-of-science/ (accessed on 15 September 2022).
- Future_Market_Insights_Inc. Optical Coherence Tomography Market. Available online: https://www.futuremarketinsights.com/reports/optical-coherence-tomography-equipment-market (accessed on 15 September 2022).
- Grand_View_Research_Inc. Optical Coherence Tomography Market Size, Share & Trends Analysis Report by Type (Doppler, Handheld), by Technology (TD-OCT, FD-OCT), by Application (Ophthalmology, Oncology), and Segment Forecasts, 2022–2030. Available online: https://www.grandviewresearch.com/industry-analysis/optical-coherence-tomography-oct-market (accessed on 15 September 2022).
- Youngquist, R.C.; Carr, S.; Davies, D.E. Optical coherence-domain reflectometry: A new optical evaluation technique. Opt. Lett. 1987, 12, 158–160. [Google Scholar] [CrossRef]
- Fercher, A.; Mengedoht, K.; Werner, W. Eye-length measurement by interferometry with partially coherent light. Opt. Lett. 1988, 13, 186–188. [Google Scholar] [CrossRef] [PubMed]
- De Carlo, T.E.; Romano, A.; Waheed, N.K.; Duker, J.S. A review of optical coherence tomography angiography (OCTA). Int. J. Retin. Vitr. 2015, 1, 5. [Google Scholar] [CrossRef] [PubMed]
- Larin, K.V.; Sampson, D.D. Optical coherence elastography—OCT at work in tissue biomechanics [Invited]. Biomed. Opt. Express 2017, 8, 1172–1202. [Google Scholar] [CrossRef] [PubMed]
- Abdulhalim, I. Spatial and temporal coherence effects in interference microscopy and full-field optical coherence tomography. Ann. Der Phys. 2012, 524, 787–804. [Google Scholar] [CrossRef]
- Drexler, W.; Fujimoto, J.G. Optical Coherence Tomography: Technology and Applications; Springer: Berlin/Heidelberg, Germany, 2015; Volume 2. [Google Scholar]
- Sudkamp, H.; Koch, P.; Spahr, H.; Hillmann, D.; Franke, G.; Münst, M.; Reinholz, F.; Birngruber, R.; Hüttmann, G. In-vivo retinal imaging with off-axis full-field time-domain optical coherence tomography. Opt. Lett. 2016, 41, 4987–4990. [Google Scholar] [CrossRef]
- Fercher, A.F.; Hitzenberger, C.K.; Kamp, G.; El-Zaiat, S.Y. Measurement of intraocular distances by backscattering spectral interferometry. Opt. Commun. 1995, 117, 43–48. [Google Scholar] [CrossRef]
- Chinn, S.R.; Swanson, E.A.; Fujimoto, J.G. Optical coherence tomography using a frequency-tunable optical source. Opt. Lett. 1997, 22, 340–342. [Google Scholar] [CrossRef]
- Bille, J.F. High Resolution Imaging in Microscopy and Ophthalmology: New Frontiers in Biomedical Optics; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Izatt, J.A.; Choma, M.A. Theory of Optical Coherence Tomography. In Optical Coherence Tomography, Biological and Medical Physics; Springer: Berlin, Germany, 2008; pp. 47–72. [Google Scholar]
- Schmitt, J.M. Optical coherence tomography (OCT): A review. IEEE J. Sel. Top. Quantum Electron. 1999, 5, 1205–1215. [Google Scholar] [CrossRef]
- Fercher, A.F.; Drexler, W.; Hitzenberger, C.K.; Lasser, T. Optical coherence tomography—principles and applications. Rep. Prog. Phys. 2003, 66, 239–303. [Google Scholar] [CrossRef]
- Tomlins, P.H.; Wang, R.K. Theory, developments and applications of optical coherence tomography. J. Phys. D Appl. Phys. 2005, 38, 2519. [Google Scholar] [CrossRef]
- Zysk, A.M.; Nguyen, F.T.; Oldenburg, A.L.; Marks, D.L.; Boppart, S.A. Optical coherence tomography: A review of clinical development from bench to bedside. J. Biomed. Opt. 2007, 12, 051403. [Google Scholar] [CrossRef]
- Marschall, S.; Sander, B.; Mogensen, M.; Jørgensen, T.M.; Andersen, P.E. Optical coherence tomography—Current technology and applications in clinical and biomedical research. Anal. Bioanal. Chem. 2011, 400, 2699–2720. [Google Scholar] [CrossRef]
- Drexler, W.; Liu, M.; Kumar, A.; Kamali, T.; Unterhuber, A.; Leitgeb, R.A. Optical coherence tomography today: Speed, contrast, and multimodality. J. Biomed. Opt. 2014, 19, 071412. [Google Scholar] [CrossRef]
- Fujimoto, J.; Swanson, E. The Development, Commercialization, and Impact of Optical Coherence Tomography. Investig. Ophthalmol. Vis. Sci. 2016, 57, OCT1–OCT13. [Google Scholar] [CrossRef]
- Dubois, A.; Boccara, C. L’OCT plein champ. M/S Méd. Sci. 2006, 22, 859–864. [Google Scholar] [CrossRef]
- Tang, D.; Henning, A.; Gao, F.; Gribble, A.; Jiang, X. Improved description of the signal formation in grating generated-optical coherence tomography. Opt. Express 2019, 27, 33999–34010. [Google Scholar] [CrossRef]
- Karamata, B.; Lambelet, P.; Laubscher, M.; Salathe, R.P.; Lasser, T. Spatially incoherent illumination as a mechanism for cross-talk suppression in wide-field optical coherence tomography. Opt. Lett. 2004, 29, 736–738. [Google Scholar] [CrossRef]
- Thouvenin, O.; Apelian, C.; Nahas, A.; Fink, M.; Boccara, C. Full-field optical coherence tomography as a diagnosis tool: Recent progress with multimodal imaging. Appl. Sci. 2017, 7, 236. [Google Scholar] [CrossRef]
- Wang, L.; Fu, R.; Xu, C.; Xu, M. Methods and applications of full-field optical coherence tomography: A review. J. Biomed. Opt. 2022, 27, 050901. [Google Scholar] [CrossRef] [PubMed]
- Regar, E.; van Leeuwen, A.; Serruys, P.W. New parallel frequency domain techniques for volumetric OCT Boris Považay, Wolfgang Drexler, Rainer A Leitgeb. In Optical Coherence Tomography in Cardiovascular Research; CRC Press: Boca Raton, FL, USA, 2007; pp. 237–246. [Google Scholar]
- Zeylikovich, I.; Alfano, R. Ultrafast dark-field interferometric microscopic reflectometry. Opt. Lett. 1996, 21, 1682–1684. [Google Scholar] [CrossRef] [PubMed]
- Beaurepaire, E.; Boccara, A.C.; Lebec, M.; Blanchot, L.; Saint-Jalmes, H. Full-field optical coherence microscopy. Opt. Lett. 1998, 23, 244–246. [Google Scholar] [CrossRef] [PubMed]
- von der Burchard, C.; Moltmann, M.; Tode, J.; Ehlken, C.; Sudkamp, H.; Theisen-Kunde, D.; König, I.; Hüttmann, G.; Roider, J. Self-examination low-cost full-field OCT (SELFF-OCT) for patients with various macular diseases. Graefe’s Arch. Clin. Exp. Ophthalmol. 2021, 259, 1503–1511. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.-U.; Pierce, M.C.; Higgins, L.; Tkaczyk, T.S. Snapshot 3D optical coherence tomography system using image mapping spectrometry. Opt. Express 2013, 21, 13758–13772. [Google Scholar] [CrossRef]
- Bonin, T.; Franke, G.; Hagen-Eggert, M.; Koch, P.; Hüttmann, G. In vivo Fourier-domain full-field OCT of the human retina with 1.5 million A-lines/s. Opt. Lett. 2010, 35, 3432–3434. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, S.-W.; Aguirre, A.D.; Fujimoto, J.G. High-resolution line-scanning optical coherence microscopy. Opt. Lett. 2007, 32, 1971–1973. [Google Scholar] [CrossRef]
- Zuluaga, A.F.; Richards-Kortum, R. Spatially resolved spectral interferometry for determination of subsurface structure. Opt. Lett. 1999, 24, 519–521. [Google Scholar] [CrossRef]
- Lee, S.-W.; Kim, B.-M. Line-field optical coherence tomography using frequency-sweeping source. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 50–55. [Google Scholar] [CrossRef]
- Zeylikovich, I.; Gilerson, A.; Alfano, R. Nonmechanical grating-generated scanning coherence microscopy. Opt. Lett. 1998, 23, 1797–1799. [Google Scholar] [CrossRef]
- Encyclopædia Britannica, Inc. Holography. In Encyclopedia Britannica; Encyclopædia Britannica, Inc.: Chicago, IL, USA, 2022. [Google Scholar]
- Schnars, U.; Jüptner, W.P. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol. 2002, 13, R85. [Google Scholar] [CrossRef]
- Hillmann, D.; Lührs, C.; Bonin, T.; Koch, P.; Hüttmann, G. Holoscopy—Holographic optical coherence tomography. Opt. Lett. 2011, 36, 2390–2392. [Google Scholar] [CrossRef]
- Liu, X.; Yu, X.; Tang, H.; Cui, D.; Beotra, M.R.; Girard, M.J.; Sun, D.; Gu, J.; Liu, L. Spectrally encoded extended source optical coherence tomography. Opt. Lett. 2014, 39, 6803–6806. [Google Scholar] [CrossRef]
- Yu, X.; Liu, X.; Chen, S.; Luo, Y.; Wang, X.; Liu, L. High-resolution extended source optical coherence tomography. Opt. Express 2015, 23, 26399–26413. [Google Scholar] [CrossRef]
- Chen, S.; Lin, K.; Liu, L. High dynamic range blood flow imaging with spectrally extended line field OCTA. In Proceedings of the Optical Coherence Tomography 2022, Fort Lauderdale, FL, USA, 24–27 April 2022; p. CM4E. 2. [Google Scholar]
- Graf, R.; Brown, W.; Wax, A. Parallel frequency-domain optical coherence tomography scatter-mode imaging of the hamster cheek pouch using a thermal light source. Opt. Lett. 2008, 33, 1285–1287. [Google Scholar] [CrossRef]
- Yurdakul, C.; Millar, D.S.; Mansour, H.; Wang, P.; Kojima, K.; Koike-Akino, T.; Parsons, K.; Orlik, P.V. Line-field Coherent Sensing with LED Illumination. arXiv 2022, arXiv:2202.12161. [Google Scholar]
- Nandakumar, H.; Srivastava, S. Low cost open-source OCT using undergraduate lab components. In Optical Coherence Tomography and Its Non-Medical Applications; IntechOpen: Rijeka, Croatia, 2020; p. 75. [Google Scholar]
- Zhang, Y.; Dong, B.; Bai, Y.; Ye, S.; Lei, Z.; Zhou, Y. Measurement of depth-resolved thermal deformation distribution using phase-contrast spectral optical coherence tomography. Opt. Express 2015, 23, 28067–28075. [Google Scholar] [CrossRef]
- Nakamura, Y.; Makita, S.; Yamanari, M.; Itoh, M.; Yatagai, T.; Yasuno, Y. High-speed three-dimensional human retinal imaging by line-field spectral domain optical coherence tomography. Opt. Express 2007, 15, 7103–7116. [Google Scholar] [CrossRef]
- Grajciar, B.; Lehareinger, Y.; Fercher, A.F.; Leitgeb, R.A. High sensitivity phase mapping with parallel Fourier domain optical coherence tomography at 512,000 A-scan/s. Opt. Express 2010, 18, 21841–21850. [Google Scholar] [CrossRef]
- Fechtig, D.J.; Schmoll, T.; Grajciar, B.; Drexler, W.; Leitgeb, R.A. Line-field parallel swept source interferometric imaging at up to 1 MHz. Opt. Lett. 2014, 39, 5333–5336. [Google Scholar] [CrossRef]
- Endo, T.; Yasuno, Y.; Makita, S.; Itoh, M.; Yatagai, T. Profilometry with line-field Fourier-domain interferometry. Opt. Express 2005, 13, 695–701. [Google Scholar] [CrossRef] [PubMed]
- Lawman, S.; Dong, Y.; Williams, B.M.; Romano, V.; Kaye, S.; Harding, S.P.; Willoughby, C.; Shen, Y.-C.; Zheng, Y. High resolution corneal and single pulse imaging with line field spectral domain optical coherence tomography. Opt. Express 2016, 24, 12395–12405. [Google Scholar] [CrossRef] [PubMed]
- Barrick, J.; Doblas, A.; Gardner, M.R.; Sears, P.R.; Ostrowski, L.E.; Oldenburg, A.L. High-speed and high-sensitivity parallel spectral-domain optical coherence tomography using a supercontinuum light source. Opt. Lett. 2016, 41, 5620–5623. [Google Scholar] [CrossRef]
- Ginner, L.; Schmoll, T.; Kumar, A.; Salas, M.; Pricoupenko, N.; Wurster, L.M.; Leitgeb, R.A. Holographic line field en-face OCT with digital adaptive optics in the retina in vivo. Biomed. Opt. Express 2018, 9, 472–485. [Google Scholar] [CrossRef] [PubMed]
- Dubois, A.; Xue, W.; Levecq, O.; Bulkin, P.; Coutrot, A.-L.; Ogien, J. Mirau-based line-field confocal optical coherence tomography. Opt. Express 2020, 28, 7918–7927. [Google Scholar] [CrossRef]
- Lawman, S.; Mason, S.; Kaye, S.B.; Shen, Y.-C.; Zheng, Y. Accurate In Vivo Bowman’s Thickness Measurement Using Mirau Ultrahigh Axial Resolution Line Field Optical Coherence Tomography. Transl. Vis. Sci. Technol. 2022, 11, 6. [Google Scholar] [CrossRef]
- Vakhtin, A.B.; Kane, D.J.; Wood, W.R.; Peterson, K.A. Common-path interferometer for frequency-domain optical coherence tomography. Appl. Opt. 2003, 42, 6953–6958. [Google Scholar] [CrossRef]
- Lawman, S.; Williams, B.M.; Zheng, Y.; Shen, Y.-C. Quasi-tomography by free space line field spectral domain optical coherence reflectometry. Meas. Sci. Technol. 2020, 31, 065203. [Google Scholar] [CrossRef]
- Robles, F.E.; Wilson, C.; Grant, G.; Wax, A. Molecular imaging true-colour spectroscopic optical coherence tomography. Nat. Photonics 2011, 5, 744–747. [Google Scholar] [CrossRef]
- Reolon, D.; Jacquot, M.; Verrier, I.; Brun, G.; Veillas, C. Broadband supercontinuum interferometer for high-resolution profilometry. Opt. Express 2006, 14, 128–137. [Google Scholar] [CrossRef]
- Grajciar, B.; Pircher, M.; Fercher, A.F.; Leitgeb, R.A. Parallel Fourier domain optical coherence tomography for in vivo measurement of the human eye. Opt. Express 2005, 13, 1131–1137. [Google Scholar] [CrossRef]
- Zhang, Y.; Rha, J.T.; Jonnal, R.S.; Miller, D.T. Adaptive optics parallel spectral domain optical coherence tomography for imaging the living retina. Opt. Express 2005, 13, 4792–4811. [Google Scholar] [CrossRef]
- Yasuno, Y.; Endo, T.; Makita, S.; Aoki, G.; Itoh, M.; Yatagai, T. Three-dimensional line-field Fourier domain optical coherence tomography for in vivo dermatological investigation. J. Biomed. Opt. 2006, 11, 014014. [Google Scholar] [CrossRef]
- Manuel, H. 3D Digital Holographic Interferometry and Spectral Optical Coherence Tomography for the Measurement of Strain in Metallic Objects and Phase in Biological Tissues. Ph.D. Thesis, M.C. Manuel Humberto De la Torre Ibarra, Centro de Investigaciones en Óptica, León, Mexico, 2006. [Google Scholar]
- Manuel, H.; Ruiz, P.D.; Huntley, J.M. Double-shot depth-resolved displacement field measurement using phase-contrast spectral optical coherence tomography. Opt. Express 2006, 14, 9643–9656. [Google Scholar]
- Yaqoob, Z.; Choi, W.; Oh, S.; Lue, N.; Park, Y.; Fang-Yen, C.; Dasari, R.R.; Badizadegan, K.; Feld, M.S. Improved phase sensitivity in spectral domain phase microscopy using line-field illumination and self phase-referencing. Opt. Express 2009, 17, 10681–10687. [Google Scholar] [CrossRef]
- Zhong, J.; Zhong, S.; Zhang, Q.; Yao, L. Two-dimensional optical coherence tomography for real-time structural dynamical characterization. Opt. Lasers. Eng. 2015, 66, 74–79. [Google Scholar] [CrossRef][Green Version]
- Nakamura, Y.; Sugisaka, J.-I.; Sando, Y.; Endo, T.; Itoh, M.; Yatagai, T.; Yasuno, Y. Complex numerical processing for in-focus line-field spectral-domain optical coherence tomography. Jpn. J. Appl. Phys. 2007, 46, 1774. [Google Scholar] [CrossRef]
- Bu, P.; Wang, X.; Sasaki, O. Full-range parallel Fourier-domain optical coherence tomography using sinusoidal phase-modulating interferometry. J. Opt. A Pure Appl. Opt. 2007, 9, 422. [Google Scholar] [CrossRef]
- Bu, P.; Wang, X.; Sasaki, O. One-shot parallel complex Fourier-domain optical coherence tomography using a spatial carrier frequency. Opt. Eng. 2008, 47, 050502. [Google Scholar] [CrossRef][Green Version]
- Witte, S.; Baclayon, M.; Peterman, E.; Toonen, R.; Mansvelder, H.; Groot, M.L. Single-shot two-dimensional full-range optical coherence tomography achieved by dispersion control. Opt. Express 2009, 17, 11335–11349. [Google Scholar] [CrossRef][Green Version]
- Kamal, M.; Narayanswamy, S.; Packirisamy, M. Optical design of a line-focused forward-viewing scanner for optical coherence tomography. Appl. Opt. 2010, 49, 6170–6178. [Google Scholar] [CrossRef]
- Kamal, M.; Sivakumar, N.R.; Packirisamy, M. Optimized off-axis cylindrical mirror-focused line-scanning system for optical coherence tomography imaging applications. J. Biomed. Opt. 2012, 17, 056006. [Google Scholar] [CrossRef] [PubMed]
- Kamal, M. Reflective Optics-Based Line-Scanning Spectral Domain Optical Coherence Tomography System. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2011. [Google Scholar]
- Robles, F.E.; Satterwhite, L.L.; Wax, A. Nonlinear phase dispersion spectroscopy. Opt. Lett. 2011, 36, 4665–4667. [Google Scholar] [CrossRef] [PubMed]
- Widjanarko, T. Hyperspectral Interferometry for Single-Shot Profilometry and Depth-Resolved Displacement Field Measurement. Ph.D. Thesis, Taufiq Widjanarko, Loughborough University, Loughborough, UK, 2011. [Google Scholar]
- Xiao, Q.; Fu, L. High resolution, real-time line-field fourier-domain interferometry. J. Innov. Opt. Health Sci. 2012, 5, 1250009. [Google Scholar] [CrossRef]
- Huang, B.J.; Bu, P.; Wang, X.Z.; Nan, N.; Guo, X. Speckle reduction in parallel optical coherence tomography by spatial compounding. Opt. Laser Technol. 2013, 45, 69–73. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, Z.-Y.; Ding, Z.-H.; Li, P.; Shen, Y.; Ni, Y. Line-field parallel spectral domain optical coherence tomography and its application in defect inspection. Acta Phys. Sin. 2014, 63, 194201. [Google Scholar] [CrossRef]
- Chen, Z.; Shen, Y.; Bao, W.; Li, P.; Wang, X.; Ding, Z. Identification of surface defects on glass by parallel spectral domain optical coherence tomography. Opt. Express 2015, 23, 23634–23646. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhao, C.; Shen, Y.; Li, P.; Wang, X.P.; Ding, Z.H. Ultrawide-field parallel spectral domain optical coherence tomography for nondestructive inspection of glass. Opt. Commun. 2015, 341, 122–130. [Google Scholar] [CrossRef]
- Briones-R, M.d.J.; De La Torre-Ibarra, M.H.; Mendoza-Santoyo, F.; Pedroza-G, J. Simultaneous birefringence imaging and depth phase resolved measurement using a Fourier domain OCT system. Opt. Lasers. Eng. 2015, 68, 104–110. [Google Scholar] [CrossRef]
- Schmidt, I. Thermal Light Tear Film Imaging with Spectral Domain Optical Coherence Tomography (SD-OCT). Diploma Thesis, Technische Universität Wien, Wien, Austria, 2016. [Google Scholar]
- Tang, D. Investigation of Line-Scan Dispersive Interferometry for In-Line Surface Metrology. Ph.D. Thesis, University of Huddersfield, Huddersfield, UK, 2016. [Google Scholar]
- Lawman, S.; Madden, P.W.; Romano, V.; Dong, Y.; Mason, S.; Williams, B.M.; Kaye, S.B.; Willoughby, C.E.; Harding, S.P.; Shen, Y.-C.; et al. Deformation velocity imaging using optical coherence tomography and its applications to the cornea. Biomed. Opt. Express 2017, 8, 5579–5593. [Google Scholar] [CrossRef]
- Lawman, S.; Williams, B.M.; Zhang, J.; Shen, Y.-C.; Zheng, Y. Scan-Less Line Field Optical Coherence Tomography, with Automatic Image Segmentation, as a Measurement Tool for Automotive Coatings. Appl. Sci. 2017, 7, 351. [Google Scholar] [CrossRef]
- Lawman, S.; Zhang, J.; Williams, B.M.; Zheng, Y.; Shen, Y. Applications of optical coherence tomography in the non-contact assessment of automotive paints. In SPIE Optical Metrology, Proceedings of the Optical Measurement Systems for Industrial Inspection X, Munich, Germany, 25–29 June 2017; SPIE: Bellingham, WA, USA, 2017. [Google Scholar]
- Al-Qazwini, Z.; Ko, Z.Y.G.; Mehta, K.; Chen, N. Ultrahigh-speed line-scan SD-OCT for four-dimensional in vivo imaging of small animal models. Biomed. Opt. Express 2018, 9, 1216–1228. [Google Scholar] [CrossRef]
- Dong, B.; Zhang, Y.; Pan, B. Enhancing the dynamic range of phase-sensitive optical coherence elastography by overcoming speckle decorrelation. Opt. Lett. 2018, 43, 5805–5808. [Google Scholar] [CrossRef]
- Lin, J.; Zhong, S.; You, T.; Zhang, Q.; Tong, J. Curvature Radius Measurement of Lens by Using Line Field Spectral Domain Optical Coherence Tomography. In FZU-OPU-NTOU Joint Symposium on Advanced Mechanical Science & Technology for Industrial Revolution 4.0; Springer: Singapore, 2016; pp. 113–119. [Google Scholar]
- Han, L.; Hosseiaee, Z.; Tan, B.; Bizheva, K. High resolution line-field SD-OCT with 2.5 kHz frame rate for cellular resolution imaging of biological tissue. In SPIE BIOS, Proceedings of Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XXIII, San Francisco, CA, USA, 2–7 February 2019; SPIE: Bellingham, WA, USA, 2019; pp. 123–128. [Google Scholar]
- Han, L.; Tan, B.; Hosseinaee, Z.; Chen, L.K.; Hileeto, D.; Bizheva, K. Line-scanning SD-OCT for in-vivo, non-contact, volumetric, cellular resolution imaging of the human cornea and limbus. Biomed. Opt. Express 2022, 13, 4007–4020. [Google Scholar] [CrossRef]
- Barrick, J. Development of a Line-Field Magneto-Motive Optical Coherence Tomography System. Ph.D. Thesis, The University of North Carolina at Chapel Hill, Ann Arbor, MI, USA, 2020. [Google Scholar]
- Xing, F.; Lee, J.-H.; Polucha, C.; Lee, J. Design and optimization of line-field optical coherence tomography at visible wavebands. Biomed. Opt. Express 2021, 12, 1351–1365. [Google Scholar] [CrossRef]
- Singh, M.; Schill, A.W.; Nair, A.; Aglyamov, S.R.; Larina, I.V.; Larin, K.V. Ultra-Fast Line-Field Optical Coherence Elastography at 11.5 MHz. In Proceedings of the Optical Coherence Tomography 2022, Fort Lauderdale, FL, USA, 24–27 April 2022; p. CTu4E. 2. [Google Scholar]
- Lawman, S.; Romano, V.; Madden, P.; Mason, S.; Williams, B.; Zheng, Y.; Shen, Y.-C. Supercontinuum Ultra-High Resolution Line-Field OCT; Experimental Spectrograph Comparison and Comparison with Current Clinical OCT Systems by the Imaging of a Human Cornea; SPIE: Bellingham, WA, USA, 2018; Volume 10591. [Google Scholar]
- Alfano, R.; Shapiro, S. Emission in the region 4000 to 7000 Å via four-photon coupling in glass. Phys. Rev. Lett. 1970, 24, 584. [Google Scholar] [CrossRef]
- Zeylikovich, I.; Alfano, R. Coherence properties of the supercontinuum source. Appl. Phys. B 2003, 77, 265–268. [Google Scholar] [CrossRef]
- Watanabe, Y.; Yamada, K.; Sato, M. Three-dimensional imaging by ultrahigh-speed axial-lateral parallel time domain optical coherence tomography. Opt. Express 2006, 14, 5201–5209. [Google Scholar] [CrossRef]
- Watanabe, Y.; Yamada, K.; Sato, M. In vivo non-mechanical scanning grating-generated optical coherence tomography using an InGaAs digital camera. Opt. Commun. 2006, 261, 376–380. [Google Scholar] [CrossRef]
- Watanabe, Y.; Takasugi, Y.; Yamada, K.; Sato, M. Axial-lateral parallel time domain OCT with an optical zoom lens and high order diffracted lights for variable imaging range. Opt. Express 2007, 15, 5208–5217. [Google Scholar] [CrossRef]
- Watanabe, Y.; Sato, M. Quasi-single shot axial-lateral parallel time domain optical coherence tomography with Hilbert transformation. Opt. Express 2008, 16, 524–534. [Google Scholar] [CrossRef] [PubMed]
- Leitgeb, R.; Hitzenberger, C.K.; Fercher, A.F. Performance of fourier domain vs. time domain optical coherence tomography. Opt. Express 2003, 11, 889–894. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Huang, S.-W.; Zhou, C.; Potsaid, B.; Fujimoto, J.G. Improved detection sensitivity of line-scanning optical coherence microscopy. IEEE J. Sel. Top. Quantum Electron. 2011, 18, 1094–1099. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, C.-H.; Schill, A.; Wu, C.; Singh, M.; Larin, K.V. Non-contact single shot elastography using line field low coherence holography. Biomed. Opt. Express 2016, 7, 3021–3031. [Google Scholar] [CrossRef] [PubMed]
- Leitgeb, R. En face optical coherence tomography: A technology review. Biomed. Opt. Express 2019, 10, 2177–2201. [Google Scholar] [CrossRef]
- Liu, C.-H.; Schill, A.; Raghunathan, R.; Wu, C.; Singh, M.; Han, Z.; Nair, A.; Larin, K.V. Ultra-fast line-field low coherence holographic elastography using spatial phase shifting. Biomed. Opt. Express 2017, 8, 993–1004. [Google Scholar] [CrossRef]
- Dubois, A.; Levecq, O.; Azimani, H.; Davis, A.; Ogien, J.; Siret, D.; Barut, A. Line-field confocal time-domain optical coherence tomography with dynamic focusing. Opt. Express 2018, 26, 33534–33542. [Google Scholar] [CrossRef]
- Ogien, J.; Levecq, O.; Azimani, H.; Dubois, A. Dual-mode line-field confocal optical coherence tomography for ultrahigh-resolution vertical and horizontal section imaging of human skin in vivo. Biomed. Opt. Express 2020, 11, 1327–1335. [Google Scholar] [CrossRef]
- OCT_News. Damae Medical Raises €5M in Series a Financing to Accelerate the European Deployment of Its Deeplive Platform and Revolutionize Skin Cancer Screening, Diagnosis and Monitoring. Available online: http://www.octnews.org/articles/12119830/damae-medical-raises-eur5m-in-series-a-financing-t/ (accessed on 16 September 2022).
- Mujat, M.; Iftimia, N.V.; Ferguson, R.D.; Hammer, D.X. Swept-source parallel OCT. In SPIE BIOS, Proceedings of the Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XIII, San Jose, CA, USA, 24–29 January 2009; SPIE: Bellingham, WA, USA, 2009; pp. 140–147. [Google Scholar]
- Fechtig, D.J.; Grajciar, B.; Schmoll, T.; Blatter, C.; Werkmeister, R.M.; Drexler, W.; Leitgeb, R.A. Line-field parallel swept source MHz OCT for structural and functional retinal imaging. Biomed. Opt. Express 2015, 6, 716–735. [Google Scholar] [CrossRef]
- Fechtig, D.J.; Kumar, A.; Drexler, W.; Leitgeb, R.A. Full range line-field parallel swept source imaging utilizing digital refocusing. J. Mod. Opt. 2015, 62, 1801–1807. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Z.; Lawman, S.J.; Yin, Z.; Hu, Y.; Xu, J.; Shen, Y. Characterization of Electrical–Thermal–Mechanical Deformation of Bonding Wires Under Silicone Gel Using LF-OCT. IEEE Trans. Power Electron. 2021, 36, 11045–11054. [Google Scholar] [CrossRef]
- Karamata, B. Multiple Scattering in Wide-Field Optical Coherence Tomography; EPFL: Lausanne, Switzerland, 2004. [Google Scholar]
- Karamata, B.; Leutenegger, M.; Laubscher, M.; Bourquin, S.; Lasser, T.; Lambelet, P. Multiple scattering in optical coherence tomography. II. Experimental and theoretical investigation of cross talk in wide-field optical coherence tomography. JOSA A 2005, 22, 1380–1388. [Google Scholar] [CrossRef]
- Karamata, B.; Lambelet, P.; Leutenegger, M.; Laubscher, M.; Bourquin, S.; Lasser, T. A semi-analytical model accounting for multiple scattering in optical coherence tomography. In SPIE BIOS, Proceedings of the Coherence Domain Optical Methods and Optical Coherence Tomography in Biomedicine IX, San Jose, CA, USA, 23–26 January 2005; SPIE: Bellingham, WA, USA, 2005; pp. 386–396. [Google Scholar]
- Hammer, D.X.; Ferguson, R.D.; Ustun, T.E.; Bigelow, C.E.; Iftimia, N.V.; Webb, R.H. Line-scanning laser ophthalmoscope. J. Biomed. Opt. 2006, 11, 041126. [Google Scholar] [CrossRef]
- Yasin Alibhai, A.; Or, C.; Witkin, A.J. Swept source optical coherence tomography: A review. Curr. Ophthalmol. Rep. 2018, 6, 7–16. [Google Scholar] [CrossRef]
- Zuluaga, A.F.; Chang, S.K.; Richards-Kortnm, R. Combined sub-surface imaging and surface spectroscopic imaging in biological samples. In Proceedings of the Biomedical Optical Spectroscopy and Diagnostics 2000, Miami Beach, FL, USA, 2 April 2000; p. SuG3. [Google Scholar]
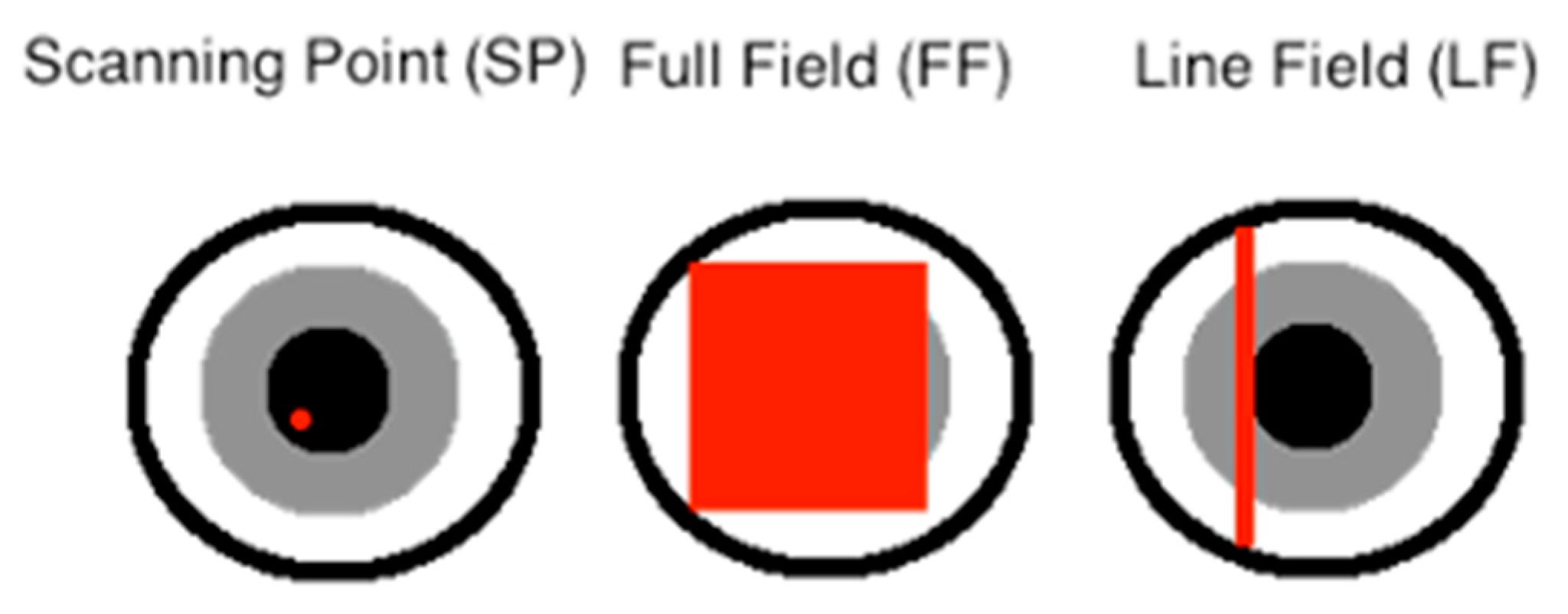




| Axial Resolution Method (Axial Format) | Pseudo-OCT | ||||
|---|---|---|---|---|---|
| Time domain (TD) (includes sequential, linear and off-axis) | Spectral domain (SD) | Swept source (SS) | Axial–lateral (AL) (also known as grating generated) | ||
| Lateral resolution method (lateral format) | Scanning point (SP) | Huang et al., 1991 [1] Early generation devices only, e.g., Zeiss OCT1 | Fercher et al., 1995 [12] Widespread use, e.g., Heidelberg Spectralis | Chin, Swanson and Fujimoto, 1997 [13] Widespread use, e.g., Tomey CASIA2 | SP basis paper [29] for LF-AL was linear TD None |
| Full/wide field (FF) | Beaurepaire et al., 1998 [30] Not widely available, but clinical studies have been carried out [31] | Achievable only via LF to FF mapping [32] None | Bonin et al., 2010 [33] Not yet available, but clinical research ongoing | - | |
| Line field (LF) | Chen et al., 2007 [34] Recent dermatology systems, e.g., DAMAE deepLive | Zuluaga and Richards-Kortum, 1999 [35] Not yet, but under clinical study | Lee and Kim, 2008 [36] None currently | Zeylikovich, Gilerson and Alfano, 1998 [37] None | |
| Full Sequential TD | En-Face Sequential Phase-Modulated and off-Axis TD (also Known as “Holographic” Misnomer) | SD | SS | AL | |
|---|---|---|---|---|---|
| Light sources that were used | Femtosecond laser [34] Supercontinuum [108] | SLD [105] | SLD [35] Thermal [61] Supercontinuum [60] Femtosecond laser [71] LED [45] | Grating cavity [36] AO modulated [50] | Femtosecond laser [37] SLD [99] LED [24] |
| Detectors used | 1D CCD [34] or CMOS [55] camera | 1D CMOS [105] | 2D CMOS or CCD camera | 1D CMOS or CCD camera | 2D CCD or CMOS |
| Scanning required to capture B-Scan | Mechanical scan along z-axis | B-Scan generally not captured | No scan necessary | Electrical scan of the light source wavelength | No scan necessary |
| Relative merits of axial method | Entire volume can be taken at focus (benefits high lateral resolution setups) High axial resolution achievable | Optimum efficiency for en-face image at single depth Ultra-high-speed monitoring of phase displacement information at en-face depth | High axial resolution achievable | High SNR, large imaging depth | None |
| Merits and drawbacks in comparison to SP version | Lower mechanical requirements for high-speed imaging Higher total optical power safety limits in some scenarios Reduced complexity of motion distortion within individual B-Scans Reduced confocal gating Not fibre optic More prone to A-Scan motion artefacts | Lower mechanical requirements for high-speed imaging Higher total optical power safety limits in some scenarios, (with a global shutter camera) no axial motion distortion or phase instability along en-face line Reduced confocal gating Not fibre optic | Lower mechanical requirements for high-speed imaging Higher total optical power safety limits in some scenarios, (with a global shutter camera) no axial motion distortion or phase instability within individual B-Scans Reduced confocal gating Not fibre optic More prone to washout | Lower mechanical requirements for high-speed imaging Higher total optical power safety limits in some scenarios Reduced complexity of phase instability within individual B-Scans Reduced confocal gating Not fibre optic More prone to A-Scan motion artefacts | N/A |
| Merits and drawbacks in comparison to FF version | Some confocal gating Requires one lateral axis scan to capture 3D volume | Some confocal gating Requires one lateral axis scan to capture 2D en-face image | Some confocal gating Requires one lateral axis scan to capture 3D volume | Some confocal gating Requires one lateral axis scan to capture 3D volume | N/A |
| Reported applications | Ex vivo tissue [34] In vivo dermatology [108] | OCE [105] Angiography [54] In vivo retinal en face [54] | Ex vivo [120] In vivo retinal [62] In vivo corneal [61] Profilometry [51] Phase displacements [65] | Retinal [112] | In vivo skin demonstration [99] |
| Challenges and future trends | 2D lock-in detection camera at affordable price Expands back out to fields outside dermatology | Ever faster dynamic measurements | Faster data transfer and higher sensitivity 2D camera In vivo ultra-fast OCM imaging with DAO enhancement | Light sources with larger tuning range at faster speed and more affordable In vivo ultra-fast imaging with DAO enhancement | Field probably dead |
| A-Scan Speed (Volume Imaging) | En-Face Speed | Highest Reflection Sensitivity (dB) | Best Axial Resolution (µm in Air) | Best Lateral Resolution (µm) | |
|---|---|---|---|---|---|
| LF-SD | 2 MHz [92] | - | 92 [92], high power extreme 113 [53] | 2.1 [52] | 2 to 3 [92] |
| LF-TD | 24.6 kHz [55] | 11.5 MHz [95] | 86 [108] | 1.5 [55] | 1.3 [55] |
| LS-SS | 1 MHz [112] | - | 93.5 [112] | 12 [112] | >7 [112] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawman, S.; Zhang, Z.; Shen, Y.-C.; Zheng, Y. Line Field Optical Coherence Tomography. Photonics 2022, 9, 946. https://doi.org/10.3390/photonics9120946
Lawman S, Zhang Z, Shen Y-C, Zheng Y. Line Field Optical Coherence Tomography. Photonics. 2022; 9(12):946. https://doi.org/10.3390/photonics9120946
Chicago/Turabian StyleLawman, Samuel, Zijian Zhang, Yao-Chun Shen, and Yalin Zheng. 2022. "Line Field Optical Coherence Tomography" Photonics 9, no. 12: 946. https://doi.org/10.3390/photonics9120946
APA StyleLawman, S., Zhang, Z., Shen, Y.-C., & Zheng, Y. (2022). Line Field Optical Coherence Tomography. Photonics, 9(12), 946. https://doi.org/10.3390/photonics9120946







