Speckle Noise-Free Interconnective Holographic Projection

Abstract

Generally, speckle noise is regarded as unavoidable in holographic projection, and it results from unexpected high spatial frequency components of diffracted light at the sharp edge of pixel openings in a spatial light modulator. Speckle noise typically reduces image contrast and degrades the image quality of the holographic projection. In this study, we propose a novel holographic optical interconnection method free of speckle noise in holographic projection. This optical interconnection is achieved by using a holographic optical element (HOE). The HOE is designed to reconstruct Gaussian beams with low divergence. These Gaussian beams become points which form target images at desired depths. Since the Gaussian beam from the HOE does not share the same position with other Gaussian beams, there is no interference at the projection image. Therefore, the image is composed of the points from the Gaussian beams and there is no reason for unexpected high spatial frequency noise to appear on the image. In this paper, we fabricate the HOE, produced with our specially manufactured hologram printer, where the directions of two Gaussian beams with low divergence are controlled by goniometers. We experimentally demonstrated a speckle noise-free interconnective holographic projection. Two images are successfully formed at different depths by optically connecting two points in pairs.

1. Introduction

Holographic projection is a method to reconstruct the optical wave that forms target images in three-dimensional (3D) space using a hologram. This holographic projection has received great interest because it has been applied in many fields, such as image formation, optical information transfer, and beam shaping [1,2,3,4]. In holographic projection technology, 3D contents are generally displayed by modulating the phase of the optical wave [5,6,7]. The optical wave propagates to one depth and forms an image expected at the given depth. Then, it propagates to the next depth and forms an image correct to the depth. So, 3D contents are represented as a set of sliced images [8,9,10]. When a sliced image enters the eye of an observer, the observer perceives 3D objects. Depending on the depth at which the observer focuses, the image at one depth looks sharp, while the images at other depths are defocused. The accommodation effect makes the 3D contents natural to the observers.

In holographic projection, the hologram needs to project different images depending on the depth for displaying sliced images as 3D contents. For this purpose, whole optical waves forming these images are multiplexed in the hologram. An image formed at a given depth looks sharp in focus at that depth, but the images formed at other depths fade out. As the observer changes his eye focus, one image in focus gradually fades out, and another image fades in. At this time, the faded-out image does not disappear completely, and it becomes the noise of the faded-in image at different depths. So, the contrast of the image is reduced. 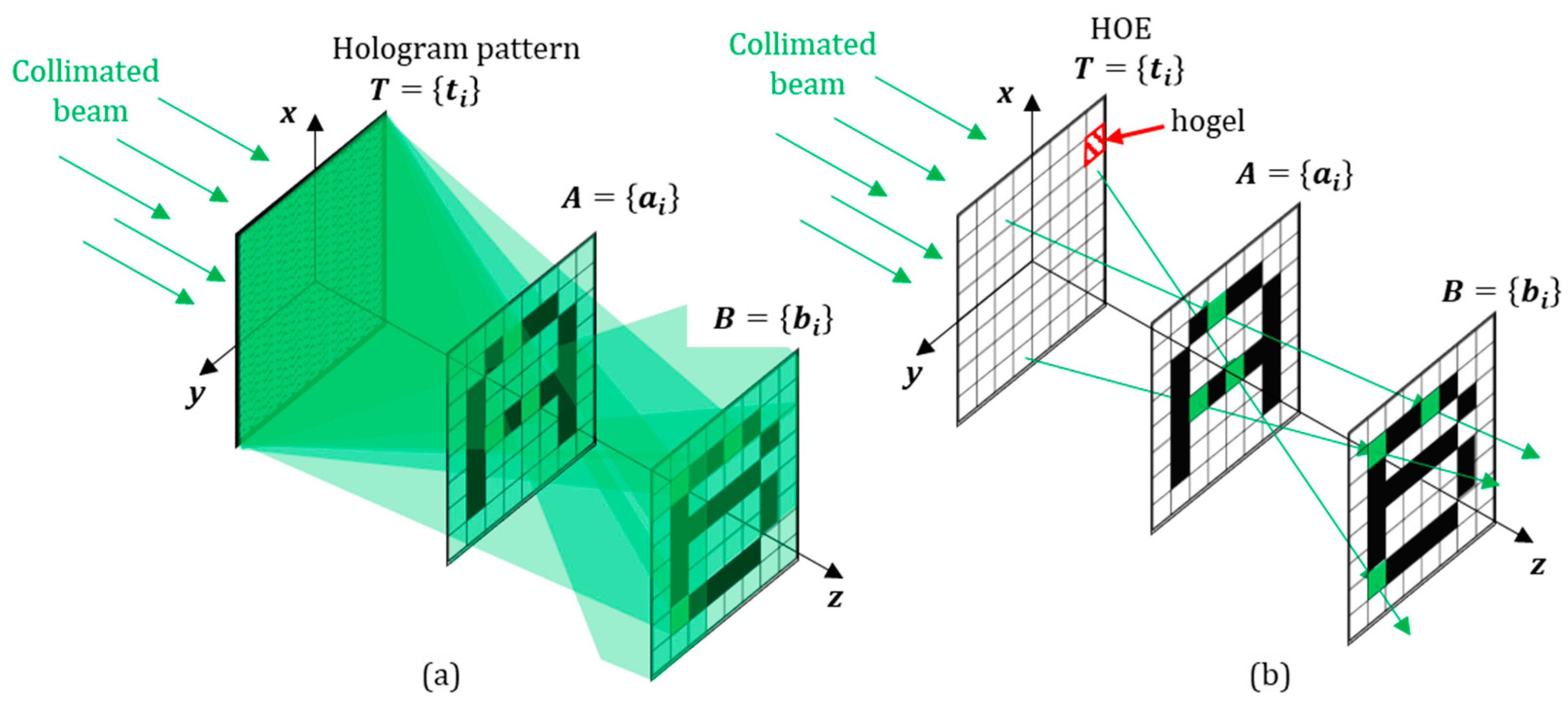Figure 1a shows that the optical wave passing through the hologram T, converges at a point on plane A, but diverges after passing through plane A. In other words, the optical wave converging at one point on plane A, diverges over a wide area on plane B, and this profile of diverging wave becomes noise. In plane B, each noise profile has a smooth distribution, but due to the coherence of the light source, one diverging wave interferes with the others. It results in spackle noise with high spatial frequencies. Recently, for the reduction of such speckle noise, techniques for optimizing the holographic pattern with a camera, by capturing the image of each layer and comparing the target image with the captured image, are proposed [11]. However, while these methods reduce speckle noise and increase the contrast of holographic projection images, the speckle noise is fundamentally unavoidable because of the speckle noise from the coherence of the light source. The light is dominantly diffracted at the sharp edges of the pixel apertures, and there is no way to eliminate noise by using conventional methods [12].

Holographic optical interconnection is a technology that transmits optical power from one point on a plane to a specific point on another plane, by diffracting the waves on fringe patterns [13,14,15]. Here, the design of the fringe pattern determines the propagation direction of the diffracted wave. Techniques for generating fringe patterns using spatial light modulators (SLMs) actively change the directions of diffracted beams [16,17,18]. Dynamic optical interconnection is implemented using the SLM, which is used as a many-to-many switching technology in optical communication. Here, the waves are transmitted through optical fibers to increase the signal-to-noise ratio. A grin lens attached to the front of the optical fiber forms a Gaussian beam with low divergence.

In this paper, we propose a speckle noise-free interconnective holographic projection (IHP) based on holographic optical interconnection. The diffraction of the incident beam to the desired direction needs a short grating period. Usually, the SLM has a relatively large interval among pixels to achieve a high diffraction angle. So, we used a holographic optical element instead of the SLM to overcome the limitations of the diffraction angle. It is noted that the HOE contains the grating patterns on each hogel, which is recorded by interference between the reference beam and the signal beam. As shown in Figure 1b, a set of T hogels is recorded on the HOE for the IHP. The HOE grating determines the direction of rays, which present dots as images at each depth. This method has an advantage in signal contrast. The beam diameter of the ray changes slightly, since the beam from the single-mode fiber has a Gaussian profile. In addition, the collimated rays propagate in free space so that the speckle noise is not generated, and a high signal-to-noise ratio is achieved.

2. Fabrication of Holographic Optical Elements for Interconnective Holographic Projection

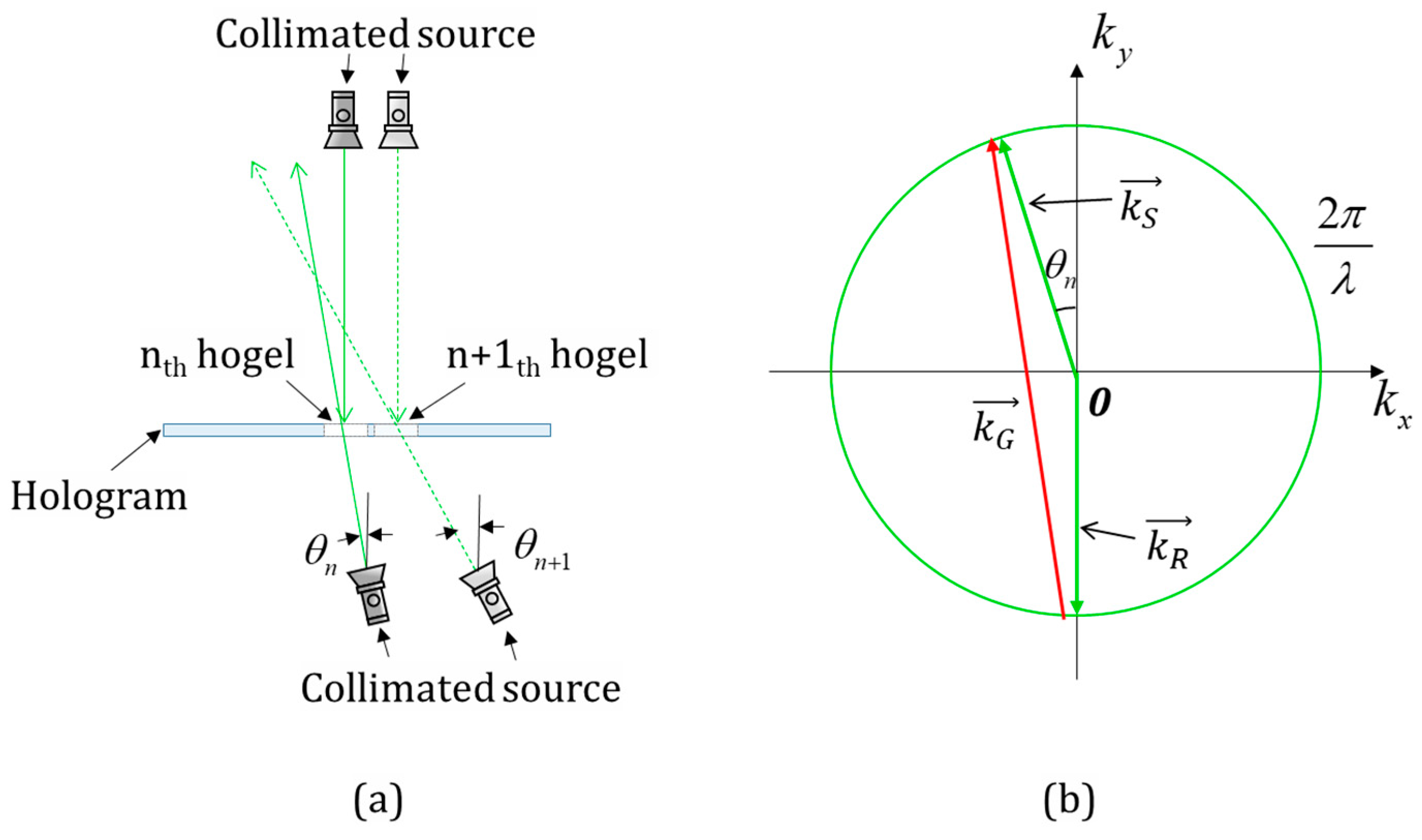
The HOE for interconnective holographic projection needs to have different gratings for individual hogels. We made a special hologram printer for recording the HOE and the concept of the printer is shown in Figure 2a. This hologram printer records the HOE at the interference between two collimated beams in a hogel. In the hologram printer, two collimators are placed on both sides of the HOE, where the upper collimator is for the reference beam and the lower collimator is for the signal beam. The reference beam is fixed so that it always illuminates every hogel on the HOE in the same direction, as one collimated beam is used as a light source for the IHP. The reference beam is depicted as an arrow in $-k_y$, as shown in Figure 2b. On the other hand, the direction of the signal beam is changeable by a mechanical tilting stage, and the direction is depicted as vector $\overrightarrow{a_i{b}_i}$, tilted by $\theta$, as shown in Figure 2b. The interference pattern from two beams is recorded on a hogel. Here, the origin of the tilting stage is placed at the same position of the hogel, and the signal beam points out the same hogel, independent of tilting angles of the stage. After recording one hogel, an xy-stage moves the HOE to record the next hogel.

For the nth hogel, the recorded linear grating is represented as grating vector $\overrightarrow{k_G}$, and is calculated as the difference between two- vectors of the signal and reference beam as follows:

$$\overrightarrow{k_G}=\overrightarrow{k_S}-\overrightarrow{k_R}$$

(1)

where $\overrightarrow{k_R}$ and $\overrightarrow{k_S}$ denote the reference and signal beams, respectively. Note that the vectors for both beams have the same length of $2\pi /\lambda$. The length of the grating vector is $2\pi /\Lambda$, where $\Lambda$ represents the period of the grating. To make the diffraction efficiency of the volume grating high, the Bragg condition must be satisfied. The Q-factor indicates whether the material is operated in the Bragg condition [19]. If it must be larger than $2\pi$, the Bragg condition is satisfied. The Q-factor is defined as follows:

$$\mathrm{Q}=\frac{2\pi \lambda T_m}{n{\Lambda }^2}$$

(2)

where $T_m$ represents the thickness of the material, and n represents the refractive index of the material. From Equation (2), the thickness of the hologram material is obtained to satisfy the Bragg condition. In this study, the maximum tilting angle and the wavelength of the signal beam are 30-degrees and 532 nm, respectively. The grating pitch becomes the minimum when it is equal to the wavelength. Therefore, the minimum thicknesses of the hologram materials are smaller than $1 \mathsf{\mu }\mathrm{m}$. Generally, the common hologram medium has a sufficient thickness of approximately $15 \mathsf{\mu }\mathrm{m}$, making it suitable for the proposed holographic projection.

Figure 3 shows the system design and the realized hologram printer [20] for fabricating the HOE for a speckle noise-free IHP. In the signal arm, the signal beam is collimated and defined by a reflective collimator and a two-axis goniometer set, as shown in Figure 3a. The reflective collimator is more suitable mounted on the goniometer than a refractive type one because the optical axis is folded. Two sets of two-axis linear stages are applied to both the reference and signal arms. The linear stages move the goniometers in the signal arm to illuminate the target hogel $t_i$. The ray passes through the reflective collimator and is propagated in a specific direction $\theta$ by the goniometers. In the reference arm, the configuration of the reference beam is almost the same as that of the signal arm, except for the goniometer, and the reference beam has a fixed angle. The tilting angle of the reference beam is adjustable using the collimator mount socket. The linear stages also change the illumination position of the reference beam with respect to hogel $t_i$, as shown in Figure 3b. The hologram material is positioned between the two collimators. Figure 3c shows a photograph of the hologram printer used to fabricate the correct HOE to the speckle noise-free IHP. Figure 3d shows the light source parts. As the light source, a pig-tailed laser (Cobolt 04 series of 532 nm and 100 mW) is used. Light from the laser is briefly exposed to the free space in a fiber-to-fiber U-bench (FBP-A-FC, Thorlabs). An optical shutter (SH1/M, Thorlabs) is also installed in the U-benches, which blocks the beam when the printer head moves from one hogel to the next. When the light passes from the U-bench to the fiber optics, it is divided into two fibers, using a 1:2 coupler. Two fibers are connected to two collimators. The collimator, RC02APC-P01 is manufactured by Thorlabs. The linear stage used in this hologram printer is LTS-300/M (Thorlabs), and the total stroke is 300 mm. A goniometer is provided by Newports, and BGS80CC and BGS50CC are assembled for tilting the heads. The tilting angles of the goniometers are ±45°and ±30°, respectively.

3. Multi-Depth Projection Based on Interconnective Holographic Projection

Generally, the beam divergence from a laser source depends on the beam width $W$. The beam divergence angle is formulated as $\theta =\lambda /\pi W$. The reflective collimator used in the hologram printer masks a beam diameter approximately 0.5 mm. In this case, the beam divergence is approximately 0.02°. Figure 4 shows the simulation results of the beam divergence. The simulation is conducted using the angular spectrum method of the wave propagation [19]. The initial beam diameter is approximately 0.457 mm (D₀). It is observed that the beam width increases very slowly up to 0.5 mm (D₁) at 400 mm and then increases with a divergence angle of 0.025° after that. The maximum projection distance is determined as approximately 1.5 m. This value is the same as the distance at which the beam width is doubled when the pitch of the points comprising images is the same. In this study, we set the IHP range from zero to 400 mm because this range maximizes the contrast of the points comprising the projected images. Therefore, the resolving power of the projected image is set to 0.5 mm.

Figure 5 shows the proposed scheme of the IHP on multi-depth planes. In particular, Figure 5a,b represent two different cases, the collimated and diverging projections. T is a set of hogels, and A and B are the sets of points consisting of two sequential images, respectively. In this study, A and B are represented as two icons: a human head and a light bulb, respectively. The incident beam at point $t_i$ on the hologram is diffracted and heads to point $b_i$, on plane $z_2$, after passing through point $a_i$, on plane $z_1$. To achieve a 1:1:1 interconnection among a hogel, and each point on the two images, the algorithm is written in the tables below.

Algorithm 1 suggests several possible interconnection combinations as n × m × k matrices. It determines the possible interconnection between two points on each image plane. Additionally, it excludes combinations in which the slope of the straight line containing two points is greater than the tilting angle expressed by the goniometer meter. Algorithm 2 chooses a combination of possible features. In Algorithm 2, P indicates the number of connections.

Algorithm 1: Count optical interconnection combination.
	Inputs:   $\mathrm{A}=\left\{{\mathit{a}}_{\mathit{i}}\right\}=\left\{\left(x,y\right)\right\}$, $\mathrm{B}=\left\{{\mathit{b}}_j\right\}=\left\{\left(x,y\right)\right\}$,    $\mathrm{T}=\left\{{\mathit{t}}_k\right\}=\left\{\left(x,y\right)| x and y are smaller than the size of HOE\right\}$
	Initialize:    let H be a new $\left|A\right|\times \left|B\right|\times \left|T\right|$ Matrix   let p be a temporal array $\left(x,y\right)$
	Output:   The number of the interconnection H
1:	while $\mathrm{i}<\left|A\right|$
2:	while $\mathrm{j}<\left|B\right|$
3:	$\mathit{p} \mathrm{is} \mathrm{the} \mathrm{intersection} \mathrm{of} \mathrm{a} \mathrm{straight} \mathrm{line} \mathrm{connecting} \mathrm{two} \mathrm{points}$
4:	if the slope of the line is larger than goniometer titling angle
5:	continue
6:	end
7:	k ← Get index of nearest point ${\mathit{t}}_k$ with p
8:	$h_{i,j,k}+=1$
9:	end
10:	end
11:	Return H

Algorithm 2: Get Interconnection Matrix.
	Inputs: H, A, B, T
	Initialize:
	m is the total number of interconnections   let C be a new $\left|A\right|\times \left|B\right|\times \left|T\right|$ Matrix   ${\mathit{P}}^T\leftarrow {\sum }_{\mathit{i}}^{\left|\mathit{A}\right|}{\sum }_{\mathit{j}}^{\left|\mathit{B}\right|}\mathit{H}$
	Output:   Connection matrix, C
1:	while${\sum }_k^{\left|T\right|}{P}^T>0$
2:	${\mathrm{k}}_M\leftarrow \mathrm{argmax}\left\{P^T\right\}$
3:	${\mathit{P}}^A\leftarrow {\sum }_{\mathit{i}}^{\left|\mathit{B}\right|}{\mathit{H}}_{k=k_M}$
4:	${\mathit{P}}^B\leftarrow {\sum }_{\mathit{i}}^{\left|\mathit{A}\right|}{\mathit{H}}_{k=k_M}$
5:	$\mathrm{i} \mathrm{or} \mathrm{j}\leftarrow \mathrm{argmax}\left[min\left\{{\mathit{P}}^A,{\mathit{P}}^B\right\}\right]$
6:	find j of which bj is interconnected with ai
7:	${\mathrm{c}}_{i,j,k}=1$
8:	end
9:	Return C

Figure 6 shows the geometric relation between the rotation angles around the x- and y-axes and the tilting angles of the upper and lower goniometers used for the hologram printer. It needs to be transformed into correct angle values for the goniometers. The rotation angles around the x- and y-axes are defined as follows:

$$tan{\varnothing }_x=\frac{a_{i,x}}{a_{i,z}}$$

(3a)

$$tan{\varnothing }_y=\frac{a_{i,y}}{a_{i,z}}$$

(3b)

In the hologram printer, two goniometers are combined to rotate the incident rays. The tilting angles of the upper and lower goniometers are not equal to the rotation angles around the x- and y-axes. The tilting angles ${\theta }_{lower}$ and ${\theta }_{upper}$ of the goniometers are obtained using a rotation matrix, as follows:

$$tan{\theta }_{lower}=\frac{sin{\varnothing }_y}{cos{\varnothing }_{x}cos{\varnothing }_y}$$

(4a)

$$tan{\theta }_{upper}=-\frac{sin{\varnothing }_x}{cos{\varnothing }_x}$$

(4b)

4. Experimental Results

In general, the holographic optical element has an inevitable direct current (DC) noise that is an unmodulated term. To avoid this DC noise, the direction of the reference beam in the hologram printer was tilted approximately 30° from the normal vector of the HOE. Figure 7 shows the experimental results for the proposed speckle noise-free IHP. The size of the HOE is 50 × 50 mm² and the number of hogels identifying connectivity is 668. Here, $z_1$ and $z_2$ are set to 100 and 400 mm, respectively. In the record parameters, the hogel pitch is set to 0.5 mm, and the dot pitch in both $z_1$ and $z_2$ is 0.5 mm. The icon sizes are designed differently depending on the depth. Here, the size of the light bulb at $z_1$ is approximately 30 × 30 mm², and the size of the human head at $z_2$ is approximately 90 × 90 mm². As shown in Figure 7a, the collimated green laser illuminates the HOE at an angle of 30° oblique. Then, the recorded hogel diffracts the incident beam, and the diffracted rays connect the dots comprising the icons at the target depth planes. The connected dots are sufficiently well arranged to represent the light bulb icon, as shown in Figure 7b. The observed icon is the same size as that of the simulation. The human head icon is also well represented by connected dots when the screen is positioned at $z_2$, as shown in Figure 7c.

Figure 8 shows the experimental results demonstrating the holographic optical interconnection in the near field. The parameters are almost the same as those used in the previous experiment. The size of the HOE is 50 × 50 mm², and the hogel and dot pitch are 0.5 mm. The size of the icon is 20 × 20 mm². The number of connections is 321. $z_1$ and $z_2$ are set to 50 and 100 mm, respectively. As shown in Figure 8a, the green laser is reflected by the mirror and collimated by a collimation lens, and the collimated beam illuminates the HOE at an angle of 30° oblique. As shown in Figure 8b, the human head is clearly observed where the screen is positioned at $z_1$. A light bulb is also formed at $z_2$, as shown in Figure 8c. This result demonstrates that the proposed method connects the two depths. The icons are formed owing to the well-separated dots.

5. Discussion

We propose a speckle noise-free IHP based on optical interconnections. The proposed method connects two points by changing the direction of the incident rays, through diffraction from a linear grating recorded on a holographic medium. It eliminates speckle and crosstalk noise by connecting two points using the low divergence of a Gaussian beam. Even though there is no clear limit, the connection of more than two images is much more difficult to solve. If the number of dots to be connected is too large, it is impossible to find a solution to connect the entire dots exclusively. Figure 9 shows the simulation results comparing the binary hologram method [17] with the proposed methods. Figure 9a shows the desired signal distribution; the signal distributions are distinguished by blue and red lines based on each depth $z_1$ and $z_2$. Figure 9b shows the simulation results obtained using the binary-phase hologram method. The simulation is conducted with a 0.3 μm pixel pitch. The signal distributions at each depth plane almost resemble the desired signal. However, owing to the random noise of the phase-modulation method, the signal-to-noise ratio is as low as 5 dB.

On the contrary, the proposed method shows a high signal-to-noise ratio of 15 dB under the same conditions owing to the low divergence of the light. The fabrication process is then simplified using the proposed hologram printer. We expect that our method will contribute to high-contrast holographic projections.

6. Conclusions

In holographic projection, the speckle noise with an undesirable high spatial frequency is considered unavoidable. The speckle noise typically reduces the contrast of a projection image. In this study, we propose a novel holographic optical interconnection method by interconnecting two points in pairs where the points comprise the projection images. The HOE is recorded by interfering with two Gaussian beams with low divergence. As the reconstructed beam from the HOE propagates with a small divergence angle, projection images are formed without speckle noise. The simulation results show that the proposed method has a larger signal-to-noise ratio of 10 dB compared to the conventional method. Experimentally, we demonstrated speckle-free interconnectivity, forming two images at different depths by connecting the points comprising the images. Experiments were conducted under two conditions: diverging and collimated projections. Two HOEs were fabricated using a hologram printer specially designed for optical interconnection. In the future, we will improve the system to include degrees of freedom, not only in the incident angle of the object beam, but also the incident angle of the reference beam. Therefore, it is possible to fabricate HOEs suitable for various reconstruction conditions with different reference beam convergence angles. The proposed method will potentially be useful for optical interconnection and holographic image projection.