Abstract
The stress’s accumulation will critically affect optical device stability, leading to components’ deviation and film peeling. Stress control techniques based on strain cancelation cannot precisely match film stress, and it is difficult to reduce the total stress of multilayer film to ultra-low levels. Existing software for film system design is mainly based on 2D design concepts such as wavelength-spectrum and does not consider 3D design concepts such as wavelength-spectrum-stress, but the stress parameter plays an essential role in film performance, and it is necessary to use it as an optimization index for film design. In this paper, we introduce mechanical synchronization design into film system design. The multilayer film’s optimal structure is precisely matched by the genetic algorithm, and an ultra-low stress and wide-spectrum optical film element is developed under the dual requirements of optical performance and mechanical performance. This technique incorporates computer-aided design and automatically seeks an optimal combination of layered film nanostructures through self-compiled optical and mechanical compatible design software. While ensuring invariant optical properties, it can effectively reduce the total stress of multilayer film. This can provide a new idea for film stress control.
1. Introduction
The presence of stress is a major problem in numerous technological applications, as excessive stress can critically affect the operational characteristics, reliability and durability of material components and devices [1,2,3,4,5]. In the film field, high-throughput and wide-spectrum components are increasing, which requires an increase in the number and thickness of film layers. For example, the total thickness of deep-cut multi-bandpass filters in optical communication reaches 40 μm [6]. For such a thick film, the stress accumulation will inevitably affect optical device stability, leading to components’ deviation and film peeling [7,8,9,10,11]. Thus, stress control is one of the central issues in current film component design and manufacturing.
The film stress originates from the interaction of its own structure and depends primarily on the deposition method, preparation process and thermal annealing technique [12,13]. Currently, researchers mainly control the film stress in the preparation process, such as substrate and film materials, deposition temperature, deposition rate and working pressure. An effective means of reducing film stress is the thermal annealing technique [14,15,16], but this is not always achievable. For example, optical components in adaptive systems cannot withstand the high-temperature environment during annealing; films prepared on laser crystals also cannot undergo high-temperature annealing due to the large difference in thermal expansion coefficients between film and crystal. In addition, the coupling relationship between film and film, film and substrate in multilayer film is complex, with significantly more factors affecting stress than in monolayer film. Existing techniques are based only on the strain cancelation principle to design multilayers by alternately selecting tensile and compressive stress materials, but this approach cannot achieve precise matching, and it is difficult to reduce the total stress of a multilayer to ultra-low levels. Therefore, it is necessary to develop a theoretical framework for stress control in multilayer films and to simultaneously optimize the optical and mechanical properties of multilayers in film design. Ultimately, this approach enables ultra-low stress levels in multilayer films.
Existing software for film system design is mainly based on 2D design concepts such as wavelength spectrum and does not consider 3D design concepts such as wavelength spectrum stress [17,18,19]. In this paper, we introduce mechanical synchronization design into film system design. The multilayer film’s optimal structure is precisely matched by the genetic algorithm, and an ultra-low stress and wide-spectrum optical film element is developed under the dual requirements of optical performance and mechanical performance. A genetic algorithm is a stochastic global search and optimization method developed by mimicking natural biological evolutionary mechanisms [20,21]. It can automatically acquire and accumulate knowledge about the search space during the search process and adaptively control the search process to obtain the optimal solution. In this paper, we complete a compatible design of optical and mechanical properties for multilayers based on a genetic algorithm. First, the optical design theory and the mechanical matching theory are established separately for the film computational model, and then the optical-mechanical integrated evaluation function is constructed, with the film’s physical thickness as a parameter. Optimal combinations of layered film nanostructures were automatically sought using self-programmed optical and mechanical compatibility design software. Finally, we obtained a perfect multilayer film structure that satisfies both optical and mechanical metrics. The software was implemented using MATLAB as a programming tool.
2. Theoretical Model
2.1. Film Optical Design Theory
The main factors that affect film’s optical performance are: refractive index n0 of incident medium, refractive index ns of substrate, which are determined by many factors such as the working environment; operating band λ, incidence Angle θ, which are generally determined by the design requirements; each film’s refractive index nj, thickness dj and total layers m, which are referred to as structural parameters of the optical film design that are varied by the designer.
According to the optical film principle, the optical properties can be calculated by successive multiplications of the film eigenmatrices [22]:
where δj is the film’s phase thickness, which can be expressed as:
where ηj is the effective admittance, which can be expressed as:
where the refraction angle θj is determined by Snell’s law:
In conclusion, the reflectance R and transmittance T of the film can be calculated as:
2.2. Film Stress Design Theory
Stress is an essential mechanical property of films, and it is also a representative parameter for strongly non-equilibrium processes during film preparation. In the stress calculation model, the film layers are considered to be independent of each other. The total stress of multilayer film is a superposition of monolayer stresses, neglecting the interfacial stress between film/film and film/substrate. The total multilayer stress is considered a function of the film’s physical thickness and each component material stress in the film system structure, which is given by Equation (7) [23,24]:
where σj and dj are the stress and physical thickness of the jth layer, and m is the maximum layer in the optical film design. Based on the monolayer film stress and thickness in the film design, the total stress of the film can be calculated using the above equation.
During the preparation of multilayer films, the stress will increase if the monolayer film stress is the same. Equation (7) also verifies the correctness of this view. Existing stress control techniques for multilayer films use only an alternating design method through tensile and compressive stress materials for stress matching, as shown in Figure 1. However, this method does not precisely match the multilayer film structure and does not guarantee that the total stress of the multilayers reaches ultra-low levels. As shown in Figure 2, when the physical thickness of any film increases, the total film stress changes and its relative change shows an increasing trend. In commonly used infrared film materials, the ZnS film’s change effect is particularly pronounced. A slight structural mismatch leads to a large change in the total film stress. Thus, the optical and mechanical properties of multilayers need to be optimized simultaneously in the film design. Conventional film system design software does not support the co-optimization of optical and mechanical properties, so optically compatible design software is preferred for film stress reduction.
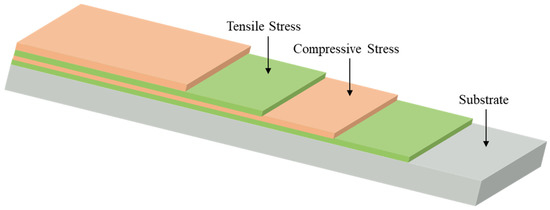
Figure 1.
Schematic diagram of the stress-matching design principle.
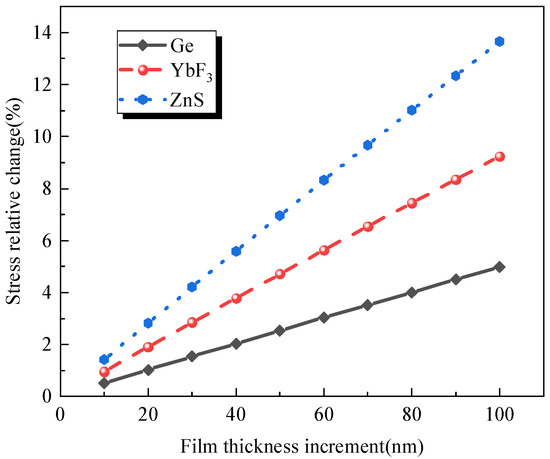
Figure 2.
The relative change in the total film stress with the film’s physical thickness.
3. Optical and Mechanical Compatible Design
When determining the materials and structures used for multilayers, only the physical thickness of each film is a design variable. Taking transmittance and reflectance as the inversion targets, the film’s transmittance and reflectance are functions of thickness d (d = d1, d2, …, dm): Td and Rd. Optical film design is the calculation of the deviation between the film optical properties under a given structural parameter and the desired target properties. In this way, the film system design problem is transformed into the problem of choosing the minimum optimal value of the structural parameters. The optimal design’s evaluation function is as follows:
where ωi and τi are the weight coefficients for transmittance and reflectance optimization, respectively. This approach essentially superimposes film transmittance and reflectance residuals at different grid points according to a certain weight.
In order to achieve zero total stress in multilayer film systems, not only is the matching design of the tensile and compressive stress film materials required, but the physical thickness in the opposite stress state also needs to be optimized. Finally, to keep the overall film stress at a low level, the integrated evaluation function for optical and mechanical properties is constructed as follows:
where κ is the optimal weight coefficient of film stress.
In the following, based on the genetic algorithm, the optical and mechanical properties are integrated into the film compatibility design, and the integrated optical and mechanical evaluation functions are used as optimization metrics to optimize the layered optical film nanostructures. The optical and mechanical integration evaluation function is a function of the film’s physical thickness; that is, by optimizing the film’s physical thickness, a perfect multilayer structure that satisfies both the optical and mechanical indices can be obtained. Optimizing layered optical film nanostructures using self-programmed optical and mechanical compatibility design software automatically selects the best combination of layered film nanostructures, resulting in a perfect multilayer structure that satisfies both optical and force metrics. The software is implemented using MATLAB as a programming tool. Figure 3 is a flowchart of the film’s optical and mechanical compatible design.
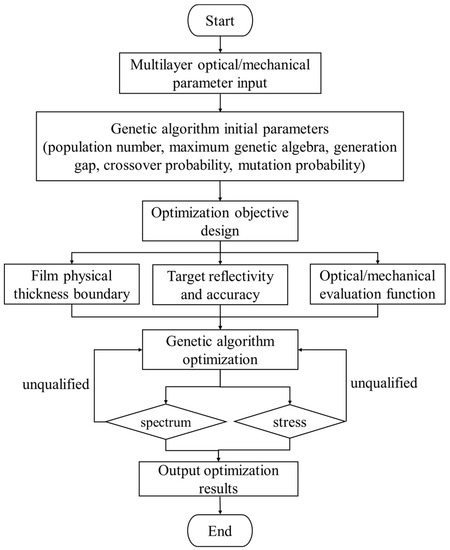
Figure 3.
Flowchart of the film’s optical and mechanical compatible design.
The process of film’s optical and mechanical compatibility design is as follows: first, input the optical and mechanical parameters of the selected film material, film structure and the initial physical thickness, and set the physical thickness boundary, target reflectance, reflectance accuracy and optical and mechanical integration evaluation functions. Then, the target optimization is performed based on a genetic algorithm, and the weight coefficients of the film stress optimization are changed to regulate the output results. Finally, a perfect multilayer structure satisfying both optical and mechanical indices is obtained. The main genetic algorithm parameters include chromosome coding, selection rate, mutation rate, crossover rate and elite selection rate, among others. The calculation procedure is shown in Figure 4. During the automatic optimization of the multi-location fitness function, the chromosome code represents the multi-location fitness function and its function value consists of an array of allocated boundary values. The selection rate, mutation rate, crossover rate and elite selection rate act on the evolution and iterative process of chromosome coding, which is represented by the optimization speed and operational accuracy of the control algorithm. The population size, crossover probability, mutation probability and population evolution times of the genetic algorithm in this paper are set to 500, 0.8, 0.1 and 1000, respectively.
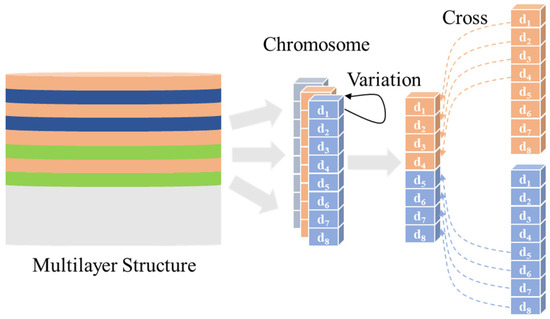
Figure 4.
Genetic algorithm process diagram.
4. Preparation of Ultra-Low Stress Long-Wave Infrared Antireflection Film
The transparent region of ZnS is 0.38–14 μm, which is an influential medium refractive index film material in the infrared band. ZnS films prepared by thermal evaporation are frequently in a compressive stress regime, with stresses as extreme as 500 MPa. ZnS stress is considerably larger than that of other commonly used infrared films, and it is one of the few compressive stress materials among the most commonly used infrared materials. Considering the requirement for a stress-matching design during multilayer film preparation, we should choose a tensile stress material to match the compressive stress of the ZnS film. Thus, the YbF3 film was chosen as a low refractive index material. In order to achieve high-quality optical performance with broadband anti-reflection, it is necessary to introduce a high-index material to improve film transmission performance. Therefore, the Ge film is selected as a high-index film layer. When assisted ion deposition is introduced, the Ge film tends to increase absorption and stress degeneration, so it is deposited with unassisted preparation parameters. In this paper, we validate the feasibility of spectrum and stress as performance optimizers for film design using a long-wave infrared antireflection film as an example. First, the optical constants and stresses of the three selected film materials are brought into the optical-mechanical integrated design software to optimize the film’s physical thickness. The process parameters, optical constant and stresses for the three selected film materials are listed in Table 1.

Table 1.
Specific parameters of the monolayer used in this paper.
The multilayer initial structure is: Sub/H M H M L M L M/Air, the central wavelength is 8 μm, and the light is incident vertically, where H: Ge; L: YbF3; M: ZnS. The film system is designed with a non-normalized structure. When only the film optical properties are considered—that is, only the reflectance parameter is added to the optimization index—the optimized multilayer structure can be obtained:
Ge/0.1H 0.32M 0.39H 0.54M 0.29L 0.05M 0.29L 0.25M/Air
The theoretical film residual reflectance in the 8–12 μm band is shown in the red curve in Figure 5. The average reflectance reaches 0.12%, the theoretical film stress is: −109.9 MPa, and the resultant force is: −232.6 GPa.
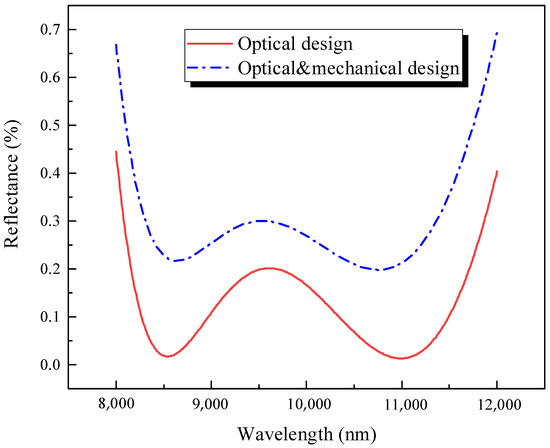
Figure 5.
Theoretical spectral curve of ultra-low stress films.
Then, the transmittance parameters and stress parameters are simultaneously optimized as optimization metrics. After the optimization is completed, the improved film structure is obtained as follows:
Ge/0.1H 0.4M 0.31H 0.46M 0.42L 0.05M 0.5L 0.1M/Air
The theoretical film residual reflectance is shown as a blue curve in Figure 5, with an average reflectance of 0.3%, a theoretical film stress of −63.5 MPa and resultant force of −154.3 GPa. It can be seen from the spectral curve that after adding the stress optimization parameters, the spectral performance can meet the design requirements, but in terms of the stress parameters, the two cases are very different: when the stress parameters are introduced for the film system design, the average film stress decreases from the original 109.9 MPa to 63.5 MPa, a decrease of 42%. Therefore, it is reasonable and feasible to use stress as a performance metric for optimizing film systems.
Based on the results of the optical-mechanical integrated design, ultra-low stress long-wave infrared anti-reflection films were prepared. The sample stress was measured with a ZYGO laser interferometer, and the value of the substrate surface shape can be directly obtained from the measurements. The peak-valley value PV can be understood as the distance from the highest point to the lowest point of the substrate surface diagram. The sagittal height Power is used to represent the overall bending direction and degree and it is a best fit value. When the substrate surface shape is excellent, PV is approximately equal to Power. Figure 6 shows the substrate surface diagram before and after coating. The PV and Power before coating are respectively: 0.253 λ, 0.234 λ. The PV and Power after coating are respectively: 0.18 λ, −0.171 λ, where λ = 632.8 nm. The relationship between Power and curvature radius R is shown in Equation (10):
where, Ds is the substrate diameter. Further, it can be obtained:
where ΔPower is the difference value before and after coating, which can be obtained directly from the ZYGO measurement results. Equation (11) is brought into the Stoney formula for calculation, and the film stress can be obtained as follows:
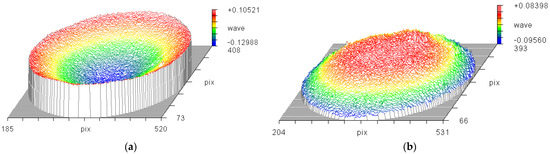
Figure 6.
Substrate surface diagram: (a) Before coating of ultra-low stress film sample; (b) After coating of ultra-low stress film sample.
The actual sample stress was −78.2 MPa. The preparation of an ultra-low stress long wave infrared antireflection film verifies the feasibility of our design and simulation. When an optical-mechanical compatible design is used, the actual film stress can be less than 80 MPa. Compared with the conventional film design, the stress decreased by about 29%. Therefore, this technology can effectively reduce film stress on the premise of ensuring that the optical properties meet the design index.
5. Conclusions
In this paper, we innovatively introduce stress into the film system design and use the stress parameter as a performance metric to evaluate the film system structure. This makes the film design three-dimensional and achieves a precisely optimized design for film stress. This self-compiled optical and mechanical compatible design software enables automatic optimization of multilayer film structures and outputs high-quality film structures under the dual requirements of optical properties and mechanical properties. As an example of a long-wave infrared antireflection film design, precise optimization of the film structure at opposite stresses was performed using optical and mechanical compatible design software, such that the film stresses cancel each other and reach extremely low levels. Under the assumption of constant optical properties, the total stress of the film is less than 80 MPa, which validates the feasibility and effectiveness of the optical and mechanical compatible design technique proposed in this paper.
Funding
This research was funded by the National Natural Science Foundation of China (61975150, 61905179), the Natural Science Foundation of Tianjin (19JCZDJC38400).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haanappel, V.A.C.; Van Corbach, H.D.; Fransen, T.; Gellings, P.J. Cracking and delamination of metal organic vapour and deposited alumina and silica films. Mater. Sci. Eng. A 1993, 167, 179–185. [Google Scholar] [CrossRef][Green Version]
- Erdem Alaca, B.; Saif, M.T.A.; Sehitoglu, H. On the interface debond at the edge of a thin film on a thick substrate. Acta Mater. 2002, 50, 1197–1209. [Google Scholar] [CrossRef]
- Forschelen, P.J.J.; Suiker, A.S.J.; van der Sluis, O. Effect of residual stress on the delamination response of film-substrate systems under bending. Int. J. Solids Struct. 2016, 97–98, 284–299. [Google Scholar] [CrossRef]
- Khaledi, K.; Brepols, T.; Reese, S. A multiscale description of bond formation in cold roll bonding considering periodic cracking of thin surface films. Mech. Mater. 2019, 137, 103142. [Google Scholar] [CrossRef]
- Stylianou, R.; Velic, D.; Daves, W.; Ecker, W.; Stark, A.; Schell, N.; Tkadletz, M.; Schalk, N.; Czettl, C.; Mitterer, C. Stress relaxation through thermal crack formation in CVD TiCN coatings grown on WC-Co with different Co contents. Int. J. Refract. Met. Hard Mater. 2020, 86, 105102. [Google Scholar] [CrossRef]
- De Denus-Baillargeon, M.M.; Schmitt, T.; Larouche, S.; Martinu, L. Design and fabrication of stress-compensated optical coatings: Fabry-perot filters for astronomical applications. Appl. Opt. 2014, 53, 2616–2624. [Google Scholar] [CrossRef]
- Stout, J.H.; Shores, D.A.; Goedjen, J.G.; Armacanqui, M.E. Stresses and cracking of oxide scales. Mater. Sci. Eng. A 1989, 120–121, 193–197. [Google Scholar] [CrossRef]
- Tamulevičius, S. Stress and strain in the vacuum deposited thin films. Vacuum 1998, 51, 127–139. [Google Scholar] [CrossRef]
- Malerba, C.; Valentini, M.; Ricardo, C.A.; Rinaldi, A.; Cappelletto, E.; Scardi, P.; Mittiga, A. Blistering in Cu2ZnSnS4 thin films: Correlation with residual stresses. Mater. Des. 2016, 108, 725–735. [Google Scholar] [CrossRef]
- Liu, D.G.; Zheng, L.; Liu, J.Q.; Luo, L.M.; Wu, Y.C. Residual stress relief of hard a-C films though buckling. Ceram. Int. 2018, 44, 3644–3648. [Google Scholar] [CrossRef]
- Li, S.J.; Wu, K.; Yuan, H.Z.; Zhang, J.Y.; Liu, G.; Sun, J. Formation of wrinkled patterns in metal films deposited on elastic substrates: Tunability and wettability. Surf. Coat. Technol. 2019, 362, 35–43. [Google Scholar] [CrossRef]
- Leplan, H.; Geenen, B.; Robic, J.Y.; Pauleau, Y. Residual stresses in evaporated silicon dioxide thin films: Correlation with deposition parameters and aging behavior. J. Appl. Phys. 1995, 78, 962–968. [Google Scholar] [CrossRef]
- Chason, E. A Kinetic Model for Stress Evolution in Thin Films. J. Am. Dent. Assoc. Dent. Cosm. 2012, 25, 1017–1024. [Google Scholar] [CrossRef]
- Xu, C.; Qiang, Y.; Zhu, Y.; Zhai, T.; Guo, L.; Zhao, Y.; Shao, J.; Fan, Z. Laser-induced damage threshold at different wavelengths of Ta2O5 films annealed over a wide temperature range. Vacuum 2010, 84, 1310–1314. [Google Scholar] [CrossRef]
- Kičas, S.; Gimževskis, U.; Melnikas, S. Post deposition annealing of IBS mixture coatings for compensation of film induced stress. Opt. Mater. Express 2016, 6, 2236. [Google Scholar] [CrossRef]
- Bischoff, M.; Nowitzki, T.; Voß, O.; Wilbrandt, S.; Stenzel, O. Postdeposition treatment of ibs coatings for uv applications with optimized thin-film stress properties. Appl. Opt. 2014, 53, 212–220. [Google Scholar] [CrossRef] [PubMed]
- Jalali, T.; Jafari, M.; Mohammadi, A. Genetic algorithm optimization of antireflection coating consisting of nanostructured thin films to enhance silicon solar cell efficacy. Mater. Sci. Eng. B 2019, 247, 114354. [Google Scholar] [CrossRef]
- Patel, S.J.; Kheraj, V. Optimization of the genetic operators and algorithm parameters for the design of a multilayer anti-reflection coating using the genetic algorithm. Opt. Laser Technol. 2015, 70, 94–99. [Google Scholar] [CrossRef]
- Patel, S.J.; Toshniwal, A.; Kheraj, V. A novel teaching-learning based optimization approach for design of broad-band anti-reflection coatings. Swarm Evol. Comput. 2017, 34, 68–74. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Ghasemi, M.; Sajjadi, Z. Evolutionary algorithm for optimization of multilayer coatings. Chin. Phys. B 2018, 27, 106802. [Google Scholar] [CrossRef]
- Patel, S.J.; Kheraj, V. Determination of refractive index and thickness of thin-film from reflectivity spectrum using genetic algorithm. AIP Conf. Proc. 2013, 1536, 509–510. [Google Scholar]
- Macleod, H.A. Thin-Film Optical Filters; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Suhir, E. Predicted thermally induced stresses in, and the bow of, a circular substrate/thin-film structure. J. Appl. Phys. 2000, 88, 2363–2370. [Google Scholar] [CrossRef]
- Klein, C.A. Normal and interfacial stresses in thin-film coated optics: The case of diamond-coated zinc sulfide windows. Opt. Eng. 2001, 40, 1115–1124. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).