Berry Phase of Two Impurity Qubits as a Signature of Dicke Quantum Phase Transition
Abstract
1. Introduction
2. Dicke Model with Two Impurity Qubits and Berry Phase of Two Impurity Qubits
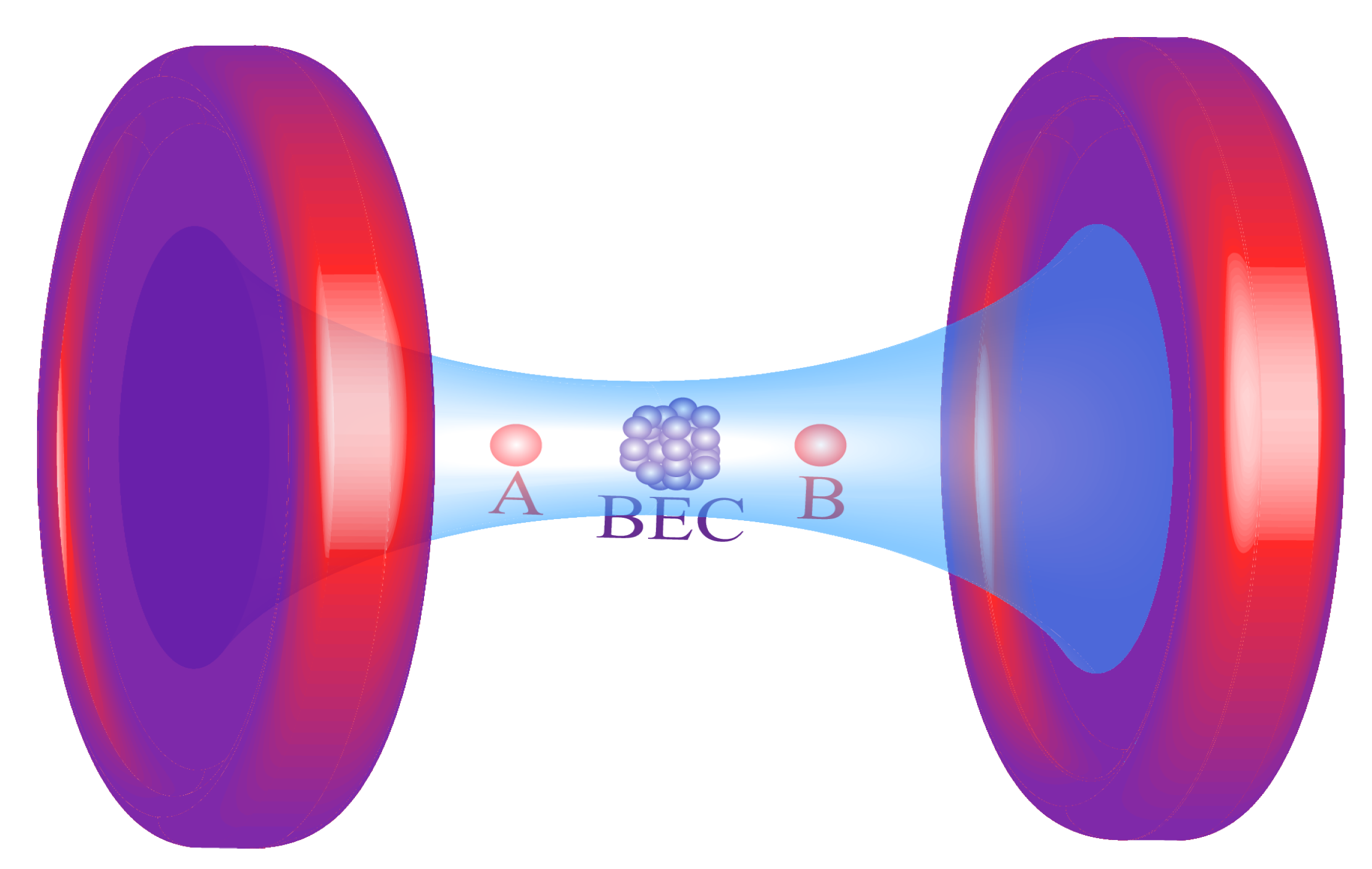
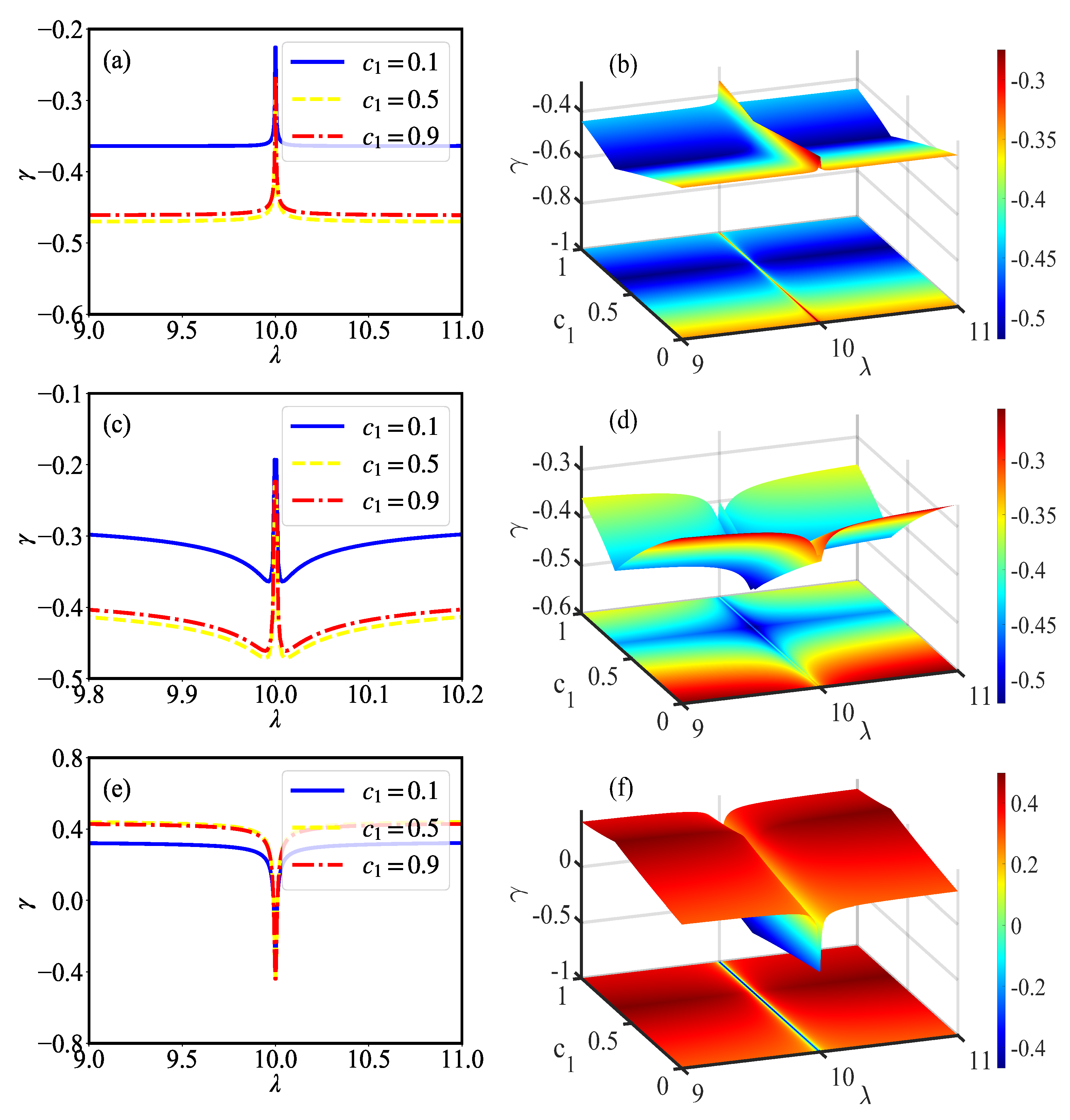
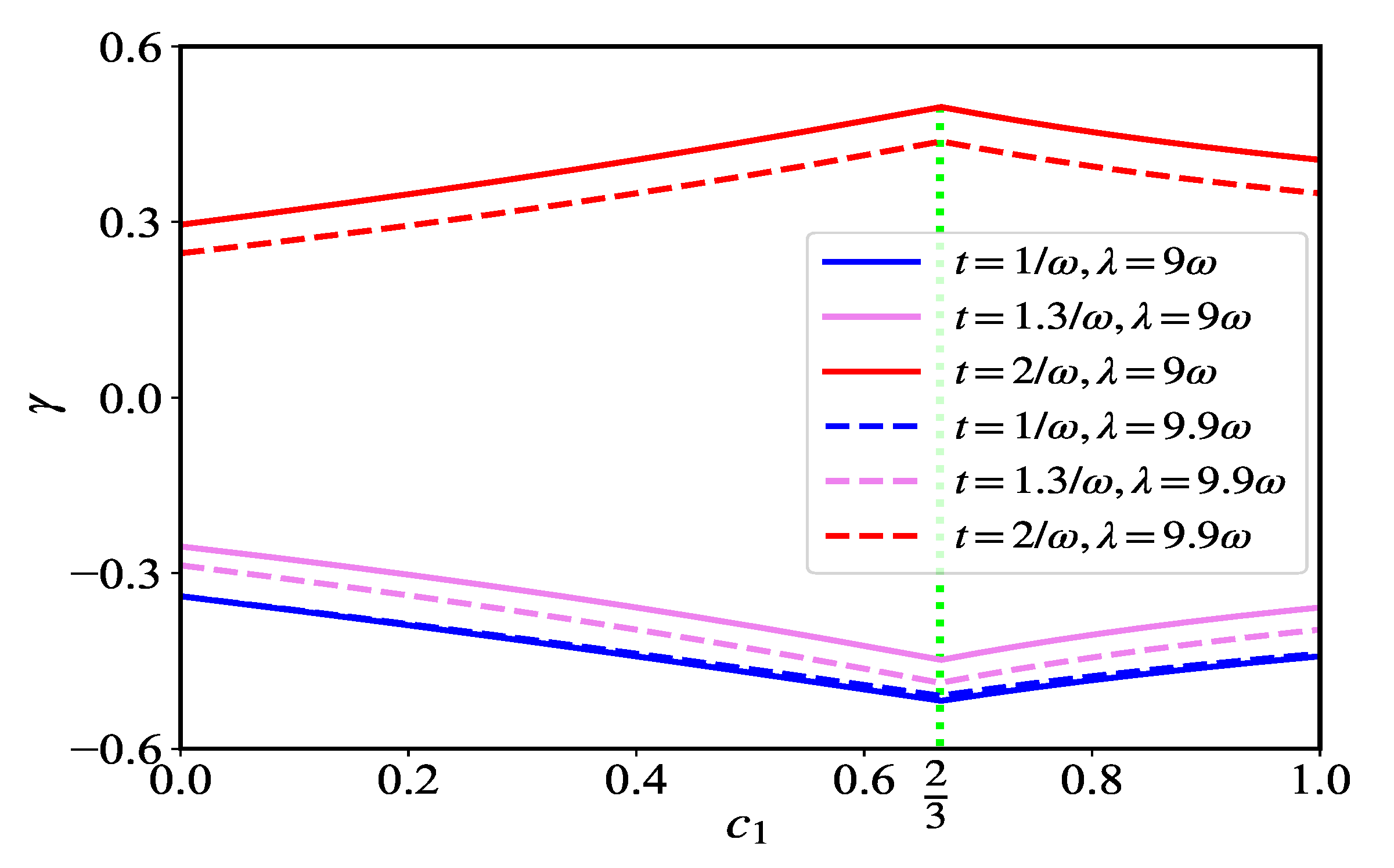
3. Effect of Dicke Quantum Phase Transition on the Berry Phase of Two Impurity Qubits

4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A Math. Phys. Sci. 1984, 392, 45–57. [Google Scholar]
- Simon, B. Holonomy, the Quantum Adiabatic Theorem, and Berry’s Phase. Phys. Rev. Lett. 1983, 51, 2167–2170. [Google Scholar] [CrossRef]
- Anandan, J.; Aharonov, Y. Geometry of quantum evolution. Phys. Rev. Lett. 1990, 65, 1697–1700. [Google Scholar] [CrossRef] [PubMed]
- Pancharatnam, S. Generalized theory of interference and its applications. Proc. Indian Acad. Sci. 1956, 44, 398–417. [Google Scholar] [CrossRef]
- Cohen, E.; Larocque, H.; Bouchard, F.; Nejadsattari, F.; Gefen, Y.; Karimi, E. Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond. Nat. Rev. Phys. 2019, 1, 437–449. [Google Scholar] [CrossRef]
- Samuel, J.; Bhandari, R. General Setting for Berry’s Phase. Phys. Rev. Lett. 1988, 60, 2339–2342. [Google Scholar] [CrossRef]
- Tomita, A.; Chiao, R.Y. Observation of Berry’s Topological Phase by Use of an Optical Fiber. Phys. Rev. Lett. 1986, 57, 937–940. [Google Scholar] [CrossRef]
- Du, J.; Zhu, J.; Shi, M.; Peng, X.; Suter, D. Experimental observation of a topological phase in the maximally entangled state of a pair of qubits. Phys. Rev. A 2007, 76, 042121. [Google Scholar] [CrossRef]
- Chen, H.; Hu, M.; Chen, J.; Du, J. Observation of geometric phases for three-level systems using NMR interferometry. Phys. Rev. A 2009, 80, 054101. [Google Scholar] [CrossRef]
- Leek, P.J.; Fink, J.; Blais, A.; Bianchetti, R.; Goppl, M.; Gambetta, J.M.; Schuster, D.I.; Frunzio, L.; Schoelkopf, R.J.; Wallraff, A. Observation of Berry’s phase in a solid-state qubit. Science 2007, 318, 1889–1892. [Google Scholar] [CrossRef]
- Möttönen, M.; Vartiainen, J.J.; Pekola, J.P. Experimental Determination of the Berry Phase in a Superconducting Charge Pump. Phys. Rev. Lett. 2008, 100, 177201. [Google Scholar] [CrossRef]
- Sjöqvist, E.; Pati, A.K.; Ekert, A.; Anandan, J.S.; Ericsson, M.; Oi, D.K.L.; Vedral, V. Geometric Phases for Mixed States in Interferometry. Phys. Rev. Lett. 2000, 85, 2845–2849. [Google Scholar] [CrossRef]
- Ericsson, M.; Achilles, D.; Barreiro, J.T.; Branning, D.; Peters, N.A.; Kwiat, P.G. Measurement of Geometric Phase for Mixed States Using Single Photon Interferometry. Phys. Rev. Lett. 2005, 94, 050401. [Google Scholar] [CrossRef]
- Tong, D.M.; Sjöqvist, E.; Kwek, L.C.; Oh, C.H. Kinematic Approach to the Mixed State Geometric Phase in Nonunitary Evolution. Phys. Rev. Lett. 2004, 93, 080405. [Google Scholar] [CrossRef]
- Ekert, A.; Ericsson, M.; Hayden, P.; Inamori, H.; Jones, J.A.; Oi, D.K.; Vedral, V. Geometric quantum computation. J. Mod. Opt. 2000, 47, 2501–2513. [Google Scholar] [CrossRef]
- Zanardi, P.; Rasetti, M. Holonomic quantum computation. Phys. Lett. A 1999, 264, 94–99. [Google Scholar] [CrossRef]
- Zhu, S.L.; Wang, Z.D. Implementation of Universal Quantum Gates Based on Nonadiabatic Geometric Phases. Phys. Rev. Lett. 2002, 89, 097902. [Google Scholar] [CrossRef]
- Zhu, S.L.; Wang, Z.D. Unconventional Geometric Quantum Computation. Phys. Rev. Lett. 2003, 91, 187902. [Google Scholar] [CrossRef]
- Huang, H.Y.; Broughton, M.; Cotler, J.; Chen, S.; Li, J.; Mohseni, M.; Neven, H.; Babbush, R.; Kueng, R.; Preskill, J.; et al. Quantum advantage in learning from experiments. Science 2022, 376, 1182–1186. [Google Scholar] [CrossRef]
- Zhou, M.G.; Cao, X.Y.; Lu, Y.S.; Wang, Y.; Bao, Y.; Jia, Z.Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Experimental quantum advantage with quantum coupon collector. Research 2022, 2022, 9798679. [Google Scholar] [CrossRef]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Zhou, N.R.; Zhang, T.F.; Xie, X.W.; Wu, J.Y. Hybrid quantum–classical generative adversarial networks for image generation via learning discrete distribution. Signal Process. Image Commun. 2022, 116891, in press. [Google Scholar] [CrossRef]
- Azimi Mousolou, V.; Canali, C.M.; Sjöqvist, E. Unifying geometric entanglement and geometric phase in a quantum phase transition. Phys. Rev. A 2013, 88, 012310. [Google Scholar] [CrossRef]
- Cui, H.T.; Yi, J. Geometric phase and quantum phase transition: Two-band model. Phys. Rev. A 2008, 78, 022101. [Google Scholar] [CrossRef]
- Ma, Y.Q.; Chen, S. Geometric phase and quantum phase transition in an inhomogeneous periodic XY spin-12 model. Phys. Rev. A 2009, 79, 022116. [Google Scholar] [CrossRef]
- Nesterov, A.I.; Ovchinnikov, S.G. Geometric phases and quantum phase transitions in open systems. Phys. Rev. E 2008, 78, 015202. [Google Scholar] [CrossRef]
- Carollo, A.C.M.; Pachos, J.K. Geometric Phases and Criticality in Spin-Chain Systems. Phys. Rev. Lett. 2005, 95, 157203. [Google Scholar] [CrossRef]
- Hamma, A. Berry phases and quantum phase transitions. arXiv 2006, arXiv:quant-ph/0602091. [Google Scholar]
- Zhu, S.L. Geometric phases and quantum phase transitions. Int. J. Mod. Phys. B 2008, 22, 561–581. [Google Scholar] [CrossRef]
- Lu, X.M.; Wang, X. Operator quantum geometric tensor and quantum phase transitions. EPL (Europhys. Lett.) 2010, 91, 30003. [Google Scholar] [CrossRef][Green Version]
- Pachos, J.K.; Carollo, A.C. Geometric phases and criticality in spin systems. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2006, 364, 3463–3476. [Google Scholar] [CrossRef]
- Plastina, F.; Liberti, G.; Carollo, A. Scaling of Berry’s phase close to the Dicke quantum phase transition. EPL (Europhys. Lett.) 2006, 76, 182. [Google Scholar] [CrossRef]
- Zhu, S.L. Scaling of Geometric Phases Close to the Quantum Phase Transition in the XY Spin Chain. Phys. Rev. Lett. 2006, 96, 077206. [Google Scholar] [CrossRef]
- Reuter, M.E.; Hartmann, M.J.; Plenio, M.B. Geometric phases and critical phenomena in a chain of interacting spins. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1271–1285. [Google Scholar] [CrossRef]
- Peng, X.; Wu, S.; Li, J.; Suter, D.; Du, J. Observation of the Ground-State Geometric Phase in a Heisenberg XY Model. Phys. Rev. Lett. 2010, 105, 240405. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Li, J.; Liang, J.Q. Critical property of the geometric phase in the Dicke model. Phys. Rev. A 2006, 74, 054101. [Google Scholar] [CrossRef]
- Cui, H.; Li, K.; Yi, X. Geometric phase and quantum phase transition in the Lipkin–Meshkov–Glick model. Phys. Lett. A 2006, 360, 243–248. [Google Scholar] [CrossRef][Green Version]
- Sjöqvist, E.; Rahaman, R.; Basu, U.; Basu, B. Berry phase and fidelity susceptibility of the three-qubit Lipkin–Meshkov–Glick ground state. J. Phys. Math. Theor. 2010, 43, 354026. [Google Scholar] [CrossRef]
- Guerra, C.A.E.; Mahecha-Gómez, J.; Hirsch, J.G. Quantum phase transition and Berry phase in an extended Dicke model. Eur. Phys. J. D 2020, 74, 1–7. [Google Scholar] [CrossRef]
- Yuan, Z.G.; Zhang, P.; Li, S.S.; Jing, J.; Kong, L.B. Scaling of the Berry phase close to the excited-state quantum phase transition in the Lipkin model. Phys. Rev. A 2012, 85, 044102. [Google Scholar] [CrossRef]
- Paunković, N.; Rocha Vieira, V. Macroscopic distinguishability between quantum states defining different phases of matter: Fidelity and the Uhlmann geometric phase. Phys. Rev. E 2008, 77, 011129. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.D.; Fu, L.B. Mean-field Berry phase of an interacting spin-1/2 system. EPL (Europhys. Lett.) 2011, 93, 30001. [Google Scholar] [CrossRef]
- Carollo, A.; Valenti, D.; Spagnolo, B. Geometry of quantum phase transitions. Phys. Rep. 2020, 838, 1–72. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Hepp, K.; Lieb, E.H. On the superradiant phase transition for molecules in a quantized radiation field: The Dicke maser model. Ann. Phys. 1973, 76, 360–404. [Google Scholar] [CrossRef]
- Hepp, K.; Lieb, E.H. Equilibrium Statistical Mechanics of Matter Interacting with the Quantized Radiation Field. Phys. Rev. A 1973, 8, 2517–2525. [Google Scholar] [CrossRef]
- Emary, C.; Brandes, T. Quantum Chaos Triggered by Precursors of a Quantum Phase Transition: The Dicke Model. Phys. Rev. Lett. 2003, 90, 044101. [Google Scholar] [CrossRef]
- Emary, C.; Brandes, T. Chaos and the quantum phase transition in the Dicke model. Phys. Rev. E 2003, 67, 066203. [Google Scholar] [CrossRef]
- Baumann, K.; Guerlin, C.; Brennecke, F.; Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 2010, 464, 1301–1306. [Google Scholar] [CrossRef]
- Baumann, K.; Mottl, R.; Brennecke, F.; Esslinger, T. Exploring Symmetry Breaking at the Dicke Quantum Phase Transition. Phys. Rev. Lett. 2011, 107, 140402. [Google Scholar] [CrossRef]
- Yuan, J.B.; Lu, W.J.; Song, Y.J.; Kuang, L.M. Single-impurity-induced Dicke quantum phase transition in a cavity-Bose–Einstein condensate. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.J.; Li, Z.; Kuang, L.M. Nonlinear Dicke quantum phase transition and its quantum witness in a cavity-Bose–Einstein-condensate system. Chin. Phys. Lett. 2018, 35, 116401. [Google Scholar] [CrossRef]
- Li, Z.; Kuang, L.M. Controlling quantum coherence of a two-component Bose–Einstein condensate via an impurity atom. Quantum Inf. Process. 2020, 19, 1–17. [Google Scholar] [CrossRef]
- Song, Y.J.; Tan, Q.S.; Kuang, L.M. Control quantum evolution speed of a single dephasing qubit for arbitrary initial states via periodic dynamical decoupling pulses. Sci. Rep. 2017, 7, 43654. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.J.; Kuang, L.M. Controlling Decoherence Speed Limit of a Single Impurity Atom in a Bose–Einstein-Condensate Reservoir. Ann. Der Phys. 2019, 531, 1800423. [Google Scholar] [CrossRef]
- Wu, X.; Jiao, Y.F.; Jia, S.P.; Zhang, J.; Zhai, C.L.; Kuang, L.M. Micro–micro and micro–macro entanglement witnessing via the geometric phase in an impurity-doped Bose–Einstein condensate. Quantum Inf. Process. 2022, 21, 1–20. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Kuang, L.M. Quantum dynamics of an impurity-doped Bose–Einstein condensate system. Commun. Theor. Phys. 2020, 72, 095102. [Google Scholar] [CrossRef]
- Jia, S.P.; Li, B.; Jiao, Y.F.; Jing, H.; Kuang, L.M. Einstein-Podolsky-Rosen steering of quantum phases in a cavity Bose–Einstein condensate with a single impurity. arXiv 2022, arXiv:2205.13938. [Google Scholar]
- Li, Z.; Han, Y.; Kuang, L.M. Complementarity between micro-micro and micro-macro entanglement in a Bose–Einstein condensate with two Rydberg impurities. Commun. Theor. Phys. 2020, 72, 025101. [Google Scholar] [CrossRef]
- Yuan, J.B.; Kuang, L.M. Quantum-discord amplification induced by a quantum phase transition via a cavity–Bose–Einstein-condensate system. Phys. Rev. A 2013, 87, 024101. [Google Scholar] [CrossRef]
- Levinsen, J.; Parish, M.M.; Bruun, G.M. Impurity in a Bose–Einstein Condensate and the Efimov Effect. Phys. Rev. Lett. 2015, 115, 125302. [Google Scholar] [CrossRef]
- Christensen, R.S.; Levinsen, J.; Bruun, G.M. Quasiparticle Properties of a Mobile Impurity in a Bose–Einstein Condensate. Phys. Rev. Lett. 2015, 115, 160401. [Google Scholar] [CrossRef]
- Lausch, T.; Widera, A.; Fleischhauer, M. Prethermalization in the cooling dynamics of an impurity in a Bose–Einstein condensate. Phys. Rev. A 2018, 97, 023621. [Google Scholar] [CrossRef]
- Lena, R.G.; Daley, A.J. Dissipative dynamics and cooling rates of trapped impurity atoms immersed in a reservoir gas. Phys. Rev. A 2020, 101, 033612. [Google Scholar] [CrossRef]
- Yoshida, S.M.; Endo, S.; Levinsen, J.; Parish, M.M. Universality of an Impurity in a Bose–Einstein Condensate. Phys. Rev. X 2018, 8, 011024. [Google Scholar] [CrossRef]
- Volya, A.; Zelevinsky, V. Invariant correlational entropy as a signature of quantum phase transitions in nuclei. Phys. Lett. B 2003, 574, 27–34. [Google Scholar] [CrossRef]
- Wang, T.L.; Wu, L.N.; Yang, W.; Jin, G.R.; Lambert, N.; Nori, F. Quantum Fisher information as a signature of the superradiant quantum phase transition. New J. Phys. 2014, 16, 063039. [Google Scholar] [CrossRef]
- Yang, L.P.; Jacob, Z. Quantum critical detector: Amplifying weak signals using discontinuous quantum phase transitions. Opt. Express 2019, 27, 10482–10494. [Google Scholar] [CrossRef]
- Paunković, N.; Sacramento, P.D.; Nogueira, P.; Vieira, V.R.; Dugaev, V.K. Fidelity between partial states as a signature of quantum phase transitions. Phys. Rev. A 2008, 77, 052302. [Google Scholar] [CrossRef]
- Relaño, A.; Arias, J.M.; Dukelsky, J.; García-Ramos, J.E.; Pérez-Fernández, P. Decoherence as a signature of an excited-state quantum phase transition. Phys. Rev. A 2008, 78, 060102. [Google Scholar] [CrossRef]
- Chen, J.J.; Cui, J.; Zhang, Y.R.; Fan, H. Coherence susceptibility as a probe of quantum phase transitions. Phys. Rev. A 2016, 94, 022112. [Google Scholar] [CrossRef]
- Hu, M.L.; Gao, Y.Y.; Fan, H. Steered quantum coherence as a signature of quantum phase transitions in spin chains. Phys. Rev. A 2020, 101, 032305. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, C.; Chen, S. Signature of a nonequilibrium quantum phase transition in the long-time average of the Loschmidt echo. Phys. Rev. B 2019, 100, 184313. [Google Scholar] [CrossRef]
- Wang, Q.; Pérez-Bernal, F. Signatures of excited-state quantum phase transitions in quantum many-body systems: Phase space analysis. Phys. Rev. E 2021, 104, 034119. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Song, Z.; Liu, X.F.; Zanardi, P.; Sun, C.P. Decay of Loschmidt Echo Enhanced by Quantum Criticality. Phys. Rev. Lett. 2006, 96, 140604. [Google Scholar] [CrossRef]
- Wu, W.; Xu, J.B. Geometric phase, quantum Fisher information, geometric quantum correlation and quantum phase transition in the cavity-Bose–Einstein-condensate system. Quantum Inf. Process. 2016, 15, 3695–3709. [Google Scholar] [CrossRef]
- Peixoto de Faria, J.G.; Nemes, M.C. Dissipative dynamics of the Jaynes-Cummings model in the dispersive approximation: Analytical results. Phys. Rev. A 1999, 59, 3918–3925. [Google Scholar] [CrossRef]
- Obada, A.S.; Hessian, H.; Mohamed, A.B. The effects of thermal photons on entanglement dynamics for a dispersive Jaynes–Cummings model. Phys. Lett. A 2008, 372, 3699–3706. [Google Scholar] [CrossRef]
- Zhang, J.S.; Chen, A.X.; Abdel-Aty, M. Two atoms in dissipative cavities in dispersive limit: Entanglement sudden death and long-lived entanglement. J. Phys. B At. Mol. Opt. Phys. 2009, 43, 025501. [Google Scholar] [CrossRef]
- Ban, M. Exact time-evolution of the dispersive Jaynes–Cummings model: The effect of initial correlation and master equation approach. J. Mod. Opt. 2011, 58, 640–651. [Google Scholar] [CrossRef]
- Guo, Y.T.; Zou, F.; Huang, J.F.; Liao, J.Q. Retrieval of photon blockade effect in the dispersive Jaynes-Cummings model. Phys. Rev. A 2022, 105, 013705. [Google Scholar] [CrossRef]
- Fröhlich, H. Theory of the Superconducting State. I. The Ground State at the Absolute Zero of Temperature. Phys. Rev. 1950, 79, 845–856. [Google Scholar] [CrossRef]
- Nakajima, S. Perturbation theory in statistical mechanics. Adv. Phys. 1955, 4, 363–380. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys. Rev. 1940, 58, 1098–1113. [Google Scholar] [CrossRef]
- Ressayre, E.; Tallet, A. Holstein-Primakoff transformation for the study of cooperative emission of radiation. Phys. Rev. A 1975, 11, 981–988. [Google Scholar] [CrossRef]
- Persico, F.; Vetri, G. Coherence properties of the N-atom-radiation interaction and the Holstein-Primakoff transformation. Phys. Rev. A 1975, 12, 2083–2091. [Google Scholar] [CrossRef]
- Thompson, R.J.; Rempe, G.; Kimble, H.J. Observation of normal-mode splitting for an atom in an optical cavity. Phys. Rev. Lett. 1992, 68, 1132–1135. [Google Scholar] [CrossRef]
- Brune, M.; Schmidt-Kaler, F.; Maali, A.; Dreyer, J.; Hagley, E.; Raimond, J.M.; Haroche, S. Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity. Phys. Rev. Lett. 1996, 76, 1800–1803. [Google Scholar] [CrossRef]
- Kimble, H.J. Strong interactions of single atoms and photons in cavity QED. Phys. Scr. 1998, 1998, 127. [Google Scholar] [CrossRef]
- Reiserer, A.; Rempe, G. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 2015, 87, 1379–1418. [Google Scholar] [CrossRef]
- Johnson, A.; Blaha, M.; Ulanov, A.E.; Rauschenbeutel, A.; Schneeweiss, P.; Volz, J. Observation of Collective Superstrong Coupling of Cold Atoms to a 30-m Long Optical Resonator. Phys. Rev. Lett. 2019, 123, 243602. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, F.C.; Villar, P.I. Corrections to the Berry phase in a solid-state qubit due to low-frequency noise. Phys. Rev. A 2014, 89, 012110. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T.; Xiang, L.; Yao, J.; Wu, J.; Yin, Y. Measuring the Berry phase in a superconducting phase qubit by a shortcut to adiabaticity. Phys. Rev. A 2017, 95, 042345. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Zhai, C.; Liu, Y.; Song, Y.; Yuan, J.; Tang, S. Berry Phase of Two Impurity Qubits as a Signature of Dicke Quantum Phase Transition. Photonics 2022, 9, 844. https://doi.org/10.3390/photonics9110844
Lu W, Zhai C, Liu Y, Song Y, Yuan J, Tang S. Berry Phase of Two Impurity Qubits as a Signature of Dicke Quantum Phase Transition. Photonics. 2022; 9(11):844. https://doi.org/10.3390/photonics9110844
Chicago/Turabian StyleLu, Wangjun, Cuilu Zhai, Yan Liu, Yaju Song, Jibing Yuan, and Shiqing Tang. 2022. "Berry Phase of Two Impurity Qubits as a Signature of Dicke Quantum Phase Transition" Photonics 9, no. 11: 844. https://doi.org/10.3390/photonics9110844
APA StyleLu, W., Zhai, C., Liu, Y., Song, Y., Yuan, J., & Tang, S. (2022). Berry Phase of Two Impurity Qubits as a Signature of Dicke Quantum Phase Transition. Photonics, 9(11), 844. https://doi.org/10.3390/photonics9110844




