Time-Varying Engineered Reservoir for the Improved Estimation of Atom-Cavity Coupling Strength
Abstract
1. Introduction
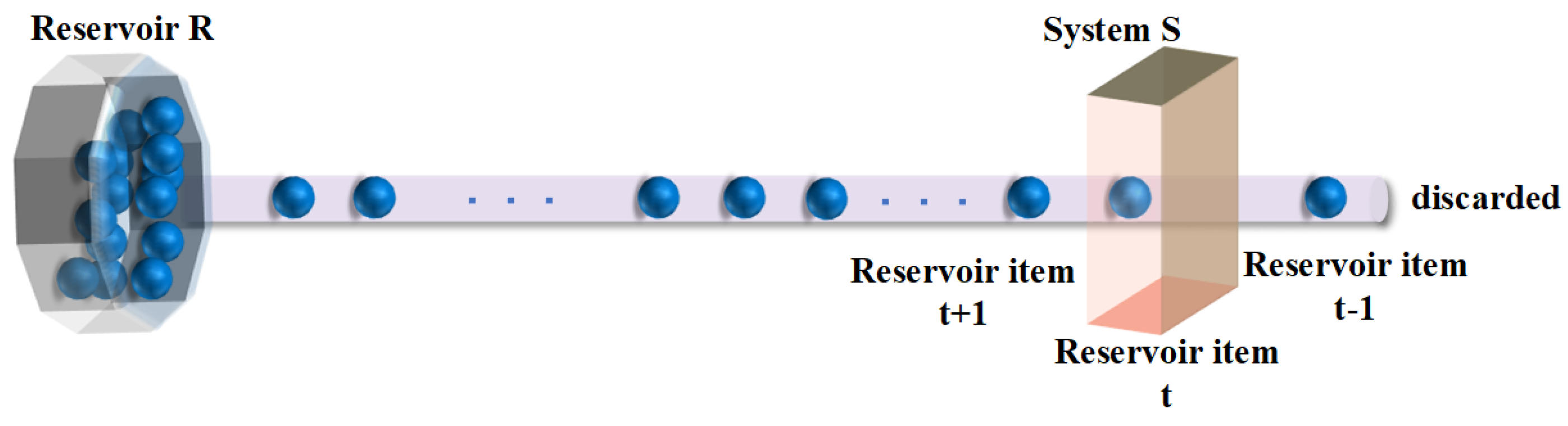
2. Mathematical Model of the System Setup and Quantification of the Estimation Precision
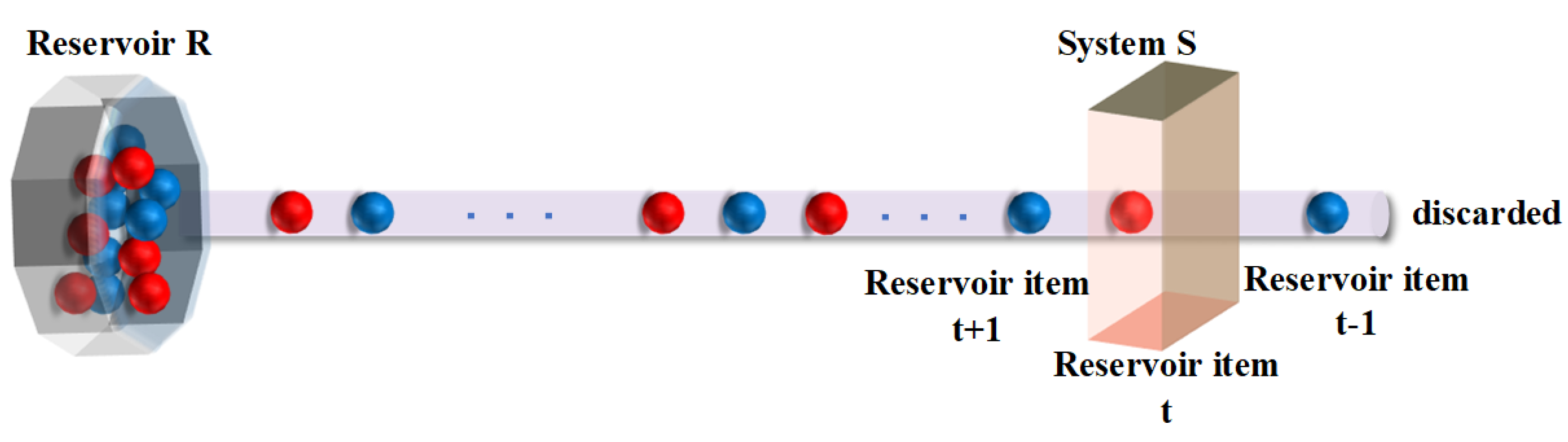
3. Quantification of the Estimation Precision in the Presence of Photonic Loss to the Environment
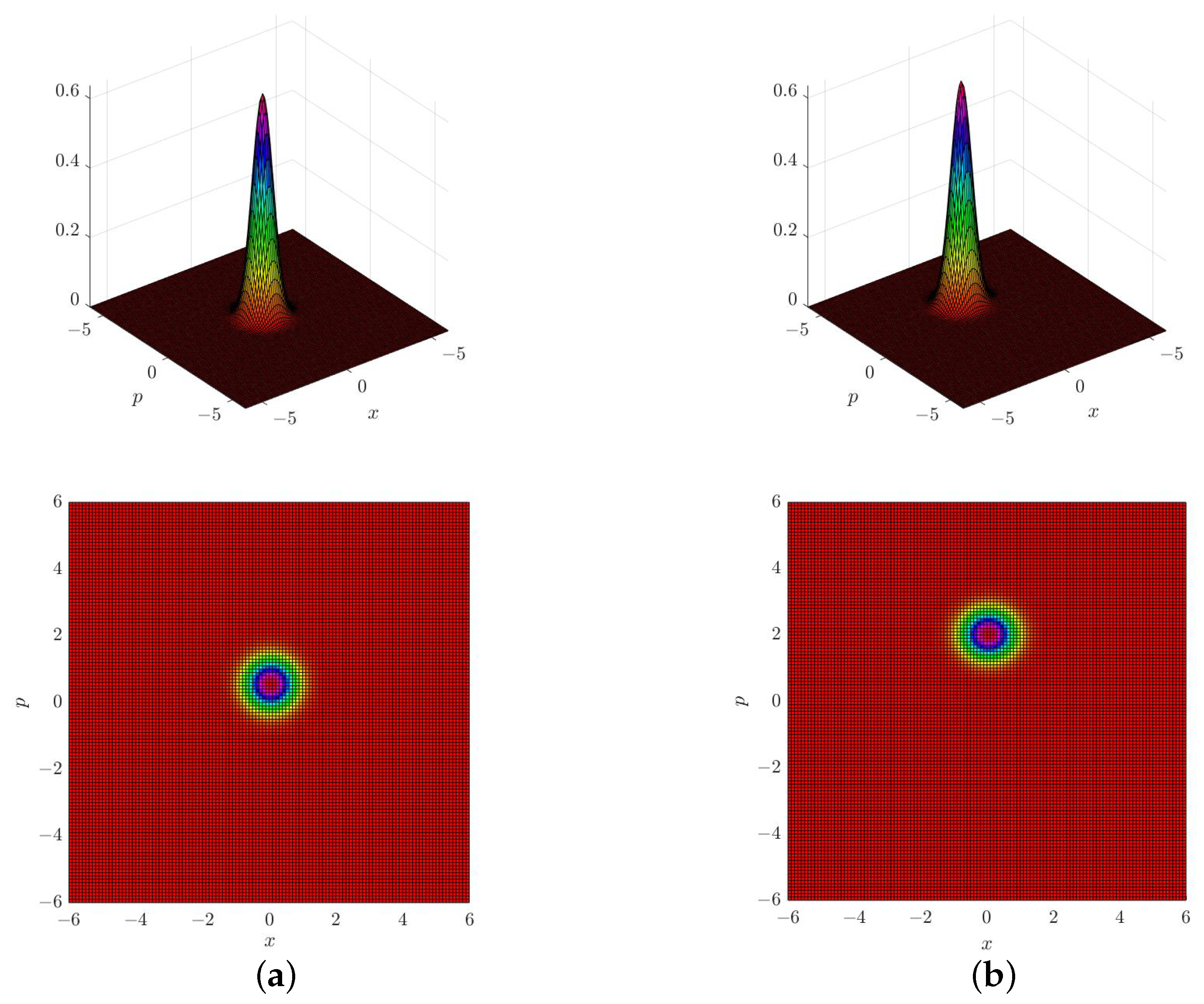
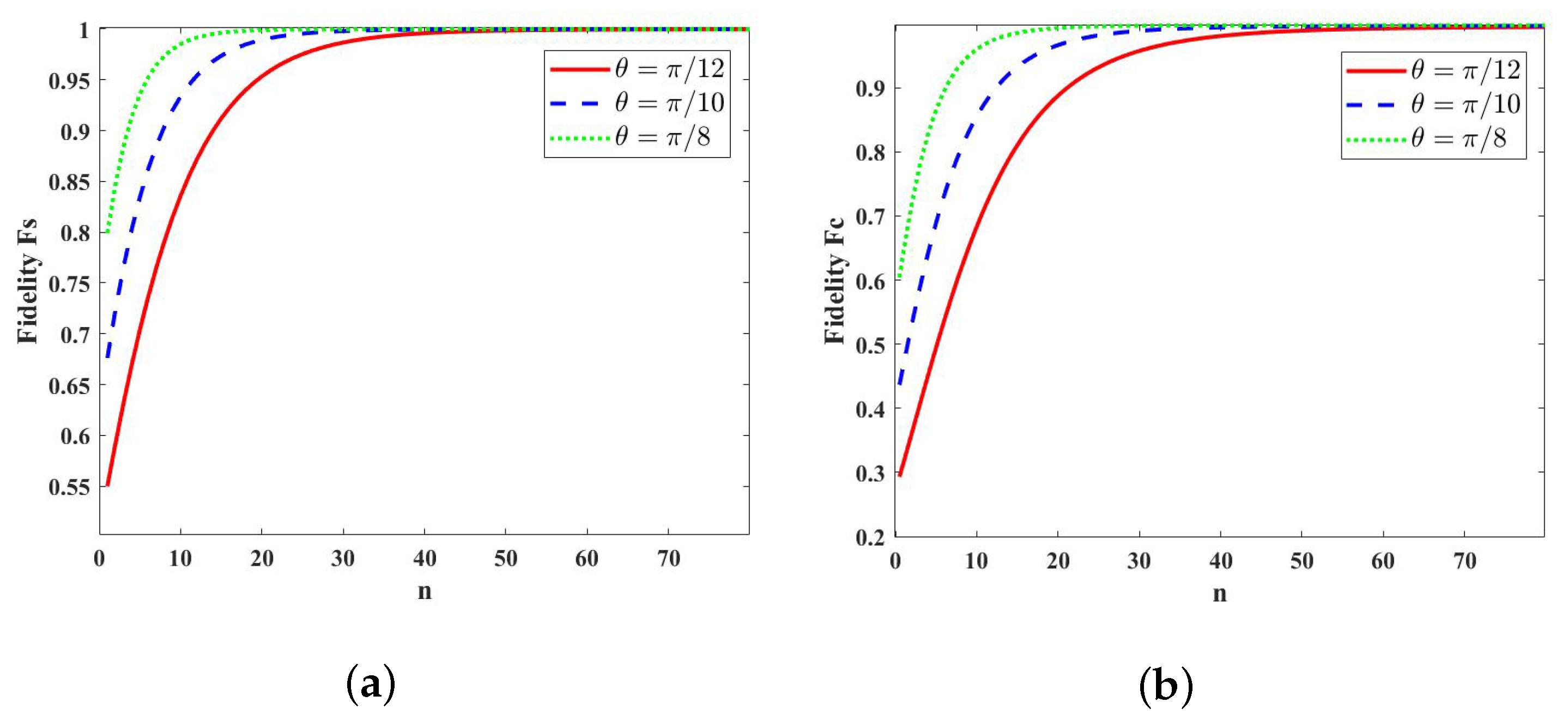
3.1. Convergence towards a Coherent State
3.2. Convergence towards a Squeezed State
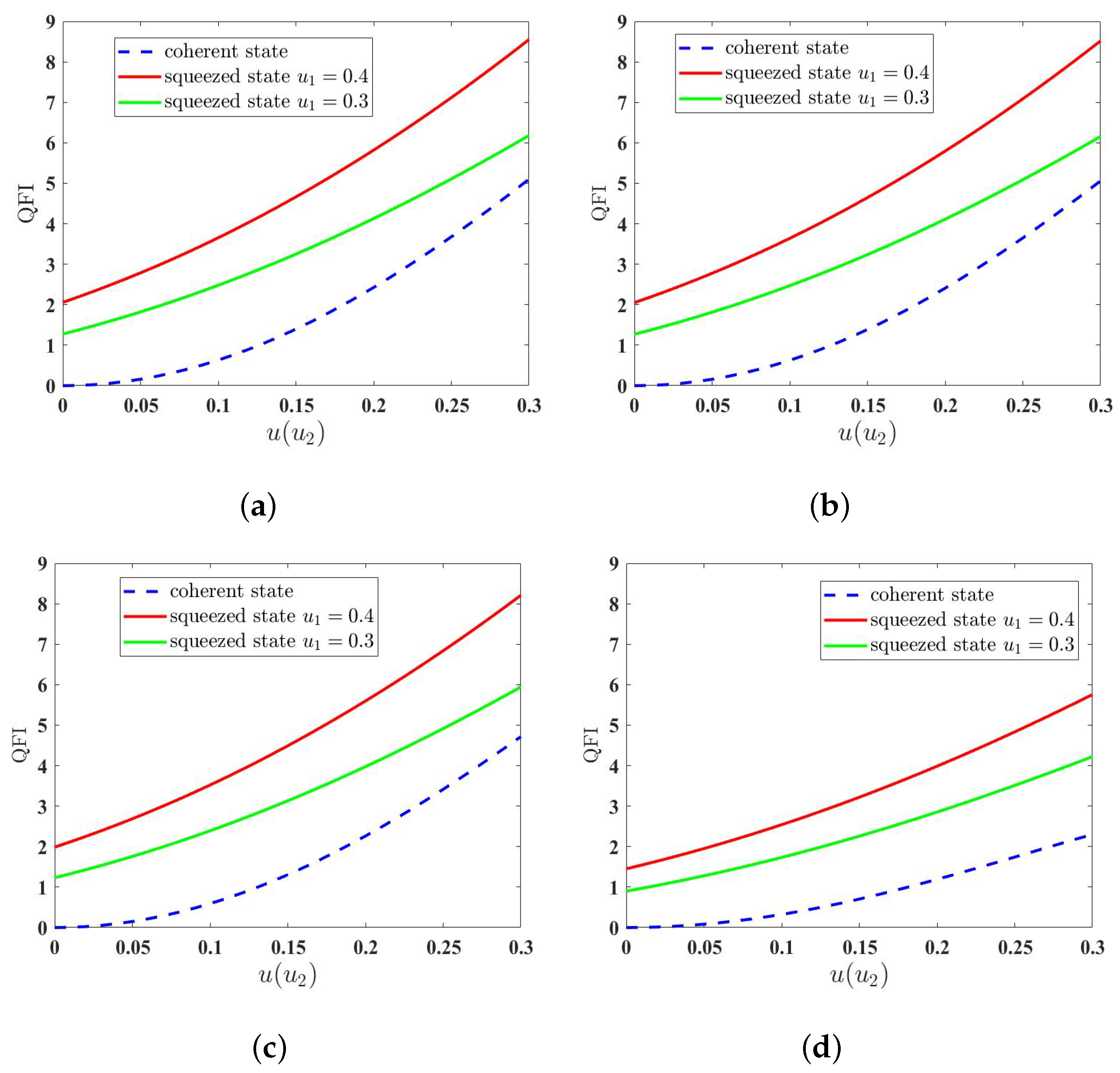
3.3. Analysis of Enhanced Estimation Precision via the Time-Varying Reservoir
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum metrology. Phys. Rev. Lett. 2006, 96, 010401. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lu, X.M.; Sun, Z.; Wang, X. Quantum multiparameter metrology with generalized entangled coherent state. J. Phys. A Math. Theor. 2016, 49, 115302. [Google Scholar] [CrossRef]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum metrology with entangled coherent states. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Sun, C.P.; Nori, F. Quantum spin squeezing. Phys. Rep. 2011, 509, 89–165. [Google Scholar] [CrossRef]
- Tan, Q.S.; Zhang, M.; Chen, Y.; Liao, J.Q.; Liu, J. Generation and storage of spin squeezing via learning-assisted optimal control. Phys. Rev. A 2021, 103, 032601. [Google Scholar] [CrossRef]
- Anisimov, P.M.; Raterman, G.M.; Chiruvelli, A.; Plick, W.N.; Huver, S.D.; Lee, H.; Dowling, J.P. Quantum metrology with two-mode squeezed vacuum: Parity detection beats the Heisenberg limit. Phys. Rev. Lett. 2010, 104, 103602. [Google Scholar] [CrossRef]
- Gazeau, J.P.; Heller, B. Positive-operator valued measure (POVM) quantization. Axioms 2014, 4, 1–29. [Google Scholar] [CrossRef]
- Singal, T.; Maciejewski, F.B.; Oszmaniec, M. Implementation of quantum measurements using classical resources and only a single ancillary qubit. Npj Quantum Inf. 2022, 8, 1–7. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693–1708. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H. Quantum parameter estimation with optimal control. Phys. Rev. A 2017, 96, 012117. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H. Control-enhanced multiparameter quantum estimation. Phys. Rev. A 2017, 96, 042114. [Google Scholar] [CrossRef]
- Xu, H.; Li, J.; Liu, L.; Wang, Y.; Yuan, H.; Wang, X. Generalizable control for quantum parameter estimation through reinforcement learning. Npj Quantum Inf. 2019, 5, 1–8. [Google Scholar] [CrossRef]
- Rams, M.M.; Sierant, P.; Dutta, O.; Horodecki, P.; Zakrzewski, J. At the limits of criticality-based quantum metrology: Apparent super-Heisenberg scaling revisited. Phys. Rev. X 2018, 8, 021022. [Google Scholar] [CrossRef]
- Gietka, K.; Metz, F.; Keller, T.; Li, J. Adiabatic critical quantum metrology cannot reach the Heisenberg limit even when shortcuts to adiabaticity are applied. Quantum 2021, 5, 489. [Google Scholar] [CrossRef]
- Hou, Z.; Jin, Y.; Chen, H.; Tang, J.F.; Huang, C.J.; Yuan, H.; Xiang, G.Y.; Li, C.F.; Guo, G.C. “Super-Heisenberg” and Heisenberg Scalings Achieved Simultaneously in the Estimation of a Rotating Field. Phys. Rev. Lett. 2021, 126, 070503. [Google Scholar] [CrossRef] [PubMed]
- Rouchon, P. Models and feedback stabilization of open quantum systems. arXiv 2014, arXiv:1407.7810. [Google Scholar]
- Sarlette, A.; Raimond, J.M.; Brune, M.; Rouchon, P. Stabilization of Nonclassical States of the Radiation Field in a Cavity by Reservoir Engineering. Phys. Rev. Lett. 2011, 107, 010402. [Google Scholar] [CrossRef]
- Sarlette, A.; Leghtas, Z.; Brune, M.; Raimond, J.M.; Rouchon, P. Stabilization of Nonclassical States of One-and Two-mode Radiation Fields by Reservoir Engineering. Phys. Rev. A 2012, 86, 012114. [Google Scholar] [CrossRef]
- Cheng, W.; Hou, S.; Wang, Z.; Yi, X. Quantum metrology enhanced by coherence-induced driving in a cavity-QED setup. Phys. Rev. A 2019, 100, 053825. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Y.H.; Daughton, W.; Li, H. Particle acceleration and plasma dynamics during magnetic reconnection in the magnetically dominated regime. Astrophys. J. 2015, 806, 167. [Google Scholar] [CrossRef]
- Miao, Z.; Sarlette, A. Discrete-time reservoir engineering with entangled bath and stabilising squeezed states. Quantum Sci. Technol. 2017, 2, 034013. [Google Scholar] [CrossRef]
- Miao, Z.; Chen, Y.; Yuan, H. Is entanglement necessary in the reservoir input? In Proceedings of the 2019 IEEE 58th Conference on Decision and Control, Nice, France, 11–13 December 2019; pp. 407–412. [Google Scholar]
- Jaekel, M.T.; Reynaud, S. Quantum limits in interferometric measurements. Europhys. Lett. 1990, 13, 301. [Google Scholar] [CrossRef]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Gu, J.; Cao, X.Y.; Fu, Y.; He, Z.W.; Yin, Z.J.; Yin, H.L.; Chen, Z.B. Experimental measurement-device-independent type quantum key distribution with flawed and correlated sources. Sci. Bull. 2022, 67, 2167–2175. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.L.; Fu, Y.; Li, C.L.; Weng, C.X.; Li, B.H.; Gu, J.; Lu, Y.S.; Huang, S.; Chen, Z.B. Experimental quantum secure network with digital signatures and encryption. arXiv 2021, arXiv:2107.14089. [Google Scholar] [CrossRef]
- Zhou, M.G.; Cao, X.Y.; Lu, Y.S.; Wang, Y.; Bao, Y.; Jia, Z.Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Experimental quantum advantage with quantum coupon collector. Research 2022, 2022, 9798679. [Google Scholar] [CrossRef] [PubMed]
- Helstrom, C.W. Quantum detection and estimation theory. J. Stat. Phys. 1969, 1, 231–252. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Maccone, L. Using entanglement against noise in quantum metrology. Phys. Rev. Lett. 2014, 113, 250801. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.C.; Yeh, Y.H.; Mendonça, P.E.; Teh, R.Y.; Reid, M.D.; Drummond, P.D. Quantum fidelity measures for mixed states. Rep. Prog. Phys. 2019, 82, 076001. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Guo, W.; Miao, Z. Time-Varying Engineered Reservoir for the Improved Estimation of Atom-Cavity Coupling Strength. Photonics 2023, 10, 157. https://doi.org/10.3390/photonics10020157
Xia Y, Guo W, Miao Z. Time-Varying Engineered Reservoir for the Improved Estimation of Atom-Cavity Coupling Strength. Photonics. 2023; 10(2):157. https://doi.org/10.3390/photonics10020157
Chicago/Turabian StyleXia, Ye, Weiming Guo, and Zibo Miao. 2023. "Time-Varying Engineered Reservoir for the Improved Estimation of Atom-Cavity Coupling Strength" Photonics 10, no. 2: 157. https://doi.org/10.3390/photonics10020157
APA StyleXia, Y., Guo, W., & Miao, Z. (2023). Time-Varying Engineered Reservoir for the Improved Estimation of Atom-Cavity Coupling Strength. Photonics, 10(2), 157. https://doi.org/10.3390/photonics10020157




