Laser Wakefield Photoneutron Generation with Few-Cycle High-Repetition-Rate Laser Systems
Abstract
1. Introduction
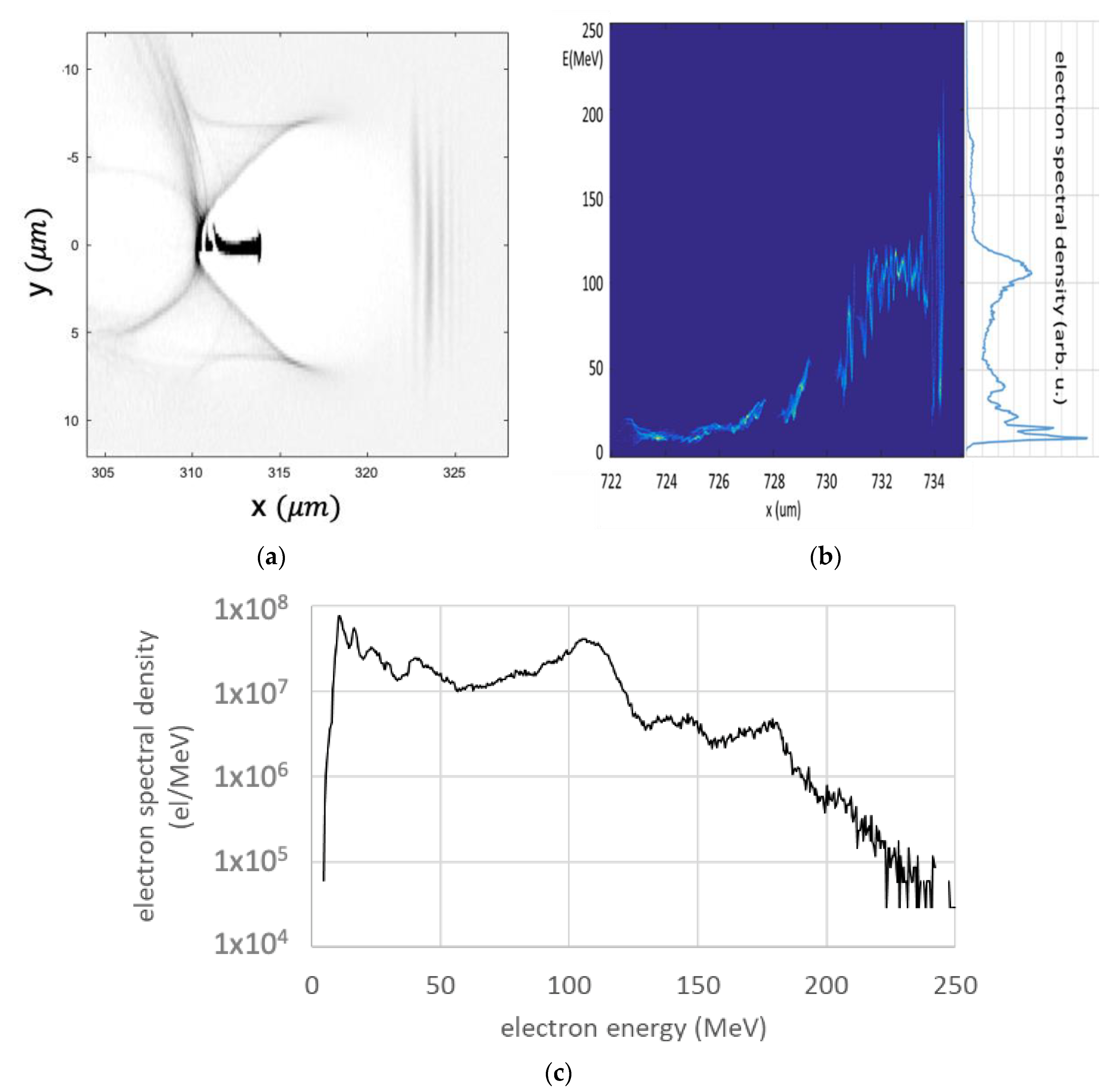
2. Laser Electron Acceleration
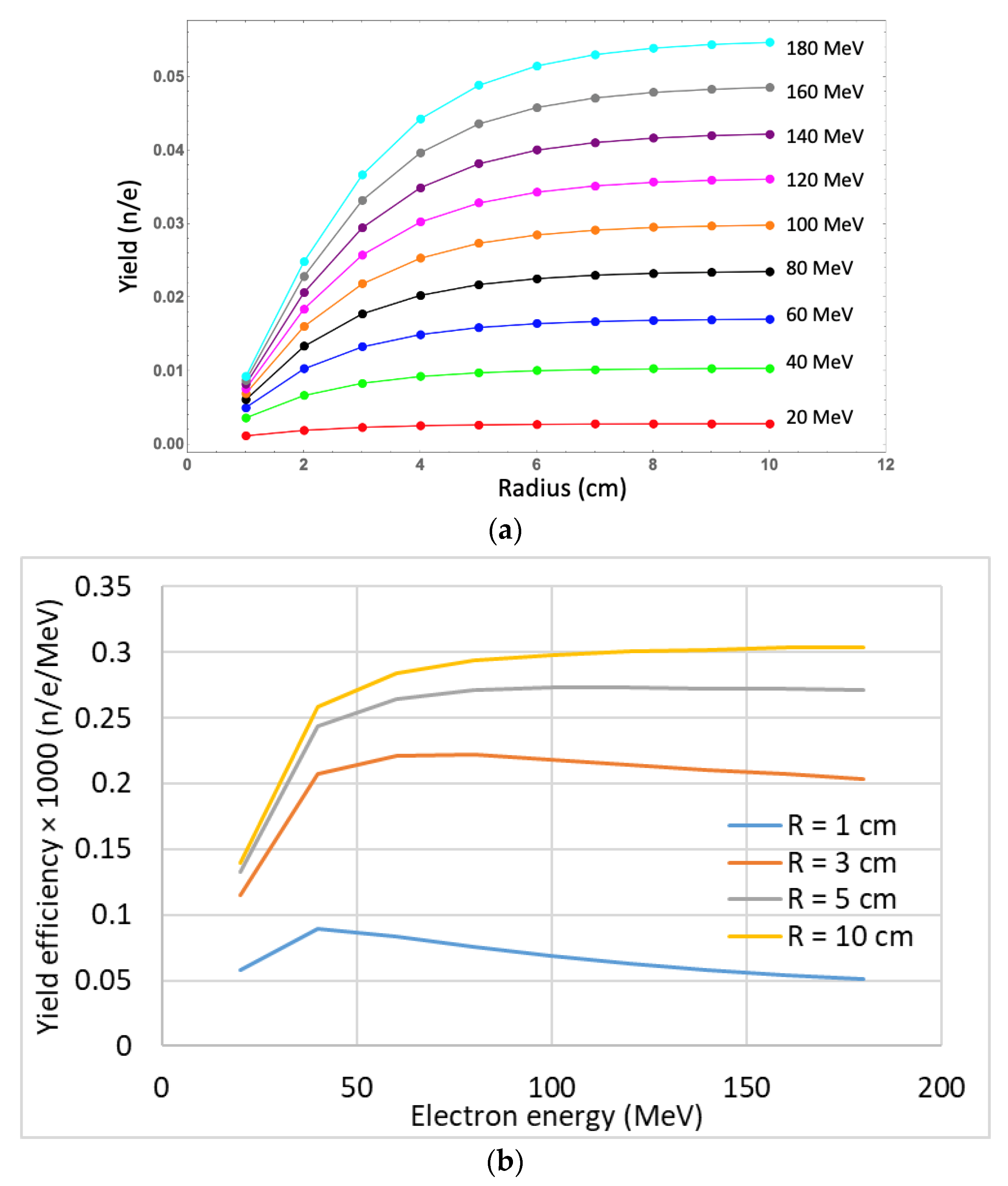
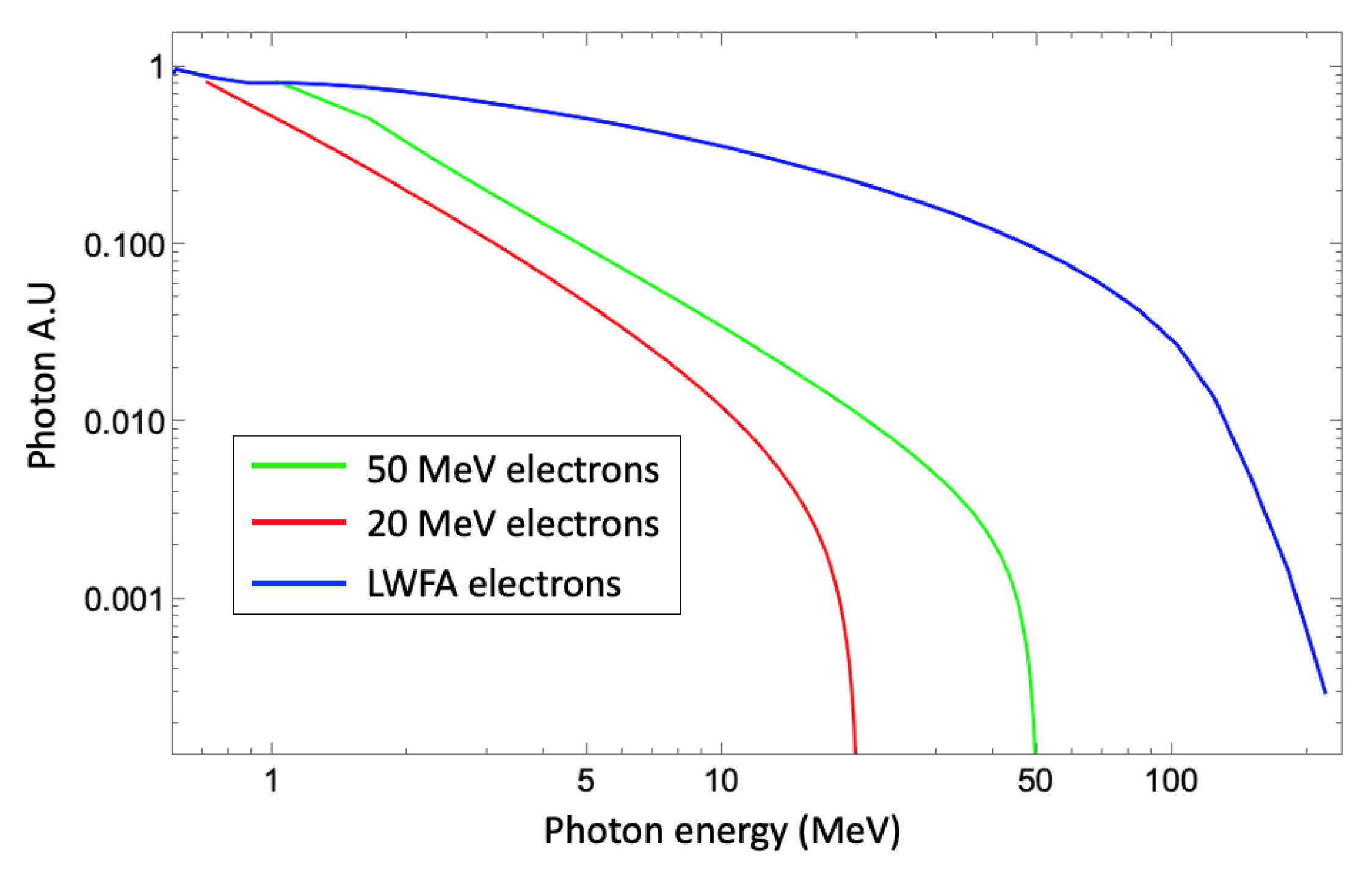
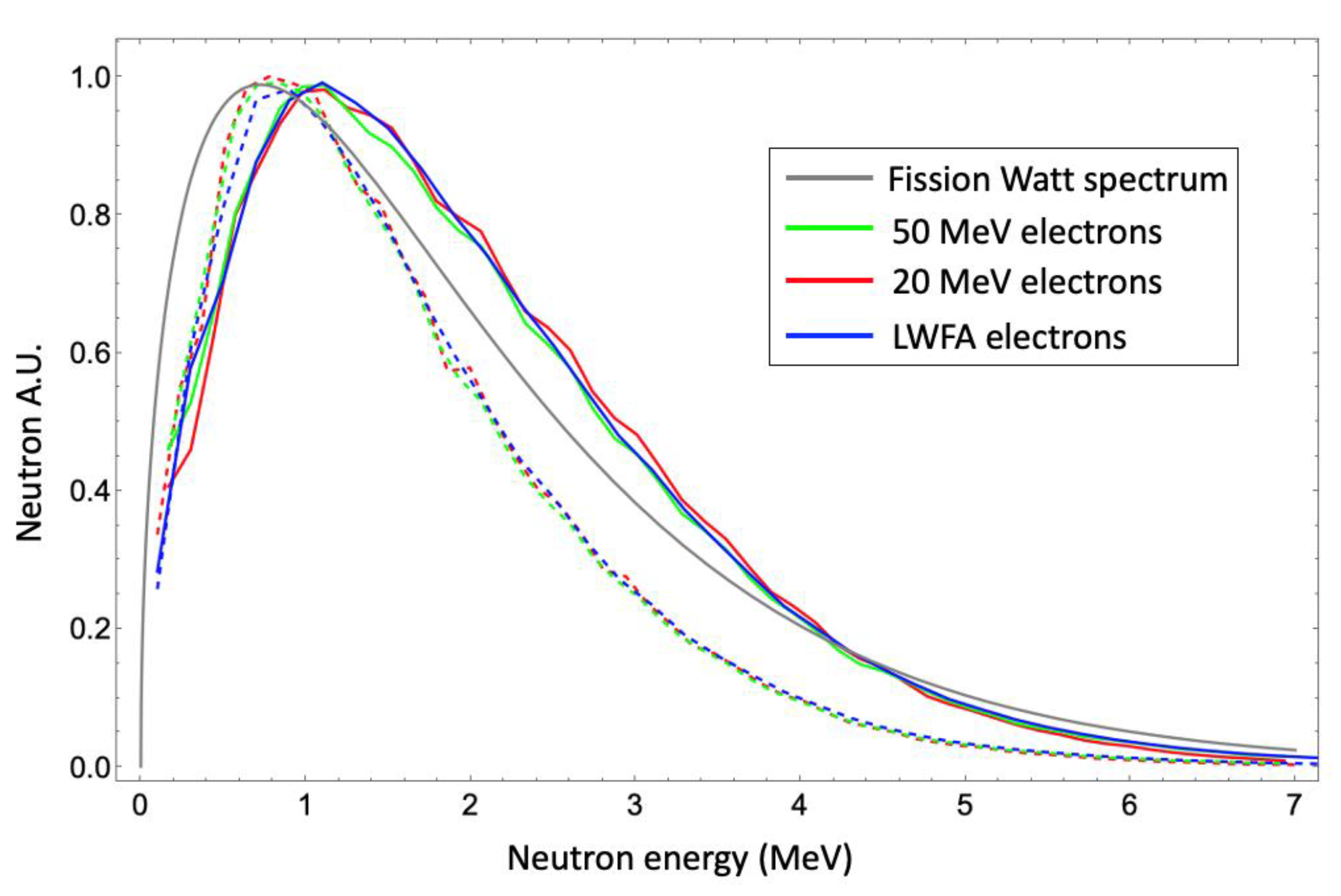
3. Photoneutron Generation
4. Photoneutron Applications
- (a)
- Medical radio-isotope production (Moly-99 to Tc-99 precursor);
- (b)
- Incineration of spent nuclear fuel;
- (c)
- Neutron radiography/imaging.
4.1. Medical Radioisotope Production
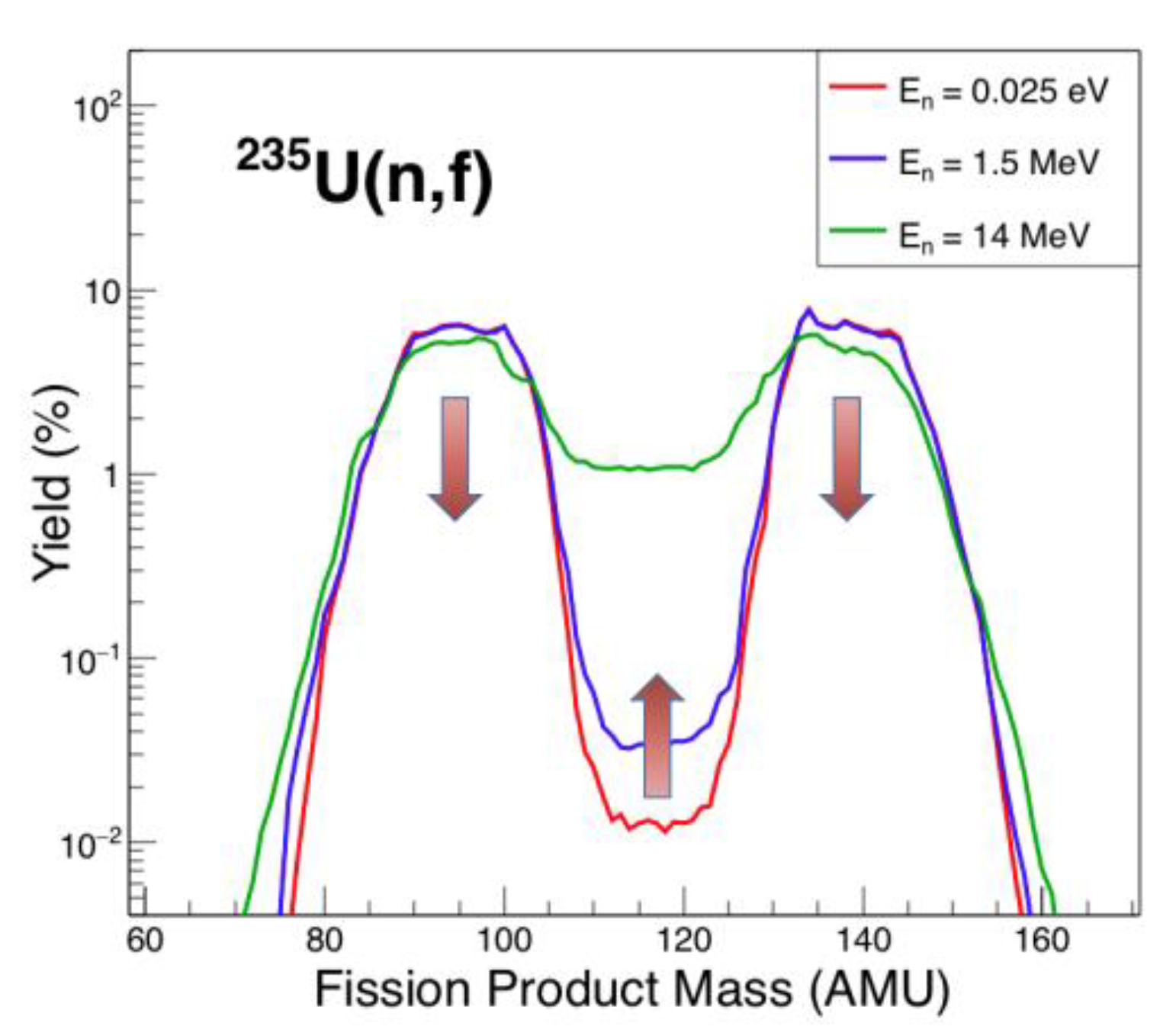
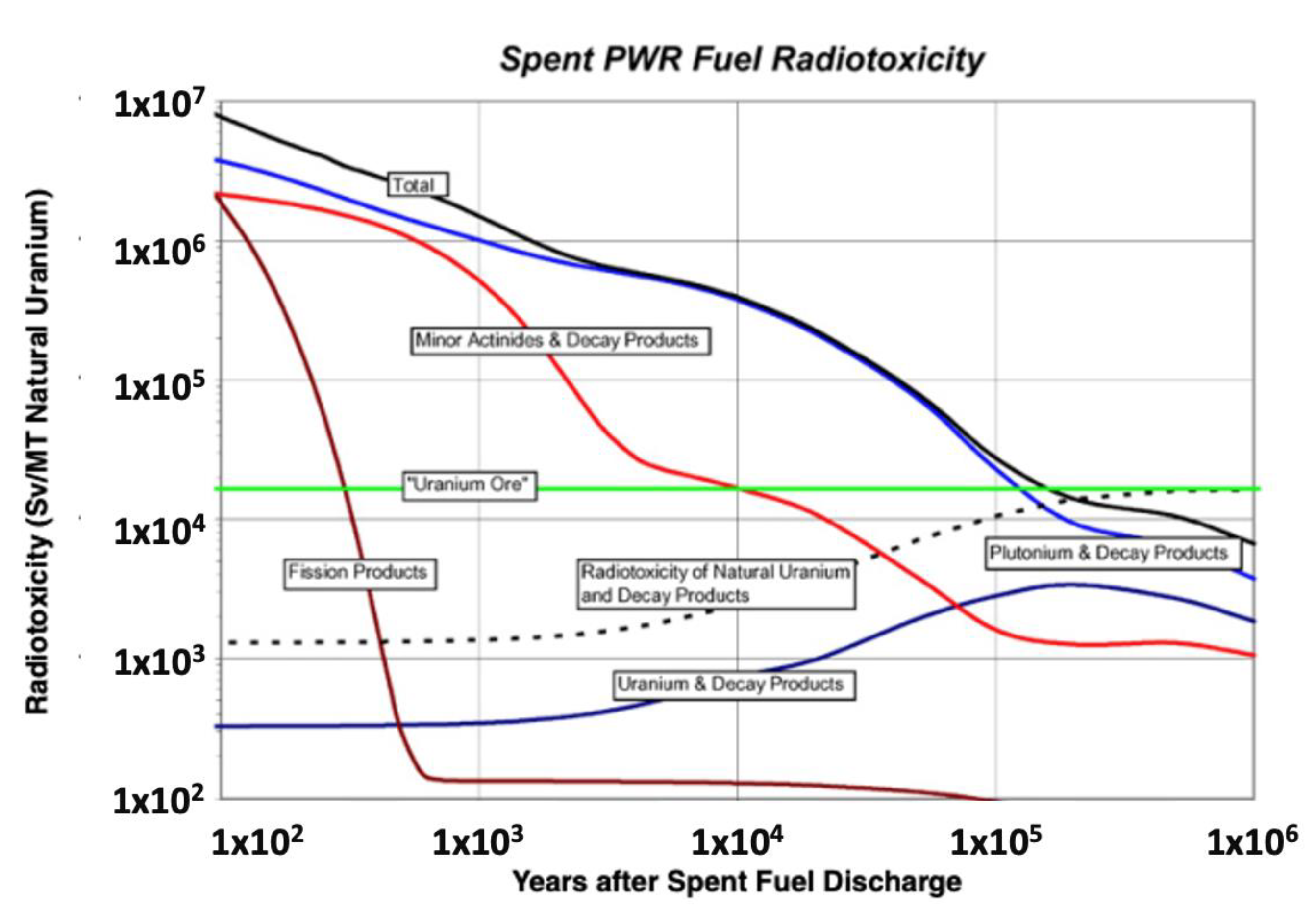
4.2. Transmutation of Spent Nuclear Fuel
- (1)
- Fission products such as iodine, strontium, molybdenum, etc.
- (2)
- Actinides such as plutonium and isotopes of uranium and thorium and minor actinides (americium, curium and neptunium).
4.3. Neutron Radiography/Imaging and Neutron Spectroscopy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Dedication
References
- Rubbia, C.; Rubio, J.; Buono, S.; Carminati, F.; Fiétier, N.; Galvez, J.; Geles, C.; Kadi, Y.; Klapisch, R.; Mandrillon, P.; et al. Conceptual Design of a Fast Neutron Operated High Power Energy Amplifier. In Proceedings of the CERN/AT/95-44, 1995; CERN: Geneva, Switzerland, 1995; pp. 187–312. [Google Scholar]
- Tajima, T.; Necas, A.; Mourou, G.; Gales, S.; Leroy, M. Spent Nuclear Fuel Incineration by Fusion-Driven Liquid Transmutator Operated in Real Time by Laser. Fusion Sci. Technol. 2021, 77, 251–265. [Google Scholar] [CrossRef]
- Woracek, R.; Santisteban, J.; Fedrigo, A.; Strobl, M. Diffraction in Neutron Imaging—A Review. Nucl. Instrum. Methods Phys. Res. A 2018, 878, 141–158. [Google Scholar] [CrossRef]
- Pudjorahardjo, D.S.; Wahyono, P.I.; Syarip. Compact Neutron Generator as External Neutron Source of Subcritical Assembly for Mo-99 Production (SAMOP). AIP Conf. Proceed. 2020, 2296, 20115. [Google Scholar]
- Moss, R.L. Critical Review, with an Optimistic Outlook, on Boron Neutron Capture Therapy (BNCT). Appl. Radiat. Isot. 2014, 88, 2–11. [Google Scholar]
- Frankle, C.M.; Dale, G.E. Unconventional Neutron Sources for Oil Well Logging. Nucl. Instrum. Methods Phys. Res. A 2013, 723, 24–29. [Google Scholar]
- Krambrock, K.; Ribeiro, L.G.M.; Pinheiro, M.V.B.; Leal, A.S.; de BC Menezes, M.Â.; Spaeth, J.-M. Color Centers in Topaz: Comparison between Neutron and Gamma Irradiation. Phys. Chem. Min. 2007, 34, 437–444. [Google Scholar] [CrossRef]
- Gulik, V.; Tkaczyk, A.H. Cost Optimization of ADS Design: Comparative Study of Externally Driven Heterogeneous and Homogeneous Two-Zone Subcritical Reactor Systems. Nucl. Eng. Des. 2014, 270, 133–142. [Google Scholar] [CrossRef]
- Gozani, T.; Morgado, R.E.; Seher, C.C. Nuclear-Based Techniques for Explosive Detection. J. Energetic Mater. 1986, 4, 377–414. [Google Scholar]
- Beyer, R.; Birgersson, E.; Elekes, Z.; Ferrari, A.; Grosse, E.; Hannaske, R.; Junghans, A.R.; Kögler, T.; Massarczyk, R.; Matić, A.; et al. Characterization of the Neutron Beam at NELBE. Nucl. Instrum. Methods Phys. Res. A 2013, 723, 151–162. [Google Scholar]
- Ibrahim, F.; Obert, J.; Bajeat, O.; Buhour, J.M.; Carminati, D.; Clapier, F.; Donzaud, C.; Ducourtieux, M.; Dufour, J.M.; Essabaa, S.; et al. Photofission for the Production of Radioactive Beams: Experimental Data from an on-Line Measurement. Eur. Phys. J. A-Hadron. Nucl. 2002, 15, 357–360. [Google Scholar] [CrossRef]
- Essabaa, S.; Arianer, J.; Ausset, P.; Bajeat, O.; Baronick, J.P.; Clapier, F.; Coacolo, L.; Donzaud, C.; Ducourtieux, M.; Galès, S.; et al. Photo-Fission for the Production of Radioactive Beams ALTO Project. Nucl. Instrum. Methods Phys. Res. B 2003, 204, 780–784. [Google Scholar] [CrossRef]
- Bezditko, A.P.; Gordienko, A.N.; Gladkikh, P.I.; Gvozd, A.M.; Kapliy, D.A.; Karnaukhov, I.M.; Karnaukhov, I.I.; Lyashchenko, V.N.; Mytsykov, A.O.; Moisieienko, M.P.; et al. 100 MeV/100 KW Accelerator Adjustment for the NSC KIPT Neutron Source Physical Start Up. Probl. At. Sci. Technol. 2020, 129, 135–142. [Google Scholar]
- Bezditko, O.; Karnaukhov, I.; Mytsykov, A.; Zelinsky, A.; Tarasov, D. Status of the NSC KIPT Neutron Source. Energy 2017, 2, 1013. [Google Scholar]
- Zelinsky, A.Y.; Bezditko, O.; Demchenko, P.O.; Karnaukhov, I.; Oleinik, V.; Peev, F.; Ushakov, I.; Vodin, O.; Gohar, Y. NSC KIPT Neutron Source on the Base of Subcritical Assembly Driven with Electron Linear Accelerator. In Proceedings of the IPAC 2013, Shanghai, China, 13–17 May 2013. [Google Scholar]
- Flaska, M.; Borella, A.; Lathouwers, D.; Mihailescu, L.C.; Mondelaers, W.; Plompen, A.J.M.; van Dam, H.; van der Hagen, T.H.J.J. Modeling of the GELINA Neutron Target Using Coupled Electron–Photon–Neutron Transport with the MCNP4C3 Code. Nucl. Instrum. Methods Phys. Res. A 2004, 531, 392–406. [Google Scholar] [CrossRef]
- Coceva, C.; Simonini, R.; Olsen, D.K. Calculation of the ORELA Neutron Moderator Spectrum and Resolution Function. Nucl. Instrum. Methods Phys. Res. 1983, 211, 459–467. [Google Scholar] [CrossRef]
- Colonna, N.; Gunsing, F.; Käppeler, F. Neutron Physics with Accelerators. Prog. Part Nucl. Phys. 2018, 101, 177–203. [Google Scholar] [CrossRef]
- Pomerantz, I.; Mccary, E.; Meadows, A.R.; Arefiev, A.; Bernstein, A.C.; Chester, C.; Cortez, J.; Donovan, M.E.; Dyer, G.; Gaul, E.W.; et al. Ultrashort Pulsed Neutron Source. Phys. Rev. Lett. 2014, 113, 184801. [Google Scholar] [CrossRef] [PubMed]
- Kleinschmidt, A.; Aumüller, S.; Bagnoud, V.; Jahn, D.; Schanz, V.A.; Zimmer, M.; Roth, M. Moderation of a Laser-Generated Neutron Beam at PHELIX. Helmholtz Inst. Jena Annu. Rep. 2018, 2017, 37. [Google Scholar]
- Günther, M.M.; Rosmej, O.N.; Tavana, P.; Gyrdymov, M.; Skobliakov, A.; Kantsyrev, A.; Zähter, S.; Borisenko, N.G.; Pukhov, A.; Andreev, N.E. Forward-Looking Insights in Laser-Generated Ultra-Intense γ-Ray and Neutron Sources for Nuclear Application and Science. Nat. Commun. 2022, 13, 170. [Google Scholar] [CrossRef]
- Prencipe, I.; Sgattoni, A.; Dellasega, D.; Fedeli, L.; Cialfi, L.; Choi, I.W.; Kim, I.J.; Janulewicz, K.A.; Kakolee, K.F.; Lee, H.W.; et al. Development of Foam-Based Layered Targets for Laser-Driven Ion Beam Production. Plasma Phys. Control Fusion 2016, 58, 34019. [Google Scholar]
- Tajima, T.; Dawson, J.M. Laser Electron Accelerator. Phys. Rev. Lett. 1979, 43, 267. [Google Scholar] [CrossRef]
- Guénot, D.; Gustas, D.; Vernier, A.; Beaurepaire, B.; Böhle, F.; Bocoum, M.; Lozano, M.; Jullien, A.; Lopez-Martens, R.; Lifschitz, A.; et al. Relativistic Electron Beams Driven by KHz Single-Cycle Light Pulses. Nat. Photonics 2017, 11, 293–296. [Google Scholar] [CrossRef]
- Gustas, D.; Guénot, D.; Vernier, A.; Dutt, S.; Böhle, F.; Lopez-Martens, R.; Lifschitz, A.; Faure, J. High-Charge Relativistic Electron Bunches from a KHz Laser-Plasma Accelerator. Phys. Rev. Accel. Beams 2018, 21, 13401. [Google Scholar] [CrossRef]
- Jiao, X.J.; Shaw, J.M.; Wang, T.; Wang, X.M.; Tsai, H.; Poth, P.; Pomerantz, I.; Labun, L.A.; Toncian, T.; Downer, M.C.; et al. A Tabletop, Ultrashort Pulse Photoneutron Source Driven by Electrons from Laser Wakefield Acceleration. Matter. Radiat. Extrem. 2017, 2, 296–302. [Google Scholar] [CrossRef]
- Papp, D.; Lécz, Z.; Kamperidis, C.; Hafz, N.A.M. Highly Efficient Few-Cycle Laser Wakefield Electron Accelerator. Plasma Phys. Control Fusion 2021, 63, 65019. [Google Scholar]
- Toth, S.; Stanislauskas, T.; Balciunas, I.; Budriunas, R.; Adamonis, J.; Danilevicius, R.; Viskontas, K.; Lengvinas, D.; Veitas, G.; Gadonas, D.; et al. SYLOS Lasers–the Frontier of Few-Cycle, Multi-TW, KHz Lasers for Ultrafast Applications at Extreme Light Infrastructure Attosecond Light Pulse Source. J. Phys. Photonics 2020, 2, 45003. [Google Scholar]
- Arber, T.D.; Bennett, K.; Brady, C.S.; Lawrence-Douglas, A.; Ramsay, M.G.; Sircombe, N.J.; Gillies, P.; Evans, R.G.; Schmitz, H.; Bell, A.R.; et al. Contemporary Particle-in-Cell Approach to Laser-Plasma Modelling. Plasma Phys. Control Fusion 2015, 57, 113001. [Google Scholar] [CrossRef]
- Briesmeister, J.F. (Ed.) MCNPTM—A General Monte Carlo N-Particle Transport Code; Code Version 4C, also Univ. of California Tech. Report UC-700; Los Alamos National Laboratory: Los Alamos, NM, USA, 2000. [Google Scholar]
- Pukhov, A.; Meyer-ter-Vehn, J. Laser Wake Field Acceleration: The Highly Non-Linear Broken-Wave Regime. Appl. Phys. B 2002, 74, 355–361. [Google Scholar] [CrossRef]
- Pukhov, A.; Gordienko, S.; Kiselev, S.; Kostyukov, I. The Bubble Regime of Laser–Plasma Acceleration: Monoenergetic Electrons and the Scalability. Plasma Phys Control Fusion 2004, 46, B179. [Google Scholar] [CrossRef]
- Lu, W.; Tzoufras, M.; Joshi, C.; Tsung, F.S.; Mori, W.B.; Vieira, J.; Fonseca, R.A.; Silva, L.O. Generating Multi-GeV Electron Bunches Using Single Stage Laser Wakefield Acceleration in a 3D Nonlinear Regime. Phys. Rev. Spec. Top.-Accel. Beams 2007, 10, 61301. [Google Scholar] [CrossRef]
- Sprangle, P.; Ting, A.; Tang, C.M. Radiation Focusing and Guiding with Application to the Free Electron Laser. Phys. Rev. Lett. 1987, 59, 202. [Google Scholar] [CrossRef] [PubMed]
- Götzfried, J.; Döpp, A.; Gilljohann, M.F.; Foerster, F.M.; Ding, H.; Schindler, S.; Schilling, G.; Buck, A.; Veisz, L.; Karsch, S. Physics of High-Charge Electron Beams in Laser-Plasma Wakefields. Phys. Rev. X 2020, 10, 41015. [Google Scholar] [CrossRef]
- Meyers, R.A. Encyclopedia of Physical Science and Technology; Academic Press: Cambridge, MA, USA, 2002; Available online: http://113.161.190.196:8080/thuvienso/handle/123456789/668 (accessed on 11 February 2022).
- Qi, W.; Zhang, X.; Zhang, B.; He, S.; Zhang, F.; Cui, B.; Yu, M.; Dai, Z.; Peng, X.; Gu, Y. Enhanced Photoneutron Production by Intense Picoseconds Laser Interacting with Gas-Solid Hybrid Targets. Phys. Plasmas 2019, 26, 43103. [Google Scholar]
- Chao, Y.; Cao, L.; Zheng, C.; Liu, Z.; He, X. Enhanced Proton Acceleration from Laser Interaction with a Tailored Nanowire Target. Appl. Sci. 2022, 12, 1153. [Google Scholar] [CrossRef]
- Pretzler, G.; Saemann, A.; Pukhov, A.; Rudolph, D.; Schätz, T.; Schramm, U.; Thirolf, P.; Habs, D.; Eidmann, K.; Tsakiris, G.D.; et al. Neutron Production by 200 MJ Ultrashort Laser Pulses. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1998, 58, 1165. [Google Scholar] [CrossRef]
- Salvatores, M.; Palmiotti, G. Radioactive Waste Partitioning and Transmutation within Advanced Fuel Cycles: Achievements and Challenges. Prog. Part. Nucl. Phys. 2011, 66, 144–166. [Google Scholar] [CrossRef]
- Kishon, I.; Kleinschmidt, A.; Schanz, V.A.; Tebartz, A.; Noam, O.; Fernandez, J.C.; Gautier, D.C.; Johnson, R.P.; Shimada, T.; Wurden, G.A.; et al. Laser Based Neutron Spectroscopy. Nucl. Instrum. Methods Phys. Res. A 2019, 932, 27–30. [Google Scholar]
- Zimmer, M.; Scheuren, S.; Kleinschmidt, A.; Mitura, N.; Tebartz, A.; Schaumann, G.; Abel, T.; Ebert, T.; Hesse, M.; Zähter, Ş.; et al. Demonstration of Non-Destructive and Isotope-Sensitive Material Analysis Using a Short-Pulsed Laser-Driven Epi-Thermal Neutron Source. Nat. Commun. 2022, 13, 1173. [Google Scholar]
- Shalloo, R.; Najmudin, Z.; Hafz, N.; Li, S.; Papp, D.; Kamperidis, C. E-SYLOS: A KHz Laser Wakefield Driven Beamline for Radiobiological and Imaging Applications at ELI-ALPS. Available online: https://agenda.infn.it/event/17304/contributions/99022/ (accessed on 10 May 2022).
- IBA. Available online: https://www.iba-industrial.com/accelerators (accessed on 10 January 2022).


| Energy (MeV) | ||||||
|---|---|---|---|---|---|---|
| 0.5 cm | 5 cm | |||||
| 20 | 2.6 | 2.0 | 1.7 | 6.3 | 5 | 0.003 |
| 50 | 4.9 | 2.0 | 1.7 | 16 | 15 | 0.01 |
| LWFA (<> = 71 MeV) | 11.3 | 2.0 | 1.7 | 23 | 23 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papp, D.; Necas, A.; Hafz, N.; Tajima, T.; Gales, S.; Mourou, G.; Szabo, G.; Kamperidis, C. Laser Wakefield Photoneutron Generation with Few-Cycle High-Repetition-Rate Laser Systems. Photonics 2022, 9, 826. https://doi.org/10.3390/photonics9110826
Papp D, Necas A, Hafz N, Tajima T, Gales S, Mourou G, Szabo G, Kamperidis C. Laser Wakefield Photoneutron Generation with Few-Cycle High-Repetition-Rate Laser Systems. Photonics. 2022; 9(11):826. https://doi.org/10.3390/photonics9110826
Chicago/Turabian StylePapp, Daniel, Ales Necas, Nasr Hafz, Toshiki Tajima, Sydney Gales, Gerard Mourou, Gabor Szabo, and Christos Kamperidis. 2022. "Laser Wakefield Photoneutron Generation with Few-Cycle High-Repetition-Rate Laser Systems" Photonics 9, no. 11: 826. https://doi.org/10.3390/photonics9110826
APA StylePapp, D., Necas, A., Hafz, N., Tajima, T., Gales, S., Mourou, G., Szabo, G., & Kamperidis, C. (2022). Laser Wakefield Photoneutron Generation with Few-Cycle High-Repetition-Rate Laser Systems. Photonics, 9(11), 826. https://doi.org/10.3390/photonics9110826





