Abstract
Recent progress of high-peak-power lasers makes researchers envisage ultra-high-field science; however, the current or near future facilities will not be strong enough to reach the vacuum breakdown intensity, i.e., the Schwinger field. To address this difficulty, a relativistic flying mirror (RFM) technology is proposed to boost the focused intensity by double the Doppler effect of an incoming laser pulse. We review the principle, theoretical, and experimental progress of the RFM, as well as its prospects.
1. Introduction
Recent progress of high-peak-power lasers such as chirped pulse amplification [1] opens a new multidisciplinary field in ultra-high-field science (UHFS), in which the plasma, laser, beam, and quantum electrodynamics are employed. One of the scientific goals of UHFS is to observe vacuum breakdown under the conditions of terrestrial laboratories by electromagnetic waves such as lasers [2,3]. Currently, multi-petawatt laser facilities are being operated, and the record focused intensity is 1.1 W/cm2 [4], of which the electric (magnetic) field is 9.1 V/m (3.0 T). The forthcoming 10 PW laser facilities may reach higher intensity, or the planned 100 PW laser facility might boost 10–100-fold focused intensity. However, this electric field is still far below the Schwinger field, which is known as the quantum electrodynamics (QED) critical field = 1.3 V/m, where m, e, c, and ℏ are the electron mass, the elementary charge, the speed of light, and the reduced Planck constant, respectively.
Several approaches have been proposed to overcome this difficulty, such as the collision of an intense laser pulse with a high-energy electron beam [5,6], a multiple laser beam focusing [7], a superposition of high- and low-frequency electromagnetic waves [8], and so on. With the help of the Lorentz boost for high-energy electron beams, the field seen by the electron in the rest frame is enhanced by twice the Lorentz factor , where E is the electron energy. The multi-beam focus effectively increases the interaction volume, thus increasing the probability of electron–positron pairs under a fixed laser energy condition. The high-frequency radiation can be used as a catastrophe singularity to be formed. As another technique, a relativistic flying mirror, was proposed for the pulse intensification due to the double-Doppler effect of reflected laser pulses from a moving focusing mirror [9]. Such mirrors are formed as electron density cusps in intense laser interaction with underdense plasma.
This review paper discusses the relativistic flying mirror model, experimental verifications, related topics, applications to UHFS, and the prospects.
2. Theoretical Model
Here, we review a simple theoretical model for relativistic flying mirrors (RFMs) [9,10,11]. As shown later, a wake wave is excited in tenuous plasma when an intense, ultrashort laser pulse propagates in the plasma by pushing plasma electrons outwards from the center of the laser due to a strong ponderomotive force. First, we start with an ideal moving mirror whose velocity is close to the speed of light in vacuum.
2.1. Ideal Moving Mirror
Let us derive the relationship between the reflection angle and the reflected light frequency [12]. The mirror propagates along the positive direction with the velocity of , where c is the speed of light in vacuum. Light with a frequency is incident on the mirror at an angle of , as seen in Figure 1.
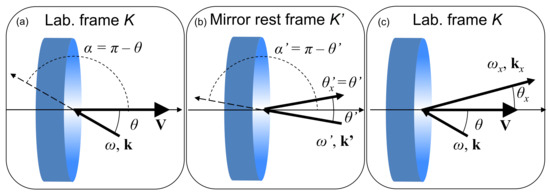
Figure 1.
The light reflection by a flying mirror propagating perpendicular to its surface, an oblique incidence case. (a,c) are shown in the laboratory frame of reference, and (b) is in the mirror rest frame. From [13].
Then, consider in the mirror rest frame by performing a Lorentz transformation , where primes (′) denote the variables in the rest frame and is the relativistic factor of the mirror. The light phase is Lorentz invariant. We obtain
and equations
In the mirror rest frame, the angle of reflection is the same as that of incidence, and the frequency does not change; thus, we obtain and . Finally, we return to the laboratory frame of reference by the inverse Lorentz transformation and obtain
and
The approximation at the end of Equation (5) is the case when the velocity of the mirror is ultra-relativistic (). The pulse duration of the reflected pulse is shortened by the same factor as the frequency upshift because the number of light cycles is Lorentz invariant.
2.2. Practical Moving (Flying) Mirror Implementation
As we saw in the previous subsection, a relativistically moving mirror has several interesting features in a thought experiment. Several methods are proposed to realize such moving mirrors, as in [13]. Here, we review a case of relativistic flying mirrors formed by the breaking plasma waves in the interaction of an intense laser pulse with underdense, gaseous plasma [9] (see Figure 2). Plasma waves are excited by the ponderomotive force of the intense laser pulse (driver), called wake waves. Such plasma waves tend to break when the laser intensity is high enough that a plasma density profile is not uniform due to phase mixing. Another laser pulse (source) is incident to the breaking wave (relativistic flying mirror) and is partially reflected by the mirror.
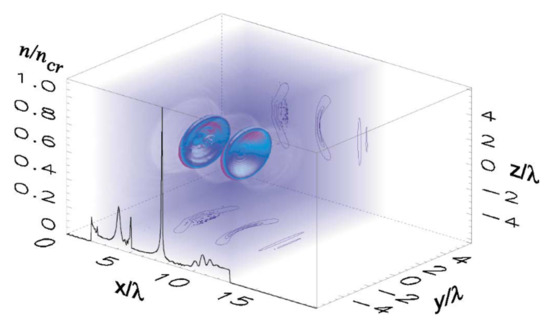
Figure 2.
Relativistic flying mirrors formed in underdense plasma. From [9].
Several reflectivities of RFMs are given in [10] depending on the kind of the formed singularity. Here, we show the reflectivities for the cases of the Dirac Delta function and Cusp structure, respectively:
where is the electron plasma frequency, is the electron plasma density, is the permittivity of free space, is the incidence angle of the source pulse (Figure 1), is the Lorentz factor associated with the group velocity of the driver in plasma, is the angular frequency of the source pulse, and is the Euler gamma function [14]. Here, the reflectivities and are in terms of the photon number; therefore, they are Lorentz invariants. Recently, Liu et al. calculated the reflectivity formula for a square-root Lorentzian distribution [15]:
where , and , is the normalized driver laser amplitude, is the angular frequency of the driver, is the plasma wavelength, and L is a characteristic length. The reflectivity for the SRLD case is
where is the modified Bessel function of the second kind. Liu et al. also presented the modified reflectivity formula for a Gaussian temporal source beam. One-dimensional PIC simulations reproduce these new formulas well.
2.3. Limitations of Relativistic Flying Mirrors
The temperature of the plasma is essential for how densely the plasma electrons form. The higher temperature typically results in lower cusp density. Nonetheless, the reflectivity is reduced, but the above-breaking limit regime can increase the reflectivity because the higher-order singularities are formed in such a case [16].
The reflected source pulse gains energy from the electron singularity, and its energy comes from the driver laser energy. Thus, the reflected source energy has a certain limit determined by the driver laser energy.
The other limitation comes from the mirror’s recoil effect during the reflection of the source laser pulse. The recoil effect degrades the upshifting factor and, thus, the performance of the RFM. Considering energy and momentum conservation, the modified formula for the upshift factor is given in [14,17].
In addition, to minimize the recoil effect, Valenta et al. proposed a characteristic time using a one-dimensional PIC simulation [14]:
where is a parameter that may be obtained from the simulation and is the source pulse irradiance. The source pulse duration should be smaller than . An example estimate for of 1.5 , an electron density of 0.01, and a normalized source laser intensity of gives a duration of 9 fs.
The modified frequency upshift factor for taking this recoil effect is described as [14,17]
where is the number of electrons in the cusp, R is the reflectivity of the RFM, is the power of the incident source pulse, and is the source pulse duration. The last expression is obtained by approximating the second term in the bracket in the last expression smaller than unity, which is typical for the RFM. Thus, we can recover Equation (5) in the limit using .
3. Experimental Demonstration
This section introduces experimental demonstrations of the relativistic flying mirror concepts and related ones. The broader experiments, including the reflection of electromagnetic radiation from moving objects, were listed in the previous review [13].
3.1. Relativistic Flying Mirrors
The relativistic flying mirror experiment was conducted with the setup [18,19] as shown in Figure 3a. The target was a gas-jet target, and the wakes were excited by irradiating a 2-TW, 76-fs Ti: sapphire laser pulse (referred to as “Driver”) onto it. The onset of the wake breaking or flying mirrors formed was the generation of energetic electrons up to 30 MeV. Another laser pulse split from the driver pulse was focused onto the gas-jet to collide with the driver pulse in plasma with a counter-crossing angle of 135° with respect to the driver propagation axis. The reason for not using the 180° colliding angle was to avoid possible damage to the laser system by the returning pulse. After the spatial and temporal overlapping high-frequency radiation was observed in the forward direction of the driver pulse. With careful statistical analysis, they concluded that the observed signals were around 13 nm.
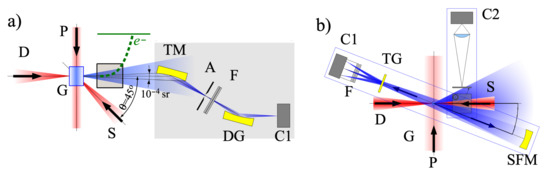
Figure 3.
Experimental setups for the RFM. (a) A counter-crossing setup where the source beam is directed to the driver at 135°. (b) A head-on colliding setup. D: driver pulse, S: source pulse, P: probe laser, G: gas-jet target, TM: toroidal mirror, DG: diffraction grating, A: aperture slit, F: filters, SFM: spherical focusing mirror, TG: transmission grating, C1: X-ray charge-coupled device (CCD), C2: image intensified camera, e: electron beam.
The same group conducted the second experiment. The setup was similar to the first experiment, except for the head-on colliding configuration thanks to the countermeasures for the returning pulse problem [20,21] (see Figure 3b). In this experiment, reflected light into (13 was detected with an imaging spectrometer, and the photon number was half the theoretical estimate (see Figure 4). Furthermore, the timing scan shows that the reflection from the flying mirrors occurred at some proper timing range.
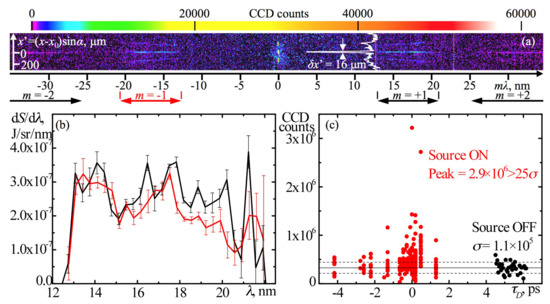
Figure 4.
Reflected signals from [20]. (a) Raw CCD image of the reflected light after the transmission grating in the spectrometer. (b) Reflected light spectra with the diffraction orders of +1 and −1. (c) The reflected light intensity (CCD counts within the 1st diffraction order) vs. time delay between the driver and source pulses with the source-off shots (time is assigned arbitrarily).
3.2. Burst Intensification of Stimulated Emission of Radiation
RFMs utilize the electron density cusps as a moving mirror. We can see other singularities in the nonlinear interaction in Figure 5. Experimentally, the intense XUV light was observed in an experiment similar to that of the flying mirror without a source laser pulse. The emission contained harmonics of the fundamental driver laser wavelength with even and odd numbers in the forward direction [22,23,24]. The emission was considered a result of collective synchrotron radiation in density singularities. This is called burst intensification by singularity emitting radiation (BISER) [25]. The duration of the XUV harmonics is calculated to be sub-fs. This regime of coherent X-ray radiation is very sensitive to the driving laser quality [26].
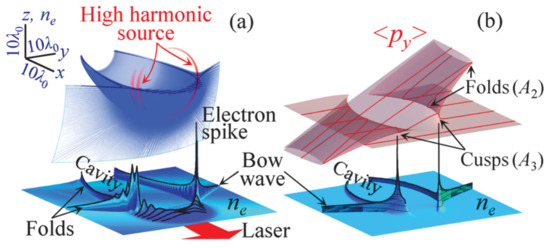
Figure 5.
(a) The 3D PIC simulation of the BISER. The electron density and its cross-section are shown together with the electromagnetic energy (shown in red). (b) Electron density and phase space distribution with the catastrophe model. (From [22]).
3.3. Measurement of Plasma Waves
We have seen in the previous subsections that the radiation of shorter wavelengths in the XUV region has been demonstrated in the flying mirror experiments and in the experiments on high-order harmonic generation in underdense plasma [22]. In both experiments, the electron density singularities play an essential role in generating the shorter-wavelength radiation. However, the direct measurement of such density cusps has not been demonstrated. Here, we describe potential methods to measure electron density singularities in future experiments.
The regular wake waves were measured with the frequency domain interferometer (FDI), which utilizes two temporally separated probe pulses to co-propagate with a driving laser of the wakes [27,28]. The timing of the two pulses is set so that one sits on the higher density region of the wake or plasma electron density oscillation and the other on the lower part. By scanning the timing between the driving laser and the two probe lasers and keeping the probes’ separation time the same, the probe pulses can map the electron density distribution as a function of time. The readout of the density is performed by the phase retrieval algorithm as in standard interferometers. The difference is that an interferogram is formed in the frequency domain. The FDI is suited for a relatively longer plasma wavelength or a lower-density plasma. The drawback of this method is that several scans are necessary to map the distributions.
The modified scheme was proposed where chirped probe pulses are used instead of short (usually, the shortest in the given experimental conditions) probe pulses. The method is referred to as frequency domain holography (FDH) [29]. The technique was demonstrated to map electron density distribution in a weakly nonlinear regime in a single shot. The feature of the curved wake structure was successfully observed, as is seen in the numerical simulations.
Another method is also used for characterizing wake waves, and the shorter probe pulse is introduced in a shadowgraphy configuration [30,31]. In a standard shadowgraph setup, a moderate pulse duration (same as the driving laser duration such as 30 fs) cannot resolve the fast oscillation of the wakes because the wake time scale is very fast, in tens of femtoseconds, driven by typical Ti: sapphire laser pulses. The shorter pulses are created by spectral broadening due to the self-phase modulation in a gas-filled, hollow capillary. Negative chirped mirrors recompress the broadened pulse. The measured images are very similar to those obtained with numerical codes showing the electron density modulations (see Figure 6). However, the RFMs or high-density singularities of electron densities are not apparent. Measuring density singularities with improved spatial and temporal resolutions may be possible [32,33].
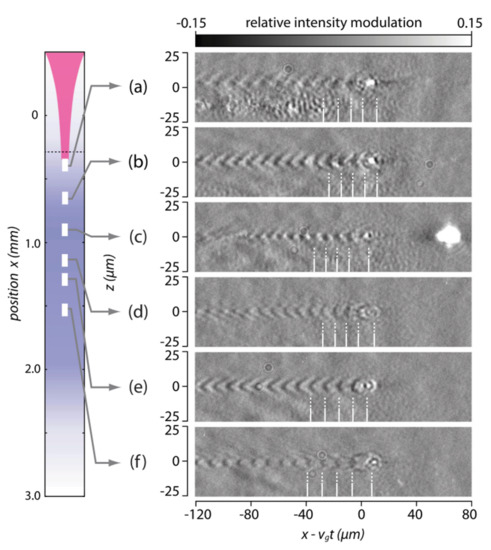
Figure 6.
Shadowgrams measured with a 5.9 fs probe laser pulse. (a–f) Measured at different longitudinal positions described in the left figure. (From [31]).
Instead of the optical probe, laser-accelerated electron beams are also used to probe plasma density modulations. The electron beam has a similar pulse duration to the laser pulse duration because the accelerating phase of the wake is somewhat limited to a shorter wake cycle that is on the order of femtoseconds. The probe electron beams are sensitive to the wake’s electromagnetic field; thus, the initially uniform distribution is modified after passing through the probing region. The measured profiles are referred to as the first measurement of breaking wakes [34].
4. Applications
In this section, applications to ultra-high field science using RFMs are discussed.
4.1. Intensification
Intensification of an incoming laser pulse is one of the favorable features of the RFM and was proposed in the original paper [9]. In the mirror rest frame, the density cusp distribution is parabolic, and the reflected light is focused to a diffraction-limited spot determined by the source wavelength in the boosted frame . The photon energy is finally multiplied as , and the pulse duration is also scaled as the same factor. A particle-in-cell (PIC) simulation demonstrates the intensification of the reflected light, as seen in Figure 7.
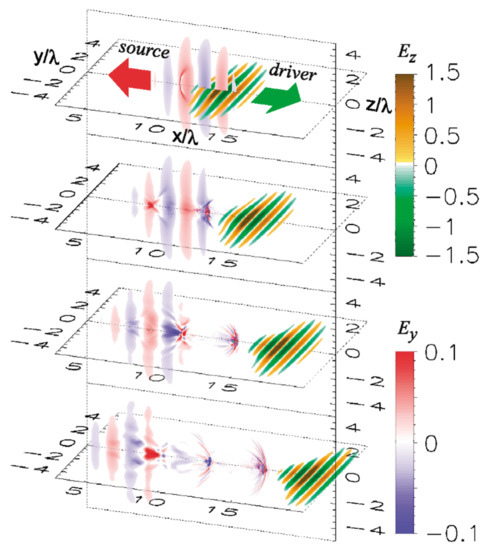
Figure 7.
Reflection of laser light by the flying mirror seen in the three-dimensional PIC simulation. The cross-sections of the electric field components are shown at each time step of t = 16, 18, 20, and 22 2 (top-down). The reflection and focusing of the source pulse are seen in Frames 3 and 4 from the top (from [9]).
Thus, the reflected pulse is ideally intensified as . Here, R is the reflectivity of the RFM in terms of the photon number. If we use a delta-function-like cusp structure as Equation (6) and , i.e., , the focused source intensity is
S. S. Bulanov et al. proposed to use a converging plasma wake by using a focusing beam to excite wake waves [35]. In the ideal case, the focused spot size of the reflected pulse is improved down to the diffraction limit, i.e., in the laboratory frame. The focused intensity may be
where we use the reflectivity of a delta function distribution in the last expression.
Recently, Jeong et al. calculated a detailed electric field distribution focused by an RFM with the vector diffraction model [17]. Jeong et al. proposed to use a colliding setup to achieve a single electron–positron pair production under the focused electric field by the RFM in a vacuum by carefully considering the recoil effect. This is one of the fascinating goals of UHFS. Using a delta-function reflectivity Equation (6), the required laser and plasma parameters are a drive laser power of 250 TW, a driver spot radius of 158 μm, a source power of 180 TW at the fourth harmonic with a duration of 3.5 fs, and a γ factor of 12.2.
4.2. Photon–Photon Scattering
Koga et al. proposed to use RFMs to observe photon–photon scattering, which has not yet been detected in experiments [36]. The experimental difficulties mainly come from the extremely small cross-section (∼ pb at a photon energy of 1 eV). The cross-section increases as the photon energy increases; thus, using coherent X-rays is a possible solution of that problem. Of course, increasing the colliding number and energy of photons and decreasing the area are essential. As is seen in the RFMs’ features, the RFMs can approach these two points. In addition, the stimulated scattering using three-photon beams is also employed to enhance the effect. Photon–photon scattering can be observed using the relativistic mirror concept and future powerful laser facilities.
4.3. Ultrashort X-ray Pulse Generation
Because the reflected pulse is compressed in time, the RFMs can offer a coherent, ultrashort X-ray pulse. If a mirror works ideally, the pulse shape of the X-ray pulse can be relatively easily modified by shaping a source laser temporal profile. Since the source pulse is generated by a near-infrared laser, several optics are available to manipulate a temporal profile, such as chirping, double-pulse, and so on. Probably, it is an upper limit for the pulse duration due to how long the cusp structure remains. Here, we give an example for an attosecond pulse duration. Assuming that cm−3, , the source energy of 180 μJ, fs, and W/cm2, the reflected pulse has a photon energy of 620 eV and a pulse energy of 0.8 μJ with a duration of 50 as. These parameters are chosen so that the source pulse does not affect the mirror due to the recoil effect.
As introduced in the previous section, the BISER can emit coherent electromagnetic radiation in the forward direction. This can be a simple mechanism to generate coherent, attosecond XUV to soft X-ray regions. The maximum harmonic number is estimated to be , where and are the critical frequency and laser frequency, respectively, and is the normalized laser amplitude. In practical units,
where P, , and are the laser peak power, the laser wavelength, and the electron density, respectively. The total emitted photon energy in cgs units is approximately equal to
where is the number of electrons in the singularity, is the Lorentz factor associated with the laser group velocity in plasma, and is the duration of the emission. Assuming practical parameters 100 TW, cm−3, = 12, , fs, and μm, the maximum harmonic number is 160 (the photon energy of 250 eV) and the maximum energy ∼0.6 mJ. This can be a very bright, soft X-ray source.
4.4. Analog Black Holes
Chen and Mourou proposed to use accelerating plasma mirrors for investigating the black hole information paradox in laboratories [37]. The current research on analog black holes is mainly theoretical because it seems impossible to address this paradox by direct astrophysical observations; typical stellar-sized black holes are too cold and young to see the paradox, which might be observed in the end-stage of black hole evaporation.
Among several proposals to investigate the Hawking effects in laboratories, an accelerating mirror is recognized that can mimic black holes and emit Hawking-like thermal radiation (Unruh radiation). According to the equivalence principle, the Hawking temperature of gravity g is expressed as , and the observer at the uniform acceleration of a feels radiation in a vacuum such as , where is the Boltzmann constant.
The acceleration of the mirror is achieved by varying a plasma density along the laser propagation [37,38,39]. Assuming that the plasma density , the acceleration is
This is an extensive experiment, and much still needs to be considered and verified before the actual experiment is conducted. An international, Analog Black Hole Evaporation via Lasers (AnaBHEL), collaboration is currently pursuing an experimental realization of the Chen–Mourou proposal. The concept, design, and status of AnaBHEL are presented in [40].
5. Discussion
The relativistic flying mirror (RFM) concept was reviewed, and the potential applications of the RFMs were also presented. Here we give the necessary theoretical considerations and technological challenges to realize the proposed visions.
The detail of the realistic parameters is owed to numerical calculations such as PIC. In PIC calculations, resolving the upshifted frequency is problematic due to the high spatial and temporal resolutions necessary for shorter wavelengths. For example, in standard parameters, a spatial grid is determined by the laser wavelength to be 0.8 μm, which is shorter than the plasma wavelength. Treating shorter wavelengths of 10 nm requires finer spatial and temporal grids. Thus, a new scheme might be necessary for resolving shorter wavelengths and/or smaller spot sizes.
As is shown in theoretical consierations, the plasma temperature effect reduces the density of the electrons in a cusp, which limits the effectiveness of the RFMs. The initial plasma temperature is strongly affected by the prepulse condition of the driving laser. Ionized electrons can be heated by absorption of the laser’s energy and transfer the energy via collisions. This effect in an actual situation has not yet been addressed in gaseous plasma.
Experimental challenges remain in many aspects. The focusability of the RFM to the theoretically estimated size has not yet been demonstrated. This is a crucial fundamental property of the RFM. Another concept to be demonstrated is the pulse compression of the reflected pulse. According to the theory, the compression must happen as long as the upshift of the frequency happens. However, the effect must be measured experimentally to prove the concept. This is crucial for ultrashort X-ray generation.
Practically, the repeatability of the reflection must be improved. This is necessary for the applications and the precise characterization mentioned above. For example, the temporal characterization in the sub-femtosecond regime requires many shots. The detailed mechanism for forming a cusp structure or singularities in plasma has been addressed experimentally, mainly investigated numerically. Singularities or breaking waves should be monitored with an ultrashort pulse (optical light or an electron beam).
6. Conclusions
We reviewed the relativistic flying mirror concept highlighting the theoretical and experimental achievements. The flying mirror has several attractive properties, such as high-frequency and ultra-short pulse generation. In addition, the intensification can be expected due to the focusing mirror shape. Some of these features are to be demonstrated experimentally. In the near term, the ultra-short, coherent source can be realized. In the long term, the RFM might enable terrestrial laboratory experiments in quantum electrodynamics and astrophysics, which would be nearly unattainable without it.
Funding
This work was partly supported by JSPS Kakenhi JP 19KK0355 and 19H00669 and the QST Director Fund Creative Research No. 20, QST IRI. S.B. acknowledges the support by the project High Field Initiative (cz.02.1.01/0.0/15_003/0000449).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BISER | Burst intensification by singularity emitting radiation |
| CCD | Charge-coupled device |
| FDI | Frequency domain interferometry |
| FDH | Frequency domain holography |
| PIC | Particle-in-cell |
| RFM | Relativistic flying mirror |
| SRLD | Square-root Lorentzian distribution |
| UHFS | Ultra-high-field science |
| QED | Quantum electrodynamics |
References
- Strickland, D.; Mourou, G. Compression of Amplified Chirped Optical Pulses. Opt. Commun. 1985, 55, 447–449. [Google Scholar] [CrossRef]
- Mourou, G.A.; Tajima, T.; Bulanov, S.V. Optics in the relativistic regime. Rev. Mod. Phys. 2006, 78, 309–371. [Google Scholar] [CrossRef]
- Piazza, A.D.; Mueller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177–1228. [Google Scholar] [CrossRef]
- Yoon, J.W.; Kim, Y.G.; Choi, I.W.; Sung, J.H.; Lee, H.W.; Lee, S.K.; Nam, C.H. Realization of laser intensity over 1023 W/cm2. Optica 2021, 8, 630. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Hayashi, Y.; Kando, M.; Kiriyama, H.; Koga, J.K.; Kondo, K.; Kotaki, H.; Pirozhkov, A.S.; Bulanov, S.S.; et al. Extreme field science. Plasma Phys. Control. Fusion 2011, 53, 124025. [Google Scholar] [CrossRef]
- Bamber, C.; Boege, S.J.; Koffas, T.; Kotseroglou, T.; Melissinos, A.C.; Meyerhofer, D.D.; Reis, D.A.; Ragg, W.; Bula, C.; McDonald, K.T.; et al. Studies of nonlinear QED in collisions of 46.6 GeV electrons with intense laser pulses. Phys. Rev. D 1999, 60, 092004. [Google Scholar] [CrossRef]
- Bulanov, S.S.; Mur, V.D.; Narozhny, N.B.; Nees, J.; Popov, V.S. Multiple Colliding Electromagnetic Pulses: A Way to Lower the Threshold of e+e− Pair Production from Vacuum. Phys. Rev. Lett. 2010, 104, 220404. [Google Scholar] [CrossRef]
- Dunne, G.V.; Gies, H.; Schützhold, R. Catalysis of Schwinger vacuum pair production. Phys. Rev. D 2009, 80, 111301. [Google Scholar] [CrossRef]
- Bulanov, S.; Esirkepov, T.Z.; Tajima, T. Light intensification towards the Schwinger limit. Phys. Rev. Lett. 2003, 91, 085001. [Google Scholar] [CrossRef]
- Panchenko, A.V.; Esirkepov, T.Z.; Pirozhkov, A.S.; Kando, M.; Kamenets, F.F.; Bulanov, S.V. Interaction of electromagnetic waves with caustics in plasma flows. Phys. Rev. E 2008, 78, 056402. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Kando, M.; Pirozhkov, A.S.; Rosanov, N.N. Relativistic mirrors in plasmas. Novel results and perspectives. Physics-Uspekhi 2013, 56, 429–464. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Ann. Der Phys. 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Kando, M.; Esirkepov, T.; Koga, J.; Pirozhkov, A.; Bulanov, S. Coherent, Short-Pulse X-ray Generation via Relativistic Flying Mirrors. Quantum Beam Sci. 2018, 2, 9. [Google Scholar] [CrossRef]
- Valenta, P.; Esirkepov, T.Z.; Koga, J.K.; Pirozhkov, A.S.; Kando, M.; Liu, Y.K.; Fang, P.; Chen, P.; Mu, J.; Korn, G.; et al. Recoil effects on reflection from relativistic mirrors in laser plasmas. Phys. Plasmas 2020, 27, 032109. [Google Scholar] [CrossRef]
- Liu, Y.-K.; Chen, P.; Fang, Y. Reflectivity and spectrum of relativistic flying plasma mirrors. Phys. Plasmas 2021, 28, 103301. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Kando, M.; Koga, J.K.; Pirozhkov, A.S.; Nakamura, T.; Bulanov, S.S.; Schroeder, C.B.; Esarey, E.; Califano, F.; et al. On the breaking of a plasma wave in a thermal plasma. II. Electromagnetic wave interaction with the breaking plasma wave. Phys. Plasmas 2012, 19, 113103. [Google Scholar] [CrossRef]
- Jeong, T.M.; Bulanov, S.V.; Valenta, P.; Korn, G.; Esirkepov, T.Z.; Koga, J.K.; Pirozhkov, A.S.; Kando, M.; Bulanov, S.S. Relativistic flying laser focus by a laser-produced parabolic plasma mirror. Phys. Rev. A 2021, 104, 053533. [Google Scholar] [CrossRef]
- Kando, M.; Fukuda, Y.; Pirozhkov, A.S.; Ma, J.; Daito, I.; Chen, L.; Esirkepov, T.Z.; Ogura, K.; Homma, T.; Hayashi, Y.; et al. Demonstration of laser-frequency upshift by electron-density modulations in a plasma wakefield. Phys. Rev. Lett. 2007, 99, 135001. [Google Scholar] [CrossRef]
- Pirozhkov, A.S.; Ma, J.; Kando, M.; Esirkepov, T.Z.; Fukuda, Y.; Chen, L.M.; Daito, I.; Ogura, K.; Homma, T.; Hayashi, Y.; et al. Frequency multiplication of light back-reflected from a relativistic wake wave. Phys. Plasmas 2007, 14, 123106. [Google Scholar] [CrossRef]
- Kando, M.; Pirozhkov, A.S.; Kawase, K.; Esirkepov, T.Z.; Fukuda, Y.; Kiriyama, H.; Okada, H.; Daito, I.; Kameshima, T.; Hayashi, Y.; et al. Enhancement of Photon Number Reflected by the Relativistic Flying Mirror. Phys. Rev. Lett. 2009, 103, 235003. [Google Scholar] [CrossRef]
- Kando, M.; Pirozhkov, A.S.; Fukuda, Y.; Esirkepov, T.Z.; Daito, I.; Kawase, K.; Ma, J.L.; Chen, L.M.; Hayashi, Y.; Mori, M.; et al. Experimental studies of the high and low frequency electromagnetic radiation produced from nonlinear laser-plasma interactions. Eur. Phys. J. D 2009, 55, 465–474. [Google Scholar] [CrossRef]
- Pirozhkov, A.S.; Kando, M.; Esirkepov, T.Z.; Gallegos, P.; Ahmed, H.; Ragozin, E.N.; Faenov, A.Y.; Pikuz, T.A.; Kawachi, T.; Sagisaka, A.; et al. Soft-X-ray Harmonic Comb from Relativistic Electron Spikes. Phys. Rev. Lett. 2012, 108, 135004. [Google Scholar] [CrossRef]
- Pirozhkov, A.S.; Kando, M.; Esirkepov, T.Z.; Gallegos, P.; Ahmed, H.; Ragozin, E.N.; Faenov, A.Y.; Pikuz, T.A.; Kawachi, T.; Sagisaka, A.; et al. High order harmonics from relativistic electron spikes. New J. Phys. 2014, 16, 093003. [Google Scholar] [CrossRef]
- Sagisaka, A.; Ogura, K.; Esirkepov, T.; Neely, D.; Pikuz, T.; Koga, J.; Fukuda, Y.; Kotaki, H.; Hayashi, Y.; Gonzalez-Izquierdo, B.; et al. Observation of Burst Intensification by Singularity Emitting Radiation generated from relativistic plasma with a high-intensity laser. High Energy Density Phys. 2020, 36, 100751. [Google Scholar] [CrossRef]
- Pirozhkov, A.S.; Esirkepov, T.Z.; Pikuz, T.A.; Faenov, A.Y.; Ogura, K.; Hayashi, Y.; Kotaki, H.; Ragozin, E.N.; Neely, D.; Kiriyama, H.; et al. Burst intensification by singularity emitting radiation in multi-stream flows. Sci. Rep. 2017, 7, 17968. [Google Scholar] [CrossRef] [PubMed]
- Pirozhkov, A.S.; Esirkepov, T.Z.; Pikuz, T.A.; Faenov, A.Y.; Sagisaka, A.; Ogura, K.; Hayashi, Y.; Kotaki, H.; Ragozin, E.N.; Neely, D.; et al. Laser Requirements for High-Order Harmonic Generation by Relativistic Plasma Singularities. Quantum Beam Sci. 2018, 2, 7. [Google Scholar] [CrossRef]
- Marquès, J.R.; Geindre, J.P.; Amiranoff, F.; Audebert, P.; Gauthier, J.C.; Antonetti, A.; Grillon, G. Temporal and Spatial Measurements of the Electron Density Perturbation Produced in the Wake of an Ultrashort Laser Pulse. Phys. Rev. Lett. 1996, 76, 3566–3569. [Google Scholar] [CrossRef]
- Siders, C.W.; Blanc, S.P.L.; Fisher, D.; Tajima, T.; Downer, M.C.; Babine, A.; Stepanov, A.; Sergeev, A. Laser Wakefield Excitation and Measurement by Femtosecond Longitudinal Interferometry. Phys. Rev. Lett. 1996, 76, 3570–3573. [Google Scholar] [CrossRef]
- Matlis, N.H.; Reed, S.; Bulanov, S.S.; Chvykov, V.; Kalintchenko, G.; Matsuoka, T.; Rousseau, P.; Yanovsky, V.; Maksimchuk, A.; Kalmykov, S.; et al. Snapshots of laser wakefields. Nat. Phys. 2006, 2, 749–753. [Google Scholar] [CrossRef]
- Buck, A.; Nicolai, M.; Schmid, K.; Sears, C.M.S.; Sävert, A.; Mikhailova, J.M.; Krausz, F.; Kaluza, M.C.; Veisz, L. Real-time observation of laser-driven electron acceleration. Nat. Phys. 2011, 7, 543–548. [Google Scholar] [CrossRef]
- Sävert, A.; Mangles, S.P.D.; Schnell, M.; Siminos, E.; Cole, J.M.; Leier, M.; Reuter, M.; Schwab, M.B.; Möller, M.; Poder, K.; et al. Direct Observation of the Injection Dynamics of a Laser Wakefield Accelerator Using Few-Femtosecond Shadowgraphy. Phys. Rev. Lett. 2015, 115, 055002. [Google Scholar] [CrossRef]
- Esirkepov, T.Z.; Mu, J.; Gu, Y.; Jeong, T.M.; Valenta, P.; Klimo, O.; Koga, J.K.; Kando, M.; Neely, D.; Korn, G.; et al. Optical probing of relativistic plasma singularities. Phys. Plasmas 2020, 27, 052103. [Google Scholar] [CrossRef]
- Kotov, A.; Esirkepov, T.; Soloviev, A.; Sagisaka, A.; Ogura, K.; Bierwage, A.; Kando, M.; Kiriyama, H.; Starodubtsev, M.; Khazanov, E.; et al. Enhanced diagnostics of radiating relativistic singularities and BISER by nonlinear post-compression of optical probe pulse. J. Instrum. 2022, 17, P07035. [Google Scholar] [CrossRef]
- Wan, Y.; Seemann, O.; Tata, S.; Andriyash, I.A.; Smartsev, S.; Kroupp, E.; Malka, V. Direct observation of relativistic broken plasma waves. Nat. Phys. 2022, 18, 1186–1190. [Google Scholar] [CrossRef]
- Bulanov, S.S.; Maksimchuk, A.; Schroeder, C.B.; Zhidkov, A.G.; Esarey, E.; Leemans, W.P. Relativistic spherical plasma waves. Phys. Plasmas 2012, 19, 020702. [Google Scholar] [CrossRef]
- Koga, J.K.; Bulanov, S.V.; Esirkepov, T.Z.; Pirozhkov, A.S.; Kando, M.; Rosanov, N.N. Possibility of measuring photon–photon scattering via relativistic mirrors. Phys. Rev. A 2012, 86, 053823. [Google Scholar] [CrossRef]
- Chen, P.; Mourou, G. Accelerating Plasma Mirrors to Investigate the Black Hole Information Loss Paradox. Phys. Rev. Lett. 2017, 118, 045001-5. [Google Scholar] [CrossRef]
- Chen, P.; Mourou, G. Trajectory of a flying plasma mirror traversing a target with density gradient. Phys. Plasmas 2020, 27, 123106. [Google Scholar] [CrossRef]
- Lobet, M.; Kando, M.; Koga, J.K.; Esirkepov, T.Z.; Nakamura, T.; Pirozhkov, A.S.; Bulanov, S.V. Controlling the generation of high frequency electromagnetic pulses with relativistic flying mirrors using an inhomogeneous plasma. Phys. Lett. A 2013, 377, 1114–1118. [Google Scholar] [CrossRef]
- Collaboration, A.; Chen, P.; Mourou, G.; Besancon, M.; Fukuda, Y.; Glicenstein, J.F.; Nam, J.; Lin, C.E.; Lin, K.N.; Liu, S.X.; et al. AnaBHEL (Analog Black Hole Evaporation via Lasers) Experiment: Concept, Design, and Status. arXiv 2022, arXiv:2205.12195. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).