Surface Depth-Mapping of Material via the Transport-of-Intensity Equation
Abstract
1. Introduction
2. Materials and Methods
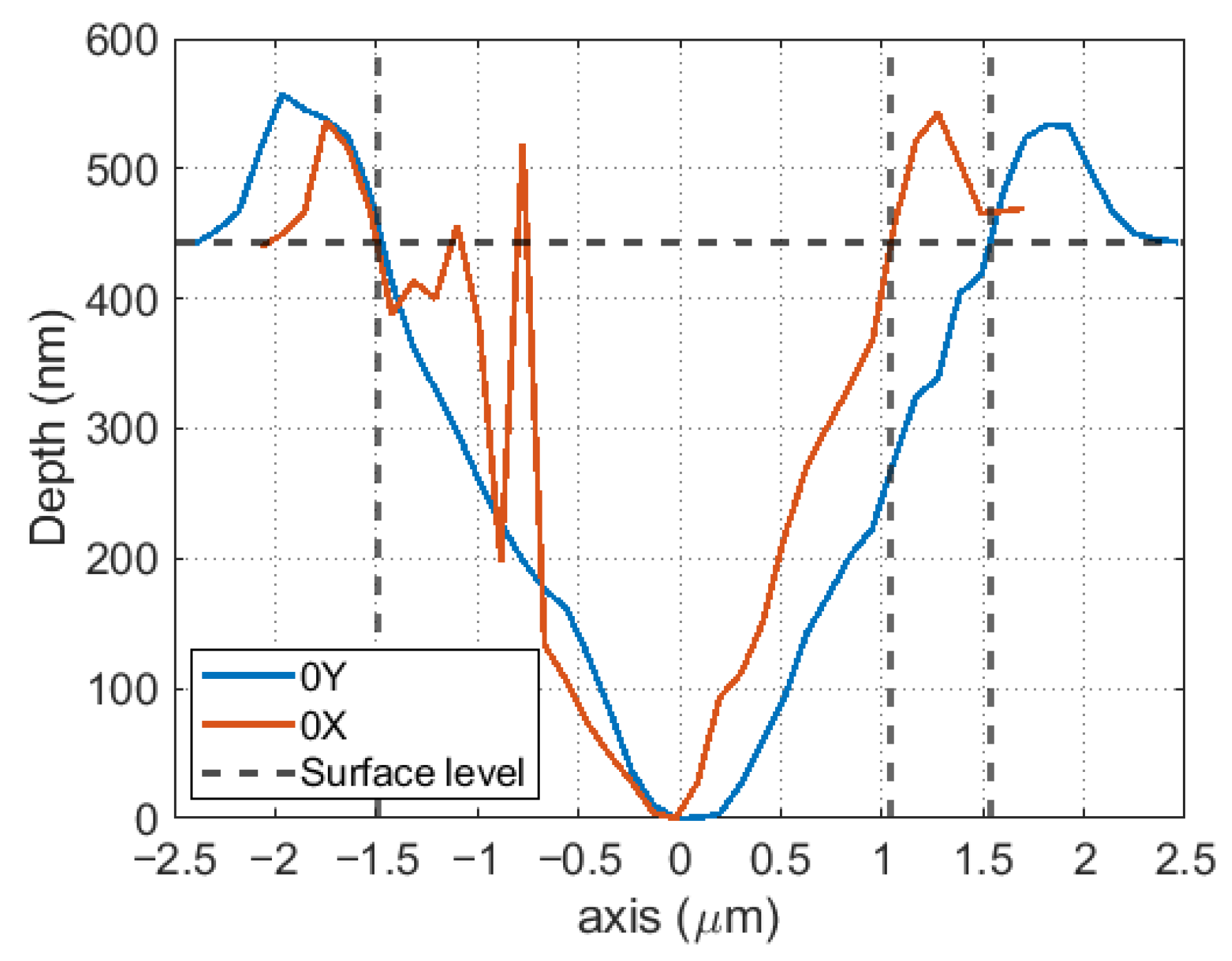
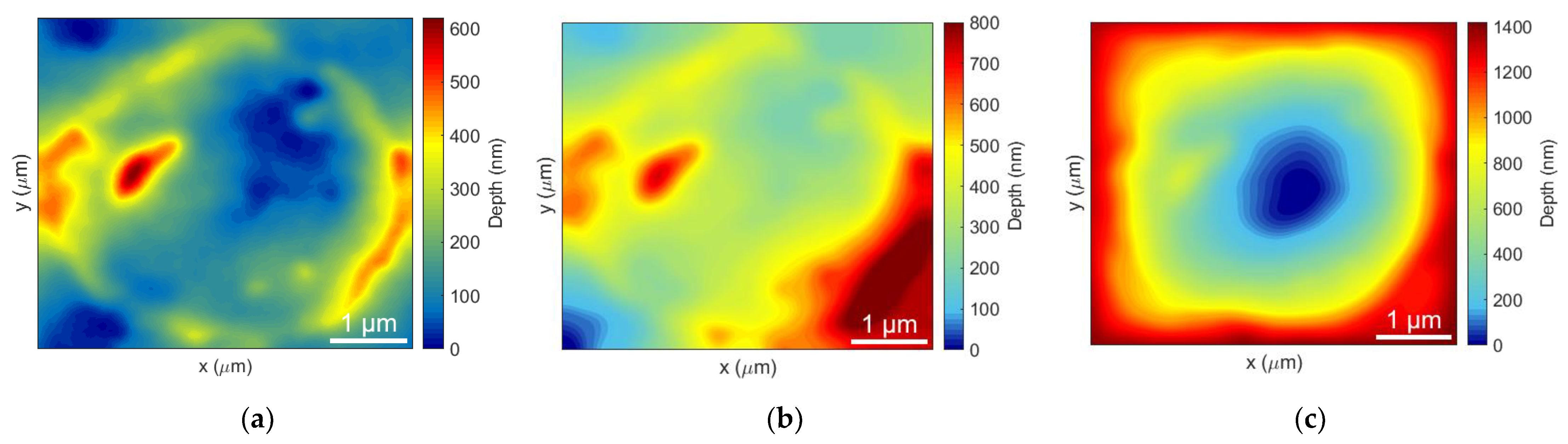
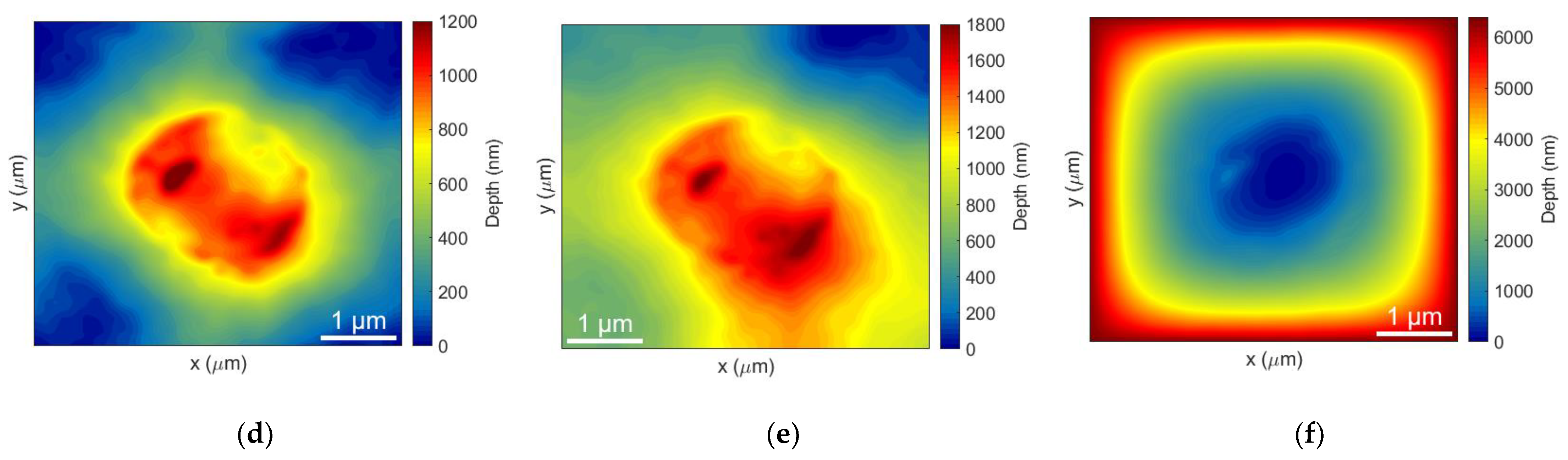
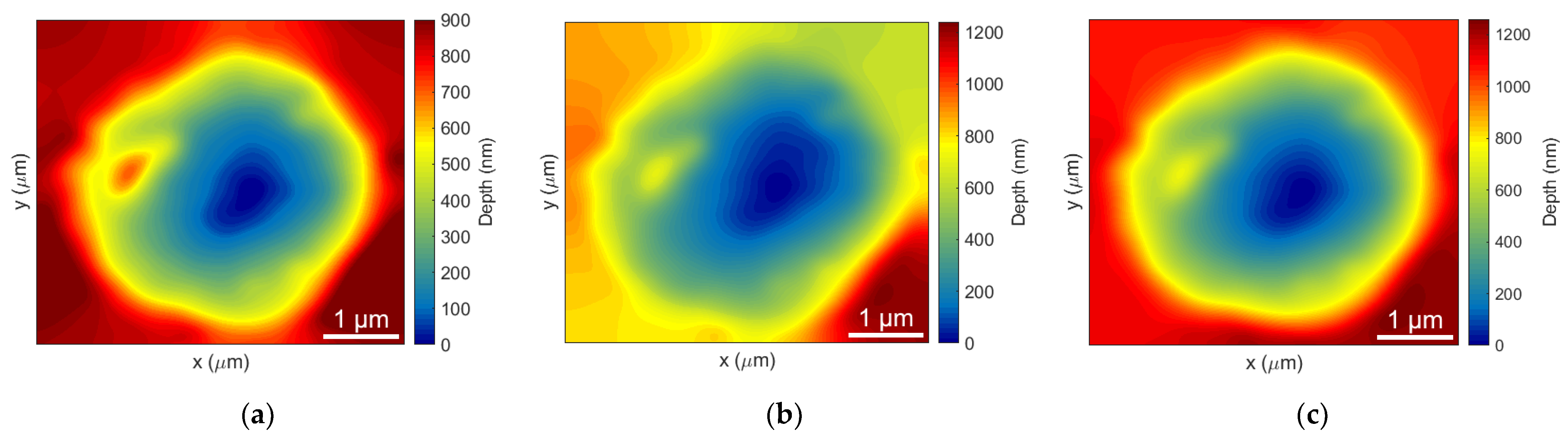
3. Experimental Demonstration
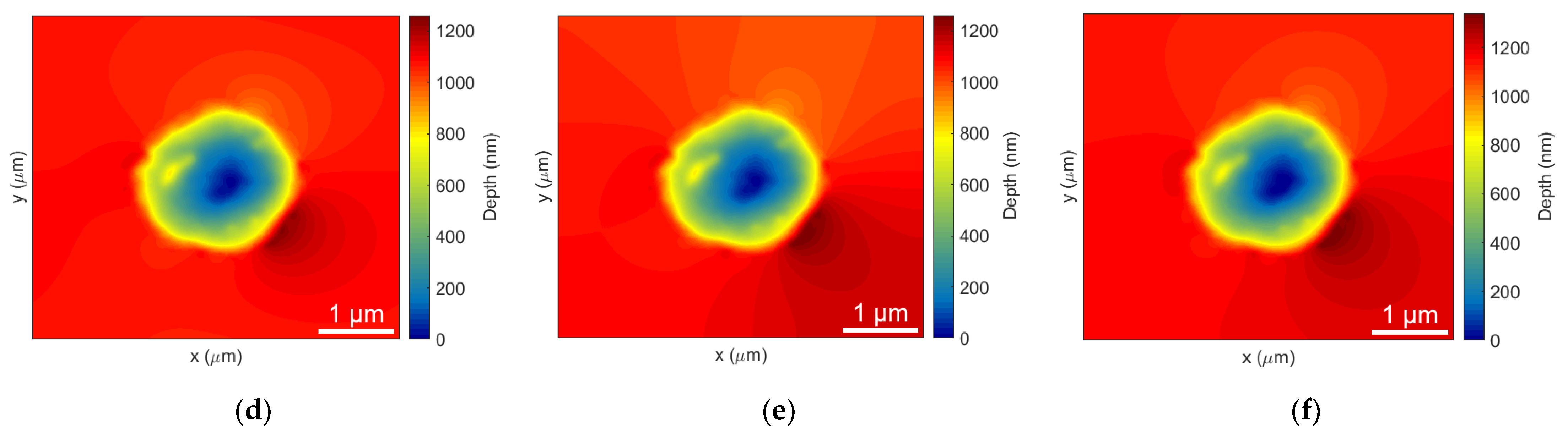
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vogel, A.; Venugopalan, V. Mechanisms of Pulsed Laser Ablation of Biological Tissues. Chem. Rev. 2003, 103, 577–644. [Google Scholar] [CrossRef]
- Assion, A.; Baumert, T.; Bergt, M.; Brixner, T.; Kiefer, B.; Seyfried, V.; Strehleand, M.; Gerber, G. Control of Chemical Reactions by Feedback-Optimized Phase-Shaped Femtosecond Laser Pulses. Science 1998, 282, 919–922. [Google Scholar] [CrossRef]
- Yangdong, W.; Haibo, Y.; Yuzhao, Z.; Ye, Q.; Peiwen, L.; Xiaoduo, W.; Boliang, J.; Lianqing, L.; Wen Jung, L. Recent Advances in Femtosecond Laser Fabrication: From Structures to Applications. IEEE Open J. Nanotechnol. 2021, 2, 161–177. [Google Scholar]
- Gattass, R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Ponkratova, E.; Ageev, E.; Komissarenko, F.; Koromyslov, S.; Kudryashov, D.; Mukhin, I.; Veiko, V.; Kuchmizhak, A.; Zuev, D. Femtosecond Laser Fabrication of Hybrid Metal-Dielectric Structures with Nonlinear Photoluminescence. Photonics 2021, 8, 121. [Google Scholar] [CrossRef]
- Patterson, J.; Bailey, B. Solid-State Physics Introduction to the Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wedler, H. Information on Surface Structure by Low Energy Electron Diffraction. Vakuum 1995, 7, 107–114. [Google Scholar] [CrossRef]
- Galiy, P.V.; Losovy, J.; Ya, B.; Nenchuk, T.; Yarovets, I.R. Low-Energy-Electron-Diffraction Structural Studies of (100) Cleavage Surfaces of In4Se3 Layered Crystals. Ukr. J. Phys. 2014, 59, 612–621. [Google Scholar] [CrossRef]
- Chen, L.X.; Lee, P.L.; Gosztola, D.; Svec, W.A.; Montano, P.A.; Wasielewski, M.R. Time-Resolved X-ray Absorption Determination of Structural Changes following Photoinduced Electron Transfer within Bis-porphyrin Heme Protein Models. J. Phys. Chem. B 1999, 103, 3270–3274. [Google Scholar] [CrossRef]
- Gawelda, W.; Saes, M.; Kaiser, M.; Tarnovsky, A.; Johnson, S.L.; Grolimund, D.; Abela, R.; Chergui, M.; Bressler, C. Structural dynamics and electronic structure changes probed with lasers and X-rays. In Femtochemistry and Femtobiology, Proceedings of the Ultrafast Events in Molecular Science VIth International Conference on Femtochemistry Maison de la Chimie, Paris, France, 6–10 July 2003; Martin, M.M., Hynes, J.T., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Petrone, L.; Ragg, N.L.C.; Girvan, L.; McQuillan, A.J. Scanning Electron Microscopy and Energy Dispersive X-Ray Microanalysis of Perna canaliculus Mussel Larvae Adhesive Secretion. J. Adhes. 2009, 85, 78–96. [Google Scholar] [CrossRef]
- Sharma, S.; Green, M.; Hyer, R.; Dark, C.; Black, T.; Chourasia, A.; Mishra, K. Growth of diamond films and characterization by Raman, scanning electron microscopy, and X-ray photoelectron spectroscopy. J. Mater. Res. 1990, 5, 2424–2432. [Google Scholar] [CrossRef]
- Sharma, S.C.; Dark, C.A.; Hyer, R.C.; Green, M.; Black, T.D. Deposition of diamond films at low pressures and their characterization by positron annihilation, Raman, scanning electron microscopy, and X-ray photoelectron spectroscopy. Appl. Phys. Lett. 1990, 56, 1781. [Google Scholar] [CrossRef]
- Hecht, B.; Sick, B.; Wild, U.P. Scanning near-field optical microscopy with aperture probes: Fundamentals and applications. J. Chem. Phys. 2000, 112, 7761. [Google Scholar] [CrossRef]
- Maurer, C.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Phase contrast microscopy with full numerical aperture illumination. Opt. Express 2008, 16, 19821–19829. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Formanek, P.; Koch, C.T.; Lubk, A. Off-axis and inline electron holography: Experimental comparison. Ultramicroscopy 2010, 110, 472–482. [Google Scholar] [CrossRef]
- Zhou, W.-J.; Guan, X.; Liu, F.; Yu, Y.; Zhang, H.; Poon, T.-C.; Banerjee, P.P. Phase retrieval based on transport of intensity and digital holography. Appl. Opt. 2018, 57, A229–A234. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, S.; Wang, C.; Zhang, H.; Yu, Y.; Poon, T.-C. Elimination of Quadratic Phase Aberration in Digital Holographic Microscopy by Using Transport of Intensity. Front. Photonics 2022, 3, 848453. [Google Scholar] [CrossRef]
- Zuo, C.; Li, J.; Sun, J.; Fan, Y.; Zhang, J.; Lu, L.; Zhang, R.; Wang, B.; Huang, L.; Chen, Q. Transport of intensity equation: A tutorial. Opt. Lasers Eng. 2020, 135, 106187. [Google Scholar] [CrossRef]
- Gritsenko, I.V.; Kovalev, M.S.; Stsepuro, N.G.; Gulina, Y.S.; Krasin, G.K.; Gonchukov, S.A.; Kudryashov, S.I. The optical refractometry using transport-of-intensity equation. Laser Phys. Lett. 2022, 19, 076201. [Google Scholar] [CrossRef]
- Kovalev, M.; Gritsenko, I.; Stsepuro, N.; Nosov, P.; Krasin, G.; Kudryashov, S. Reconstructing the Spatial Parameters of a Laser Beam Using the Transport-of-Intensity Equation. Sensors 2022, 22, 1765. [Google Scholar] [CrossRef]
- McCray, A.R.C.; Cote, T.; Li, Y.; Petford-Long, A.K.; Phatak, C. Understanding Complex Magnetic Spin Textures with Simulation-Assisted Lorentz Transmission Electron Microscopy. Phys. Rev. Applied 2012, 15, 044025. [Google Scholar] [CrossRef]
- Zhidong, H.; Dongsheng, S.; Weiwei, W.; Ning, W.; Binghui, G.; Shouguo, W.; Mingliang, T.; Haifeng, D. Visualizing Emergent Magnetic Flux of Antiskyrmions in Mn1.4PtSn Magnet. Adv. Funct. Mater. 2022, 32, 2112661. [Google Scholar]
- Cao, F.; Donnarumma, F.; Murray, K.K. Wavelength dependent atomic force microscope tip-enhanced laser ablation. Appl. Surf. Sci. 2018, 447, 437–441. [Google Scholar] [CrossRef]
- Smirnov, N.A.; Kudryashov, S.I.; Rudenko, A.A.; Zayarny, D.A.; Ionin, A.A. Pulsewidth and ambient medium effects during ultrashort-pulse laser ablation of silicon in air and water. Appl. Surf. Sci. 2021, 5621, 150243. [Google Scholar] [CrossRef]
- Teague, M.R. Irradiance moments: Their propagation and use for unique retrieval of phase. J. Opt. Soc. Am. 1982, 72, 1199–1209. [Google Scholar] [CrossRef]
- Teague, M.R. Deterministic phase retrieval: A green’s function solution. J. Opt. Soc. Am. 1983, 73, 1434–1441. [Google Scholar] [CrossRef]
- Teague, M.R. Image formation in terms of the transport equation. J. Opt. Soc. Am. A 1985, 2, 2019–2026. [Google Scholar] [CrossRef]
- Philip, M.M.; Feshbach, H. Methods of Theoretical Physics, Part I.; McGraw-Hill: New York, USA, 1953. [Google Scholar]
- Semichaevsky, A.; Testorf, M. Phase-space interpretation of deterministic phase retrieval. JOSA A 2004, 21, 2173–2179. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Roberts, A.; Nugent, K.A. Partially coherent fields, the transport of intensity equation and phase uniqueness. JOSA A 1995, 12, 1942–1946. [Google Scholar] [CrossRef]
- Paganin, D.; Nugent, K.A. Noninterferometric Phase Imaging with Partially Coherent Light. Phys. Rev. Lett. 1998, 80, 2586–2589. [Google Scholar] [CrossRef]
- De Graef, M. Lorentz microscopy: Theoretical basis and image simulations. In Magnetic Imaging and Its Applications to Materials, 1st ed.; De Graef, M., Zhu, Y., Eds.; Academic Press: Cambridge, MA, USA, 2001; Volume 38, pp. 27–67. [Google Scholar]
- Paganin, D. Coherent X-ray optics. Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Gureyev, T.E.; Nugent, K.A. Phase retrieval with the transport-of-intensity equation. II. Orthogonal series solution for nonuniform illumination. J. Opt. Soc. Am. A 1996, 13, 1670–1682. [Google Scholar] [CrossRef]
- Martinez-Carranza, J.; Falaggis, K.; Kozacki, T.; Kujawinska, M. Effect of imposed boundary conditions on the accuracy of transport of intensity equation based. Model. Asp. Opt. Metrol. IV 2013, 8789, 195–208. [Google Scholar]
- Volkov, V.; Zhu, Y.; De Graef, M. A new symmetrized solution for the phase retrieval using the Transport of Intensity Equation. Micron 2002, 33, 411–416. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Li, H.; Qu, W.; Asundi, A. Boundary-artifact-free phase retrieval with the transport of intensity equation II: Applications to microlens characterization. Opt. Express 2014, 22, 18310–18324. [Google Scholar] [CrossRef] [PubMed]
- Piskunov, N. Differential and Integral Calculus; Noordhoff: Groningen, The Netherlands, 1965. [Google Scholar]
- Available online: https://www.tescan.com (accessed on 20 September 2022).
- Palchoudhury, S.; Baalousha, M.; Lead, J.R. Methods for Measuring Concentration (Mass, Surface Area and Number) of Nanomaterials. In Frontiers of Nanoscience; Baalousha, M., Lead, J.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 8, pp. 153–181. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stsepuro, N.; Kovalev, M.; Krasin, G.; Podlesnykh, I.; Gulina, Y.; Kudryashov, S. Surface Depth-Mapping of Material via the Transport-of-Intensity Equation. Photonics 2022, 9, 815. https://doi.org/10.3390/photonics9110815
Stsepuro N, Kovalev M, Krasin G, Podlesnykh I, Gulina Y, Kudryashov S. Surface Depth-Mapping of Material via the Transport-of-Intensity Equation. Photonics. 2022; 9(11):815. https://doi.org/10.3390/photonics9110815
Chicago/Turabian StyleStsepuro, Nikita, Michael Kovalev, George Krasin, Ivan Podlesnykh, Yulia Gulina, and Sergey Kudryashov. 2022. "Surface Depth-Mapping of Material via the Transport-of-Intensity Equation" Photonics 9, no. 11: 815. https://doi.org/10.3390/photonics9110815
APA StyleStsepuro, N., Kovalev, M., Krasin, G., Podlesnykh, I., Gulina, Y., & Kudryashov, S. (2022). Surface Depth-Mapping of Material via the Transport-of-Intensity Equation. Photonics, 9(11), 815. https://doi.org/10.3390/photonics9110815







