Two-Dimensional Elliptical Microresonator Arrays for Wide Flat Bandwidth and Boxlike Filter Response
Abstract
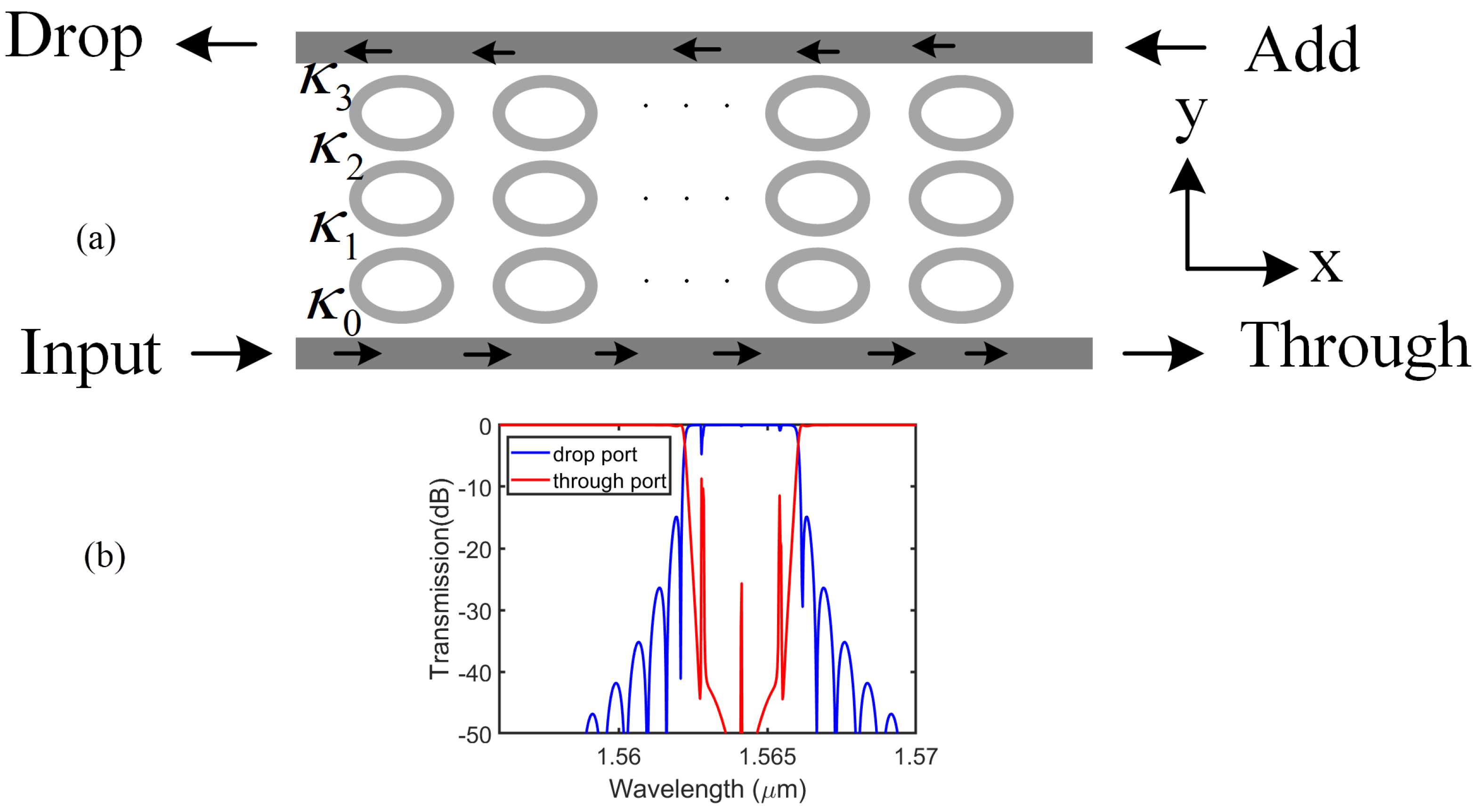
1. Introduction
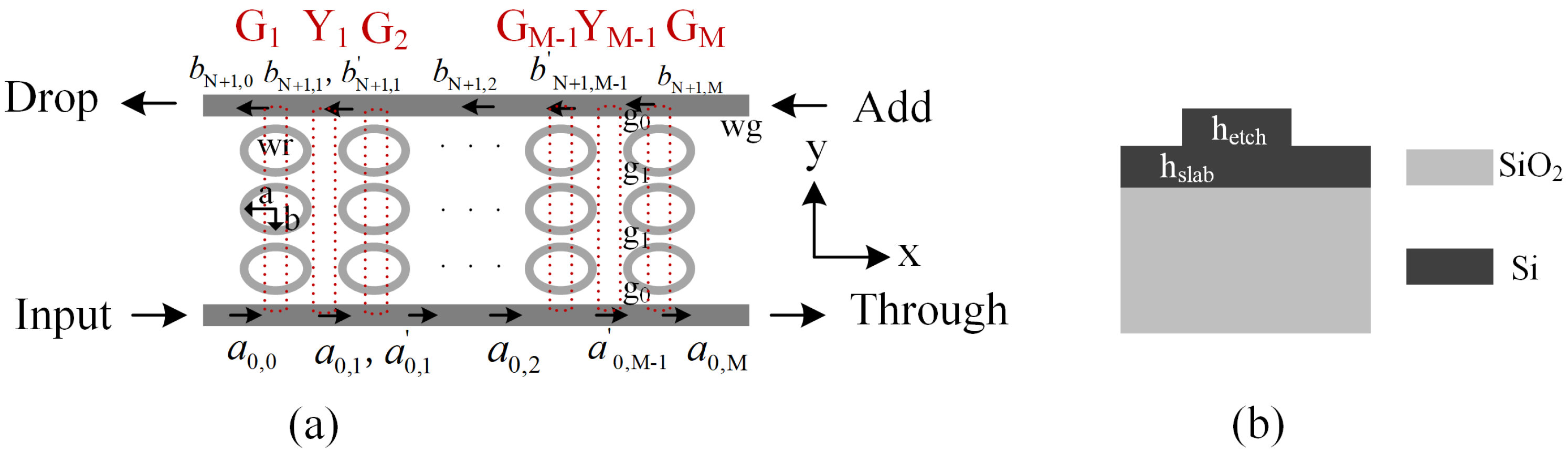
2. Methods
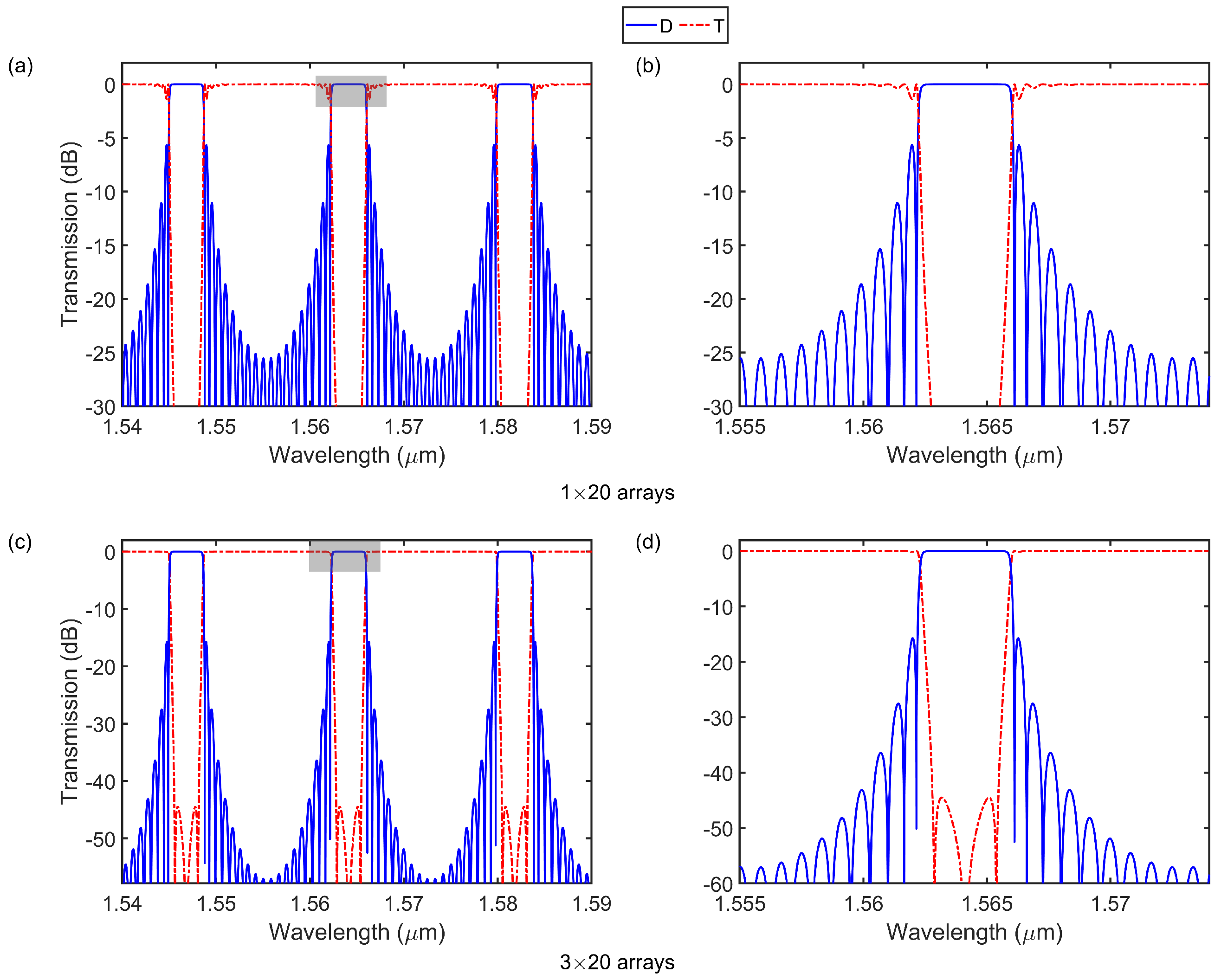
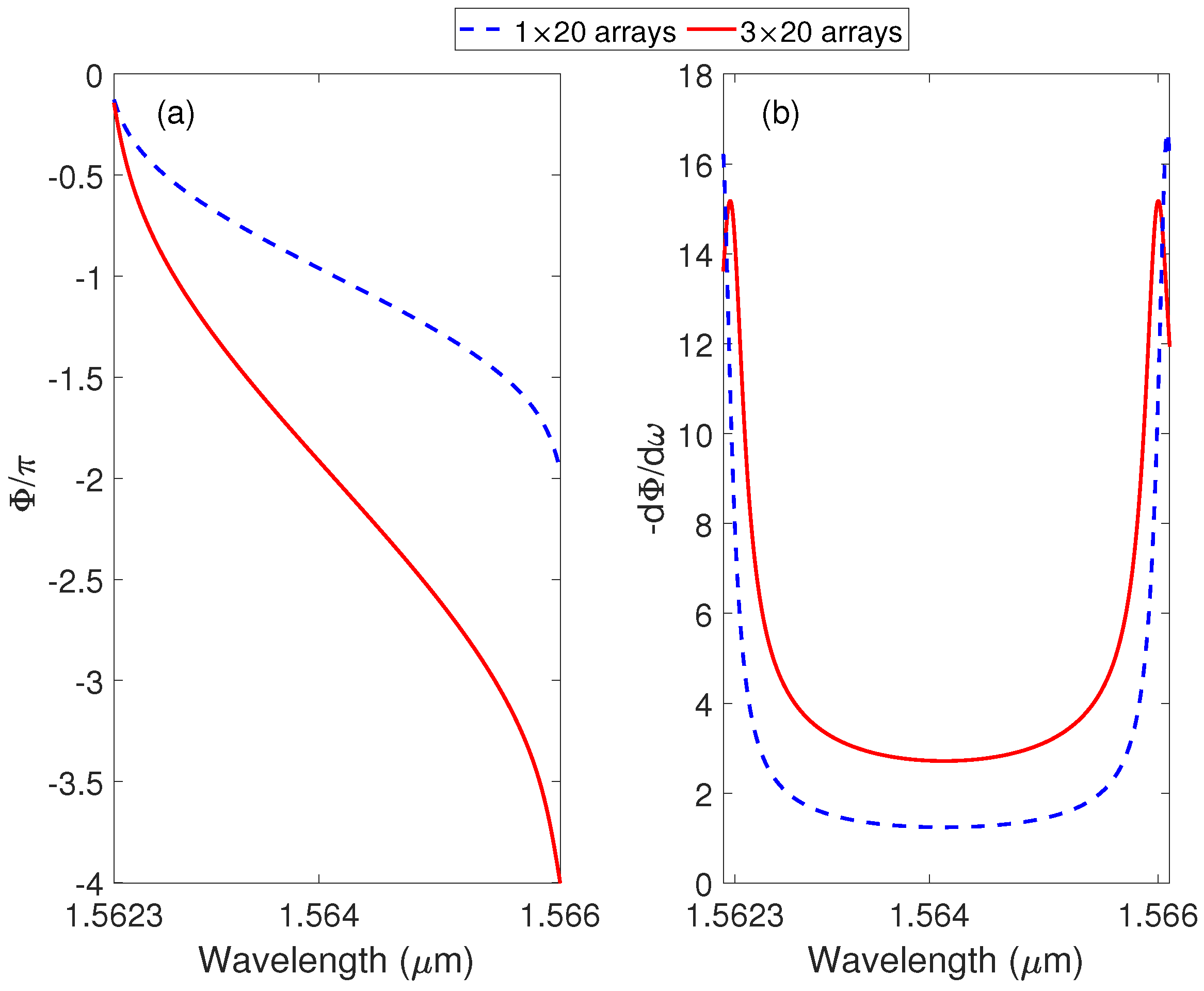
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, Y.; Perron, D.; Aurangozeb, F.; Jiang, Z.; Hossain, M.; Van, V. Silicon Photonic Vernier Cascaded Microring Filter for Broadband Tunability. IEEE Photonics Technol. Lett. 2019, 31, 1503–1506. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, C.; Liang, D.; Dai, D. Submicron-resonator-based add-drop optical filter with an ultra-large free spectral range. Opt. Express 2019, 27, 416–422. [Google Scholar] [CrossRef]
- Poulopoulos, G.; Giannoulis, G.; Iliadis, N.; Kalavrouziotis, D.; Apostolopoulos, D.; Avramopoulos, H. Flexible Filtering Element on SOI With Wide Bandwidth Tunability and Full FSR tuning. J. Light. Technol. 2019, 37, 300–306. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Huang, B.; Zhang, Z.; Cheng, C.; Gao, T.; Yu, Y.; Li, Y.; Chen, H. Multi-channel silicon photonic receiver based on compact second-order microring resonators. Opt. Commun. 2019, 437, 168–173. [Google Scholar] [CrossRef]
- Yang, H.; Li, J.; Zheng, P.; Hu, G.; Yun, B.; Cui, Y. A Stopband and Passband Switchable Microwave Photonic Filter Based on Integrated Dual Ring Coupled Mach-Zehnder Interferometer. IEEE Photonics J. 2019, 11, 5502608. [Google Scholar] [CrossRef]
- Mistry, A.; Hammood, M.; Shoman, H.; Chrostowski, L.; Jaeger, N.A.F. Bandwidth-tunable, FSR-free, microring-based, SOI filter with integrated contra-directional couplers. Opt. Lett. 2018, 43, 6041–6044. [Google Scholar] [CrossRef]
- Ciminelli, C.; Dell’Olio, F.; Brunetti, G.; Conteduca, D.; Armenise, M.N. New microwave photonic filter based on a ring resonator including a photonic crystal structure. In Proceedings of the 2017 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Ciminelli, C.; Innone, F.; Brunetti, G.; Conteduca, D.; Dell’Olio, F.; Tatoli, T.; Armenise, M.N. Rigorous model for the design of ultra-high Q-factor resonant cavities. In Proceedings of the 2016 18th International Conference on Transparent Optical Networks (ICTON), Trento, Italy, 10–14 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Spencer, D.T.; Bauters, J.F.; Heck, M.J.R.; Bowers, J.E. Integrated waveguide coupled Si3N4 resonators in the ultrahigh-Q regime. Optica 2014, 1, 153–157. [Google Scholar] [CrossRef]
- Brunetti, G.; Dell’Olio, F.; Conteduca, D.; Armenise, M.N.; Ciminelli, C. Ultra-Compact Tuneable Notch Filter Using Silicon Photonic Crystal Ring Resonator. J. Light. Technol. 2019, 37, 2970–2980. [Google Scholar] [CrossRef]
- Kang, Y.M.; Arbabi, A.; Goddard, L.L. Engineering the spectral reflectance of microring resonators with integrated reflective elements. Opt. Express 2010, 18, 16813–16825. [Google Scholar] [CrossRef]
- Shen, L.; Lu, L.; Guo, Z.; Zhou, L.; Chen, J. Silicon optical filters reconfigured from a 16 × 16 Benes switch matrix. Opt. Express 2019, 27, 16945–16957. [Google Scholar] [CrossRef]
- Chew, S.X.; Yi, X.; Song, S.; Li, L.; Bian, P.; Nguyen, L.; Minasian, R.A. Silicon-on-Insulator Dual-Ring Notch Filter for Optical Sideband Suppression and Spectral Characterization. J. Light. Technol. 2016, 34, 4705–4714. [Google Scholar] [CrossRef]
- Grover, R.; Van, V.; Ibrahim, T.; Absil, P.; Calhoun, L.; Johnson, F.; Hryniewicz, J.; Ho, P. Parallel-cascaded semiconductor microring resonators for high-order and wide-FSR filters. J. Light. Technol. 2002, 20, 872–877. [Google Scholar] [CrossRef]
- Capmany, J.; Munoz, P.; Domenech, J.D.; Muriel, M.A. Apodized coupled resonator waveguides. Opt. Express 2007, 15, 10196–10206. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, G.; Sasanelli, N.; Armenise, M.N.; Ciminelli, C. High performance and tunable optical pump-rejection filter for quantum photonic systems. Opt. Laser Technol. 2021, 139, 106978. [Google Scholar] [CrossRef]
- Capmany, J.; Domenech, D.; Muñoz, P. Silicon Graphene Reconfigurable CROWS and SCISSORS. IEEE Photonics J. 2015, 7, 2700609. [Google Scholar] [CrossRef]
- Dong, P.; Qian, W.; Liang, H.; Shafiiha, R.; Wang, X.; Feng, D.; Li, G.; Cunningham, J.E.; Krishnamoorthy, A.V.; Asghari, M. 1x4 reconfigurable demultiplexing filter based on free-standing silicon racetrack resonators. Opt. Express 2010, 18, 24504–24509. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Guan, H.; Liu, Y.; Chang, L.; Kuang, Y.; Tan, M.; Yu, Y.; Li, Z. Compact and Broadband Optical Add-Drop De-Multiplexer With Cascaded Elliptical Micro-Rings on SOI. IEEE Photonics Technol. Lett. 2019, 31, 451–454. [Google Scholar] [CrossRef]
- Chak, P.; Sipe, J.E. Minimizing finite-size effects in artificial resonance tunneling structures. Opt. Lett. 2006, 31, 2568–2570. [Google Scholar] [CrossRef]
- Landobasa, Y.; Darmawan, S.; Chin, M. Matrix analysis of 2-D microresonator lattice optical filters. IEEE J. Quantum Electron. 2005, 41, 1410–1418. [Google Scholar] [CrossRef]
- Little, B.E.; Chu, S.T.; Hryniewicz, J.V.; Absil, P.P. Filter synthesis for periodically coupled microring resonators. Opt. Lett. 2000, 25, 344–346. [Google Scholar] [CrossRef]
- Liu, H.C.; Yariv, A. Synthesis of high-order bandpass filters based on coupled-resonator optical waveguides (CROWs). Opt. Express 2011, 19, 17653–17668. [Google Scholar] [CrossRef] [PubMed]
- Chremmos, I.; Uzunoglu, N. Modes of the infinite square lattice of coupled microring resonators. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 2008, 25, 3043–3050. [Google Scholar] [CrossRef] [PubMed]
- Radjenovic, B.; Radmilovic-Radjenovic, M.; Belicev, P. Eigenmodes of finite length silicon-on-insulator microring resonator arrays. Opt. Quantum Electron. 2017, 49, 149. [Google Scholar] [CrossRef]
- Tobing, L.Y.M.; Dumon, P.; Baets, R.; Chin, M.K. Boxlike filter response based on complementary photonic bandgaps in two-dimensional microresonator arrays. Opt. Lett. 2008, 33, 2512–2514. [Google Scholar] [CrossRef]
- Guan, H.; Li, Z.Y.; Shen, H.H.; Wang, R.; Yu, Y.D. A Highly Compact Third-Order Silicon Elliptical Micro-Ring Add-Drop Filter with a Large Free Spectral Range. Chin. Phys. Lett. 2017, 34, 034210. [Google Scholar] [CrossRef]
- Popović, M.A.; Manolatou, C.; Watts, M.R. Coupling-induced resonance frequency shifts in coupled dielectric multi-cavity filters. Opt. Express 2006, 14, 1208–1222. [Google Scholar] [CrossRef]



| Structure | Passband Width | Sidelobe Suppression | OBR | IL |
|---|---|---|---|---|
| GHz | dB | dB | dB | |
| 2 rings [1] | 26.5 | NG | 40 | 1.05 |
| 2 rings [3] | 9–103 | 31–7.5 | NG | <3 |
| ring+grating [6] | 25–60 | >26.7 | NG | <3 |
| Benes switch [12] | 132.5 | 10 | >30 | 14.5 |
| arrays [26] | 755 | −25 | 50 | <3 |
| this work | 951 | −46 | 50 | ≤1.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, H.; Huang, X.; Tu, D.; Yu, H.; Yin, Y.; Yu, Z.; Li, Z. Two-Dimensional Elliptical Microresonator Arrays for Wide Flat Bandwidth and Boxlike Filter Response. Photonics 2022, 9, 814. https://doi.org/10.3390/photonics9110814
Guan H, Huang X, Tu D, Yu H, Yin Y, Yu Z, Li Z. Two-Dimensional Elliptical Microresonator Arrays for Wide Flat Bandwidth and Boxlike Filter Response. Photonics. 2022; 9(11):814. https://doi.org/10.3390/photonics9110814
Chicago/Turabian StyleGuan, Huan, Xingrui Huang, Donghe Tu, Hang Yu, Yuxiang Yin, Zhiguo Yu, and Zhiyong Li. 2022. "Two-Dimensional Elliptical Microresonator Arrays for Wide Flat Bandwidth and Boxlike Filter Response" Photonics 9, no. 11: 814. https://doi.org/10.3390/photonics9110814
APA StyleGuan, H., Huang, X., Tu, D., Yu, H., Yin, Y., Yu, Z., & Li, Z. (2022). Two-Dimensional Elliptical Microresonator Arrays for Wide Flat Bandwidth and Boxlike Filter Response. Photonics, 9(11), 814. https://doi.org/10.3390/photonics9110814





