Sensing Performance of Triple-Band Terahertz Metamaterial Absorber Based on Snowflake-Shaped Resonators
Abstract
1. Introduction
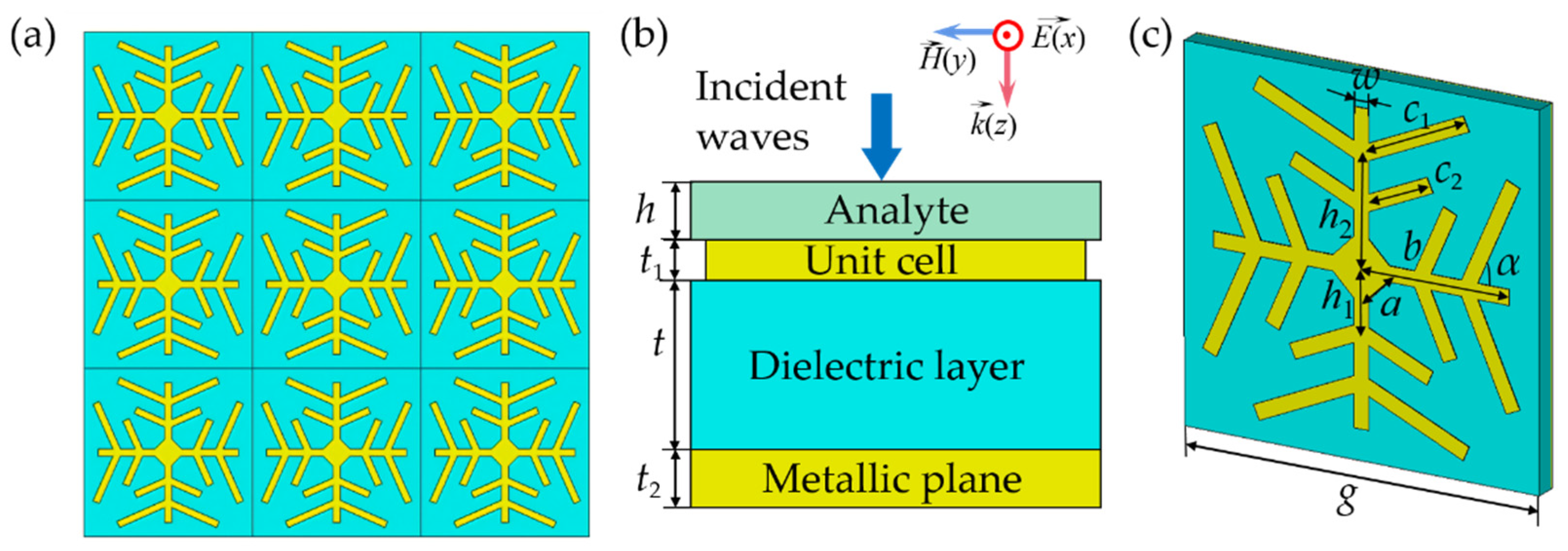
2. Structures and Methods
3. Results and Discussion
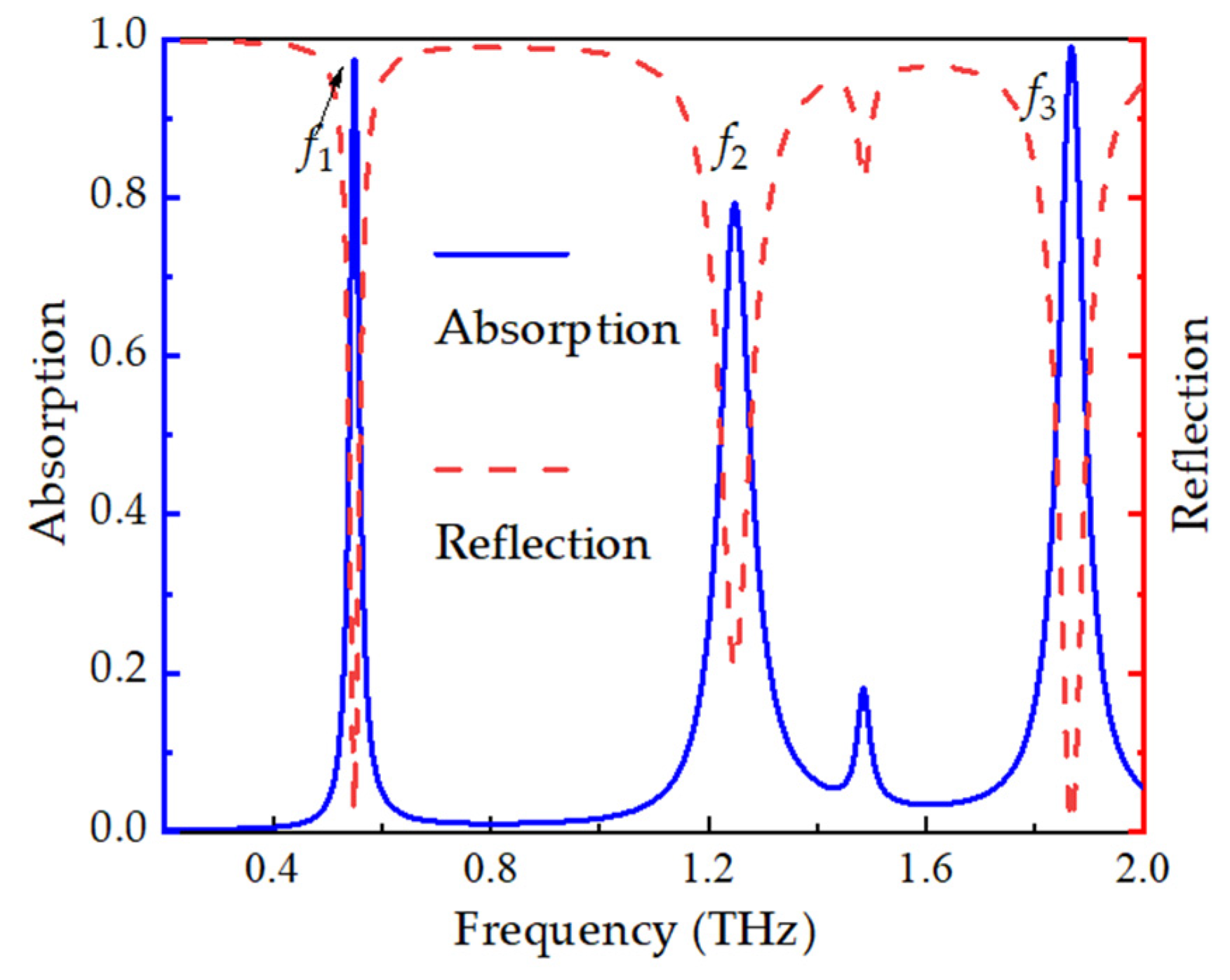
3.1. Structural Design of the Triple-Band THz Metamaterial Absorber
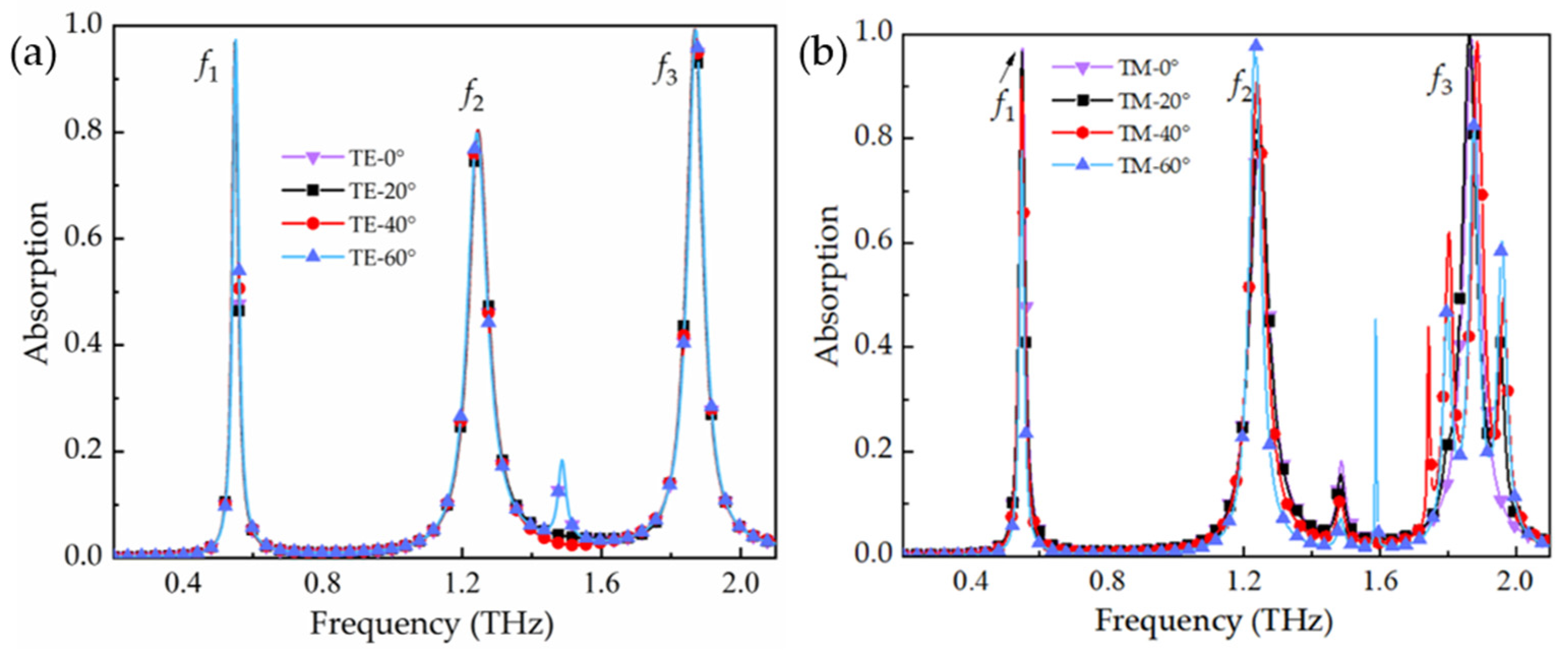
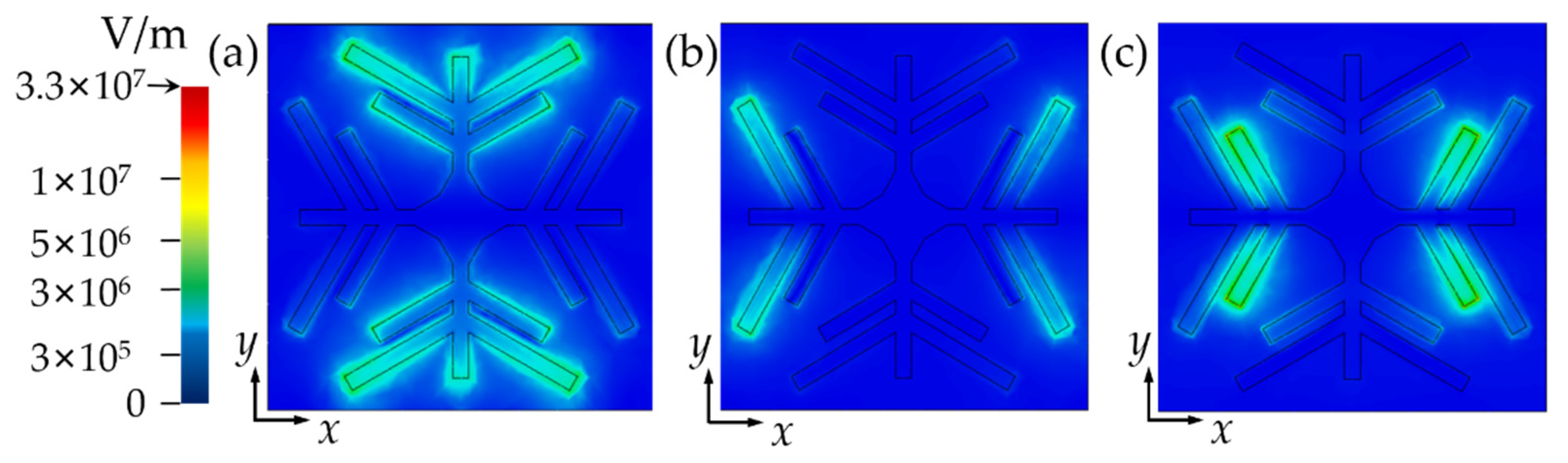
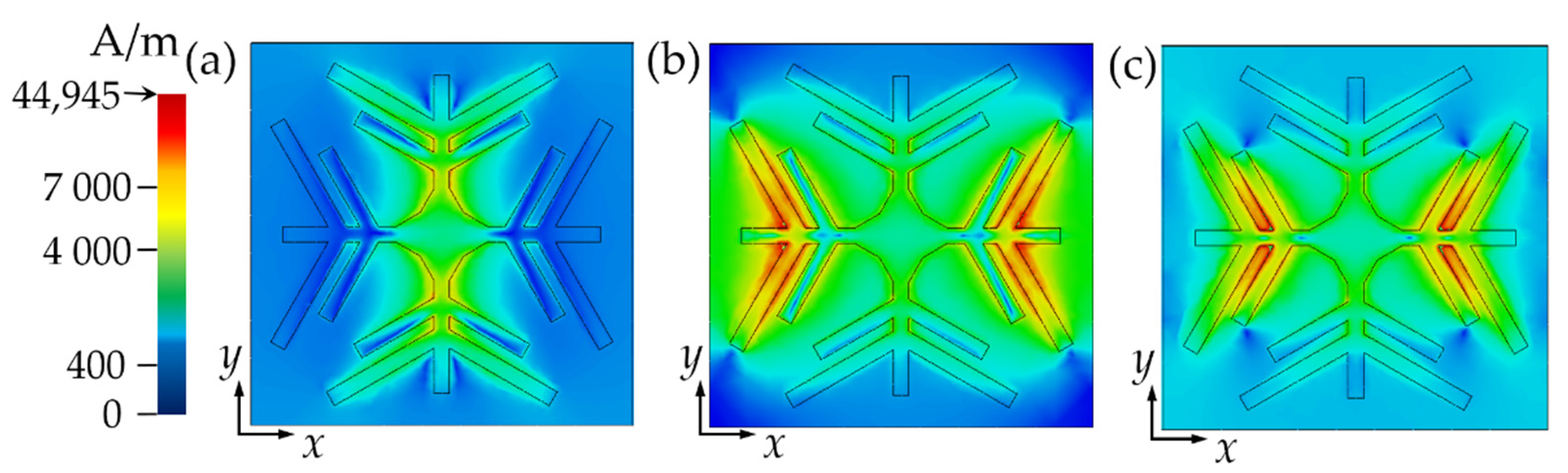
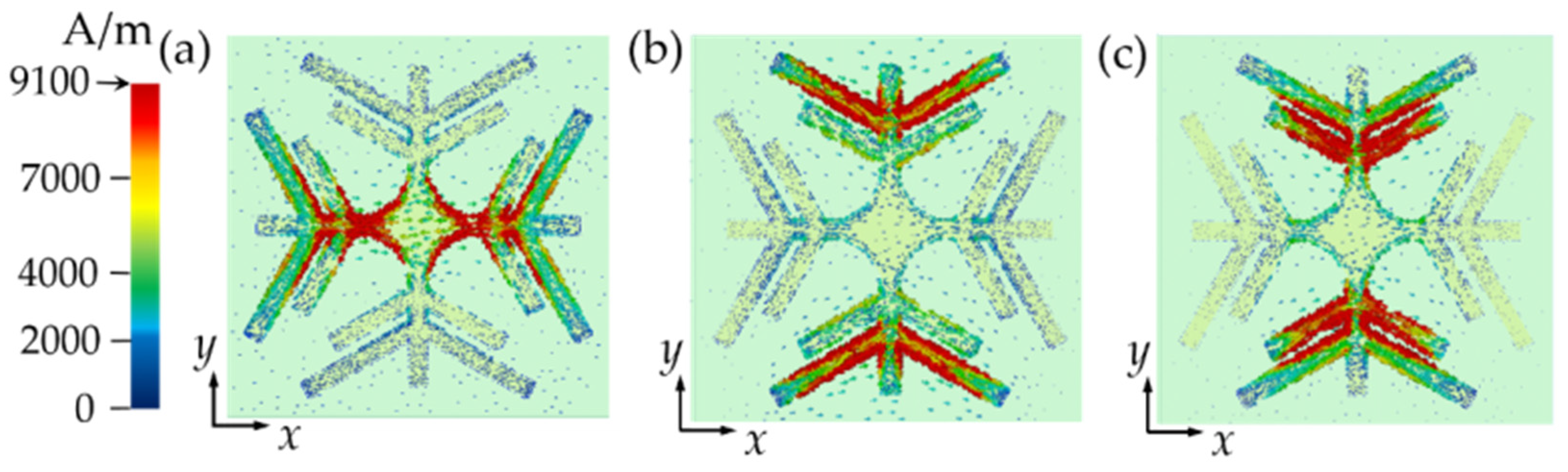
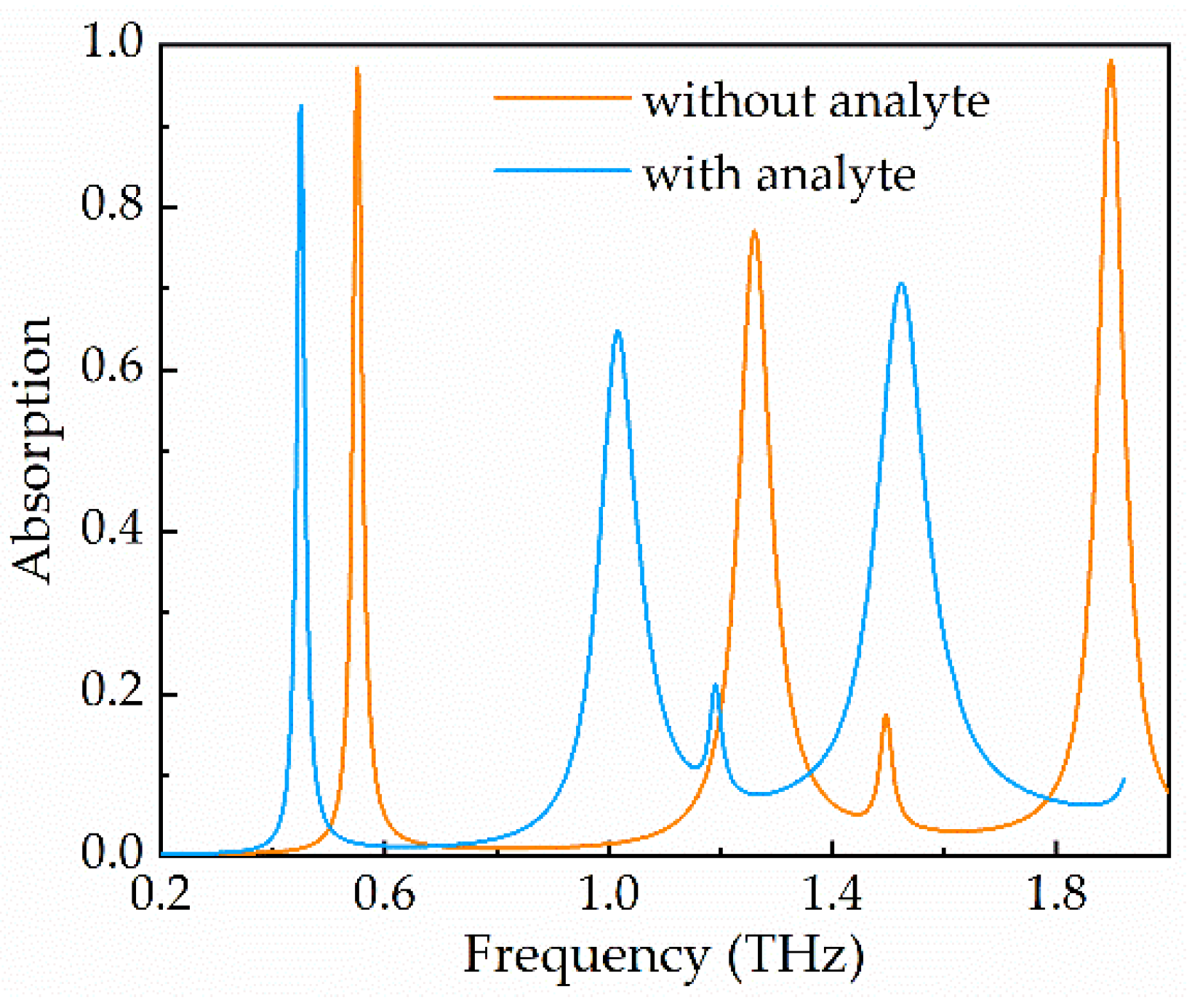
3.2. Absorption Mechanism of Triple-Band THz Metamaterial Absorber
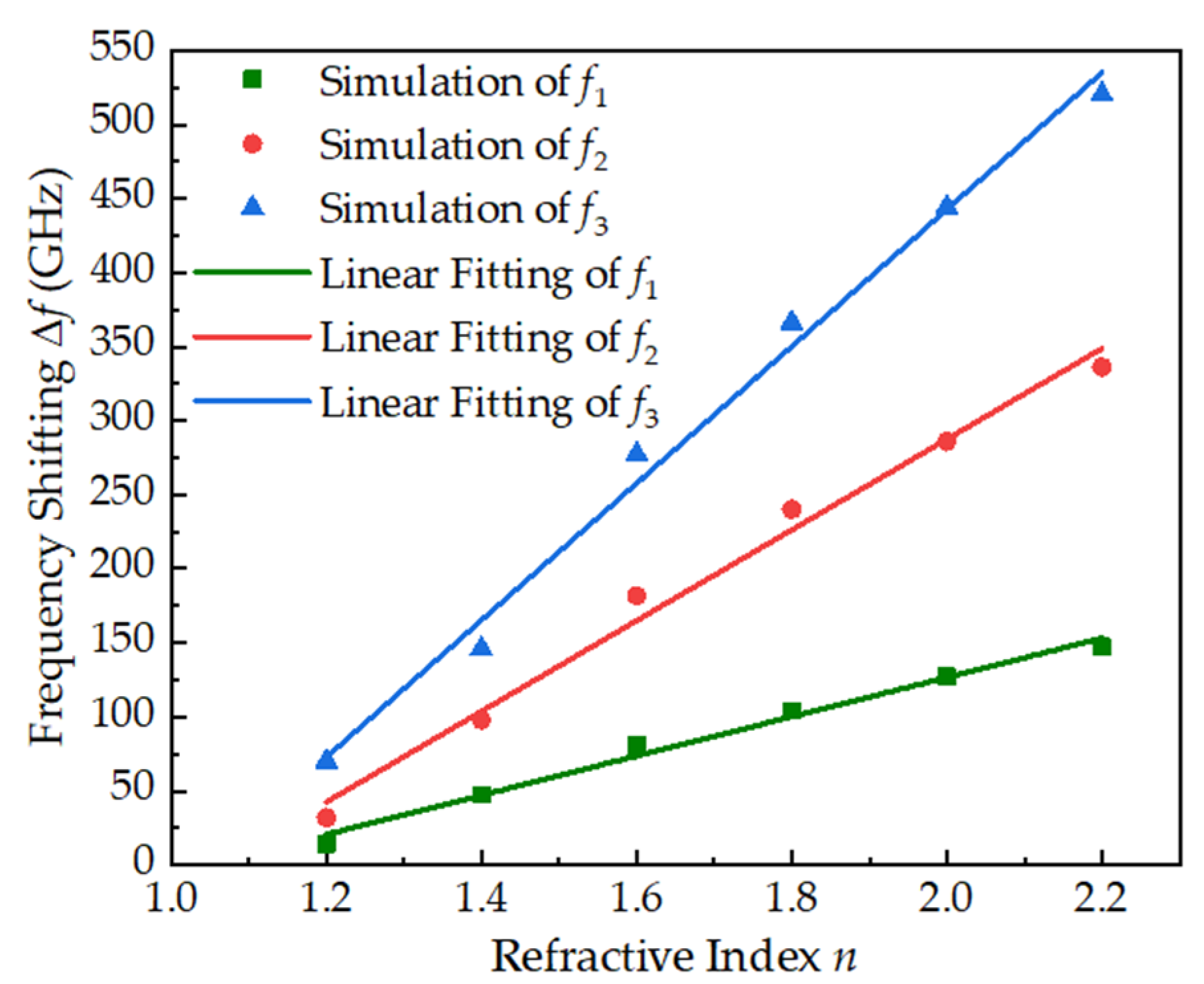
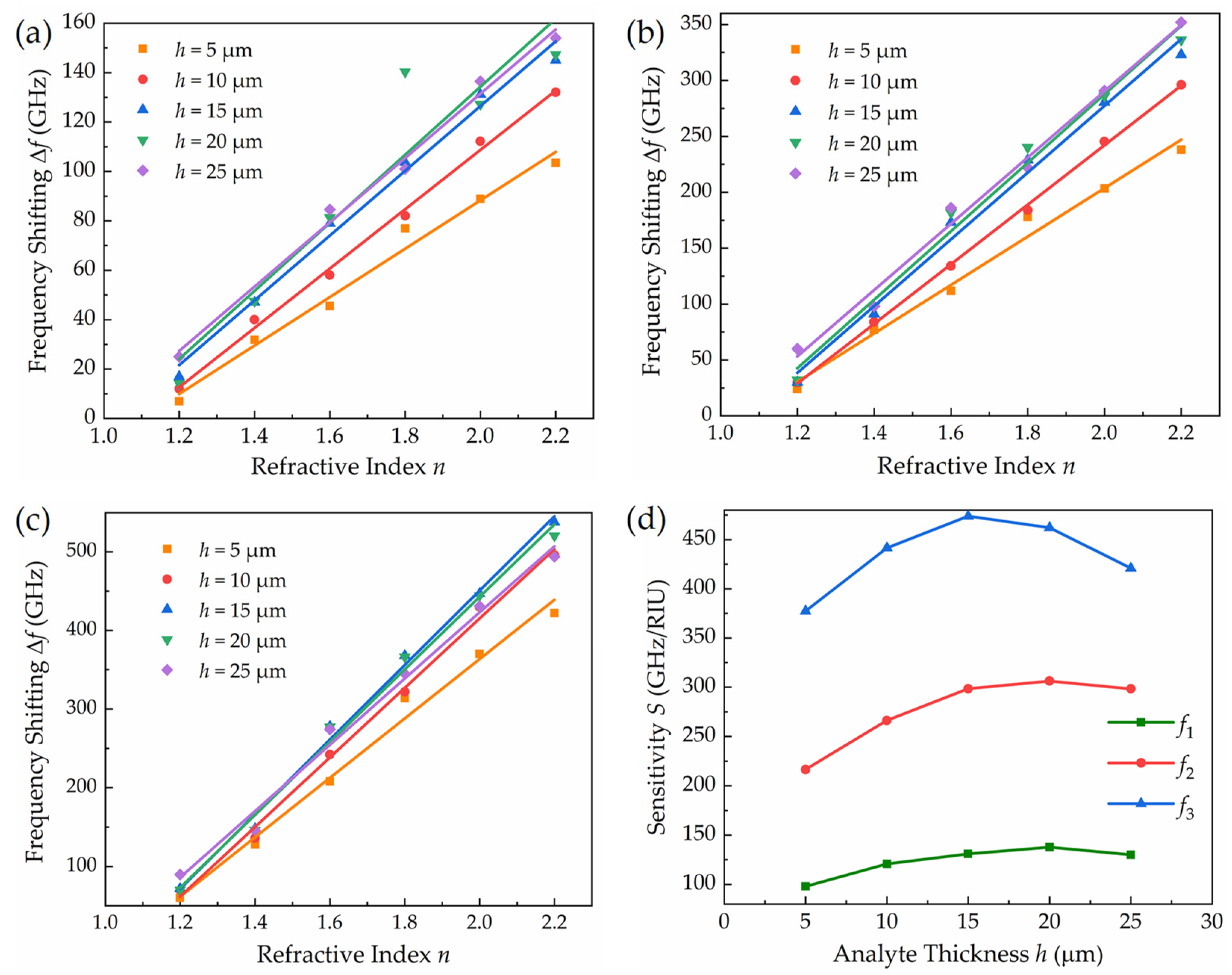
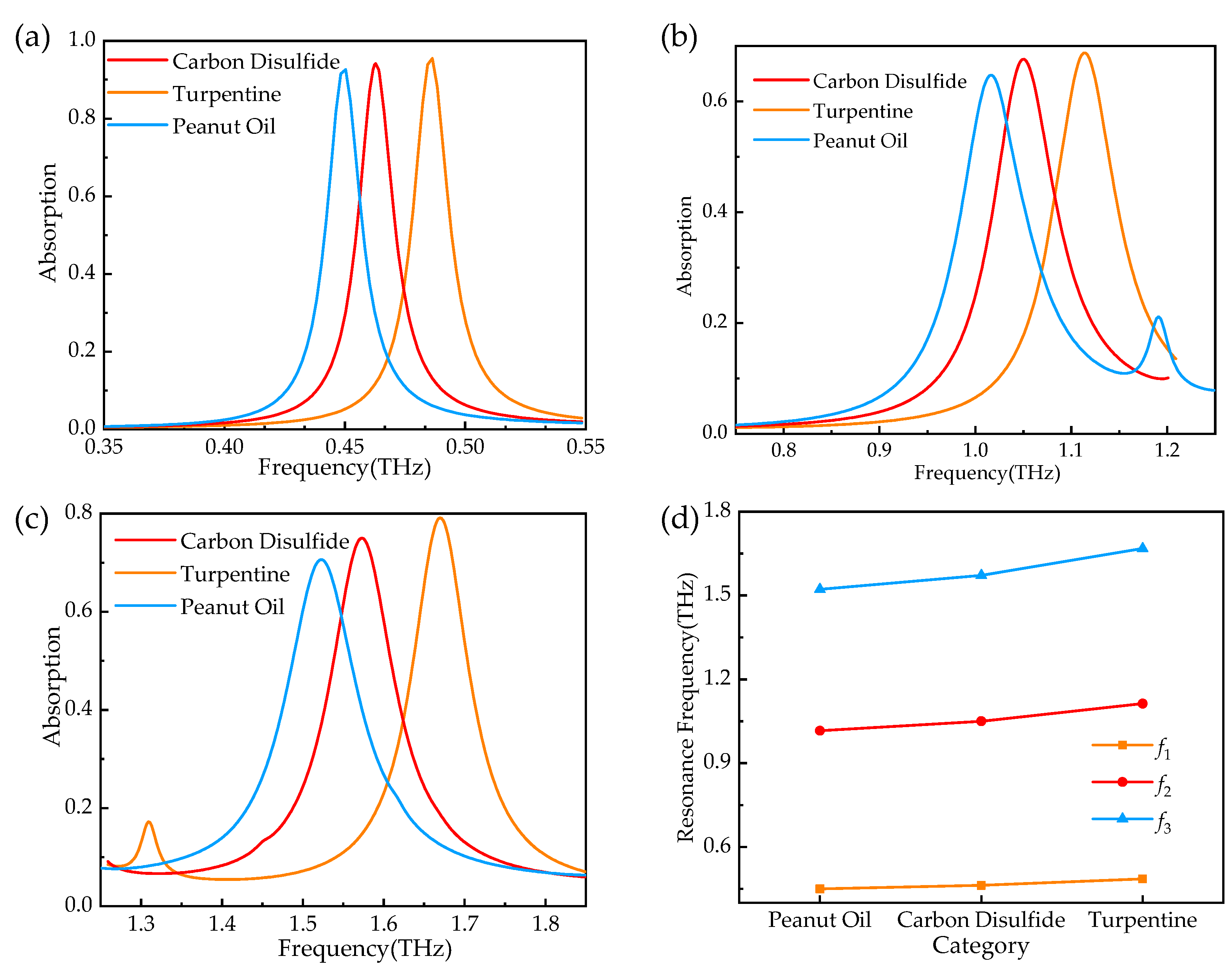
3.3. Sensing Characteristics of Triple-Band THz Metamaterial Absorber
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kayal, S.; Shaw, T.; Mitra, D. Design of miniaturized highly sensitive liquid sensor at microwave frequency. Int. J. RF Microw. Comput.-Aided Eng. 2020, 30, e22387. [Google Scholar] [CrossRef]
- Ma, X.X.; Chen, K.X.; Wu, J.Y.; Wang, L.F. Low-Cost and Highly Sensitive Liquid Refractive Index Sensor Based on Polymer Horizontal Slot Waveguide. Photonic Sens. 2020, 10, 7–15. [Google Scholar] [CrossRef]
- Romain, X.; Baida, F.; Boyer, P. Extended Malus’ Law with THz metallic metamaterials for sensitive detection with giant tunable quality factor. Phys. Rev. B 2016, 5, 045407. [Google Scholar] [CrossRef]
- Su, Z.X.; Yin, J.B.; Zhao, X.P. Terahertz dual-band metamaterial absorber based on graphene/MgF2 multilayer structures. Opt. Express 2015, 23, 1679–1690. [Google Scholar] [CrossRef]
- Sun, S.L.; He, Q.; Hao, J.M.; Xiao, S.Y.; Zhou, L. Electromagnetic metasurfaces: Physics and applications. Adv. Opt. Photonics. 2019, 380, 380–479. [Google Scholar] [CrossRef]
- Sotsky, A.B.; Nazarov, M.M.; Miheev, S.S.; Sotskaya, L.I. Sensitivity of Reflecting Terahertz Sensors of Aqueous Solutions. Tech. Phys. 2021, 66, 305–315. [Google Scholar] [CrossRef]
- Hossain, B.; Rahaman, E.; Mondal, H.S.; Kabiraj, S.; Raihan, M. Design and optimization of the perilous chemical sensor in the terahertz frequency range. Mater. Today Proc. 2020, 43, 3720–3724. [Google Scholar]
- Tang, Q.; Liang, M.; Lu, Y.; Wong, P.K.; Wilmink, G.J.; Zhang, D.; Xin, H. Microflfluidic devices for terahertz spectroscopy of live cells toward lab-on-a-chip applications. Sensors 2016, 16, 476. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Chang, H.C.; Chan, P.Y.; Friend, J.R. Microflfluidic devices for bioapplications. Small 2011, 7, 12–48. [Google Scholar] [CrossRef]
- Zhang, R.; Cherr, Q.M.; Liu, K.; Chen, Z.F.; Li, K.D.; Xu, J.B. Terahertz Microfluidic Metamaterial Biosensor for Tiny Volume Liquid Samples. In Proceedings of the 2018 43rd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Nagoya, Japan, 9–14 September 2018; pp. 1–2. [Google Scholar]
- Barroso, R.H.; Malpica, W. An Overview of Electromagnetic Metamaterials. IEEE Lat. Am. Trans. 2020, 18, 1862–1873. [Google Scholar] [CrossRef]
- Mirzaei, S.; Green, N.G.; Rotaru, M.; Pu, S.H. Detecting and identifying DNA via the THz backbone frequency using a metamaterial-based label-free biosensor. In Terahertz, RF, Millimeter, and Submillimeter-Wave Technology and Applications X; Proc SPIE: Bellingham, WA, USA, 2017; Volume 12, pp. 101031–101038. [Google Scholar]
- Janneh, M.; Marcellis, A.D.; Palange, E.; Tenggara, A.T.; Byun, D. Design of a metasurface-based dual-band Terahertz perfect absorber with very high Q-factors for sensing applications,ptics Communications. Opt. Commun. 2018, 416, 152–159. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Hameed, M.F.O.; Elkaramany, E.M.A.; Obayya, S.S.A. Highly Sensitive Terahertz Metamaterial Sensor. IEEE Sens. J. 2019, 19, 7993–7999. [Google Scholar] [CrossRef]
- Mayani, M.G.; Herraiz-Martínez, F.J.; Domingo, J.M.; Giannetti, R. Resonator-Based Microwave Metamaterial Sensors for Instrumentation: Survey, Classification, and Performance Comparison. IEEE Trans. Instrum. Meas. 2021, 70, 9503414. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Pratap, D.; Srivastava, K.V.; Ramakrishna, S.A. Highly Sensitive Permittivity Sensor Using an Inhomogeneous Metamaterial Cylindrical Waveguide. IEEE Sens. J. 2021, 21, 9120–9127. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.L. Terahertz Metamaterial Absorber Sensor Based on Three-Dimensional Split-Ring Resonator Array and Microfluidic Channel. Acta Optica Sinica 2020, 19, 19–26. [Google Scholar]
- Cheng, Q.Q.; Zhang, C.S.; Yu, D.; Chen, L.; Xie, J.Y.; Zang, X.F.; Shkurinov, A.; Zhu, Y.M.; Zhang, S.L. Manipulation of the terahertz leaky wave by metal–dielectric–metal metasurface. Appl. Phys. Express 2019, 12, 072008. [Google Scholar] [CrossRef]
- Wang, B.X.; Wang, G.Z.; Sang, T. Simple design of novel triple-band terahertz metamaterial absorber for sensing application. Phys. D Appl. Phys. 2016, 46, 165307. [Google Scholar] [CrossRef]
- Pang, H.Z.; Wang, X.; Wang, J.L.; Wang, Z.L.; Liu, S.Y.; Tian, H.Q. Sensing characteristics of dual band terahertz metamaterial absorber sensor. Acta Phys. 2021, 70, 168101. [Google Scholar] [CrossRef]
- Lan, F.; Luo, F.; Mazumder, P.; Yang, Z.Q.; Meng, L.; Bao, Z.Q.; Zhou, J.; Zhang, Y.X.; Liang, L.X.; Shi, Z.J.; et al. Dual-band refractometric terahertz biosensing with intense wave-matter-overlap microfluidic channel. Biomed. Opt. Express 2019, 10, 3789–3799. [Google Scholar] [CrossRef]
- Yang, J.P.; Wang, M.C.; De, H.; Kang, Y.; Li, Z.R.; Liu, Q.C.; Xiong, L.; Wu, Z.X.; Qu, W.W.; Shang, L.P. Dual-Band Terahertz Sensor Based on Metamaterial Absorber Integrated Microfluidic. Acta Optica Sinica 2021, 41, 2428001. [Google Scholar]
- Lu, T.G.; Zhang, D.; Qiu, P.; Lian, J.; Jing, M.; Yu, B.; Wen, J. Ultrathin Terahertz Dual-Band Perfect Metamaterial Absorber Using Asymmetric Double-Split Rings Resonator. Symmetry 2018, 10, 293. [Google Scholar] [CrossRef]
- Yao, Y.; Li, S.; Zhu, L.; Wu, F.; He, X.; Jiang, J. Multi-band terahertz metamaterial absorber for sensing application. Integr. Ferroelectr. 2018, 190, 149–155. [Google Scholar] [CrossRef]
- Yin, X.; Chen, L.; Li, X. Ultra-Broadband Super Light Absorber Based on Multi-Sized Tapered Hyperbolic Metamaterial Waveguide Arrays. J. Light. Technol. 2015, 33, 3704–3710. [Google Scholar] [CrossRef]
- Yin, X.; Long, C.; Li, J.H.; Zhu, H.; Chen, L.; Guan, J.G.; Li, X. Ultra-wideband microwave absorber by connecting multiple absorption bands of two different-sized hyperbolic metamaterial waveguide arrays. Sci. Rep. 2015, 5, 15367. [Google Scholar] [CrossRef] [PubMed]
- Fan, R.H.; Xiong, B.; Peng, R.W.; Wang, M. Constructing Metastructures with Broadband Electromagnetic Functionality. Adv. Mater. 2019, 32, 1904646. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Ou, Y.H.; Wang, S.Y.; Meng, Y.Z.; Wang, Z.; Zhai, X.; Wang, L.L.; Xia, S.X. Ultrahigh-Q Tunable Terahertz Absorber Based on Bulk Dirac Semimetal with Surface Lattice Resonance. Photonics 2022, 9, 22. [Google Scholar] [CrossRef]
- Yan, F.; Li, L.; Wang, R.; Tian, H.; Liu, J.; Liu, J.; Tian, F.; Zhang, J. Ultrasensitive Tunable Terahertz Sensor with Graphene Plasmonic Grating. J. Light. Technol. 2019, 12, 1103–1112. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Q.; Yang, J.; Zhao, J.; Cui, T.J. Broadband metamaterial for optical transparency and microwave absorption. Appl. Phys. Lett. 2017, 110, 143511. [Google Scholar] [CrossRef]
- Xiao, W.F.; Ou, Y.H.; Wang, S.Y.; Wang, S.; Meng, Y.Z.; Xiang, Z.; Xia, S.X.; Wang, L. Ultra-high sensitivity terahertz sensor based on a five-band absorber. J. Opt. 2022, 24, 055102. [Google Scholar] [CrossRef]

| References | Resonant Frequency (THz) | Absorption | Sensitivity (GHz/RIU) | Q Factor | FoM | |
|---|---|---|---|---|---|---|
| Ref. [10] | 2.06 | / | 72 | / | 1.58 | |
| Ref. [17] | 0.79 | 98.8% | 379 | 53 | 25 | |
| Ref. [21] | 0.378 0.694 | 99% 98% | 39.5 85 | 28.1 29.3 | 2.94 12.5 | |
| Ref. [22] | Design A | 0.64 0.88 | 99% 99% | 32 44 | 10.3 15 | / / |
| Design B | 0.6 0.86 | 96.8% 96.8% | 30 43 | 9.7 14.8 | / / | |
| Ref. [23] | 4.48 4.76 | 98.6% 98.5% | / / | / / | / / | |
| Ref. [24] | 0.64 1.94 2.67 | / / / | 119 248 662 | / / / | / / / | |
| This paper | 0.55 1.249 1.867 | 97.43% 79.22% 99.02% | 137.70 306.25 473.86 | 26.01 17.83 58.04 | 3.14 2.33 6.46 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Liu, Y.; Zhu, Y.; Gu, W. Sensing Performance of Triple-Band Terahertz Metamaterial Absorber Based on Snowflake-Shaped Resonators. Photonics 2022, 9, 777. https://doi.org/10.3390/photonics9100777
Ma L, Liu Y, Zhu Y, Gu W. Sensing Performance of Triple-Band Terahertz Metamaterial Absorber Based on Snowflake-Shaped Resonators. Photonics. 2022; 9(10):777. https://doi.org/10.3390/photonics9100777
Chicago/Turabian StyleMa, Limin, Yuhuang Liu, Yongkai Zhu, and Wenhua Gu. 2022. "Sensing Performance of Triple-Band Terahertz Metamaterial Absorber Based on Snowflake-Shaped Resonators" Photonics 9, no. 10: 777. https://doi.org/10.3390/photonics9100777
APA StyleMa, L., Liu, Y., Zhu, Y., & Gu, W. (2022). Sensing Performance of Triple-Band Terahertz Metamaterial Absorber Based on Snowflake-Shaped Resonators. Photonics, 9(10), 777. https://doi.org/10.3390/photonics9100777





