Broadband Supercontinuum Generation in Dispersion Decreasing Fibers in the Spectral Range 900–2400 nm
Abstract
1. Introduction
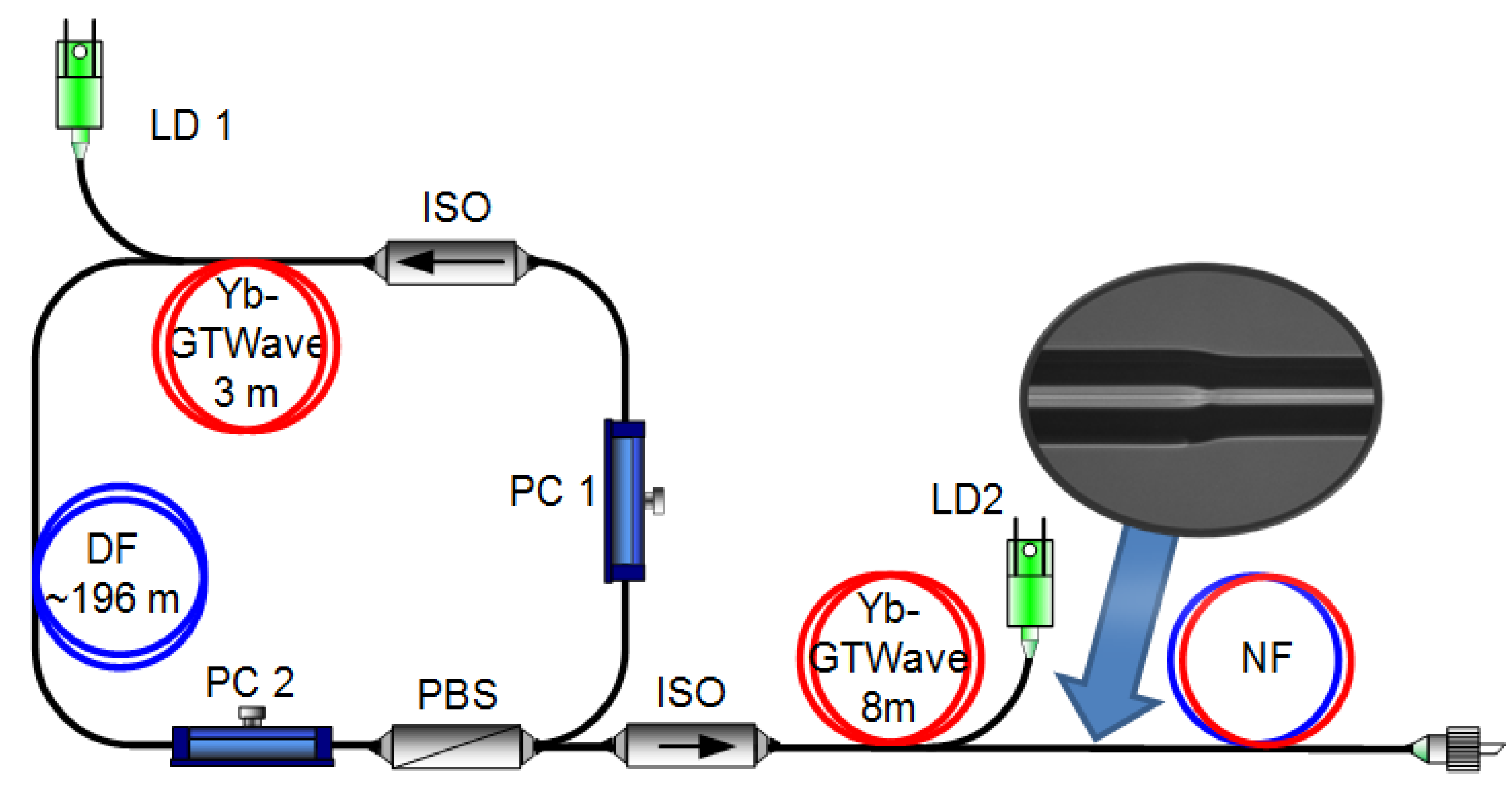
2. Experimental Setup
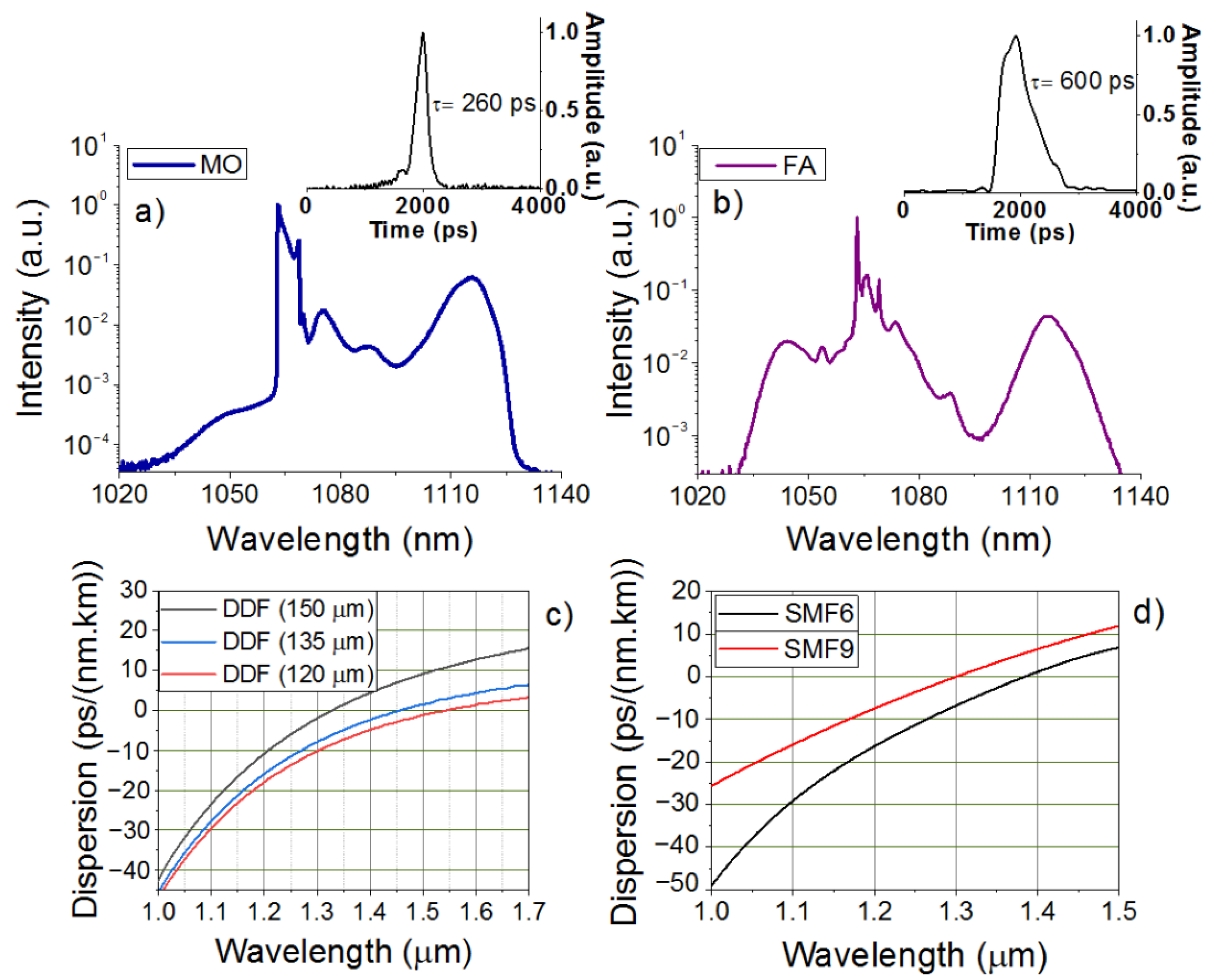
2.1. MO and Amplifier
2.2. Researched Fibers
3. Results and Discussion
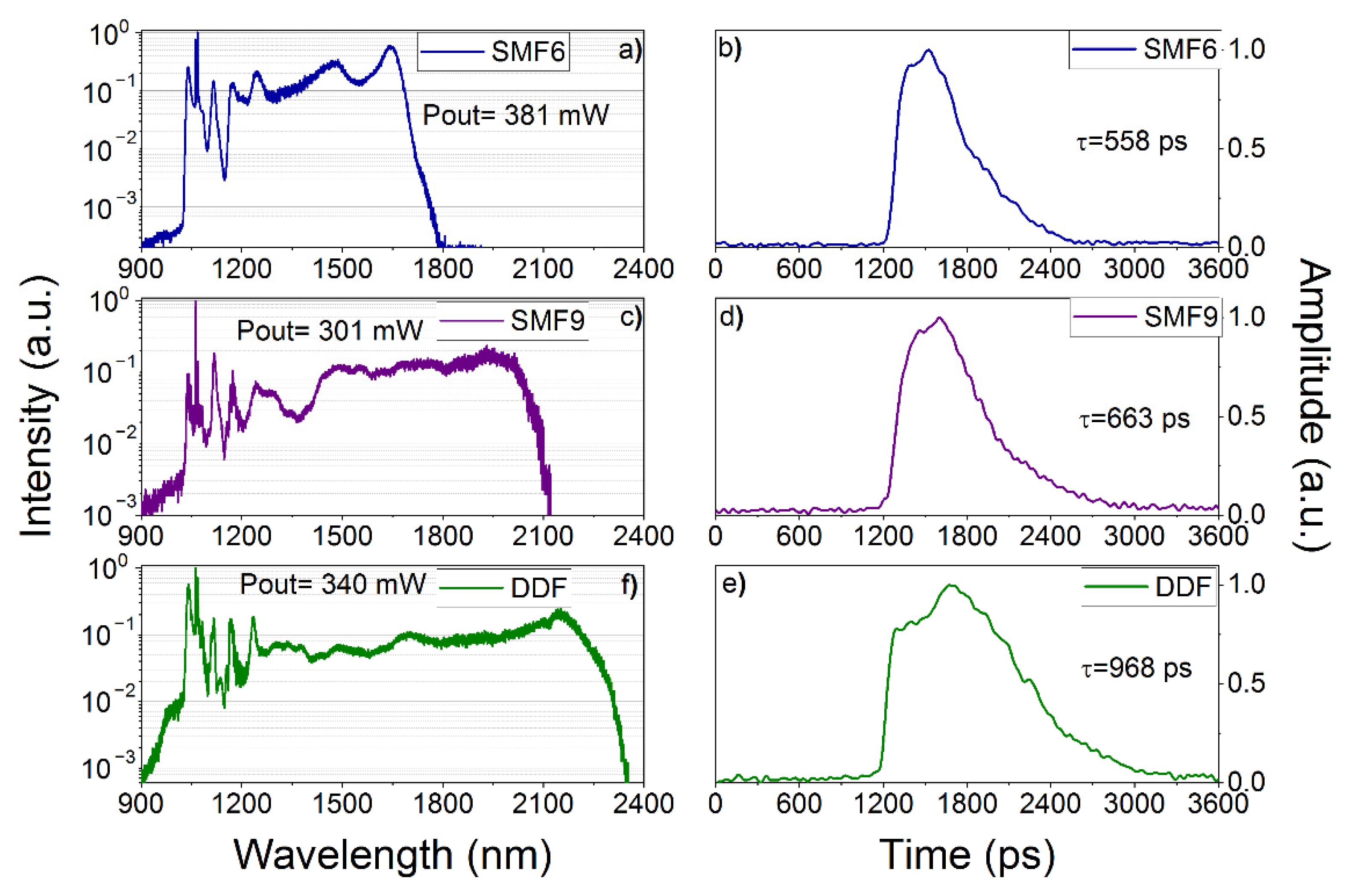
3.1. Standard Fibers versus DDF
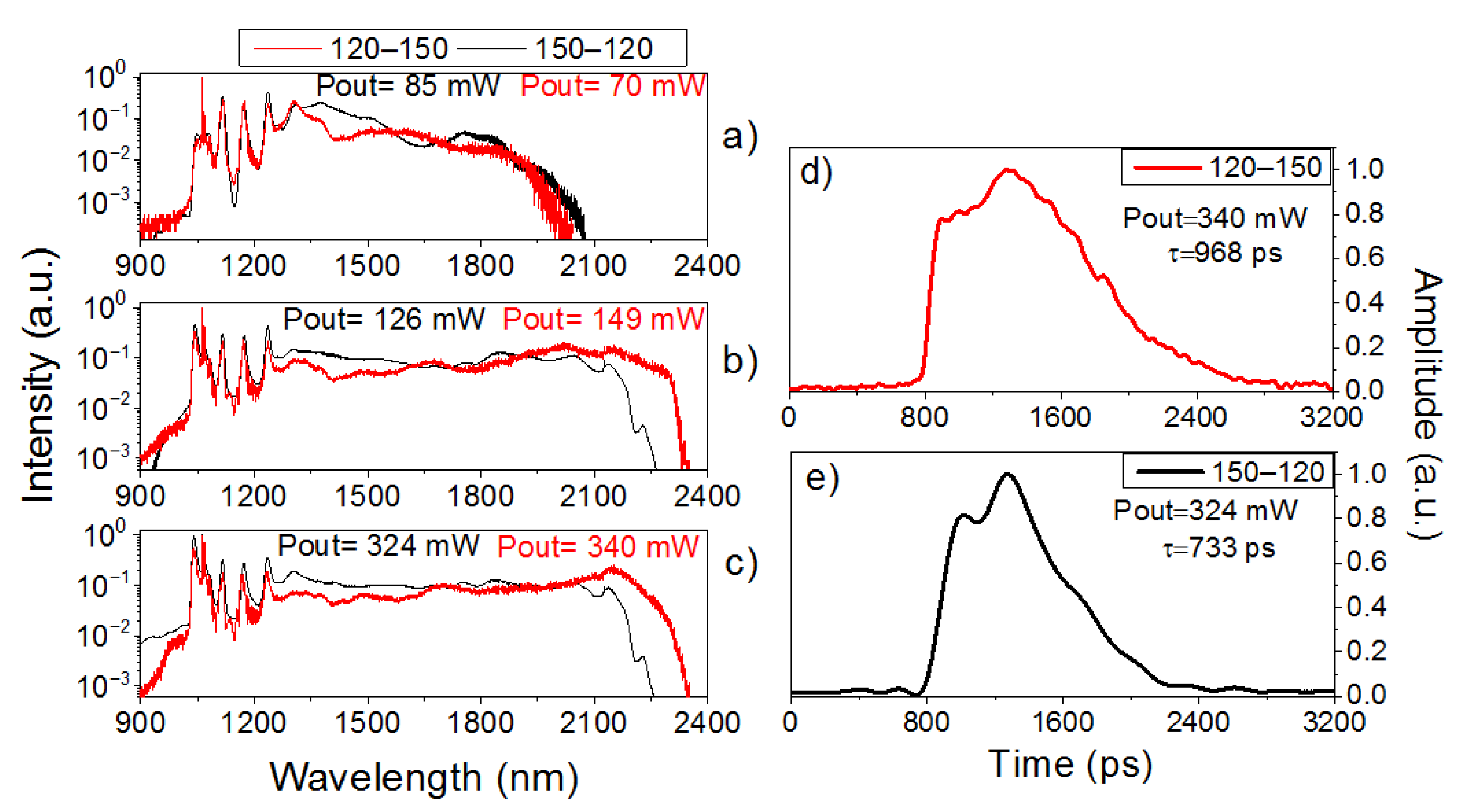
3.2. SC Generation Depending on Propagation Direction in DDF
3.3. Numerical Simulation of SC Generation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dorsinville, R.; Ho, P.P.; Manassah, J.T.; Alfano, R.R. Applications of Supercontinuum: Present and Future. In Book The Supercontinuum Laser Source; Alfano, R.R., Ed.; Springer: New York, NY, USA, 1989; Volume 9, pp. 377–398. [Google Scholar]
- Lambert-Girard, S.; Allard, M.; Piché, M.; Babin, F. Differential Optical Absorption Spectroscopy Lidar for Mid-Infrared Gaseous Measurements. Appl. Opt. 2015, 54, 1647. [Google Scholar] [CrossRef]
- Bartlome, R.; Sigrist, M.W. Laser-Based Human Breath Analysis: D/H Isotope Ratio Increase Following Heavy Water Intake. Opt. Lett. 2009, 34, 866. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Reyes, A.; Hou, Z.; van Mastrigt, E.; Horsten, R.C.; de Jongste, J.C.; Pijnenburg, M.W.; Urbach, H.P.; Bhattacharya, N. Multicomponent Gas Analysis Using Broadband Quantum Cascade Laser Spectroscopy. Opt. Express 2014, 22, 18299. [Google Scholar] [CrossRef] [PubMed]
- Dupont, S.; Petersen, C.; Thøgersen, J.; Agger, C.; Bang, O.; Keiding, S.R. IR Microscopy Utilizing Intense Supercontinuum Light Source. Opt. Express 2012, 20, 4887. [Google Scholar] [CrossRef] [PubMed]
- Seddon, A.B. Mid-Infrared (IR)—A Hot Topic: The Potential for Using Mid-IR Light for Non-Invasive Early Detection of Skin Cancerin Vivo. Phys. Status Solidi B 2013, 250, 1020–1027. [Google Scholar] [CrossRef]
- Hartl, I.; Li, X.D.; Chudoba, C.; Ghanta, R.K.; Ko, T.H.; Fujimoto, J.G.; Ranka, J.K.; Windeler, R.S. Ultrahigh-Resolution Optical Coherence Tomography Using Continuum Generation in an Air–Silica Microstructure Optical Fiber. Opt. Lett. 2001, 26, 608. [Google Scholar] [CrossRef]
- Ohara, T.; Takara, H.; Yamamoto, T.; Masuda, H.; Morioka, T.; Abe, M.; Takahashi, H. Over-1000-Channel Ultradense WDM Transmission with Supercontinuum Multicarrier Source. J. Lightwave Technol. 2006, 24, 2311–2317. [Google Scholar] [CrossRef]
- Pivtsov, V.S.; Nyushkov, B.N.; Korel’, I.I.; Koliada, N.A.; Farnosov, S.A.; Denisov, V.I. Development of a Prototype Compact Fibre Frequency Synthesiser for Mobile Femtosecond Optical Clocks. Quantum Electron. 2014, 44, 507–514. [Google Scholar] [CrossRef]
- Smirnov, S.V.; Ania-Castanon, J.D.; Ellingham, T.J.; Kobtsev, S.M.; Kukarin, S.; Turitsyn, S.K. Optical Spectral Broadening and Supercontinuum Generation in Telecom Applications. Opt. Fiber Technol. 2006, 12, 122–147. [Google Scholar] [CrossRef]
- Genty, G.; Coen, S.; Dudley, J.M. Fiber Supercontinuum Sources (Invited). J. Opt. Soc. Am. B 2007, 24, 1771. [Google Scholar] [CrossRef]
- Fotiadi, A.A.; Mégret, P. Self-Q-Switched Er-Brillouin Fiber Source with Extra-Cavity Generation of a Raman Supercontinuum in a Dispersion-Shifted Fiber. Opt. Lett. 2006, 31, 1621. [Google Scholar] [CrossRef] [PubMed]
- Dolg, M.; Stoll, H. Handbook on the physics and chemistry of rare earths. Z. Fur Krist. Cryst. Mater. 1995, 22, 976–977. [Google Scholar]
- Lei, C.; Song, R.; Chen, Z.; Pu, D.; Hou, J. Supercontinuum Generation in an Ytterbium-Doped Fiber Amplifier With Cascaded Double-Clad Passive Fiber Tapers. IEEE Photonics J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Tao, G.; Ebendorff-Heidepriem, H.; Stolyarov, A.M.; Danto, S.; Badding, J.V.; Fink, Y.; Ballato, J.; Abouraddy, A.F. Infrared Fibers. Adv. Opt. Photon. 2015, 7, 379. [Google Scholar] [CrossRef]
- Sylvestre, T.; Genier, E.; Ghosh, A.N.; Bowen, P.; Genty, G.; Troles, J.; Mussot, A.; Peacock, A.C.; Klimczak, M.; Heidt, A.M.; et al. Recent Advances in Supercontinuum Generation in Specialty Optical Fibers [Invited]. J. Opt. Soc. Am. B 2021, 38, F90. [Google Scholar] [CrossRef]
- Zheltikov, A.M. Let there be white light: Supercontinuum generation by ultrashort laser pulses. Usp. Fiz. Nauk 2006, 176, 623. [Google Scholar] [CrossRef]
- Dai, S.; Wang, Y.; Peng, X.; Zhang, P.; Wang, X.; Xu, Y. A Review of Mid-Infrared Supercontinuum Generation in Chalcogenide Glass Fibers. Appl. Sci. 2018, 8, 707. [Google Scholar] [CrossRef]
- Harshavardhan Reddy, P.; Kir’yanov, A.V.; Dhar, A.; Das, S.; Dutta, D.; Pal, M.; Barmenkov, Y.O.; Minguella-Gallardo, J.A.; Bhadra, S.K.; Paul, M.C. Fabrication of Ultra-High Numerical Aperture GeO_2-Doped Fiber and Its Use for Broadband Supercontinuum Generation. Appl. Opt. 2017, 56, 9315. [Google Scholar] [CrossRef]
- Jain, D.; Sidharthan, R.; Woyessa, G.; Moselund, P.M.; Bowen, P.; Yoo, S.; Bang, O. Scaling Power, Bandwidth, and Efficiency of Mid-Infrared Supercontinuum Source Based on a GeO2-Doped Silica Fiber. J. Opt. Soc. Am. B 2018, 36, A86. [Google Scholar] [CrossRef]
- Kamynin, V.A.; Kurkov, A.S.; Mashinsky, V.M. Supercontinuum Generation up to 2.7 Μm in the Germanate-Glass-Core and Silica-Glass-Cladding Fiber. Laser Phys. Lett. 2012, 9, 219–222. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Andrianov, A.V.; Koptev, M.Y.; Muravyev, S.V.; Kim, A.V. Towards Mid-Infrared Supercontinuum Generation With Germano-Silicate Fibers. IEEE J. Select. Topics Quantum Electron. 2014, 20, 643–650. [Google Scholar] [CrossRef]
- Wang, X.; Yao, C.; Li, P.; Yang, L.; Ren, G.; Wu, Y.; Wang, C. High-Power All-Fiber Supercontinuum Laser Based on Germania-Doped Fiber. IEEE Photon. Technol. Lett. 2021, 33, 1301–1304. [Google Scholar] [CrossRef]
- Tausenev, A.V.; Kryukov, P.G.; Bubnov, M.M.; Likhachev, M.E.; Romanova, E.Y.; Yashkov, M.V.; Khopin, V.F.; Salganskii, M.Y. Efficient Source of Femtosecond Pulses and Its Use for Broadband Supercontinuum Generation. Quantum Electron. 2005, 35, 581–585. [Google Scholar] [CrossRef]
- Yu, C.X.; Haus, H.A.; Ippen, E.P.; Wong, W.S.; Sysoliatin, A. Gigahertz-Repetition-Rate Mode-Locked Fiber Laser for Continuum Generation. Opt. Lett. 2000, 25, 1418. [Google Scholar] [CrossRef] [PubMed]
- Hudson, D.D.; Antipov, S.; Li, L.; Alamgir, I.; Hu, T.; Amraoui, M.E.; Messaddeq, Y.; Rochette, M.; Jackson, S.D.; Fuerbach, A. Toward All-Fiber Supercontinuum Spanning the Mid-Infrared. Optica 2017, 4, 1163. [Google Scholar] [CrossRef]
- Qi, X.; Chen, S.; Li, Z.; Liu, T.; Ou, Y.; Wang, N.; Hou, J. High-Power Visible-Enhanced All-Fiber Supercontinuum Generation in a Seven-Core Photonic Crystal Fiber Pumped at 1016 Nm. Opt. Lett. 2018, 43, 1019. [Google Scholar] [CrossRef] [PubMed]
- Chernikov, S.V.; Richardson, D.J.; Dianov, E.M.; Payne, D.N. Picosecond Soliton Pulse Compressor Based on Dispersion Decreasing Fibre. Electron. Lett. 1992, 28, 1842. [Google Scholar] [CrossRef]
- Gordon, J.P. Theory of the Soliton Self-Frequency Shift. Opt. Lett. 1986, 11, 662. [Google Scholar] [CrossRef]
- Cundiff, S.T.; Weiner, A.M. Optical Arbitrary Waveform Generation. Nature Photon 2010, 4, 760–766. [Google Scholar] [CrossRef]
- Bres, C.-S.; Glesk, I.; Prucnal, P.R. Demonstration of an Eight-User 115-Gchip/s Incoherent OCDMA System Using Supercontinuum Generation and Optical Time Gating. IEEE Photon. Technol. Lett. 2006, 18, 889–891. [Google Scholar] [CrossRef]
- Bufetov, I.A.; Bubnov, M.M.; Mel’kumov, M.A.; Dudin, V.V.; Shubin, A.V.; Semenov, S.L.; Kravtsov, K.S.; Gur’yanov, A.N.; Yashkov, M.V.; Dianov, E.M. Yb-, Er—Yb-, and Nd-Doped Fibre Lasers Based on Multi-Element First Cladding Fibres. Quantum Electron. 2005, 35, 328–334. [Google Scholar] [CrossRef]
- Zhluktova, I.V.; Filatova, S.A.; Trikshev, A.I.; Kamynin, V.A.; Tsvetkov, V.B. All-Fiber 1125 Nm Spectrally Selected Subnanosecond Source. Appl. Opt. 2020, 59, 9081. [Google Scholar] [CrossRef] [PubMed]
- Kharenko, D.S.; Efremov, V.D.; Evmenova, E.A.; Babin, S.A. Generation of Raman Dissipative Solitons near 13 Microns in a Phosphosilicate-Fiber Cavity. Opt. Express 2018, 26, 15084. [Google Scholar] [CrossRef] [PubMed]
- Bogatyrev, V.A.; Bubnov, M.M.; Dianov, E.M.; Kurkov, A.S.; Mamyshev, P.V.; Prokhorov, A.M.; Rumyantsev, S.D.; Semenov, V.A.; Semenov, S.L.; Sysoliatin, A.A.; et al. A Single-Mode Fiber with Chromatic Dispersion Varying along the Length. J. Lightwave Technol. 1991, 9, 561–566. [Google Scholar] [CrossRef]
- Mostofi, A.; Hatami-Hanza, H.; Chu, P.L. Optimum Dispersion Profile for Compression of Fundamental Solitons in Dispersion Decreasing Fibers. IEEE J. Quantum Electron. 1997, 33, 620–628. [Google Scholar] [CrossRef]
- Kamynin, V.A.; Kurkov, A.S.; Tsvetkov, V.B. Supercontinuum Generation in the Range 1.6–2.4 Μm Using Standard Optical Fibres. Quantum Electron. 2011, 41, 986–988. [Google Scholar] [CrossRef]
- Kurkov, A.S.; Sadovnikova, Y.E.; Marakulin, A.V.; Sholokhov, E.M. All Fiber Er-Tm Q-Switched Laser. Laser Phys. Lett. 2010, 7, 795–797. [Google Scholar] [CrossRef]
- Swiderski, J.; Maciejewska, M. Watt-Level, All-Fiber Supercontinuum Source Based on Telecom-Grade Fiber Components. Appl. Phys. B 2012, 109, 177–181. [Google Scholar] [CrossRef]
- Hernandez-Garcia, J.C.; Pottiez, O.; Estudillo-Ayala, J.M. Supercontinuum Generation in a Standard Fiber Pumped by Noise-like Pulses from a Figure-Eight Fiber Laser. Laser Phys. 2011, 22, 221–226. [Google Scholar] [CrossRef]
- Li, B.; Chen, S. Experimental Research of Supercontinuum Generation in a 1030nm Fiber Amplifier. In Proceedings of the 24th National Laser Conference & Fifteenth National Conference on Laser Technology and Optoelectronics, Shanghai, China, 2 December 2020. [Google Scholar] [CrossRef]
- Krupa, K.; Louot, C.; Couderc, V.; Fabert, M.; Guenard, R.; Shalaby, B.M.; Tonello, A.; Pagnoux, D.; Leproux, P.; Bendahmane, A.; et al. Spatiotemporal Characterization of Supercontinuum Extending from the Visible to the Mid-Infrared in a Multimode Graded-Index Optical Fiber. Opt. Lett. 2016, 41, 5785. [Google Scholar] [CrossRef]
- Teğin, U.; Ortaç, B. Cascaded Raman Scattering Based High Power Octave-Spanning Supercontinuum Generation in Grad-ed-Index Multimode Fibers. Sci. Rep. 2018, 8, 12470. [Google Scholar] [CrossRef] [PubMed]
- Korobko, D.A.; Rastogi, V.; Sysoliatin, A.A.; Zolotovskii, I.O. Generation of 2 μm radiation due to single-mode fibers with longitudinally varying diameter. Opt. Fiber Technol. 2019, 47, 38–42. [Google Scholar] [CrossRef]
- Korobko, D.A.; Okhotnikov, O.G.; Stoliarov, D.A.; Sysolyatin, A.A.; Zolotovskii, I.O. Broadband infrared continuum generation in dispersion shifted tapered fiber. J. Opt. Soc. Am. B 2015, 32, 692–700. [Google Scholar] [CrossRef]

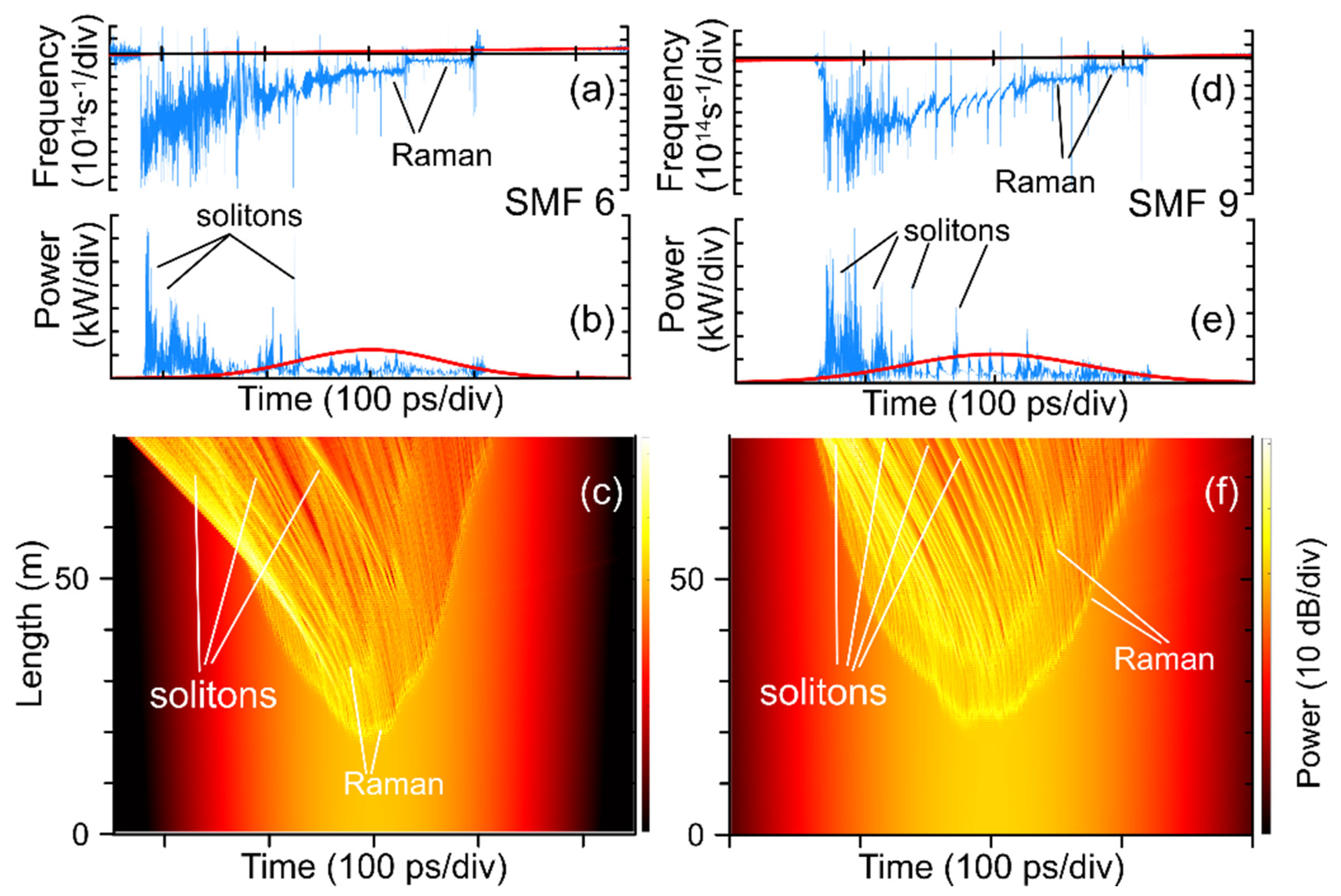
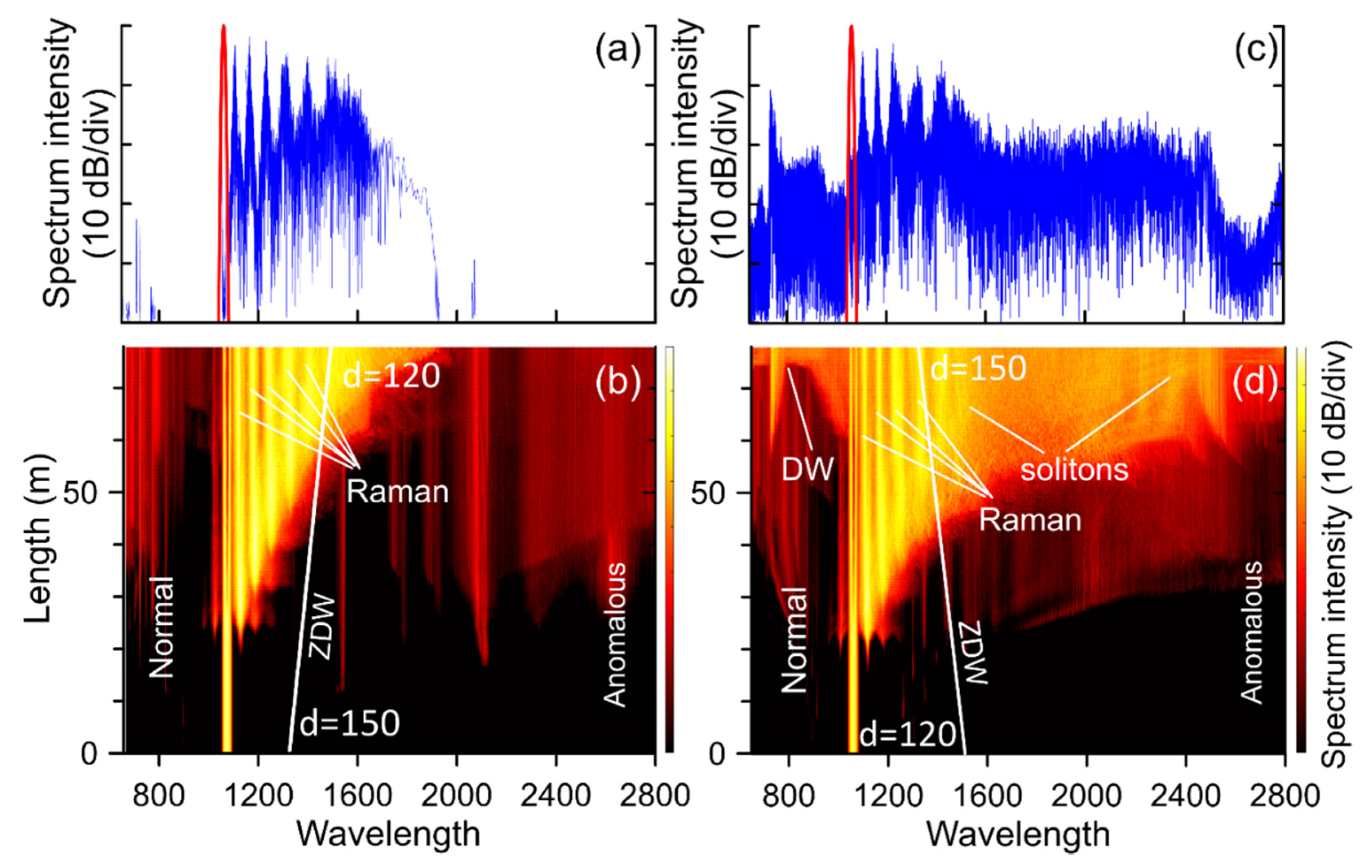
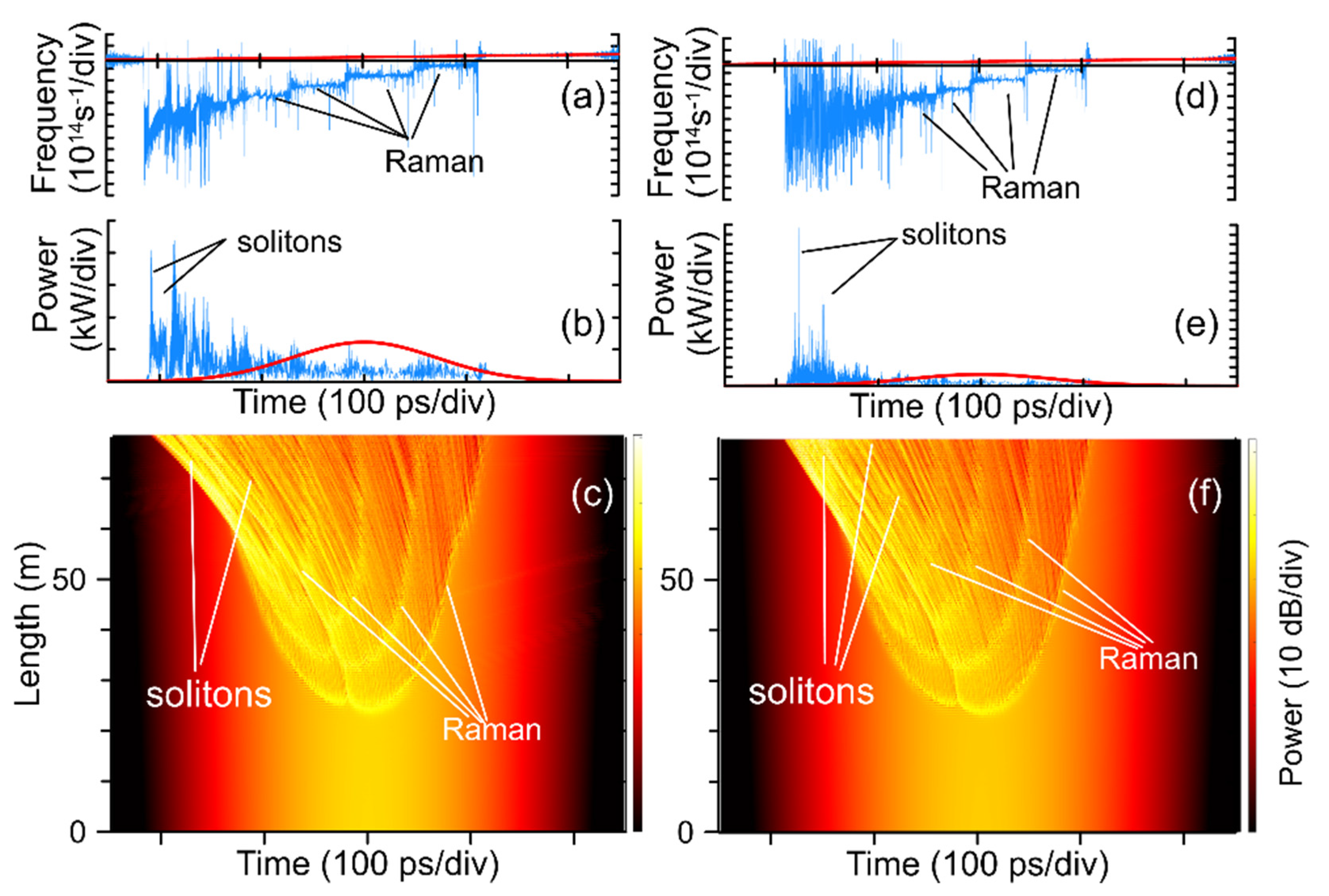
| Sample | d1 1, µm | d2 1, µm | L 2, m | α 3, dB/km |
|---|---|---|---|---|
| DDF | 6 (120) | 9 (150) | 78 | 0.9 |
| SMF6 | 6 | 6 | 78 | 0.2 |
| SMF9 | 9 | 9 | 78 | 0.2 |
| Sample | Δλ 1 (−30 dB), nm | Long-Wave Length Limit, nm | Pav 2, mW | τ 3, ps |
|---|---|---|---|---|
| DDF (120–150 µm) | 1496 | Up to 2354 | 340 | 970 |
| DDF (150–120 µm) | 1355 | Up to 2246 | 324 | 730 |
| SMF6 | 895 | Up to 1810 | 381 | 560 |
| SMF9 | 1212 | Up to 2100 | 301 | 660 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhluktova, I.V.; Kamynin, V.A.; Korobko, D.A.; Abramov, A.S.; Fotiadi, A.A.; Sysoliatin, A.A.; Tsvetkov, V.B. Broadband Supercontinuum Generation in Dispersion Decreasing Fibers in the Spectral Range 900–2400 nm. Photonics 2022, 9, 773. https://doi.org/10.3390/photonics9100773
Zhluktova IV, Kamynin VA, Korobko DA, Abramov AS, Fotiadi AA, Sysoliatin AA, Tsvetkov VB. Broadband Supercontinuum Generation in Dispersion Decreasing Fibers in the Spectral Range 900–2400 nm. Photonics. 2022; 9(10):773. https://doi.org/10.3390/photonics9100773
Chicago/Turabian StyleZhluktova, Irina V., Vladimir A. Kamynin, Dmitry A. Korobko, Aleksei S. Abramov, Andrei A. Fotiadi, Alexej A. Sysoliatin, and Vladimir B. Tsvetkov. 2022. "Broadband Supercontinuum Generation in Dispersion Decreasing Fibers in the Spectral Range 900–2400 nm" Photonics 9, no. 10: 773. https://doi.org/10.3390/photonics9100773
APA StyleZhluktova, I. V., Kamynin, V. A., Korobko, D. A., Abramov, A. S., Fotiadi, A. A., Sysoliatin, A. A., & Tsvetkov, V. B. (2022). Broadband Supercontinuum Generation in Dispersion Decreasing Fibers in the Spectral Range 900–2400 nm. Photonics, 9(10), 773. https://doi.org/10.3390/photonics9100773





