Design and Characteristics of Diamond-Assisted Ring-Core Fiber for Space Division Multiplexing
Abstract
1. Introduction
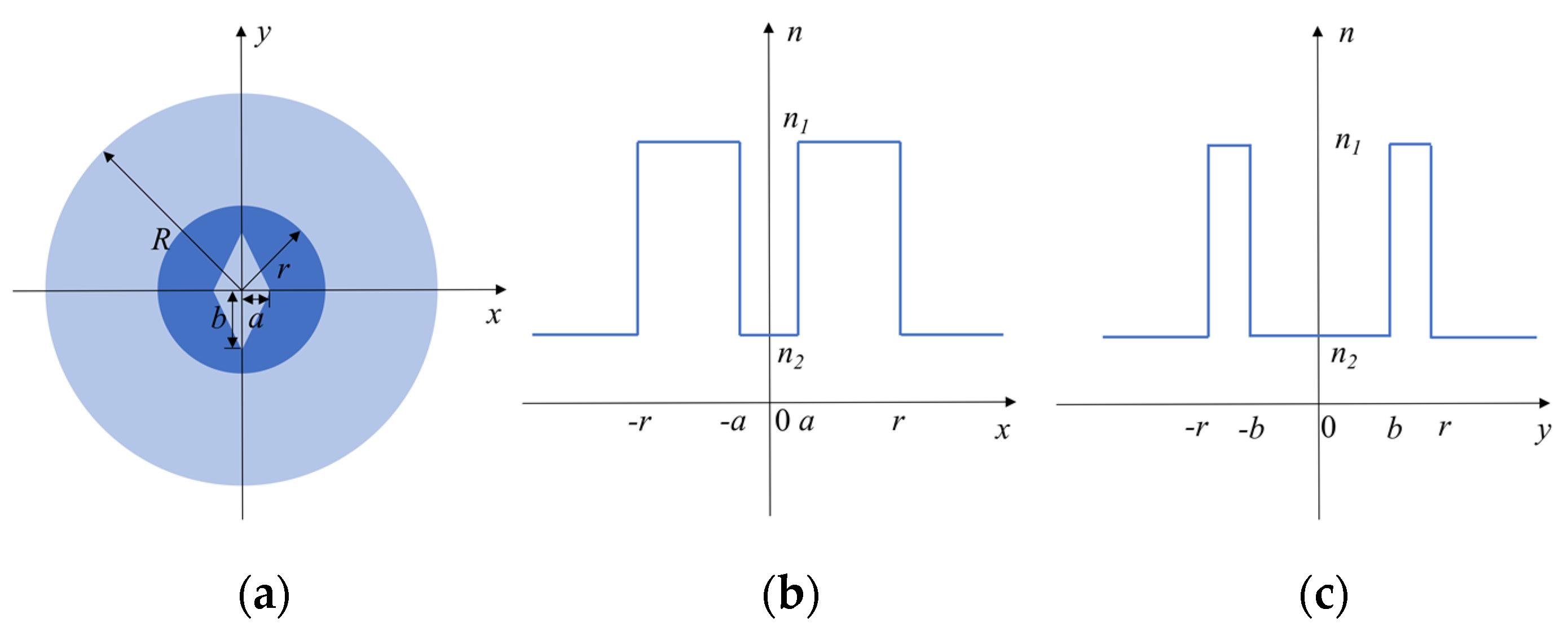
2. Fiber Structure
3. Characteristic Analysis of DRF
3.1. Modal Properties of DRF
3.2. Influence of Structural Parameters on Fiber Properties
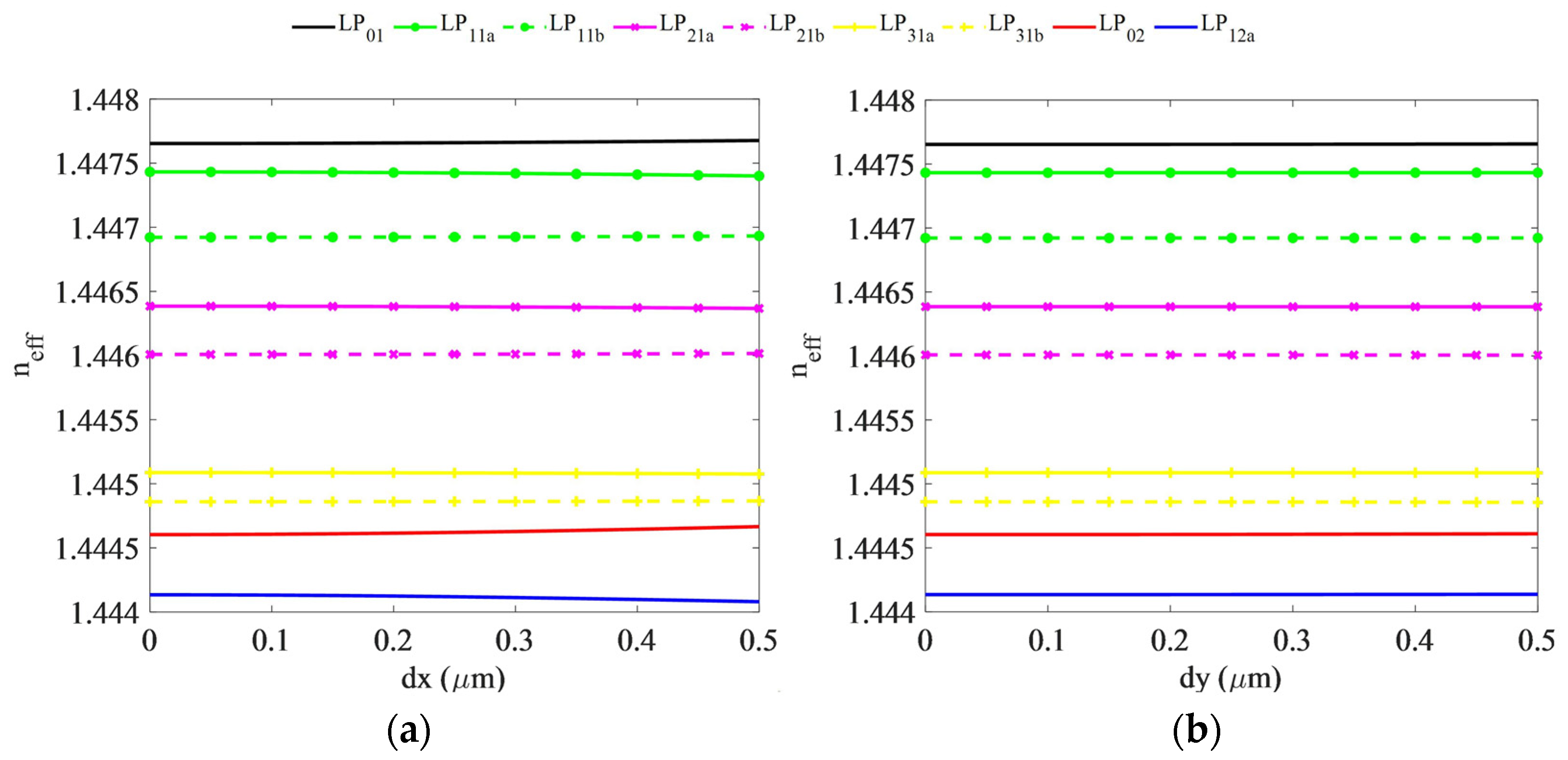
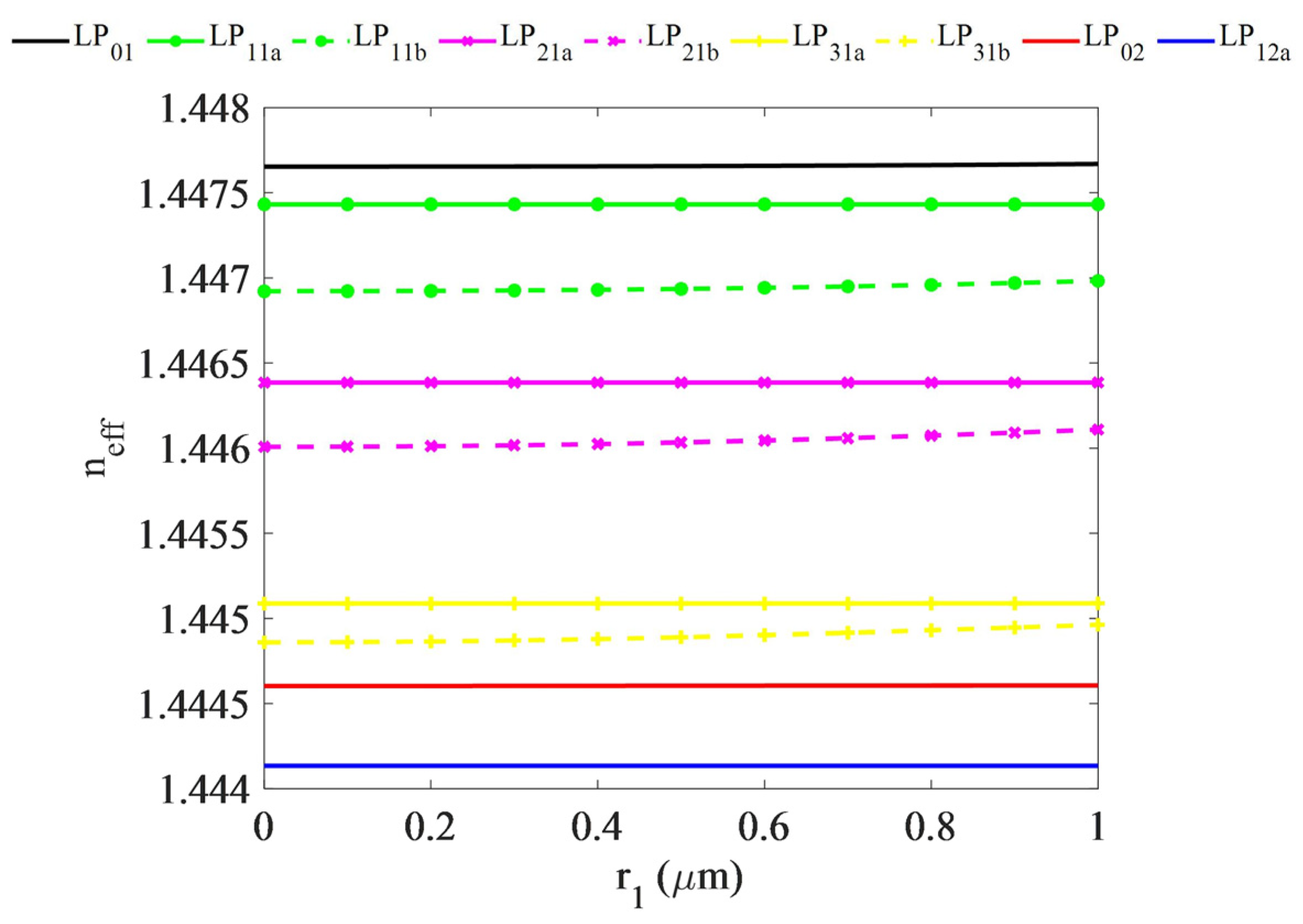
3.3. Fabrication Tolerance
4. Discussion of the Relationship between the Structural Symmetry and Spatial Mode Degenerate Separation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Winzer, P.J. Scaling Optical Fiber Networks: Challenges and Solutions. Opt. Photonics News 2015, 26, 28–35. [Google Scholar] [CrossRef]
- Saitoh, K.; Matsuo, S. Multicore Fiber Technology. J. Light. Technol. Jt. IEEE/OSA Publ. 2016, 34, 55–66. [Google Scholar] [CrossRef]
- Mizuno, T.; Miyamoto, Y. High-capacity dense space division multiplexing transmission. Opt. Fiber Technol. 2016, 35, 108–117. [Google Scholar] [CrossRef]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Winzer, P.J. Energy-Efficient Optical Transport Capacity Scaling Through Spatial Multiplexing. IEEE Photonics Technol. Lett. 2011, 23, 851–853. [Google Scholar] [CrossRef]
- Sillard, P.; Bigot-Astruc, M.; Molin, D. Few-Mode Fibers for Mode-Division-Multiplexed Systems. J. Light. Technol. 2014, 32, 2824–2829. [Google Scholar] [CrossRef]
- Chebaane, S.; Seleem, H.E.; Fathallah, H.; Machhout, M. Design tradeoffs of few-mode step index fiber for next generation mode division multiplexing optical networks. In Proceedings of the International Conference on Information & Communication Technology Research, Abu Dhabi, United Arab Emirates, 17–19 May 2015. [Google Scholar]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Sierra, A. Mode-Division Multiplexing Over 96 km of Few-Mode Fiber Using Coherent 6 × 6 MIMO Processing. J. Light. Technol. 2012, 30, 521–531. [Google Scholar] [CrossRef]
- Inan, B.; Spinnler, B.; Ferreira, F.; van den Borne, D.; Lobato, A.; Adhikari, S.; Sleiffer, V.A.; Kuschnerov, M.; Hanik, N.; Jansen, S.L. DSP complexity of mode-division multiplexed receivers. Opt. Express 2012, 20, 10859–10869. [Google Scholar] [CrossRef]
- Ramachandran, S.; Fini, J.M.; Mermelstein, M.; Nicholson, J.W.; Ghalmi, S.; Yan, M.F. Ultra-large effective-area, higher-order mode fibers: A new strategy for high-power lasers. Laser Photonics Rev. 2008, 2, 429–448. [Google Scholar] [CrossRef]
- Wang, L.; Nejad, R.M.; Corsi, A.; Lin, J.; Larochelle, S. Linearly polarized vector modes: Enabling MIMO-free mode-division multiplexing. Opt. Express 2017, 25, 11736. [Google Scholar] [CrossRef]
- He, Z.; Du, J.; Chen, X.; Shen, W.; Huang, Y.; Wang, C.; Xu, K.; He, Z. Machine learning aided inverse design for few-mode fiber weak-coupling optimization. Opt. Express 2020, 28, 21668–21681. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, Y.; Takenaga, K.; Matsuo, S.; Aikawa, K.; Saitoh, K. Few-mode multicore fibers for long-haul transmission line. Opt. Fiber Technol. 2017, 35, 19–27. [Google Scholar] [CrossRef]
- Zhao, J.J.; Tang, M.; Oh, K.; Feng, Z.H.; Zhao, C.; Liao, R.L.; Fu, S.N.; Shum, P.P.; Liu, D.M. Polarization-maintaining few mode fiber composed of a central circular-hole and an elliptical-ring core. Photonics Res. 2017, 5, 261–266. [Google Scholar] [CrossRef]
- Zheng, J.J.; Song, Y.J.; Li, P.; Zi, T.; Chen, W.X.; Ning, T.; Li, J.; Wang, J.; Bai, B. Design and Characteristics of Rectangular-Assistant Ring-Core Fiber for Space Division Multiplexing. Acta Opt. Sin. 2022, 42, 1606006. [Google Scholar] [CrossRef]
- Song, Y.J.; Zheng, J.J.; Pei, L.; Huang, J.; Wang, J.S.; Ning, T.; Li, J.; Bai, B. Design and characteristics of ellipse-assisted ring-core fiber for space division multiplexing. Opt. Fiber Technol. 2022, 72, 102984. [Google Scholar] [CrossRef]
- Xiao, H.; Li, H.S.; Jian, S.S. Hole-assisted polarization-maintaining few-mode fiber. Opt. Laser Technol. 2018, 107, 162–168. [Google Scholar] [CrossRef]
- Liang, J.P.; Mo, Q.; Fu, S.N.; Tang, M.; Shum, P.; Liu, D.M. Design and fabrication of elliptical-core few-mode fiber for MIMO-less data transmission. Opt. Lett. 2016, 41, 3058–3061. [Google Scholar] [CrossRef]
- Yang, Y.; Mo, Q.; Fu, S.; Liu, B.; Tang, M.; Liu, D. Panda type elliptical core few-mode fiber. APL Photonics 2019, 4, 022901. [Google Scholar] [CrossRef]
- Song, W.; Chen, H.; Wang, J.; Liu, C.; Chen, Y.; Li, Z.; Liu, M. Panda type elliptical ring core few-mode fiber. Opt. Fiber Technol. 2020, 60, 102361. [Google Scholar] [CrossRef]
- Parmigiani, F.; Jung, Y.; Gruner-Nielsen, L.; Geisler, T.; Richardson, D.J. Elliptical Core Few Mode Fibers for Multiple-Input Multiple Output-Free Space Division Multiplexing Transmission. IEEE Photonics Technol. Lett. 2017, 29, 1764–1767. [Google Scholar] [CrossRef]
- Shi, C.; Wang, J. Design of PANDA-type elliptical-core multimode fiber supporting 24 fully lifted eigenmodes. Opt. Lett. 2018, 43, 3718–3721. [Google Scholar] [CrossRef]
- Shi, C.; Jian, W. Fully degeneracy-lifted bow-tie elliptical ring-core multi-mode fiber. Opt. Express 2018, 26, 18773. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, Y.; Yu, X.; Han, J.; Jie, Z. Design and characterization of 16-mode PANDA polarization-maintaining few-mode ring-core fiber for spatial division multiplexing. Opt. Eng. 2017, 56, 116102. [Google Scholar] [CrossRef]
- Yan, H.; Li, S.; Xie, Z.; Zheng, X.; Zhang, H.; Zhou, B. Design of PANDA ring-core fiber with 10 polarization-maintaining modes. Photonics Res. 2017, 5, 1–5. [Google Scholar] [CrossRef]
- Xiao, H.; Li, H.S.; Wu, B.L.; Dong, Y.; Xiao, S.Y.; Jian, S.S. Elliptical hollow-core optical fibers for polarization-maintaining few-mode guidance. Opt. Fiber Technol. 2019, 48, 7–11. [Google Scholar] [CrossRef]
- Corsi, A.; Chang, J.H.; Rusch, L.A.; LaRochelle, S. Design of Highly Elliptical Core Ten-Mode Fiber for Space Division Multiplexing with 2 × 2 MIMO. IEEE Photonics J. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Wang, L.; LaRochelle, S. Design of eight-mode polarization-maintaining few-mode fiber for multiple-input multiple-output-free spatial division multiplexing. Opt. Lett. 2015, 40, 5846–5849. [Google Scholar] [CrossRef]
- Cui, Z.; Yuan, C.; Li, C. Modeling the splice loss of ultra-low loss fiber and single-mode optical fiber in high altitude area. Opt. Fiber Technol. 2021, 67, 102696. [Google Scholar] [CrossRef]
- Song, Y.J.; Zheng, J.J.; Pei, L.; Huang, J.; Wang, J.S.; Ning, T.; Li, J.; Bai, B. Design and characteristics of square-assisted ring-core fiber for mode space degenerate modulating. In Proceedings of the 13th International Conference on Information Optics and Photonics, Xi’an, China, 7–10 August 2022. accepted. [Google Scholar]
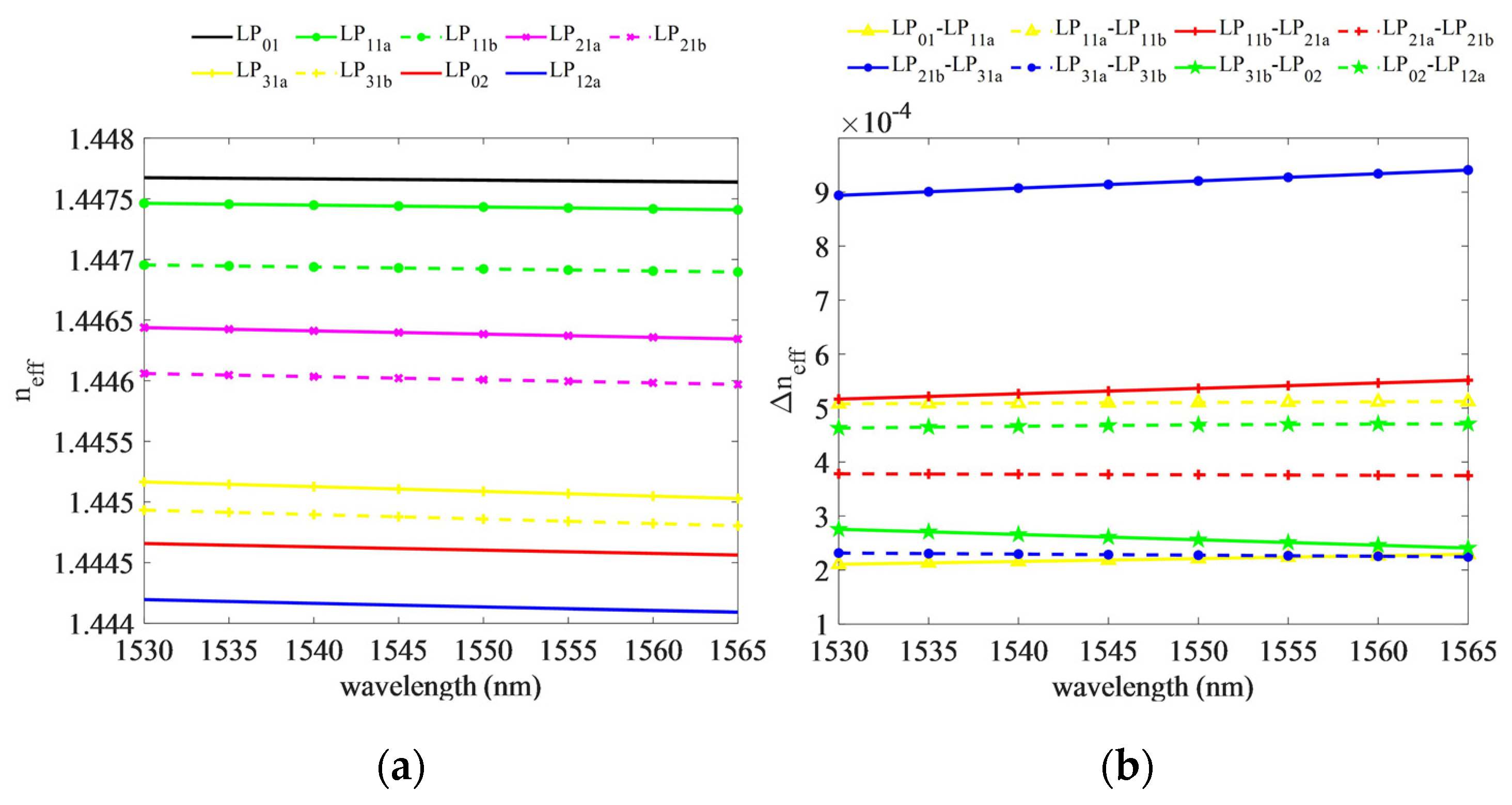
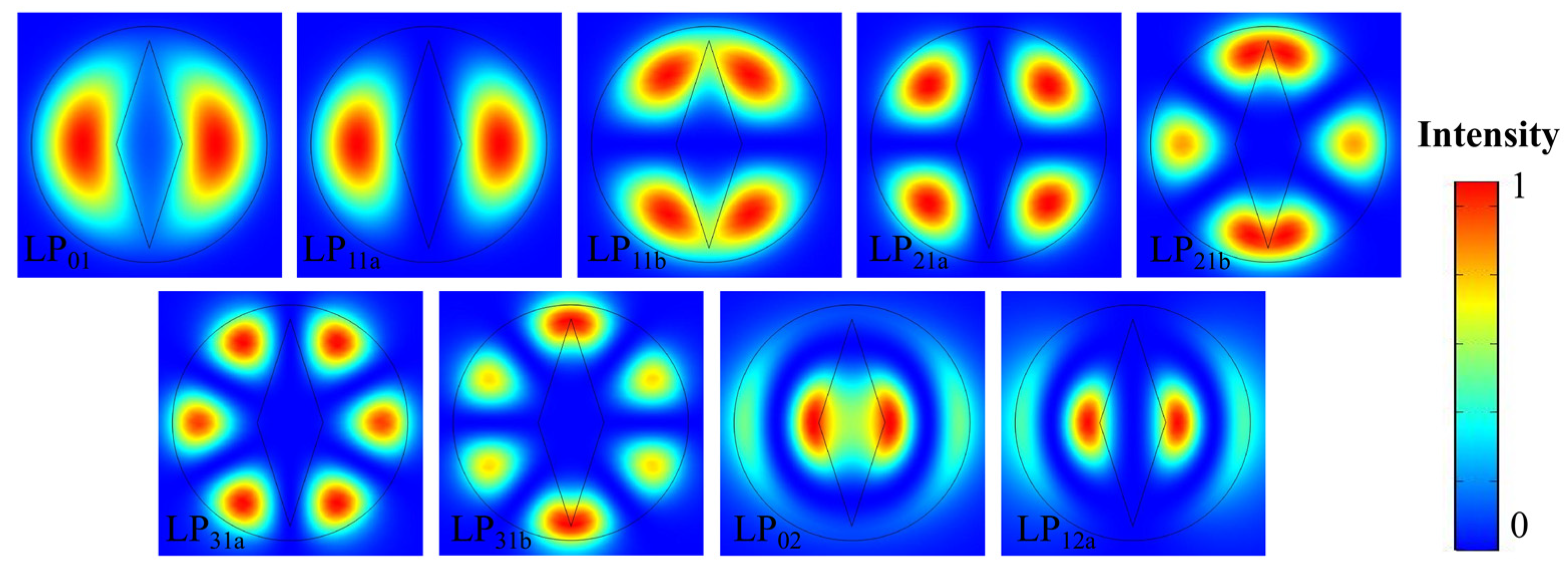
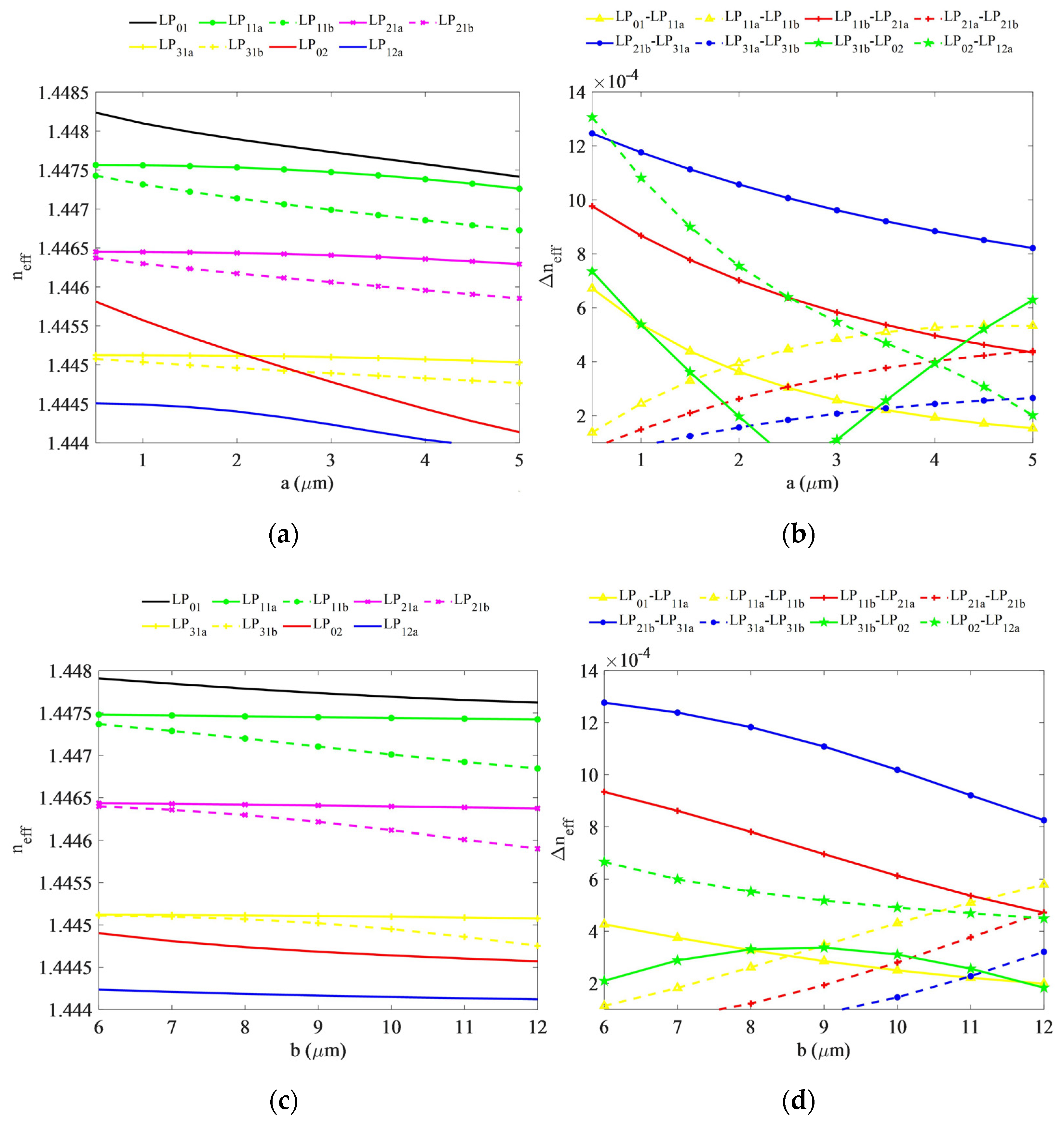
| LP01 | LP11a | LP11b | LP21a | LP21b | LP31a | LP31b | LP02 | LP12a | |
|---|---|---|---|---|---|---|---|---|---|
| 1530 nm | 2.48 | 2.94 | 0.39 | 1.47 | 0.42 | 1.19 | 1.01 | 3.01 | 3.68 |
| 1535 nm | 2.49 | 2.96 | 0.37 | 1.48 | 0.43 | 1.19 | 1.01 | 2.99 | 3.61 |
| 1540 nm | 2.50 | 2.97 | 0.37 | 1.49 | 0.43 | 1.20 | 1.02 | 2.97 | 3.53 |
| 1545 nm | 2.51 | 2.99 | 0.37 | 1.49 | 0.44 | 1.20 | 1.02 | 2.94 | 3.45 |
| 1550 nm | 2.51 | 3.01 | 0.36 | 1.49 | 0.45 | 1.21 | 1.02 | 2.92 | 3.36 |
| 1555 nm | 2.53 | 3.02 | 0.35 | 150 | 0.45 | 1.21 | 1.02 | 2.89 | 3.27 |
| 1560 nm | 2.53 | 3.04 | 0.35 | 1.51 | 0.46 | 1.21 | 1.02 | 2.87 | 3.17 |
| 1565 nm | 2.54 | 3.05 | 0.34 | 1.51 | 0.46 | 1.21 | 1.02 | 2.84 | 3.06 |
| Rectangle-Assisted Ring-Core Fiber (RRF) [15] | Ellipse-Assisted Ring-Core Fiber (ERF) [16] | Square-Assisted Ring-Core Fiber (SRF) [30] | Diamond-Assisted Ring-Core Fiber (DRF) | |
|---|---|---|---|---|
| Schematic cross-section |  | 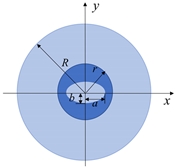 | 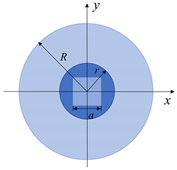 | 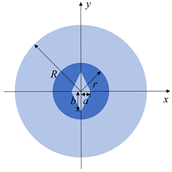 |
| Core diameter (μm) | 25 | 25 | 30.8 | 25 |
| Assisted area parameters (μm) | a = 19 b = 2 | a = 12.5 b = 1 | a = 16.6 | a = 3.5 b = 11 |
| Core-clad refractive index difference | 0.005 | 0.005 | 0.01 | 0.005 |
| Number of symmetry axes | 2 | 2 | 4 | 2 |
| LPmn mode supporting degenerate separation of spatial modes | LP11 LP21 LP31 | LP11 LP21 LP31 LP12 | LP21 LP41 LP61 LP22 | LP11 LP21 LP31 LP12 |
| Δneff between spatial modes | >2.2 × 10−4 | >3.16 × 10−4 | >1.13 × 10−4 | >2.25 × 10−4 |
| Δneff between polarization modes | <2.1 × 10−6 | <3.23 × 10−6 | <7.12 × 10−6 | <3.68 × 10−6 |
| The Shape of the Central-Assisted Area: Regular Hexagon | ||||||
|---|---|---|---|---|---|---|
| Schematic Cross-Section | Structural Parameters | Δneff between Spatial Modes (If Degenerated) | ||||
 | Core diameter (μm) | Assisted area parameters (μm) | LP01 | LP11 | LP21 | LP31 |
| 30 | a = 13 | - | - | - | 6.21 × 10−4 | |
| Core-clad refractive index difference | Number of symmetry axes | LP41 | LP51 | LP61 | ||
| 0.01 | 6 | - | - | 1.76 × 10−4 | ||
| The Shape of the Central-Assisted Area: Concave Polygon | ||||||
|---|---|---|---|---|---|---|
| Schematic Cross-Section | Structural Parameters | Δneff between Spatial Modes (If Degenerated) | ||||
 | Core diameter (μm) | Assisted area parameters (μm) | LP01 | LP11 | LP21 | LP31 |
| 25 | a = 8 b = 18 | - | 2.98 × 10−4 | 1.44 × 10−4 | 2.11 × 10−4 | |
| Core-clad refractive index difference | Number of symmetry axes | LP02 | ||||
| 0.005 | 2 | - | ||||
| The Shape of the Central-Assisted Area: Convex Polygon | ||||||
|---|---|---|---|---|---|---|
| Schematic Cross-Section | Structural Parameters | Δneff between Spatial Modes (If Degenerated) | ||||
 | Core diameter (μm) | Assisted area parameters (μm) | LP01 | LP11 | LP21 | LP02 |
| 25 | a = 2 b = 13 ra = 1.5 | - | 4.86 × 10−4 | 3.58 × 10−4 | - | |
| Core-clad refractive index difference | Number of symmetry axes | LP31 | LP12 | |||
| 0.005 | 2 | 1.98 × 10−4 | - | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Zheng, J.; Pei, L.; Huang, J.; Ning, T.; Li, J.; Wang, J.; Bai, B. Design and Characteristics of Diamond-Assisted Ring-Core Fiber for Space Division Multiplexing. Photonics 2022, 9, 766. https://doi.org/10.3390/photonics9100766
Song Y, Zheng J, Pei L, Huang J, Ning T, Li J, Wang J, Bai B. Design and Characteristics of Diamond-Assisted Ring-Core Fiber for Space Division Multiplexing. Photonics. 2022; 9(10):766. https://doi.org/10.3390/photonics9100766
Chicago/Turabian StyleSong, Yujing, Jingjing Zheng, Li Pei, Jing Huang, Tigang Ning, Jing Li, Jianshuai Wang, and Bing Bai. 2022. "Design and Characteristics of Diamond-Assisted Ring-Core Fiber for Space Division Multiplexing" Photonics 9, no. 10: 766. https://doi.org/10.3390/photonics9100766
APA StyleSong, Y., Zheng, J., Pei, L., Huang, J., Ning, T., Li, J., Wang, J., & Bai, B. (2022). Design and Characteristics of Diamond-Assisted Ring-Core Fiber for Space Division Multiplexing. Photonics, 9(10), 766. https://doi.org/10.3390/photonics9100766






