Nonlinear Spectrum Modulation in the Anomalous Dispersion Regime Using Second- and Third-Order Solitons
Abstract
1. Introduction
2. Theory and Numerical Methods
2.1. Channel Model
2.2. Signal Generation
2.3. Performance Measurement
3. Results
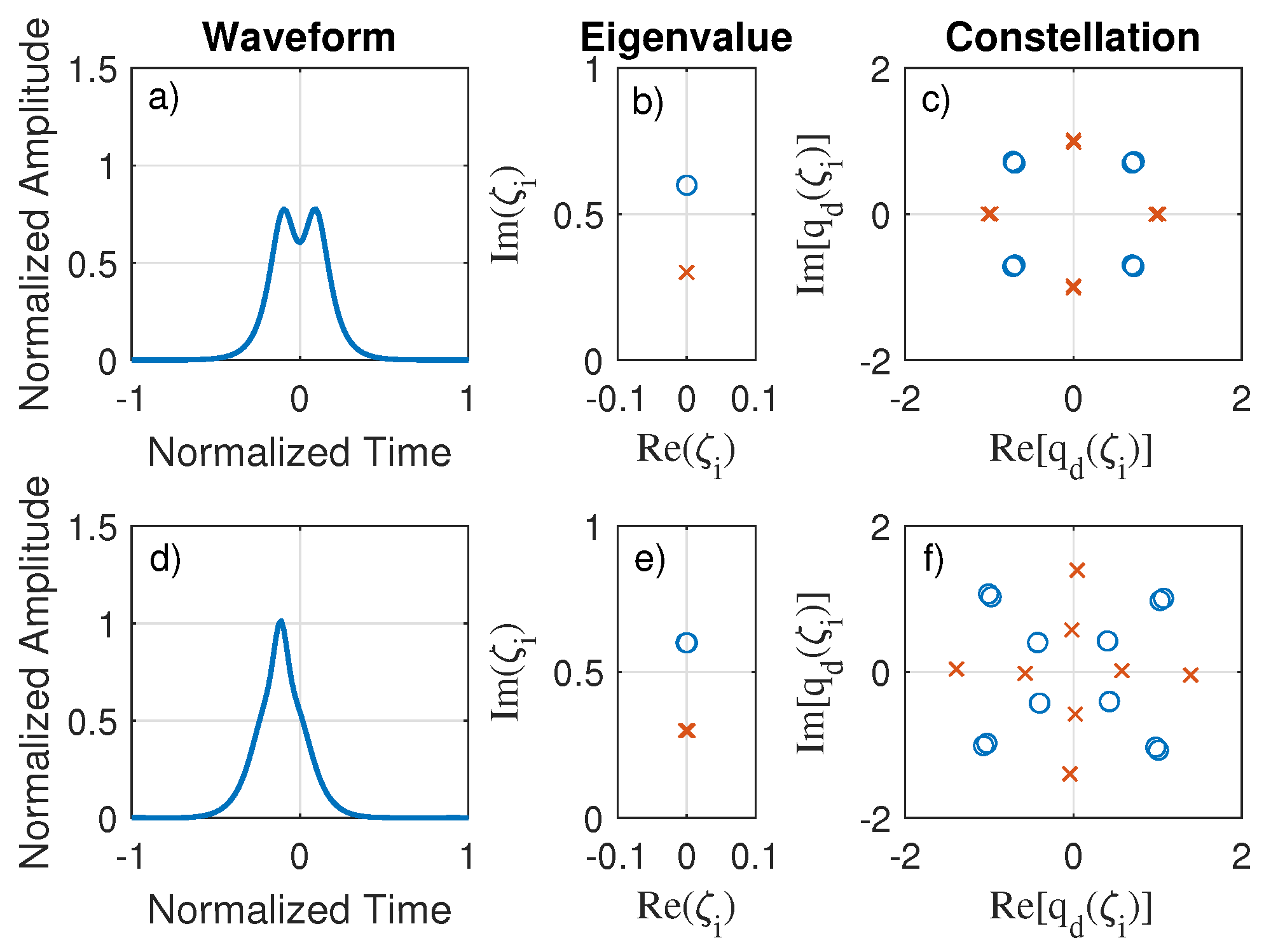
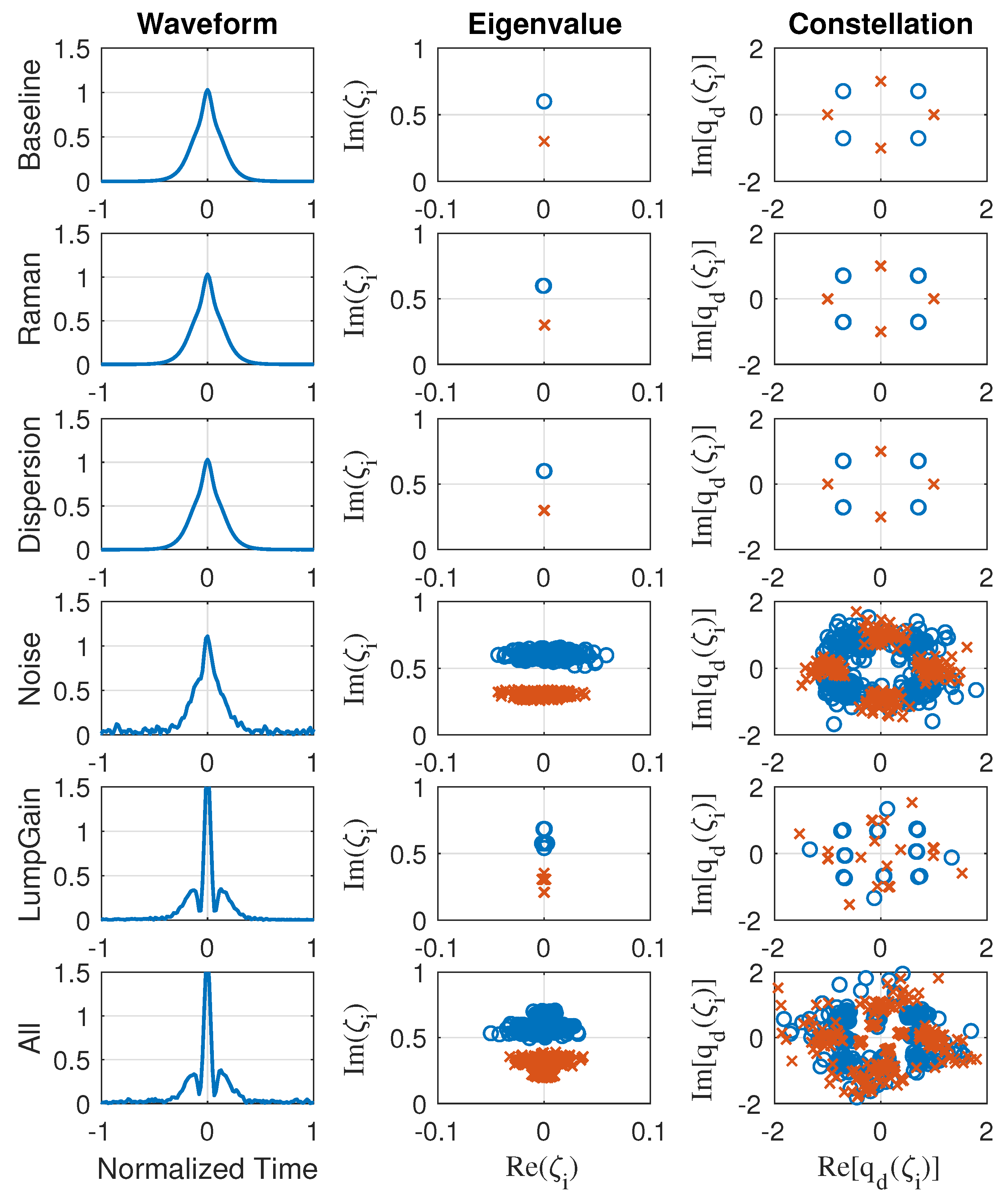
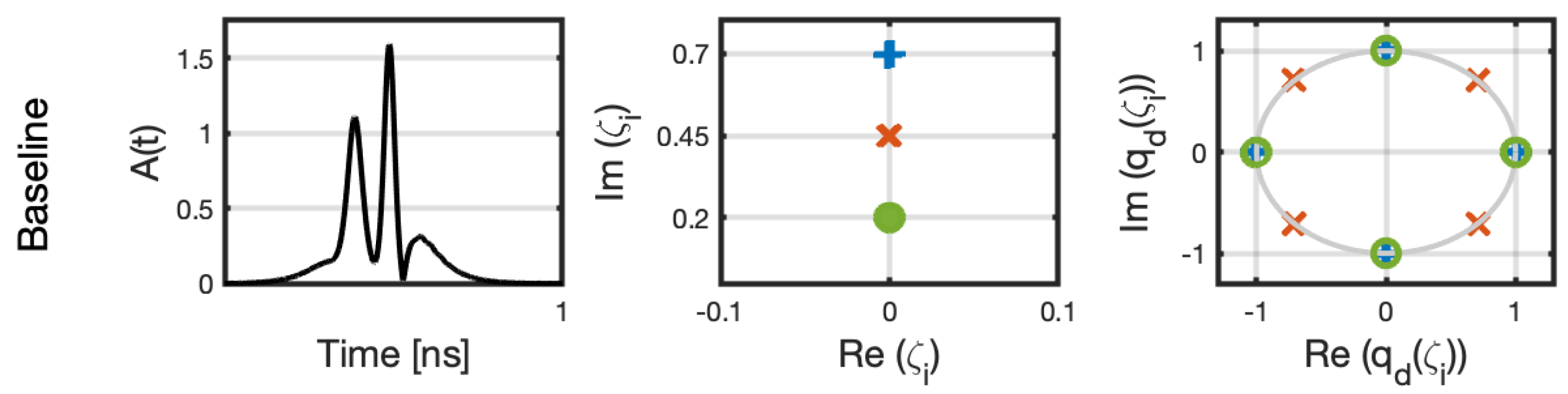
3.1. Baseline Simulation
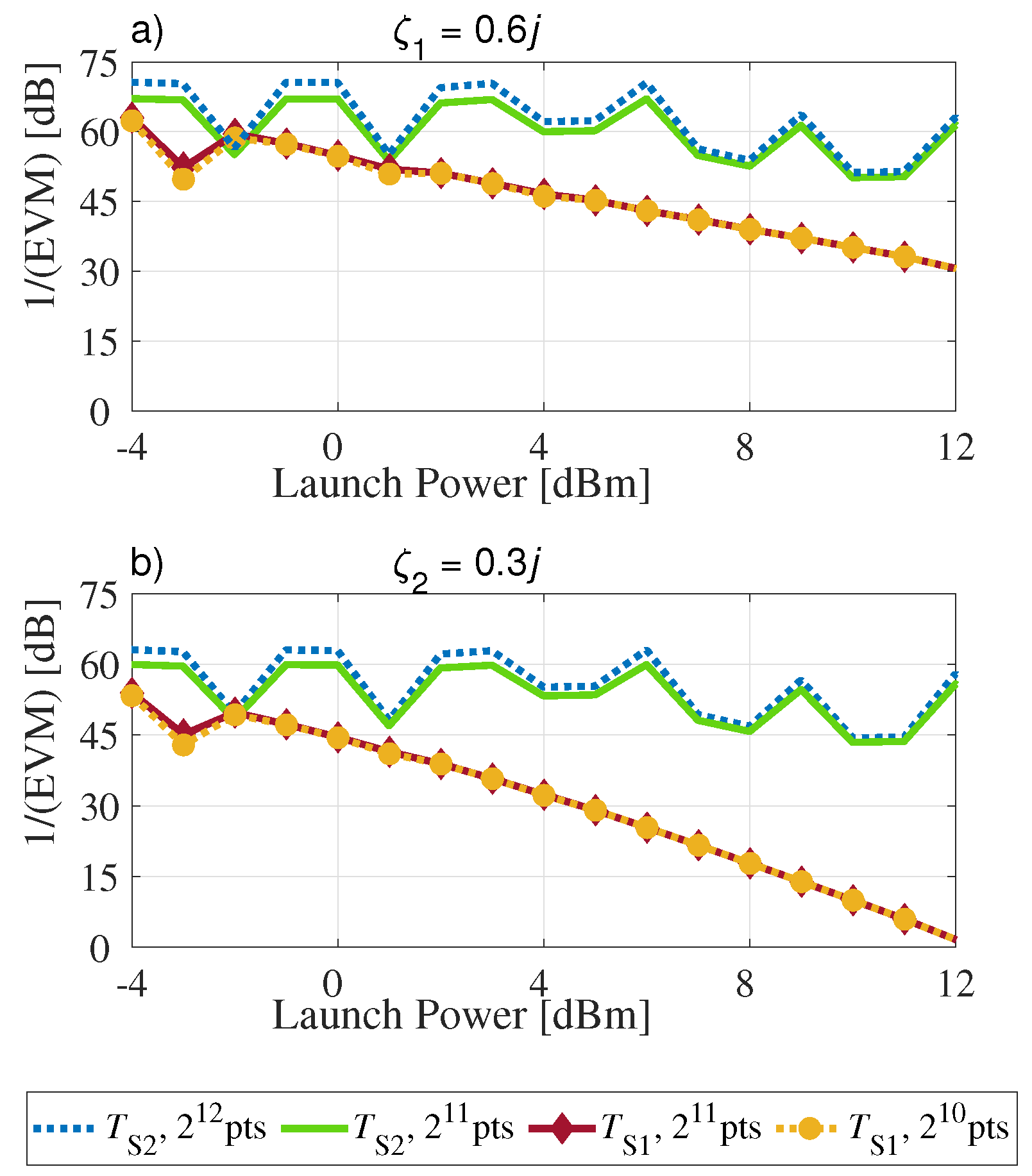
3.1.1. Mitigating Inter-Symbol Interference and Truncation Errors
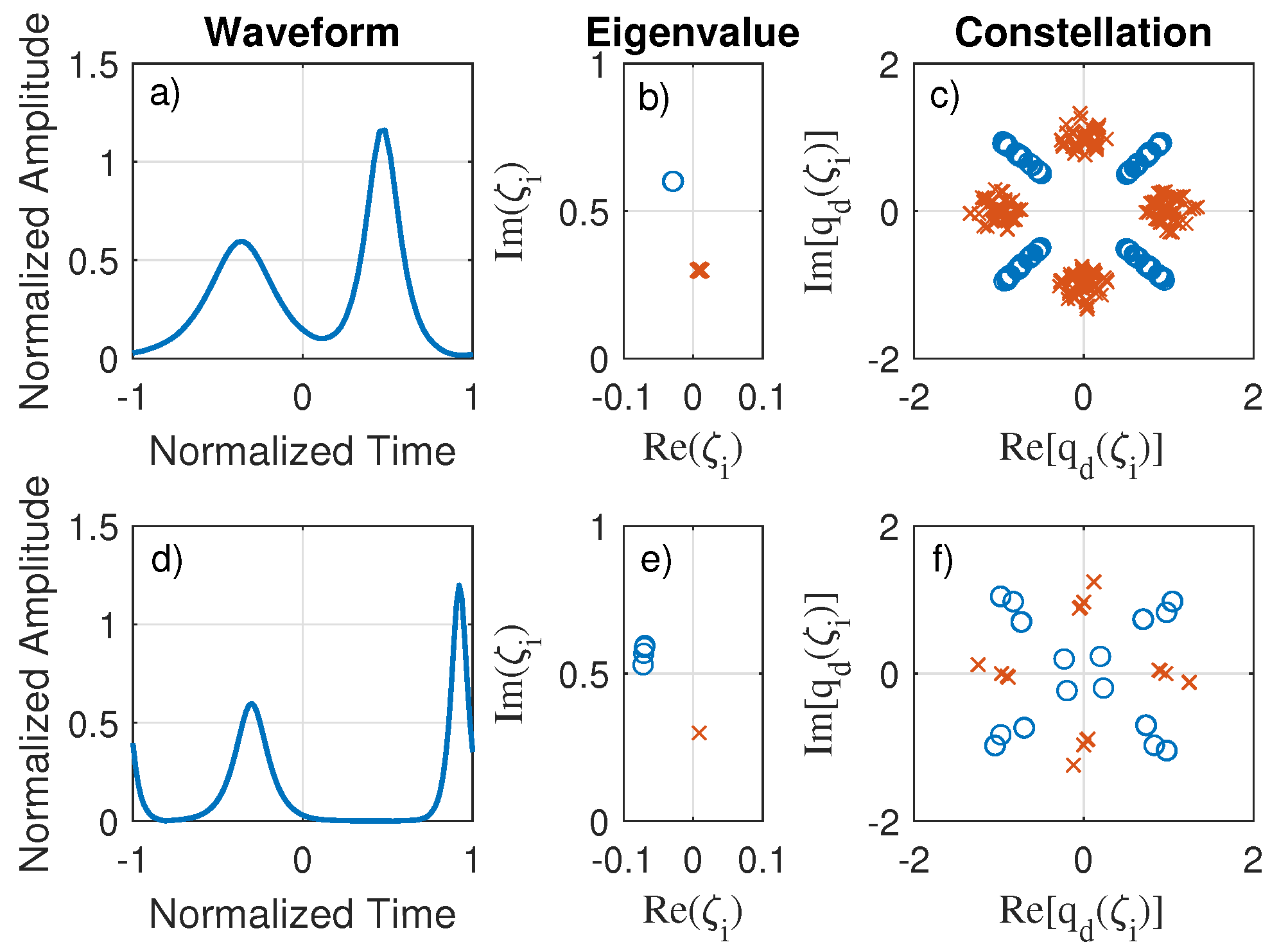
3.1.2. Constellation Analysis
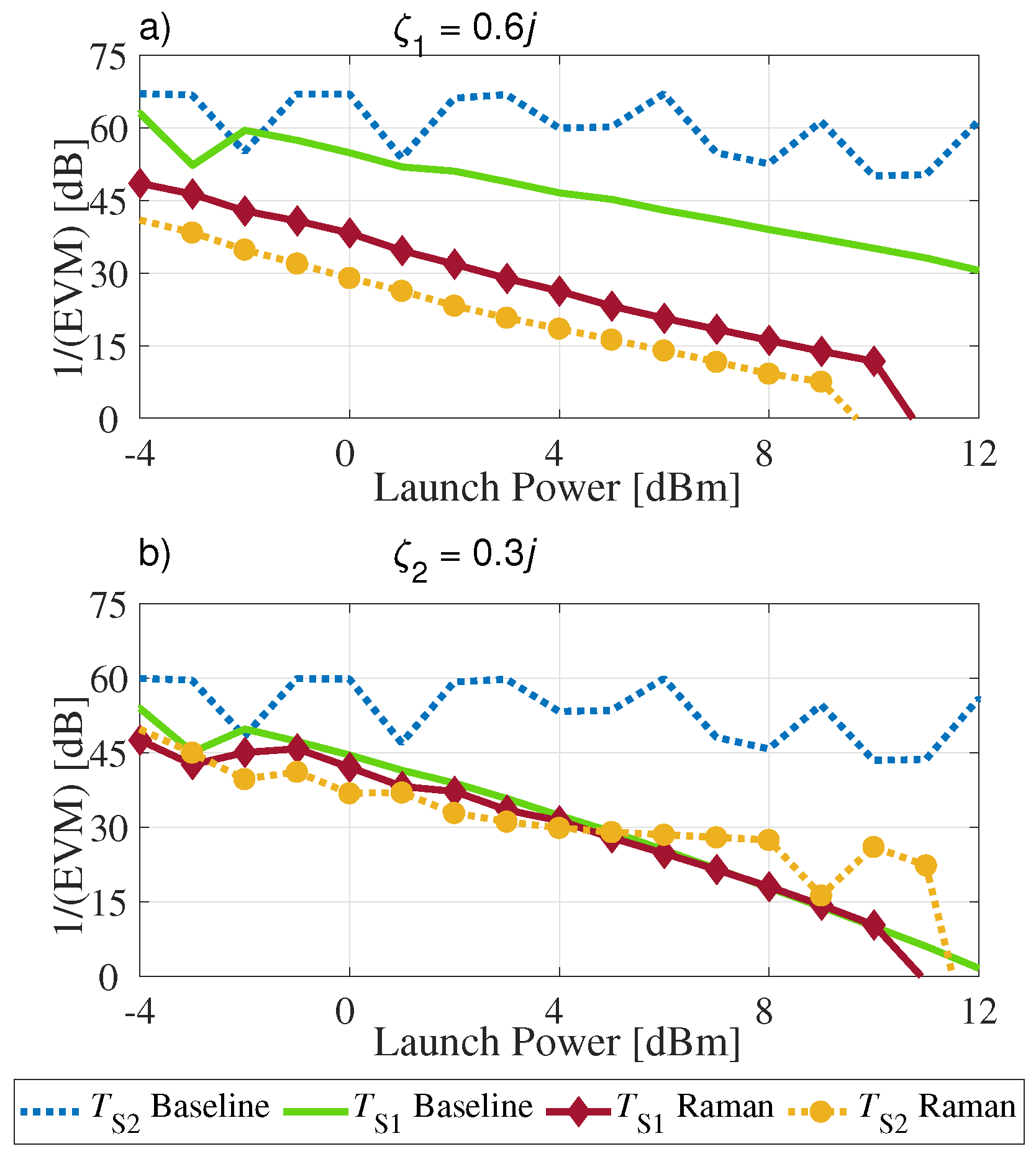
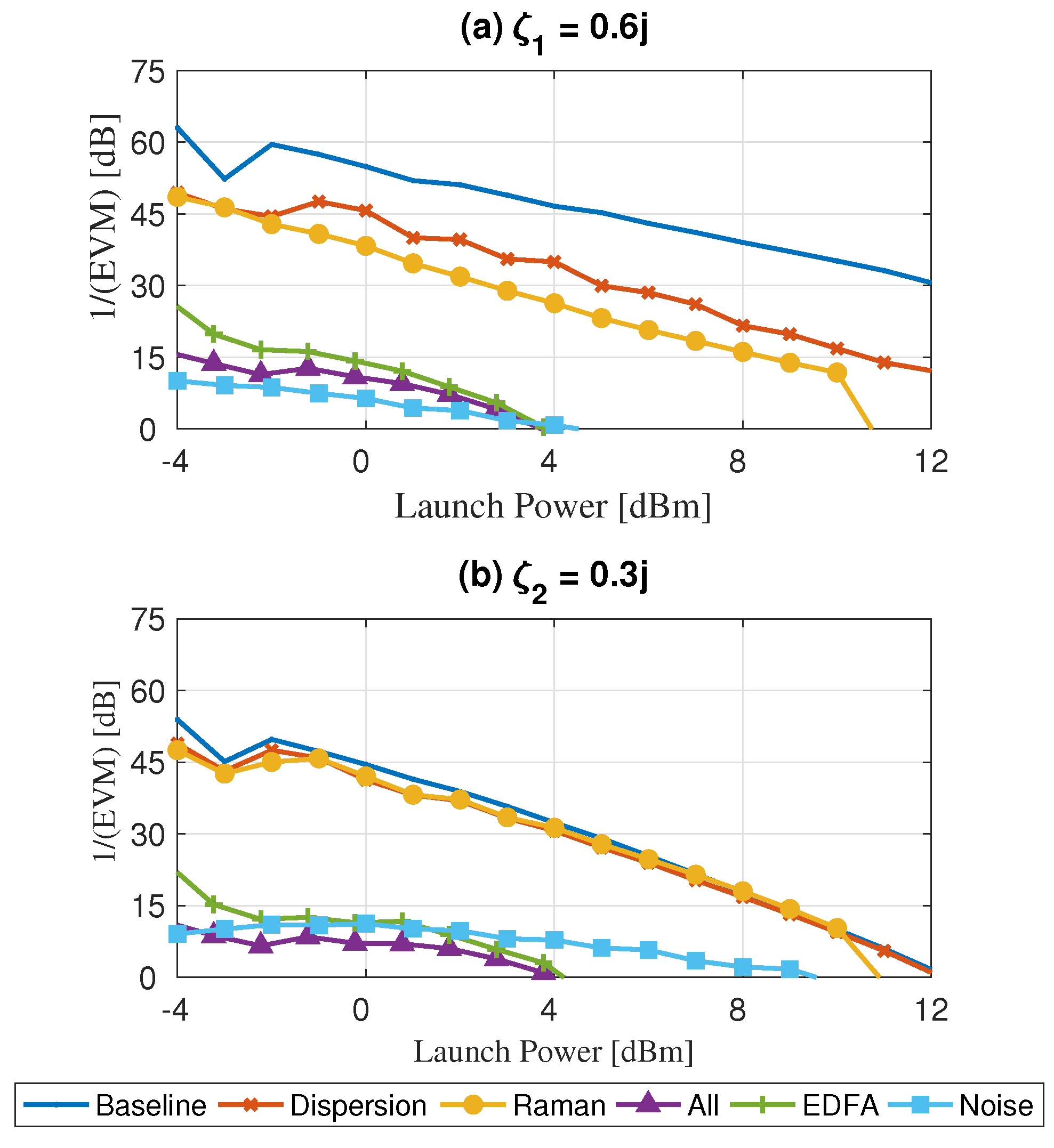
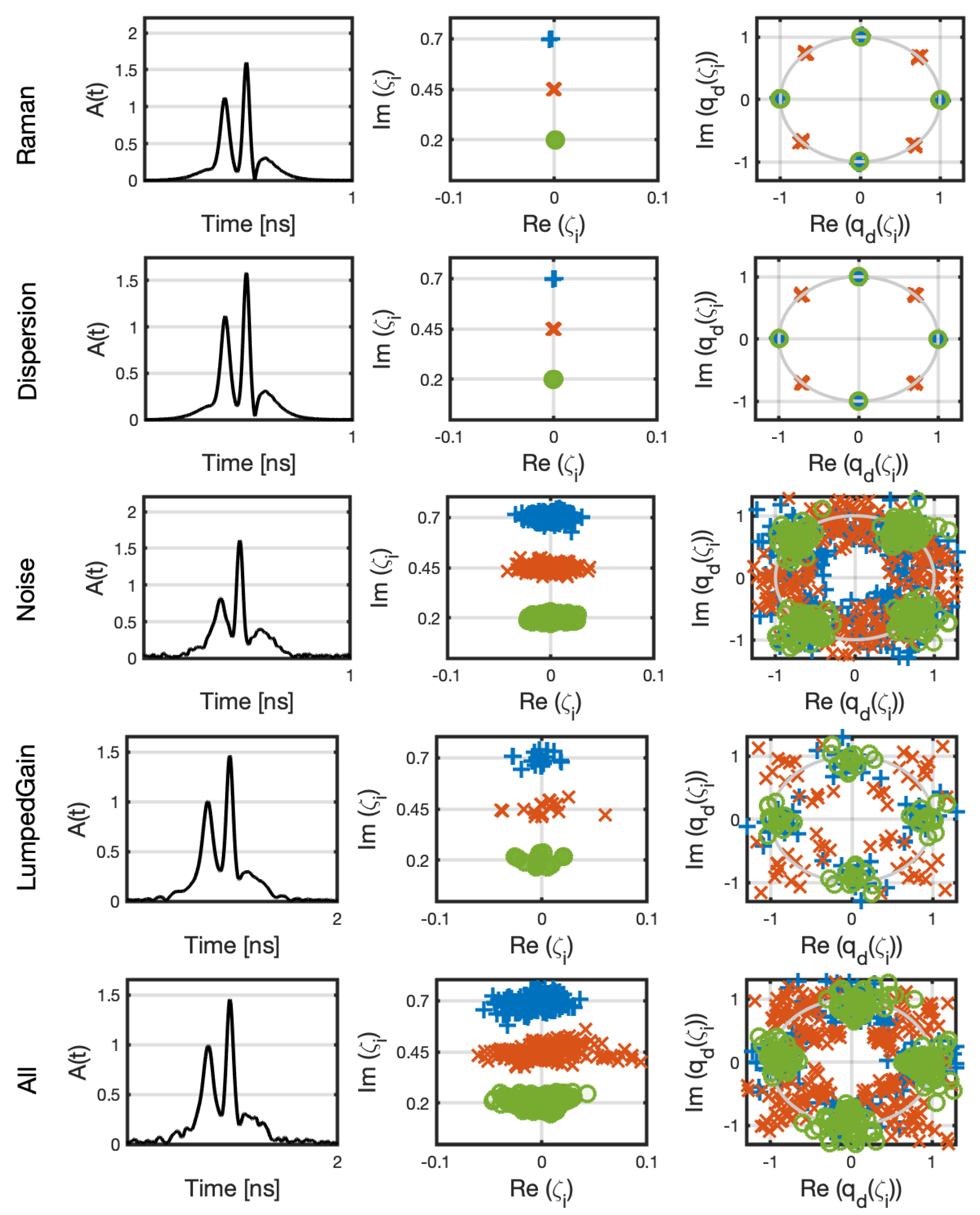
3.2. Raman Effect
Constellation Analysis
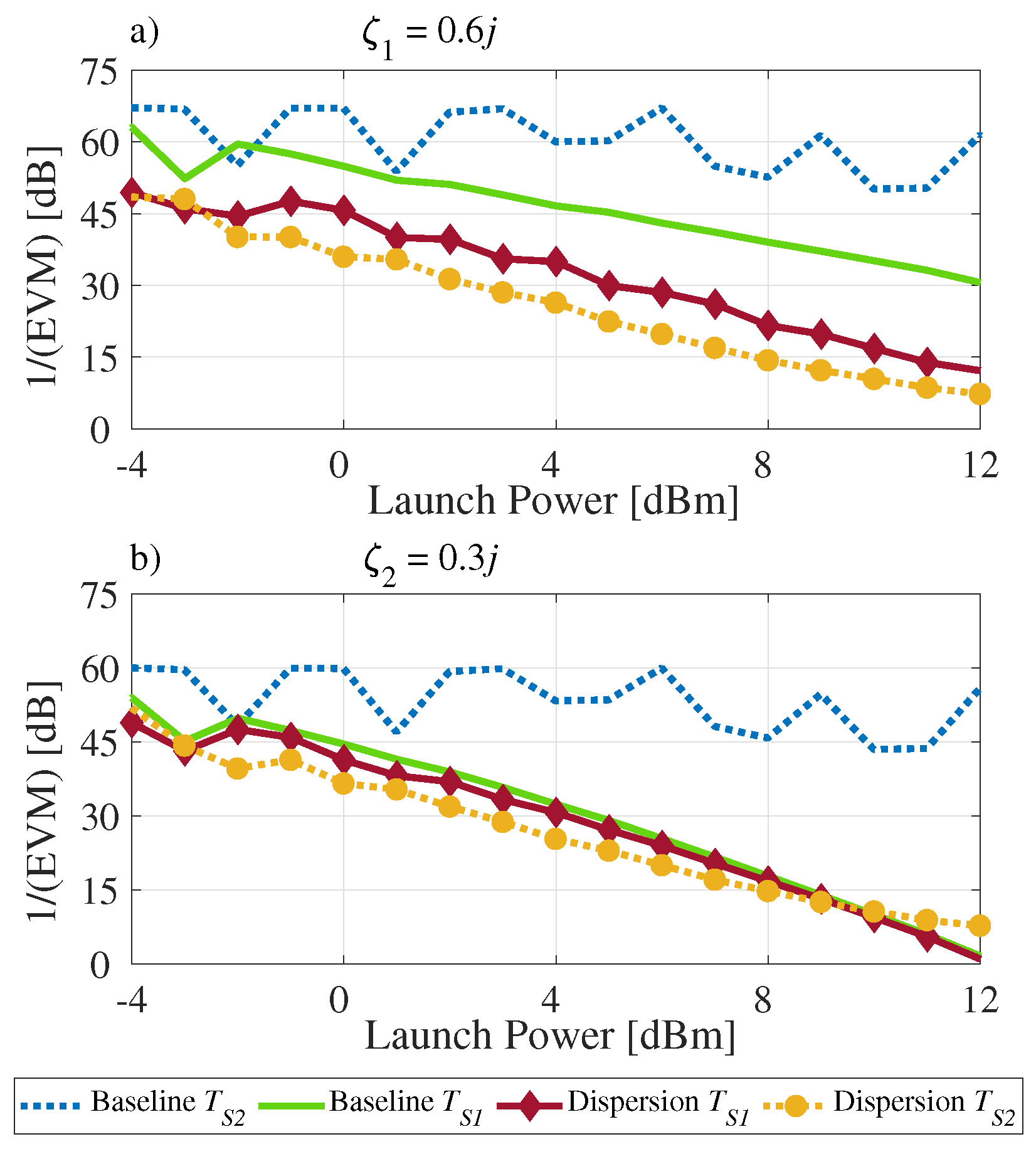
3.3. Third-Order Dispersion
Constellation Analysis
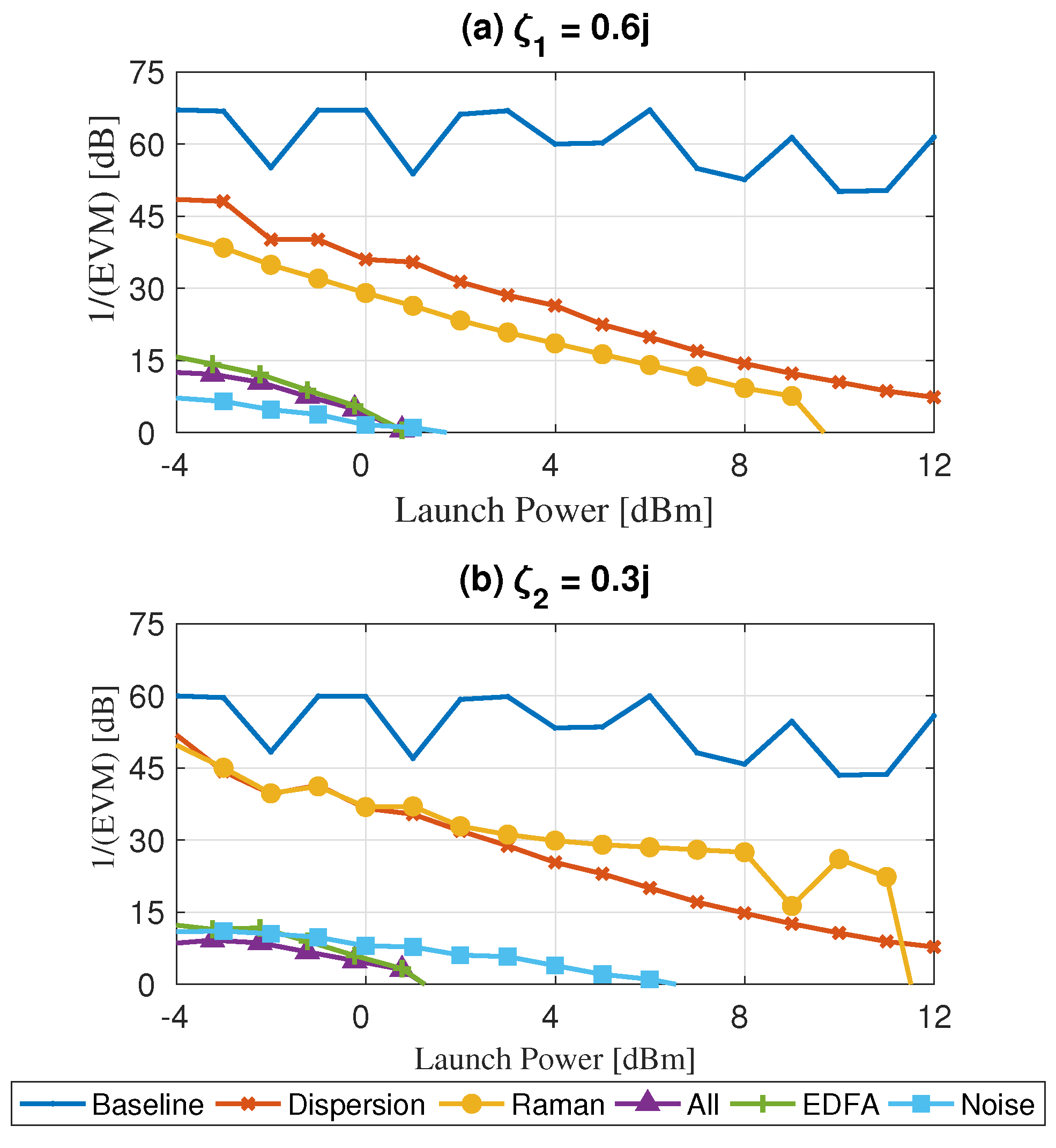
3.4. Lumped Gain
Constellation Analysis
3.5. Ase Noise
3.6. All Impairments Combined
Constellation Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Pre-Compensation For Raman Shift


References
- Essiambre, R.J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. J. Light. Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Yousefi, M.I.; Kschischang, F.R. Information transmission using the nonlinear Fourier transform, part III: Spectrum modulation. IEEE Trans. Info. Theory 2014, 60, 4346–4369. [Google Scholar] [CrossRef]
- Redor, I.; Barthélemy, E.; Michallet, H.; Onorato, M.; Mordant, N. Experimental Evidence of a Hydrodynamic Soliton Gas. Phys. Rev. Lett. 2019, 122, 214502. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lucas, E.; Raja, A.S.; He, J.; Riemensberger, J.; Wang, R.N.; Karpov, M.; Guo, H.; Bouchand, R.; Kippenberg, T.J. Photonic microwave generation in the X- and K-band using integrated soliton microcombs. Nat. Photonics 2020, 14, 486–491. [Google Scholar] [CrossRef]
- Wang, W.; Wang, L.; Zhang, W. Advances in soliton microcomb generation. Adv. Photonics 2020, 2, 034001. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Shemer, L.; Arie, A. Observation of accelerating solitary wavepackets. Phys. Rev. E 2020, 101, 050201. [Google Scholar] [CrossRef] [PubMed]
- Rozenman, G.G.; Schleich, W.P.; Shemer, L.; Arie, A. Periodic Wave Trains in Nonlinear Media: Talbot Revivals, Akhmediev Breathers, and Asymmetry Breaking. Phys. Rev. Lett. 2022, 128, 214101. [Google Scholar] [CrossRef] [PubMed]
- Lannig, S.; Schmied, C.M.; Prüfer, M.; Kunkel, P.; Strohmaier, R.; Strobel, H.; Gasenzer, T.; Kevrekidis, P.G.; Oberthaler, M.K. Collisions of Three-Component Vector Solitons in Bose-Einstein Condensates. Phys. Rev. Lett. 2020, 125, 170401. [Google Scholar] [CrossRef] [PubMed]
- Rozenman, G.G.; Fu, S.; Arie, A.; Shemer, L. Quantum mechanical and optical analogies in surface gravity water waves. Fluids 2019, 4, 96. [Google Scholar] [CrossRef]
- Pernet, N.; St-Jean, P.; Solnyshkov, D.D.; Malpuech, G.; Carlon Zambon, N.; Fontaine, Q.; Real, B.; Jamadi, O.; Lemaître, A.; Morassi, M.; et al. Gap solitons in a one-dimensional driven-dissipative topological lattice. Nat. Phys. 2022, 18, 678–684. [Google Scholar] [CrossRef]
- Qi, Y.; Yang, S.; Wang, J.; Li, L.; Bai, Z.; Wang, Y.; Lv, Z. Recent advance of emerging low-dimensional materials for vector soliton generation in fiber lasers. Mater. Today Phys. 2022, 23, 100622. [Google Scholar] [CrossRef]
- Hari, S.; Kschischang, F.; Yousefi, M. Multi-eigenvalue communication via the nonlinear Fourier transform. In Proceedings of the 2014 27th Biennial Symposium on Communications (QBSC), Kingston, ON, Canada, 1–4 June 2014; pp. 92–95. [Google Scholar]
- Le, S.T.; Prilepsky, J.E.; Turitsyn, S.K. Nonlinear inverse synthesis for high spectral efficiency transmission in optical fibers. Opt. Express 2014, 22, 26720–26741. [Google Scholar] [CrossRef]
- Le, S.T.; Prilepsky, J.E.; Turitsyn, S.K. Nonlinear inverse synthesis technique for optical links with lumbed amplification. Opt. Express 2015, 23, 8317–8325. [Google Scholar] [CrossRef] [PubMed]
- Hari, S.; Yousefi, M.I.; Kschischang, F.R. Multieigenvalue Communication. J. Light. Technol. 2016, 34, 3110–3117. [Google Scholar] [CrossRef]
- Bülow, H.; Aref, V.; Idler, W. Transmission of waveforms determined by 7 eigenvalues with PSK-modulated spectral amplitudes. In Proceedings of the European Conference on Optical Communication, ECOC, Dusseldorf, Germany, 18–22 September 2016; pp. 412–414. [Google Scholar]
- Aref, V.; Bülow, H. Design of 2-Soliton spectral phase modulated pulses over lumped amplified link. In Proceedings of the European Conference on Optical Communication (ECOC), Dusseldorf, Germany, 18–22 September 2016; pp. 409–411. [Google Scholar]
- Bülow, H.; Len, S.T.; Aref, V. Modulation of the nonlinear spectrum in experiment. In Proceedings of the Optics InfoBase Conference Papers—Advanced Photonics Conference, New Orleans, LA, USA, 24–27 July 2017; pp. 10–12. [Google Scholar]
- Gui, T.; Chan, T.H.; Lu, C.; Lau, A.P.T.; Wai, P.A. Alternative Decoding Methods for Optical Communications Based on Nonlinear Fourier Transform. J. Light. Technol. 2017, 35, 1542–1550. [Google Scholar] [CrossRef]
- Aref, V.; Le, S.T.; Buelow, H. Modulation over Nonlinear Fourier Spectrum: Continuous and Discrete Spectrum. J. Light. Technol. 2018, 36, 1289–1295. [Google Scholar] [CrossRef]
- Bülow, H.; Aref, V.; Schmalen, L. Modulation on Discrete Nonlinear Spectrum: Perturbation Sensitivity and Achievable Rates. IEEE Photonics Technol. Lett. 2018, 30, 423–426. [Google Scholar] [CrossRef]
- Leible, B.; Chen, Y.; Yousefi, M.I.; Hanik, N. Soliton Transmission with 5 Eigenvalues over 2000km of Raman-Amplified Fiber. In Proceedings of the International Conference on Transparent Optical Networks, Bucharest, Romania, 1–5 July 2018; pp. 1–4. [Google Scholar]
- Turitsyna, E.G.; Turitsyn, S.K. Digital signal processing based on inverse scattering transform. Opt. Lett. 2013, 38, 4186–4188. [Google Scholar] [CrossRef] [PubMed]
- Wahls, S.; Le, S.T.; Prilepsk, J.E.; Poor, V.H.; Turitsyn, S.K. Digital backpropagation in the nonlinear Fourier domain. In Proceedings of the IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 445–449. [Google Scholar] [CrossRef]
- Lima Jr., I.T.; Grigoryan, V.S.; O’Sullivan, M.; Menyuk, C.R. Computational Complexity of Nonlinear Transforms Applied to Optical Communications Systems with Normal Dispersion Fibers. In Proceedings of the 2015 IEEE Photonics Conference (IPC), Reston, VA, USA, 4–8 October 2015; pp. 277–278. [Google Scholar]
- Lima, I.T., Jr.; DeMenezes, T.D.S.; Grigoryan, V.S.; O’Sullivan, M.; Menyuk, C.R. Nonlinear Compensation in Optical Communication Systems with Normal Dispersion Fiber Using Nonlinear Fourier Transform. J. Light. Technol. 2017, 35, 5056–5068. [Google Scholar] [CrossRef]
- Chimmalgi, S.; Prins, P.J.; Wahls, S. Nonlinear Fourier transform algorithm using a higher order exponential integrator. In Proceedings of the OSA Advanced Photonics Congress, Zurich, Switzerland, 2–5 July 2018; pp. 7–8. [Google Scholar]
- Medvedev, S.; Vaseva, I.; Chekhovskoy, I.; Fedoruk, M. Novel numerical algorithm with fourth-order accuracy for the direct Zakharov-Shabat problem. arXiv 2019, arXiv:1902.09736v7. [Google Scholar]
- Wahls, S.; Chimmalgi, S.; Prins, P.J. Wiener-Hopf Method for b-Modulation. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–2. [Google Scholar]
- Zhang, Q.; Kschischang, F. Correlation-Aided Nonlinear Spectrum Detection. J. Light. Technol. 2021, 39, 4923–4931. [Google Scholar] [CrossRef]
- Kamalian, M.; Vasylchenkova, A.; Prilepsky, J.; Shepelsky, D.; Turitsyn, S. Communication System Based on Periodic Nonlinear Fourier Transform with Exact Inverse Transformation. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018. [Google Scholar]
- Hasegawa, A.; Kodama, Y. Solitonsn in Optical Communications; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Bülow, H.; Aref, V.; Schuh, K.; Idler, W. Experimental Nonlinear Frequency Domain Equalization of QPSK Modulated 2-Eigenvalue Soliton. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016; pp. 1–3. [Google Scholar]
- Dong, Z.; Hari, S.; Gui, T.; Zhong, K.Y.M.I.; Lu, C.; Wai, P.K.A.; Kschishang, F.R.; Lau, A.P.T. Nonlinear frequency division multiplexed based on NFT. IEEE Photonics Tehcnol. Lett. 2015, 27, 1621–1623. [Google Scholar] [CrossRef]
- Span, A.; Aref, V.; Bulow, H.; Ten Brink, S. Efficient Precoding Scheme for Dual-Polarization Multi-Soliton Spectral Amplitude Modulation. IEEE Trans. Commun. 2019, 67, 7604–7615. [Google Scholar] [CrossRef]
- Civelli, S.; Forestieri, E.; Secondini, M. A Novel Detection Strategy for Nonlinear Frequency-Division Multiplexing. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Bülow, H. Experimental demonstration of optical signal detection using nonlinear Fourier transform. J. Light. Technol. 2015, 33, 1433–1439. [Google Scholar] [CrossRef]
- Da Ros, F.; Civelli, S.; Gaiarin, S.; Da Silva, E.P.; De Renzis, N.; Secondini, M.; Zibar, D. Dual-Polarization NFDM Transmission with Continuous and Discrete Spectral Modulation. J. Light. Technol. 2019, 37, 2335–2343. [Google Scholar] [CrossRef]
- Shevchenko, N.A.; Prilepsky, J.E.; Derevyanko, S.A.; Alvarado, A.; Bayvel, P.; Turitsyn, S.K. A lower bound on the per soliton capacity of the nonlinear optical fibre channel. In Proceedings of the ITW 2015—2015 IEEE Information Theory Workshop, Jeju Island, Korea, 11–15 October 2015; pp. 104–108. [Google Scholar]
- Gui, T.; Lo, S.K.; Zhou, X.; Lu, C.; Tao Lau, A.P.; Wai, P.K. High-order modulation on a single discrete eigenvalue for optical communications based on nonlinear Fourier transform. Opt. Express 2017, 25, 20286–20297. [Google Scholar] [CrossRef] [PubMed]
- Buchberger, A.; Graell I Amat, A.; Aref, V.; Schmalen, L. Probabilistic eigenvalue shaping for nonlinear fourier transform transmission. J. Light. Technol. 2018, 36, 4799–4807. [Google Scholar] [CrossRef]
- Span, A.; Aref, V.; Henning, B. On Time-Bandwidth Product of Multi-Soliton Pulses. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 61–65. [Google Scholar]
- Geisler, A.; Leibrich, J.; Schäffer, C.G. Influence of non-ideal first order counter-propagating Raman amplification on discrete nonlinear fourier spectrum based communication. In Proceedings of the ITG-Fachbericht—Photonische Netze, Leipzig, Germany, 11–12 June 2018; Volume 279, pp. 83–89. [Google Scholar]
- Yousefi, M.; Yangzhang, X. Linear and Nonlinear Frequency-Division Multiplexing. IEEE Trans. Inf. Theory 2020, 66, 478–495. [Google Scholar] [CrossRef]
- Yousefi, M.I.; Kschischang, F.R. Information transmission using the nonlinear Fourier transform, part I: Mathematical tools. IEEE Trans. Info. Theory 2014, 60, 4312–4328. [Google Scholar] [CrossRef]
- Yousefi, M.I.; Kschischang, F.R. Information transmission using the nonlinear Fourier transform, part II: Numerical methods. IEEE Trans. Info. Theory 2014, 60, 4329–4345. [Google Scholar] [CrossRef]
- DeMenezes, T.D.S.; Grigoryan, V.S.; O’Sullivan, M.; Menyuk, C.R.; Lima Jr., I.T. Performance Limits of a Nonlinear Frequency Division Multiplexed System due to the Raman effect. In Proceedings of the 2017 IEEE Photonics Conference (IPC), Orlando, FL, USA, 1–5 October 2017. [Google Scholar]
- Bajaj, V.; Chimmalgi, S.; Aref, V.; Wahls, S. Exact NFDM Transmission in the Presence of Fiber-Loss. J. Light. Technol. 2020, 38, 3051–3058. [Google Scholar] [CrossRef]
- Gaiarin, S.; Perego, A.M.; da Silva, E.P.; da Ros, F.; Zibar, D. Dual-polarization nonlinear Fourier transform-based optical communication system. Optica 2018, 5, 263–270. [Google Scholar] [CrossRef]
- Gaiarin, S.; Da Ros, F.; De Renzis, N.; da Silva, E.P.; Zibar, D. Dual-Polarization NFDM Transmission Using Distributed Raman Amplification and NFT-Domain Equalization. IEEE Photonics Technol. Lett. 2018, 30, 1983–1986. [Google Scholar] [CrossRef]
- Yangzhang, X.; Lavery, D.; Bayvel, P.; Yousefi, M.I. Impact of Perturbations on Nonlinear Frequency-Division Multiplexing. J. Light. Technol. 2018, 36, 485–494. [Google Scholar] [CrossRef]
- Tavakkolnia, I.; Safari, M. The Impact of PMD on Single-Polarization Nonlinear Frequency Division Multiplexing. J. Light. Technol. 2019, 37, 1264–1272. [Google Scholar] [CrossRef]
- Koch, J.; Chan, K.; Schaeffer, C.G.; Pachnicke, S. Signal Processing Techniques for Optical Transmission Based on Eigenvalue Communication. IEEE J. Sel. Top. Quantum Electron. 2021, 27. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 3rd ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Keiser, G. Optical Fiber Communications, 4th ed.; McGraw-Hill Education: Berkshire, UK, 2010. [Google Scholar]
- Ablowitz, M.J.; Ladik, J.F. Nonlinear differential-difference equations. J. Math. Phys. 1975, 16, 598–603. [Google Scholar] [CrossRef]
- Bülow, H. Experimental Assessment of Nonlinear Fourier Transform Based Detection under Fiber Nonlinearity. In Proceedings of the 2014 European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014. [Google Scholar]
- Bülow, H. Nonlinear Fourier Transformation Based Coherent Detection Scheme for Discrete Spectrum. In Proceedings of the Optical Fiber Communications Conference and Exhibition, Los Angeles, CA, USA, 22–26 March 2015; pp. 1–3. [Google Scholar]
- Aref, V.; Bülow, H.; Schuh, K.; Idler, W. Experimental Demonstration of Nonlinear Frequency Division Multiplexed Transmission. In Proceedings of the European Conference on Optical Communication, Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar]
- Schmogrow, R.; Nebendahl, B.; Winter, M.; Josten, A.; Hillerkuss, D.; Koenig, S.; Meyer, J.; Dreschmann, M.; Huebner, M.; Koos, C.; et al. Error Vector Magnitude as a Performance Measure for Advanced Modulation Formats. IEEE Photonics Technol. Lett. 2012, 24, 61–63. [Google Scholar] [CrossRef]
- Gordon, J.P. Interaction forces among solitons in optical fibers. Opt. Lett. 1983, 8, 596–598. [Google Scholar] [CrossRef]
- Agrawal, G.P. Applied Nonlinear Fiber Optics; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Gordon, J.P. Theory of the soliton self-frequency shift. Opt. Lett. 1986, 11, 662–664. [Google Scholar] [CrossRef] [PubMed]
- Hause, A.; Mitschke, F. Soliton trains in motion. Phys. Rev. A 2010, 82, 043838. [Google Scholar] [CrossRef]
- Le, S.T.; Prilepsky, J.E.; Rosa, P.; Ania-Castanon, J.D.; Turitsyn, S.K. Nonlinear Inverse Synthesis for Optical Links With Distributed Raman Amplification. J. Light. Technol. 2016, 34, 1778–1786. [Google Scholar] [CrossRef]
- Wang, P.; Hinton, K.; Farrell, P.M.; Pillai, B.S.G. On EDFA and Raman Fiber Amplifier Energy Efficiency. In Proceedings of the IEEE International Conference on Data Science and Data Intensive Systems, Sydney, Australia, 11–13 December 2015; pp. 268–275. [Google Scholar]
- Derevyanko, S.A.; Prilepsky, J.E.; Turitsyn, S.K. Capacity estimates for optical transmission based on the nonlinear Fourier transform. Nat. Comm. 2016, 7, 12710. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.T.; Gaiarin, S.; Yankov, M.P.; Zibar, D. Time-Domain Neural Network Receiver for Nonlinear Frequency Division Multiplexed Systems. IEEE Photonics Technol. Lett. 2018, 30, 1079–1082. [Google Scholar] [CrossRef]









| SR (GBd) | Launch Power (dBm) | |
|---|---|---|
| Baseline, Raman, Dispersion, Noise | Lumped Gain, All Effects | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Menezes, T.D.S.; Tu, C.; Besse, V.; O’Sullivan, M.; Grigoryan, V.S.; Menyuk, C.R.; Lima Jr., I.T. Nonlinear Spectrum Modulation in the Anomalous Dispersion Regime Using Second- and Third-Order Solitons. Photonics 2022, 9, 748. https://doi.org/10.3390/photonics9100748
De Menezes TDS, Tu C, Besse V, O’Sullivan M, Grigoryan VS, Menyuk CR, Lima Jr. IT. Nonlinear Spectrum Modulation in the Anomalous Dispersion Regime Using Second- and Third-Order Solitons. Photonics. 2022; 9(10):748. https://doi.org/10.3390/photonics9100748
Chicago/Turabian StyleDe Menezes, Thiago D. S., Chaoran Tu, Valentin Besse, Maurice O’Sullivan, Vladimir S. Grigoryan, Curtis R. Menyuk, and Ivan T. Lima Jr. 2022. "Nonlinear Spectrum Modulation in the Anomalous Dispersion Regime Using Second- and Third-Order Solitons" Photonics 9, no. 10: 748. https://doi.org/10.3390/photonics9100748
APA StyleDe Menezes, T. D. S., Tu, C., Besse, V., O’Sullivan, M., Grigoryan, V. S., Menyuk, C. R., & Lima Jr., I. T. (2022). Nonlinear Spectrum Modulation in the Anomalous Dispersion Regime Using Second- and Third-Order Solitons. Photonics, 9(10), 748. https://doi.org/10.3390/photonics9100748






