1. Introduction
Floquet resonance in a periodically driven field is of fundamental importance in quantum control and manipulation in which periodic driving [
1,
2,
3,
4] has emerged as a technique to realize different applications, for instance, in population trapping [
5], quantum phase transition [
6,
7], atomic transportation [
8,
9] and quantum information processing [
10,
11]. Among various models, the paradigmatic two-level and there-level systems, e.g., Rydberg-excited atoms [
12], Bose-Einstein condensate (BEC) [
13,
14,
15], coupled waveguide arrays [
16,
17] and Dirac electrons [
18], have been intensively investigated and exhibit interesting effects including dynamical localization [
19], coherent destruction of tunneling (CDT) [
20,
21] and photo-assisted tunneling (PAT) [
22]. Recently, dynamics of monolayer graphene in a time-periodic potential are widely studied in the framework of the Floquet approach and exhibit a number of novel quantum effects [
23] such as photon-induced tunneling of electrons [
24], chiral tunneling [
25], Floquet scatting [
26] and voltage-driven quantum oscillations [
27]. These findings and approaches that are related to Floquet dynamics open the possibility of controlling quantum states in multiple nanotechnological applications.
In particular, recent numerical algorithms and experimental conditions have developed driving schemes from monochromatic [
28] to bichromatic [
29], three-frequency [
30] and even random-frequency driving models [
31], and consequently provide more intriguing results such as multiphoton resonance and fractional photon-assisted tunneling [
32]. Esmann and coworkers [
33] have revealed that 1/2-photon, 1/3-photon, and 1/4-photon resonances can have large effects on the particle transfer. Strictly speaking, there is no true photon absorption in a driven system and the
photons are provided by the external driving field. In this paper, resonances corresponding to integer or fractional multiples of a driving frequency are still called photon resonances, which in essence are analogous to those in solids. These extensions of photon resonance in a periodically driven system are of significance and provide a more flexible way to realize how such effects could be applied. For instance, an analog of photon-assisted tunneling [
34] is achieved in a coupled optical waveguide system by only modulating one waveguide and adjusting the distance between two adjacent ones, which may offer benefits for controlling light propagation and realizing all-optical switches.
For these periodically driven systems, Floquet theory provides a useful tool to understand the physical mechanism of some new quantum effects derived from the time-dependent schr
ödinger equations (TDSE) [
35,
36] with a time-periodic Hamiltonian
where
is the period of external driving fields for all time
t. Recently, Floquet approaches have developed into many types such as Shirley’s formulation of Floquet theory (SFT) [
37], many-mode Floquet theory (MMFT) [
38,
39,
40] and instantaneous Floquet state (IFS) [
41]. In special cases of multiple periodic fields with commensurate frequencies (integer multiples of a common frequency), Poertner and Martin [
42] have proved the equivalence of SFT and MMFT.
These powerful approaches enable us to qualitatively understand Floquet resonances in multiple frequency driving conditions. In this paper, we focus on the peculiar behaviors of tunneling probability at and beyond the resonance by investigating a particle in a three-well lattice subjected to a dc field plus two ac fields. We propose that through driving-induced resonances, one can engineer the parameter space involving six relevant driving parameters for both coherent tunneling and complete population trapping. Also, the ratio between driving amplitude and frequency plays a vital role in exploring features of tunneling dynamics. Our results further demonstrate that pairs of avoided crossings of quasienergies account for the photon-assisted tunneling which is closely related to the symmetrical and anti-symmetrical states. Furthermore, in two-frequency driving conditions, we find that integer and fractional photon-assisted tunneling show obvious dependence on driving amplitudes and phase differences, which provides us with a way to coherently control the tunneling probability between different quantum states.
The rest of this paper is structured as follows. In
Section 2, we present the physical model, Floquet theory and SFT method and then introduce a useful transformation in the high-frequency approximation. To characterize the particle’s evolution behaviors, we define a physical quantity, namely the tunneling probability, to directly describe the tunneling rate. In
Section 3, we revisit integer multiple photon resonances and their physical mechanisms under monochromatic cases. Floquet-based interpretations reveal that pairs of avoided crossings of quasienergies account for photon-assisted tunneling. In
Section 4, we indulge in the two-frequency driving cases and find that fractional-order resonances being a large effect on tunneling dynamics can have an excellent explanation by utilizing the Floquet theory under certain conditions. Then, we further analyze dynamic dependences on driving amplitude and phase difference and establish a close connection with Floquet properties. Finally, we summarize our results in
Section 5.
2. Model and Method
We study a particle confined in a driven system consisting of a linear arrangement of three quantum wells, in which the left-most well (well-1) is driven by a dual-frequency field and the other two wells denoted by
are undriven. Such a three-well (state) model illustrated in
Figure 1a can be realized by subjecting ultracold neutral atoms to spatially periodic light-shift potentials arising in the interference patterns of multiple laser beams [
43,
44]. In particular, Frederik et al. [
45] proposed a two-frequency driving case by modulating the position of an optical lattice at two frequencies simultaneously. These experimental results establish the possibility of artificially generating two-frequency driving quantum potentials in an optical lattice. Alternatively, a three-engineered-waveguide system can provide an ideal platform to investigate such driving-induced phenomena by mapping the temporal evolution of quantum dynamics into spatial propagation of light waves. Experimentally, the technology of fs laser written waveguide arrays (see Ref. [
46] for full details of the fabrication method) permits our specific setting of the two-frequency driving properties of the waveguides. S. Longhi et al. have provided several methods to realize the selective harmonic modulations by periodically bending particular waveguides [
2,
47,
48] or by harmonically modulating the refractive index of partial waveguides while keeping the rest fixed [
49]. As in the experiments [
46], in
Figure 1b, we set the top boundary waveguide to have a different refractive index profile compared to the rest waveguides. The width of the individual waveguides is set to be 3 μm and the adjacent waveguide spacing amounts to 32 μm. The input power of light intensity is on the order of
. Thus, selectively irradiating the top waveguide with two harmonic frequencies is well within the reach of the related experimental setup.
Dynamics of the system is governed by the dimensionless Hamiltonian (
) [
50,
51,
52],
where
represent the localized state in the three wells correspondingly. Here, the dual-frequency field
acts on well-1 with
being the dc field, and
and
being the driving amplitudes and frequencies of the external driving ac field-1 and field-2 with a phase difference
. The six driving parameters can be tuned to explore the driving-induced photon resonances.
g is the coupling intensity between adjacent wells and couplings between next-nearest-neighbor wells have been neglected. As in the Ref. [
53], all the parameters
and
are normalized in units of a reference frequency
on the order of
, and time
t is normalized in units of
. Dynamics of this system can be obtained by numerically solving the TDSE
, where the quantum state
is expanded with the localized state. Here
represents the probability amplitude at the jth well and satisfies normalization condition
. We will use the population probability
to characterize the dynamics.
2.1. Floquet Theory and SFT Method
When two driving frequencies are rational, i.e.,
with
and
being integers, Hamiltonian (
1) is periodic in time
t with a common frequency
. According to the Floquet theory [
35,
36], for a Hamiltonian that is both periodic and hermitian, one could write three independent solutions for quantum state
of the form,
where we have labeled each solution with index
j.
and
are the quasienergies and corresponding Floquet states with a same periodicity as the Hamiltonian,
. Hence we find
and the unitarity of
at all times guarantees that diagonal elements
of quasienergies are real.
Since Hamiltonian (
1) is also hermitian, we can define a unitary time evolution operator,
, satisfying,
for all time
t. Here, we have assumed that the initial time for evolution is given at
. From the equation of TDSE, one can find that
where
denotes the time-ordering operator. Then, for the unitary case [
53], the operator
is obtained formally,
Therefore, the quasienergies and quasistates of Equation (
2) can be obtained by numerically solving the time evolution operator over one period of the driving.
Based on Floquet’s theorem, Shirley [
37,
42] provides an alternative to direct integration, namely the SFT method, which relates the semiclassic time-dependent Hamiltonian to a time-independent Hamiltonian represented by an infinite matrix. In the following, we present briefly the SFT method in the case of a single frequency field. It can be extended to multiple frequencies [
37,
42]. However, we find the method is more convenient in dealing with single frequency fields as insights revealed by the method. Due to the periodicity of
, one can apply the SFT method through Fourier decomposition of the Floquet states,
where
and
n to be an integer. Here we have defined SFT Floquet state
, where
denotes the modes of the driving fields and forms an orthonormal basis. Note that Equation (
2) can also be written as
. Therefore, the SFT method is considered as the famous replicas of Floquet states, and their quasienergies are given by,
Because the periodic Hamiltonian (
1) can also be expanded as
where
m is also an integer, the TDSE can be expressed in terms of the
and
and expansion coefficients are determined from a time-independent matrix (the Floquet Hamiltonian). In our system, each
is a
matrix. The coupled time-independent equation is,
where
j runs over all the atomic states before each change in
n. This result is a linear eigenvalue problem and the Floquet Hamiltonian
can be conveniently defined by Dirac notation [
37],
where the index
represents an atomic state, but the index
represents a Fourier component. We can see that the Floquet Hamiltonian has a periodic structure with multiple
in the diagonal elements. Based on this SFT method, Floquet quasienergies and Floquet states are determined by an infinity time-independent matrix
which is solvable by appropriately truncating the standard basis for the Fourier space. Instead of summation over all integer m, here we only consider a finite set
and for the validity and simplicity, we select
. Then as Poertner and Martin have pointed out in Ref. [
42], the truncated Fourier series
is necessary to compute Equation (
7).
2.2. High-Frequency Approximation
As an effective analytical method, a high-frequency approximation is required to obtain approximate analytical solutions to the governing equation as analytical results can provide a better intuitive understanding of the physics. High-frequency approximation arises when the driving frequency exceeds other characteristic frequencies of the system [
54,
55,
56,
57,
58]. In that case, one can construct a high-frequency expansion of an effective time-independent Hamiltonian of the system by averaging out the high-frequency terms. In this paper, it is found that the high-frequency limit works well under the condition of
. We first apply the high-frequency approximation to gain some insight into the tunneling dynamics. By introducing the transformation
, we use the slowly varying function of time
to describe the evolution of tunneling dynamics and then obtain a coupled equation,
where the terms
describe the coupling between the driven well-1 and undriven well-2, which is effectively modified by six driving parameters. After further using the Jacobi-Anger expansion
with
being the
th-order ordinary Bessel function of
x, we can get the expansion
=
where
,
and
are integers. In the high-frequency approximation, the higher-order terms which are proportional to
and
where
vary rapidly and their average over a time scale larger than
(
) is zero. These terms can therefore be neglected. Hence we could obtain some analytical solutions which display fascinating physical phenomena such as dynamical stabilization and multiple photon resonances. For instance, when
, our model is identical to that of the periodically driven three-level system by a monochromatic field [
59,
60]. In the high-frequency regime,
, the effective coupling between well-1 and well-2 is
. The CDT effect occurs at a series of isolated driving parameter points which satisfy
[
20,
21].
To characterize dynamic behaviors, we define the tunneling probability
as,
where
denotes the population probability of the particle at the
jth well and
is the minimum value of
within a finite time interval (
). Under this definition,
means the probability of the particle initially trapped at the jth well can completely tunnel into other wells, while
indicates the occurrence of population trapping or dynamical localization of the state
in the simulation. Therefore, the value of
allows to directly measure the tunneling rate from state
to other states.
3. Integer Photon Resonance with a Single-Frequency Driving Field
In this section, we investigate integer photon resonances with one ac field (i.e.,
). In particular, we reveal a close relation between resonance dynamics and Floquet mode properties. To illustrate this relation, we first show dynamical evolution of
versus
and
in
Figure 1c, where we change parameters
and
and fix
. The initial conditions are
and we choose
. When
varies from 0 to 2.5, one finds that, in the horizontal direction, three pairs of resonance features are illustrated, and bright colors indicate higher tunneling rates. It is seen that quantum tunneling from well 1 to the other two wells is greatly restored when
is about an integer. If assuming
where
and
n being an integer, parameters corresponding to
where
are usually called resonance points. One can define the tunneling near these points as
n-photon-assisted tunneling, i.e., zeroth-order, 1st-order and 2nd-order PAT as marked in
Figure 1c. In the vertical direction, it is seen that the zeroth-order photon-assisted tunneling is almost completely suppressed when
equals to 2.4, and 5.5, satisfying
. According to the high-frequency approximation in Equation (
9), one can see that the right-hand side of the equation vanishes, which suppresses the tunneling. Similarly, one can find the suppression of other orders. For example, the 1st-order photon-assisted tunneling is inhibited when
equals 3.8 satisfying
. Finally, we rewrite Equation (
9) in the high-frequency approximation using the Bessel functions,
Clearly, tunneling probabilities between wells are completely inhibited under the conditions of , indicating the occurrence of population trapping and the particle will be localized at the initial well.
3.1. Physical Explanation of Photon-Assisted Tunneling
To understand the physical mechanism of integer photon-assisted tunneling, we first investigate the properties of Floquet quasienergies based on the SFT method. Driven by the single-frequency field, the relevant Floquet Hamiltonian has a simple form,
We can diagonalize
(truncated at
) to obtain the quasienergies for
. Three replicas are presented in
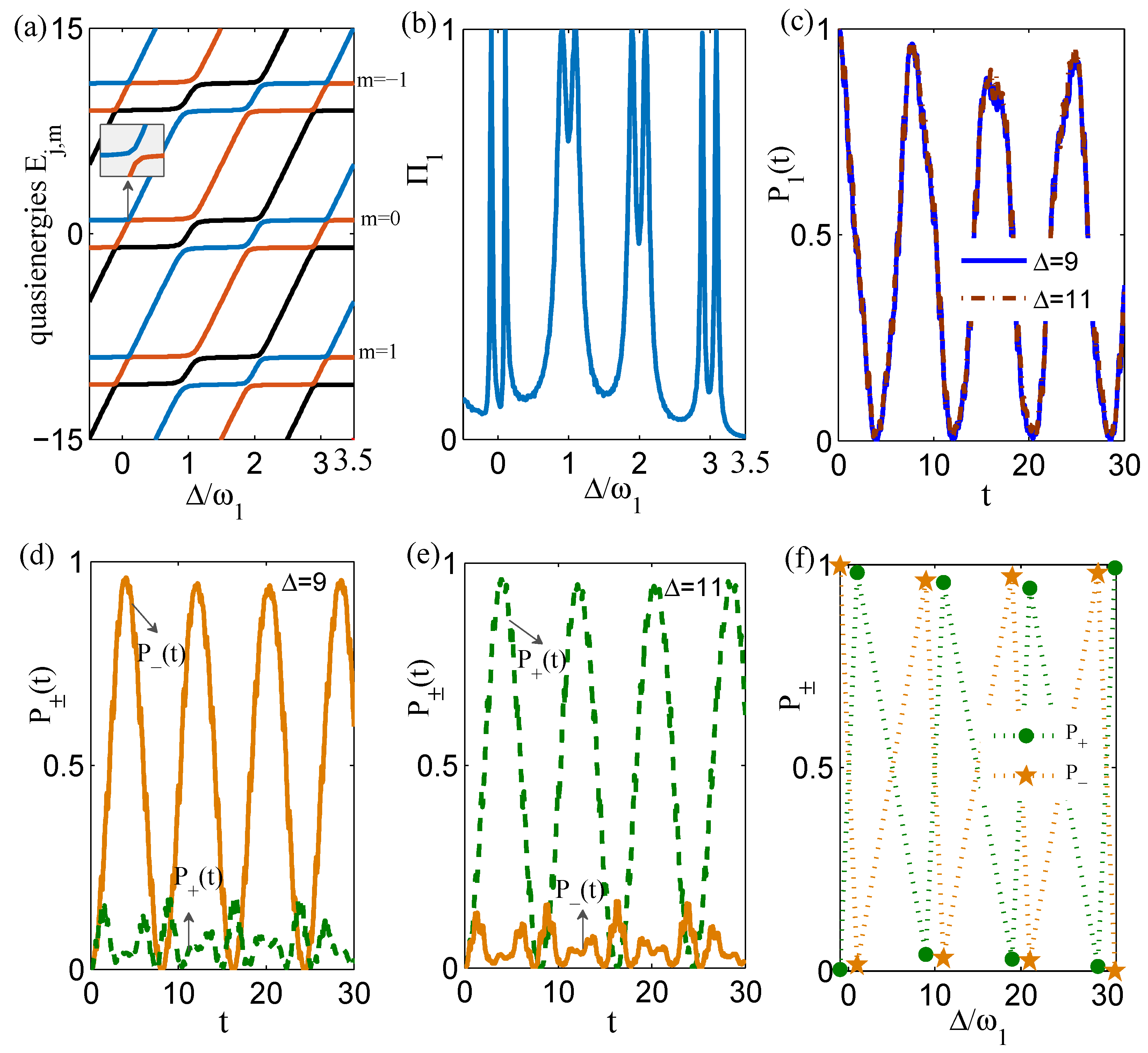
Figure 2a corresponding to
. The ratio
is varied by changing
and fixing
. Other parameters are
and
. Avoided level crossings of the quasienergy are clearly displayed near
. The partially enlarged illustration (the insert in
Figure 2a) shows that there are no degeneracy points in this quasienergy spectrum. The hybridization between different quantum states around the avoided level crossing leads to photon-assisted tunneling. To confirm this, we numerically solve the TDSE and plot
as a function of
for
in
Figure 2b. It is seen that at these avoided crossings, photon-assisted tunneling is identified as pairs of sharp peaks in
.
As an important aspect within this analysis, we further identify which states are actually excited at the avoided crossings by looking at the occupation in the basis of
,
and
. Evolutions of occupations at well 1
for two cases of
and
are plotted in
Figure 2c. It is seen that evolutions for the 1st-order resonance tunneling under these two conditions keep the same properties. Then occupations at the symmetrical state
, i.e.,
and the anti-symmetrical state
, i.e.,
are displayed in
Figure 2d,e. For
,
oscillates with a higher amplitude, while
keeps a lower value. However, for
, we see the opposite. Moreover, occupations at the symmetrical state
and the antisymmetrical state
at four pairs of avoided crossings are carefully checked, as shown in
Figure 2f, which demonstrates that when
, the particle tunnels into a hybrid state between well 2 and well 3. These values are numerically derived when
reaches zero for the first time. Therefore, the left tunneling peak at the nth-order resonance is closely related to the anti-symmetrical state and the right one is associated with the symmetrical state. In a brief, we attribute pairs of photon-assisted tunneling in
Figure 1c and
Figure 2b to avoid crossings in the quasienergies which, in essence, are the quantum feature of the hybridization between different quantum states.
3.2. Manipulation of Nth-Order Photon-Assisted Tunneling
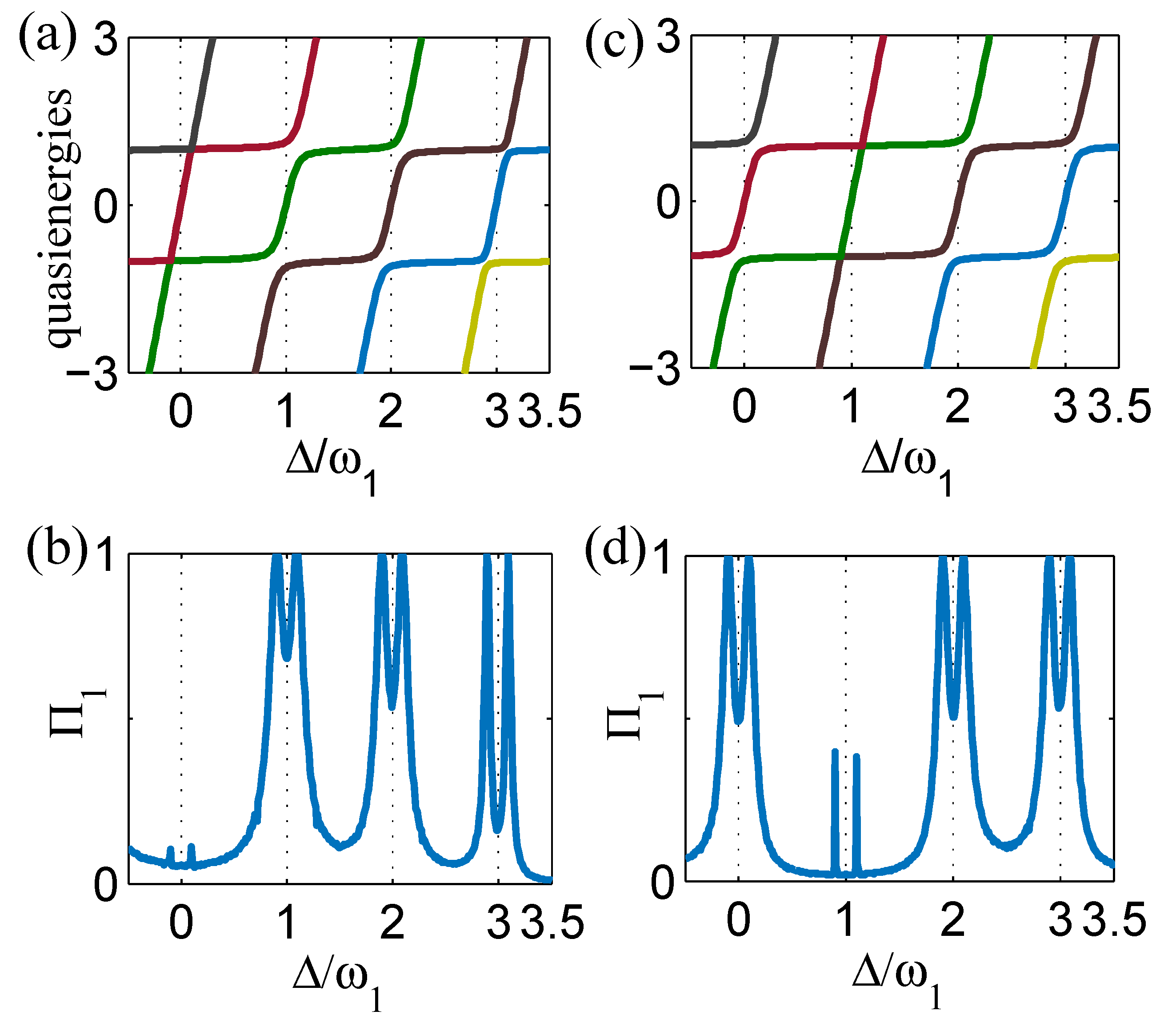
In this subsection, we focus on the control of tunneling dynamics. From
Figure 1c, we learn that
n-photon-assisted tunneling will be greatly suppressed once the conditions
are satisfied. Inspired by this, we provide a scheme to manipulate the
nth-order resonance dynamics. In
Figure 3, we show the Floquet spectra and tunneling probabilities
in terms of
with
and
. The left column is for
satisfying
, while the right column is for
which is a zero solution of
. We find that for
, as shown in
Figure 3a,b, when quasienergy levels tend to be degenerate near
, the zeroth-order tunneling peaks in
are suppressed. Then, for
, as shown in
Figure 3c,d, the Floquet spectrum becomes almost a crossing point near
where 1st-order photon-assisted tunneling is inhibited. Such conclusions can be extended to suppress nth-order photon-assisted tunneling by changing ratio
to satisfy
. Analytically, when
, the 1st-order photon-assisted tunneling is inhibited where
. For
, profiles of
is nearly identical (in
Figure 3d) due to
. These results provide an opportunity to control nth-order photon-assisted tunneling by choosing the driving amplitude and frequency.
4. Fractional Floquet Resonance under Two-Frequency Driving
In this section, we investigate fractional photon resonance when the system is driven by a two-frequency field. For concreteness, we set
such that the driving field becomes a superposition of two simple harmonic driving fields
. To illustrate the dynamics, we first present numerical results by considering
and
, as shown in
Figure 4a, in which pairs of straight lines with bright colors denoting high tunneling rates (or large
) are observed at different ratios of
, such as
. These
-photon-assisted tunneling effects come from the applied ac field-2 without which the particle has a very low probability of tunneling into other wells because
belonging to a particular tunneling suppression phenomenon [
59]. It is seen that in regions where tunneling should be suppressed, tunneling can be restored when the other drive frequency
is an integer multiple or fraction of the drive frequency
. In the low-frequency region, tunneling dynamics display a complex resonance pattern, while in the high-frequency region, it tends to have a stable constant value. Compared to the single frequency driving case, the two-frequency driving scheme offers richer dynamics, i.e., leading to both integer and fractional Floquet resonances. Considering the physics of the side with fractional
is just the same as the one with integer
in
Figure 4a, we incorporate the fractional transitions like
into integer ones like
. In the following, we just investigate in detail the fractional transitions, such as
.
4.1. Fractional Photon-Assisted Tunneling
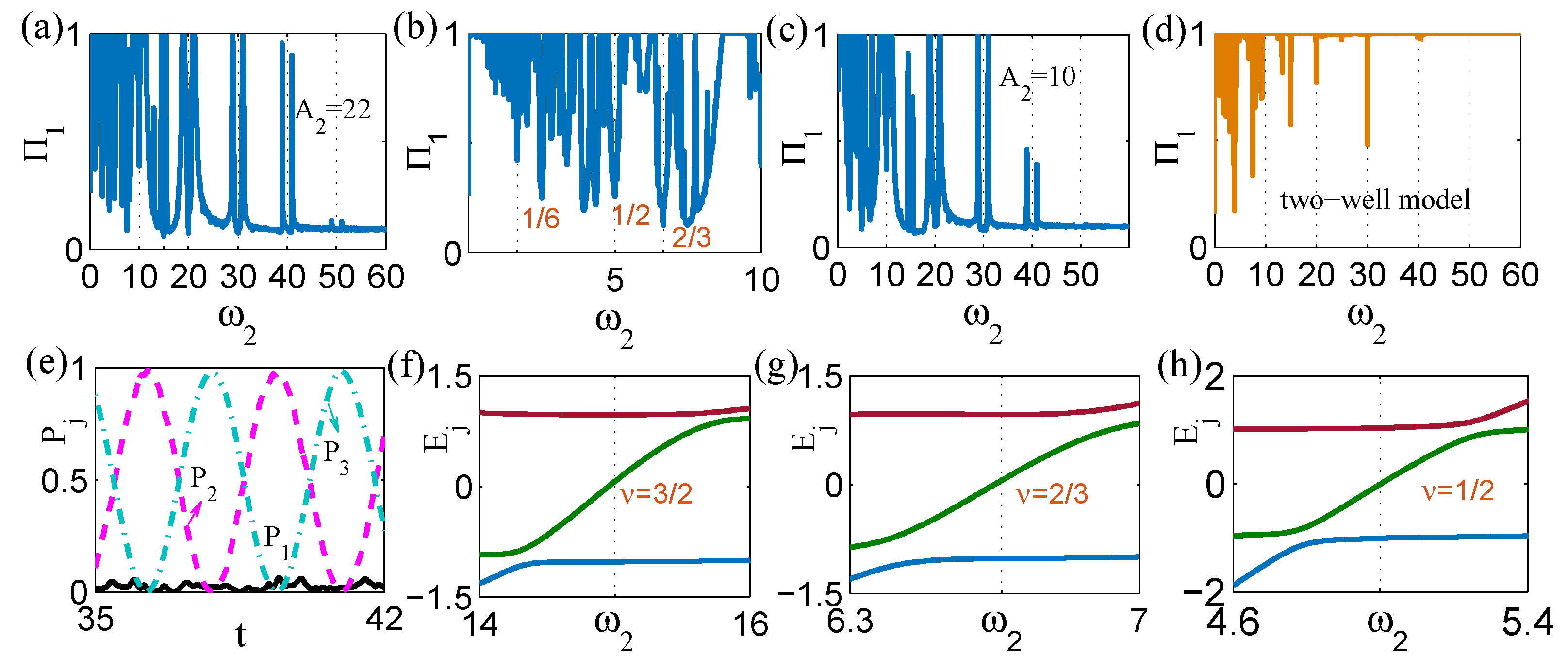
To explore the physical mechanism of these resonances, we show
versus
in
Figure 5a,b for
. Other parameters are
and
. When
varies in the low-frequency region (
),
increases to 1 and followed by multiple transitions between coherent tunneling and its suppression. As shown in
Figure 5b, the dip positions, from left to right, exactly correspond to the ratios
,
and
etc. What’s more, values of
are less than 0.5 when
and even
, suggesting that tunneling suppression at
th-order fractional photon resonances are not trivial effects. In the moderate-frequency region, when
, we note that when
, i.e.,
, there exists a pair of fractional photon-assisted tunneling peaks, together with a series of integer-multiphoton-like resonances. As expected, when
is in the high-frequency region (
), the curve ends up with a plateau representing a very low tunneling rate. More simulation results reveal that such resonance effects still exist even if
, as shown in
Figure 5c which is plotted under the condition of
and
. Other parameters are the same as in
Figure 5a. Then one may wonder whether the integer and fractional resonances appear particularly in driven three-wells. For this reason, we particularly plot the evolution of
versus
for the driven two-well system (i.e., by disconnecting the 3rd well) in
Figure 5d with the same parameters as in
Figure 5a. A series of dips without tunneling peaks (photon-assisted tunneling) is observed and clearly, in such a two-well model, resonance effects manifest as a series of tunneling suppression, as discussed in Ref. [
12]. Therefore, this suggests that the driven three-well system is the simplest model to investigate integer and fractional Floquet resonances.
To find out where the particle is when fractional photon-assisted tunneling occurs, we calculate the population probabilities at well 2 and well 3 when
. Taking
nd-order PAT as an example, as shown in
Figure 5e, when
reaches zero within a short time interval (between 35-time units and 42-time units), we find that the particle oscillates between well 2 and well 3. Thus, pairs of fractional PAT still correspond to the two hybrid states between wells 2 and 3.
As discussed in
Section 2, if
can be expressed as the ratio of two integers
, the Hamiltonian (
1) has a common frequency
. However, it is challenging for us to obtain accurate quasienergies for such a condition with two varying frequencies because the common frequency always changes for different
. Considering inconveniences of the SFT method in solving the variable dual-frequency problem, we turn to the basic Floquet theory and choose a finite narrow parameter range around the resonance to obtain some Floquet-based quasienergy spectra by solving the time evolution operator
over one period of
. For example, in the case of
, as shown in
Figure 5f, we set the common frequency
to calculate the quasienergies when
varies between 14 and 16. When
, as shown in
Figure 5g, the common frequency is
and
varies from 6.3 to 7. Other parameters are chosen as
,
and
. We find that at the resonance, three quasienergy levels are separated and the tunneling dynamics are inhibited. While near the resonance, pairs of avoided crossings are attributed to the fractional photon-assisted tunneling. Similarly, utilizing this method, we carefully check all the dips and their corresponding quasienergy spectra, as shown in
Figure 5h, in which we list another typical case of
. Comparing these results, we can have a deeper understanding of the complicated
-photon resonance. For very low values of
, the common frequency
must be much lower than
and the three quasienergies oscillating in the range (−
,
) tend to be degenerated, leading to high tunneling rates. When two quasienergy levels form the structure of avoided crossing, the particle can transfer from one state to another. Due to the common frequencies, the spectrum has a complicated energy level structure, resulting in complex resonance patterns in the low-frequency region. These numerical results reveal that Floquet theory still works well near the resonance even if the common frequency changes slightly and we can conclude that it is the avoided crossing of the Floquet quasienergy that brings the occurrence of integer or fractional photon-assisted tunneling.
4.2. Analytical Analysis in the High-Frequency Approximation
To obtain more intuitive explanations, we focus on the analytical analysis in this part. It is observed that when both
and
, as shown in
Figure 4a, these parameters fall in the high-frequency region, and the result can be explained analytically with the high-frequency approximation. The coupling intensity between well-1 and well-2
(see Equation (
9)) can be rewritten by assuming
where
as,
For small values of
and
, the effective coupling is mainly governed by
. This analytical result of
, as shown in
Figure 4b, has a good agreement with the numerical ones in
Figure 4a in the high frequency ranges. For instance,
tends to
if both
and
hold high values, resulting in a higher tunneling rate. However, we haven’t found any evidence of fractional photon-assisted tunneling in
Figure 4b, which proves that fractional resonance could be a combination of higher-order transitions. The further analytical result of the population amplitude at well-1 is yielded by solving the coupled Equation (
9),
where
. If the two driving frequencies are very high,
tends to be 1, determining the values of population amplitude at well-1 varying between 0 and 1. These analytical predictions agree well with the numerical results.
In addition, we also note that when one driving frequency is fixed,
tends to be a constant value with the increase of another frequency. For instance, when
and
is larger than 50, as shown in
Figure 5a,
is almost zero, exhibiting the occurrence of coherent population trapping. The higher
is, the weaker the influence of
on the coupling intensity. Therefore, in the parameter range
,
, we see almost decoupling between well 1 and well 2 in
Figure 5a. The analysis shows that the effective coupling intensity plays a critically important role in controlling tunneling.
4.3. Dependence on Driving Amplitudes
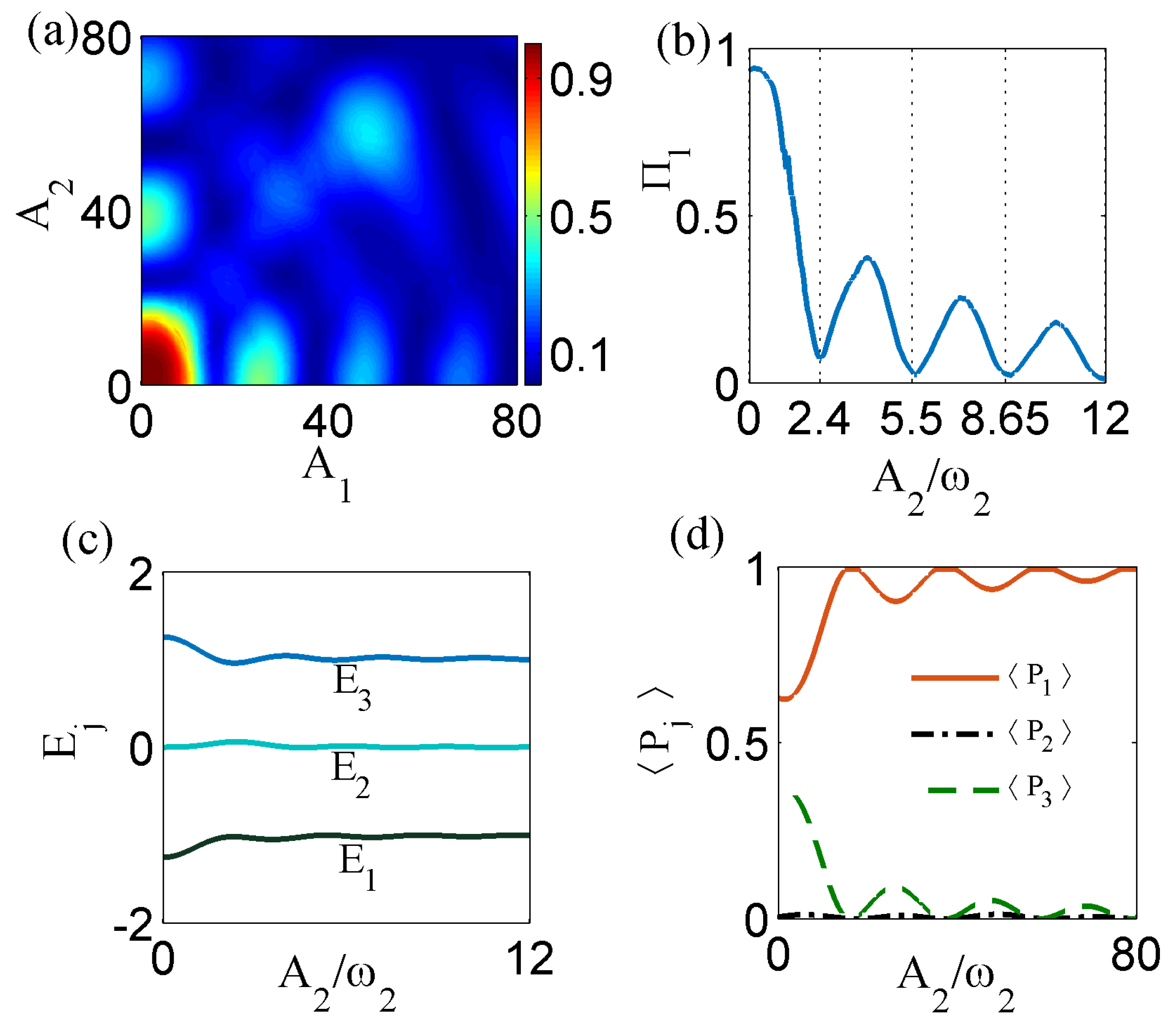
Using the
rd-order resonance as an example, we investigate the dependence on the driving amplitude. The evolution of
versus
and
is plotted in
Figure 6a with
and
. For
, the 2/3rd-order photon-assisted tunneling effect becomes significant in the weak-driving parameter region, i.e.,
and
being very small, in which the value of
can reach 1, manifesting that the particle can almost completely tunnel into other wells. This result can be understood because the weak-driving conditions are similar to those in the high-frequency approximation. when
and
are very small, the effective coupling
in Equation (
13) may also tend to be
g. Interestingly, we note that the complete tunneling suppression can be observed in a wide parameter range except for some special cases such as
and
, in which
oscillates around 0.5, indicating the particle has half the probability to tunnel into other states. More simulations show that when the condition of
changes, the dependence of tunneling dynamics on driving amplitudes will be different and these results provide us a scheme to enter or exist
-photon resonance.
We further reveal the dependence of resonance dynamics on driving amplitudes by a peculiar condition for
in
Figure 6b. With the increase of
,
first experiences a transition from tunneling to almost complete suppression at
and then oscillates with a lower amplitude, implying partial tunneling suppression. The minimum values of
are well consistent with zeros of
due to the decoupling effect. So, particle’s transfer between three states can be adjusted with appropriate driving amplitudes even if at fractional-
th-order resonances.
Here, due to
, Floquet theory works well for a common frequency
. Quasienergy spectrum as a function of
is plotted in
Figure 6c in which
and
are weakly influenced by varying amplitude
in the absence of avoided crossings or degeneracy. Based on the significant dependence of
on driving amplitudes, we further check their eigenstates and find that the property of Floquet state corresponding to quasi-zero energy level
is consistent with
, as shown in
Figure 6d (The other two Floquet states with no localized states are not listed here). Therefore, we can see that driving amplitudes dependence is attributed to the modulated localized Floquet state.
4.4. Dependence on Phase Differences
In the above discussion, we have not considered the roles played by the phase difference. In fact,
is useful in realizing quantum control if applied appropriately. Focusing on the 2/3rd-order resonance (
) again,
Figure 7a shows tunneling probability
with varying
and
for a driving amplitudes
. Significant influence of
is observed in the parameter region
. So, tunneling probability can be enhanced by more than 0.5 by choosing appropriate values of
and
. Therefore, the phase difference can have a large contribution to improving or suppressing tunneling probability.
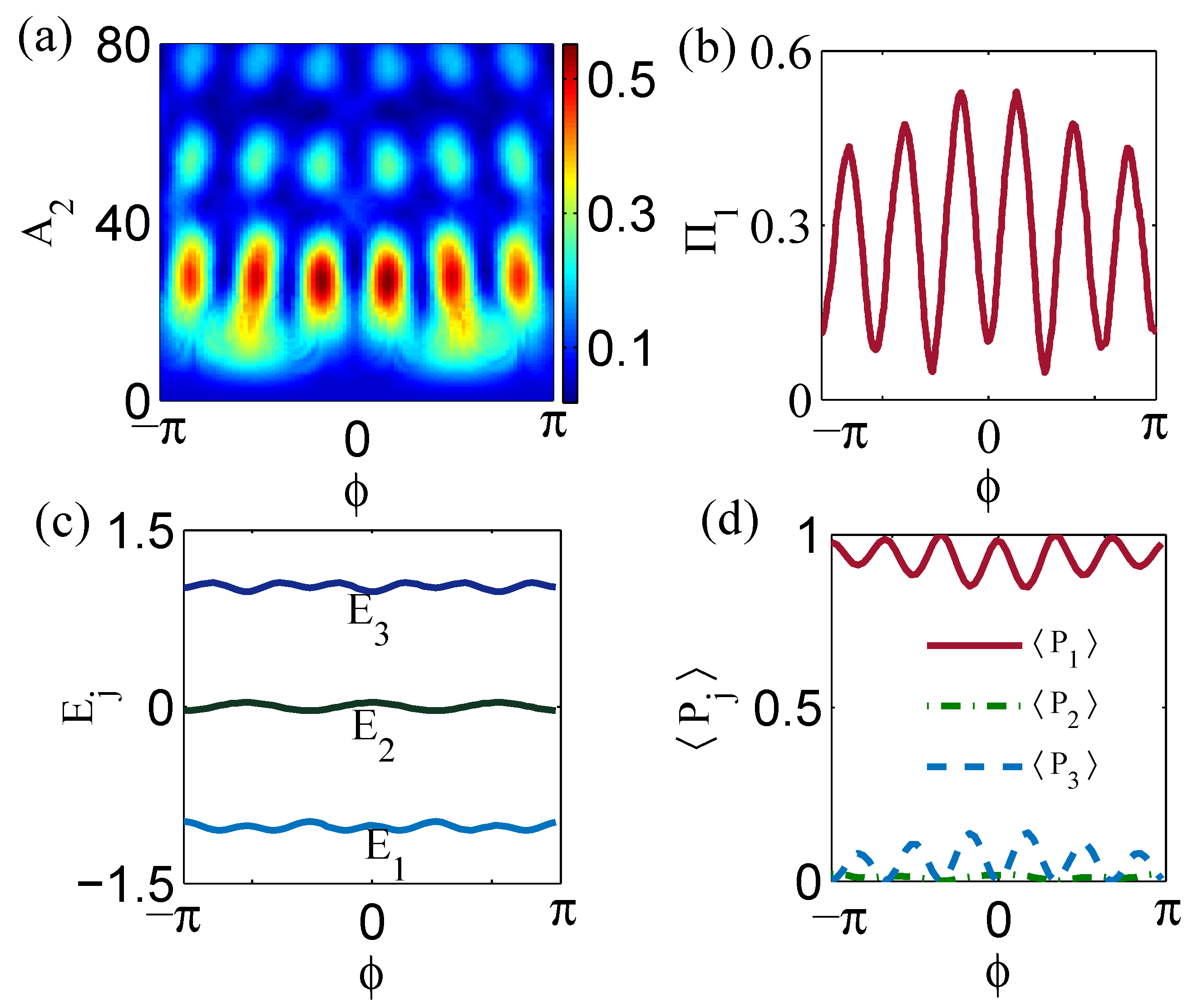
To establish a connection between phase dependence and Floquet properties, we plot
as a function of
in
Figure 7b under the condition of
which satisfies
. It is found that as
varies from
to
, tunneling probability
can be enhanced
. Also, the quasienergy spectra, as shown in
Figure 7c, display that
,
and
are all changed by the phase and the medium one
slightly oscillates around zero. Further study on the Floquet states, plotted in
Figure 7d reveals that the phase dependence on
is originated from the localized Floquet state corresponding to
with a negligible population at
. The other two Floquet states with no localized states are not shown here. Therefore, it is also the modulated dark Floquet state that leads to the change of tunneling probabilities.