SHG in Micron-Scale Layers of Glasses: Electron Beam Irradiation vs. Thermal Poling
Abstract
1. Introduction
2. Materials and Methods
3. Results
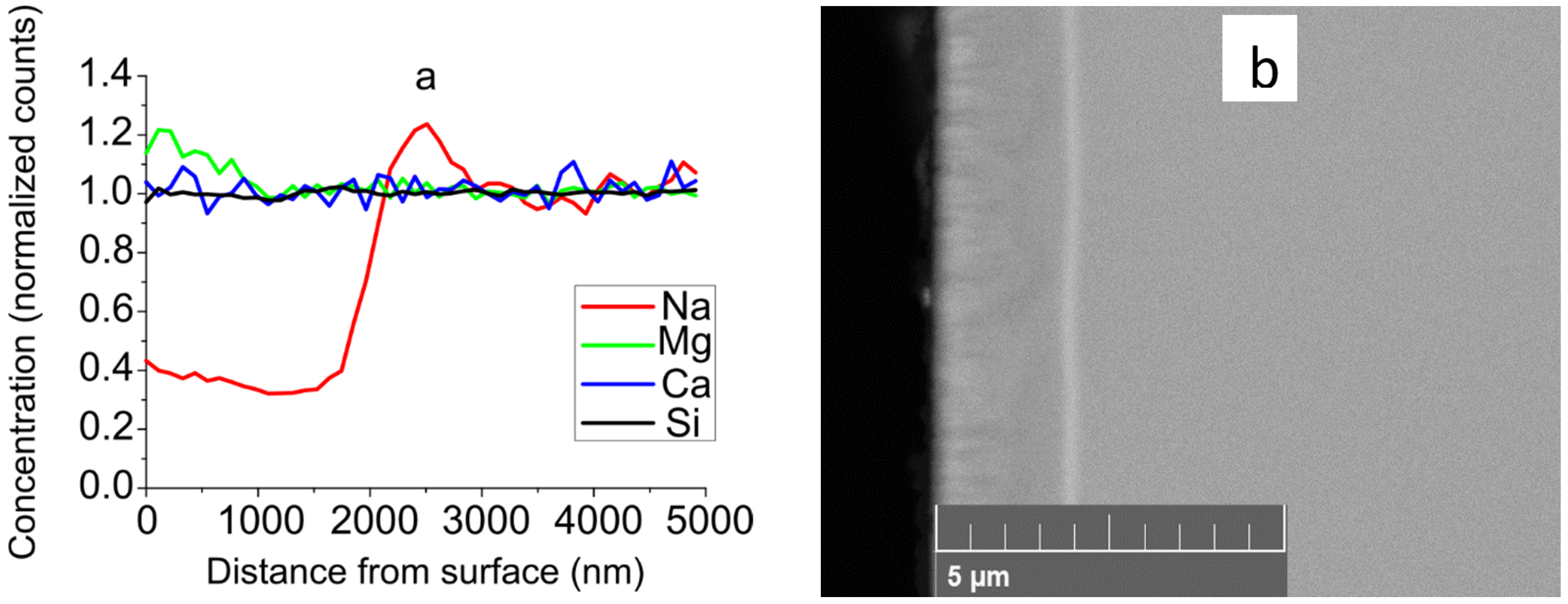
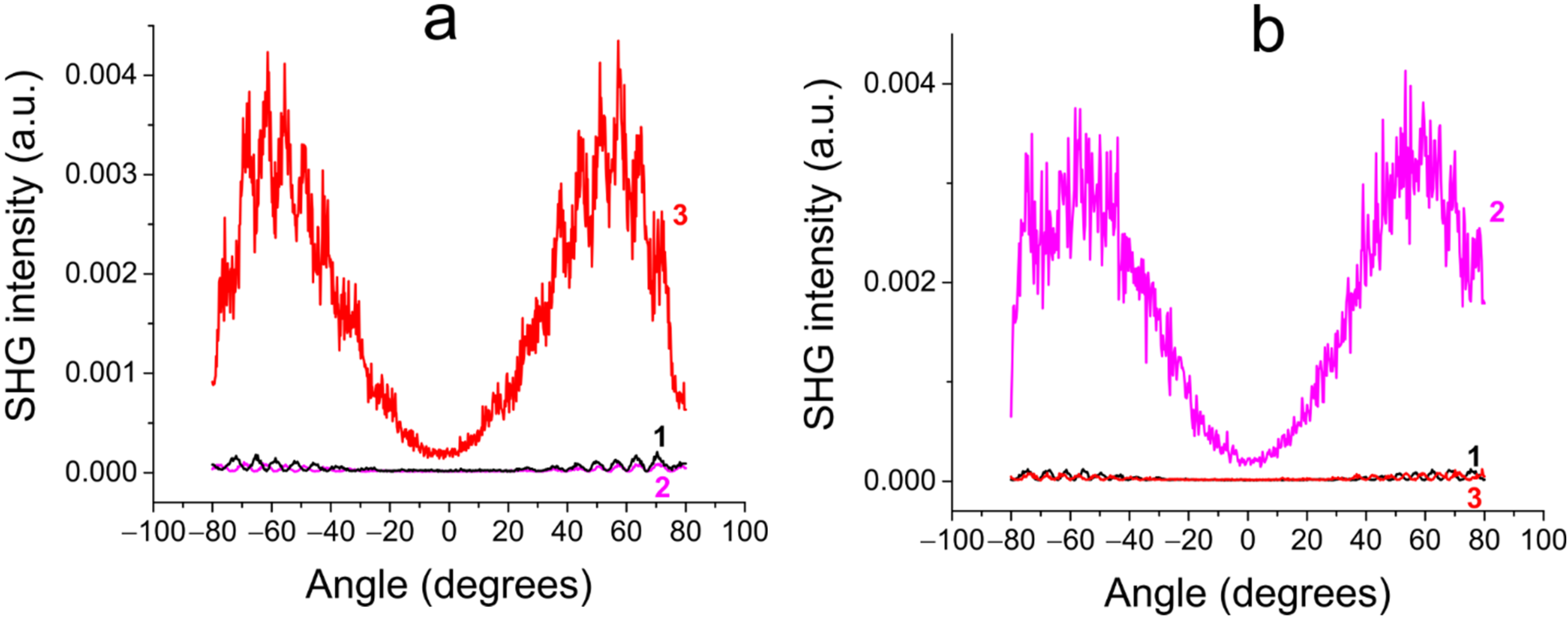
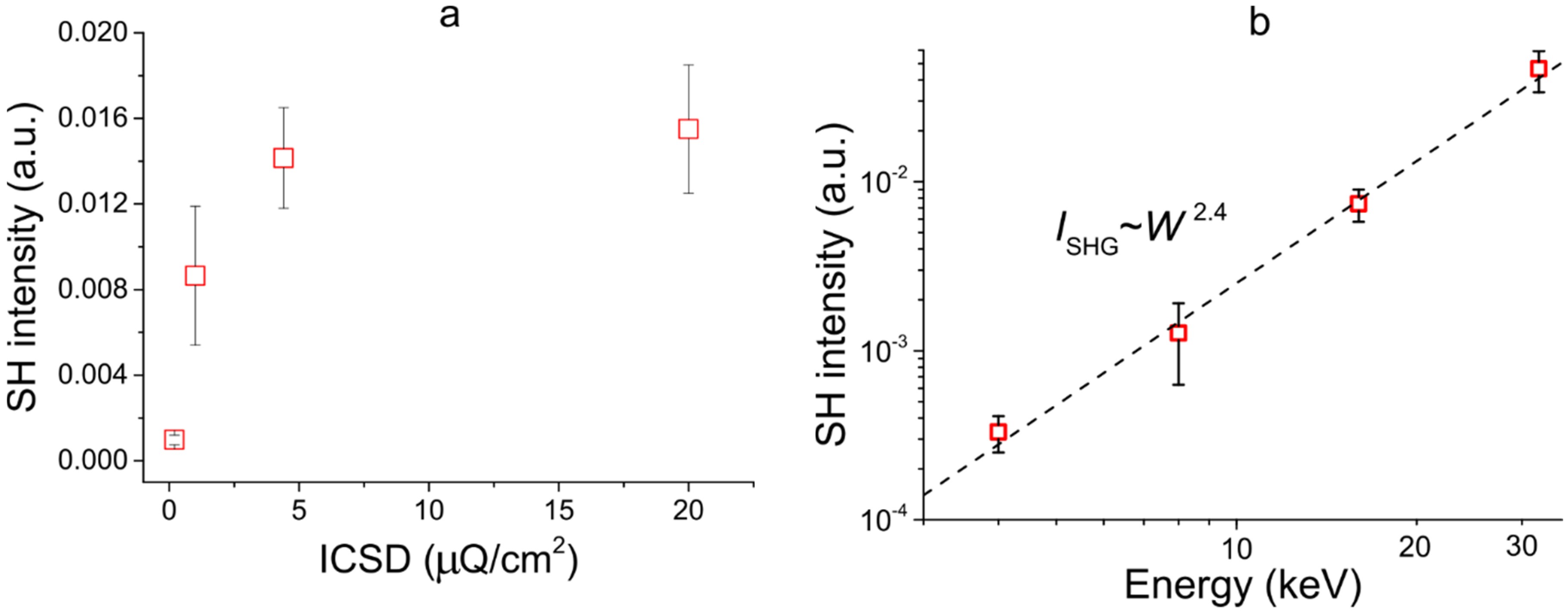
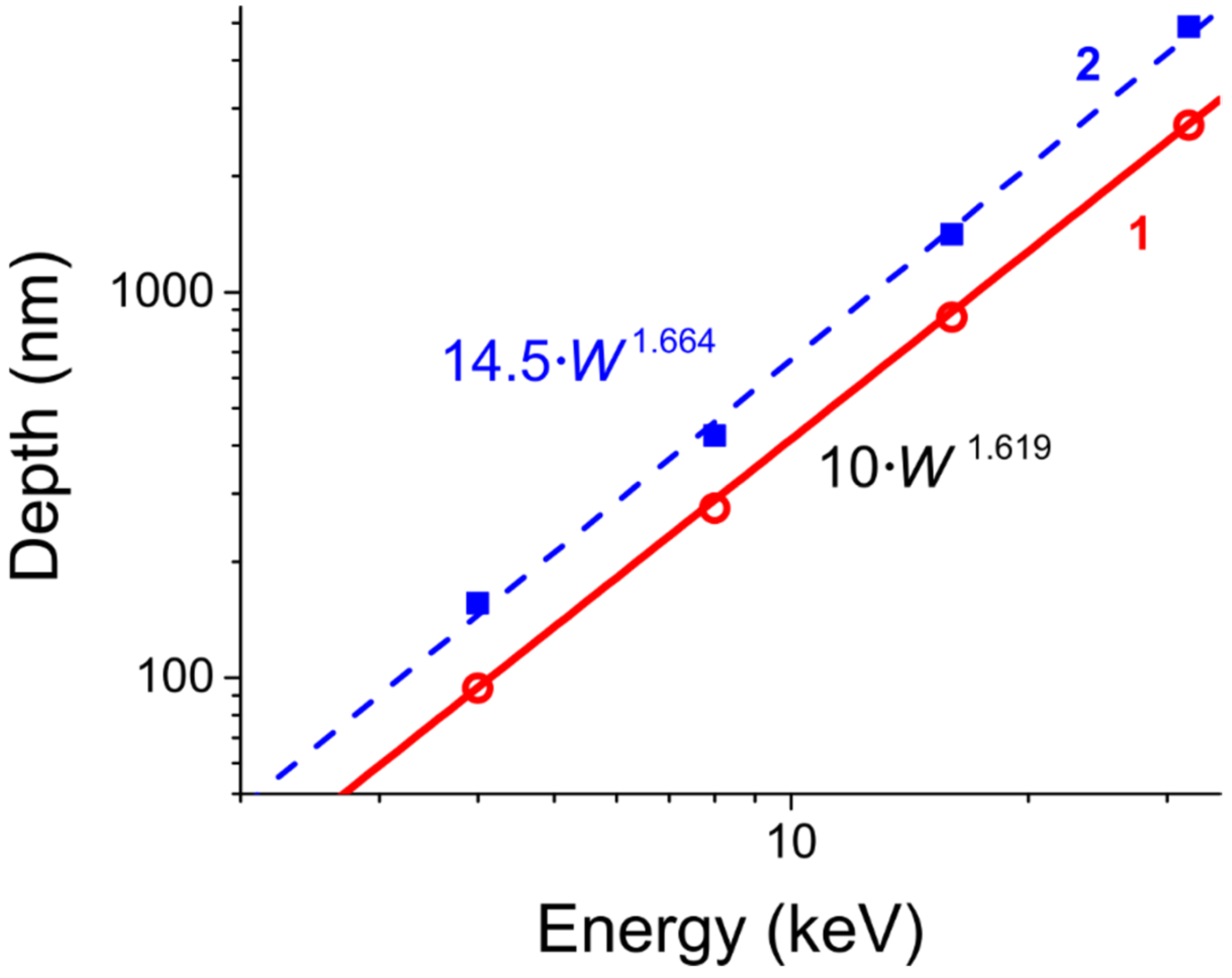
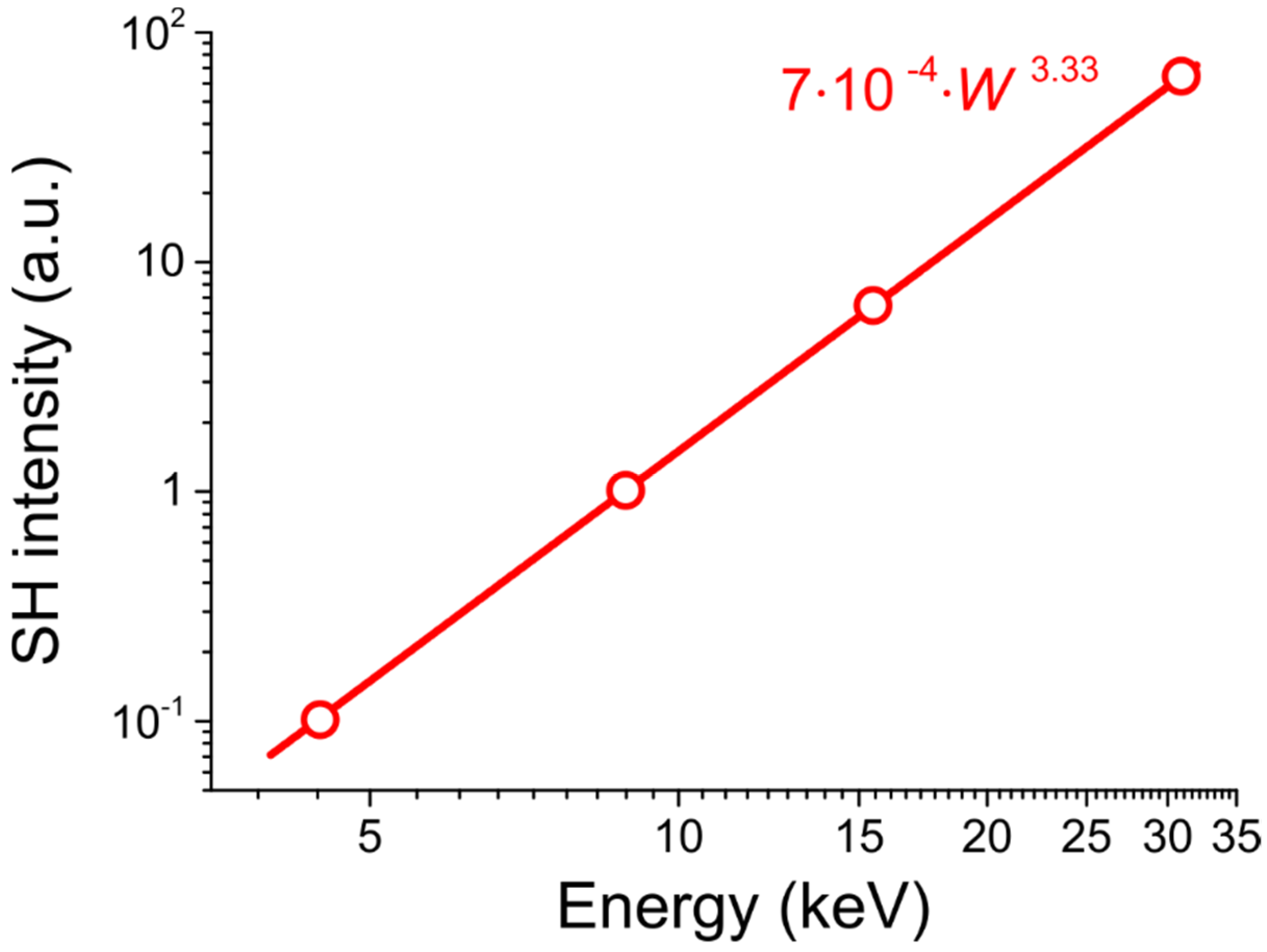
3.1. Measurements
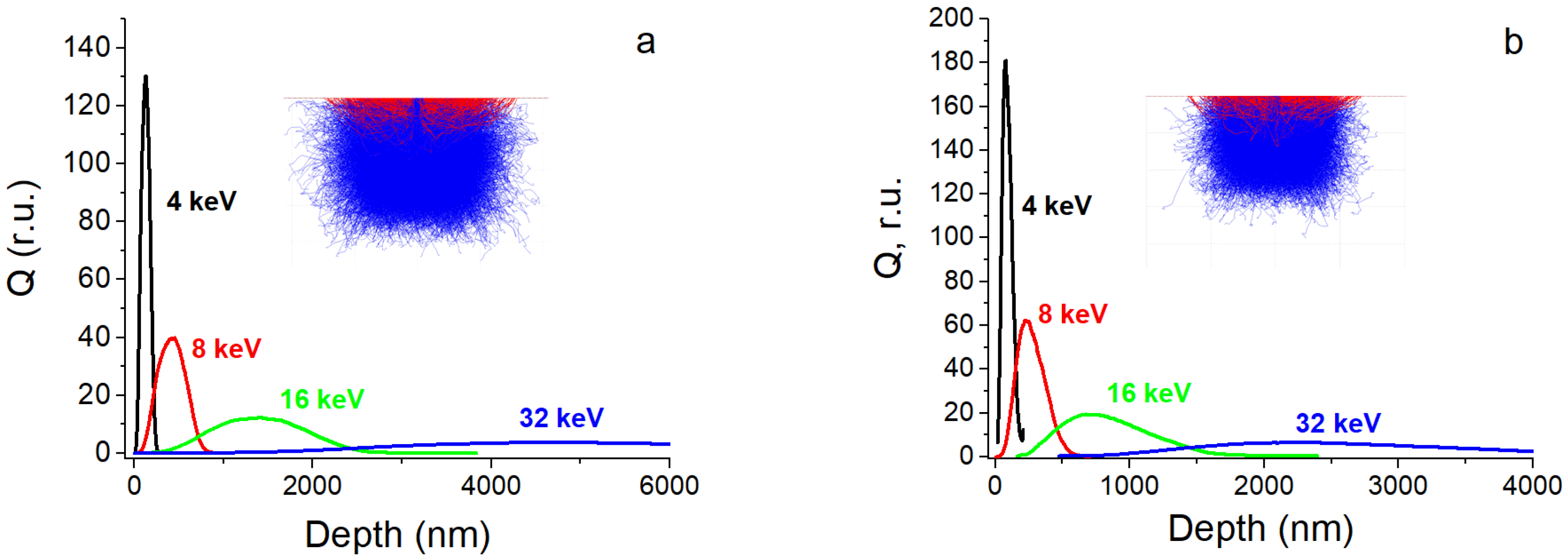
3.2. Modeling
4. Discussion
4.1. Origin of the Difference of Experimental and Modeled Dependence of SHG Efficiency on Electron Energy
4.2. Nature of SON in BF16 and Menzel Glasses
4.2.1. Electric Field Magnitude
4.2.2. Nonlinear Interaction Length
4.2.3. Nonlinear Constants
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Okada, A.; Ishii, K.; Mito, K.; Sasaki, K. Phase-matched Second-harmonic Generation in Novel Corona Poled Glass Waveguides. Appl. Phys. Lett. 1992, 60, 2853–2855. [Google Scholar] [CrossRef]
- Russell, P.S.; Kazansky, P.G.; Kamal, A. Electron Implantation: A New Technique for Creation and Modification of Second-Order Susceptibility in Glasses. SPIE Proc. 1993, 2044, 192–201. [Google Scholar] [CrossRef]
- Kazansky, P.G.; Kamal, A.; Russell, P.S.J. High Second-Order Nonlinearities Induced in Lead Silicate Glass by Electron-Beam Irradiation. Opt. Lett. 1993, 18, 693–695. [Google Scholar] [CrossRef]
- Corbari, C.; Ajitdoss, L.C.; Carvalho, I.C.S.; Deparis, O.; Mezzapesa, F.P.; Kazansky, P.G.; Sakaguchi, K. The Problem of Achieving High Second-Order Nonlinearities in Glasses: The Role of Electronic Conductivity in Poling of High Index Glasses. J. Non-Cryst. Solids 2010, 356, 2742–2749. [Google Scholar] [CrossRef][Green Version]
- Smith, N.J.; Pantano, C.G. Structural and Compositional Modification of a Barium Boroaluminosilicate Glass Surface by Thermal Poling. Appl. Phys. A 2014, 116, 529–543. [Google Scholar] [CrossRef]
- Lepicard, A.; Bondu, F.; Kang, M.; Sisken, L.; Yadav, A.; Adamietz, F.; Rodriguez, V.; Richardson, K.; Dussauze, M. Long-Lived Monolithic Micro-Optics for Multispectral GRIN Applications. Sci. Rep. 2018, 8, 7388. [Google Scholar] [CrossRef] [PubMed]
- Chervinskii, S.; Sevriuk, V.; Reduto, I.; Lipovskii, A. Formation and 2D-Patterning of Silver Nanoisland Film Using Thermal Poling and out-Diffusion from Glass. J. Appl. Phys. 2013, 114, 224301. [Google Scholar] [CrossRef]
- Qiu, M.; Pi, F.; Orriols, G. The Role of Lead Component in Second-Harmonic Generation in Lead Silica by Electron-Beam Irradiation. Appl. Phys. Lett. 1998, 73, 3040–3042. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, X.; Tanaka, K.; Narazaki, A.; Hirao, K.; Gan, F. Second-Harmonic Generation in Ge-As-S Glasses by Electron Beam Irradiation and Analysis of the Poling Mechanism. Opt. Commun. 2001, 198, 187–192. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, C.; Li, H.; Zhao, X. The Generation and Stability of Second-Harmonic in Electron-Beam Irradiated GeS2—In2S3—CdS Chalcogenide Glasses. Solid State Commun. 2009, 149, 266–268. [Google Scholar] [CrossRef]
- Kassab, L.R.P.; Miedzinski, R.; Kityk, I.V.; Ebothe, J.; da Silva, D.M.; Reshak, A.H. Electron Beam Induced Second-Harmonic Generation in Er 3+ Doped PbO-GeO 2 Glasses Containing Silver Nanoparticles. J. Mater. Sci. Mater. Electron. 2009, 20, 87–91. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, Q.; Dong, G.; Zhao, X. Second-Order Optical Nonlinearity in Sb2S3 Microcrystal Doped Glasses by Electron Beam Irradiation. Opt. Commun. 2007, 274, 456–460. [Google Scholar] [CrossRef]
- Guillet de Chatellus, H.; Freysz, E. Measurement of the Third-Order Susceptibility of Glasses by EFISH of Femtosecond Pulses. Opt. Express 2001, 9, 586–591. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-Y.; Lin, H.-Y. Thermal Poling Induced Second-Order Optical Nonlinearity in Phosphosilicate Glass Thin Films. J. Mod. Opt. 2019, 66, 2053–2062. [Google Scholar] [CrossRef]
- Le Calvez, A.; Freysz, E.; Ducasse, A. A Model for Second Harmonic Generation in Poled Glasses. Eur. Phys. J. D 1998, 1, 223–226. [Google Scholar] [CrossRef]
- Kazansky, P.G.; Russel, P.S.J. Thermally Poled Glass: Frozen-in Electric Field or Oriented Dipoles? Opt. Commun. 1994, 110, 611–614. [Google Scholar] [CrossRef]
- Reshetov, I.; Scherbak, S.; Tagantsev, D.; Zhurikhina, V.; Lipovskii, A. Giant Enhancement of Optical Second Harmonic in Poled Glasses by Cold Repoling. J. Phys. Chem. Lett. 2022, 13, 5932–5937. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; He, H.; Podraza, N.J.; Qian, L.; Pantano, C.G.; Kim, S.H. Thermal Poling of Soda-Lime Silica Glass with Nonblocking Electrodes—Part 1: Effects of Sodium Ion Migration and Water Ingress on Glass Surface Structure. J. Am. Ceram. Soc. 2016, 99, 1221–1230. [Google Scholar] [CrossRef]
- Dussauze, M.; Rodriguez, V.; Lipovskii, A.; Petrov, M.; Smith, C.; Richardson, K.; Cardinal, T.; Fargin, E.; Kamitsos, E.I. How Does Thermal Poling Affect the Structure of Soda-Lime Glass? J. Phys. Chem. C 2010, 114, 12754–12759. [Google Scholar] [CrossRef]
- Cremoux, T.; Dussauze, M.; Fargin, E.; Cardinal, T.; Talaga, D.; Adamietz, F.; Rodriguez, V. Trapped Molecular and Ionic Species in Poled Borosilicate Glasses: Toward a Rationalized Description of Thermal Poling in Glasses. J. Phys. Chem. C 2014, 118, 3716–3723. [Google Scholar] [CrossRef]
- Jbara, O.; Cazaux, J.; Trebbia, P. Sodium Diffusion in Glasses during Electron Irradiation. J. Appl. Phys. 1995, 78, 868–875. [Google Scholar] [CrossRef]
- Jiang, N. Electron Beam Damage in Oxides: A Review. Rep. Prog. Phys. 2015, 79, 016501. [Google Scholar] [CrossRef]
- Sidorov, A.I.; Kirpichenko, D.A.; Yurina, U.V.; Podsvirov, O.A. Structural Changes in Silica Glass under the Action of Electron Beam Irradiation: The Effect of Irradiation Dose. Glass Phys. Chem. 2021, 47, 118–125. [Google Scholar] [CrossRef]
- Gedeon, O.; Zemek, J.; Jurek, K. Changes in Alkali-Silicate Glasses Induced with Electron Irradiation. J. Non-Cryst. Solids 2008, 354, 1169–1171. [Google Scholar] [CrossRef]
- Dudko, Y.V.; Kravchenko, A.A.; Cherednichenko, D.I. Electron-Beam Modification of Silicate Glass Surfaces. J. Non-Cryst. Solids 1995, 188, 87–92. [Google Scholar] [CrossRef]
- Thermo Scientific™ Microscope Slides, 45°. Available online: https://www.fishersci.pt/shop/products/microscope-slides-45/12164682 (accessed on 6 October 2022).
- Scherbak, S.A.; Kaasik, V.P.; Zhurikhina, V.V.; Lipovskii, A.A. SEM-Visualization of a Spatial Charge and a Giant Potassium Peak in a Corona-Poled Glass. J. Phys. Condens. Matter 2021, 33, 235702. [Google Scholar] [CrossRef]
- Hovington, P.; Drouin, D.; Gauvin, R. CASINO: A New Monte Carlo Code in C Language for Electron Beam Interaction-Part I: Description of the Program. Scanning 2006, 19, 1–14. [Google Scholar] [CrossRef]
- Jerphagnon, J.; Kurtz, S.K. Maker Fringes: A Detailed Comparison of Theory and Experiment for Isotropic and Uniaxial Crystals. J. Appl. Phys. 1970, 41, 1667–1681. [Google Scholar] [CrossRef]
- Tong, A.S.K.; Bondu, F.; Senthil Murugan, G.; Wilkinson, J.S.; Dussauze, M. Effect of sodium addition and thermal annealing on second-order optical nonlinearity in thermally poled amorphous Ta2O5 thin films. J. Appl. Phys. 2019, 125, 015104. [Google Scholar] [CrossRef]
- Bethe, H.; Ashkin, J. Experimental Nuclear Physics; Segré, E., Ed.; John Wiley: New York, NY, USA, 1953; p. 253. [Google Scholar]
- Yariv, A.; Yeh, P. Optical Waves in Crystals: Propagation and Control of Laser Radiation; John Wiley & Sons, Inc.: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada; Singapore, 2002; ISBN 978-0-471-43081-0. [Google Scholar]
- Quiquempois, Y.; Martinelli, G.; Duthérage, P.; Bernage, P.; Niay, P.; Douay, M. Localization of the Induced Second-Order Non-Linearity within Infrasil and Suprasil Thermally Poled Glasses. Opt. Commun. 2000, 176, 479–487. [Google Scholar] [CrossRef]
- Melchinger, A.; Hofmann, S. Dynamic Double Layer Model: Description of Time Dependent Charging Phenomena in Insulators under Electron Beam Irradiation. J. Appl. Phys. 1995, 78, 6224–6232. [Google Scholar] [CrossRef]
- Rau, É.I.; Evstaf’eva, E.N.; Andrianov, M.V. Mechanisms of Charging of Insulators under Irradiation with Medium-Energy Electron Beams. Phys. Solid State 2008, 50, 621–630. [Google Scholar] [CrossRef]
- Liu, W. Resist Charging in Electron Beam Lithography. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. 1995, 13, 1979–1983. [Google Scholar] [CrossRef]
- Doremus, R.H. Mechanism of Electrical Polarization of Silica Glass. Appl. Phys. Lett. 2005, 87, 232904. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H. Mechanism Analysis of Thermal/Electric Field Poling in Fused Silica. Jpn. J. Appl. Phys. 2002, 41, 2958–2961. [Google Scholar] [CrossRef]
- Lipovskii, A.A.; Melehin, V.G.; Petrov, M.I.; Svirko, Y.P.; Zhurikhina, V.V. Bleaching versus Poling: Comparison of Electric Field Induced Phenomena in Glasses and Glass-Metal Nanocomposites. J. Appl. Phys. 2011, 109, 011101. [Google Scholar] [CrossRef]
- Redkov, A.V.; Melehin, V.G.; Lipovskii, A.A. How Does Thermal Poling Produce Interstitial Molecular Oxygen in Silicate Glasses? J. Phys. Chem. C 2015, 119, 17298–17307. [Google Scholar] [CrossRef]
- Dussauze, M.; Cremoux, T.; Adamietz, F.; Rodriguez, V.; Fargin, E.; Yang, G.; Cardinal, T. Thermal Poling of Optical Glasses: Mechanisms and Second-Order Optical Properties. Int. J. Appl. Glass Sci. 2012, 3, 309–320. [Google Scholar] [CrossRef]
- Zverev, V.A.; Krivopustova, E.V.; Tochilina, T.V. Optical Materials. Part 1; ITMO University: St. Petersburg, Russia, 2009. (In Russian) [Google Scholar]
- RefractiveIndex. INFO Refractive Index Database. Available online: https://refractiveindex.info/?shelf=glass&book=LZOS-BF&page=BF16 (accessed on 6 October 2022).
- Adair, R.; Chase, L.L.; Payne, S.A. Nonlinear Refractive-Index Measurements of Glasses Using Three-Wave Frequency Mixing. J. Opt. Soc. Am. B 1987, 4, 875–881. [Google Scholar] [CrossRef]
- Aber, J.E.; Newstein, M.C.; Garetz, B.A. Femtosecond Optical Kerr Effect Measurements in Silicate Glasses. J. Opt. Soc. Am. B 2000, 17, 120–127. [Google Scholar] [CrossRef]
- Thomazeau, I.; Etchepare, J.; Grillon, G.; Migus, A. Electronic Nonlinear Optical Susceptibilities of Silicate Glasses. Opt. Lett. 1985, 10, 223–225. [Google Scholar] [CrossRef] [PubMed]
- Smith, N.J.; Lanagan, M.T.; Pantano, C.G. Thermal Poling of Alkaline Earth Boroaluminosilicate Glasses with Intrinsically High Dielectric Breakdown Strength. J. Appl. Phys. 2012, 111, 083519. [Google Scholar] [CrossRef]
- Pruneri, V.; Samoggia, F.; Bonfrate, G.; Kazansky, P.G.; Yang, G.M. Thermal Poling of Silica in Air and under Vacuum: The Influence of Charge Transport on Second Harmonic Generation. Appl. Phys. Lett. 1999, 74, 2423–2425. [Google Scholar] [CrossRef]

| Si | O | Al | B | K | Na | Pb | Ba | Zn | Ca | Mg | Other 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Menzel | 24.77 | 60.08 | 0.49 | - | 0.53 | 9.51 | - | - | - | 2.35 | 2.20 | 0.07 |
| BF16 | 15.32 | 59.86 | 1.66 | 6.63 | - | - | 1.52 | 9.31 | 2.37 | 3.07 | - | 0.36 |
| Thermal Poling | e-Beam Poling | |
|---|---|---|
| Menzel | high SHG signal | weak SHG signal |
| BF16 | weak SHG signal | high SHG signal |
| SiO2 | Al2O3 | B2O3 | PbO | BaO | K2O | Na2O | ZnO | CaO | MgO | Other 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Menzel | 72.2 | 1.2 | - | - | - | 1.2 | 14.3 | - | 6.4 | 4.3 | 0.33 |
| BK7 | 69.13 | - | 10.75 | - | 3.07 | 6.29 | 10.4 | - | - | - | 0.36 |
| BF16 | 27.04 | 2.49 | 6.79 | 9.95 | 42 | - | - | 5.68 | 5.05 | - | 1.03 |
| SF6 | 57.6 | - | - | 40.4 | - | 2 | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reshetov, I.; Kaasik, V.; Kan, G.; Shestakov, S.; Scherbak, S.; Zhurikhina, V.; Lipovskii, A. SHG in Micron-Scale Layers of Glasses: Electron Beam Irradiation vs. Thermal Poling. Photonics 2022, 9, 733. https://doi.org/10.3390/photonics9100733
Reshetov I, Kaasik V, Kan G, Shestakov S, Scherbak S, Zhurikhina V, Lipovskii A. SHG in Micron-Scale Layers of Glasses: Electron Beam Irradiation vs. Thermal Poling. Photonics. 2022; 9(10):733. https://doi.org/10.3390/photonics9100733
Chicago/Turabian StyleReshetov, Ilya, Vladimir Kaasik, Gennadiy Kan, Sergey Shestakov, Sergey Scherbak, Valentina Zhurikhina, and Andrey Lipovskii. 2022. "SHG in Micron-Scale Layers of Glasses: Electron Beam Irradiation vs. Thermal Poling" Photonics 9, no. 10: 733. https://doi.org/10.3390/photonics9100733
APA StyleReshetov, I., Kaasik, V., Kan, G., Shestakov, S., Scherbak, S., Zhurikhina, V., & Lipovskii, A. (2022). SHG in Micron-Scale Layers of Glasses: Electron Beam Irradiation vs. Thermal Poling. Photonics, 9(10), 733. https://doi.org/10.3390/photonics9100733






