Second-Harmonic Generation in Aggregates of Lithium Niobate Particles Formed upon Suspension Freezing
Abstract
1. Introduction
2. Materials and Methods
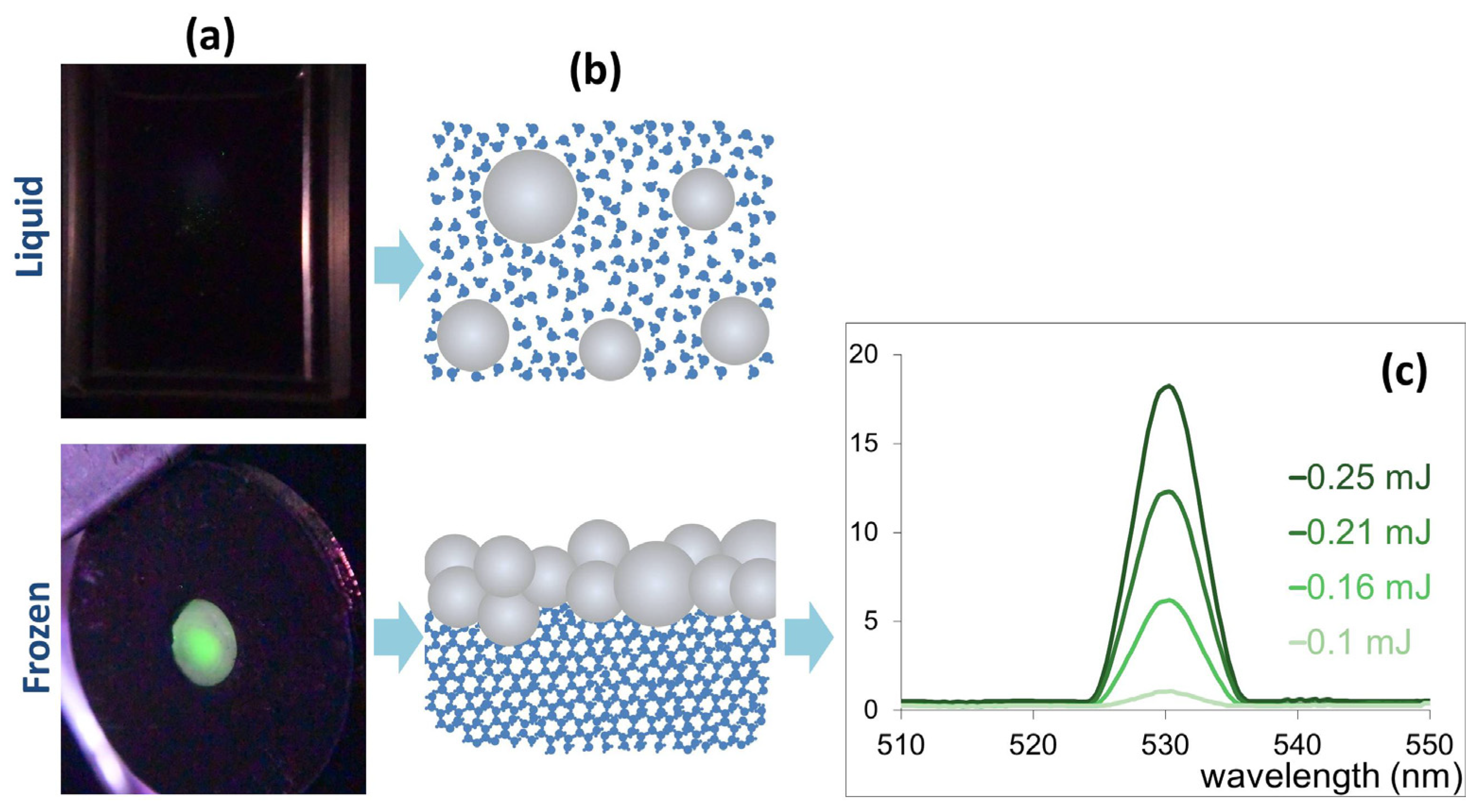
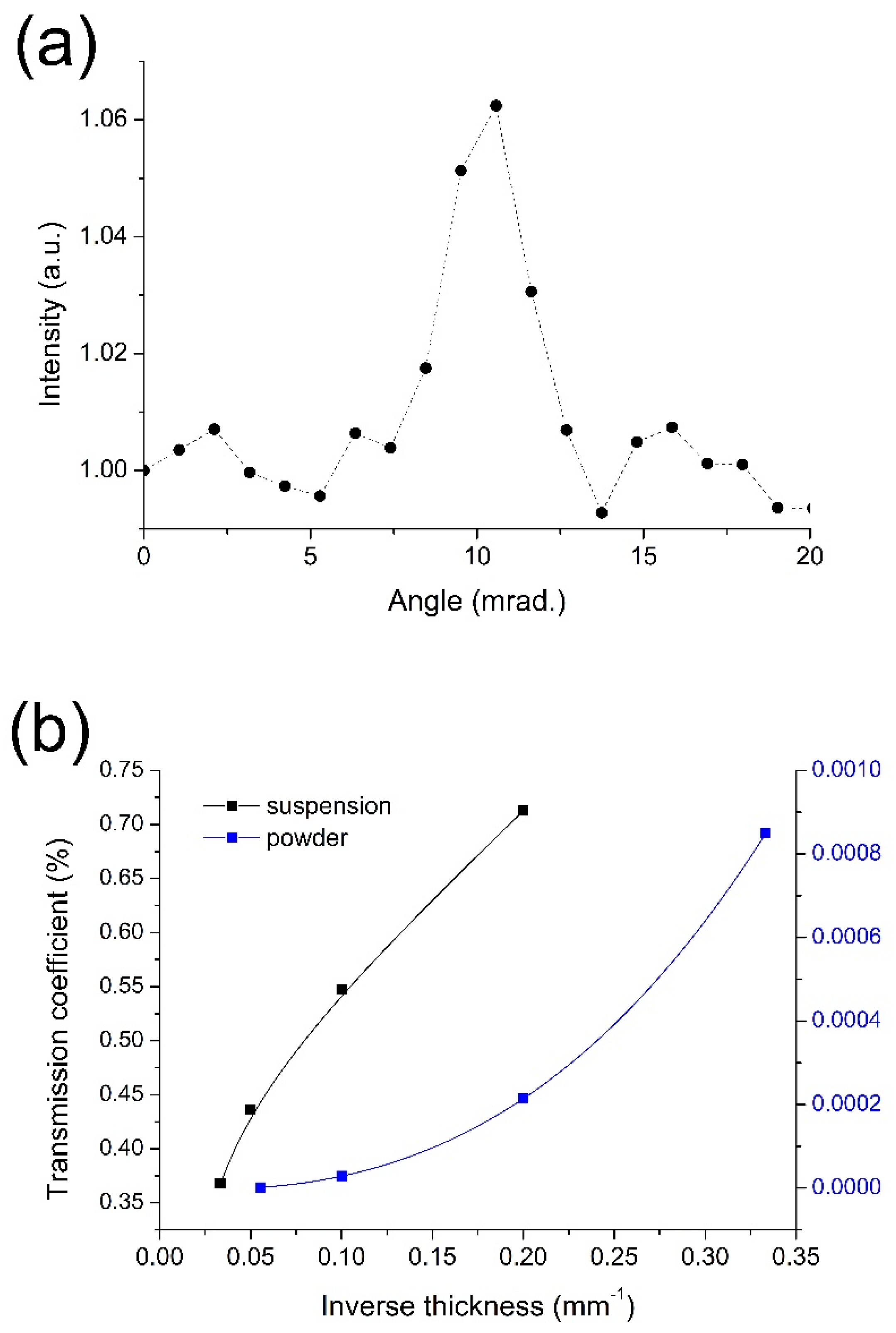
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ogov, A.; Mugnier, Y.; Bonacina, L. Harmonic nanoparticles: Noncentrosymmetric metal oxides for nonlinear optics. J. Opt. 2015, 17, 033001. [Google Scholar]
- Staedler, D.; Magouroux, T.; Hadji, R.; Joulaud, C.; Extermann, J.; Schwung, S.; Passemard, S.; Kasparian, C.; Clarke, G.; Gerrmann, M.; et al. Harmonic nanocrystals for biolabeling: A survey of optical properties and biocompatibility. ACS Nano 2012, 6, 2542–2549. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, P.; Maloney, J.; Wu, D.; Fraser, S.E. Second harmonic generating (SHG) nanoprobes for in vivo imaging. Proc. Natl. Acad. Sci. USA 2010, 107, 14535–14540. [Google Scholar] [CrossRef]
- Slenders, E.; Bové, H.; Urbain, M.; Mugnier, Y.; Sonay, A.Y.; Pantazis, P.; Bonacina, L.; Berghe, P.V.; Vandeven, M.; Ameloot, M. Image Correlation Spectroscopy with Second Harmonic Generating Nanoparticles in Suspension and in Cells. J. Phys. Chem. Lett. 2018, 9, 6112–6118. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y.; Centurion, M.; Psaltis, D. Harmonic holography: A new holographic principle. Appl. Opt. 2008, 47, A103–A110. [Google Scholar] [CrossRef] [PubMed]
- Denk, W.; Strickler, J.H.; Webb, W.W. Two-photon laser scanning fluorescence microscopy. Science 1990, 248, 73–76. [Google Scholar] [CrossRef]
- Linnenbank, H.; Grynko, Y.; Förstner, J.; Linden, S. Second harmonic generation spectroscopy on hybrid plasmonic/dielectric nanoantennas. Light Sci. Appl. 2016, 5, e16013. [Google Scholar] [CrossRef]
- Winter, S.; Zielinski, M.; Chauvat, D.; Zyss, J.; Oron, D. The Second Order Nonlinear Susceptibility of Quantum Confined Semiconductors—A Single Dot Study. J. Phys. Chem. C 2011, 115, 4558–4563. [Google Scholar] [CrossRef]
- Lisinski, S.; Ratke, L.; Schaniel, D.; Jungk, T.; Soergel, E.; Boysen, H.; Woike, T. Second-harmonic generation in nano-structured LiTaO3- and LiNbO3-xerogels with randomly oriented ferroelectric grains. Opt. Mater. 2010, 32, 504–509. [Google Scholar] [CrossRef]
- Rodríguez, E.M.; Kumar, K.U.; Speghini, A.; Piccinelli, F.; Nodari, L.; Cannas, C.; Bettinelli, M.; Jaque, D.; Solé, J.G. Non-linear niobate nanocrystals fot two-photon imaging. Opt. Mater. 2011, 33, 258–266. [Google Scholar] [CrossRef]
- Smirnova, D.; Smirnov, A.I.; Kivshar, Y.S. Multipolar second-harmonic generation by Mie-resonant dielectric nanoparticles. Phys. Rev. A 2018, 97, 013807. [Google Scholar] [CrossRef]
- Martorell, J.; Vilaseca, R.; Corbalan, R. Second harmonic generation in a photonic crystal. Appl. Phys. Lett. 1997, 70, 702–704. [Google Scholar] [CrossRef]
- Qiao, Y.; Ye, F.; Zheng, Y.; Chen, X. Cavity-enhanced second-harmonic generation in strongly scattering nonlinear media. Phys. Rev. A 2019, 99, 043844. [Google Scholar] [CrossRef]
- Hewageegana, P.; Apalkov, V. Second harmonic generation in disordered media: Random resonators. Phys. Rev. B 2008, 77, 075132. [Google Scholar] [CrossRef]
- Polson, R.C.; Vardeny, Z.V. Random lasing in human tissues. Appl. Phys. Lett. 2004, 85, 1289–1291. [Google Scholar] [CrossRef]
- Hokr, B.H.; Bixler, J.N.; Cone, M.T.; Mason, J.D.; Beier, H.T.; Noojin, G.D.; Petrov, G.I.; Golovan, L.A.; Thomas, R.J.; Rockwell, B.A.; et al. Bright emission from a random Raman laser. Nat. Commun. 2014, 5, 4356. [Google Scholar] [CrossRef]
- Shevchenko, M.; Zemskov, K.; Karpov, M.; Kudryavtseva, A.; Maresev, A.; Tcherniega, N.; Umanskaya, S. Raman random lasing—Extremely high conversion efficiency and temperature dependence. Opt. Commun. 2022, 508, 127795. [Google Scholar] [CrossRef]
- Ismail, W.Z.W.; Liu, G.; Zhang, K.; Goldys, E.M.; Dawes, J. Dopamine sensing and measurement using threshold and spectral measurements in random lasers. Opt. Express 2016, 24, A85–A91. [Google Scholar] [CrossRef]
- Rempel, A.; Worster, M. The interaction between a particle and an advancing solidification front. J. Cryst. Growth 1999, 205, 427–440. [Google Scholar] [CrossRef]
- Bouville, F.; Maire, E.; Deville, S. Self-Assembly of Faceted Particles Triggered by a Moving Ice Front. Langmuir 2014, 30, 8656–8663. [Google Scholar] [CrossRef]
- You, J.; Wang, J.; Wang, L.; Wang, Z.; Wang, Z.; Li, J.; Lin, X. Dynamic particle packing in freezing colloidal suspensions. Colloids Surf. A Physicochem. Eng. Asp. 2017, 531, 93–98. [Google Scholar] [CrossRef][Green Version]
- Dedovets, D.; Deville, S. Multiphase imaging of freezing particle suspensions by confocal microscopy. J. Eur. Ceram. Soc. 2018, 38, 2687–2693. [Google Scholar] [CrossRef]
- Deville, S.; Maire, E.; Bernard-Granger, G.; Lasalle, A.; Bogner, A.; Gauthier, C.; Leloup, J.; Guizard, C. Metastable and unstable cellular solidification of colloidal suspensions. Nat. Mater. 2009, 8, 966–972. [Google Scholar] [CrossRef] [PubMed]
- Van Albada, M.P.; Lagendijk, A. Observation of Weak Localization of Light in a Random Medium. Phys. Rev. Lett. 1985, 55, 2692–2695. [Google Scholar] [CrossRef]
- Wolf, P.E.; Maret, G. Weak localization and coherent backscattering of photons in disordered media. Phys. Rev. Lett. 1985, 55, 2696. [Google Scholar] [CrossRef]
- De Oliveira, P.C.; Perkins, A.E.; Lawandy, N.M. Coherent backscattering from high-gain scattering media. Opt. Lett. 1996, 21, 1685. [Google Scholar] [CrossRef]
- Anderson, P.W. The question of classical localization A theory of white paint? Philos. Mag. Part B 1985, 52, 505–509. [Google Scholar] [CrossRef]
- Faez, S.; Johnson, P.M.; Mazurenko, D.A.; Lagendijk, A. Experimental observation of second-harmonic generation and diffusion inside random media. J. Opt. Soc. Am. B 2009, 26, 235–243. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matrokhin, A.A.; Shevchenko, M.A.; Umanskaya, S.F.; Tareeva, M.V.; Kudryavtseva, A.D.; Tcherniega, N.V. Second-Harmonic Generation in Aggregates of Lithium Niobate Particles Formed upon Suspension Freezing. Photonics 2022, 9, 705. https://doi.org/10.3390/photonics9100705
Matrokhin AA, Shevchenko MA, Umanskaya SF, Tareeva MV, Kudryavtseva AD, Tcherniega NV. Second-Harmonic Generation in Aggregates of Lithium Niobate Particles Formed upon Suspension Freezing. Photonics. 2022; 9(10):705. https://doi.org/10.3390/photonics9100705
Chicago/Turabian StyleMatrokhin, Anton A., Mikhail A. Shevchenko, Sofia F. Umanskaya, Maria V. Tareeva, Anna D. Kudryavtseva, and Nikolay V. Tcherniega. 2022. "Second-Harmonic Generation in Aggregates of Lithium Niobate Particles Formed upon Suspension Freezing" Photonics 9, no. 10: 705. https://doi.org/10.3390/photonics9100705
APA StyleMatrokhin, A. A., Shevchenko, M. A., Umanskaya, S. F., Tareeva, M. V., Kudryavtseva, A. D., & Tcherniega, N. V. (2022). Second-Harmonic Generation in Aggregates of Lithium Niobate Particles Formed upon Suspension Freezing. Photonics, 9(10), 705. https://doi.org/10.3390/photonics9100705




